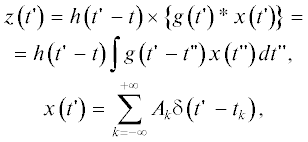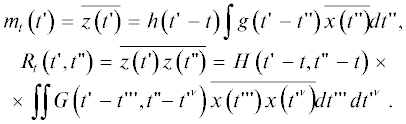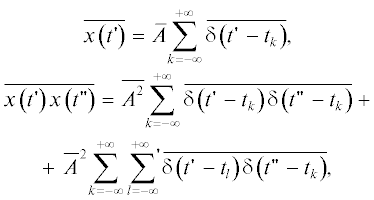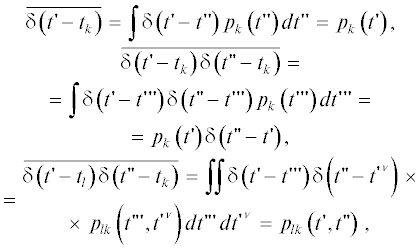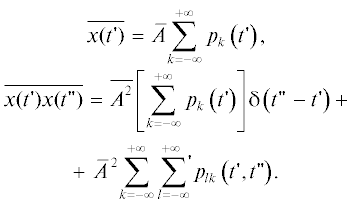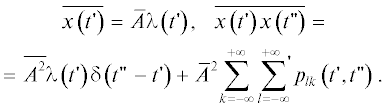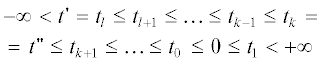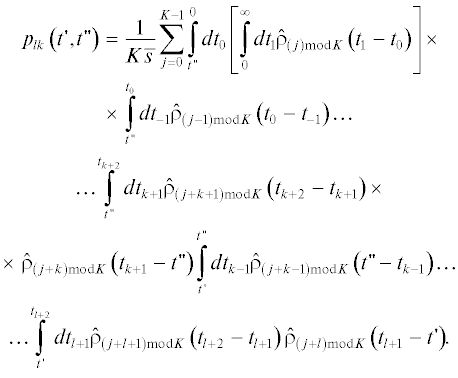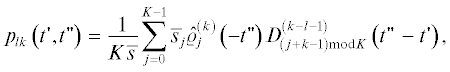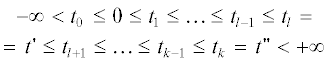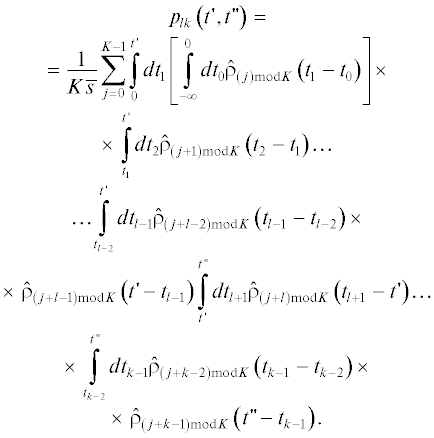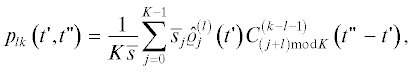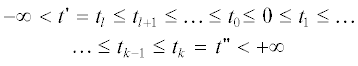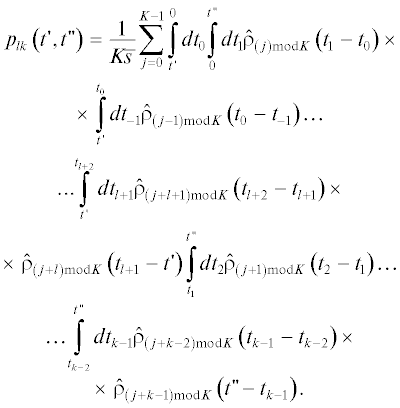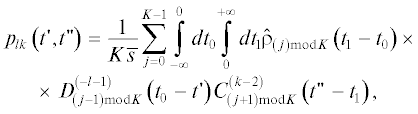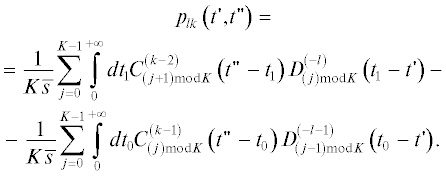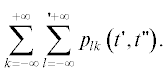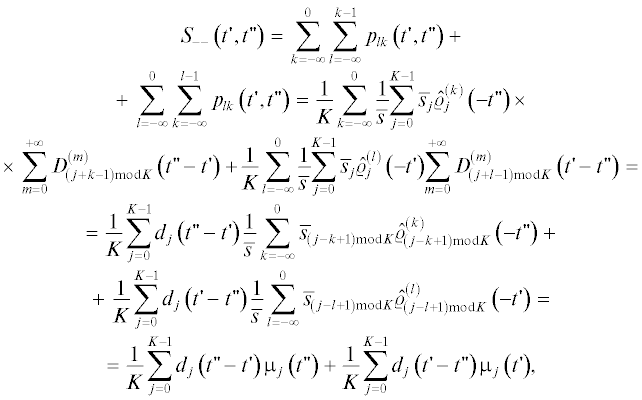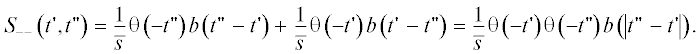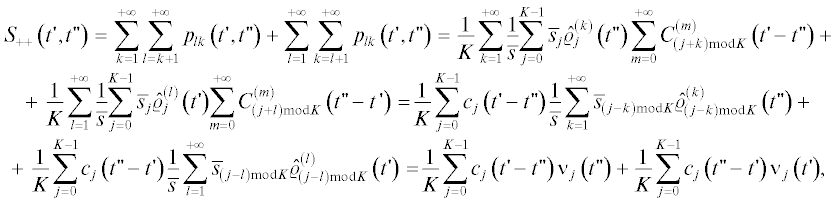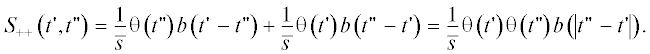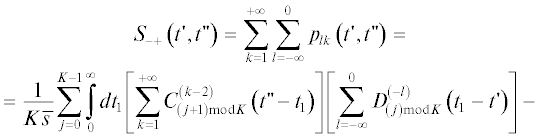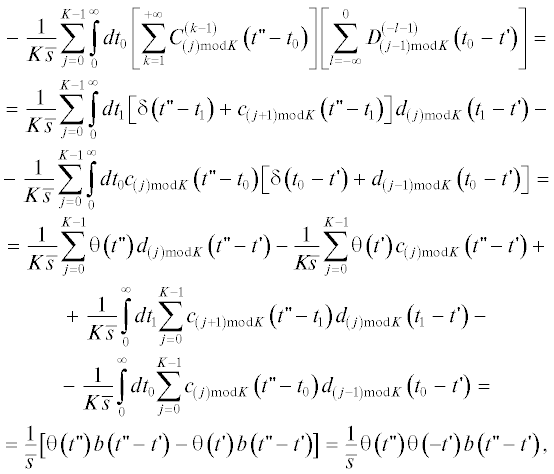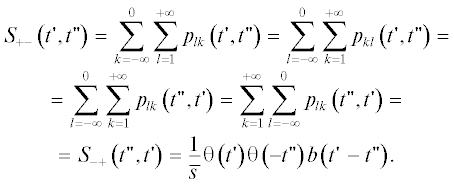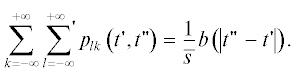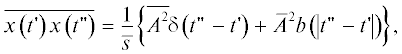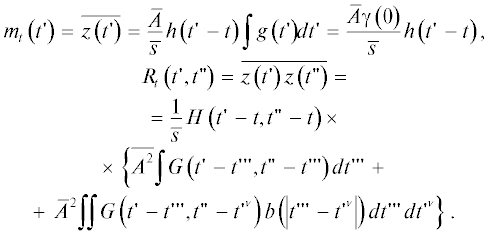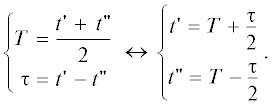Радиотехника и электроника, 2020, T. 65, № 8, стр. 774-797

ВВЕДЕНИЕ

Многие важные импульсные сигналы в природе и в технике являются результатом взаимодействия периодических процессов и связанных с ними случайных событий. Хотя реализации подобных сигналов сами не являются строго периодическими функциями, их средние статистические характеристики обладают свойством периодичности. Часто подобные сигналы называются циклостационарными, они встречаются в телекоммуникационных системах, радарах, телеметрии, астрономии, механике, эконометрии и биологии. Обширный список моделей, алгоритмов и приложений циклостационарных сигналов представлен в работе [1].

Для моделирования импульсных сигналов циклостационарного типа часто используются профильтрованные с некоторой импульсной передаточной функцией случайные точечные процессы. Широкий класс используемых для этих целей точечных процессов составляют так называемые точечные процессы с ограниченным последействием (в терминологии Ф.Я. Хинчина [2]). Процессы с ограниченным последействием являются далеко идущими обобщениями простого пуассоновского процесса, наследующими от него свойство статистической независимости длительностей интервалов между импульсами. Одними из популярных семейств точечных процессов этого класса являются рекуррентные процессы [3], характеризующиеся одинаковым распределением длительностей интервалов. В теории систем массового обслуживания такие процессы также называются процессами восстановления [4]. Рекуррентные процессы нашли широкое применение в теориях связи, очередей, распределения ресурсов и т.д. Однако для задач моделирования сигналов биомедицинского происхождения, они оказались не вполне адекватными. Проблема состоит в том, что описываемые рекуррентными процессами потоки импульсов имеют постоянный средний ритм, а для биомедицинских сигналов свойственна вариабельность ритма во времени [5]. К счастью, эту проблему можно разрешить оставаясь в рамках класса процессов с ограниченным последействием. Это достигается на пути включения в анализ моделей циклических точечных процессов. Для циклических процессов условие одинакового распределения длительностей интервалов между импульсами заменяется условием цикличности их последовательных распределений [6].

Цель данной работы состоит в разработке ${{L}_{2}}$ теории циклических точечных процессов с ограниченным последействием, подобной аналогичной теории для рекуррентных процессов, и анализа на основе характеристик второго смешанного момента циклических процессов временных масштабов ритма импульсных сигналов циклостационарного типа.

1. КВАЗИСТАЦИОНАРНАЯ МОДЕЛЬ ИМПУЛЬСНЫХ СИГНАЛОВ

Зададим рабочую модель выделенного фрагмента импульсного сигнала $z\left( {t{\kern 1pt} '} \right)$ в виде последовательности подобных по форме $g\left( {t{\kern 1pt} '} \right)$ случайных импульсов на заданном весовым окном $h\left( {t{\kern 1pt} '} \right)$ интервале:

где t – момент времени анализа, положение весового окна. Моменты времени появления импульсов $\left\{ {{{t}_{k}}} \right\}$ и соответствующие им амплитуды $\left\{ {{{A}_{k}}} \right\}$, $ - \infty < k < + \infty $, предполагаются (бесконечными) совокупностями случайных величин, статистика которых детализируется ниже.

В отношении окна $h\left( {t{\kern 1pt} '} \right)~$ примем, что оно представляет собой некоторую положительную функцию, существенно отличную от нуля в области квазистационарности сигнала:

где величина $2\Sigma $ представляет собой характерную длительность интервалов квазистационарности. Для определенности примем $h\left( 0 \right) = 1$.

Функцию формы импульса $g\left( {t{\kern 1pt} '} \right)$ также будем считать существенно отличной от нуля на интервале длительности ~2σ: $g\left( {t{\kern 1pt} '} \right){\text{\;}} \approx 0,~~\left| {~t{\kern 1pt} '~} \right| \geqslant \sigma $, но не обязательно положительной. Для определенности нормируем ее на единицу (в квадратичной норме):

где $j$ – мнимая единица. В (3) также представлена частотная характеристика $\gamma \left( f \right)$ формы импульса $g\left( {t{\kern 1pt} '} \right)$, которая ввиду действительности последней является комплексной эрмитово-симметричной $\gamma {\text{*}}\left( f \right) = \gamma \left( { - f} \right)$ функцией частоты.

Известным фактом спектральной теории является то, что в случае $\sigma \ll \Sigma $ ширина $\Omega {\text{\;}}\sim {1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma }$ характеристики $\gamma \left( f \right)$ (3) задает ширину частотного диапазона (полосу) всего сигнала $z\left( {t{\kern 1pt} '} \right)$ (1). Далее соотношение $\sigma \ll \Sigma $ будем считать выполненным. Более того, будем считать $\sigma \ll \bar {s},~\,\,~\bar {s} \ll \Sigma $, где $\bar {s}$ – средняя длительность интервала следования импульсов. Из $\sigma \ll \bar {s}$ следует, что, помимо прочего, в (1) предполагается отсутствие существенного перекрытия импульсов. Неравенство же $\bar {s} \ll \Sigma $, означает, что на анализируемом фрагменте число импульсов существенно больше единицы. Далее параметр $\bar {s}$ будет определен строго, пока же отметим, что с учетом сделанных предположений модель (1) характеризуется по крайней мере тремя временными масштабами $\sigma \ll \bar {s} \ll \Sigma $.

Предполагаемая многомасштабность сигнала $z\left( {t{\kern 1pt} '} \right)$ (1) уже достаточна для анализа простых процедур его обработки, включая анализ специализированных представлений. Отметим, что при этом всегда остается возможность дальнейшего уточнения модели, посредством добавления в нее ряда деталей для более глубокого анализа конкретных случаев. В данной работе, выбирая между характеристиками модели такими, как общность и простота, с одной стороны, или специализация и сложность, с другой, будем в основном придерживаться первой альтернативы. C этой целью представим $z\left( {t{\kern 1pt} '} \right)$ (1) в виде результата последовательных линейных операций над некоторым еще более простым импульсным сигналом – идеальным точечным процессом (сигналом) $x\left( {t{\kern 1pt} '} \right)$, см. работы [7–11]:

где $\delta \left( {t{\kern 1pt} ''} \right)$ – дельта-функции Дирака, задающая форму импульсов $x\left( {t{\kern 1pt} '} \right)$. В отличие от $z\left( {t{\kern 1pt} '} \right)$ (1) все временные масштабы процесса $x\left( {t{\kern 1pt} '} \right)$ (4) связаны только со статистикой моментов времени импульсов $\left\{ {{{t}_{k}}} \right\}$. Внутренний же $\sigma $ и внешний $\Sigma $ масштабы результирующего сигнала $z\left( {t'} \right)$ определяются характеристиками ядра $g\left( {t{\kern 1pt} '} \right)$ операции свертки “*” и окна $h\left( {t{\kern 1pt} '} \right)$ операции взвешивания "×”, применяемых к точечному процессу $x\left( {t{\kern 1pt} '} \right)$. Отметим, что ввиду линейности перечисленных операций статистические моменты $z\left( {t{\kern 1pt} '} \right)$ – первый ${{m}_{t}}\left( {t{\kern 1pt} '} \right)$, второй смешанный ${{R}_{t}}\left( {t{\kern 1pt} ',t{\kern 1pt} ''} \right)$ и т.д. – также линейно связаны с соответствующими моментами $x\left( {t{\kern 1pt} '} \right)$:

Здесь и далее чертой сверху обозначается операция усреднения. В (5) весовое окно 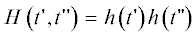и ядро свертки 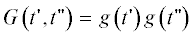имеют на плоскости $\left\{ {\left( {t{\kern 1pt} ',t''} \right)} \right\}$ носители с теми же характерными размерами ~$\Sigma $ и $\sigma $.

В отношении статистики $x\left( {t{\kern 1pt} '} \right)$ (4) примем следующие общие предположения. Будем считать совокупность моментов времени появления импульсов $\left\{ {{{t}_{k}}} \right\}$ и совокупность амплитуд $\left\{ {{{A}_{k}}} \right\}$ статистически независимыми друг от друга. Более того, будем считать все ${{A}_{k}}$ независимыми в совокупности, одинаково распределенными случайными величинами с первым и вторым статистическими моментами, равными соответственно $\bar {A}$ и $\overline {{{A}^{2}}} $. При этом первый и второй смешанный моменты сигнала $x\left( {t{\kern 1pt} '} \right)$ (4) принимают вид

где 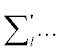означает суммирование по индексу $l \ne k.$

Из (6) следует, что для нахождения требуемых статистических моментов необходимо, по крайней мере, задание одно- и двумерных распределений вероятностей всех моментов времени ${{t}_{k}}$ и всех пар $({{t}_{l}},{{t}_{k}})$:

где ${{p}_{k}}(t{\kern 1pt} ')$ и ${{p}_{{lk}}}(t{\kern 1pt} ',~t{\kern 1pt} '')$ – плотности соответствующих распределений. С учетом введенных обозначений соотношения (6) можно записать в явном виде:

Некоторого упрощения выражений в правых частях (7) можно добиться, если принять достаточно общее допущение об ординарности процесса $x\left( {t{\kern 1pt} '} \right)$ [3]. Ординарность означает, что для интервалов времени малой длительности ${\Delta }$ вероятность появления в них только одного импульса имеет первый порядок малости по ${\Delta }$: ${{P}_{1}}\left( {t,{\Delta }} \right) \approx \lambda \left( t \right){\Delta }$, а двух и более импульсов – порядок выше первого: ${{P}_{n}}\left( {t,{\Delta }} \right) = o\left( {\Delta } \right)$,$~n = 2,3, \ldots $, где ${{P}_{n}}\left( {t,{\Delta }} \right)$ – вероятность появления $n$ импульсов в $\left( {t,t + {\Delta }} \right)$. Зависящий в общем случае от времени коэффициент $\lambda \left( t \right) \geqslant 0$ носит название (средней) интенсивности потока импульсов [3]. Последнее обстоятельство связано с тем, что среднее число импульсов $\bar {n}$ на интервале $\left( {t,t + {\Delta }} \right)$ имеет следующее разложение по ${\Delta }$:

Интенсивность $\lambda \left( t \right)$ ординарного процесса напрямую связана с плотностями $\left\{ {{{p}_{k}}\left( t \right)} \right\}$ распределений вероятностей моментов импульсов $\left\{ {{{t}_{k}}} \right\}$. Эта связь следует из того факта, что здесь события ${{t}_{k}} \in \left( {t,t + {\Delta }} \right)$ для разных $k$ несовместны, имеют вероятности ${{p}_{k}}\left( t \right){\Delta }$ и в совокупности составляют в точности событие появления одного импульса на этом интервале$.$ Поэтому исходя из ${{P}_{1}}\left( {t,{\Delta }} \right) = $ $ = \sum\nolimits_{k = - \infty }^{ + \infty } {{{p}_{k}}} \left( t \right){\Delta } = \lambda \left( t \right){\Delta }$ получим

С учетом соотношения (8) выражения (7) для первого и второго смешанных статистических моментов $x\left( {t{\kern 1pt} '} \right)$ принимают следующий окончательный вид:

Для нахождения правых частей (9) (в конечном счете (5)) достаточно задания интенсивности $\lambda \left( {t{\kern 1pt} '} \right)$ и совокупности двумерных плотностей $\left\{ {{{p}_{{lk}}}\left( {t{\kern 1pt} ',~t{\kern 1pt} ''} \right)} \right\}$. Однако ввиду известных условий согласованности распределений весьма желательно, чтобы все они были заданы не эвристически, а в рамках некоторого полного статистического описания случайных моментов $\left\{ {{{t}_{k}}} \right\}$, содержащего все конечномерные плотности распределения вероятностей ${{p}_{{l, \ldots ,k}}}\left( {{{t}_{l}}, \ldots ,{{t}_{k}}} \right)$. В контексте задач оценивания параметров модели (1) подобное задание, как отмечалось выше, не должно быть чрезмерно сложным, чтобы допускать построение (синтез) трактуемых, поддающихся простому анализу оценок. Очевидно, наиболее простым было бы предположение о статистической независимости моментов $\left\{ {{{t}_{k}}} \right\}$. Однако в отличие от амплитуд $\left\{ {{{A}_{k}}} \right\}$ предположение о статистической независимости совокупности $\left\{ {{{t}_{k}}} \right\}$ для реалистических моделей является, как правило, сверхупрощением.

Следующим по сложности классом точечных процессов являются рекуррентные процессы [3], характеризующиеся статистической независимостью и одинаковым распределением (iid – independent and identically-distributed) не самих $\left\{ {{{t}_{k}}} \right\}$, а длительностей $\left\{ {{{s}_{k}}} \right\},$ $~{{s}_{k}} = {{t}_{{k + 1}}} - {{t}_{k}} \geqslant 0,$ интервалов между импульсами. В теории систем массового обслуживания такие процессы также называются процессами восстановления [4]¹¹ . Оказалось, однако, что хотя область применимости рекуррентных процессов и является достаточно широкой [3], она недостаточна для моделирования важных классов сигналов ряда современных приложений. Например, общепризнанным фактом является то, что для задач моделирования сигналов биомедицинского происхождения, рекуррентные процессы не вполне адекватны: описываемые ими потоки импульсов имеют постоянный средний ритм, а для биомедицинских сигналов характерна вариабельность ритма во времени [5].

К счастью, для решения проблемы моделирования сигналов с переменным ритмом оказалось возможным лишь несколько обобщить модель рекуррентных точечных процессов, оставаясь в рамках класса процессов с ограниченным последействием [2]. Это достигается на пути включения в анализ моделей циклических точечных процессов. Для циклических процессов сохраняется условие независимости интервалов $\left\{ {{{s}_{k}}} \right\},~~$но условие их одинакового распределения заменяется более слабым условием циклического повторения последовательных распределений [6].

Ввиду того, что класс точечных циклических процессов с ограниченным последействием используется в радиотехнических приложениях не так часто (за исключением альтернирующих процессов [4, 12]), напомним его место в семействе процессов с ограниченным последействием и дадим на этой основе его полное статистическое описание. Затем воспользуемся полным статистическим описанием циклических процессов для вывода используемого в дальнейшем локального описания асимптотического поведения процесса.

2. ЦИКЛИЧЕСКИЕ ТОЧЕЧНЫЕ ПРОЦЕССЫ С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ

Широким семейством точечных процессов, описывающих потоки событий появления точек (узких импульсов) на временной оси в случайные моменты ${{t}_{1}} \leqslant {{t}_{2}} \leqslant ... < \infty $ начиная с некоторого неслучайного момента времени начала наблюдения ${{t}_{0}}$, являются процессы с ограниченным последействием. По определению А.Я. Хинчина [2] это процессы, у которых длительности интервалов между моментами событий ${{s}_{0}},...,{{s}_{k}}, \ldots ,$ ${\text{\;}}{{s}_{k}} = {{t}_{{k + 1}}} - {{t}_{k}}$ независимы в совокупности и имеют заданные плотности распределения вероятностей ${{\rho }_{0}}\left( s \right),...,{{\rho }_{k}}\left( s \right), \ldots ;$ $s \geqslant 0$. Если все плотности, исключая ${{\rho }_{0}}\left( s \right)$, совпадают между собой: ${{\rho }_{k}}\left( s \right) = \hat {\rho }\left( s \right),$ то процесс называется рекуррентным (процессом восстановления). Можно показать [12], что если рекуррентный процесс является стационарным, то обязательно ${{\rho }_{0}}\left( s \right)$ совпадает с сопряженной к $\hat {\rho }\left( s \right)$ плотностью

где $\bar {s}$ – математическое ожидание $\hat {\rho }\left( s \right).$

Более того, асимптотически при неограниченном увеличении времени анализа $t \to \infty $ всякий рекуррентный процесс по отношению к $t$ как к началу наблюдения процесса становится стационарным и его интенсивность $\lambda \left( t \right)$ асимптотически стремится к ${1 \mathord{\left/ {\vphantom {1 {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$ [1] (элементарная теорема восстановления). Отметим, что к рекуррентным процессам относится также простейший точечный процесс – однородный пуассоновский процесс, стационарный относительно любого момента времени $t \geqslant {{t}_{0}}$.

Простым обобщением рекуррентных процессов являются альтернирующие процессы (с ограниченным последействием) [4, 12]. Для этих процессов требование одинакового распределения интервалов заменяется требованиями одинаковых распределений с плотностью ${{\hat {\rho }}_{0}}\left( s \right)$ четных интервалов и с плотностью ${{\hat {\rho }}_{1}}\left( s \right)$ нечетных. Если ${{\hat {\rho }}_{0}}\left( s \right)$ и ${{\hat {\rho }}_{1}}\left( s \right)$ являются экспоненциальными функциями, то процесс является альтернирующим пуассоновским. Для альтернирующих процессов также выполняется соответствующее утверждение о асимптотической стационарности [4].

Следующим шагом обобщения является замена условия совпадения плотностей распределения вероятностей через событие, условием их совпадения через $K$ событий (K – период цикличности). Такие процессы с ограниченным последействием называются циклическими [6] и задаются они наборами $K$ плотностей распределения вероятностей ${{\hat {\rho }}_{0}}\left( s \right),~$ ${{\hat {\rho }}_{1}}\left( s \right),...,{{\hat {\rho }}_{{K - 1}}}\left( s \right),~$ $~s \geqslant 0$. Таким образом, для циклических процессов имеет место ${{\rho }_{k}}\left( s \right) = \,\,~{{\hat {\rho }}_{{k{\text{mod}}K}}}\left( s \right)$ для произвольных $k$, где бинарная операция ${\text{mod}}$ означает, как обычно, остаток от деления целого $k$ на период $K$.

Удобно представлять себе циклический процесс как некоторую систему из $K$ состояний $\left\{ {0,~1, \ldots ,\left( {K - 1} \right)} \right\}$, в которой состояния детерминированным образом циклически сменяют друг друга $0 \to 1 \to $ … $ \to \left( {K - 1} \right) \to 0 \to \ldots $, но эти смены происходят в случайные моменты времени, такие, что распределение вероятностей интервалов ${{s}_{k}}$ между соседними моментами (времена пребывания в состояниях) зависит от номера состояния $k$. Если в этой интерпретации снять условие детерминированности переходов, то будет осуществлен переход к следующему обобщению – к определению полумарковских процессов [4].

Заметим, что для общих процессов с ограниченным последействием, ввиду ${{t}_{{k + 1}}}$ = ${{t}_{0}} + {{s}_{0}} + \ldots + {{s}_{k}}$ и независимости ${{s}_{0}},...,{{s}_{k}}{\text{\;\;}}$в совокупности, условные плотности распределения моментов $\left\{ {{{t}_{k}}} \right\}$ обладают следующим марковским свойством:

Для циклических процессов свойство (10) уточняется следующим образом:

Используя это свойство, можно на основе цепного правила записать для циклических процессов следующие выражения конечномерных плотностей распределения вероятностей моментов $\left\{ {{{t}_{k}}} \right\}$ [12]:

Выражения (12) задают в общем виде структуру полного статистического описания циклических точечных процессов с ограниченным последействием. Однако для целей данной работы удобнее другое – локальное задание статистики процесса. Именно, выбирая произвольным образом момент времени анализа процесса $t > {{t}_{0}},$ перенумеруем последовательные моменты точек процесса относительно этого $t$ следующим образом ($~~l < 0 < 1 < k$):

где моменты $t_{l}^{'}$ c индексами $l$, значения которых меньше некоторого номера $L \leqslant 0,$ полагаются равными начальному моменту времени ${{t}_{0}}$. Используя рассуждения, подобные применявшимся при выводе (8), с помощью (12) находятся плотности распределения вероятностей моментов в локальном описании $\left\{ {t_{k}^{'}} \right\}$. А именно, учтем, что событие, соответствующее заданной конечной последовательности моментов $t_{l}^{'} \leqslant \ldots \leqslant t_{k}^{'},~$ $\left( {~t \in \left( {t_{l}^{'},t_{k}^{'}} \right)~} \right),$ может быть представлено в терминах исходного описания процесса ${{t}_{1}} \leqslant {{t}_{2}} \leqslant ... < \infty $ как сумма следующих несовместных событий: во-первых, события $\left( {{{t}_{1}} = t_{l}^{'}} \right) \cap \left( {{{t}_{2}} = t_{{l + 1}}^{'}} \right)$ $ \cap \ldots \cap \left( {{{t}_{{k - l + 1}}} = t_{k}^{'}} \right)$, во-вторых, события $({{t}_{2}} = t_{l}^{'}) \cap ({{t}_{3}} = t_{{l + 1}}^{'})$ $ \cap \ldots \cap ({{t}_{{k - l + 2}}} = t_{k}^{'})$ и т.д. Суммируя заданные описанием (12) плотности вероятностей этих событий, получим

где в соответствии с (12) использованы обозначения

для одномерных плотностей вероятности $\left\{ {{{{\tilde {p}}}_{k}}\left( t \right)} \right\}$ моментов $\left\{ {{{t}_{k}}} \right\}$ в терминах исходного описания процесса. Кроме того, в (13) сгруппированы слагаемые с кратными периоду $K$ номерами $\left\{ {j + qK} \right\},~$ $~j = 1, \ldots ,K$, поскольку в силу цикличности процесса все они имеют одинаковые сомножители при ${{\tilde {p}}_{{j + qK}}}\left( t \right)$. Если учесть, что при разных сомножителях в (13) ряды одномерных плотностей по форме подобны $\lambda \left( t \right)$ (8), то естественно считать их парциальными интенсивностями процесса и обозначить как ${{\lambda }_{j}}\left( t \right)$:

Парциальные интенсивности {λ_j(t)} можно интерпретировать как интенсивности версий исходного циклического процесса (с общим началом ${{t}_{0}}$), прореженных с периодом $K$, начиная с моментов ${{t}_{j}},~j = 1,~ \ldots ,~K$. Нетрудно заметить, что все эти версии представляют собой обычные рекуррентные точечные процессы с разными начальными плотностями ${{\rho }_{0}}\left( s \right)$, но с одинаковой плотностью $\hat {\rho }\left( s \right)$, являющейся сверткой всех $K$ плотностей ${{\hat {\rho }}_{0}}\left( s \right),$ $~{{\hat {\rho }}_{1}}\left( s \right),...,{{\hat {\rho }}_{{K - 1}}}\left( s \right)$. Из теории рекуррентных процессов известно [12], что асимптотически, при $t \to + \infty $, вне зависимости от начальной плотности, интенсивность такого процесса стремится к постоянному пределу ${1 \mathord{\left/ {\vphantom {1 {\bar {S}}}} \right. \kern-0em} {\bar {S}}}$, где $\bar {S}$ – математическое ожидание $\hat {\rho }\left( s \right)$. Поскольку математическое ожидание свертки есть сумма математических ожиданий $\left\{ {{{{\bar {s}}}_{j}}} \right\}$ ее сомножителей, $\bar {S} = {{\bar {s}}_{0}} + \ldots + {{\bar {s}}_{{K - 1}}},$ асимптотический предел для всех $\left\{ {{{\lambda }_{j}}\left( t \right)} \right\}$ можно представить и как ${1 \mathord{\left/ {\vphantom {1 {K\bar {s}}}} \right. \kern-0em} {K\bar {s}}}$, где $\bar {s}$ есть средний интервал времени между точками процесса $\bar {s} = {{\left( {{{{\bar {s}}}_{0}} + \ldots + {{{\bar {s}}}_{{K - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\bar {s}}}_{0}} + \ldots + {{{\bar {s}}}_{{K - 1}}}} \right)} K}} \right. \kern-0em} K}$.

Из сделанных замечаний следует, что для циклических процессов при $t \to + \infty $ конечномерные плотности распределения вероятностей ${{p}_{{l, \ldots ,k}}}(t_{l}^{'}, \ldots ,t_{k}^{'})$ (13) будут зависеть только от разностей последовательных аргументов $(t_{{i + 1}}^{'} - t_{i}^{'})$, т.е. асимптотически они становятся стационарными. Это свойство обобщает упоминавшиеся выше аналогичные факты для рекуррентного и альтернирующего процессов, являющихся частными случаями циклического.

Предполагая далее для циклического процесса асимптотику $t \to + \infty $, т.е. предполагая для него выполненным условие стационарности ${{\lambda }_{j}}\left( t \right) = {1 \mathord{\left/ {\vphantom {1 {K{\kern 1pt} \bar {s}}}} \right. \kern-0em} {K{\kern 1pt} \bar {s}}},$ перепишем статистическое задание (13) распределений наборов подряд идущих моментов времени с l-го по k-й ($l \leqslant 0 < 1 \leqslant k$) в виде

где использованы локальные относительно момента времени анализа $t$ координаты ${{t}_{i}} = t_{i}^{'} - t,~~$ $ - \infty < i < \infty $. При этом, очевидно, момент времени анализа процесса переносится в начало координат, и это предполагает его расположение между крайними моментами времени набора: ${{t}_{l}} \leqslant 0$ и $0 \leqslant {{t}_{k}}$. Если в (16) произвести замену индекса $j{\kern 1pt} ' = \left( {j - l} \right){\text{mod}}K$, то при суммировании по $j$ новый индекс $j{\kern 1pt} '$ будет пробегать значения из $\left\{ {0, \ldots ,K - 1} \right\}$, что позволяет плотности распределений вероятностей (16) переписать в следующем окончательном виде ($l \leqslant 0 < 1 \leqslant k$):

где возвращено обозначение индекса суммирования $j{\kern 1pt} ' \to j$. Отметим, что каждое слагаемое в (17) может интерпретироваться как совместная плотность распределения вероятности набора ${{t}_{l}}, \ldots ,{{t}_{k}}$ и определенного состояния $j$ процесса в момент времени анализа 0 (или в течение времени от ${{t}_{0}}$ до ${{t}_{1}}$).

Условие $l \leqslant 0 < 1 \leqslant k$ для (17) не является ограничением для полного статистического задания процесса. С помощью (17) также можно вычислить конечномерные плотности наборов ${{t}_{l}} \leqslant \ldots \leqslant {{t}_{k}}$, расположенных по одну сторону от нуля. Они вычисляются как маргинальные для распределений бóльших наборов подряд идущих моментов, содержащих в себе данный поднабор, но имеющих крайние моменты по разные стороны от нуля. Заметим, что поскольку при этом приходится интегрировать $~{{\hat {\rho }}_{j}}\left( {{{t}_{1}} - {{t}_{0}}} \right)$ вдоль положительной ${{t}_{1}} \geqslant 0$ и/или отрицательной ${{t}_{0}} \leqslant 0$ полуосей, полезно заменить плотности $~{{\hat {\rho }}_{j}}\left( {{{t}_{1}} - {{t}_{0}}} \right)$ выражениями $\theta \left( {{{t}_{1}}} \right)\theta \left( { - {{t}_{0}}} \right)~{{\hat {\rho }}_{j}}\left( {{{t}_{1}} - {{t}_{0}}} \right)$ и интегрировать его уже вдоль полных осей координат $ - \infty < {{t}_{0}} < \infty $ и $ - \infty < {{t}_{1}} < \infty $. При этом, поскольку ${{\hat {\rho }}_{j}}\left( s \right) \equiv 0,~$ $~s < 0,$ оказывается полезным следующее тождество:

Найдем, например, одномерные плотности распределения ${{p}_{k}}\left( t \right)$ для моментов времени ${{t}_{k}} = t,~$ $~k \geqslant 1,$ процесса. Для этого используем набор моментов ${{t}_{0}} \leqslant 0 \leqslant {{t}_{1}} \leqslant \ldots \leqslant {{t}_{{k - 1}}} \leqslant t~$ и проинтегрируем соответствующую ему плотность ${{p}_{{0, \ldots ,k}}}\left( {{{t}_{0}},{{t}_{1}}, \ldots ,{{t}_{{k - 1}}},t} \right)$ (17) по ${{t}_{0}}$ от $ - \infty $ до 0 и по ${{t}_{1}} \leqslant \ldots \leqslant {{t}_{{k - 1}}}$ от 0 до $t$:

где пределы всех интегралов заменены на бесконечные ввиду автоматического обращения подынтегральных выражений в нуль вне интервалов интегрирования ${{t}_{{i - 1}}} \leqslant {{t}_{i}} \leqslant t$ и искусственного введения функций Хэвисайда $\theta \left( {{{t}_{1}}} \right)$ и $\theta \left( { - {{t}_{0}}} \right)$ в первых двух интегралах.

Используя для интеграла по ${{t}_{0}}$ в (19) тождество (18), получим

где использована сопряженная к $~{{\hat {\rho }}_{j}}\left( s \right)$ плотность ${{\hat {\varrho }}_{j}}\left( t \right)$ (см. выше).

Подставляя полученное выражение в (19), окончательно получим

Частным случаем (20) является распределение первого момента ${{t}_{1}}$ (последующего времени пребывания в состоянии на момент анализа), равное

Отметим, что плотность (21) можно интерпретировать как формулу полной вероятности, если понимать под ${{\hat {\varrho }}_{j}}\left( t \right)$ плотности условных распределений вероятностей находиться в течение времени $t$, начиная с нуля, в состоянии $j$, а под ${{{{{\bar {s}}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{j}}} {K{\kern 1pt} \bar {s}}}} \right. \kern-0em} {K{\kern 1pt} \bar {s}}} = {{\pi }_{j}}$ ‒ безусловные вероятности оказаться в этом состоянии на момент времени анализа 0.

Из (20) следует, что все ${{p}_{k}}\left( t \right)$ являются взвешенными (с весами ${{\pi }_{j}} = {{{{{\bar {s}}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{j}}} {K{\kern 1pt} \bar {s}}}} \right. \kern-0em} {K{\kern 1pt} \bar {s}}}$) суммами $\left( {k - 1} \right)$-кратных сверток $~{{\hat {\varrho }}_{j}}\left( s \right)$ и последовательных $\left( {k - 1} \right)$ плотностей $~{{\hat {\rho }}_{{\left( {j + 1} \right){\text{mod}}K}}}\left( s \right),$ …, $~{{\hat {\rho }}_{{\left( {j + k - 1} \right){\text{mod}}K}}}\left( s \right)$. Для компактной записи выражений, подобных (20), полезно ввести специальные обозначения $C_{j}^{{\left( k \right)}}\left( t \right),$ $~j = 0, \ldots ,K - 1,$ для $k$-кратных сверток подряд следующих (k + 1) плотностей $~{{\hat {\rho }}_{{\left( j \right){\text{mod}}K}}}\left( s \right)$,…, $~{{\hat {\rho }}_{{\left( {j + k} \right){\text{mod}}K}}}\left( s \right)$, $k = 0,1, \ldots $ (понимая под 0-сверткой $C_{j}^{{\left( 0 \right)}}\left( t \right) = \,\,~{{\hat {\rho }}_{j}}\left( t \right)$):

Функции $C_{j}^{{\left( k \right)}}\left( t \right)$ (22), будучи плотностями распределений сумм $\left( {k + 1} \right)$ независимых положительных случайных величин, тождественно обращаются в нуль на отрицательной полуоси $t < 0$, а на положительной $t > 0$ они положительны и нормированы на единицу. Кроме того, их средние и дисперсии равны суммам средних и суммам дисперсий всех входящих под свертку плотностей.

Доопределив $C_{j}^{{\left( k \right)}}\left( t \right)$ для значений $k = - 1$ посредством $C_{j}^{{\left( { - 1} \right)}}\left( t \right) = \delta \left( t \right),$ $~j = 0, \ldots ,K - 1$, из (22) можно получить следующие рекуррентные соотношения:

С учетом определений $C_{j}^{{\left( k \right)}}\left( t \right)$ (22) одномерные плотности (20) принимают следующий более компактный вид:

где

могут интерпретироваться как плотности распределения условных вероятностей моментов ${{t}_{k}},~~k > 0$, при условии прохождения процесса через состояние $j$ в момент времени анализа 0, а ${{\pi }_{j}} = {{{{{\bar {s}}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{j}}} {K{\kern 1pt} \bar {s}}}} \right. \kern-0em} {K{\kern 1pt} \bar {s}}}$ – как (безусловные) вероятности оказаться в этом состоянии. В частном случае $k = 1$ из определения (25) следует $\hat {\varrho }_{j}^{{\left( 1 \right)}}\left( t \right) = {{\hat {\varrho }}_{j}}\left( t \right).$

Просуммировав обе части (24) по $k$ от 1 до $\infty $, в соответствии с (8) получим

Продифференцировав $\lambda \left( t \right)$ и учитывая, что ${{\bar {s}}_{j}}\hat {\varrho }_{j}^{'}\left( t \right) = \delta \left( t \right) - ~{{\hat {\rho }}_{j}}\left( t \right)$, получим

где также использованы рекуррентные соотношения (23). Интегрируя это соотношение с учетом ${{p}_{k}}\left( t \right) \equiv 0$ при $t < 0$, получим ${{\lambda }_{ + }}\left( t \right) = {{\theta \left( t \right)} \mathord{\left/ {\vphantom {{\theta \left( t \right)} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}.$

Все, что сделано выше для вероятностей ${{p}_{k}}\left( t \right)$ моментов ${{t}_{k}} = t,~~k \geqslant 1$ с равным успехом может быть повторено и для вероятностей p_l(t) моментов ${{t}_{l}} = t,~$ $l \leqslant 0.$ Для этого возьмем набор ${{t}_{l}} \leqslant {{t}_{{l + 1}}} \leqslant \ldots \leqslant {{t}_{0}} \leqslant 0 \leqslant {{t}_{1}}~$ и проинтегрируем соответствующую ему плотность ${{p}_{{l, \ldots ,1}}}\left( {t,{{t}_{{l + 1}}}, \ldots ,{{t}_{0}},{{t}_{1}}} \right)$ (17) по ${{t}_{1}}$ от 0 до $\infty $ и по ${{t}_{{l + 1}}} \leqslant \ldots \leqslant {{t}_{0}}$ от $t$ до 0:

где пределы всех интегралов заменены на бесконечные ввиду автоматического обращения подынтегральных выражений в нуль вне интервалов интегрирования $t \leqslant {{t}_{i}} \leqslant {{t}_{{i + 1}}}$ и искусственного введения функций Хэвисайда $\theta \left( {{{t}_{1}}} \right)$ и $\theta \left( { - {{t}_{0}}} \right)$ в первых двух интегралах.

Используя для интеграла по t₁ в (26) тождество (18), получим

Подставляя полученное выражение в (26), окончательно получим

Частным случаем (27) является распределение нулевого момента ${{t}_{0}}$ (предшествующего времени пребывания в состоянии на момент анализа):

Плотность (28) можно интерпретировать как формулу полной вероятности, понимая под $~{{\hat {\varrho }}_{j}}\left( { - t} \right)$ плотности условных вероятностей находиться в течение времени $\left( { - t} \right)$ вплоть до нуля в состоянии $j$, а под ${{{{{\bar {s}}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{j}}} {K\bar {s}}}} \right. \kern-0em} {K\bar {s}}} = {{\pi }_{j}}$ – безусловные вероятности оказаться в состоянии $j$ в момент времени анализа 0.

Из (27) следует, что все ${{p}_{l}}\left( t \right)$ являются взвешенными суммами $\left( { - l} \right)$-кратных сверток $~{{\hat {\varrho }}_{j}}\left( s \right)$ и предшествующих в обратном порядке плотностей $~{{\hat {\rho }}_{{\left( {j - 1} \right){\text{mod}}K}}}\left( s \right)$, …, $~{{\hat {\rho }}_{{\left( {j + l} \right){\text{mod}}K}}}\left( s \right)$. Для компактной записи выражений, подобных (27), полезно ввести специальные обозначения $D_{j}^{{\left( k \right)}}\left( t \right),~$ $~j = 0, \ldots ,K - 1,$ для $k$-кратных сверток подряд следующих в обратном порядке $\left( {k + 1} \right)$ плотностей $~{{\hat {\rho }}_{{\left( j \right){\text{mod}}K}}}\left( s \right)$, …, $~{{\hat {\rho }}_{{\left( {j - k} \right){\text{mod}}K}}}\left( s \right),~$ $~k = 0,1, \ldots $ (понимая под 0-сверткой $D_{j}^{{\left( 0 \right)}}\left( t \right) = \,\,~{{\hat {\rho }}_{j}}\left( t \right)$):

Функции $D_{j}^{{\left( k \right)}}\left( t \right)$ (29), будучи плотностями распределений сумм (k + 1) независимых положительных случайных величин, тождественно обращаются в нуль на отрицательной полуоси t < 0, а на положительной t > 0 они положительны и нормированы на единицу. Кроме того, их средние и дисперсии равны суммам средних и суммам дисперсий всех входящих под свертку плотностей.

Сравнивая определения $D_{j}^{{\left( k \right)}}\left( t \right)$ (29) и $C_{j}^{{\left( k \right)}}\left( t \right)$ (22), легко заметить, что

Просуммировав соотношения (30) по j от 0 до K – 1, получим тождество

Доопределив $D_{j}^{{\left( k \right)}}\left( t \right)$ для значений $k = - 1$ посредством $D_{j}^{{\left( { - 1} \right)}}\left( t \right) = \delta \left( t \right),$ $~j = 0, \ldots ,K - 1$, из (29) можно получить следующие рекуррентные соотношения:

С учетом определения $D_{j}^{{\left( k \right)}}\left( t \right)$ (29) одномерные плотности (27) принимают следующий более компактный вид:

где

могут интерпретироваться как плотности распределения условных вероятностей моментов t_l, l ≤ 0, при условии прохождения процесса через состояние j в момент времени анализа 0, а ${{\pi }_{j}} = {{{{{\bar {s}}}_{j}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{j}}} {K\bar {s}}}} \right. \kern-0em} {K\bar {s}}}$ – как (безусловные) вероятности оказаться в этом состоянии. В частном случае, $l = 0,$ из определения (34) следует $\hat {\varrho }_{j}^{{\left( 0 \right)}}\left( t \right) = {{\hat {\varrho }}_{j}}\left( t \right)$.

Просуммировав обе части (33) по l от –∞ до 0, в соответствии с (8) получим

Продифференцировав λ_–(t) и учитывая, что ${{\bar {s}}_{j}}\hat {\varrho }_{j}^{'}\left( t \right) = \delta \left( t \right) - ~{{\hat {\rho }}_{j}}\left( t \right)$, получим

${\text{где}}$ также использованы рекуррентные соотношения (32). Интегрируя это соотношение с учетом ${{p}_{l}}\left( t \right) \equiv 0$ при $t > 0$, получим ${{\lambda }_{ - }}\left( t \right) = {{\theta \left( { - t} \right)} \mathord{\left/ {\vphantom {{\theta \left( { - t} \right)} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$.

Исходя из того, что $\lambda \left( {t{\kern 1pt} '} \right) = {{\lambda }_{ - }}\left( {t{\kern 1pt} '} \right) + {{\lambda }_{ + }}\left( {t{\kern 1pt} '} \right)$ для всех $t{\kern 1pt} '$, получаем, что первый момент (среднее) стационарного циклического процесса $x\left( {t{\kern 1pt} '} \right)$ (9) в явном виде есть:

3. ВТОРОЙ МОМЕНТ СТАЦИОНАРНОГО ЦИКЛИЧЕСКОГО ПРОЦЕССА В ЛОКАЛЬНОЙ ВЕРСИИ

Возвращаясь к соотношениям (9), найдем на основе локального описания (17) двумерные плотности распределения вероятностей 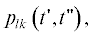$~l \ne k~$. Воспользуемся методом, подобным использованному в предыдущем разделе при нахождении одномерных распределений ${{p}_{k}}\left( t \right)$, где случаи $~k \geqslant 1~$ и $k \leqslant 0~$ рассматривались отдельно. Для определенности найдем ${{p}_{{lk}}}\left( {t{\kern 1pt} ',~t{\kern 1pt} ''} \right)$ при $l < k$, дополнительный случай $k < \,\,~l$ получается в результате одновременных перестановок $k \leftrightarrow \,\,~l$ и $t{\kern 1pt} ' \leftrightarrow ~\,\,t{\kern 1pt} {\kern 1pt} ''$. Таким образом, рассмотрим три случая: А) $l < k \leqslant 0$, Б) $l \leqslant {\kern 1pt} \,~0 < k$ и В) $1 \leqslant l < k$.

Случай A: $l < ~\,\,k \leqslant 0$.

В группе моментов

проинтегрируем соответствующую плотность (17) по моменту ${{t}_{1}}$ от 0 до $\infty $, по ${{t}_{{k + 1}}} \leqslant \ldots \leqslant {{t}_{0}}$ от 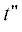до 0 и по ${{t}_{{l + 1}}} \leqslant \ldots \leqslant {{t}_{{k - 1}}}$ от $t{\kern 1pt} '$ до :

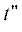Воспользовавшись выведенным ранее соотношением

а также соотношениями (29) и (34), перепишем (36) в компактном виде:

откуда следует, что 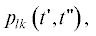$~l < ~\,\,k \leqslant 0,~$ отлична от нуля при .

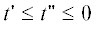Случай Б: $0 \leqslant l < ~\,\,k$.

В группе моментов

проинтегрируем соответствующую плотность (17) по моменту ${{t}_{0}}$ от $ - \infty $ до 0, по ${{t}_{1}} \leqslant \ldots \leqslant {{t}_{{l - 1}}}$ от 0 до $t{\kern 1pt} '$ и по ${{t}_{{l + 1}}} \leqslant \ldots \leqslant {{t}_{{k - 1}}}$ от $t{\kern 1pt} '$ до :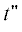

Воспользовавшись выведенным ранее соотношением

а также соотношениями (22) и (25), перепишем (38) в компактном виде:

откуда следует, что 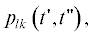$0 \leqslant l < ~k~$ отлична от нуля при .

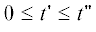Случай В: $l \leqslant 0 < k.$

В группе моментов

проинтегрируем соответствующую плотность (17) по моментам ${{t}_{{l + 1}}} \leqslant \ldots \leqslant {{t}_{0}}$ от $t{\kern 1pt} '$ до 0 и по ${{t}_{1}} \leqslant \ldots \leqslant {{t}_{{k - 1}}}$ от 0 до :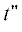

Воспользовавшись (22) и (29), перепишем (40) в компактном виде:

откуда следует, что 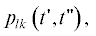$~l \leqslant 0 < \,\,~k~$ отлична от нуля при .

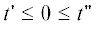Далее, используя соотношение (18) и рекуррентные тождества (23) и (32), окончательно получим

Для дальнейших целей полезно ввести набор связанных с $C_{j}^{{\left( k \right)}}\left( t \right)$ (22) и $D_{j}^{{\left( k \right)}}\left( t \right)$ (29) функций ${{c}_{j}}\left( t \right),$ $~{{d}_{j}}\left( t \right)~~j = 0, \ldots ,K - 1$:

Функции ${{c}_{j}}\left( t \right)$ и ${{d}_{j}}\left( t \right)$ (43) тождественно обращаются в нуль на отрицательной полуоси $t < 0,$ а на положительной $t > 0$ они положительны, но не нормированы, т.е. не являются плотностями распределения вероятностей. Из соотношений (31) можно получить следующую связь между ними:

Для определения второго момента $\overline {x\left( {t{\kern 1pt} '} \right)x\left( {t{\kern 1pt} ''} \right)} $ согласно (9) необходимо найти двойную сумму

Разобьем сумму на четыре слагаемых: A') $~l,k \leqslant 0$, Б') $l,~k \geqslant 1$, В') $l \leqslant 0,~\,\,k \geqslant 1~$, В") $l \geqslant 1,~\,\,k \leqslant 0~$ и в соответствии с результатами рассмотренных выше случаев A–В найдем их.

A'. Сумма :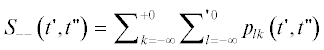

где введено ${{\mu }_{j}}\left( t \right) = \frac{1}{{\overline {s~} }}\sum\nolimits_{k = 0}^{ + \infty } {{{{\bar {s}}}_{{\left( {j + k + 1} \right){\text{mod}}K}}}} \hat {\varrho }_{{\left( {j + k + 1} \right){\text{mod}}K}}^{{\left( { - k} \right)}}\left( { - t} \right)$.

С учетом определения $\hat {\varrho }_{j}^{{\left( l \right)}}\left( t \right),\,\,~l \leqslant 0$ (34):

Продифференцируем ${{\mu }_{j}}\left( t \right)$ с учетом ${{\bar {s}}_{j}}\hat {\varrho }_{j}^{'}\left( t \right) = \delta \left( t \right) - ~{{\hat {\rho }}_{j}}\left( t \right)$:

где было использовано рекуррентное тождество (32). Интегрируя $\mu _{j}^{'}\left( t \right)$ и учитывая, что ${{\mu }_{j}}\left( t \right) \equiv 0$ при $t > 0$, получим ${{\mu }_{j}}\left( t \right) = {{\theta \left( { - t} \right)} \mathord{\left/ {\vphantom {{\theta \left( { - t} \right)} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$. С учетом этого имеем

Б'. Сумма :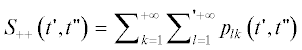

где введено

С учетом определения $\hat {\varrho }_{j}^{{\left( k \right)}}\left( t \right),~\,\,k \geqslant 0$ (25), получаем

Продифференцируем ${{\nu }_{j}}\left( t \right)$ с учетом ${{\bar {s}}_{j}}\hat {\varrho }_{j}^{'}\left( t \right) = \delta \left( t \right) - ~{{\hat {\rho }}_{j}}\left( t \right)$:

где было использовано рекуррентное тождество (23). Интегрируя $\nu _{j}^{'}\left( t \right)$ и учитывая, что ${{\nu }_{j}}\left( t \right) \equiv 0$ при $t < 0$, получим ${{\nu }_{j}}\left( t \right) = {{\theta \left( t \right)} \mathord{\left/ {\vphantom {{\theta \left( t \right)} {\bar {s}~}}} \right. \kern-0em} {\bar {s}~}}$. С учетом этого имеем

В'. Сумма :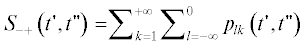

где использовано тождество (18).

В". Сумма :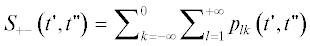

Суммируя выражения (44)–(47), получим следующий окончательный результат:

Теперь, с учетом найденного выражения (49) для двойной суммы и (35) для интенсивности $\lambda \left( {t{\kern 1pt} '} \right)$ может быть окончательно выписан явный вид второго момента $\overline {x\left( {t{\kern 1pt} '} \right)x\left( {t{\kern 1pt} ''} \right)} $ (9):

регулярная часть которого полностью задается функцией $b\left( t \right)$ (44), однозначно определяемой через свертки $C_{j}^{{\left( k \right)}}\left( t \right)$ (22) подряд следующих плотностей распределения вероятностей $~{{\hat {\rho }}_{{\left( j \right){\text{mod}}K}}}\left( s \right)$, …, $~{{\hat {\rho }}_{{\left( {j + k} \right){\text{mod}}K}}}\left( s \right)$.

Отметим, что 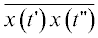(50) зависит от разности аргументов , что также является признаком стационарности процесса.

Если ввести характеристические функции $\left\{ {~{{\chi }_{k}}\left( f \right)} \right\}$ для задающих циклический процесс плотностей распределения вероятностей $\left\{ {~{{{\hat {\rho }}}_{k}}\left( s \right)} \right\},$ $k = 0,~1, \ldots ,K - 1$ :

то в соответствии с определением (22) характеристическими функциями сверток $C_{j}^{{\left( k \right)}}\left( t \right)$ будут:

Отметим, что все $\left\{ {~{{\chi }_{k}}\left( f \right)} \right\}$ и $\left\{ {\psi _{l}^{{\left( k \right)}}\left( f \right)} \right\}$, будучи характеристическими функциями распределений, которые обращаются в нуль на отрицательной оси, являются аналитическими функциями в нижней комплексной полуплоскости ${\text{Im}}\left( f \right) < 0$, где также имеют место ограничения $\left| {~{{\chi }_{k}}\left( f \right)} \right| < 1$ и $\left| {\psi _{l}^{{\left( k \right)}}\left( f \right)} \right| < 1$.

С помощью (52) может быть найдено преобразованием Фурье $b\left( t \right)$ (44):

Если в суммах рядов (53) сгруппировать члены с кратными периоду $K$ номерами $k = m + nK,~$ $m = 0, \ldots ,\left( {K - 1} \right),~$ $~~n = 0, \ldots $ , то в силу их циклического характера можно по крайней мере в нижней комплексной полуплоскости $Im\left( f \right) < 0$ привести эти ряды к конечным суммам вида:

Подставляя эти выражения в (53), найдем $\Psi \left( f \right)$ в удобном для анализа виде:

Представление (54) полезно тем, что из него следует явное уравнение для полюсов $\Psi \left( f \right)$, которые, как известно, определяют многие черты поведения исходной функции $b\left( t \right)$ (44). Из (54) следует, что уравнение для полюсов есть

В частности, ввиду равенства характеристических функций в нуле единице, нуль всегда является корнем (55). Соответствующий этому корню вычет $\Psi \left( f \right)$ легко находится (см. (51)) и равен ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\pi j\bar {s}$. Отсюда, например, вытекает асимптотическое поведение $b\left( t \right) \to {1 \mathord{\left/ {\vphantom {1 {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$ при $t \to \infty .$

С помощью $\Psi \left( f \right)$ (54) может быть найден спектр второго момента $\overline {x\left( {t{\kern 1pt} '} \right)x\left( {t{\kern 1pt} ''} \right)} $:

Из (56), в частности, следует, что $S\left( f \right)$ имеет в нуле особенность ${{{{{\bar {A}}}^{2}}\delta \left( f \right)} \mathord{\left/ {\vphantom {{{{{\bar {A}}}^{2}}\delta \left( f \right)} {{{{\bar {s}}}^{2}}}}} \right. \kern-0em} {{{{\bar {s}}}^{2}}}}$, которая ведет к асимптотике $\overline {x\left( 0 \right)x\left( t \right)} \to {{{{{\bar {A}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\bar {A}}}^{2}}} {{{{\bar {s}}}^{2}}}}} \right. \kern-0em} {{{{\bar {s}}}^{2}}}} = {{\bar {x}}^{2}}$ при $t \to \pm \infty $. В невырожденных случаях $~\Psi \left( f \right)$, за исключением f = 0, не имеет особенностей на действительной оси (уравнение (55) имеет единственный действительный корень – нуль). Поэтому $\Psi \left( f \right) - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\pi jf\bar {s}$ является регулярной функцией действительных частот и спектр $S\left( f \right)$ (56) можно представить в виде суммы сингулярной и регулярной частей:

Отметим здесь формальную аналогию (57) со спектром рекуррентного импульсного процесса, обсуждаемого в [13] (см. там же ссылки).

4. СОДЕРЖАТЕЛЬНАЯ КОНКРЕТИЗАЦИЯ МОДЕЛИ ЦИКЛИЧЕСКИХ ТОЧЕЧНЫХ ПРОЦЕССОВ

Уравнения (50) и (57) задают наиболее общий вид представлений второго момента $\overline {x\left( {t{\kern 1pt} '} \right)x\left( {t{\kern 1pt} ''} \right)} $ (9) точечного циклического процесса во временной и в частотной областях. При этом задающие процесс плотности распределения вероятностей ${{\hat {\rho }}_{0}}\left( s \right),~{{\hat {\rho }}_{1}}\left( s \right),...,{{\hat {\rho }}_{{K - 1}}}\left( s \right),$ $s \geqslant 0$, могут иметь произвольный вид ‒ любую форму, статистические моменты, включая моду, масштаб и т.д. Однако для конкретизации анализа в отношении определенного класса задач, необходимо, как это отмечалось в разд. 1, ввести некоторые элементы детализации модели, ограничив ее на определенные частные случаи. Одним из распространенных в приложениях частных случаев является ситуация, в которой плотности $\left\{ {~{{{\hat {\rho }}}_{k}}\left( s \right)} \right\}$ имеют одинаковую форму, но различаются расположением на полуоси $s \geqslant 0$. Формально, в данном случае центрированные статистические моменты всех $~{{\hat {\rho }}_{k}}\left( s \right)$ предполагаются равными, за исключением математических ожиданий ${{\bar {s}}_{k}}$. Рассмотрим эту частную модель более подробно.

Будем считать, что все $K$ плотностей распределения вероятностей циклического процесса имеют одинаковую форму $~{{\hat {\rho }}_{0}}\left( s \right)$, но сдвинуты относительно нее на ${\Delta }{{s}_{k}}$: $~{{\hat {\rho }}_{k}}\left( s \right) = \,\,~{{\hat {\rho }}_{0}}\left( {s - {\Delta }{{s}_{k}}} \right),~$ $k = 1, \ldots ,~K - 1$. При этом будем считать, что сдвиги заданы явным образом в виде синусоидальной последовательности ${\Delta }{{s}_{k}} = \theta \sin \left( {{{2\pi k} \mathord{\left/ {\vphantom {{2\pi k} K}} \right. \kern-0em} K}} \right)$. Математические ожидания введенных плотностей $\left\{ {{{{\hat {\rho }}}_{k}}\left( s \right)} \right\}$ очевидно равны ${{\bar {s}}_{k}} = {{\bar {s}}_{0}} + \theta ~\sin \left( {{{2\pi k} \mathord{\left/ {\vphantom {{2\pi k} K}} \right. \kern-0em} K}} \right)$, где ${{\bar {s}}_{0}}$ – математическое ожидание ${{\hat {\rho }}_{0}}\left( s \right)$. Среднее значение и размах $\left\{ {{{{\bar {s}}}_{k}}} \right\}$ составляют соответственно ${{\bar {s}}_{0}}$ и $2\theta $. Другими словами, параметр ${{\bar {s}}_{0}}$ совпадает с введенным ранее средним $\bar {s}$ интервалов между точками процесса, а величина $Q = {{2\theta } \mathord{\left/ {\vphantom {{2\theta } {{{{\bar {s}}}_{0}}}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}}}$ может рассматриваться как параметр их вариабельности. Очевидно, что у введенного таким образом набора плотностей все (центрированные) статистические моменты совпадают. В частности, у них совпадают стандартные отклонения $\beta $, удвоенную величину которых примем в качестве эффективной ширины каждой из $\left\{ {~{{{\hat {\rho }}}_{k}}\left( s \right)} \right\}$. Для обеспечения условия ${{\hat {\rho }}_{k}}\left( s \right) \equiv 0$ при $s < 0~$ требуется, очевидно, условие $\beta + \theta \ll {{\bar {s}}_{0}}$, которое в дальнейшем будет предполагаться выполненным.

Попутно отметим, что ввиду $K$-периодичности синуса имеет место ${\Delta }{{s}_{{\left( k \right){\text{mod}}K}}} = {\Delta }{{s}_{k}}$, поэтому далее в обозначениях вида ${{\hat {\rho }}_{{\left( {j + k} \right){\text{mod}}K}}}\left( t \right),$ ${{\chi }_{{\left( {l + i} \right){\text{mod}}K}}}\left( f \right)$ и т.д. операцию $\left( \ldots \right){\text{mod}}K$ приведения индекса по модулю $K$ можно в явном виде не выписывать.

С учетом введенных обозначений характеристические функции (51) плотностей распределения вероятностей $~{{\hat {\rho }}_{k}}\left( s \right)$ в рассматриваемом случае представляются в виде

Как следует из (54), в выражение для спектра $\Psi \left( f \right)$ характеристические функции (58) входят только как элементы следующих структурных блоков:

где использовано обозначение ${{U}_{{m,K}}}$ для коэффициентов ${{\sin \left( {\frac{{\pi \left( {m + 1} \right)}}{K}} \right)} \mathord{\left/ {\vphantom {{\sin \left( {\frac{{\pi \left( {m + 1} \right)}}{K}} \right)} {\sin \left( {\frac{\pi }{K}} \right)}}} \right. \kern-0em} {\sin \left( {\frac{\pi }{K}} \right)}}$, являющихся значениями полиномов Чебышева второго рода ${{U}_{m}}\left( x \right)$ в точке $x = \cos \left( {{\pi \mathord{\left/ {\vphantom {\pi K}} \right. \kern-0em} K}} \right)$.

В частности, из полученного выражения ввиду ${{U}_{{m,K - 1}}} = 0,$ следует:

что представляет собой входящее в знаменатель $\Psi \left( f \right)$ (54) блок-произведение характеристических функций.

Вводя временно обозначение ${{z}_{m}} = 2\pi {{U}_{{m,K}}}f\theta $ и воспользовавшись разложением $\exp \left( { - j{{z}_{m}}\sin \left( \varphi \right)} \right)$ в ряд Фурье по $\varphi $ (формула Якоби–Ангера, см. Приложение (П3) ), найдем

где ${{\mathcal{J}}_{n}}\left( z \right)$ – функции Бесселя первого рода (см. Приложение (П1) ).

Вводя спектральные окна $W_{m}^{{\left( K \right)}}\left( f \right)$:

можно записать структурные блоки ${{\Psi }^{{\left( m \right)}}}\left( f \right)$ (59) в более компактном виде:

Ввиду того, что при любых $n \ne 0$ значениями ${{\mathcal{J}}_{n}}\left( z \right)$ в нуле является нуль и только ${{\mathcal{J}}_{0}}\left( 0 \right) = 1$, общим свойством спектральных окон (60) при любых $K$ и $m$ является $W_{m}^{{\left( K \right)}}\left( 0 \right) = 1$. Частным свойством окон (60), выполняющимся при нечетных $K$ и являющимся следствием известного свойства функций Бесселя ${{\mathcal{J}}_{{ - n}}}\left( z \right) = {{\left( { - 1} \right)}^{n}}{{\mathcal{J}}_{n}}\left( z \right)$, является то, что члены ряда в $W_{m}^{{\left( K \right)}}\left( f \right)$ (60) с нечетными номерами $ \pm p$ взаимно сокращаются, а с четными – удваиваются, что позволяет в случае нечетного $K$ несколько упростить выражение для $W_{m}^{{\left( K \right)}}\left( f \right)$ (60):

Отметим, что в этом случае все окна $W_{m}^{{\left( K \right)}}\left( f \right)$ выражаются через $W_{0}^{{\left( K \right)}}\left( f \right)$ с помощью масштабного преобразования частоты:

Масштаб ${{U}_{{m,K}}}$ изменяется от 1 до ${{\sim \,K} \mathord{\left/ {\vphantom {{\sim \,K} \pi }} \right. \kern-0em} \pi }$ при изменении $m$ от 0 до ${{\left( {K - 1} \right)} \mathord{\left/ {\vphantom {{\left( {K - 1} \right)} 2}} \right. \kern-0em} 2}$ и обратно от ${{\sim {\kern 1pt} K} \mathord{\left/ {\vphantom {{\sim {\kern 1pt} K} \pi }} \right. \kern-0em} \pi }$ до 1 при изменении $m$ от ${{\left( {K - 1} \right)} \mathord{\left/ {\vphantom {{\left( {K - 1} \right)} 2}} \right. \kern-0em} 2}$ до $K - 2$. При $m = K - 1$ масштабный множитель ${{U}_{{K - 1,K}}} = 0$ и $W_{{K - 1}}^{{\left( K \right)}}\left( f \right) = W_{0}^{{\left( K \right)}}\left( 0 \right) \equiv 1$.

Во избежание громоздких выражений ниже будет рассматриваться только случай нечетных $K$, в котором все $W_{m}^{{\left( K \right)}}\left( f \right)$ являются масштабированными версиями $W_{0}^{{\left( K \right)}}\left( f \right)$.

В наиболее интересном случае $K \gg 1,$ ряд из функций Бесселя (62) можно приблизить его конечным отрезком исходя из нижеприведенных оценок. На основе оценки $\left| {{{\mathcal{J}}_{n}}\left( z \right)} \right| \leqslant {{{{{\left| {{z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2}} \right|}}^{n}}} \mathord{\left/ {\vphantom {{{{{\left| {{z \mathord{\left/ {\vphantom {z 2}} \right. \kern-0em} 2}} \right|}}^{n}}} {n!}}} \right. \kern-0em} {n!}}$ (см. Приложение (П10)) можно, воспользовавшись формулой Стирлинга, выписать следующую верхнюю границу ${{\mathcal{J}}_{{2qK}}}\left( z \right),\,\,~q \geqslant 1$ для интервала $\left| z \right| < M$:

Если положить $M\sim K\hat {q}$, то приведенная оценка принимает вид

откуда следует, что при больших $K$ слагаемыми с $q \geqslant \hat {q}$ в (62) на интервале $\left| z \right| < K\hat {q}$ можно пренебречь и вместо бесконечных рядов использовать для $W_{m}^{{\left( K \right)}}\left( f \right)$ их конечные отрезки. Как отмечалось выше, в связи с вопросами о масштабном подобии, при больших $K$ максимальный (при $m = {{\left( {K - 1} \right)} \mathord{\left/ {\vphantom {{\left( {K - 1} \right)} 2}} \right. \kern-0em} 2}$) диапазон изменений $z = 2\pi {{U}_{{m,K}}}f\theta $ в ${{\sim K} \mathord{\left/ {\vphantom {{\sim K} \pi }} \right. \kern-0em} \pi }$ раз больше существенного диапазона $2\pi f\theta $ или в $\sim 2K\theta $ раз больше существенного диапазона изменений частоты $f$. Последний определяется полушириной $~{{\chi }_{0}}\left( f \right)$ и в соответствии с (51) равен обратной полуширине ${{\hat {\rho }}_{0}}\left( s \right)$, т.е. ${{\beta }^{{ - 1}}}$. Другими словами, необходимо $M~\sim {{2K\theta } \mathord{\left/ {\vphantom {{2K\theta } \beta }} \right. \kern-0em} \beta }$ и, соответственно, $\hat {q}~\sim {{2\theta } \mathord{\left/ {\vphantom {{2\theta } \beta }} \right. \kern-0em} \beta }$. Обрывая соответствующий ряд на членах с $q = \hat {q} - 1$, получим следующую аппроксимацию для $W_{0}^{{\left( K \right)}}\left( f \right)$ (62) на интервале $\left| f \right| \leqslant {{\beta }^{{ - 1}}}$:

Подставляя полученные структурные блоки ${{\Psi }^{{\left( m \right)}}}\left( f \right)$ (61) в спектр $\Psi \left( f \right)$ (54), получим следующее его приближение, содержащее конечное число слагаемых в числителе/знаменателе:

Отметим, что при любом $K$, при $\theta \to 0$ рассматриваемый циклический точечный процесс вырождается в рекуррентный, а спектр (64) – в выражение:

которое совпадает с приведенным в [16] спектром стационарных рекуррентных процессов.

Несколько примеров $\Psi \left( f \right)$ (64) для$~K = 7$ и плотности ${{\hat {\rho }}_{0}}\left( s \right)$ гауссовской формы с ${{\bar {s}}_{0}} = 1$, $\beta = 0.02$ при нескольких значениях параметра вариабельности $Q = {{2\theta } \mathord{\left/ {\vphantom {{2\theta } {{{{\bar {s}}}_{0}}}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}}}$ представлены на рис. 1 (вырожденный случай $Q = 0$ соответствует рекуррентному процессу с теми же $K,{{\bar {s}}_{0}},\beta $).

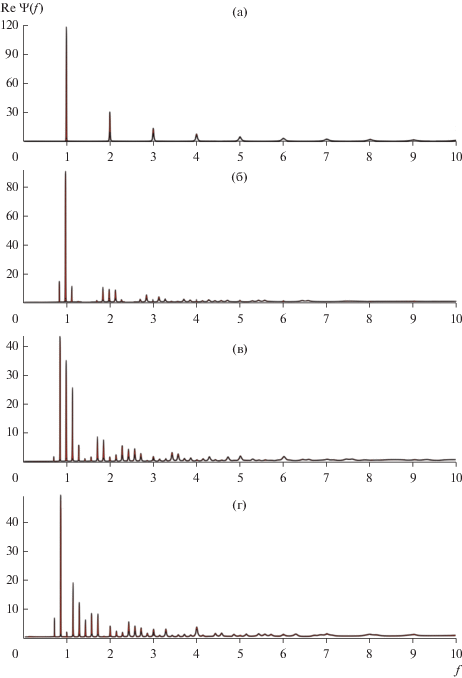
Поскольку, как отмечалось ранее, для действительных $f \ne 0$ имеет место $\left| {{{\chi }_{0}}\left( f \right)} \right| < 1$, можно разложить знаменатель (64) в ряд по $\chi _{0}^{K}\left( f \right)$ и получить разложение спектра $\Psi \left( f \right)$ по степеням ${{\chi }_{0}}\left( f \right)$:

где использована формальная периодичность $\left| {{{U}_{{m,K}}}} \right| = {{U}_{{\left( m \right){\text{mod}}K,K}}}$ по $m$.

Взяв от (66) обратное преобразование Фурье, получим согласно определению $\Psi \left( f \right)$ (53) функцию $b\left( t \right)$, являющуюся не сингулярной частью второго момента $\overline {x\left( {t{\kern 1pt} '} \right)x\left( {t{\kern 1pt} ''} \right)} $ (50) точечного циклического процесса:

где $R_{0}^{{\left( m \right)}}\left( t \right)$, так же как и $C_{j}^{{\left( k \right)}}\left( t \right)$ (22), – $m$-кратная свертка, но только плотности ${{\hat {\rho }}_{0}}\left( s \right)$ с собой. По существу, $R_{0}^{{\left( m \right)}}\left( t \right)$ представляет собой плотность распределения суммы $\left( {m + 1} \right)$ независимых, одинаково распределенных с ${{\hat {\rho }}_{0}}\left( s \right)$ случайных интервалов. В соответствии с этим $R_{0}^{{\left( m \right)}}\left( t \right)$ в (67) имеют форму положительных пиков ширины $\sim 2\sqrt {m + 1} ~\beta $, расположенных в точках ${{t}_{{m + 1}}} = \left( {m + 1} \right){{\bar {s}}_{0}}$. При увеличении номера $m$ форма пиков стремится к форме гауссовых распределений.

В выражении (67) звездочка * обозначает операцию свертки $R_{0}^{{\left( m \right)}}\left( t \right)$ c масштабированным на $\left| {{{U}_{{m,K}}}} \right|$ ядром $\Pi _{\theta }^{{\left( K \right)}}\left( \xi \right)$, представляющим собой обратное преобразование Фурье от спектрального окна $\hat {W}_{0}^{{\left( K \right)}}\left( f \right)$ :

где ${{T}_{{2qK}}}\left( \xi \right)$ – многочлены Чебышева первого рода (см. Приложение (П7)) .

Замечательным результатом является то, что ядро $\Pi _{\theta }^{{\left( K \right)}}\left( \xi \right)$ (68) есть финитная функция: его значения при $\left| \xi \right| \leqslant \theta $ задаются выражением (68), а вне этого отрезка ядро тождественно обращается в нуль. Несколько примеров ядер $\Pi _{\theta }^{{\left( K \right)}}\left( \xi \right)$ и их преобразований Фурье $\hat {W}_{0}^{{\left( K \right)}}\left( f \right)$ для$~K = 7$ и $\theta = 0.1$ при разных значениях параметра $\hat {q} = {{2\theta } \mathord{\left/ {\vphantom {{2\theta } \beta }} \right. \kern-0em} \beta }$ приведены на рис. 2.

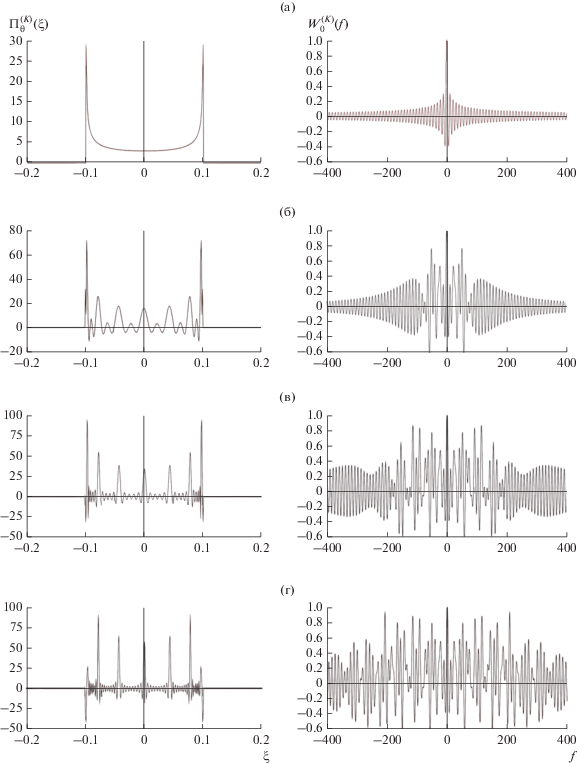
Согласно приведенному выше анализу, слагаемые ряда $b\left( t \right)$ (67) представляют собой свертки $R_{0}^{{\left( m \right)}}\left( t \right)$ с финитными функциями ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}} \times $ $ \times \,\,\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right)$, носители которых составляют отрезки $\left( { - \theta \left| {{{U}_{{m,K}}}} \right|;\theta \left| {{{U}_{{m,K}}}} \right|} \right)$. Результирующий ряд (67) по структуре отчасти напоминает ряд вырожденного (при $\theta \to 0$) рекуррентного процесса с плотностью распределения интервалов ${{\hat {\rho }}_{0}}\left( s \right)$, для которого согласно (65) $\tilde {b}\left( t \right)$ имеет вид

Ряд $\tilde {b}\left( t \right)$ (69) представлен эквидистантно расположенными в точках ${{t}_{{m + 1}}} = \left( {m + 1} \right){{\bar {s}}_{0}}$ пиками с монотонно возрастающей шириной ${\sim 2}\sqrt {m + 1} ~\beta $, как это было отмечено выше. Ввиду условия ${\beta \mathord{\left/ {\vphantom {\beta {{{{\bar {s}}}_{0}}}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}}} \ll 1$ пики с небольшими номерами $m$ будут изолированными. Они начнут заметно перекрываться начиная с номеров $m~\sim ~\hat {m} = {{\left( {{{{{{\bar {s}}}_{0}}} \mathord{\left/ {\vphantom {{{{{\bar {s}}}_{0}}} {2\beta }}} \right. \kern-0em} {2\beta }}} \right)}^{2}} \gg 1$, постепенно формируя постоянный асимптотический уровень ${{{\sim }1} \mathord{\left/ {\vphantom {{{\sim }1} {{{{\bar {s}}}_{0}}~}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}~}}$ на бесконечности.

Ряд общего циклического процесса $b\left( t \right)$ (67) также содержит пики вида $R_{0}^{{\left( m \right)}}\left( t \right),$ но только при $m = pK - 1$, в точках ${{t}_{{m + 1}}} = pK{{\bar {s}}_{0}},~$ $~p = 1,2, \ldots $ , ввиду ${{U}_{{m,K}}} \to 0$ и, соответственно, ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}} \times $ $ \times \,\,\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right) \to \delta \left( t \right)$. Однако в отличие от (69) в промежутках между этими пиками ($m \ne pK - 1$) соответствующие пики $R_{0}^{{\left( m \right)}}\left( t \right)$ из $b\left( t \right)$ (67) будут уширены на величину $\sim 2\theta \left| {{{U}_{{m,K}}}} \right|$ и деформированы за счет сглаживания с ядром ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}}\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right)$ (см. рис. 2), что при вариабельности интервалов ${{2\theta } \mathord{\left/ {\vphantom {{2\theta } {{{{\bar {s}}}_{0}}}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}}} > \pi {{K}^{{ - 1}}}$ приведет к их перекрытию еще до первого неискаженного пика $R_{0}^{{\left( {K - 1} \right)}}\left( t \right)$ (в основном в середине интервала $\left( {0;K{{{\bar {s}}}_{0}}} \right)$). Кроме того, деформация приводит к разбиению каждого из $R_{0}^{{\left( m \right)}}\left( t \right)$ пиков на несколько (вплоть до $K$) локальных пиков, что при их перекрытии ведет к усложнению картины $b\left( t \right)$ в промежутках между точками ${{t}_{{m + 1}}} = pK{{\bar {s}}_{0}}$. Ряд примеров $b\left( t \right)$ (67) для$~K = 7$ и плотности ${{\hat {\rho }}_{0}}\left( s \right)$ гауссовской формы с ${{\bar {s}}_{0}} = 1$, $\beta = 0.02$ при нескольких значениях параметра вариабельности $Q = {{2\theta } \mathord{\left/ {\vphantom {{2\theta } {{{{\bar {s}}}_{0}}}}} \right. \kern-0em} {{{{\bar {s}}}_{0}}}}$ представлены на рис. 3 (вырожденный случай $Q = 0$ соответствует рекуррентному процессу с теми же $K,{{\bar {s}}_{0}},\beta $).

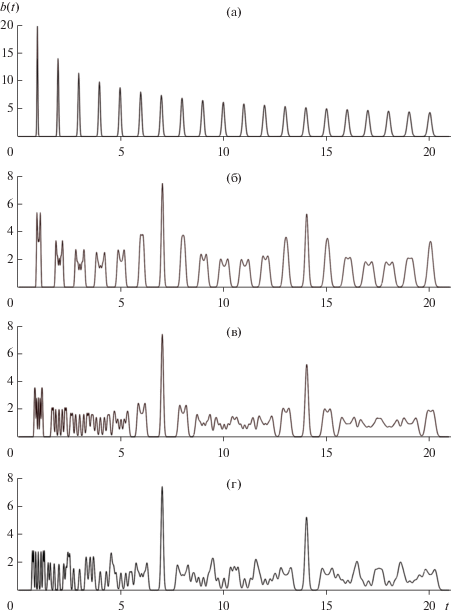
5. АНАЛИЗ ВРЕМЕННЫХ МАСШТАБОВ ИМПУЛЬСНЫХ ПРОЦЕССОВ НА ОСНОВЕ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ЦИКЛИЧЕСКИХ ТОЧЕЧНЫХ ПРОЦЕССОВ

Возвращаясь к исходной модели фрагмента импульсного сигнала $z\left( {t{\kern 1pt} '} \right)$ (1) и его статистическим моментам ${{m}_{t}}\left( {t{\kern 1pt} '} \right)$ и ${{R}_{t}}\left( {t{\kern 1pt} ',t''} \right)$ (5), подставим в них найденные выше выражения для $\overline {x\left( {t{\kern 1pt} '} \right)} $ (35) и 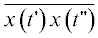(50):

В (70) для интеграла от формы импульса $g\left( {t{\kern 1pt} '} \right)$ в ${{m}_{t}}\left( {t{\kern 1pt} '} \right)$ использовано значение частотной характеристики $\gamma \left( f \right)$ (3) в нуле. Заметим, что перед формированием по измеренному сигналу некоторых оценок или представлений, подобных (70), он обычно подвергается предобработке. Последняя, как правило, включает в себя некоторую предварительную фильтрацию, обеспечивающую подавление медленных составляющих сигнала, в частности устранение постоянного уровня. Несложно показать, что в модели (1) результаты подобной фильтрации скажутся также на изменении формы импульсов ‒ новая форма $g\left( {t{\kern 1pt} '} \right)$ будет представлять из себя свертку старой формы с импульсной реакцией предварительного фильтра. В частотной области эта операция соответствует перемножению спектров, поэтому ввиду режекции низких частот предварительным фильтром будем иметь $\gamma \left( 0 \right) = 0$. В силу этого обстоятельства согласно (70) будем иметь ${{m}_{t}}\left( {t{\kern 1pt} '} \right) = \overline {z\left( {t{\kern 1pt} '} \right)} \equiv 0$, т.е. главным источником информации о сигнале $z\left( {t{\kern 1pt} '} \right)$ (1) в описанной ситуации становится 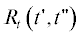. Для того чтобы наглядно связать структуру 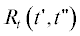с выявленной структурой вторых моментов подлежащих точечных циклических процессов $x\left( {t{\kern 1pt} '} \right)$, перейдем от переменных 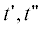к линейно связанным с ними $T,\tau $:

Роль весового окна 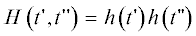в новых переменных легче оценить, если хотя бы приближенно разделить в нем переменные $T,\tau $: $H\left( {t{\kern 1pt} ',t{\kern 1pt} ''} \right) \approx U\left( T \right)u\left( \tau \right)$. Это можно сделать точно, например, в случае, когда окно $h\left( {t{\kern 1pt} '} \right)$ имеет гауссову форму:

В новых переменных представление сигнала ${\text{его}}$ вторым моментом 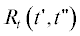(70) записывается в виде

где введена “автоковариация” формы импульса сигнала $\Gamma \left( \tau \right)$ ‒ квадратичная по $g\left( {t{\kern 1pt} '} \right)~$функция:

Как отмечалось выше, частотная характеристика $\gamma \left( f \right)$ имеет ширину $\Omega {\text{\;}}\sim {1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma }$. То же относится и к квадрату ее огибающей ${{\left| {\gamma \left( f \right)} \right|}^{2}}$. Соответственно, эффективная ширина $\Gamma \left( \tau \right)$ (73) совпадает по порядку величины с длительностью импульса ~2$\sigma $ ‒ с наименьшим временным масштабом сигнала $z\left( {t{\kern 1pt} '} \right)$ (1). Наоборот, функции $U\left( T \right)$ и $u\left( \tau \right)$, факторизующие $H\left( {t{\kern 1pt} ',t{\kern 1pt} ''} \right)$, имеют эффективную ширину ~2Σ, соответствующую наибольшему временному масштабу. Учитывая эти соотношения и тот факт, что $u\left( 0 \right) = 1$, запишем окончательное выражение для ${{\hat {R}}_{t}}\left( {T,\tau } \right)$ (72):

Как следует из (74), в данном “диагональном” представлении переменные $T$ и $\tau $ разделяются. Это позволяет связать структуру двумерного представления ${{\hat {R}}_{t}}\left( {T,\tau } \right)$ на интервале анализа $\left( {t - \Sigma ,t + \Sigma } \right)$ со структурой одномерного локального-стационарного представления ${{\hat {r}}_{t}}\left( \tau \right)$:

Как следует из (74), в ~$~\Sigma $-окрестности момента времени анализа $t$ представление сигнала ${{\hat {R}}_{t}}\left( {T,\tau } \right)$ с точностью до множителя $U\left( {T - t} \right) \approx 1$ определяется функцией ${{\hat {r}}_{t}}\left( \tau \right)$ (75), непосредственно связанной с функцией $b\left( t \right)$ (44), (67), задающей структуру второго момента точечного процесса $x\left( {t{\kern 1pt} '} \right)$. Именно, с точностью до слагаемого ${{\overline {{{A}^{2}}} \Gamma \left( \tau \right)} \mathord{\left/ {\vphantom {{\overline {{{A}^{2}}} \Gamma \left( \tau \right)} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$ представление ${{\hat {r}}_{t}}\left( \tau \right)$ есть результат последовательных линейных операций свертки с ядром $\Gamma \left( \tau \right)$ (73) и взвешивания с окном ${{{{{\bar {A}}}^{2}}u\left( \tau \right)} \mathord{\left/ {\vphantom {{{{{\bar {A}}}^{2}}u\left( \tau \right)} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$ над $b\left( {\left| t \right|} \right)$. Другими словами, ${{\hat {r}}_{t}}\left( \tau \right)$ представляет собой симметричный относительно нуля фрагмент длительности ~2Σ, сглаженной с окном (ядром) длительности ~2σ функции $b\left( {\left| t \right|} \right)$. Отметим, что при этом согласно (73) вся требуемая информация о форме импульса сигнала $g\left( {t{\kern 1pt} '} \right)$ содержится в огибающей ее частотной характеристики $\left| {\gamma \left( f \right)} \right|$ (в АЧХ). В частотной области соответствующая интерпретация (75) следующая: спектр ${{\hat {r}}_{t}}\left( \tau \right)$ с точностью до подстилающей ${{\overline {{{A}^{2}}} {{{\left| {\gamma \left( f \right)} \right|}}^{2}}} \mathord{\left/ {\vphantom {{\overline {{{A}^{2}}} {{{\left| {\gamma \left( f \right)} \right|}}^{2}}} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$ представляет собой взвешенную с окном ${{{{{\bar {A}}}^{2}}{{{\left| {\gamma \left( f \right)} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\bar {A}}}^{2}}{{{\left| {\gamma \left( f \right)} \right|}}^{2}}} {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$, сглаженную с ядром $\nu \left( f \right)$ длительности ~${1 \mathord{\left/ {\vphantom {1 \Sigma }} \right. \kern-0em} \Sigma }$ регулярную часть спектра $S\left( f \right)$ (57), где $\nu \left( f \right)$ ‒ частотная характеристика $u\left( \tau \right)$. Отметим, что в отличие от симметричного унимодального ядра $\nu \left( f \right)$ весовое окно и кратная ему подстилающая – пропорциональные ${{\left| {\gamma \left( f \right)} \right|}^{2}}$ функции, ввиду отмеченного условия $\gamma \left( 0 \right) = 0$, имеют максимумы в ненулевых симметричных частотах, определяемых колебательной составляющей формы импульса сигнала $g\left( {t{\kern 1pt} '} \right)$.

Более детальная характеризация структуры ${{\hat {R}}_{t}}\left( {T,\tau } \right)$, вытекающая из анализа ${{\hat {r}}_{t}}\left( \tau \right)$ (75), может быть осуществлена в рассмотренном выше частном случае циклических процессов с одинаковыми по форме, но различно расположенными на полуоси $s \geqslant 0$ плотностями $\left\{ {~{{{\hat {\rho }}}_{k}}\left( s \right)} \right\}$. Детализация структуры связана здесь с наличием у $b\left( {\left| t \right|} \right)$ дополнительных (помимо $\bar {s}$) временных параметров $\beta $ ‒ полуширины каждой из $\left\{ {~{{{\hat {\rho }}}_{k}}\left( s \right)} \right\},$ и $\theta $ ‒ половины размаха их расположений $\left\{ {~{{s}_{k}}} \right\}$. В наиболее интересном, рассмотренном выше случае, $\beta + \theta \ll \bar {s}$, особенности структуры ${{\hat {r}}_{t}}\left( \tau \right)$ (75) будут определяться соотношением между$~\sigma $ и $\beta ,\theta ,$ с одной стороны, и между самими $\beta $ и $\theta $ ‒ с другой.

Именно в случае $\beta > \theta $ циклический процесс по существу, как это выше отмечалось ($\theta \to 0$), вырождается в рекуррентный со структурой функции $b\left( t \right)$, задаваемой выражением (69). При этом представление ${{\hat {r}}_{t}}\left( \tau \right)$(75) принимает следующий вид:

где ${{R}^{{\left( m \right)}}}\left( t \right)$ являются результатом свертки $R_{0}^{{\left( m \right)}}$ и $\Gamma \left( \tau \right)$ (73). Другими словами, при $\beta > \sigma $ практически ${{R}^{{\left( m \right)}}}\left( t \right) \approx R_{0}^{{\left( m \right)}}$ и второе, содержательное слагаемое в ${{\hat {r}}_{t}}\left( \tau \right)$ (76) имеет структуру второго момента связанного рекуррентного точечного процесса. В противном случае $\beta < \sigma ,$ пики ${{R}^{{\left( m \right)}}}\left( t \right)$ до номеров $m\sim {{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma \beta }} \right. \kern-0em} \beta }} \right)}^{2}}$ практически имеют форму $\Gamma \left( t \right)$ и только затем ${{R}^{{\left( m \right)}}}\left( t \right) \approx R_{0}^{{\left( m \right)}}.$ Отметим также, что за счет весового окна $u\left( \tau \right)$ на самом деле количество пиков ${{R}^{{\left( m \right)}}}\left( t \right)$ в ${{\hat {r}}_{t}}\left( \tau \right)$ конечно и равно ~${\Sigma \mathord{\left/ {\vphantom {\Sigma {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$.

В другом случае $\beta < \theta $, подставляя выражение $b\left( t \right)$ (67) в ${{\hat {r}}_{t}}\left( \tau \right)$(75), получим

где $\Delta _{\theta }^{{\left( K \right)}}\left( t \right)$ является сверткой финитных ядер ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}}\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right)$ и $\Gamma \left( \tau \right)$ (73). При $\theta > \sigma $ сглаженные ядра $~\Delta _{\theta }^{{\left( K \right)}}\left( t \right)$ практически совпадают с ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}}\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right)$ (небольшая модификация может касаться коррекции величины $\hat {q}~$ в (63) при $\beta < \sigma $: вместо ${{2\theta } \mathord{\left/ {\vphantom {{2\theta } \beta }} \right. \kern-0em} \beta }$ целесообразно использовать ${{2\theta } \mathord{\left/ {\vphantom {{2\theta } \sigma }} \right. \kern-0em} \sigma }$). При $\theta < \sigma ~$ функция автоковариации $\Gamma \left( \tau \right)$ полностью размоет структуру ядер ${{\left| {{{U}_{{m,K}}}} \right|}^{{ - 1}}}\Pi _{\theta }^{{\left( K \right)}}\left( {{t \mathord{\left/ {\vphantom {t {\left| {{{U}_{{m,K}}}} \right|}}} \right. \kern-0em} {\left| {{{U}_{{m,K}}}} \right|}}} \right)$ и данный случай будет практически не отличим от вырожденного случая $\beta > \theta $ при $\beta < \sigma $. Повторим еще раз, что здесь, так же как и ранее, за счет весового окна $u\left( \tau \right)$ количество пиков $\Delta _{\theta }^{{\left( K \right)}}\left( t \right){\text{*}}R_{0}^{{\left( m \right)}}\left( t \right)$ в ${{\hat {r}}_{t}}\left( \tau \right)$ конечно и равно ~${\Sigma \mathord{\left/ {\vphantom {\Sigma {\bar {s}}}} \right. \kern-0em} {\bar {s}}}$.

ЗАКЛЮЧЕНИЕ

Оценивая итоги изложенных выше рассмотрений, хотелось бы отметить следующее. Как нам представляется, разработка ${{L}_{2}}$ теории (стационарных) циклических точечных процессов с ограниченным последействием может считаться на данный момент полностью выполненной. Именно, для общих циклических процессов в явном виде получены аналитические выражения первого и второго статистических моментов, также получена аналитическая формула спектра второго момента. Для локального описания циклического точечного процесса найдены его одно- и двумерные плотности распределения моментов времени точек (событий) процесса. Определены подобные функции восстановления в теории рекуррентных процессов, структурные функции теории циклических точечных процессов, такие как $C_{j}^{{\left( k \right)}}\left( t \right)~$ (22), $D_{j}^{{\left( k \right)}}\left( t \right)$ (29), ${{c}_{j}}\left( t \right),~{{d}_{j}}\left( t \right)$ (42) и $b\left( t \right)$ (44).

Другими словами, полностью разработан инструментарий для исследования в рамках ${{L}_{2}}$ теории циклических точечных процессов практически всех теоретических аспектов, известных в рамках соответствующей теории рекуррентных процессов.

Приведенный в работе детальный анализ важного частного случая циклических процессов ‒ случая, в котором плотности распределения длительностей интервалов имеют одинаковую форму, но различаются расположениями, – открывает дорогу к применению разработанной теории в целом ряде приложений. В частности, отдельные элементы теории ранее были использованы для анализа сигналов ЭКГ на предмет оценки вариабельности сердечного ритма. В работах [8–11] изложен ряд результатов этих исследований, касающиеся дифференциации ЭКГ-записей без существенных аритмий или каких-либо других нарушений сердечного ритма и записей пациентов с гипертонической болезнью и высоким риском развития сосудистых событий. Полученные результаты позволяют выразить осторожный оптимизм также и в отношении перспектив развития прикладных аспектов разработанной теории.