Радиотехника и электроника, 2021, T. 66, № 11, стр. 1133-1139
Параметрическая накачка магнонов в гибридном магнон-фононном резонаторе
Н. И. Ползикова a, *, С. Г. Алексеев a, А. О. Раевский b
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
* E-mail: polz@cplire.ru
Поступила в редакцию 12.06.2021
После доработки 12.06.2021
Принята к публикации 21.06.2021
Аннотация
Рассмотрены условия параметрической неустойчивости магнонов под действием чисто упругой накачки, представляющей собой моды составного резонатора акустических волн, содержащего пленки ферримагнетика и пьезоэлектрика на монокристаллической подложке. Электрическое возбуждение объемных акустических волн происходит за счет пьезоэффекта (в пленке ZnO) на резонансных частотах резонатора fn. В магнитоупорядоченном слое (в пленке железоиттриевого граната) акустические моды при превышении пороговой мощности возбуждают магноны на частотах fn/2. Показано, что в случае накачки поперечными акустическими модами величина порога в несколько десятков раз меньше, чем в случае накачки продольными модами и составляет примерно 100 мкВт, что согласуется с экспериментальными данными.
ВВЕДЕНИЕ
В последнее время наблюдается значительный интерес к процессам взаимодействия акустических волн (как поверхностных, так и объемных) с электронами, магнонами, квантовыми кубитами и другими квазичастицами и квантовыми объектами в различных микро и наноструктурах [1–7]. Явления, связанные с магнон-фононным взаимодействием, описанным более полувека назад [8–10], являются весьма важными, если не ключевыми, для современных областей микро- и наноэлектроники, таких как как стрэйнтроника, спиновая калоритроника, микрорезонаторная магномеханика и др.
Одним из важнейших следствий магнитоупругой связи является возможность возбуждения спиновых волн (СВ), как линейного, так и параметрического, с помощью акустических волн (АВ), а не переменного магнитного поля и создающих его токов [8–11]. Это позволяет существенно снизить омические потери в низкоэнергетических гибридных магнон-фононных устройствах микроволновой спинтроники и магноники [1–3, 12–18]. Далее мы будем называть возбужденные таким образом спиновые волны акустическими или ADSW (Acoustically Driven Spin Waves) [19]. В структурах, содержащих пьезоэлектрические (ПЭ) и ферро(ферри)магнитные (ФМ) слои, ADSW возбуждаются с помощью переменного электрического поля за счет пьезоэффекта и магнитострикции в соответствующих слоях.
Ранее [19–22] мы экспериментально продемонстрировали ПЭ-возбуждение как линейных, так и параметрических ADSW в гибридном резонаторе объемных АВ, а также электрическое детектирование ADSW с помощью эффектов спиновой накачки (СН) [23] и обратного спинового эффекта Холла (Inverse Spin Hall Effect – ISHE) [24]. В гиперзвуковом резонаторе объемных волн (High overtone Bulk Acoustic wave Resonator – HBAR) в качестве преобразователя АВ использовалась ПЭ-пленка окиси цинка ZnO, магнитоупорядоченной системы – ФМ-пленки железоиттриевого граната (ЖИГ) на подложке из галлий-гадолиниевого граната граната (ГГГ), а в качестве детектора – тонкая полоска Pt, нанесенная на свободную пленку ЖИГ. Теоретическое описание особенностей линейного магнитоупругого взаимодействия в таком композитном резонаторе было приведено в работах [19, 21].
В данной работе рассмотрены условия параметрической неустойчивости магнонов под действием акустической накачки, представляющей собой моды описанного выше резонатора. Приводится сравнение величин порогов для случаев накачки продольными и поперечными акустическими волнами. Показано, что подаваемая на резонатор пороговая СВЧ-мощность в случае продольных волн в несколько десятков раз выше, чем в случае поперечных волн. В последнем случае оценка величины порога согласуется с наблюдавшейся в работе [22].
1. СТРУКТУРА РЕЗОНАТОРА И ЕГО ХАРАКТЕРИСТИКИ
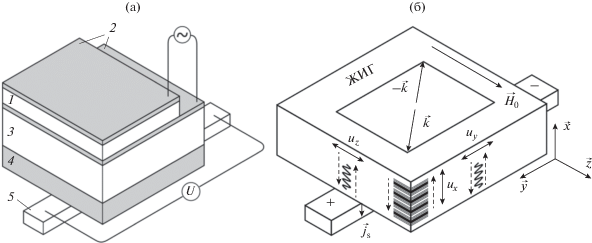
На рис. 1а представлена схема рассматриваемой структуры HBAR, соответствующая экспериментальному образцу из работы [22]. Преобразователь, включенный во внешнюю электрическую цепь, за счет прямого и обратного пьезоэффекта в пленке ZnO 1 возбуждает и регистрирует объемные АВ, распространяющиеся по толщине и отражающиеся как от свободных границ структуры, так и от границ разных слоев. Когда частота f подаваемого на электроды 2 СВЧ-напряжения соответствует одной из резонансных частот структуры fn, амплитуды всех отраженных волн складываются в фазе и формируется стоячая волна. Если пренебречь отраженными волнами на границах многослойной структуры (отличием акустических импедансов слоев [25, 26]), то резонансные частоты могут быть оценены из условия
(1)
$\theta = {{2\pi {{f}_{n}}D} \mathord{\left/ {\vphantom {{2\pi {{f}_{n}}D} {{{V}_{{{\text{эф}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{эф}}}}}}} = \pi n,\,\,\,\,n = 1,~2, \ldots ~,~1000,~ \ldots ~,$Рис. 1.
Схема (не в масштабе) структуры гибридного магнон-фононного HBAR (a) и направления основных векторов относительно декартовой системы координат (x, y, z) и слоев ЖИГ и Pt (б). Принятые обозначения: 1 – пленка ZnO, 2 – электроды СВЧ-напряжения, 3 – ГГГ, 4 – слой ЖИГ, 5 – слой Pt, двойные стрелки – направления поляризации в АВ, штриховые – направления распространения толщинных АВ с частотой f и с волновыми векторами $ \pm {{\vec {\xi }}_{x}},$ векторы $ \pm \vec {k}$ показывают латеральные компоненты квазиимпульсов параметрических магнонов на частоте f/2 (вырожденный случай параметрической накачки).
которое означает, что в результате распространения фронта АВ по всей толщине структуры $D = \sum\nolimits_i {{{l}_{i}}} $ c эффективной фазовой скоростью Vэф = $ = {{\left( {\sum\nolimits_k {{{l}_{k}}{{V}_{k}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_k {{{l}_{k}}{{V}_{k}}} } \right)} D}} \right. \kern-0em} D}$ полный набег фазы θ кратен π [27]. Здесь ${{l}_{k}}$ и ${{V}_{k}}$ – толщины и фазовые скорости для каждого из слоев структуры с номером k, n – номер обертона. При этом для типичных толщин $D$ ~ 500 мкм, определяемых в основном толщинами подложки, и гигагерцовых резонансных частот fn, наиболее интересных для магнитоакустики, номера обертонов лежат в диапазоне $n~~$ ~ ~ 102…103.
Основной характеристикой HBAR является частотная зависимость входного электрического импеданса преобразователя или связанного с ним и измеряемого в эксперименте комплексного коэффициента отражения ${{S}_{{11}}}\left( f \right).$ Типичная зависимость $\left| {{{S}_{{11}}}\left( f \right)} \right|$ имеет вид гребенки с основанием ${{\left| {{{S}_{{11}}}\left( f \right)} \right|}_{0}}\sim 1$ и квазиэквидистантными провалами с глубиной ${{\left| {{{S}_{{11}}}\left( f \right)} \right|}_{0}} - \left| {{{S}_{{11}}}\left( {{{f}_{n}}} \right)} \right|$ на частотах ${{f}_{n}}.$ В зависимости от того, как расположены активные пьезоэлектрические направления (для текстурированной ПЭ-пленки это ось текстуры $~\vec {c}$) относительно нормали к слоям структуры, преобразователь может возбуждать либо продольные волны со смещением $~{{\vec {u}}^{L}} = \left( {{{u}_{x}},0,~0} \right),$ если $\vec {c}\parallel \vec {x},$ либо сдвиговые со смещением, ${{\vec {u}}^{S}} = \left( {0,{{u}_{y}},{{u}_{z}}} \right),$ если ось $\vec {c}$ наклонена по отношению к нормали на определенный угол. На практике возбуждение продольных волн всегда сопровождается возбуждением поперечных, и наоборот. Однако области эффективного возбуждения продольных и сдвиговых мод лежат в различных частотных диапазонах, а межмодовые расстояния $f_{{n + 1,~m + 1}}^{{L,S}} - f_{{n,~m}}^{{L,S}}$ = ${{V_{{{\text{эф}}}}^{{L,S}}} \mathord{\left/ {\vphantom {{V_{{{\text{эф}}}}^{{L,S}}} {2D}}} \right. \kern-0em} {2D}}$ отличаются почти в два раза, поскольку, как правило, $~V_{{{\text{эф}}}}^{L} \approx 2V_{{{\text{эф}}}}^{S}.$ Таким образом, в ряде задач можно рассматривать отдельно продольные и сдвиговые моды, что мы и будем делать в дальнейшем. Типичные широкополосные (в диапазоне частот 0.5…6 ГГц) экспериментальные и теоретические спектры композитных акустомагнитных HBAR, а также их детальное обсуждение приведены, в частности, в работах [22, 26, 28].
Далее будем считать, что в плоскости слоев приложено внешнее магнитное поле ${{\vec {H}}_{0}} = \left( {0,~0,~{{H}_{0}}} \right),$ которое намагничивает пленки ЖИГ до насыщения, и намагниченность насыщения есть ${{\vec {M}}_{0}} = \left( {0,~0,~{{M}_{0}}} \right).$ Примем, что приведенные на рис. 1б оси $\vec {x},\vec {y},\vec {z},$ совпадают с кристаллографическими кубическими осями как в ГГГ, так и в ЖИГ. Вследствие магнитоупругого взаимодействия в пленке ЖИГ акустические колебания могут возбуждать ADSW. При этом эффективная генерация линейных ADSW происходит на резонансных частотах fn при выполнении условий синхронизма акустической и спиновой волн (магнитоупругий резонанс, МУР [8]) в соответствующем магнитном поле ${{H}_{0}} = {{H}_{{{\text{МУР}}}}}.$ В данной работе мы будем рассматривать только область полей, в которых возможно возбуждение параметрических ADSW на половинной частоте акустической накачки fn/2. При той же частоте возбуждения АВ эти поля лежат ниже поля HМУР и ограничены снизу только полем насыщения.
На рис. 1 также показана схема детектирования как линейных, так и параметрических ADSW с использованием эффектов спиновой накачки (генерации спинового тока ${{\vec {j}}_{s}}$) и ISHE, которая применялась в работах [20, 22]. Постоянное напряжение U, возникающее на разомкнутых концах полоски Pt 5, оказывается мерой числа возбужденных магнонов в пленке ЖИГ (строго говоря, на границе ЖИГ/Pt), причем как линейных, так и параметрических [18]. Расположение полоски обеспечивает наилучшие условия детектирования магнитной динамики, когда электрическое поле ISHE оказывается параллельным ее длинной стороне.
2. МАГНИТОУПРУГАЯ ЭНЕРГИЯ, УПРУГАЯ НАКАЧКА
Описанная выше геометрия структуры была выбрана с учетом свойств симметрии пьезоэлектрического, магнитоупругого и спин-орбитального механизмов взаимодействия квазичастиц. Центральное место в комбинации этих механизмов занимает явление магнитоупругости, обусловленное зависимостью энергии магнитной кристаллической анизотропии от тензора деформации
где i и j принимают значения x, y, z. Магнитоупругий (МУ) вклад в энергию ${{W}^{{{\text{МУ}}}}}$ имеет вид [8]
(2)
${{W}^{{{\text{МУ}}}}} = \int {\left[ {\frac{{{{B}_{1}}}}{{M_{s}^{2}}}\left( {M_{x}^{2}{{u}_{{xx}}} + M_{y}^{2}{{u}_{{yy}}} + M_{z}^{2}{{u}_{{zz}}}} \right) + \frac{{2{{B}_{2}}}}{{M_{s}^{2}}}\left( {{{M}_{x}}{{M}_{y}}{{u}_{{xy}}} + ~~{{M}_{x}}{{M}_{z}}{{u}_{{xz}}} + {{M}_{y}}{{M}_{z}}{{u}_{{yz}}}} \right)} \right]} \,dV.$Здесь B1,2 – константы МУ-связи, ${{M}_{i}}$ – компоненты вектора намагниченности $\vec {M} = {{\vec {M}}_{0}}~\, + \vec {m},$ $\vec {m} = \left( {{{m}_{x}},~{{m}_{y}},{{m}_{z}}} \right)$ – переменная намагниченность, V – объем.
Обсудим особенности параметрической генерации магнонов за счет упругой накачки в нашей структуре. Уравнение Ландау–Лифшица для прецессии намагниченности $\vec {M}$ и уравнение Ньютона для упругого смещения $\vec {u}~$ в среде с плотностью ρ имеют вид
(4)
$\rho \frac{{{{\partial }^{2}}{{u}_{i}}}}{{\partial {{t}^{2}}}} = \frac{{\partial {{T}_{{ij}}}}}{{\partial {{x}_{j}}}}.$Здесь эффективные поле $\vec {H}$ и упругое напряжение ${{T}_{{ij}}}$ находятся через вариационные производные от полной энергии и, соответственно, содержат следующие МУ-вклады:
(5)
$\begin{gathered} {{{\vec {H}}}^{{{\text{МУ}}}}} = {{ - \,\delta {{W}^{{{\text{МУ}}}}}} \mathord{\left/ {\vphantom {{ - \,\delta {{W}^{{{\text{МУ}}}}}} {\delta \vec {M}}}} \right. \kern-0em} {\delta \vec {M}}}, \\ T_{{ij}}^{{{\text{МУ}}}} = \left( {{{\delta {{W}^{{{\text{МУ}}}}}} \mathord{\left/ {\vphantom {{\delta {{W}^{{{\text{МУ}}}}}} {\delta {{u}_{{ij}}}}}} \right. \kern-0em} {\delta {{u}_{{ij}}}}}} \right){{\left( {1 + {{\delta }_{{ij}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {{\delta }_{{ij}}}} \right)} 2}} \right. \kern-0em} 2}, \\ \end{gathered} $где ${{\delta }_{{ij}}}$ – символ Кронеккера.
Поскольку мы рассматриваем упругую подсистему как накачку, то будем пренебрегать обратным действием на нее параметрических ADSW, полагая $T_{{ij}}^{{{\text{МУ}}}} = 0.$ Тогда для МУ-вклада в эффективное поле из (2) и (5) получаем
(6)
$H_{x}^{{{\text{МУ}}}} = ~\left( { - \frac{2}{{M_{0}^{2}}}} \right)\,~\left[ {{{B}_{1}}{{u}_{{xx}}}{{m}_{x}} + ~{{B}_{2}}\left( {{{u}_{{xy}}}{{m}_{y}} + {{u}_{{xz}}}{{M}_{{\text{0}}}}} \right)} \right],$(7)
$H_{y}^{{{\text{МУ}}}} = ~\left( { - \frac{2}{{M_{0}^{2}}}} \right)\,~\left[ {{{B}_{1}}{{u}_{{yy}}}{{m}_{y}} + ~{{B}_{2}}\left( {{{u}_{{xy}}}{{m}_{x}} + {{u}_{{yz}}}{{M}_{{\text{0}}}}} \right)} \right],$(8)
$H_{z}^{{{\text{МУ}}}} = ~\left( { - \frac{2}{{{{M}_{{\text{0}}}}}}} \right)\left[ {{{B}_{1}}{{u}_{{zz}}} + {{B}_{2}}\left( {{{u}_{{xz}}}{{m}_{x}} + {{u}_{{yz}}}{{m}_{y}}} \right)} \right].$Ограничимся случаем сравнительно малых колебаний, для которых справедливо условие сохранения длины вектора намагниченности $\left| {\vec {M}} \right| = {{M}_{0}}.$ При этом в уравнении (8) следует оставить только первый член в квадратных скобках, пропорциональный ${{B}_{1}}.$
Из уравнений (6)–(8) видно, что действие упругой накачки существенно зависит от ее поляризации и в целом не сводится к эффективному полю (продольному, либо поперечному), аналогичному полю электромагнитной накачки. Это обусловлено тем, что МУ-энергия (2) квадратична по намагниченности, а зеемановская энергия взаимодействия с переменным магнитным полем накачки линейна по намагниченности [17].
Рассмотрим возможность упругой параметрической накачки за счет различных компонент тензора деформации. При этом ограничимся параметрическими процессами первого порядка и используем упрощенный подход, аналогичный работам [9, 10]. А именно, будем рассматривать однородную упругую накачку c поляризацией, зависящей от времени и координат, как
где ωp = 2πfр, – частота накачки, а к.с. означает комплексное сопряжение. Волновой вектор волны накачки $\vec {\xi } = {{\vec {\xi }}_{x}} + {{\vec {\xi }}_{\parallel }}$ в общем случае имеет как нормальную, так и тангенциальную компоненты относительно слоев структуры: ${{\vec {\xi }}_{x}}$ и ${{\vec {\xi }}_{\parallel }}.$ Будем рассматривать только трехчастичные процессы распада одного фонона волны накачки на два магнона с частотами $\omega \left( {{{{\vec {q}}}_{1}}} \right),$ $\omega \left( {{{{\vec {q}}}_{2}}} \right)$ и квазиимпульсами $~{{\vec {q}}_{{1,2}}} = {{\vec {q}}_{{1x,2x}}} + {{\vec {k}}_{{1,2}}}.$ Законы сохранения энергии и квазиимпульса, связанные с временной и трансляционной симметрией, накладывают соответствующие условия:
(9)
$\omega \left( {{{{\vec {q}}}_{1}}} \right) + \omega \left( {{{{\vec {q}}}_{2}}} \right) = ~~{{\omega }_{p}},\,\,\,\,{{\vec {k}}_{1}} + {{\vec {k}}_{2}} = {{\vec {\xi }}_{\parallel }}.$Отметим, что в ограниченном по толщине образце закон сохранения квазиимпульса должен выполняться для компонент, лежащих в плоскости пленки ${{\vec {k}}_{{1,2}}},$ но не для компонент по толщине ${{\vec {q}}_{{1x,2x~}}},$ поскольку в направлении Ox отсутствует трансляционная симметрия [9, 17].
Для нахождения пороговых амплитуд фононной накачки с теми или иными компонентами тензора деформации используется традиционный метод. Исходные уравнения (3), записанные для компонент намагниченности mx, my, сводятся к уравнениям для связанных осцилляторов, которыми в данном случае являются СВ с волновыми векторами ${{\vec {q}}_{1}}$ и ${{\vec {q}}_{2}}.$ Затухание СВ учитывается с помощью замены
где ${{\Delta }}H\left( {{{{\vec {q}}}_{{1,2}}}} \right)$ – феноменологический параметр релаксации. Решение указанных уравнений ищется в виде колебаний с частотами $\omega \left( {{{{\vec {q}}}_{1}}} \right)$ и $\omega \left( {{{{\vec {q}}}_{2}}} \right)$ и медленно меняющимися по времени амплитудами $ \propto {\text{exp}}\left( { - {{\Gamma }}t} \right),$ где ${{\Gamma }}$ – вещественная величина. При определенной пороговой амплитуде накачки может произойти смена знака этой величины, что приводит к экспоненциальному росту амплитуд СВ.
Далее будем считать, что накачка создает только одну отличную от нуля компоненту тензора деформации ${{u}_{{ij}}},$ т.е. вектор поляризация накачки ${{\vec {u}}_{0}}$ и волновой вектор накачки $\vec {\xi }$ направлены каждый по одной из осей – $\vec {x}$, $\vec {y}$ или $\vec {z}$. При этом их направления могут совпадать (тогда волна будет продольной – L) или быть перпендикулярными (тогда волна будет сдвиговой – S). Для безграничной среды компоненты волновых векторов находятся из дисперсионных уравнений $\xi _{i}^{{L,S}} = {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} {V_{i}^{{L,S}}}}} \right. \kern-0em} {V_{i}^{{L,S}}}},$ где $V_{i}^{{L,S}}$ – скорости продольной или сдвиговой волны в направлении i = x, y, z. Для слоев конечной толщины можно говорить о квази-L- или квази-S-модах, поскольку строгое разделение на чисто продольные и чисто сдвиговые моды в общем случае не происходит даже в изотропном приближении.
3. ПОРОГОВЫЕ УПРУГИЕ СМЕЩЕНИЯ ДЛЯ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ ВОЛН НАКАЧКИ
Продольные волны. Начнем с наиболее простого типа накачки в виде продольной волны плотности, поляризованной в направлении постоянной намагниченности:
В этом случае действие упругой накачки, создающей деформацию
(10)
${{u}_{{zz}}} = - i\xi _{z}^{L}{{\left[ {u_{{0z}}^{L}{\text{exp}}\left( {i{{\omega }_{p}}t - i\xi _{z}^{L}z} \right) - {\text{к}}{\text{.с}}.} \right]} \mathord{\left/ {\vphantom {{\left[ {u_{{0z}}^{L}{\text{exp}}\left( {i{{\omega }_{p}}t - i\xi _{z}^{L}z} \right) - {\text{к}}{\text{.с}}.} \right]} 2}} \right. \kern-0em} 2},$аналогично действию продольной электромагнитной накачки, т.е. сводится к продольному эффективному магнитному полю (8), колеблющемуся с частотой ωp. Продольная акустическая накачка была описана в работах [9, 10]. Минимальное пороговое поле ${{h}_{{{\text{пор}}}}} = \left| {H_{z}^{{{\text{MУ}}}}} \right|$ соответствует возбуждению пары магнонов с $\omega \left( {{{{\vec {q}}}_{1}}} \right) = ~\omega \left( {{{{\vec {q}}}_{2}}} \right) = {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} 2}} \right. \kern-0em} 2}$ и ${{\vec {q}}_{1}} = - {{\vec {q}}_{2}},$ а для порогового упругого смещения получается выражение
(11)
$\left| {u_{{0z}}^{L}} \right| = \frac{{{{f}_{{{\text{p\;}}}}}\Delta {{H}_{q}}}}{{4\pi \gamma {{B}_{1}}\xi _{z}^{L}{\text{si}}{{{\text{n}}}^{2}}{{\theta }}}}.$Здесь $\Delta {{H}_{q}} \equiv {{\Delta }}H\left( {{{{\vec {q}}}_{{1,2}}}} \right)~$ – параметр диссипации, определяемый полной шириной резонансной кривой для доминантной группы магнонов с квазиимпульсом ${{\vec {q}}_{1}}$ и ${{\vec {q}}_{2}},$ направленными под углами ${{\theta }}$ и $\pi ~\,\, - \,\,{{\theta }}$ к направлению статической намагниченности.
Перейдем теперь к случаям накачки продольными акустическими волнами, распространяющимися перпендикулярно намагниченности либо в направлении [100] (${{\xi }_{{y,z}}} = 0,~~$uxx ≠ 0), либо вдоль направления [010] (${{\xi }_{{x,z}}} = 0,~~$uyy ≠ 0). Соответствующие деформации имеют вид
Для пороговых величин смещений получаем следующие выражения:
(12a)
$\left| {u_{{0x}}^{L}} \right| = \frac{{{{M}_{{0~}}}\Delta {{H}_{q}}}}{{{{B}_{1}}\xi _{x}^{L}}},$(12б)
$\left| {u_{{0y}}^{L}} \right| = \frac{{{{M}_{{0~}}}\Delta {{H}_{q}}}}{{{{B}_{1}}\xi _{y}^{L}}}~.$Поперечные волны. Как видно из уравнений (6)–(8), поперечные волны накачки, поляризованные перпендикулярно направлению распространения, влияют на динамику намагниченности через поперечные эффективные поля. При этом только поперечные волны накачки с поляризациями и волновыми векторами, перпендикулярными постоянной намагниченности, дают вклад в эффективное поле $H_{{x,y}}^{{{\text{MУ}}}} = - \frac{2}{{M_{0}^{2}}}~{{B}_{2}}{{u}_{{xy}}}{{m}_{{y,x}}},$ приводящий к параметрической неустойчивости. В частности, для волн с $\vec {\xi } = \vec {\xi }_{x}^{{~S}}$ либо с $~\vec {\xi } = \vec {\xi }_{y}^{{~S}}$ и с соответствующими поляризациями –
либо
пороговые смещения находятся из формул [9]
(13a)
$\left| {u_{{0y}}^{S}} \right| = \frac{{{{M}_{{0~}}}\Delta {{H}_{q}}}}{{{{B}_{2}}\xi _{x}^{S}}},$(13б)
$\left| {u_{{0x}}^{S}} \right| = \frac{{{{M}_{{0~}}}\Delta {{H}_{q}}}}{{{{B}_{2}}\xi _{y}^{S}}}.$Что же касается сдвиговых волн, поляризованных в направлении поля и создающих деформации $~{{u}_{{zx}}}$ либо ${{u}_{{zy}}},$ то их вклад в поперечные компоненты эффективного поля (6), (7) приводит только к перенормировке частоты спиновых волн, но не влияет на величину затухания Г.
Возвращаясь к нашей резонаторной структуре (см. рис. 1а), напомним, что накачкой являются толщинные моды многослойного резонатора, т.е. волны распространяются преимущественно перпендикулярно слоям структуры и, следовательно, $\xi _{{y,z}}^{{L,~S}} \ll \xi _{x}^{{L,~S}}.$ Поэтому согласно (11) и (12) среди продольных волн наименьшим пороговым смещением $\left| {u_{{0x}}^{L}} \right|$ обладает волна плотности, схематически представленная штриховкой на рис. 1б. Среди поперечных волн наименьшим пороговым смещением $\left| {u_{{0y}}^{S}} \right|~$ также обладает волна накачки, распространяющаяся по толщине структуры. Поэтому далее будем обсуждать только толщинные моды накачки с волновыми числами
(14)
${{\xi }^{{L,~S}}} \approx \xi _{x}^{{L,~S}} = {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} {{{V}^{{L,S}}}}}} \right. \kern-0em} {{{V}^{{L,S}}}}}.$Сравним теперь величины пороговых смещений для квазипродольной и квазисдвиговой мод. Отношение пороговых смещений находится из (12а), (13а) и (14) в виде
(15)
$~{{R}_{u}} = {{\left| {u_{{0x}}^{L}} \right|} \mathord{\left/ {\vphantom {{\left| {u_{{0x}}^{L}} \right|} {\left| {u_{{0y}}^{S}} \right|}}} \right. \kern-0em} {\left| {u_{{0y}}^{S}} \right|}} = \left( {{{{{B}_{2}}} \mathord{\left/ {\vphantom {{{{B}_{2}}} {{{B}_{1}}}}} \right. \kern-0em} {{{B}_{1}}}}} \right)\left( {{{{{V}^{L}}} \mathord{\left/ {\vphantom {{{{V}^{L}}} {{{V}^{S}}}}} \right. \kern-0em} {{{V}^{S}}}}} \right).$При этом считается, что параметры магнитного затухания $\Delta {{H}_{q}}$ не зависят от поляризации накачки. Для характерных магнитоупругих параметров пленок ЖИГ, приведенных в табл. 1, получаем ${{{{B}_{2}}} \mathord{\left/ {\vphantom {{{{B}_{2}}} {{{B}_{1}}}}} \right. \kern-0em} {{{B}_{1}}}} \approx 2,$ ${{{{V}^{L}}} \mathord{\left/ {\vphantom {{{{V}^{L}}} {{{V}^{S}}}}} \right. \kern-0em} {{{V}^{S}}}} \approx 2$ и, следовательно, ${{R}_{u}} \approx 4.$
Таблица 1.
Параметры пленок ЖИГ [29], использованные в расчетах
| ρ, 103 кг/м3 | VL, 103 м/с | VS, 103 м/с | 4πM0, Гс | ${{B}_{1}},$ 106 эрг/cм3 | ${{B}_{2}},$ 106 эрг/cм3 | $\Delta {{H}_{q}},$ Э | |
|---|---|---|---|---|---|---|---|
| легированный Ga, La | чистый ЖИГ | ||||||
| 5.18 | 7.2 | 3.85 | 845 [22] | 1750…1770 | 6.96 | 3.48 | 0.25 |
4. ПОРОГОВЫЕ МОЩНОСТИ АКУСТИЧЕСКОЙ НАКАЧКИ
На практике вместо амплитуд волны накачки целесообразно бывает оценивать их мощности. После подстановки выражений (12а), (13а) и (14) в соотношение Умова–Пойнтинга пороговые мощности накачки $~{{P}^{S}}$ и ${{P}^{L}}$ на единицу площади $A$ акустического потока могут быть найдены в виде
(16)
$\begin{gathered} {{{{P}^{S}}} \mathord{\left/ {\vphantom {{{{P}^{S}}} A}} \right. \kern-0em} A} = \rho {{V}^{S}}{{\left( {2\pi {{f}_{{{\text{p}}~}}}} \right)}^{2}}\frac{{{{{\left| {u_{{0x}}^{S}} \right|}}^{2}}}}{2} = \\ = \frac{1}{2}\rho {{\left( {{{V}^{S}}} \right)}^{3}}{{\left( {\frac{{{{M}_{0}}\Delta {{H}_{q}}}}{{{{B}_{2}}}}} \right)}^{2}}, \\ \end{gathered} $(17)
$\begin{gathered} {{{{P}^{L}}} \mathord{\left/ {\vphantom {{{{P}^{L}}} A}} \right. \kern-0em} A} = \rho {{V}^{L}}{{\left( {2\pi {{f}_{{{\text{p}}~}}}} \right)}^{2}}\frac{{{{{\left| {u_{{0x}}^{L}} \right|}}^{2}}}}{2} = \\ = \frac{1}{2}\rho {{\left( {{{V}^{L}}} \right)}^{3}}{{\left( {\frac{{{{M}_{0}}\Delta {{H}_{q}}}}{{{{B}_{1}}}}} \right)}^{2}}. \\ \end{gathered} $Далее под площадью акустического потока будем подразумевать площадь преобразователя, заданную диаметром электродов $a.$
Отношение пороговых мощностей находится в виде
что для принятых выше отношений параметров дает ${{R}_{P}} \approx 30.$
Таким образом, величина пороговой мощности для квазипродольной волны накачки оказывается более чем на порядок выше, чем для квазисдвиговой волны.
Для оценки величины пороговой мощности используем приведенные в табл. 1 параметры ЖИГ, причем для намагниченности возьмем значение $4\pi {{M}_{0}} = 845$ Гс, характерное для использованной в эксперименте Ga, La замещенной пленки ЖИГ [22]. Тогда из (16) получаем ${{{{P}^{S}}} \mathord{\left/ {\vphantom {{{{P}^{S}}} A}} \right. \kern-0em} A} = 87.5$ мВт/см2, что при диаметре преобразователя $a = 170$ мкм, дает пороговую акустическую мощность ${{P}^{S}} = 20$ мкВт.
Для того чтобы связать акустическую мощность с подаваемой на электроды преобразователя электромагнитной мощностью ${{P}_{{{\text{вх\;}}}}},$ удобно использовать экспериментально измеряемые S-параметры. Энергетический баланс между подаваемой мощностью, отраженной мощностью ${{P}_{{{\text{отр}}}}}$ = ${{\left| {{{S}_{{11}}}\left( f \right)} \right|}^{2}}{{P}_{{{\text{вх}}}}}$ и мощностью ${{P}^{S}},$ переданной в акустические колебания, приводит к следующему соотношению:
Чтобы исключить из экспериментальных данных различные высокочастотные потери, не связанные с акустическим возбуждением образца, измерения проводятся обычно при предварительной калибровке измерительного тракта. Однако полностью избежать их вклада в параметр ${{S}_{{11}}}\left( f \right)$ в широком диапазоне частот достаточно сложно. Поэтому, учитывая резонансный характер полезного акустического отклика, для более точной оценки пороговой электромагнитной мощности воспользуемся модифицированной формулой [12]
(18)
${{P}_{{{\text{вх}}}}}\left( f \right) = {{{{P}^{S}}} \mathord{\left/ {\vphantom {{{{P}^{S}}} {{{\Delta }}{{{\left| {{{S}_{{11}}}{\text{\;}}\left( f \right)} \right|}}^{2}}}}} \right. \kern-0em} {{{\Delta }}{{{\left| {{{S}_{{11}}}{\text{\;}}\left( f \right)} \right|}}^{2}}}}{\text{\;}}.$Здесь ${{\Delta }}{{\left| {{{S}_{{11}}}\left( f \right)} \right|}^{2}}$ = $\left| {{{S}_{{11}}}\left( f \right)} \right|_{0}^{2} - {{\left| {{{S}_{{11}}}\left( {{{f}_{n}}} \right)} \right|}^{2}}$ – глубина провалов в частотной зависимости ${{\left| {{{S}_{{11}}}\left( f \right)} \right|}^{2}}$ в окрестности резонансной частоты fn. Как следует из экспериментальных данных работы [22], при возбуждении резонатора в частотном диапазоне fn = 2.4 ГГц величина ${{\Delta }}{{\left| {{{S}_{{11}}}\left( f \right)} \right|}^{2}}{\text{\;}} \approx 0.2.$ Тогда из (16) и (18) пороговое значение мощности составляет ${{P}_{{{\text{вх}}}}} = 100$ мкВт. Экспериментально в той же работе наблюдался минимальный порог 400 мкВт, что, учитывая возможные отклонения реальных магнитоупругих параметров от приведенных в табл. 1, следует считать хорошим соответствием найденной выше теоретической оценке.
ЗАКЛЮЧЕНИЕ
Рассмотрены условия параметрического возбуждения спиновых волн под действием чисто акустической накачки в виде толщинных резонансных мод гиперзвукового композитного резонатора. Характерно, что к параметрической неустойчивости спиновых волн может привести накачка с упругой поляризацией, направленной перпендикулярно намагниченности. Сравнение пороговых мощностей показало, что при прочих равных условиях и для типичных параметров ЖИГ порог параметрического возбуждения спиновых волн для накачки сдвиговыми толщинными модами резонатора в 30 раз ниже, чем для накачки поперечными модами, и по величине согласуется с ранее наблюдавшимся в эксперименте.
Список литературы
Delsing P., Cleland A.N., Schuetz M.J.A. et al. // J. Phys. D Appl. Phys. 2019. V. 52. № 35. P. 353001.
Barman A., Gubbiotti G., Ladak S. et al. // J. Phys. Condens Matter. 2021. V. 33. P. 117146.R1.
Bozhko D.A., Vasyuchka V.I., Chumak A.V., Serga A.A. // Low Temp. Phys. 2020. V. 46. № 4. P. 383.
Gokhale V.J., Downey B.P., Katzer D.S. et al. // Nature Commun. 2020. V. 11. P. 2314.
Bas D.A., Shah P.J., McConney M.E., Page M.R. // J. Appl. Phys. 2019. V. 126. № 11. P. 114501.
Li Y., Zhao C., Zhang W. et al. // APL Materials. 2021. V. 9. № 6. P. 060902.
Azovtsev A.V., Nikitchenko A.I., Pertsev N.A. // Phys. Rev. Materials. 2021. V. 5. № 5. P. 054601.
Kittel C. // Phys. Rev. 1958. V. 110. № 4. P. 836.
Haas C.W. // J. Phys. Chem. Solids. 1966. V. 27. № 10. P. 1687.
Matthews H., Morgenthaler F.R. // Phys. Rev. Lett. 1964. V. 13. № 21. P. 614.
Pomerantz M. // Phys. Rev. Lett. 1961. V. 7. № 8. P. 312.
Weiler M., Huebl H., Goerg F.S. et al. // Phys. Rev. Lett. 2012. V. 108. № 17. P. 176601.
Uchida K., An T., Kajiwara Y. et al. // Appl. Phys. Lett. 2011. V. 99. № 21. P. 212501.
Polzikova N., Alekseev S., Kotelyanskii I. et al. // J. Appl. Phys. 2013. V. 113. № 17. P. 17C704.
Cherepov S., Amiri P.K., Alzate J.G. et al. // Appl. Phys. Lett. 2014. V. 104. № 8. P. 082403.
Chowdhury P., Jander A., Dhagat P. // IEEE Magnetics Lett. 2017. V. 8. P. 3108204.
Lisenkov I., Jander A., Dhagat P. // Phys. Rev. B. 2019. V. 99. № 18. P. 184433.
Keshtgar H., Zareyan M., Bauer G.E.W. // Solid State Commun. 2014. V. 198. P. 30.
Ползикова Н.И., Алексеев С.Г., Лузанов В.А., Раевский А.О. // ФТТ. 2018. Т. 60. № 11. С. 2170.
Polzikova N.I., Alekseev S.G., Pyataikin I.I. et al. // AIP Advances. 2018. V. 8. № 5. P. 56128.
Polzikova N.I., Alekseev S.G., Luzanov V.A., Raevskiy A.O. // J. Magn. Magn. Mater. 2019. V. 479. P. 38.
Alekseev S.G., Dizhur S.E., Polzikova N.I. et al. // Appl. Phys. Lett. 2020. V. 117. № 7. P. 72408.
Tserkovnyak Y., Brataas A., Bauer G.E.W. // Phys. Rev. Lett. 2002. V. 88. № 11. P.117601.
Saitoh E., Ueda M., Miyajima H., Tatara G. // Appl. Phys. Lett. 2006. V. 88. № 18. P. 182509.
Li J., Liu M., Wang Ch. // Micromachines. 2016. V. 7. № 9. P. 159.
Алексеев С.Г., Котелянский И.М., Ползикова Н.И., Мансфельд Г.Д. // РЭ. 2015. Т. 60. № 3. С. 317.
Мансфельд Г.Д., Алексеев С.Г., Ползикова Н.И. // Акуст. журн. 2008. Т. 54. № 4. P. 552.
Алексеев С.Г., Лузанов В.А., Ползикова Н.И. // РЭ. 2020. Т. 65. № 11. С. 1131.
Comstock R.L., Nilsen W.G. // Phys. Rev. 1964. V. 136. № 2A. P. A442.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


