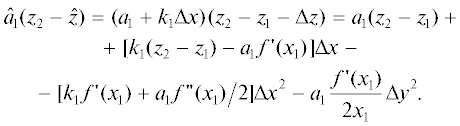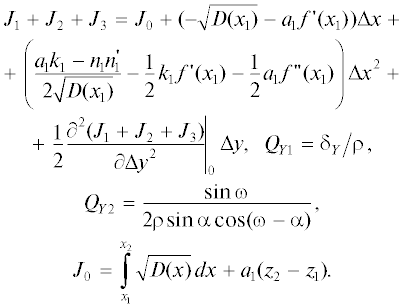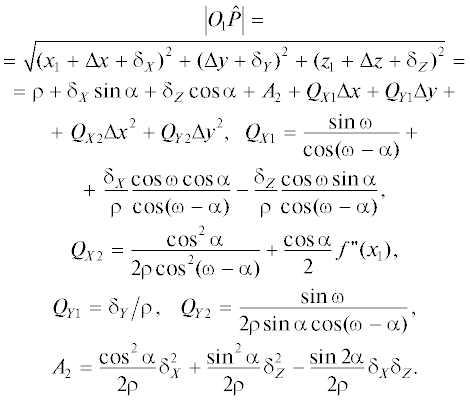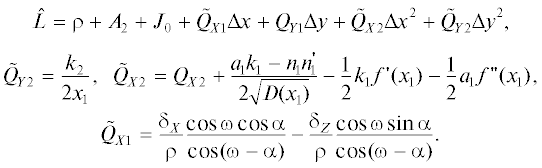Радиотехника и электроника, 2021, T. 66, № 11, стр. 1071-1077

О распределении эйконала на поверхности градиентной осесимметричной линзы

А. С. Венецкий^*

Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

^* E-mail: AVenetsky@yandex.ru

Поступила в редакцию 28.07.2020
После доработки 28.07.2020
Принята к публикации 17.09.2020

DOI: 10.31857/S0033849421110097

Полный текст (PDF)

Аннотация

Получена формула для эйконала на выходной поверхности осесимметричной диэлектрической линзы c радиальным градиентом показателя преломления в цилиндрической системе координат при смещении источника из фокуса, расположенного на оси линзы. Формула представляет собой сумму членов первого и второго порядка малости разложения эйконала по степеням величин радиального и продольного смещений источника из фокуса. Коэффициенты при членах разложения имеют особенность на оси, поэтому найдены их параксиальные разложения, в которых эта особенность устранена. Проведено исследование погрешности полученных формул при вычислении эйконала в апертуре апланатических линз.

ВВЕДЕНИЕ

Осесимметричные линзы из плавно неоднородного (градиентного) диэлектрика с зависимостью коэффициента преломления от радиальной координаты используются как в оптическом, так и в радиодиапазоне электромагнитных волн и обладают дополнительной степенью свободы по сравнению с линзами из однородного диэлектрика. Исследование аберрационных свойств таких линз усложняется из-за криволинейных траекторий лучей. Классическая (оптическая) теория аберраций таких линз описывает области фокусировки лучей в виде разложения по степеням угла зрения и апертуры линзы [1]. В работах [2–4] развита новая теория аберраций для однородных диэлектрических линз с использованием разложения эйконала по одному параметру – величине смещения источника. В работах [5, 6] эта теория обобщается для линз с цилиндрической симметрией и градиентом диэлектрической проницаемости вдоль декартовой координаты. В данной работе эта теория развивается для градиентных линз с осевой симметрией.

Рассмотрим осесимметричную диэлектрическую линзу с коэффициентом преломления n, зависящим от расстояния от оси линзы. Продольное и поперечное сечение линзы показано на рис. 1а, 1б.

Рис. 1.

Геометрия лучей в линзе: а – продольное сечение, б – поперечное сечение.

При расположении источника в фокусе О на оси системы (оси z) на выходной поверхности линзы формируется плоский фронт. Предположим, что через любую точку В на выходной поверхности линзы проходит только один луч, выходящий из источника под углом α к оси системы, т.е. обеспечивается взаимно-однозначное соответствие между углом α и расстоянием от оси системы до точки В, которое описывается функцией отображения:

(1)

$r = \sqrt {X_{B}^{2} + Y_{B}^{2}} = r(\alpha ),\,\,\,\,\alpha = \alpha (r).$

Луч, выходящий из источника, лежит в плоскости, проходящей через ось линзы в плоскости xOz (см. рис. 1а), и его уравнение имеет вид

(2)

$z = {{z}_{1}} + \int\limits_{{{x}_{1}}}^x {\frac{{{{a}_{1}}dx}}{{\sqrt {{{n}^{2}}(x) - a_{1}^{2}} }}} ,$

где а₁ – параметр луча.

Пусть точка О₁ с координатами (–δ_R, 0, –δ_Z) – положение смещенного источника (см. рис. 1б). Предположим, что при смещении источника в точку О₁ взаимно-однозначное соответствие множества точек выходной апертуры множеству выходящих из О₁ лучей сохраняется. При этом всегда существует луч, соединяющий точку О₁ и точку В.

Выберем систему координат $\tilde {x}\tilde {y}\tilde {z}$ с центром в фокусе О так, чтобы точка В имела координаты (x₂, 0, z₂). Тогда другие точки будут иметь координаты P(x₁, 0, z₁), $\hat {P}$(x₁+ Δx, Δy, z₁+ Δz), O₁(–δ_Х, –δ_Y, –δ_Z), O(0, 0, 0). При этом z₂= F(x₂), z₁= f(х₁), где z = F(x) и z = f(x) – уравнения образующих поверхности линзы соответственно, δ_Х = δ_R cosφ, δ_Y = –δ_Rsinφ .

Уравнение луча, соединяющего точки В и $\hat {P}$ имеет вид [7]

(3)

${{z}_{2}} = \hat {z} + \int\limits_{\hat {r}}^{{{r}_{2}}} {\frac{{{{{\hat {a}}}_{1}}dr}}{{\sqrt {D(r)} }}} ,$

(4)

$\Delta \varphi = \int\limits_{\hat {r}}^{{{r}_{2}}} {\frac{{{{a}_{2}}dr}}{{{{r}^{2}}\sqrt {D(r)} }}} ,$

где $D(r) = {{n}^{2}}(r) - \hat {a}_{1}^{2} - {{a_{2}^{2}} \mathord{\left/ {\vphantom {{a_{2}^{2}} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}},$ $\Delta \varphi = {{\varphi }_{2}} - \hat {\varphi },$ $\hat {z} = {{z}_{1}} + \Delta z,$ ${{\hat {a}}_{1}} = {{a}_{1}} + {{k}_{1}}\Delta x,$ ${{a}_{2}} = {{k}_{2}}\Delta y,$ $\hat {r} = {{x}_{1}} + \Delta r,$ $\Delta r = \Delta x + {{\Delta {{y}^{2}}} \mathord{\left/ {\vphantom {{\Delta {{y}^{2}}} {2{{x}_{1}}}}} \right. \kern-0em} {2{{x}_{1}}}},$

${{r}_{2}} = {{x}_{2}},$ (${{\hat {a}}_{1}},{{a}_{2}}$) – лучевые параметры возмущенного луча, (а₁, 0) – лучевые параметры невозмущенного луча, k₁, k₂ – неизвестные пока коэффициенты.

Эйконал луча, соединяющего точки О₁ и В, имеет вид

(5)

$\hat {L} = \left| {{{O}_{1}}\hat {P}} \right| + \int\limits_{\hat {r}}^{{{r}_{2}}} {\sqrt {D(r)} } dr + {{a}_{2}}\Delta \varphi + {{\hat {a}}_{1}}({{z}_{2}} - \hat {z}).$

Отметим, что в выбранной системе координат невозмущенный луч (т.е. луч при Δх = Δу = 0) лежит в плоскости хОz, и из уравнения (3) следует:

(6)

${{z}_{2}} = {{z}_{1}} + \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{a}_{1}}dx}}{{\sqrt {{{n}^{2}}(x) - a_{1}^{2}} }}} ,$

где точка Р имеет координаты (x₁, 0, z₁), а точка В – (x₂, 0, z₂).

Для нахождения неизвестного параметра k₁ разложим выражение (3) в ряд по Δх в точке х₁ при условии, что Δу = 0, и ограничимся членами первого порядка малости:

$\begin{gathered} {{z}_{2}} = {{z}_{1}} + f{\kern 1pt} '({{x}_{1}})\Delta x + \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{a}_{1}}}}{{\sqrt {D(х)} }}} \,dx + \\ + \,\,\left( {{{k}_{1}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{n}^{2}}(x)}}{{D{{{(х)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \,dx - \frac{{{{a}_{1}}}}{{\sqrt {D({{x}_{1}})} }}} \right)\Delta x + ... \\ \end{gathered} $

Приравнивая сумму членов при Δх к 0 и учитывая соотношение (6), получим уравнение

$f{\kern 1pt} '({{x}_{1}}) + {{k}_{1}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{n}^{2}}(x)}}{{{{D}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} dx - {\text{ctg}}{{\xi }_{{\text{1}}}} = 0,$

из которого находим

(7)

${{k}_{1}} = \frac{{{\text{ctg}}{{\xi }_{{\text{1}}}} - f{\kern 1pt} '({{x}_{1}})}}{{\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {{{{{n}^{2}}} \mathord{\left/ {\vphantom {{{{n}^{2}}} {{{D}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}dx}}} \right. \kern-0em} {{{D}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}dx}}} }},$

где ${\text{ctg}}{{\xi }_{{\text{1}}}} = \frac{{{{a}_{1}}}}{{\sqrt {D({{x}_{1}})} }},$ $D(x) = {{n}^{2}}(x) - a_{1}^{2}.$

С одной стороны, из выражения (4) можно получить

(8)

${{\left. {\frac{{\partial \Delta \varphi }}{{\partial \Delta y}}} \right|}_{{{{\Delta }}x,{{\Delta }}y = 0}}} = {{k}_{2}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{x}^{2}}\sqrt D }}} .$

С другой –

$\Delta \varphi = {\text{arctg}}\left( {\frac{{\Delta y}}{{{{x}_{1}} + \Delta x}}} \right) = \frac{{\Delta y}}{{{{x}_{1}}}} - \frac{{\Delta x\Delta y}}{{x_{1}^{2}}} + ....$

Следовательно,

(9)

${{\left. {\frac{{\partial \Delta \varphi }}{{\partial \Delta y}}} \right|}_{{{{\Delta }}x,{{\Delta }}y = 0}}} = \frac{1}{{{{x}_{1}}}}.$

Сравнивая (8) и (9), находим

(10)

$\frac{1}{{{{k}_{2}}}} = {{x}_{1}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{x}^{2}}\sqrt D }}} \,.$

Представим эйконал (5) в виде ряда по степеням Δх и Δу. Для этого запишем его в виде

$\hat {L} = \left| {{{O}_{1}}\hat {P}} \right| + {{J}_{1}} + {{J}_{2}} + {{J}_{3}},$

где ${{J}_{1}} = \int_{\hat {r}}^{{{r}_{2}}} {\sqrt {D(r)} } dr,$ ${{J}_{2}} = {{a}_{2}}\Delta \varphi ,$ ${{J}_{3}} = {{\hat {a}}_{1}}({{z}_{2}} - \hat {z}),$ и продифференцируем:

$\begin{gathered} \frac{{\partial {{J}_{1}}}}{{\partial \Delta x}} = - {{k}_{1}}\int\limits_{\hat {r}}^{{{r}_{2}}} {\frac{{{{{\hat {a}}}_{1}}}}{{\sqrt D }}dr - \sqrt {D(\hat {r})} } , \\ {{\left. {\frac{{\partial {{J}_{1}}}}{{\partial \Delta x}}} \right|}_{0}} = - {{k}_{1}}({{z}_{2}} - {{z}_{1}}) - \sqrt {D({{x}_{1}})} . \\ \end{gathered} $

Используя соотношение ${\text{ctg}}{{\xi }_{1}} = {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} {\sqrt {D({{x}_{1}})} }}} \right. \kern-0em} {\sqrt {D({{x}_{1}})} }},$ а также выражение (7) для k₁, можно получить

$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}{{J}_{1}}}}{{\partial \Delta {{x}^{2}}}}} \right|}_{0}} = - {{k}_{1}}\left( {{{k}_{1}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{n}^{2}}(x)}}{{{{D}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}dx - \frac{{{{a}_{1}}}}{{\sqrt {D({{x}_{1}})} }}} } \right) - \frac{{{{n}_{1}}n_{{\text{1}}}^{'} - {{a}_{1}}{{k}_{1}}}}{{\sqrt {D({{x}_{1}})} }} = \\ = {{k}_{1}}f{\kern 1pt} '({{x}_{1}}) - \frac{{{{n}_{1}}n_{{\text{1}}}^{'} - {{a}_{1}}{{k}_{1}}}}{{\sqrt {D({{x}_{1}})} }}. \\ \end{gathered} $

Нетрудно получить

Продифференцируем J₁, J₂, J₃ по Δу:

$\begin{gathered} \frac{{\partial {{J}_{1}}}}{{\partial \Delta y}} = - {{k}_{2}}\int\limits_{\hat {r}}^{{{r}_{2}}} {\frac{{{{a}_{2}}}}{{{{r}^{2}}\sqrt D }}dr - \sqrt {D(\hat {r})} \frac{{\Delta y}}{{{{x}_{1}}}}} ,\,\,\,\,{{\left. {\frac{{\partial {{J}_{1}}}}{{\partial \Delta y}}} \right|}_{0}} = 0, \\ {{\left. {\frac{{{{\partial }^{2}}{{J}_{1}}}}{{\partial \Delta {{y}^{2}}}}} \right|}_{0}} = - k_{2}^{2}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{x}^{2}}\sqrt {D(x)} }} - \frac{{\sqrt {D({{x}_{1}})} }}{{{{x}_{1}}}} = - \frac{{{{k}_{2}}}}{{{{x}_{1}}}} - } \frac{{\sqrt {D({{x}_{1}})} }}{{{{x}_{1}}}} \\ \end{gathered} $

(была использована формула (10) для k₂),

${{\left. {\frac{{{{\partial }^{2}}{{J}_{2}}}}{{\partial \Delta {{y}^{2}}}}} \right|}_{0}} = \frac{{2{{k}_{2}}}}{{{{x}_{1}}}},\,\,\,\,{{\left. {\frac{{{{\partial }^{2}}{{J}_{3}}}}{{\partial \Delta {{y}^{2}}}}} \right|}_{0}} = - \frac{{f{\kern 1pt} '({{x}_{1}})}}{{{{x}_{1}}}}{{a}_{1}}.$

Используя соотношение, выражающее закон преломления невозмущенного луча в точке Р:

$\begin{gathered} \sqrt {D({{x}_{1}})} + {{a}_{1}}f{\kern 1pt} '({{x}_{1}}) = {{n}_{1}}\sin {{\xi }_{1}} + {{n}_{1}}\cos {{\xi }_{1}}{\text{tg(}}\omega - \alpha {\text{)}} = \\ = {{{{n}_{1}}\sin ({{\xi }_{1}} + \omega - \alpha )} \mathord{\left/ {\vphantom {{{{n}_{1}}\sin ({{\xi }_{1}} + \omega - \alpha )} {\cos (\omega - \alpha )}}} \right. \kern-0em} {\cos (\omega - \alpha )}} = {{\sin \omega } \mathord{\left/ {\vphantom {{\sin \omega } {\cos (\omega - \alpha )}}} \right. \kern-0em} {\cos (\omega - \alpha )}}, \\ \end{gathered} $

можно найти

$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}({{J}_{1}} + {{J}_{2}} + {{J}_{3}})}}{{\partial \Delta {{y}^{2}}}}} \right|}_{0}} = \frac{{{{k}_{2}}}}{{{{x}_{1}}}} - \frac{{\sqrt {D({{x}_{1}})} }}{{{{x}_{1}}}} - \frac{{f{\kern 1pt} '({{x}_{1}})}}{{{{x}_{1}}}}{{a}_{1}} = \\ = \frac{{{{k}_{2}}}}{{{{x}_{1}}}} - {{n}_{1}}(\sin {{\xi }_{1}} + \cos {{\xi }_{1}}{\text{tg(}}\omega - \alpha {\text{))}} = \\ = \frac{{{{k}_{2}}}}{{{{x}_{1}}}} - \frac{{\sin \omega }}{{\rho \sin \alpha \cos (\omega - \alpha )}}. \\ \end{gathered} $

Тогда можно записать

Раскроем также $\left| {{{О}_{1}}\hat {P}} \right|$ в выражении (5):

Окончательно получаем выражение для эйконала (5):

(11)

Из принципа Ферма следует, что эйконал на истинной траектории достигает минимума и, следовательно, удовлетворяются уравнения:

$\frac{{\partial{ \hat {L}}}}{{\partial \Delta x}} = 0,\,\,\,\,\frac{{\partial{ \hat {L}}}}{{\partial \Delta x}} = 0,$

из которых можно найти неизвестные Δх и Δу:

$\Delta x = - \frac{{{{{\tilde {Q}}}_{{X1}}}}}{{4{{{\tilde {Q}}}_{{X2}}}}},\,\,\,\,\Delta y = - \frac{{{{Q}_{{Y1}}}}}{{4{{{\tilde {Q}}}_{{Y2}}}}}.$

После подстановки полученных Δх, Δу в выражение для эйконала (11), получаем

$\hat {L} = \rho + {{A}_{2}} + {{J}_{0}} - \frac{{\tilde {Q}_{{X1}}^{2}}}{{4{{{\tilde {Q}}}_{{X2}}}}} - \frac{1}{2}\frac{{{{x}_{1}}}}{{{{k}_{2}}}}Q_{{Y1}}^{2}.$

В исходной системе координат, в которой точка В имеет координаты (Rcosφ, Rsinφ, z₂), формула для эйконала будет иметь вид:

(12)

$\hat {L}(R,\varphi ) = \rho + {{A}_{2}} + {{J}_{0}} - \frac{{{{{\cos }}^{2}}\omega \,{{{({{\delta }_{R}}\cos \varphi \cos \alpha - {{\delta }_{Z}}\sin \alpha )}}^{2}}}}{{4{{{\tilde {Q}}}_{{X2}}}{{{\cos }}^{2}}(\omega - \alpha ){{\rho }^{2}}}} - \frac{{{{x}_{1}}}}{{2{{k}_{2}}}}\frac{{\delta _{R}^{2}{{{\sin }}^{2}}\varphi }}{{{{\rho }^{2}}}}.$

Полученная формула имеет особенность при R = 0 и в силу этого теряет точность в малой окрестности оси. В окрестности 0 закон изменения коэффициента преломления можно считать квадратичным:

${{n}^{2}}(x) = n_{0}^{2} - {{c}_{2}}{{x}^{2}}.$

Тогда интеграл, входящий в (7), можно представить в виде

(13)

$\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{n}^{2}}(x)dx}}{{{{{\left( {{{n}^{2}}(x) - a_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} = \frac{{n_{0}^{2}}}{{c_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{t}^{3}}}}} - \frac{1}{{\sqrt {{{c}_{2}}} }}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{x}^{2}}dx}}{{{{t}^{3}}}}} ,$

где

$\begin{gathered} t = \sqrt {{{p}^{2}} - {{x}^{2}}} ,\,\,\,\,{{p}^{2}} = {{\left( {n_{0}^{2} - a_{1}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {n_{0}^{2} - a_{1}^{2}} \right)} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}, \\ \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{t}^{3}}}}} = \frac{1}{{{{p}^{2}}}}\left( {\frac{{{{x}_{2}}}}{{\sqrt {{{p}^{2}} - x_{2}^{2}} }} - \frac{{{{x}_{1}}}}{{\sqrt {{{p}^{2}} - x_{1}^{2}} }}} \right), \\ \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{x}^{2}}dx}}{{{{t}^{3}}}}} = \frac{{{{x}_{2}}}}{{\sqrt {{{p}^{2}} - x_{2}^{2}} }} - \frac{{{{x}_{1}}}}{{\sqrt {{{p}^{2}} - x_{1}^{2}} }} - \arcsin \frac{{{{x}_{2}}}}{p} + \arcsin \frac{{{{x}_{1}}}}{p}. \\ \end{gathered} $

В заданном законе отображения (1) r= x₂, а угол α можно выразить через х₁, используя соотношения

$\begin{gathered} f(x) = {{f}_{0}} + {{f}_{2}}{{x}^{2}} + {{f}_{4}}{{x}^{4}} + ..., \\ \alpha = {\text{arctg}}\left( {\frac{{{{x}_{1}}}}{{f({{x}_{1}})}}} \right) = \frac{{{{x}_{1}}}}{{{{f}_{0}}}} - \left( {\frac{{{{f}_{2}}}}{{f_{0}^{2}}} + \frac{1}{{3f_{0}^{3}}}} \right)x_{1}^{3}. \\ \end{gathered} $

Закон отображения x₂ = r(α) можно привести к виду

$x_{2}^{2} = {{\beta }_{2}}x_{1}^{2} - {{\beta }_{4}}x_{1}^{4},$

где ${{\beta }_{2}} = {{f_{e}^{2}} \mathord{\left/ {\vphantom {{f_{e}^{2}} {f_{0}^{2}}}} \right. \kern-0em} {f_{0}^{2}}},$ а f_e – коэффициент разложения r(α) = f_eα + pα³+….

Используя соотношения $\omega = {\text{arctg[}}f{\kern 1pt} '({{x}_{1}})] + \alpha $ и_{$\sin \omega = n({{x}_{1}})\sin (\omega - \alpha + {{\xi }_{1}}),$ лучевой параметр можно представить в виде}

$a_{1}^{2} = {{n}^{2}}({{x}_{1}}){{\cos }^{2}}{{\xi }_{1}} = n_{0}^{2} - ({{c}_{2}} + {{g}_{2}})x_{1}^{2} + {{A}_{4}}x_{1}^{4}.$

Теперь интеграл (13) можно записать в виде

$\begin{gathered} \int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{{{n}^{2}}(x)dx}}{{D{{{(x)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} = \frac{{{{I}_{0}}}}{{x_{1}^{2}}} + {{I}_{2}},\,\,\,\,{{I}_{0}} = \frac{{n_{0}^{2}}}{{({{c}_{2}} + {{g}_{2}})}}\left( {\frac{1}{{{{g}_{1}}}} - \frac{1}{{{{h}_{1}}}}} \right), \\ {{I}_{2}} = \frac{{n_{0}^{2}}}{{({{c}_{2}} + {{g}_{2}})}}\left[ {\frac{{{{A}_{4}}}}{{{{c}_{2}} + {{g}_{2}}}}\left( {\frac{1}{{{{g}_{1}}}} - \frac{1}{{{{h}_{1}}}}} \right) + S{{Q}_{{21}}}} \right] + \frac{1}{{{{g}_{1}}}} - \frac{1}{{{{h}_{1}}}} + \\ + \,\,\frac{1}{{\sqrt {{{c}_{2}}} }}\left( {\arcsin \frac{{\sqrt {{{c}_{2}}} }}{{\sqrt {{{c}_{2}} + {{g}_{2}}} }} - \arcsin \frac{{\sqrt {{{\beta }_{2}}{{c}_{2}}} }}{{\sqrt {{{c}_{2}} + {{g}_{2}}} }}} \right), \\ S{{Q}_{{21}}} = \frac{{{{A}_{4}}}}{{2g_{1}^{3}}} - \frac{{{{{{A}_{4}} - {{\beta }_{4}}({{c}_{2}} + {{g}_{2}})} \mathord{\left/ {\vphantom {{{{A}_{4}} - {{\beta }_{4}}({{c}_{2}} + {{g}_{2}})} {{{\beta }_{2}}}}} \right. \kern-0em} {{{\beta }_{2}}}}}}{{2{{\beta }_{2}}h_{1}^{3}}}, \\ \end{gathered} $

(14)

${{k}_{1}} = {\rm K}{{x}_{1}}\left( {1 - {{{\rm M}}_{2}}x_{1}^{2}} \right),$

$\begin{gathered} {\rm K} = \frac{{{{h}_{1}}({{c}_{2}} + {{g}_{2}})}}{{{{n}_{0}}({{g}_{1}} - {{h}_{1}})}},\,\,\,\,{{{\rm M}}_{2}} = {{\Xi _{1}^{2}} \mathord{\left/ {\vphantom {{\Xi _{1}^{2}} 2}} \right. \kern-0em} 2} + 2{{f}_{2}}{{\Xi }_{1}} + \\ + \,\,{\rm K}\left[ {\left( {{{\Xi }_{3}} - {{\Xi _{1}^{3}} \mathord{\left/ {\vphantom {{\Xi _{1}^{3}} 6}} \right. \kern-0em} 6}} \right){{I}_{0}} + {{\Xi }_{1}}{{I}_{2}}} \right],\,\,\,\,{{\Xi }_{1}} = {{ - {{g}_{1}}} \mathord{\left/ {\vphantom {{ - {{g}_{1}}} {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}, \\ {{\Xi }_{3}} = - \frac{{{{f}_{2}}}}{{f_{0}^{2}}} - \frac{1}{{3f_{0}^{3}}} + \frac{{{{c}_{2}}{{\omega }_{1}}}}{{2n_{0}^{3}}} + \frac{{\omega _{1}^{3}}}{{6{{n}_{0}}}}\left( {\frac{1}{{n_{0}^{2}}} - 1} \right) + {{\omega }_{3}}\left( {\frac{1}{{{{n}_{0}}}} - 1} \right), \\ {{\omega }_{1}} = 2{{f}_{2}} + {1 \mathord{\left/ {\vphantom {1 {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}},\,\,\,\,{{\omega }_{3}} = 4{{f}_{4}} - \frac{8}{3}f_{2}^{3} - \frac{{{{f}_{2}}}}{{f_{0}^{2}}} - \frac{1}{{3f_{0}^{3}}}, \\ {{A}_{4}} = {{c}_{2}}\Xi _{1}^{2} + n_{0}^{2}\left( {\Xi _{1}^{4} - 2{{\Xi }_{1}}{{\Xi }_{3}}} \right), \\ {{g}_{1}} = 2{{f}_{2}}({{n}_{0}} - 1) - {1 \mathord{\left/ {\vphantom {1 {{{f}_{0}}}}} \right. \kern-0em} {{{f}_{0}}}},\,\,\,\,{{h}_{1}} = 2{{\psi }_{2}}({{n}_{0}} - 1),\,\,\,\,{{g}_{2}} = g_{1}^{2}, \\ \end{gathered} $

f₂, f₄, ψ₂ – коэффициенты разложений поверхностей линзы (см. рис. 1а)

$\begin{gathered} f(x) = {{f}_{0}} + {{f}_{2}}{{x}^{2}} + {{f}_{4}}{{x}^{4}} + ..., \\ \psi (x) = {{f}_{0}} + {{d}_{0}} + {{\psi }_{2}}{{x}^{2}} + {{\psi }_{4}}{{x}^{4}} + ... \\ \end{gathered} $

С учетом найденного k₁ (14) выражение для_{${{\tilde {Q}}_{{X2}}}$ можно привести к виду}

$\begin{gathered} {{{\tilde {Q}}}_{{X2}}} = \frac{{{{g}_{2}} + {{c}_{2}}}}{{2({{h}_{1}} - {{g}_{1}})}} + \left( {\frac{1}{{2{{g}_{1}}}}{{W}_{2}} + {{F}_{2}}} \right)x_{1}^{2}, \\ \frac{1}{{4{{{\tilde {Q}}}_{{X2}}}}} = \frac{{{{h}_{1}} - {{g}_{1}}}}{{2({{c}_{2}} + {{g}_{2}})}} - \frac{{{{{({{h}_{1}} - {{g}_{1}})}}^{2}}}}{{{{{({{c}_{2}} + {{g}_{2}})}}^{2}}}}\left( {\frac{1}{{2{{g}_{1}}}}{{W}_{2}} + {{F}_{2}}} \right)x_{1}^{2}, \\ \end{gathered} $

$\begin{gathered} {{W}_{2}} = {\rm K}{{n}_{0}}\left( {\frac{{{{c}_{2}} + {{g}_{2}}}}{{2n_{0}^{2}}} + {{{\rm M}}_{2}}} \right) + \\ + \,\,{{W}_{0}}{\rm K}\left[ {{{n}_{0}}\left( {{{\Xi }_{3}} - {{\Xi _{1}^{3}} \mathord{\left/ {\vphantom {{\Xi _{1}^{3}} 6}} \right. \kern-0em} 6}} \right) - \frac{{{{c}_{2}}{{\Xi }_{1}}}}{{2{{n}_{0}}}}} \right],\,\,\,\,{{W}_{0}} = {{n}_{0}}{\rm K} + {{c}_{2}}, \\ {{F}_{2}} = \frac{{2f_{2}^{2}}}{{{{f}_{0}}}} - \frac{{{{f}_{2}}}}{{f_{0}^{2}}} - \frac{3}{{4f_{0}^{3}}} + \frac{{{{f}_{2}}}}{{{{n}_{0}}}}({{c}_{2}} + {{g}_{2}})\left( {\frac{1}{2} - \frac{{{{h}_{1}}}}{{{{g}_{1}} - {{h}_{1}}}}} \right) + \\ + \,\,6(1 - {{n}_{0}}){{f}_{4}}. \\ \end{gathered} $

Теперь раскроем особенность в члене с k₂. Из формулы (10) следует:

$\begin{gathered} \frac{{{{x}_{1}}}}{{{{k}_{2}}}} = x_{1}^{2}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{x}^{2}}\sqrt D }} = } \frac{{x_{1}^{2}}}{{\sqrt {{{c}_{2}}} }}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\frac{{dx}}{{{{x}^{2}}\sqrt {{{p}^{2}} - {{x}^{2}}} }}} = \\ = \frac{{x_{1}^{2}}}{{{{p}^{2}}\sqrt {{{c}_{2}}} }}\left( {\frac{{\sqrt {{{p}^{2}} - x_{1}^{2}} }}{{{{x}_{1}}}} - \frac{{\sqrt {{{p}^{2}} - x_{2}^{2}} }}{{{{x}_{2}}}}} \right). \\ \end{gathered} $

Используя зависимости х₂ и р от х₁ и оставляя члены не выше второго порядка по х₁, можно получить

$\begin{gathered} \frac{{{{x}_{1}}}}{{2{{k}_{2}}}} = \frac{{{{h}_{1}} - {{g}_{1}}}}{{2({{c}_{2}} + {{g}_{2}})}} + {{H}_{2}}x_{1}^{2}, \\ {{H}_{2}} = \frac{1}{{2({{c}_{2}} + {{g}_{2}})}}\left( {\frac{{{{A}_{4}}({{h}_{1}} - {{g}_{1}})}}{{{{c}_{2}} + {{g}_{2}}}} - \frac{{{{\beta }_{4}}({{h}_{2}} + {{c}_{2}}) - {{A}_{4}}}}{{2{{h}_{1}}{{\beta }_{2}}}} + \frac{{{{A}_{4}}}}{{2{{g}_{1}}}}} \right). \\ \end{gathered} $

Формулу для эйконала луча в точке В теперь можно записать в виде

(15)

$\begin{gathered} \hat {L}(R,\varphi ) = \rho + {{A}_{2}} + {{J}_{0}} - \frac{{{{{\cos }}^{2}}\omega }}{{{{{\cos }}^{2}}(\omega - \alpha ){{\rho }^{2}}}}\left( {{{Q}_{0}} + {{G}_{2}}x_{1}^{2}} \right) \times \\ \times \,\,{{({{\delta }_{R}}\cos \varphi \cos \alpha - {{\delta }_{Z}}\sin \alpha )}^{2}} - \\ - \,\,\frac{1}{{{{\rho }^{2}}}}\left( {{{Q}_{0}} + {{H}_{2}}x_{1}^{2}} \right)\delta _{R}^{2}{{\sin }^{2}}\varphi , \\ \end{gathered} $

где

${{Q}_{0}} = \frac{{{{h}_{1}} - {{g}_{1}}}}{{2({{c}_{2}} + {{g}_{2}})}},\,\,\,\,{{G}_{2}} = - 4Q_{0}^{2}\left( {\frac{1}{{2{{g}_{1}}}}{{W}_{2}} + {{F}_{2}}} \right).$

Если положить x₁ = 0, то выведенная формула (15) будет иметь вид

(16)

$\begin{gathered} \hat {L}(R,\varphi ) = \rho + {{A}_{2}} + {{J}_{0}} - \frac{{{{Q}_{0}}{{{\cos }}^{2}}\omega }}{{{{{\cos }}^{2}}(\omega - \alpha ){{\rho }^{2}}}} \times \\ \times \,\,{{({{\delta }_{R}}\cos \varphi \cos \alpha - {{\delta }_{Z}}\sin \alpha )}^{2}} - \frac{{{{Q}_{0}}}}{{{{\rho }^{2}}}}\delta _{R}^{2}{{\sin }^{2}}\varphi . \\ \end{gathered} $

На рис. 2–5 приведены результаты исследования точности полученных формул – графики разностей точного геометрооптического значения эйконала и найденного по приближенным формулам (12) и (16) эйконала при смещении источника из фокуса для двух апланатических линз с координатами смещенного источника (–0.2, 0.01). На рис. 6, 7 приведены графики аберрации эйконала, посчитанные строгим геометро-оптическим методом, т.е. графики эйконала после вычета линейной составляющей для обоих линз. Все величины на графиках нормированы на диаметр апертуры линз.

Рис. 2.

Ошибка вычисления эйконала на выходной поверхности линзы с параметрами: f₀ = 0.7, d₀ = 0.8, f_е = 1.1, n₀ = 1.6, c₂ = 1.5, а – меридиональная плоскость, б – сагиттальная плоскость; кривая 1 соответствует формуле (12), кривая 2 – формуле (16).

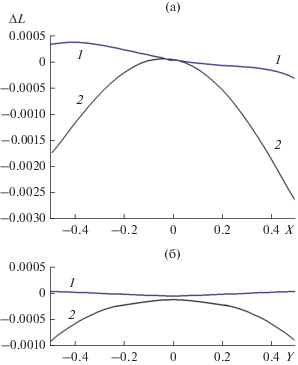
Рис. 3.

Ошибка вычисления эйконала на выходной поверхности линзы с параметрами: f₀ = 0.7, d₀ = 0.8, f_е = 1.1, n₀ = 1.6, c₂ = 0.5; а – меридиональная плоскость, б – сагиттальная плоскость; кривая 1 соответствует формуле (12), кривая 2 – формуле (16).

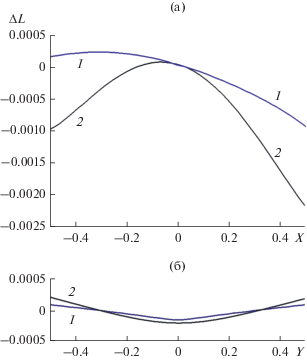
Рис. 4.

Ошибка вычисления эйконала на выходной поверхности линзы с параметрами: f₀ = 1, d₀ = 0.5, f_е = = 1.3, n₀ = 1.6, c₂ = 1.5; а – меридиональная плоскость, б – сагиттальная плоскость; кривая 1 соответствует формуле (12), кривая 2 – формуле (16).

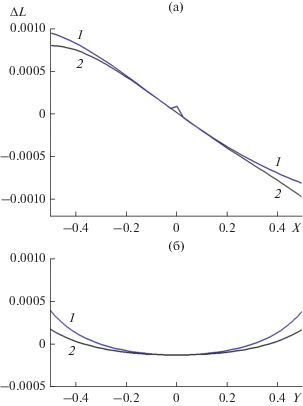
Рис. 5.

Ошибка вычисления эйконала на выходной поверхности линзы с параметрами: f₀ = 1, d₀ = 0.5, f_е = = 1.3, n₀ = 1.6, c₂ = 1.5, с₄ = –1.5; а – меридиональная плоскость, б – сагиттальная плоскость; кривая 1 соответствует формуле (12), кривая 2 – формуле (16).

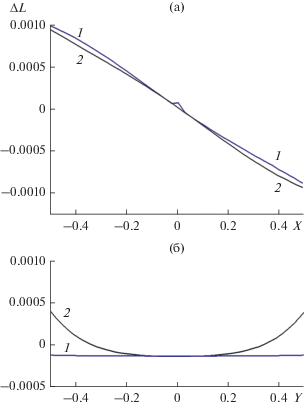
Рис. 6.

Аберрация эйконала в меридиональной плоскости на выходной поверхности линзы с параметрами: f₀ = 0.7, d₀ = 0.8, f_е = 1.1, n₀ = 1.6, c₂ = 1.5.

Рис. 7.

Аберрация эйконала в меридиональной плоскости на выходной поверхности линзы с параметрами: f₀ = 1, d₀ = 0.5, f_е = 1.3, n₀ = 1.6, c₂ = 1.5.

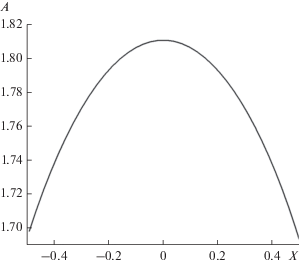
Из сравнения рис. 6, 7 с рис. 2–5 видно, что величина аберрации в меридиональной плоскости для линзы с f₀ = 0.7 примерно в 30 раз больше ошибки формулы (16), и в 140 раз больше ошибки формулы (12); для линзы с f₀ = 1 величина аберрации в меридиональной плоскости примерно в 50 раз больше ошибки по формулам (12) и (16) даже без учета линейной составляющей, которая не влияет на величину аберраций. Это позволяет использовать приближенные формулы для исследования аберраций в градиентных линзах.

Список литературы

Marchand E.W. Gradient Index Optics. N.Y.: Academic Press, Inc., 1978.
Венецкий А.С., Калошин В.А. // ДАН. 2015. Т. 463. № 5. С. 533.
Венецкий А.С., Калошин В.А. // РЭ. 2017. Т. 62. № 6. С. 533.
Венецкий А.С., Калошин В.А. // РЭ. 2018. Т. 63. № 2. С. 144.
Венецкий А.С. // Журн. радиоэлектроники. 2018. № 8. http://jre.cplire.ru/jre/aug18/7/text.pdf.
Венецкий А.С., Калошин В.А. // РЭ. 2020. Т. 65. № 9. С. 872.
Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. М.: Наука, 1980.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал