Радиотехника и электроника, 2021, T. 66, № 5, стр. 436-442

Электродный датчик электрического поля представляет собой пару электродов, расположенных на некотором расстоянии друг от друга. Он нашел широкое применение в геофизике при измерении напряженности электрических полей в океане для изучения строения земной коры и разведки полезных ископаемых на шельфе, в электромагнитных расходомерах, в системах радиосвязи с глубокопогруженными исследовательскими объектами в океане на сверхнизких частотах [1–3]. Основной причиной, ограничивающей чувствительность электродного датчика при движении в морской воде, является специфический электродный шум, представляющий собой флуктуации потенциала электродов, возникающие вследствие движения электродов относительно жидкости. Величина шумового напряжения в экспериментах при движении датчика была на 10…20 дБ больше, чем в состоянии покоя [4–6]. Экспериментально и теоретически установлена связь пульсаций напряжения между электродами с пульсациями скорости жидкости относительно электродов [6–9].

Цель работы – повышение чувствительности электродного датчика за счет уменьшения электродного шума движения.

В работе [10] рассмотрен механизм возникновения пульсаций электродного потенциала в результате модуляции толщины диффузионного слоя на границе электрод–электролит набегающим пульсирующим потоком жидкости. Потенциал электрода относительно электролита определяется отношением заряда поверхности электрода к емкости электрода относительно электролита. Заряд поверхности электрода формируется за счет адсорбции диффундирующих к электроду атомов растворенного в воде кислорода. При адсорбции одного моля кислорода в соответствии с его валентностью заряд поверхности изменяется на $2F$ Кулон (F – число Фарадея). Плотность потока j диффундирующего кислорода (${{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {{\text{с}}\,\,{{{\text{м}}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с}}\,\,{{{\text{м}}}^{{\text{2}}}}}}$) зависит от градиента концентрации кислорода в диффузионном слое электролита, который можно считать равным отношению концентрации кислорода в толще электролита к толщине диффузионного слоя [11]:

где $D \approx 2.6 \times {{10}^{{ - 9}}}{\text{ }}{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ – коэффициент диффузии кислорода, ${{c}_{0}}$ – концентрация кислорода в толще электролита, $\delta $ – толщина диффузионного слоя. Диффузионный слой – это прилегающий к электроду слой электролита, в котором концентрация с кислорода в направлении оси z, перпендикулярной к поверхности электрода, изменяется по закону, близкому к линейному, от нуля на поверхности электрода до значения, мало отличающегося от ${{c}_{0}}$. Толщина диффузионного слоя зависит от скорости набегающего на электрод электролита. Поэтому при наличии пульсаций скорости жидкости заряд поверхности электрода получает пульсационную составляющую. Изменение потенциала электрода, вызванное изменением заряда, составляет

где $C$ – емкость электрода относительно электролита. Как показано в [10], заряд, приобретаемый электродом при адсорбции атомов кислорода, содержит две составляющих. Первая медленно возрастает, а вторая, связанная с пульсацией скорости жидкости, вызывает сравнительно быстрые пульсации потенциала электрода, которые и представляют собой шум движения. Амплитуда пульсаций заряда пропорциональна амплитуде пульсаций потока диффундирующего кислорода. Следовательно, амплитуда пульсаций потенциала электрода также пропорциональна амплитуде пульсаций потока кислорода. Поэтому уменьшение шума движения можно оценивать по уменьшению пульсаций потока кислорода к поверхности электрода при одинаковых прочих условиях.

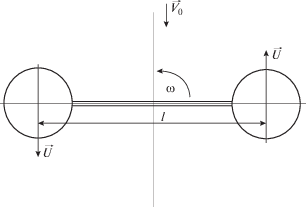
Пусть электрод выполнен в виде пары плоских контактных площадок в форме круга с радиусом R, установленных на расстоянии l между их центрами на концах перекладины, вращающейся с угловой скоростью $\omega $ вокруг оси, проходящей через ее середину (рис. 1). На электрод набегает поток жидкости со скоростью V₀, вектор которой параллелен плоскости контактных площадок.

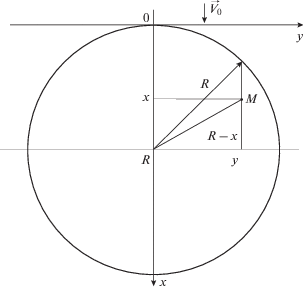
Рассмотрим сначала движение электролита относительно одной контактной площадки в отсутствие вращения перекладины (рис. 2). Расстояние от произвольной точки M(x; y) до края площадки в направлении оси x равно $\sqrt {{{R}^{2}} - {{y}^{2}}} + x - R$. Заряд поверхности площадки определяется количеством адсорбированных атомов кислорода, которое в свою очередь определяется величиной потока кислорода при его диффузии на поверхность площадки. Толщина диффузионного слоя на гладкой пластинке, на край которой набегает поток электролита со скоростью ${{\vec {V}}_{0}}$ [12], определяется по формуле

где $x$ – расстояние от передней кромки пластинки до точки наблюдения, $\nu $ – кинематическая вязкость электролита. У водного электролита $\nu \approx {{10}^{{ - 6}}}\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Толщина диффузионного слоя в нашем случае в точке M (x; y) равна

Плотность потока диффузии кислорода к поверхности площадки имеет вид

Поток на всю контактную площадку вычисляем по формуле

Применив тригонометрическую подстановку $y = \cos \varphi $, приведем интеграл к табличному виду, выражающемуся через гамма-функцию:

Сравнивая полученное значение с потоком на квадратную площадку той же площади (вектор скорости перпендикулярен к стороне квадрата), можно убедиться, что последний больше всего на 3.6%, т.е. они практически равны.

Найдем эффективную толщину диффузионного слоя, полагая, что на всей площади круглой контактной площадки она одинакова:

Вычислим теперь поток диффузии кислорода на весь электрод. Рассмотрим положение перекладины, при котором первая контактная площадка со скоростью $U = {{\omega l} \mathord{\left/ {\vphantom {{\omega l} 2}} \right. \kern-0em} 2}$ движется навстречу потоку электролита, а вторая – с такой же скоростью – по направлению потока (см. рис. 1). В результате первая из них имеет скорость относительно жидкости $U + {{V}_{0}}$, а вторая $U - {{V}_{0}}$. Полагаем, что U $ \gg $ V₀. В соответствии с (7) поток кислорода, диффундирующего из толщи электролита к поверхности двух контактных площадок (${{{\text{моль}}} \mathord{\left/ {\vphantom {{{\text{моль}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$), имеет вид

При скачке скорости $\Delta {{V}_{0}} \ll {{V}_{0}}$ ($U \gg {{V}_{0}}$) получим скачок потока кислорода (здесь мы не учитываем инерционность процесса изменения толщины диффузионного слоя, которая проявляется на частотах выше 30 Гц [10]):

В отсутствие вращения электрода поток кислорода на обе площадки будет иметь вид

Скачок потока, соответствующий скачку скорости $\Delta {{V}_{0}}$, имеет вид

Сравнивая (10) и (12), видим, что при вращении электрода абсолютная пульсация потока, а следовательно, и пульсация потенциала электрода уменьшилась в $2{{({U \mathord{\left/ {\vphantom {U {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}})}^{{1.5}}}$. При $U = 10{{V}_{0}}$ это уменьшение составляет 63 раза.

Вследствие круглой формы площадок гидродинамика их обтекания при вращении перекладины не меняется. Изменяется лишь модуль скорости жидкости относительно поверхности площадки. Рассмотрим теперь положение перекладины после ее поворота на 90^о против часовой стрелки, при котором контактные площадки движутся перпендикулярно к вектору скорости набегающего потока электролита. В этом случае в формулу (7) вместо ${{V}_{0}}$ следует подставить $\sqrt {V_{0}^{2} + {{U}^{2}}} $. При этом поток кислорода на обе контактные площадки определяется выражением

а изменение потока на обе площадки, вызванное скачком скорости $\Delta {{V}_{0}} \ll U$, примет вид

Как видно из сравнения (12) и (14), пульсации потенциала электрода уменьшились в ${{({U \mathord{\left/ {\vphantom {U {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}})}^{{1.5}}}$, что составляет 31.5 раз.

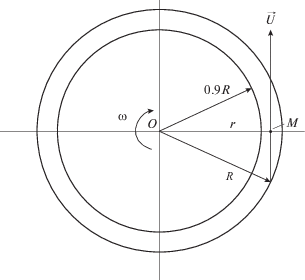
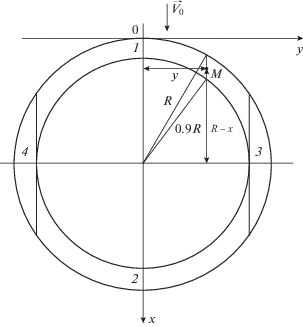
Более интересной для практического применения является форма электрода в виде кольца или диска. Пусть электрод выполнен в форме узкого кольца с внешним радиусом R и внутренним радиусом 0.9R. Найдем поток диффузии кислорода на неподвижное кольцо, на которое вдоль оси x (рис. 3) набегает поток электролита со скоростью ${{\vec {V}}_{0}}$. Разделим кольцо на четыре части. Две из них – это правый и левый сегменты (1, 2), ограниченные хордами, проходящими по внутренней стороне кольца. Две другие – это верхняя и нижняя части кольца (3, 4), отсеченные хордами. Условия обтекания их можно считать одинаковыми, поскольку кольцо узкое. Также одинаковы и условия обтекания сегментов. Найдем поток диффузии на верхнюю часть кольца (см. рис. 3, 1). Произвольная точка M(x; y) отстоит от верхнего края кольца по направлению вектора ${{\vec {V}}_{0}}$ на расстояние $\sqrt {{{R}^{2}} - {{y}^{2}}} + x - R$. Толщина диффузионного слоя в точке M (x; y) определяется выражением (4). Поток диффузии кислорода на верхнюю часть кольца определяется таким же интегралом, что и (6), только с другими пределами интегрирования:

Поток диффузии на обе части кольца, верхнюю и нижнюю, в два раза больше и определяется следующей формулой:

Найдем поток диффузии на правый сегмент, обозначенный цифрой 3. Он тоже определяется интегралом (6), но с другими пределами интегрирования:

Сделав замену ${y \mathord{\left/ {\vphantom {y R}} \right. \kern-0em} R} = \cos \varphi $, получим

Поток ${{I}_{4}}$ на левый сегмент такой же, поток диффузии на все кольцо –

Пульсация потока диффузии при пульсации скорости жидкости $\Delta {{V}_{0}}$ имеет вид

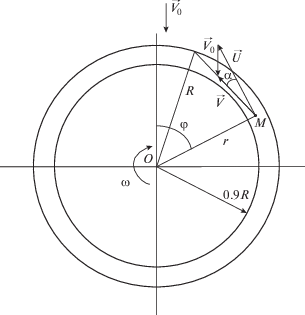
Рассмотрим теперь диффузию кислорода на кольцевой электрод, вращающийся с угловой скоростью $\omega $ в неподвижной жидкости. В системе отсчета, связанной с кольцом, жидкость вращается относительно него с той же угловой скоростью в противоположную сторону. Расстояние от произвольной точки $M$, расположенной на расстоянии $r$ от центра кольца, до внешнего края кольца по направлению вектора $\vec {U}$ скорости жидкости относительно электрода (по перпендикуляру к радиусу OM) равно $\sqrt {{{R}^{2}} - {{r}^{2}}} $ (рис. 4). При этом модуль вектора скорости жидкости равен $U = \omega r$. В соответствии с (3) толщину диффузионного слоя вычисляем по

Поток диффузии на элементарную площадку $rdrd\varphi $ в окрестностях точки M определяем по формуле

а поток на весь кольцевой электрод –

Эффективная толщина диффузионного слоя на кольцевом вращающемся электроде с внутренним радиусом 0.9 R равна

Сравним полученную формулу (22) с потоком ${{I}_{{\text{д}}}}$ на диск радиусом R, известным из [12]. Получаем ${{{{I}_{{\text{к}}}}} \mathord{\left/ {\vphantom {{{{I}_{{\text{к}}}}} {{{I}_{{\text{д}}}}}}} \right. \kern-0em} {{{I}_{{\text{д}}}}}} = 0.285$, т.е. наш результат не противоречит известному. Отношение потока диффузии на вращающееся кольцо к потоку на такой же неподвижный электрод в соответствии с (18) и (22) равно $0.4\sqrt {{{\omega R} \mathord{\left/ {\vphantom {{\omega R} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}} $. При высокой скорости вращения это отношение больше единицы вследствие уменьшения толщины диффузионного слоя.

Пусть теперь на вращающийся кольцевой электрод набегает поток электролита, имеющий скорость ${{V}_{0}}$ и пульсацию скорости $\Delta {{V}_{0}}$. Вектор $\vec {V}$ скорости жидкости относительно электрода в точке М определяется суммой вектора $\vec {U}$ скорости неподвижной жидкости относительно электрода и вектора ${{\vec {V}}_{0}}$ скорости набегающего на электрод потока. Из треугольника скоростей в соответствии с рис. 5 по теореме синусов получаем

где $V$ – скорость жидкости относительно электрода в точке $M$. По теореме косинусов имеем

Также по теореме косинусов найдем расстояние $l$ от точки $M$ до внешнего края кольца по направлению вектора $\vec {V}$:

Принимая во внимание, что $\sin \alpha = \frac{{{{V}_{0}}}}{V}\cos \varphi $, имеем

В соответствии с (3) толщина диффузионного слоя в точке $M$ равна

Сделаем упрощения. При ${{V}_{0}} \ll \omega r$ получим $V \approx \omega r$. Тогда

Поток диффузии на элементарную площадку в окрестностях точки M будет равен

а поток диффузии на весь электрод –

После введения новой переменной $t = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$ интеграл принимает вид, более удобный для вычисления:

Пусть ${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {\omega R}}} \right. \kern-0em} {\omega R}} = 0.05$. Тогда

Поток практически не отличается от (22), что ожидаемо. Посмотрим, как влияет на поток диффузии пульсация скорости ${{V}_{0}}$. Обозначим через $J(x)$ двойной интеграл в (30), где $x = {{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {\omega R}}} \right. \kern-0em} {\omega R}}$. Расчет по формуле (30) при ${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {\omega R}}} \right. \kern-0em} {\omega R}} = 0.05$ дает значение ${{\Delta J} \mathord{\left/ {\vphantom {{\Delta J} {\Delta x}}} \right. \kern-0em} {\Delta x}} = 0.43$ (вычислено при ${{\Delta {{V}_{0}}} \mathord{\left/ {\vphantom {{\Delta {{V}_{0}}} {\omega R}}} \right. \kern-0em} {\omega R}} = 0.001$, т.е. для изменения скорости ${{V}_{0}}$ на 2%). Это значит, что пульсация потока диффузии за счет пульсации скорости $\Delta {{V}_{0}}$ равна

Сравнивая формулы (32) и (19), можно видеть, что пульсация потока диффузии на вращающийся электрод в $3.56\sqrt {{{\omega R} \mathord{\left/ {\vphantom {{\omega R} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}} = 15$ раз меньше, чем на неподвижный. Убедимся, что отношение ${{\omega R} \mathord{\left/ {\vphantom {{\omega R} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$, равное 20, достижимо в практических задачах. Пусть скорость вращения электрода равна 100 об/с, т.е. $\omega = 628\,\,{{{\text{с}}}^{{ - 1}}}$. Такая скорость технически реализуема и гарантирует, что помеха, связанная с эксцентриситетом электрода, не попадет в диапазон частот измеряемого сигнала, который обычно находится в области ниже 100 Гц. При внешнем радиусе кольца R = 0.2 м линейная скорость точек на краю кольцевого электрода имеет величину около 126 м/с. Если скорость набегающего потока ${{V}_{0}}$, равная скорости буксировки датчика, в 20 раз меньше, то она составляет около 6.3 м/с. Такая скорость буксировки датчика вполне соответствует практическим задачам. Следовательно, влияние пульсаций набегающего потока можно уменьшить, как минимум, на порядок.

Таким образом, применение вращающихся электродов в датчике электрического поля в электролите позволяет уменьшить электродный шум движения более чем на порядок и практически во столько же раз повысить чувствительность датчика. Физически уменьшение шума движения объясняется тем, что, во-первых, толщина диффузионного слоя нелинейно зависит от скорости жидкости. Поэтому вращение электрода снижает чувствительность электрода к пульсациям скорости. Во-вторых, пульсации потока диффузии в диаметрально противоположных точках электрода противофазны, поэтому частично вычитаются. Размер электрода вносит ограничение в величину выигрыша по чувствительности. При большой величине радиуса R становится заметна неоднородность набегающего потока жидкости по скорости в пределах одного электрода. Скачок скорости $\Delta {{V}_{0}}$ в диаметрально противоположных точках кольца становится неодинаковым, поэтому невозможно полное вычитание пульсаций потока диффузии. Кроме того, если на неподвижный датчик набегает поток морской воды со скоростью ${{V}_{0}}$ порядка единиц метров в секунду, то при радиусе электрода порядка десятых долей метра временная задержка в воздействии пульсации скорости на диаметрально противоположные участки кольца достигает величины порядка десятых долей секунды. Это приводит к тому, что эффективно подавляются только низкочастотные составляющие шума движения. Уменьшая размер электрода, можно расширить диапазон частот, в котором шум движения в значительной степени подавлен, до нескольких десятков герц. Чтобы не увеличивать тепловой шум датчика, можно вместо одного большого вращающегося электрода применить несколько небольших электродов, электрически соединенных между собой. Если же датчик буксируется за кораблем, то пульсации скорости, связанные с буксировкой, действуют на всей площади электрода одновременно и ограничения на полосу частот, в которой шум движения эффективно подавляется, отсутствуют. Для исключения влияния помехи, связанной с недостаточной балансировкой электрода, частота вращения электрода должна превышать верхнюю границу частотного диапазона принимаемого сигнала.

Вычислить пульсацию потока кислорода на вращающийся дисковый электрод значительно сложнее, поскольку при его вращении вектор скорости жидкости относительно электрода имеет три пространственные компоненты. При этом толщина диффузионного слоя постоянна практически на всей площади электрода и определяется скоростью вращения, поэтому влияние пульсаций скорости набегающей жидкости ослаблено, как и у кольцевого электрода. Также вычитание пульсаций потока диффузии в диаметрально противоположных точках при пульсациях скорости буксировки происходит как у кольцевого, так и у дискового электрода. Поэтому для дискового электрода можно ожидать такого же подавления шума движения, т.е. в десятки раз.