Радиотехника и электроника, 2021, T. 66, № 5, стр. 431-435

Решение задачи рассеяния на теле вращения с кусочно-аналитической формой образующей гибридным методом. Осевое падение

В. А. Калошин^a, *, Д. Т. Луу^b, **

^a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, корп. 7, Российская Федерация

^b Московский физико-технический институт (национальный исследовательский университет)
141700 Долгопрудный, Московской обл., Институтский пер., 9, Российская Федерация

^* E-mail: vak@cplire.ru
^** E-mail: luuductho@phystech.edu

Поступила в редакцию 24.12.2019
После доработки 15.01.2020
Принята к публикации 17.01.2020

DOI: 10.31857/S0033849421050065

Полный текст (PDF)

Аннотация

Рассмотрена задача рассеяния плоской электромагнитной волны, падающей вдоль оси на круглый идеально-проводящий цилиндр, ограниченный по торцам полусферами. Для решения задачи использован гибридный метод, сочетающий метод собственных функций, последовательных дифракций и принцип эквивалентности. Проведено сравнение результатов расчета диаграммы рассеяния двумя вариантами гибридного метода, методом моментов и методом Гюйгенса–Френеля–Кирхгофа.

ВВЕДЕНИЕ

При решении задач рассеяния акустических и электромагнитных волн на телах вращения с кусочно-аналитической формой поверхности применяются как численные методы: моментов, конечных элементов, конечных разностей во временной области, Т-матриц, так и асимптотические: метод Гюйгенса–Френеля–Кирхгофа (ГФК), геометрическая теория дифракции, метод параболического уравнения [1–5].

В случае когда хотя бы один из характерных электрических размеров задачи мал, асимптотические методы приводят к серьезным погрешностям. Если хотя бы один из этих размеров велик, использование численных методов требует больших размеров оперативной памяти компьютера. В работах [6, 7] предложен гибридный метод решения подобных задач и в качестве примера решена двумерная задача рассеяния на цилиндре с кусочно-аналитической образующей.

Гибридный метод основан на сочетании метода собственных функций, последовательных дифракций и принципа эквивалентности (строгой формулировки метода ГФК).

В данной работе гибридный метод, предложенный в работах [6, 7], использован для решения трехмерной задачи рассеяния плоской электромагнитной волны на теле вращения в виде кругового цилиндра, ограниченного по торцам полусферами.

1. РЕШЕНИЕ ЗАДАЧИ ГИБРИДНЫМ МЕТОДОМ

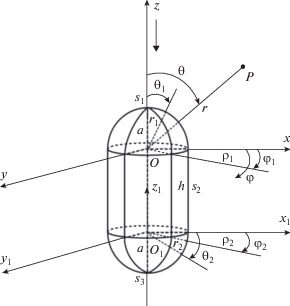
Пусть на идеально-проводящей цилиндр вдоль его оси падает плоская электромагнитная волна, вектор электрического поля которой для определенности параллелен оси x, где a – радиус полусфер, h – длина цилиндра (рис. 1). Решение задачи рассеяния плоской волны сводится к задаче нахождения тока на поверхности тела S. Разобьем поверхность S на три участка: S₁ и S₃ (поверхности полусфер) и S₂ (поверхность цилиндра), и рассмотрим последовательное рассеяние плоской волны на этих поверхностях.

Рис. 1.

Геометрия задачи.

Решение задачи рассеяния на поверхности S₁ будем искать в виде ряда по собственным функциям (ряда Ми) [1, 2]. Компоненты полного поля в сферических координатах (r₁, θ₁, φ₁) при этом имеют вид:

$\begin{gathered} {{E}_{{{{r}_{1}}}}} = \frac{1}{{{{r}_{1}}}}\sum\limits_{m = 0}^\infty {m(m + 1)} U_{m}^{э},\,\,\,\,{{H}_{{{{\varphi }_{1}}}}} = i\omega {{\varepsilon }_{a}}\sum\limits_{m = 0}^\infty {\frac{{\partial U_{m}^{э}}}{{\partial {{\theta }_{1}}}}} + \\ + \,\,\frac{1}{{{{r}_{1}}\sin ({{\theta }_{1}})}}\sum\limits_{m = 0}^\infty {\frac{{{{\partial }^{2}}({{r}_{1}}U_{m}^{м})}}{{\partial {{\varphi }_{1}}\partial {{r}_{1}}}}} ,\,\,\,\,{{H}_{{{{r}_{1}}}}} = \frac{1}{{{{r}_{1}}}}\sum\limits_{m = 0}^\infty {m(m + 1)} U_{m}^{м}, \\ \end{gathered} $

(1)

$\begin{gathered} {{H}_{{{{\theta }_{1}}}}} = \frac{{ - i\omega {{\varepsilon }_{a}}}}{{\sin ({{\theta }_{1}})}}\sum\limits_{m = 0}^\infty {\frac{{\partial U_{m}^{э}}}{{\partial {{\varphi }_{1}}}}} + \frac{1}{{{{r}_{1}}}}\sum\limits_{m = 0}^\infty {\frac{{{{\partial }^{2}}({{r}_{1}}U_{m}^{м})}}{{\partial {{\theta }_{1}}\partial {{r}_{1}}}}} , \\ {{E}_{{{{\varphi }_{1}}}}} = \frac{1}{{{{r}_{1}}\sin ({{\theta }_{1}})}}\sum\limits_{m = 0}^\infty {\frac{{{{\partial }^{2}}({{r}_{1}}U_{m}^{э})}}{{\partial {{\varphi }_{1}}\partial {{r}_{1}}}}} - i\omega {{\mu }_{a}}\sum\limits_{m = 0}^\infty {\frac{{\partial U_{m}^{м}}}{{d{{\theta }_{1}}}}} , \\ {{E}_{{{{\theta }_{1}}}}} = \frac{1}{{{{r}_{1}}}}\sum\limits_{m = 0}^\infty {\frac{{{{\partial }^{2}}({{r}_{1}}U_{m}^{э})}}{{\partial {{\theta }_{1}}\partial {{r}_{1}}}}} + \frac{{i\omega {{\mu }_{a}}}}{{\sin {{\theta }_{1}}}}\sum\limits_{m = 0}^\infty {\frac{{\partial U_{m}^{м}}}{{\partial {{\varphi }_{1}}}}} , \\ U_{m}^{э} = \frac{{2m + 1}}{{m(m + 1)}}\frac{{{{{\left( { - i} \right)}}^{{m - 1}}}}}{k} \times \\ \times \,\,\left[ {{{\psi }_{m}}(k{{r}_{1}}) - \xi _{m}^{{(1)}}(k{{r}_{1}})\frac{{\frac{{\partial (a{{\psi }_{m}}(ka))}}{{\partial a}}}}{{\frac{{\partial (a\xi _{m}^{{(1)}}(ka))}}{{\partial a}}}}} \right]P_{m}^{1}\left( {cos({{\theta }_{1}})} \right)cos({{\varphi }_{1}}), \\ U_{m}^{м} = - \frac{{2m + 1}}{{m(m + 1)}}\frac{{{{{\left( { - i} \right)}}^{{m - 1}}}\omega {{\varepsilon }_{a}}}}{{{{k}^{2}}}} \times \\ \times \,\,\left[ {{{\psi }_{m}}(k{{r}_{1}}) - \xi _{m}^{{(1)}}(k{{r}_{1}})\frac{{{{\psi }_{m}}(ka)}}{{\xi _{m}^{{(1)}}(ka)}}} \right]P_{m}^{1}\left( {cos({{\theta }_{1}})} \right)sin({{\varphi }_{1}}), \\ \end{gathered} $

где ${{\psi }_{m}}$ – сферические функции Бесселя, $\xi _{m}^{1}$ – сферические функции Ханкеля, $P_{m}^{1}$ – функция Лежандра.

Токи на полусфере S₁ определяются по формулам: ${{j}_{{{{\theta }_{1}}}}} = {{H}_{{{{\varphi }_{1}}}}}$, ${{j}_{{{{\varphi }_{1}}}}} = - {{H}_{{{{\theta }_{1}}}}}$, r₁ = a, а выражения для компонент магнитного поля приведены в (1).

В цилиндрической системе координат (ρ₁, φ₁, z) эквивалентные токи на плоскости xy имеют вид:

(2)

$J_{{{{\varphi }_{1}}}}^{э} = - {{H}_{{{{\rho }_{1}}}}},\,\,\,\,J_{{{{\rho }_{1}}}}^{м} = - {{E}_{{{{\varphi }_{1}}}}},\,\,\,\,J_{{{{\rho }_{1}}}}^{э} = {{H}_{{{{\varphi }_{1}}}}},\,\,\,\,J_{{{{\varphi }_{1}}}}^{м} = {{E}_{{{{\rho }_{1}}}}}.$

Далее определим векторные потенциалы в области между плоскостями xy и x₁y₁ по формулам:

(3)

$\begin{gathered} {{A}_{r}} = \oint\limits_S {\left[ {{{J}_{r}}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) + {{J}_{\varphi }}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} \,GdS, \\ {{A}_{\varphi }} = \oint\limits_S {\left[ {{{J}_{\varphi }}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) - {{J}_{r}}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} \,GdS. \\ \end{gathered} $

В результате получим

(4)

$\begin{gathered} A_{{{{\varphi }_{2}}}}^{э} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{1}}\left[ {J_{{{{\varphi }_{1}}}}^{э}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) - J_{{{{\rho }_{1}}}}^{э}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} } \times \\ \times \,\,{{G}_{1}}d{{\varphi }_{1}}d{{\rho }_{1}}, \\ A_{{{{\varphi }_{2}}}}^{м} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{1}}\left[ {J_{{{{\varphi }_{1}}}}^{м}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) - J_{{{{\rho }_{1}}}}^{м}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} } \times \\ \times \,\,{{G}_{1}}d{{\varphi }_{1}}d{{\rho }_{1}}, \\ A_{{{{\rho }_{2}}}}^{э} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{1}}\left[ {J_{{{{\rho }_{1}}}}^{э}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) + J_{{{{\varphi }_{1}}}}^{э}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} } \times \\ \times \,\,{{G}_{1}}d{{\varphi }_{1}}d{{\rho }_{1}}, \\ A_{{{{\rho }_{2}}}}^{м} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{1}}\left[ {J_{{{{\rho }_{1}}}}^{м}\cos ({{\varphi }_{2}} - {{\varphi }_{1}}) + J_{{{{\varphi }_{1}}}}^{м}sin({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} } \times \\ \times \,\,{{G}_{1}}d{{\varphi }_{1}}d{{\rho }_{1}}, \\ \end{gathered} $

где

$\begin{gathered} {{G}_{1}} = \frac{{ - 1}}{{8\pi i}}\sum\limits_{m = - \infty }^\infty {\exp \left[ {im({{\varphi }_{2}} - {{\varphi }_{1}})} \right]} \times \\ \times \,\,\int\limits_{\eta = - \infty }^\infty {\left[ {{{J}_{m}}(\eta {{\rho }_{ < }}) - \frac{{\Omega {{J}_{m}}(\eta a)}}{{\Omega H_{m}^{{(1)}}(\eta a)}}H_{m}^{{(1)}}(\eta {{\rho }_{ < }})} \right]H_{m}^{{(1)}}(\eta {{\rho }_{ > }})} \times \\ \times \,\,\frac{{exp\left[ {i\sqrt {{{k}^{2}} - {{\eta }^{2}}} \left| z \right|} \right]}}{{\sqrt {{{k}^{2}} - {{\eta }^{2}}} }}\eta d\eta \\ \end{gathered} $

– функция Грина на цилиндре [2], $\Omega = 1$ – для нахождения компонент поля ${{E}_{{{{\varphi }_{2}}}}}$ и ${{H}_{{{{\rho }_{2}}}}}$, $\Omega = {\partial \mathord{\left/ {\vphantom {\partial {\partial a}}} \right. \kern-0em} {\partial a}}$ – для нахождения компоненты поля ${{H}_{{{{\varphi }_{2}}}}}$, ${{E}_{{{{\rho }_{2}}}}}$ и ${{H}_{z}}$, ρ_< = ρ₁, ρ_> = ρ₂ при ρ₂ > ρ₁ и ρ_< = ρ₂, ρ_> = ρ₁ при ρ₂ < ρ₁.

Компоненты полного поля в области между плоскостями xy и x₁y₁ вычисляются по формулам

$\begin{gathered} {{E}_{{{{\varphi }_{2}}}}} = \frac{1}{{ - i\omega {{\varepsilon }_{a}}}}\left[ {{{k}^{2}}A_{{{{\varphi }_{2}}}}^{э} + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}} \right. \times \\ \times \,\,\left. {\left[ {\frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\rho }_{2}}}}\left( {{{\rho }_{2}}A_{{{{\rho }_{2}}}}^{э}} \right) + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\varphi }_{2}}}}^{э}} \right]} \right] - \frac{\partial }{{\partial z}}A_{{{{\rho }_{2}}}}^{м}, \\ {{H}_{{{{\rho }_{2}}}}} = \frac{1}{{ - i\omega {{\mu }_{a}}}}\left[ {{{k}^{2}}A_{{{{\rho }_{2}}}}^{м} + \frac{\partial }{{\partial {{\rho }_{2}}}}} \right. \times \\ \times \,\,\left. {\left[ {\frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\rho }_{2}}}}\left( {{{\rho }_{2}}A_{{{{\rho }_{2}}}}^{м}} \right) + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\varphi }_{2}}}}^{м}} \right]} \right] - \frac{\partial }{{\partial z}}A_{{{{\varphi }_{2}}}}^{э}, \\ {{H}_{z}} = \frac{1}{{ - i\omega {{\mu }_{a}}}}\frac{\partial }{{\partial z}}\left[ {\frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\rho }_{2}}}}({{\rho }_{2}}A_{{{{\rho }_{2}}}}^{м}) + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\varphi }_{2}}}}^{м}} \right] + \\ + \,\,\frac{1}{{{{\rho }_{2}}}}\left[ {\frac{\partial }{{\partial {{\rho }_{2}}}}\left( {{{\rho }_{2}}A_{{{{\varphi }_{2}}}}^{э}} \right) - \frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\rho }_{2}}}}^{э}} \right], \\ \end{gathered} $

(5)

$\begin{gathered} {{E}_{{{{\rho }_{2}}}}} = \frac{1}{{ - i\omega {{\varepsilon }_{a}}}}\left[ {{{k}^{2}}A_{{{{\rho }_{2}}}}^{э} + \frac{\partial }{{\partial {{\rho }_{2}}}}} \right. \times \\ \times \,\,\left. {\left[ {\frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\rho }_{2}}}}\left( {{{\rho }_{2}}A_{{{{\rho }_{2}}}}^{э}} \right) + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\varphi }_{2}}}}^{э}} \right]} \right] + \frac{\partial }{{\partial z}}A_{{{{\varphi }_{2}}}}^{м}, \\ {{H}_{{{{\varphi }_{2}}}}} = \frac{1}{{ - i\omega {{\mu }_{a}}}}\left[ {{{k}^{2}}A_{{{{\varphi }_{2}}}}^{м} + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}} \right. \times \\ \times \,\,\left. {\left[ {\frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\rho }_{2}}}}\left( {{{\rho }_{2}}A_{{{{\rho }_{2}}}}^{м}} \right) + \frac{1}{{{{\rho }_{2}}}}\frac{\partial }{{\partial {{\varphi }_{2}}}}A_{{{{\varphi }_{2}}}}^{м}} \right]} \right] + \frac{\partial }{{\partial z}}A_{{{{\rho }_{2}}}}^{э}. \\ \end{gathered} $

Подставляя в формулу (5) значение ρ₂ = a, находим компоненты магнитного поля и тока ${{j}_{{{{\varphi }_{2}}}}} = {{H}_{z}}$, ${{j}_{z}} = - {{H}_{{{{\varphi }_{2}}}}}$ на поверхности S₂. Далее находим токи на полусфере S₃ с использованием токового варианта гибридного метода:

(6)

$\begin{gathered} {{j}_{{{{\theta }_{3}}}}} = \frac{1}{{{{r}_{3}}}}\left[ {\frac{\partial }{{\partial {{r}_{3}}}}({{r}_{3}}A_{{{{\theta }_{3}}}}^{э}) - \frac{\partial }{{\partial {{\theta }_{3}}}}A_{{{{r}_{3}}}}^{э}} \right] + \exp (ikh){{j}_{{{{\theta }_{1}}}}}, \\ {\text{при}}\,\,{{r}_{3}} = a, \\ {{j}_{{{{\varphi }_{3}}}}} = \frac{{ - 1}}{{{{r}_{3}}}}\left[ {\frac{1}{{\sin {{\theta }_{3}}}}\frac{\partial }{{\partial {{\varphi }_{3}}}}(A_{{{{r}_{3}}}}^{э}) - \frac{\partial }{{\partial {{r}_{3}}}}({{r}_{3}}A_{{{{\varphi }_{3}}}}^{э})} \right] + \exp (ikh){{j}_{{{{\varphi }_{1}}}}}, \\ \end{gathered} $

где

$\begin{gathered} A_{{{{r}_{3}}}}^{э} = \sin {{\theta }_{3}}\int\limits_0^h {\int\limits_0^{2\pi } {a {{j}_{{{{\varphi }_{2}}}}}\sin ({{\varphi }_{3}} - {{\varphi }_{2}})} } \,{{G}_{2}}dzd{{\varphi }_{2}} + \\ + \,\,\cos {{\theta }_{3}}\int\limits_0^h {\int\limits_0^{2\pi } {a {{j}_{z}}} } {{G}_{2}}dzd{{\varphi }_{2}}, \\ A_{{{{\theta }_{3}}}}^{э} = \cos {{\theta }_{3}}\int\limits_0^h {\int\limits_0^{2\pi } {a {{j}_{{{{\varphi }_{2}}}}}\sin ({{\varphi }_{3}} - {{\varphi }_{2}})} } \,{{G}_{2}}dzd{{\varphi }_{2}} - \\ - \,\,\sin {{\theta }_{3}}\int\limits_0^h {\int\limits_0^{2\pi } {a {{j}_{z}}} } {{G}_{2}}dzd{{\varphi }_{2}}, \\ A_{{{{\varphi }_{3}}}}^{э} = \int\limits_0^h {\int\limits_0^{2\pi } {a {{j}_{{{{\varphi }_{2}}}}}cos({{\varphi }_{3}} - {{\varphi }_{2}})\,} } {{G}_{2}}dzd{{\varphi }_{2}}, \\ {{G}_{2}} = \frac{{ - k}}{{4\pi i}}\sum\limits_{m = 0}^\infty {\sum\limits_{n = m}^\infty {{{\varepsilon }_{m}}\frac{{\left( {2n + 1} \right)\left( {n - m} \right)!}}{{\left( {n + m} \right)!}} \times } } \\ \times \,\,\left[ {{{\psi }_{n}}(k{{r}_{3}}) - \frac{{{{\partial (a{{\psi }_{n}}(ka))} \mathord{\left/ {\vphantom {{\partial (a{{\psi }_{n}}(ka))} {\partial a}}} \right. \kern-0em} {\partial a}}}}{{\partial (a\xi _{n}^{{(1)}}{{(ka))} \mathord{\left/ {\vphantom {{(ka))} {\partial a}}} \right. \kern-0em} {\partial a}}}}\xi _{n}^{{(1)}}(k{{r}_{3}})} \right]\xi _{n}^{{(1)}}(k\sqrt {{{a}^{2}} + {{z}^{2}}} ), \\ \cos m({{\varphi }_{3}} - {{\varphi }_{2}})P_{n}^{m}(cos{{\theta }_{3}})P_{n}^{m}\left( {cos\left( {\operatorname{arct} {\kern 1pt} {\text{g}}({a \mathord{\left/ {\vphantom {a z}} \right. \kern-0em} z})} \right)} \right) \\ \end{gathered} $

– функция Грина на сфере [2].

Найдем токи на полусфере S₃ с использованием апертурного варианта гибридного метода. Подставляя в формулу (5) значения z = –h, находим компоненты поля в плоскости x₁y₁ по формулам:

(7)

$J_{{{{\varphi }_{2}}}}^{э} = - {{H}_{{{{\rho }_{2}}}}},\,\,\,\,J_{{{{\rho }_{2}}}}^{м} = - {{E}_{{{{\varphi }_{2}}}}},\,\,\,\,J_{{{{\rho }_{2}}}}^{э} = {{H}_{{{{\varphi }_{2}}}}},\,\,\,\,J_{{{{\varphi }_{2}}}}^{м} = {{E}_{{{{\rho }_{2}}}}}.$

Векторные потенциалы в сферических координатах имеют вид:

(8)

$\begin{gathered} A_{{{{\varphi }_{3}}}}^{э} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\varphi }_{2}}}}^{э}\cos ({{\varphi }_{3}} - {{\varphi }_{2}}) - J_{{{{\rho }_{2}}}}^{э}sin({{\varphi }_{3}} - {{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}, \\ A_{{{{\varphi }_{3}}}}^{м} = \int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\varphi }_{2}}}}^{м}\cos ({{\varphi }_{3}} - {{\varphi }_{2}}) - J_{{{{\rho }_{2}}}}^{м}sin({{\varphi }_{3}} - {{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}, \\ A_{{{{r}_{3}}}}^{э}\, = \,\sin {{\theta }_{3}}\int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\rho }_{2}}}}^{э}\cos ({{\varphi }_{3}}\, - \,{{\varphi }_{2}})\, + \,J_{{{{\varphi }_{2}}}}^{э}sin({{\varphi }_{3}}\, - \,{{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}, \\ A_{{{{r}_{3}}}}^{м}\, = \,\sin {{\theta }_{3}}\int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\rho }_{2}}}}^{м}\cos ({{\varphi }_{3}}\, - \,{{\varphi }_{2}})\, + \,J_{{{{\varphi }_{2}}}}^{м}sin({{\varphi }_{3}}\, - \,{{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}, \\ A_{{{{\theta }_{3}}}}^{э} = \cos {{\theta }_{3}}\int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\rho }_{2}}}}^{э}\cos ({{\varphi }_{3}} - {{\varphi }_{2}}) + J_{{{{\varphi }_{2}}}}^{э}sin({{\varphi }_{3}} - {{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}, \\ A_{{{{\theta }_{3}}}}^{м} = \cos {{\theta }_{3}}\int\limits_a^\infty {\int\limits_0^{2\pi } {{{\rho }_{2}}\left[ {J_{{{{\rho }_{2}}}}^{м}\cos ({{\varphi }_{3}} - {{\varphi }_{2}}) + J_{{{{\varphi }_{2}}}}^{м}sin({{\varphi }_{3}} - {{\varphi }_{2}})} \right]} } \,{{G}_{2}}d{{\varphi }_{2}}d{{\rho }_{2}}. \\ \end{gathered} $

В результате для тока на поверхности S₃ (r₃ = a) получаем:

(9)

$\begin{gathered} j_{{{{\theta }_{3}}}}^{э} = \frac{{ - 1}}{{i\omega {{\mu }_{a}}}}\left[ {{{k}^{2}}A_{{{{\varphi }_{3}}}}^{м} + \frac{1}{{{{r}_{3}}\sin {{\theta }_{3}}}}\frac{\partial }{{\partial {{\varphi }_{3}}}}\left( {\frac{1}{{{{r}_{3}}^{2}}}\frac{{\partial ({{r}_{3}}^{2}A_{{{{r}_{3}}}}^{м})}}{{\partial {{r}_{3}}}}} \right.} \right. + \left. {\left. {\,\,\frac{1}{{{{r}_{3}}\sin {{\theta }_{3}}}}\frac{{\partial (sin{{\theta }_{3}}A_{{{{\theta }_{3}}}}^{м})}}{{\partial {{\theta }_{3}}}} + \frac{1}{{{{r}_{3}}\sin {{\theta }_{3}}}}\frac{{\partial A_{{{{\varphi }_{3}}}}^{м}}}{{\partial {{\varphi }_{3}}}}} \right)} \right] + \,\,\frac{1}{{{{r}_{3}}}}\left[ {\frac{\partial }{{\partial {{r}_{3}}}}\left( {{{r}_{3}}A_{{{{\theta }_{3}}}}^{э}} \right) - \frac{\partial }{{\partial {{\theta }_{3}}}}A_{{{{r}_{3}}}}^{э}} \right], \\ j_{{{{\varphi }_{3}}}}^{э} = \frac{1}{{i\omega {{\mu }_{a}}}}\left[ {{{k}^{2}}A_{{{{\theta }_{3}}}}^{м} + \frac{1}{{{{r}_{3}}}}\frac{\partial }{{\partial {{\theta }_{3}}}}\left( {\frac{1}{{{{r}_{3}}^{2}}}\frac{{\partial ({{r}_{3}}^{2}A_{{{{r}_{3}}}}^{м})}}{{\partial {{r}_{3}}}}} \right.} \right. + \left. {\left. {\,\frac{1}{{{{r}_{3}}\sin {{\theta }_{3}}}}\frac{{\partial (sin{{\theta }_{3}}A_{{{{\theta }_{3}}}}^{м})}}{{\partial {{\theta }_{3}}}} + \frac{1}{{{{r}_{3}}\sin {{\theta }_{3}}}}\frac{{\partial A_{{{{\varphi }_{3}}}}^{м}}}{{\partial {{\varphi }_{3}}}}} \right)} \right] + \\ + \,\,\frac{1}{{{{r}_{3}}}}\left[ {\frac{1}{{\sin {{\theta }_{3}}}}\left( {{{r}_{3}}A_{{{{\theta }_{3}}}}^{э}} \right) - \frac{\partial }{{\partial {{\theta }_{3}}}}A_{{{{r}_{3}}}}^{э}} \right]. \\ \end{gathered} $

Таким образом, мы нашли токи на всей поверхности тела с использованием двух вариантов гибридного метода. Далее находим диаграмму рассеяния по известной формуле [1]:

(10)

$E = \frac{{ - 1}}{{i\omega {{\varepsilon }_{a}}}}({{k}^{2}}{{A}^{э}} + grad div {{A}^{э}}).$

При интегрировании по S₁ и S₃ будем использовать сферические координаты (r₁, θ₁, φ₁) и (r₃, θ₃, φ₃) с центрами в точке O и O₁ соответственно, а при интегрировании по S₂ – цилиндрическую систему координат.

В результате для диаграммы рассеяния при учете токов на S₁ получаем:

$E_{\varphi }^{1} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\varphi }^{э},\,\,\,\,E_{{_{\theta }}}^{1} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\theta }^{э},$

$\begin{gathered} {\text{где}}\,\,A_{\theta }^{э} = {{a}^{2}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_0^{2\pi } {\sin ({{\theta }_{1}})\frac{\partial }{{\partial \theta }}} } \times \\ \times \,\,\left[ {{{j}_{{{{\theta }_{1}}}}}\frac{{\partial \cos \beta }}{{\partial {{\theta }_{1}}}} + {{j}_{{{{\varphi }_{1}}}}}\frac{1}{{\sin ({{\theta }_{1}})}}\frac{{\partial \cos \beta }}{{\partial {{\varphi }_{1}}}}} \right]{{G}_{0}} d{{\varphi }_{1}}d{{\theta }_{1}}, \\ A_{\varphi }^{э} = \frac{{{{a}^{2}}}}{{\sin (\theta )}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\int\limits_0^{2\pi } {\sin ({{\theta }_{1}})\frac{\partial }{{\partial \varphi }}} } \times \\ \times \,\,\left[ {{{j}_{{{{\theta }_{1}}}}}\frac{{\partial \cos \beta }}{{\partial {{\theta }_{1}}}} + {{j}_{{{{\varphi }_{1}}}}}\frac{1}{{\sin ({{\theta }_{1}})}}\frac{{\partial \cos \beta }}{{\partial {{\varphi }_{1}}}}} \right]{{G}_{0}} d{{\varphi }_{1}}d{{\theta }_{1}}, \\ {{G}_{0}} = \frac{1}{{4\pi }}\frac{{\exp (ikr)}}{r} \times \\ \times \,\,\exp \left[ { - ika\left( {\cos \theta cos{{\theta }_{1}} + sin\theta sin{{\theta }_{1}}cos(\varphi - {{\varphi }_{1}})} \right)} \right] \\ \end{gathered} $

– функция Грина свободного пространства в сферических координатах, $\cos \beta = cos(\theta )cos({{\theta }_{1}}) + $ $ + sin(\theta )sin({{\theta }_{1}})cos(\varphi - {{\varphi }_{1}}).$

Вклад токов на поверхности S₂ в диаграмму рассеяния:

(12)

$E_{\varphi }^{2} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\varphi }^{э},\,\,\,\,E_{{_{\theta }}}^{2} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\theta }^{э},$

где $A_{\theta }^{э}\, = \, - a \sin {\kern 1pt} \theta \int_0^{ - h} {\int_0^{2\pi } {{{j}_{z}}{{G}_{0}}d{{\varphi }_{2}}} } dz,$ $A_{\varphi }^{э}\, = \,a \times $ $ \times \,\,\int_0^{ - h} {\int_0^{2\pi } {\cos (\varphi - {{\varphi }_{2}})} } {{j}_{{{{\varphi }_{2}}}}}{{G}_{0}}d{{\varphi }_{2}}dz.$

Вклад токов на поверхности S₃ в диаграмму рассеяния:

(13)

$E_{\varphi }^{3} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\varphi }^{э},\,\,\,\,E_{{_{\theta }}}^{3} = \frac{{{{k}^{2}}}}{{ - i\omega {{\varepsilon }_{a}}}}A_{\theta }^{э},$

$\begin{gathered} {\text{где}}\,\,A_{\theta }^{э} = {{a}^{2}}\int\limits_{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}}^\pi {\int\limits_0^{2\pi } {\sin ({{\theta }_{3}})\frac{\partial }{{\partial \theta }}} } \times \\ \times \,\,\left[ {{{j}_{{{{\theta }_{3}}}}}\frac{{\partial \cos \beta }}{{\partial {{\theta }_{3}}}} + {{j}_{{{{\varphi }_{3}}}}}\frac{1}{{\sin ({{\theta }_{3}})}}\frac{{\partial \cos \beta }}{{\partial {{\varphi }_{3}}}}} \right]{{G}_{0}} d{{\varphi }_{3}}d{{\theta }_{3}}, \\ A_{\varphi }^{э} = \frac{{{{a}^{2}}}}{{\sin (\theta )}}\int\limits_{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}}^\pi {\int\limits_0^{2\pi } {\sin ({{\theta }_{3}})\frac{\partial }{{\partial \varphi }}} \times } \\ \times \,\,\left[ {{{j}_{{{{\theta }_{3}}}}}\frac{{\partial \cos \beta }}{{\partial {{\theta }_{3}}}} + {{j}_{{{{\varphi }_{3}}}}}\frac{1}{{\sin ({{\theta }_{3}})}}\frac{{\partial \cos \beta }}{{\partial {{\varphi }_{3}}}}} \right]{{G}_{0}} d{{\varphi }_{3}}d{{\theta }_{3}}, \\ \cos \beta = cos(\theta )cos({{\theta }_{3}}) + sin(\theta )sin({{\theta }_{3}})cos(\varphi - {{\varphi }_{3}}). \\ \end{gathered} $

В результате, суммируя вклады всех токов для диаграммы рассеяния, получаем

(14)

$\begin{gathered} {{E}_{\varphi }} = E_{\varphi }^{1} + E_{\varphi }^{2} + \exp \left[ {ikh\cos (\theta )} \right]E_{\varphi }^{3}, \\ {{E}_{\theta }} = E_{\theta }^{1} + E_{\theta }^{2} + \exp \left[ {ikh\cos (\theta )} \right]E_{\theta }^{3}. \\ \end{gathered} $

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

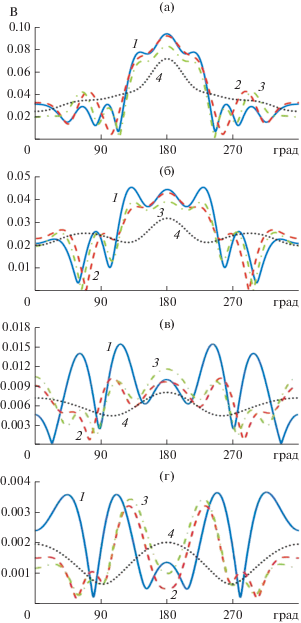
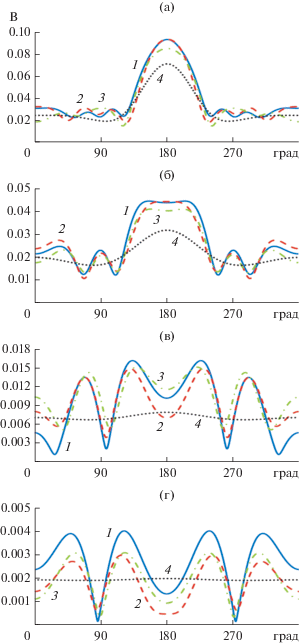
На рис. 2, 3 приведены результаты расчета диаграммы рассеяния плоской волны на цилиндре с электрической длиной kh = 5 для различных ka в Е- и Н-плоскостях соответственно. Кривая 1 показывает результаты расчета методом моментов, 2 – гибридным методом (апертурный вариант), 3 – гибридным методом (токовый вариант), 4 – методом ГФК.

Рис. 2.

Диаграммы рассеяния в E-плоскости (φ = 0) при ka = 3 (а), 2 (б), 1 (в), 0.5 (г).

Рис. 3.

Диаграммы рассеяния в H-плоскости (φ = 90°) при ka = 3 (а), 2 (б), 1 (в), 0.5 (г).

Как видно из рис. 2 и 3 , диаграммы рассеяния в Е-плоскости, рассчитанные методом моментов и гибридным методом, достаточно хорошо совпадают при ka > 2. При этом лучшее совпадение обеспечивает апертурный вариант гибридного метода. Метод ГФК дает только качественное описание диаграммы рассеяния. При ka = 1 и менее совпадение наблюдается только в области рассеяния вперед. В Н-плоскости совпадение результатов, полученное двумя вариантами гибридного метода и методом моментов, наблюдается для всех исследованных значений ka. При этом разница между этими результатами, как и в Е‑плоскости, уменьшается с ростом ka. Метод ГФК не дает даже качественного описания диаграммы рассеяния в Н-плоскости. Наиболее точные результаты расчета при использовании гибридного метода наблюдаются в обеих плоскостях при рассеянии вперед, наименее точные – при рассеянии назад.

ЗАКЛЮЧЕНИЕ

На основании сравнения результатов расчета диаграммы рассеяния двумя вариантами гибридного метода и методом моментов можно сделать следующие выводы.

1. Применение обоих вариантов гибридного метода, в отличие от метода Гюйгенса–Френеля–Кирхгофа, позволяет обеспечить хорошее совпадение с результатами расчета диаграммы рассеяния методом моментов при соотношении радиуса тела вращения к длине волны более 0.3, а в Н-плоскости и для меньших значений.

2. Наиболее точные результаты расчета при использовании гибридного метода наблюдаются при рассеянии вперед, наименее точные – при рассеянии назад, что можно объяснить, во-первых, приближенным характером моделей при вычислении токов на различных частях тела, а во-вторых, учетом последовательных дифракций только в одном направлении.

Список литературы

Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.; Л.: Энергия, 1967.
Фелсен Л., Маркувиц Н. Излучение и рассеяние волн. М.: Мир, 1978.
Боровиков В.А., Кинбер Б.Е. Геометрическая теория дифракции. М.: Связь, 1978.
Фок В.А. Проблемы дифракции и распространения электромагнитных волн. М.: Сов. радио, 1970.
Kleshchev A.A. // J. Acoustics. 2016. V. 6. № 4. P. 45.
Kaloshin V.A., Luu D.T. // Int. Sci. Conf. “Radiation and Scattering of Electromagnetic Waves RSEMW-2019”, Divnomorskoe, 24–28 Jun, 2019. N.Y.: IEEE, P. 232. https:// ieeexplore.ieee.org/document/8792743.
Калошин В.А., Луу Д.Т. // РЭ. 2020. Т. 65. № 5. С. 457.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал