Радиотехника и электроника, 2021, T. 66, № 8, стр. 748-759

ВВЕДЕНИЕ

Для решения задач оптимальной обработки сигналов широкое применение находит теория условных марковских процессов, основы которой были разработаны Р.Л. Стратоновичем [1]. Помимо основных четырех видов марковских процессов [2, 3] могут быть более сложные – дискретно-непрерывные марковские процессы (ДНМП), часть компонентов которых принимает непрерывное, а часть дискретное множество значений [4]. Описание радиоэлектронных систем, успешно функционирующих в сложной динамически изменяющейся сигнально-помеховой обстановке, с помощью аппарата ДНМП оказалось чрезвычайно эффективным. Впервые аппарат ДНМП был применен для решения задачи фильтрации сообщений при непрерывных наблюдениях в работах В.И. Тихонова [5, 6] и затем получил развитие в многочисленных работах других авторов [7–11]. В них получены интегро-дифференциальные уравнения, описывающие эволюцию апостериорной плотности вероятности ДНМП.

Цифровая реализация полученных на основе аппарата ДНМП при непрерывных наблюдениях алгоритмов встречает значительные трудности, вызванные сильной зависимостью точности и устойчивости алгоритмов от величины шага дискретизации. Дальнейшее развитие этот подход получил при решении задач оптимальной обработки ДНМП в дискретном времени [7, 12]. При формировании же цифровых сигналов погрешность квантования ДНМП носит шумовой характер и может моделироваться путем добавления аддитивного шума к сигналу, что не всегда справедливо, так как погрешность квантования аналого-цифровых преобразователей (АЦП) далеко не случайна и, как правило, коррелирована с процессом. Конечно, уменьшение погрешности квантования возможно путем увеличения числа уровней квантования. Однако в системах передачи аналоговых сообщений по цифровым каналам связи [13] и радиолокации [14] это не всегда возможно, кроме того, в некоторых случаях необходимо учитывать статистические характеристики квантователей при расчете коэффициентов чувствительности показателя качества систем управления конечным положением в условиях противодействия среды [15].

Все эти факторы вызывают необходимость разработки методов оптимального оценивания ДНМП в дискретном времени с учетом статистических характеристик квантователей АЦП, адекватных реальным задачам цифровой обработки сигналов радиоэлектронных систем.

1. ПОСТАНОВКА ЗАДАЧИ

Теория построения алгоритмов распознавания и оценивания состояний ДНМП рассмотрена достаточно полно в [5–11], где получены непрерывные уравнения для законов распределения фазовых координат, их моментов и вероятностей состояний дискретных компонентов ДНМП. Для реализации этих уравнений на цифровых вычислительных машинах указанные алгоритмы необходимо синтезировать в дискретной форме в виде рекуррентных соотношений. В связи с этим при синтезе оптимальных алгоритмов цифровой фильтрации непрерывных компонентов ДНМП центральным является вопрос о статистически эквивалентном дискретном представлении стохастических дифференциальных уравнений (СДУ) непрерывных компонентов ДНМП и алгебраических уравнений измерений. Традиционно при формулировке эквивалентной задачи с дискретным временем используются два подхода.

1. Дискретные модели записываются непосредственно для этих уравнений (см., например, в [12]).

2. Априорные уравнения объекта и измерителя в непрерывном времени записываются в разностной форме с интервалом дискретизации ${{\Delta }}$. При этом в уравнении измерений непрерывный белый гауссовский шум (БГШ) приближенно заменяется его допредельной моделью – некоррелированной последовательностью центрированных случайных величин с ковариационной матрицей ${{\mathbf{I}} \mathord{\left/ {\vphantom {{\mathbf{I}} {{\Delta }}}} \right. \kern-0em} {{\Delta }}}$ (например, в [4]), где ${\mathbf{I}}$ – единичная матрица интенсивностей исходного непрерывного БГШ. Применительно к задачам цифровой фильтрации непрерывных компонентов ДНМП это представление является некорректным уже потому, что оно не согласовано с каким-либо техническим способом формирования отсчетов непрерывного измеряемого процесса, а также противоречит физике рассматриваемых явлений [16]. В частности, при увеличении интервала дискретизации $\Delta $ точность оценивания непрерывных компонентов будет увеличиваться, так как будет уменьшаться интенсивность шумов измерений.

Следует отметить, что физически процессы, протекающие в радиоэлектронных системах, являются непрерывными случайными процессами, поэтому для этих систем актуальна задача оптимизации алгоритмов оценивания ДНМП по наблюдаемым цифровым сигналам на основе корректного эквивалентного дискретного представления непрерывных компонентов ДНМП.

Рассмотрим задачу оценивания ${{n}_{x}}$-мерного вектора состояния ${\mathbf{x}}(t)$, описывающего в пространстве состояний динамику фазовых координат ДНМП. Пусть СДУ вектора состояния и уравнение измерений имеют вид

где ${\mathbf{v}}(t)$ – ${{n}_{y}}$-мерный вектор измерений; s(t_k) = $ = {{\left[ {{{a}_{j}}({{t}_{k}}),{{b}_{m}}({{t}_{k}})} \right]}^{T}}$ – дискретная компонента ДНМП – условная марковская цепь с матрицами вероятностей переходов, T – знак транспонирования. смена состояний которой может происходить только в фиксированные моменты времени ${{t}_{k}} = {{t}_{0}} + k\Delta $, k = 1, 2, …, разделенные постоянным интервалом $\Delta = {{t}_{k}} - {{t}_{{k - 1}}}$; ${{M}_{1}}$, ${{M}_{2}}$ – число значений дискретных параметров ${{a}_{j}}$, ${{b}_{m}}$ соответственно; ${\mathbf{\xi }}(t)$, ${\mathbf{\zeta }}(t)$ – независимые между собой ${{n}_{{{\xi }}}}$-, ${{n}_{{{\varsigma }}}}$-мерные векторы БГШ с нулевыми математическими ожиданиями и единичными матрицами интенсивностей соответствующей размерности.

По условию задачи известны матрицы ${\mathbf{F}}\left( \cdot \right)$, ${{{\mathbf{G}}}_{x}}\left( \cdot \right)$, ${\mathbf{H}}\left( \cdot \right)$, ${{{\mathbf{G}}}_{y}}\left( \cdot \right)$, а также начальные распределения марковского вектора ${{\left[ {{{{\mathbf{x}}}^{T}}(t),{{{\mathbf{v}}}^{T}}(t),{{a}_{j}}({{t}_{k}}),{{b}_{m}}({{t}_{k}})} \right]}^{Т}}$, причем компонент марковской цепи ${{b}_{m}}({{t}_{k}})$, характеризующий нарушения в канале измерения, не зависит от процесса ${\mathbf{x}}(t)$ и от компонента ${{a}_{j}}({{t}_{k}})$, характеризующего изменения статистических свойств непрерывных компонентов ДНМП. Непрерывный процесс ${\mathbf{v}}(t)$ подвергается дискретизации с постоянным шагом Δ в моменты времени ${{t}_{k}} = {{t}_{0}} + k\Delta $ и амплитудному квантованию по уровням в квантователях многоканального АЦП измерителя. Особенностью задачи является то, что для оценивания отсчетов ${\mathbf{x}}(t)$ непосредственному наблюдению доступны только цифровые выходные сигналы АЦП. Требуется по наблюдаемым цифровым сигналам

найти апостериорное распределение отсчетов вектора ${\mathbf{x}}(t)$ и дискретной компоненты ДНМП ${\mathbf{s}}({{t}_{k}})$ с точным учетом характеристик АЦП: нормированных оптимальных уровней и порогов квантования, а также нормированного равномерного шага квантования. Здесь и далее знак $ \triangleq $ обозначает равенство по определению.

2. ЭКВИВАЛЕНТНАЯ ЗАДАЧА ОЦЕНИВАНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА В ДИСКРЕТНОМ ВРЕМЕНИ

Для корректного статистически эквивалентного дискретного представления непрерывных моделей вектора состояния ДНМП и измерителя воспользуемся методами теории условных марковских процессов [1], в соответствии с которыми модели (1), (2) описываются в виде совместного условно-марковского процесса. При помощи равенства [15]

введем векторный процесс у(t), статистическая динамика которого согласно (2) описывается стохастическим дифференциальным уравнением

Согласно (1), (4) совместный процесс z = $ = {{\left[ {{{{\mathbf{x}}}^{Т}}(t),{{{\mathbf{y}}}^{Т}}(t)} \right]}^{Т}}$ является условно-марковским и описывается СДУ

где

Уравнение (5) может быть представлено в статистически эквивалентной форме [2] в виде разностного уравнения с шагом дискретизации Δ

в котором используются обозначения где N_z – (n_x + n_y)-мерный вектор независимых гауссовских случайных величин с нулевыми математическими ожиданиями и единичными дисперсиями. Элементы блочных матриц ${{{\mathbf{\Phi }}}_{{zz}}}$, ${{{\mathbf{\Gamma }}}_{{zz}}}$, где ${{{\mathbf{\Gamma }}}_{{zz}}}$ – нижняя треугольная матрица априорной корреляционной матрицы ${{{\mathbf{B}}}_{{zz}}}(k,k - 1,{\mathbf{s}}({{t}_{k}}))$, определяются из решения системы уравнений [2, 6] где блочная корреляционная матрица ${{{\mathbf{B}}}_{{zz}}}$ имеет вид

Эквивалентное дискретное представление (6) непрерывных моделей векторов состояния маневрирующего объекта (1) и измерения (3) является абсолютно точным в том смысле, что для любых ${{t}_{k}} - {{t}_{{k - 1}}} > 0$ оно позволяет получить случайные процессы с теми же статистическими характеристиками, что и решение СДУ (6), без погрешностей аппроксимации [16]. Особенность задачи состоит в том, что требуемые уравнения апостериорного закона распределения ненаблюдаемого вектора состояния эквивалентной дискретной системы ${{\left[ {{{{\mathbf{x}}}^{Т}}\left( k \right),{{{\mathbf{y}}}^{Т}}\left( k \right),{{{\mathbf{s}}}^{Т}}({{t}_{k}})} \right]}^{Т}}$ определяются по наблюдаемым цифровым сигналам ${\mathbf{d}}\left( k \right)$, которые формируются квантователями АЦП путем амплитудного квантования ${{n}_{y}}$-мерного вектора

Каждый квантователь АЦП представляет собой устройство с нулевой памятью и осуществляет безынерционную нумерацию областей квантования, в которые попадает входная величина ${{y}_{u}}\left( k \right)$, $u = \overline {1,{{n}_{y}}} $. Динамический диапазон u-го квантователя разбит на соприкасающиеся области ${{\Omega }_{u}}\left[ {k,{{l}_{u}}} \right]$, ${{l}_{u}} = \overline {1,{{L}_{u}}} $ [17]. Каждая область ограничивается порогами квантования ${{{{\eta }}}^{{(u)}}}(k,{{l}_{u}} - 1)$ и ${{{{\eta }}}^{{(u)}}}(k,{{l}_{u}})$. Цифровой сигнал ${{d}_{u}}\left( k \right)$, $\forall $ $u = \overline {1,{{n}_{y}}} $, формируется в соответствии с алгоритмом [18]

где ${{L}_{u}}$ – число областей квантования. Если условие (7) выполняется для всех компонентов вектора ${\mathbf{y}}\left( k \right)$, то формируется вектор цифровых сигналов ${\mathbf{d}}\left( k \right) = {{\left[ {{{d}_{1}}\left( k \right),...,{{d}_{u}}\left( k \right),...,{{d}_{{{{n}_{y}}}}}\left( k \right)} \right]}^{Т}}$.

3. ЗАКОН РАСПРЕДЕЛЕНИЯ РАСШИРЕННОГО ВЕКТОРА СОСТОЯНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА

На основании свойств марковских процессов в дискретном времени запишем рекуррентные уравнения, описывающие апостериорную плотность вероятности вектора

по наблюдаемым цифровым сигналам ${\mathbf{D}}_{1}^{k} \triangleq $ $ \triangleq \left\{ {{\mathbf{d}}\left( 1 \right),{\mathbf{d}}\left( 2 \right),...,{\mathbf{d}}\left( k \right)} \right\}$

В (8) и далее для простоты записи аргументы k, $k - 1$, ${{t}_{k}}$, ${{t}_{{k - 1}}}$ всех функций, где это возможно и не вызывает сомнений, опущены, а интегрирование по переменной ${\mathbf{z}}$ ведется в области ${{\Re }^{{{{n}_{x}}}}} \times \Omega $ $\left( {\Omega \subset {{\Omega }_{1}} \times \cdot \cdot \cdot \times {{\Omega }_{{{{n}_{y}}}}}} \right)$.

Представим апостериорную плотность вероятности вектора z при условии ${{a}_{j}}({{t}_{k}})$, ${{b}_{m}}({{t}_{k}})$ – (8) в виде системы рекуррентных уравнений

где ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{z}}\left( k \right)} \right) = f\left( {{\mathbf{z}}\left( k \right)\left| {{{a}_{j}},{{b}_{m}},{\mathbf{D}}_{1}^{{k - 1}}} \right.} \right)$ – условная плотность вероятности вектора ${{\left[ {{{{\mathbf{z}}}^{Т}}(k),{{a}_{j}}({{t}_{k}}),{{b}_{m}}({{t}_{k}})} \right]}^{Т}}$.

Апостериорная вероятность дискретной компоненты ДНМП при условии ${{a}_{j}}({{t}_{k}})$, ${{b}_{m}}({{t}_{k}})$ – ${{\hat {P}}_{{jm}}}(k)$ описывается системой рекуррентных уравнений:

где $P\left( {{\mathbf{d}}\left( k \right),{{a}_{j}},{{b}_{m}}\left| {{\mathbf{D}}_{1}^{{k - 1}}} \right.} \right)$ – условная вероятность одношагового предсказания наблюдаемого цифрового сигнала (вывод уравнений (8)–(14) приведен в Приложении).

Для замыкания систем уравнений (10)–(14) необходимо выполнить двухмоментную параметрическую гауссовскую аппроксимацию условной плотности вероятности ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{z}}\left( k \right)} \right)$. Эта аппроксимация состоит в замене неизвестных функций ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{z}}\left( k \right)} \right)$ некоторыми известными функциями, в частности ${\mathbf{\tilde {z}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\tilde {R}}}}_{{zz}}}(k,{{a}_{j}},{{b}_{m}})$ – математического ожидания и корреляционной функции условной плотности вероятности ${{\tilde {f}}_{{jm}}}\left( {{\mathbf{z}}\left( k \right)} \right)$ соответственно [19].

4. КВАЗИОПТИМАЛЬНЫЙ АЛГОРИТМ ОЦЕНИВАНИЯ ВЕКТОРА СОСТОЯНИЯ ДИСКРЕТНО-НЕПРЕРЫВНОГО МАРКОВСКОГО ПРОЦЕССА ПО НАБЛЮДАЕМЫМ ЦИФРОВЫМ СИГНАЛАМ

Задача оценивания считается практически решенной, если на выходе рекуррентного цифрового фильтра (ЦФ) на каждом k-м шаге формируется безусловная оптимальная оценка, соответствующая определенному критерию оптимальности. Байесовское решение может быть получено на основе минимизации условного апостериорного риска (УАР), которая выполняется в два этапа: сначала по непрерывному компоненту (при каждом фиксированном значении дискретного компонента), а затем по дискретному компоненту. На втором этапе на основе сравнения УАР ${{\gamma }_{{jm}}}\left( k \right)$ выбираются оптимальные оценки ${{\hat {a}}_{j}}({{t}_{k}})$, ${{\hat {b}}_{m}}({{t}_{k}})$дискретных параметров, если выполняется условие

В (15) выражение УАР для функции потерь простой по дискретному и квадратичной по непрерывному компонентам имеет вид [12]

где ${\mathbf{\hat {z}}}(k,{{a}_{j}},{{b}_{m}})$ – оптимальная условная оценка [20], ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }}(k,{{a}_{{{\mu }}}},{{b}_{{{\nu }}}})$, ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }}(k,{{a}_{{{\mu }}}},{{b}_{{{\nu }}}})$ – математическое ожидание и корреляционная матрица условной апостериорной плотности вероятности ${{\hat {f}}_{{{{\mu \nu }}}}}\left( {{\mathbf{z}}\left( k \right)} \right)$ соответственно; ${{g}_{{{{\mu \nu }}}}}$, ${{c}_{{{{\mu \nu }}}}}$ – коэффициенты потерь; ${{{{\delta }}}_{{jm{{\mu \nu }}}}}$ – символ Кронекера.

При выполнении условия (15) за окончательную оценку отсчетов вектора состояния ${\mathbf{z}}\left( k \right)$ принимается соответствующая условная оценка ${\mathbf{\hat {z}}}(k,{{a}_{j}},{{b}_{m}})$. Из (15) и (16) следует, что в качестве оценок дискретных компонентов ${{\hat {a}}_{j}}({{t}_{k}})$, ${{\hat {b}}_{m}}({{t}_{k}})$ берется решение, для которого взвешенная сумма потерь (выражение в фигурных скобках в (16)) минимальна. Причем эта сумма растет с уменьшением апостериорной точности фильтрации вектора ${\mathbf{z}}\left( k \right)$, что является важным для практических приложений [21]. Для определения УАР ${{\gamma }_{{jm}}}(k)$, $\forall j = \overline {1,{{M}_{1}}} $, $m = \overline {1,{{M}_{2}}} $, может быть использован квазиоптимальный алгоритм цифровой фильтрации непрерывных компонентов вектора состояния ДНМП, который описывается системой рекуррентных уравнений и получен с учетом гауссовской аппроксимации условной плотности вероятности $\tilde {f}({\mathbf{z}}\left( k \right),{{a}_{j}},{{b}_{m}})$ и оптимизации процедуры квантования

Уравнения ${\text{o}}$ценивания дискретных компонентов вектора состояния (10), (11) остаются без изменения, при этом условная вероятность одношагового предсказания наблюдаемого цифрового сигнала имеет вид

где ${{\tilde {y}}_{u}}(k,{{a}_{j}},{{b}_{m}})$ – и-й элемент вектора ${\mathbf{\tilde {y}}}(k,{{a}_{j}},{{b}_{m}})$; ${{{{\tau }}}_{u}}$ ($u = \overline {1,{{n}_{y}}} $) – диагональный элемент нижней треугольной матрицы ${{{\mathbf{T}}}_{{yy}}}\left( {k,{{a}_{j}},{{b}_{m}}} \right)$; $F\left\{ \cdot \right\}$ – интеграл вероятности. Значения ${{\delta }}_{{{\text{opt}}}}^{{(u)}}$, ${{\varepsilon }}_{{{\text{opt}}}}^{{(u)}}$ оптимального равномерного шага и среднего квадрата ошибок квантования для заданного числа уровней квантования ${{L}_{u}}$ приведены в [13]. Квазиоптимальный ЦФ, реализующий алгоритм (10), (11), (17)–(28), является многоканальным с числом каналов $M = {{M}_{1}} \times {{M}_{2}}$ (рис. 1). Каждый канал состоит из многоканального АЦП (МКАЦП), цифроаналогового преобразователя ЦАП; блока вычисления коэффициента усиления КУ ${\mathbf{K}}(k,{{a}_{j}},{{b}_{m}})$, блока оценки БО, в котором вычисляются ${\mathbf{\hat {x}}}(k,{{a}_{j}},{{b}_{m}})$, ${\mathbf{\hat {x}}}(k - 1,{{a}_{i}},{{b}_{n}})$; блока прогноза БП, в котором вычисляются ${\mathbf{\tilde {x}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\tilde {y}}}}_{{jm}}}(k)$; блока апостериорных вероятностей БАВ, в котором вычисляются ${{\hat {P}}_{{jm}}}(k)$, ${{\hat {P}}_{{in}}}(k - 1)$, ${{\tilde {P}}_{{jm}}}(k)$, и блока корреляционных матриц БКМ, в котором вычисляются ${{{\mathbf{\tilde {R}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\tilde {R}}}}_{{xy}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\tilde {R}}}}_{{yy}}}(k,{{a}_{j}},{{b}_{m}})$, ${{{\mathbf{\hat {R}}}}_{{xx}}}(k,{{a}_{j}},{{b}_{m}})$ и ${{{\mathbf{\hat {R}}}}_{{xx}}}\left( {k - 1,{{a}_{i}},{{b}_{n}}} \right)$. Окончательное решение о принятии оценок ${\mathbf{\hat {x}}}(k)$, ${{\hat {a}}_{j}}({{t}_{k}})$, ${{\hat {b}}_{m}}({{t}_{k}})$ производится в решающем устройстве РУ.

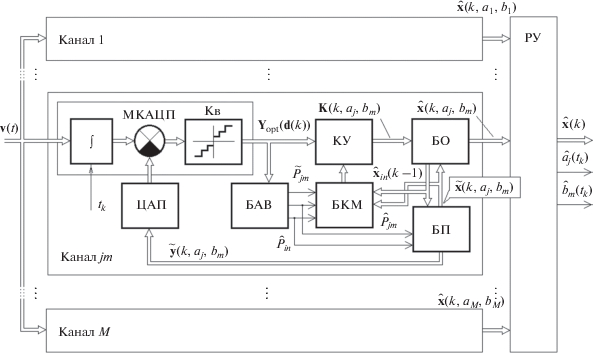
Основной особенностью МКAЦП является формирование значений вектора ${\mathbf{y}}\left( k \right)$ накоплением аналоговым путем измеряемого процесса ${\mathbf{v}}\left( t \right)$ на интеграторе со сбросом в конце каждого интервала дискретизации. Полученная таким образом последовательность ${\mathbf{y}}\left( k \right)$ преобразуется квантователем Кв в цифровые сигналы ${\mathbf{d}}\left( k \right)$, которые далее участвуют в алгоритме формирования оценок.

Пример. В качестве примера использования полученных квазиоптимальных алгоритмов рассмотрим задачу синтеза цифрового фильтра ДНМП вида

где $\alpha $ – коэффициент, характеризующий ширину спектральной плотности ДНМП; ${{\sigma }}_{x}^{2}\left( {{{a}_{j}}({{t}_{k}})} \right)$ – дисперсия оцениваемого ДНМП, значение которой изменяется по закону марковской цепи в дискретные моменты времени ${{t}_{k}}$; ${{\xi }}\left( t \right)$ – стандартный БГШ с нулевым математическим ожиданием и единичной интенсивностью.

Пусть на вход АЦП цифрового фильтра поступает непрерывный случайный процесс

где h – известный коэффициент; ${{\varsigma }}\left( t \right)$ – стандартный БГШ с нулевым математическим ожиданием и единичной интенсивностью, N₀ – спектральная плотность БГШ. Требуется по наблюдаемым цифровым сигналам получить текущую оценку $\hat {x}\left( {{{t}_{k}}} \right)$ отсчетов ДНМП $x\left( t \right)$, описываемого стохастическим дифференциальным уравнением (30).

С учетом (4) совместный марковский процесс ${\mathbf{z}} = {{\left[ {\begin{array}{*{20}{c}} x&y \end{array}} \right]}^{T}}$ в этом случае описывается уравнением (5), в котором

Элементы фундаментальной матрицы ${\mathbf{\Phi }}_{{zz}}^{{}}\left( \Delta \right)$ и матрица ${\mathbf{B}}_{{zz}}^{{}}\left( {\Delta ,{{a}_{j}}({{t}_{k}})} \right)$ определяются соотношениями

где αΔ, χ = h/α – безразмерные коэффициенты; q – отношение сигнал–шум; $\Delta = {{t}_{k}} - {{t}_{{k - 1}}}$ – интервал дискретизации.

Алгоритм оценивания ДНМП $x\left( t \right)$ по наблюдаемым цифровым сигналам описывается уравнениями (19)–(29). Оценка дискретного компонента определяется по решающему правилу (12)–(14). Квазиоптимальный ЦФ, реализующий алгоритм (12)–(14), (19)–(29), является двухканальным. Окончательное решение о принятии оценок $\hat {x}(k)$, ${{\hat {a}}_{j}}({{t}_{k}})$ производится в РУ.

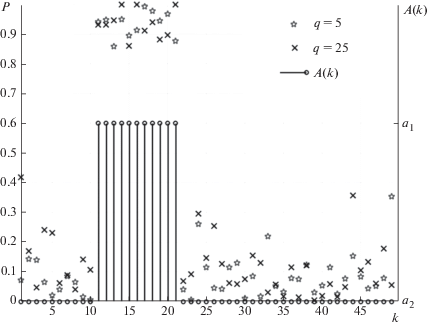
Проверка качества квазиоптимального алгоритма проведена с помощью статистического моделирования на ЭВМ для случая, когда параметры уравнений (30), (31): ${{\alpha }}$ = 0.1 с^–1, $\Delta $ = 1 с, $h$ = 1, $q$ = = 1 … 1000, а цепь Маркова принимает значения ${{a}_{1}}$ = 1, ${{a}_{2}}$ = 10. Вероятности перехода ${{{{\pi }}}_{{11}}}$ = 0.8; ${{{{\pi }}}_{{12}}}$ = 0.2. В целях повышения наглядности функционирования алгоритма была сформирована тестовая реализации для дискретного компонента $A\left( k \right)$. При этом было принято, что длина реализации $k = \overline {1,50} $, а цепь Маркова принимает значения

При определении статистических характеристик квазиоптимальных алгоритмов фильтрации методом Монте-Карло проводилось 100 испытаний, при этом тестовая реализация дискретной цепи Маркова A(k) сохранялась неизменной, а независимые гауссовские последовательности n_x(k), n_y(k) формировались с помощью датчика случайных чисел.

На рис. 2 представлены графики зависимости относительного среднего квадрата ошибки цифровой фильтрации $\varepsilon $ от отношения сигнал/шум q при различных значениях числа уровней квантования L. Здесь же для сравнения приведена зависимость $\varepsilon $ от q при аналоговой оптимальной фильтрации ДНМП [5]. Все кривые получены интерполяцией значений оценок $\varepsilon $, полученных при моделировании.

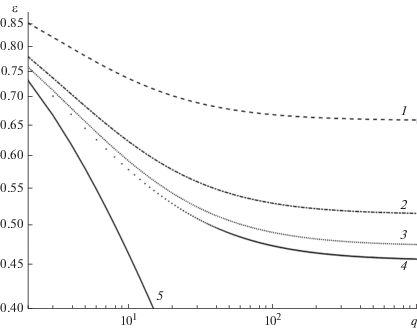
Следует отметить, что полученное при синтезе ЦФ ДНМП значение отношения сигнал/шум q (исходя из его физической сущности) является единым для цифровых (дискретных) и аналоговых алгоритмов фильтрации [16]. Это позволяет достаточно просто сравнить точность и помехоустойчивость квазиоптимальной цифровой, дискретной и аналоговой фильтрации.

На рис. 3 представлены зависимости вероятности правильного определения значений марковской цепи A(k) от дискретного времени при различных отношениях сигнал/шум q. Здесь же приведена тестовая последовательность марковской цепи A(k).

ЗАКЛЮЧЕНИЕ

Для оптимизации алгоритмов оценивания дискретно-непрерывных марковских процессов по наблюдаемым цифровым сигналам применено эквивалентное дискретное представление непрерывных компонентов этих процессов. Полученный квазиоптимальный алгоритм оценивания вектора состояния дискретно-непрерывных марковских процессов позволяет построить практически реализуемый ЦФ на базе высокопроизводительной вычислительной техники.