Радиотехника и электроника, 2021, T. 66, № 9, стр. 845-852

1. БАЗОВЫЕ ПОЛОЖЕНИЯ СИНТЕЗА СЛОИСТЫХ ДИЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ

Теория синтеза слоистых диэлектрических фильтров (СДФ) составляет существенный раздел фундаментальной радиоэлектроники, так как в ее современных приложениях, а также в оптике практически нет ни одного общезначимого устройства, которое бы не имело в своем составе некоторого, обычно достаточно большого, количества фильтров.

Построению СДФ посвящена обширная литература (см., например, [1–13]). Обычно математическая постановка задачи синтеза использует сильно нелинейный по основным параметрам задачи функционал качества синтезируемой системы:

где κ – волновое число, R(κ) или T(κ) – энергетические коэффициенты соответственно отражения и пропускания слоистой диэлектрической системы (СДС), реализующей фильтр.

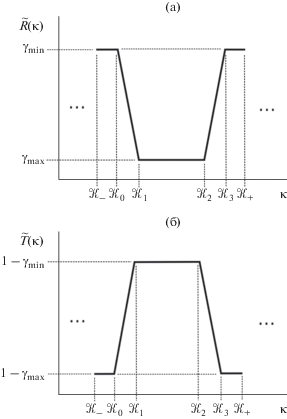
Желаемое поведение энергетического коэффициента отражения или пропускания в заданной полосе волновых чисел $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ задается спектральными характеристиками этого фильтра $\tilde {R}\left( \kappa \right)$ или $\tilde {T}\left( \kappa \right)$, достаточно условно изображенными на рис. 1а и 1б. Функции типа $\tilde {R}\left( \kappa \right)$, $\tilde {T}\left( \kappa \right)$ в данной работе будем называть идеалами для соответствующих физически реализуемых конкретным фильтром спектральных характеристик.

Качество проектируемой системы оценивается величиной разности между функциями $R\left( \kappa \right)$ и $\tilde {R}\left( \kappa \right)$ [или $T\left( \kappa \right)$ и $\tilde {T}\left( \kappa \right)]$ по норме линейного нормированного пространства $\mathbb{L}\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$.

В данной работе, как и в [3] в качестве пространства сравнения с идеальными спектральными характеристиками фильтра $\tilde {R}\left( \kappa \right){\text{\;}}\left[ {\tilde {T}\left( \kappa \right)} \right]$ выбрано пространство $\mathbb{C}\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ всех непрерывных на фиксированном отрезке $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ функций с нормой

Рассмотренная в [3] математическая постановка задачи оптимального синтеза СДФ в смысле П.Л. Чебышева состоит в том, чтобы для заданного интервала волновых чисел [𝒦₁, 𝒦₂] и заданного идеала энергетического коэффициента отражения $\tilde {R}\left( \kappa \right)$ минимизировать функционал:

где электрические толщины $\vec {\nu }$ и импедансы $\vec {p}$ всех слоев СДС.

По многим теоретическим и особенно практическим соображениям полезно дополнить постановку задачи синтеза в смысле П.Л. Чебышева, наложив дополнительные ограничения на электродинамические параметры задачи $\vec {p}$ и записав математическую постановку задачи в виде

где электрические толщины $\vec {\nu }$ есть элементы пространства всех возможных электрических толщин ${{\mathcal{N}}_{N}}$, а импедансы $\vec {p}$ слоев СДС есть элементы заданного параллелепипеда ${{{\mathbf{P}}}_{N}}$ из пространства всех возможных импедансов ${{\mathcal{P}}_{N}}$ материалов слоистых систем. С учетом реализуемости на практике импедансы материалов слоев удовлетворяют двойному неравенству: $\hat {p} \leqslant {{p}_{j}} \leqslant \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} $, $j = 1,2, \ldots ,N,$ где ${{p}_{j}}$ – импедансы слоев, а $N$ – порядок фильтра. Такую постановку задачи синтеза СДФ естественно называть задачей оптимизации в смысле П.Л. Чебышева с ограничениями.

Определение. Идеал фильтра $\tilde {R}\left( \kappa \right){\text{\;}}\left[ {\tilde {T}\left( \kappa \right)} \right]$ будем называть правильным на заданном интервале волновых чисел $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$, если он может быть на этом интервале сколь угодно точно равномерно приближен $R\left( \kappa \right){\text{\;}}\left[ {T\left( \kappa \right)} \right]$, реализуемыми СДС в классе рассматриваемых. Это естественное требование корректности идеальных характеристик формализуется в виде предположения о том, что $\tilde {R}\left( \kappa \right)$ [$\tilde {T}\left( \kappa \right)$] принадлежит замыканию в метрике $\mathbb{C}\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ множества всех возможных коэффициентов отражения (пропускания) СДС рассматриваемого класса.

Тогда, как будет показано далее, вычислительная сложность функционала качества определяется дробно-рациональной структурой энергетического коэффициента отражения от любой СДС данного класса и может быть существенно уменьшена при помощи эффективной процедуры построения идеала не для сложных коэффициентов отражения или пропускания $R\left( \kappa \right){\text{\;}}\left[ {T\left( \kappa \right)} \right]$, а для квадратичных профилирующих функций, введенных в [1, 2, 14], что существенно упрощает анализ и решение соответствующих оптимизационных задач.

По сравнению с работами [1, 2, 14], в постановку задачи синтеза в данной работе включены принципиальные ограничения на допустимые для задачи синтеза параметры материалов слоев. Проведен представляющий самостоятельный интерес анализ прямой задачи об описании всех возможных в СДС с кусочно-непрерывными физическими параметрами плоских электромагнитных полей с плоскостями постоянной фазы, параллельными слоям СДС. Ранее в [1, 2, 14] подобный анализ был проведен только для сред с кусочно-постоянными параметрами.

В этой части работы особенно важен факт доказательства основного энергетического тождества для СДС без потерь (17) (см. [1, 2, 14]), в отличие от обычно постулируемой формы закона сохранения энергии¹¹:

Замечание. Доказанное в работе основное энергетическое тождество для СДС без потерь (17), эквивалентное в своей основе тождеству (3), показывает, что все спектральные характеристики слоистых диэлектрических систем с кусочно-непрерывными параметрами $\varepsilon \left( x \right) > 0,~$ $~\mu \left( x \right) > 0$ от координаты $x$, отсчитываемой от поверхности покрытия вглубь слоя, определяются исключительно величинами скачков функций $\varepsilon \left( {{{x}_{j}}} \right),$ ${\text{\;}}\mu \left( {{{x}_{j}}} \right)$ в точках ${{x}_{j}}$ разрывов этих функций и совершенно не зависят от “непрерывного” поведения этих функций между точками разрыва.

Более детально вычислительные аспекты предлагаемого подхода к задачам синтеза полосовых фильтров будут рассмотрены в наших следующих работах.

2. ПОСТАНОВКА ПРЯМОЙ ЗАДАЧИ

Пусть часть пространства ${{\mathbb{R}}^{3}}$ между двумя параллельными плоскостями $\pi $ и $\pi {\kern 1pt} {\text{'}}$, расстояние между которыми $d$, $d > 0$, заполнена диэлектрической средой, параметры которой – диэлектрическая и магнитная проницаемости – являются кусочно-непрерывными функциями от координаты $x$ оси $Ox$ декартовой системы координат, направленной по нормали от $\pi $ к $\pi {\kern 1pt} {\text{'}}$. Начало координат находится на плоскости $\pi $:

с конечным, общим для обеих функций, числом точек разрыва первого рода, которые будем обозначать ${{a}_{0}} = 0 < {{a}_{1}} < ... < {{a}_{N}} = d$, не заботясь о том, какая из двух функций, $\varepsilon \left( x \right)$ или $\mu \left( x \right),$ терпит разрыв в точке ${{a}_{j}}$. Интервалы непрерывности обеих функций $\varepsilon \left( x \right)$ и $\mu \left( x \right)$ будем обозначать

Пусть полупространство $\mathbb{R}_{ - }^{3}$ слева от $\pi $ заполнено однородной средой с диэлектрической ${{\varepsilon }_{ - }}$ и магнитной ${{\mu }_{ - }}$ проницаемостями, а полупространство $\mathbb{R}_{ + }^{3}$ справа от $\pi {\text{'}}$ – однородной средой с проницаемостями ${{\varepsilon }_{ + }}$ и ${{\mu }_{ + }}$.

Прямая задача о распространении плоских электромагнитных волн в пространстве ${{\mathbb{R}}^{3}}$, заполненном слоистым диэлектриком, состоит в описании класса всех возможных плоских электромагнитных полей в определенной выше СДС: требуется, во-первых, указать количество свободных параметров, определяющих все возможные в указанной системе электромагнитные поля, и, во-вторых, определить коэффициенты отражения и пропускания от СДС $\left[ {0,d} \right]$ слева и справа от нее.

Известно (см., например, [9]), что комплексные амплитуды векторов электрической и магнитной напряженностей

плоского электромагнитного поля (зависимость от времени – ${\text{exp}}\left( { - i\omega t} \right)$) с волновым вектором $\vec {k}$, параллельным оси $Ox$ внутри каждого интервала непрерывности ${{{{\Delta }}}_{j}}$ функций $\varepsilon \left( x \right)$ и $\mu \left( x \right)$, удовлетворяют системе дифференциальных уравнений, записанной в матричной форме, которые получаются для плоских волн из общих уравнений Максвелла:

Кроме того, на каждой плоскости ${{\pi }_{j}}:x = {{a}_{j}}$ разрыва коэффициентов $\varepsilon \left( x \right)$ или $\mu \left( x \right)$ должны выполняться вытекающие из уравнений Максвелла электродинамические граничные условия, совпадающие в нашем случае ${\text{c}}$ условиями непрерывности амплитуд электрического и магнитного полей:

где $\left( {{{a}_{j}} - 0} \right)$ и $\left( {{{a}_{j}} + 0} \right)$ – пределы слева и справа в точках разрыва ${{a}_{j}},j = 0,1,2,...,N$, коэффициентов $\varepsilon \left( x \right)$ или $\mu \left( x \right)$ уравнений Максвелла.

Всевозможные плоские электромагнитные поля рассматриваемого выше типа слева и справа от СДС $\left[ {0,d} \right]$ (в полупространствах $\mathbb{R}_{ \mp }^{3}$) определяются уравнением (4) с постоянными коэффициентами ${{\varepsilon }_{ - }},{{\mu }_{ - }}$ слева от плоскости $\pi $ и ${{\varepsilon }_{ + }},{{\mu }_{ + }}$ – справа от $\pi {\kern 1pt} {\text{'}}$.

Поэтому в полупространствах $\mathbb{R}_{ \mp }^{3}$ общее решение системы (4) имеет вид

где величины, помеченные индексами минус и $0$, относятся к плоской волне, распространяющейся в $\mathbb{R}_{ - }^{3}$ к плоскости π, а с индексами минус и $1$ соответствуют плоской волне, распространяющейся в $\mathbb{R}_{ - }^{3}$ от плоскости π²².

Аналогично этому в (4) все величины, помеченные индексами $ + $ и $0$, относятся к плоской волне, распространяющейся в $\mathbb{R}_{ + }^{3}$ от плоскости $\pi {\kern 1pt} {\text{'}}$, а с индексами $ + $ и $1$ соответствуют плоской волне, распространяющейся в $\mathbb{R}_{ + }^{3}$ к плоскости $\pi {\kern 1pt} {\text{'}}$.

Замечание. Вектор Пойнтинга $\vec {W} = \left[ {\vec {E},\vec {H}{\text{*}}} \right]$ для волны в $\mathbb{R}_{ - }^{3}$, распространяющейся к плоскости $\pi $, равен ${{p}_{ - }}{{\left| {C_{0}^{ - }} \right|}^{2}}~{{\vec {x}}_{0}}$, а для распространяющейся от $\pi $, равен $ - {{p}_{ - }}{{\left| {C_{1}^{ - }} \right|}^{2}}~{{\vec {x}}_{0}}$. Аналогично, вектор Пойнтинга для волны в $\mathbb{R}_{ + }^{3}$, распространяющейся к плоскости $\pi {\kern 1pt} '$, равен $ - {{p}_{ + }}{{\left| {C_{1}^{ + }} \right|}^{2}}~{{\vec {x}}_{0}}$, а для распространяющейся от $\pi {\kern 1pt} '$ равен ${{p}_{ + }}{{\left| {C_{0}^{ + }} \right|}^{2}}~{{\vec {x}}_{0}}$.

Общее решение уравнений (4) в $\mathbb{R}_{ \mp }^{3}$ в векторно-матричной записи имеет вид

где $x_{0}^{ - } = 0,\,\,x_{0}^{ + } = d$. При этом

В (6) и (7) введены обозначения: $\lambda _{s}^{ \mp }$ – собственные значения и $\vec {l}_{s}^{ \mp },\,\,\left( {s = 0,1} \right)$ – собственные векторы матриц ${{{\mathbf{P}}}_{ \mp }}$ для полупространств $\mathbb{R}_{ \mp }^{3}$, имеют вид

где ${{n}_{ \mp }} = {{\left( {{{\varepsilon }_{ \mp }}{{\mu }_{ \mp }}} \right)}^{{1/2}}},$ ${\text{\;}}{{p}_{ \mp }} = {{\left( {\frac{{{{\varepsilon }_{ \mp }}}}{{{{\mu }_{ \mp }}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Таким образом, в соответствии с (5) на плоскостях $\pi $ и $\pi {\kern 1pt} {\text{'}}$ справедливы равенства ${{{\mathbf{B}}}_{ - }}{{\vec {C}}_{ - }} = {{\vec {u}}_{1}}\left( 0 \right)$ и ${{\vec {u}}_{N}}\left( d \right) = {{{\mathbf{B}}}_{ + }}{{\vec {C}}_{ + }}$.

3. ОСНОВНЫЕ СВОЙСТВА ПРЯМОЙ ЗАДАЧИ

Лемма. Матрицы ${{{\mathbf{B}}}_{ \mp }}$ обладают свойством:

Доказательство леммы проводится перемножением нужных матриц.

Для произвольного решения $\vec {u}\left( x \right)$ (4) рассмотрим квадратичную форму:

Лемма (основная). Для произвольного решения $\vec {u}\left( x \right)$ системы уравнений (4) на всяком интервале непрерывности ее коэффициентов ${{{{\Delta }}}_{j}},j = 1, \ldots ,N$, квадратичная форма (9) сохраняет постоянное значение:

Доказательство. Производная от квадратичной формы (7) с учетом уравнений (4) тождественно равна нулю на всяком интервале непрерывности ${{{{\Delta }}}_{j}}$ коэффициентов системы уравнений (4) в силу тождества:

4. АМПЛИТУДНАЯ ПАРАМЕТРИЗАЦИЯ ПРЯМОЙ ЗАДАЧИ

Для решения прямой задачи используем представление решения (4) с начальным условием ${{\vec {u}}_{j}}\left( {{{a}_{j}}} \right) = \vec {u}_{j}^{0}$ на всяком интервале ${{{{\Delta }}}_{j}},j = 1,2,...,N$:

где

– фундаментальная матрица, столбцы которой ${{\vec {m}}_{0}}$ и ${{\vec {m}}_{1}}$ образуют фундаментальную систему решений (4) на ${{{{\Delta }}}_{j}}$,

– постоянный на ${{{{\Delta }}}_{j}},j = 1,2,...,N$ вектор коэффициентов – комплексных амплитуд “волн” ${{\vec {m}}_{0}}$ и ${{\vec {m}}_{1}}$.

Чтобы получить представление (11), достаточно решить матричное дифференциальное уравнение

с начальным условием:

Далее рассмотрим два разных представления фундаментальных матриц ${{{\mathbf{M}}}_{j}}\left( x \right)$ в (12), $j = 1,2,...,N$, отвечающих разным начальным условиям (13). Во-первых, будем говорить про “тригонометрическое” представление (t-представление)³³, когда ${{{\mathbf{M}}}_{j}}\left( {{{a}_{j}}} \right) = {\mathbf{I}}$, где ${\mathbf{I}}$ – единичная матрица, и, во-вторых, про “экспоненциальное” представление (e‑представление), когда

а ${{p}_{j}}\left( {{{a}_{j}}} \right)$ – величина импеданса в правом конце ${{{{\Delta }}}_{j}},j = 1,2,...,N$.

В силу тождества (10) и нужного начального условия (13) на интервале ${{{{\Delta }}}_{j}}$:

Из этих тождеств следует невырожденность матриц ${\mathbf{M}}_{j}^{{\left( e \right)}}\left( x \right),{\mathbf{M}}_{j}^{{\left( t \right)}}\left( x \right)$ для всякого $x$ из ${{{{\Delta }}}_{j}},j = 1,2,...,N$, а также выражения для постоянных векторов ${{\vec {C}}_{j}}$:

Представления (15) аналогичны представлению (8) для всякого $x$ из ${{{{\Delta }}}_{j}}$.

Используя первое из тождеств (13) и непрерывность электромагнитного поля в каждой точке разрыва коэффициентов уравнений (4), получим основное энергетическое тождество, показывающее сохранение направления и величины потока энергии электромагнитного поля слева от СДС $\left[ {0,d} \right]$ и справа от нее:

Из последнего тождества видно, что решение прямой задачи для ${{\mathbb{R}}^{3}}$ зависит от двух произвольных постоянных, в качестве которых можно взять ${{\vec {C}}_{ - }}$ или ${{\vec {C}}_{ + }}$.

При интерпретации решения прямой задачи как задачи о распространении плоской электромагнитной волны через слоистую систему ${{\mathbb{R}}^{3}}$ слева направо удобно выбрать произвольные постоянные в виде

где второе условие – отсутствие отражения на $ + \infty $, а первое – нормировка “по прохождению” волны, прошедшей через СДС $\left[ {0,d} \right]$ с кусочно-непрерывными параметрами.

С учетом указанного выбора свободных параметров тождество (17) примет вид

где $\theta = {{{{p}_{ + }}} \mathord{\left/ {\vphantom {{{{p}_{ + }}} {{{p}_{ - }}}}} \right. \kern-0em} {{{p}_{ - }}}},$ из которого вытекает ряд важных следствий для рассматриваемых полей: ${{\left| {C_{0}^{ - }} \right|}^{2}} = $ $ = {{\left| {C_{1}^{ - }} \right|}^{2}} + \theta \geqslant \theta $, т.е. оценка величины ${{\left| {C_{0}^{ - }} \right|}^{2}}$ снизу: ${{\left| {C_{0}^{ - }} \right|}^{2}} \geqslant \theta > 0$, в силу которой для всех $\kappa $ обязательна конечность энергетических коэффициентов отражения слева от СДС и пропускания справа от СДС с кусочно-непрерывными физическими параметрами:

и, как следствие этого и (17), оказывается обоснованным тождество (3).

Подстановка решений (12) в условия непрерывности (5) приводит к основной системе уравнений (см. [1, 2, 14]) относительно амплитуд прямой и обратной волн ${{\vec {C}}_{j}} = \left( {\begin{array}{*{20}{l}} {C_{0}^{{\left( j \right)}}} \\ {C_{1}^{{\left( j \right)}}} \end{array}} \right)$ в $j$-м слое $\left( {j = 0,1, \ldots ,N + 1} \right)$:

где $j = 0$ отвечает индексу минус, а $j = N + 1$ индексу плюс в предыдущем тексте.

Определение. При распространении волны слева направо будем называть профилирующими функциями следующие функции от волнового числа $\kappa $:

Эти функции, а также аналогичные им при распространении волны справа налево, являются функционалами от кусочно-непрерывных параметров СДС $\left[ {0,d} \right]$. В силу (17), будет справедливо тождество

Замечание. При интерпретации решения прямой задачи, как задачи о распространении плоской электромагнитной волны через слоистую систему справа налево, удобно выбрать произвольные постоянные в (14) в виде $C_{0}^{ - } = 0,\,\,C_{1}^{ - } = 1,$ где первое условие означает отсутствие отражения на $ - \infty $, а второе – нормировку “по прохождению” волны, прошедшей через кусочно-непрерывную СДС.

С учетом указанного ${\text{в}}$ыбора свободных параметров и изменения знаков тождество (17) примет вид

из которого, как и выше, вытекает ряд следствий для рассматриваемых полей: ${{\left| {C_{1}^{ + }} \right|}^{2}} = {{\left| {C_{0}^{ + }} \right|}^{2}} + {{\theta }^{{ - 1}}} \geqslant {{\theta }^{{ - 1}}}$, т.е. оценка величины ${{\left| {C_{1}^{ + }} \right|}^{2}}$ снизу: ${{\left| {C_{1}^{ + }} \right|}^{2}} \geqslant {{\theta }^{{ - 1}}} > 0$, в силу которой для всех κ следует не обращение в нуль: ${{\left| {C_{1}^{ + }} \right|}^{2}} > 0$, и вытекающая из этого факта конечность энергетических коэффициентов отражения справа от СДС и пропускания слева от СДС с кусочно-непрерывными физическими параметрами:

Следствием этих обозначений и (17) выступает обоснование тождества (2), которое, как и при распространении волны слева направо, позволяет в случае правильных идеалов для коэффициентов отражения (пропускания) обосновать переход от стандартных постановок задач синтеза к их эффективным постановкам.

5. ОБОСНОВАНИЕ ПЕРЕХОДА К ЭФФЕКТИВНЫМ ПОСТАНОВКАМ ЗАДАЧ СИНТЕЗА

Лемма. Если идеальные спектральные характеристики $\tilde {R}\left( \kappa \right)$ и $\tilde {T}\left( \kappa \right)$ связаны между собой соотношением $\tilde {R}\left( \kappa \right) + \tilde {T}\left( \kappa \right) \equiv 1$, то оба идеала могут быть правильными только одновременно.

Лемма. Если хотя бы один из идеалов ${{\tilde {R}}_{ - }}\left( \kappa \right)$ или ${{\tilde {T}}_{ + }}\left( \kappa \right)$ имеет представление

где ${{\tilde {F}}_{1}}\left( \kappa \right)$ – идеал для профилирующей функции ${{F}_{1}}\left( \kappa \right)$, а ${{\tilde {F}}_{0}}\left( \kappa \right)$ – идеал для профилирующей функции ${{F}_{0}}\left( \kappa \right)$, то правильность любого из идеалов ${{\tilde {R}}_{ - }}\left( \kappa \right)$, ${{\tilde {T}}_{ + }}\left( \kappa \right)$, ${{\tilde {F}}_{0}}\left( \kappa \right)$ или ${{\tilde {F}}_{1}}\left( \kappa \right)$ влечет правильность остальных идеалов из перечисленных.

Формулы пересчета идеала для стандартного коэффициента отражения ${{\tilde {R}}_{ - }}\left( \kappa \right)$ в идеалы для профилирующих функций ${{\tilde {F}}_{1}}\left( \kappa \right)$ и ${{\tilde {F}}_{0}}\left( \kappa \right)$ таковы:

Из первой формулы следует ${{\tilde {F}}_{1}}\left( \kappa \right) = {{\tilde {R}}_{ - }}\left( \kappa \right){{\tilde {F}}_{0}}\left( \kappa \right)$ и, подставляя это соотношение во вторую формулу, получаем

В приведенных формулах для оценки точности замены на интервале $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ исходного неравенства $\left| {{{R}_{ - }}\left( \kappa \right) - {{{\tilde {R}}}_{ - }}\left( \kappa \right)} \right| < \varepsilon $ на $\left| {{{F}_{1}}\left( \kappa \right) - {{{\tilde {F}}}_{1}}\left( \kappa \right)} \right| < \delta \left( \varepsilon \right)$, нужно использовать модуль непрерывности функции

производная которой на $\left( {0, + \infty } \right)$ монотонно спадает от $y{\kern 1pt} '\left( 0 \right) = {{\theta }^{{ - 1}}}$ до нуля, с заменой ее аргумента $x$ на ${{F}_{1}}\left( \kappa \right)$, а ее значений $y$ на $R\left( \kappa \right)$.

6. ЗАПИСЬ УПРОЩЕННОЙ ПОСТАНОВКИ ЗАДАЧИ СИНТЕЗА ПО П.Л. ЧЕБЫШЕВУ

Задача оптимального синтеза СДФ в смысле П.Л. Чебышева (1) для энергетического коэффициента отражения в силу тождества (3) полностью эквивалентна такой же задаче для энергетического коэффициента пропускания, если $\tilde {T}\left( \kappa \right) = 1 - \tilde {R}\left( \kappa \right)$. Аналогично, в силу (17) эквивалентны между собой задачи оптимального синтеза для каждой из профилирующих функций ${{F}_{0}}\left( \kappa \right),{{F}_{1}}\left( \kappa \right)$.

Тождество

позволяет дать простую двухстороннюю оценку для функционала задачи (1) через аналогичные функционалы для профилирующих функций:

где $\theta \leqslant {{F}_{0}}\left( \kappa \right) \leqslant \alpha $, $\theta \leqslant {{\tilde {F}}_{0}}\left( \kappa \right) \leqslant \beta $, что позволяет говорить об эквивалентности (1) и существенно более простой задачи:

Аналогичный переход от (24) к его аналогу:

где $v\left( \kappa \right) = {1 \mathord{\left/ {\vphantom {1 {{{{\tilde {F}}}_{0}}\left( \kappa \right)}}} \right. \kern-0em} {{{{\tilde {F}}}_{0}}\left( \kappa \right)}}$ – фиксированная весовая функция для равномерной метрики, позволяет говорить об асимптотической (при $n \to + \infty $) эквивалентности задачи (1), аналогичной “весовой” задаче для профилирующей функции ${{\tilde {F}}_{0}}\left( \kappa \right)$.

Замечание. Неравенства (24) и следующее за ним, справедливы для всех $\vec {p},{\text{\;\;}}\vec {\nu }$ из пространств ${{\mathcal{P}}_{N}}$, ${{\mathcal{N}}_{N}}$ соответственно и, следовательно, справедливы при замене пространства ${{\mathcal{P}}_{N}}$ на его подмножество – параллелепипед ${{{\mathbf{P}}}_{N}}$.

Таким образом, задача оптимального синтеза СДФ в смысле П.Л. Чебышева с ограничениями (2) для энергетического коэффициента отражения или пропускания в силу тождества (3), с учетом проведенных выше рассуждений, эквивалентна такой же задаче для профилирующих функций.

ВЫВОДЫ

Проведен анализ прямой задачи о распространении плоских электромагнитных волн в слоистой среде в пространстве ${{\mathbb{R}}^{3}}$ с кусочно-непрерывными физическими параметрами $\varepsilon \left( x \right)$ и $\mu \left( x \right)$, являющийся единственно надежной основой для постановки и решения всех возможных оптимизационных и обратных задач, связанных с этой тематикой. При указанных предположениях, установлены основные для всей теории слоистых сред тождества (19) и (23).

Приведены явные формулы пересчета для “идеалов” энергетических коэффициентов отражения и пропускания в “идеалы” для профилирующих функций.

Обоснована эквивалентность традиционных постановок задач синтеза слоистых диэлектрических фильтров по их “желаемым” спектральным характеристикам типа энергетических коэффициентов отражения и пропускания, названных в работе “идеалами” для соответствующих спектральных характеристик, значительно более простым по структуре функционалам – задачам синтеза по “идеалу” для профилирующих функций.

Сформулированы принципиально новые постановки задач синтеза полосовых фильтров при помощи идеалов для профилирующих функций с учетом практических ограничений на импедансы слоев реализующих фильтры СДС.