Радиотехника и электроника, 2022, T. 67, № 11, стр. 1067-1075
Геометрия пространства адмитансов N-слойных диэлектрических структур и задачи синтеза
Ю. И. Худак a, *, Д. В. Парфенов a, М. И. Джиоева a
a МИРЭА – Российский технологический университет
119454 Москва, просп. Вернадского, 78, Российская Федерация
* E-mail: hudak@mirea.ru
Поступила в редакцию 02.02.2022
После доработки 24.02.2022
Принята к публикации 01.03.2022
- EDN: ZTCZDH
- DOI: 10.31857/S0033849422110031
Аннотация
Известно, что уровень аналитического моделирования прямых задач электродинамики слоистых диэлектрических структур (СДС) серьезно отстал от потребностей задач оптимизационного синтеза фильтров и решения обратных задач в этой области. Рассмотрена постановка задачи синтеза полосового оптического фильтра на базе заданного в полосе волновых чисел $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ идеала его энергетического коэффициента отражения – $\tilde {R}\left( \kappa \right)$ в метрике пространства $\mathbb{C}\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$. Осуществлено упрощение и дополнение этой постановки задачи важными для практики условиями принадлежности адмитансов системы $\vec {p}\mathop = \limits^{{\text{def}}} \left( {{{p}_{1}}, \ldots ,{{p}_{N}}} \right)$ кубу ${{{\text{K}}}_{{\vec {p}}}}\mathop = \limits^{{\text{def}}} \left\{ {\hat {p} \leqslant {{p}_{j}} \leqslant \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} ,\left( {j = 1, \ldots ,N} \right)} \right\}$ допустимых адмитансов и электрических толщин слоев системы $\vec {\nu }\mathop = \limits^{{\text{def}}} \left( {{{\nu }_{1}}, \ldots ,{{\nu }_{N}}} \right)$ параллелепипеду ${{{{\Pi }}}_{{\vec {\nu }}}}\mathop = \limits^{{\text{def}}} \left\{ {{{{\hat {\nu }}}_{j}} \leqslant {{\nu }_{j}} \leqslant {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\nu } }}_{j}},\left( {j = 1, \ldots ,N} \right)} \right\}$ ограничений СДС по толщинам. Изучено взаимодействие структур пространств электродинамических параметров ${{\mathcal{P}}_{N}}\mathop = \limits^{{\text{def}}} \left\{ {\vec {p}} \right\}$ адмитансов и ${{\mathcal{N}}_{N}}\mathop = \limits^{{\text{def}}} \left\{ {\vec {\nu }} \right\}$ электрических толщин слоев СДС, чего до последнего времени сделано не было.
1. ПОСТАНОВКА ЗАДАЧИ
Если плоское электромагнитное поле11 существует в пространстве ${{\mathbb{R}}^{3}}$, разделенном системой диэлектрических слоев на два полупространства $\mathbb{R}_{ - }^{3}$ и $\mathbb{R}_{ + }^{3}$, то, в общем случае, в $\mathbb{R}_{ - }^{3}$ и $\mathbb{R}_{ + }^{3}$ имеются по две плоские волны, одна из которых распространяется к СДС, а другая – от нее. Обозначим22 $C_{0}^{{\left( - \right)}}$ амплитуду волны, распространяющейся к СДС в $\mathbb{R}_{ - }^{3}$, $C_{1}^{{\left( - \right)}}$ – от СДС в $\mathbb{R}_{ + }^{3}$, $C_{1}^{{\left( + \right)}}$ – распространяющейся к СДС в $\mathbb{R}_{ + }^{3}$, а $C_{0}^{{\left( + \right)}}$ – от СДС в $\mathbb{R}_{ + }^{3}$. Показано, что при не слишком больших величинах электромагнитных полей существует линейная связь между векторами амплитуд ${{{\mathbf{C}}}_{ - }}$ и ${{{\mathbf{C}}}_{ + }}$
Описание любых спектральных характеристик произвольных СДС может быть основано на существенно расширенном толковании анонсированных в [3] и обоснованных в [4] формул, положенных в основу работ авторов [1, 2].
Выяснилось удобство использования электродинамических параметров44, отличных от адмитансов:
Полученные формулы для коэффициентов Фурье экспоненциального представления элементов ${{\tau }_{{lk}}}$ матрицы передачи $\mathcal{T}$ приводят к рассмотрению вопросов вырождения $N$-слойных СДС в $\left( {N - 1} \right)$-слойные и еще “менее” слойные системы, доходя в крайнем случае $0$-слойной системы до случая Френеля – “составного” пространства ${{\mathbb{R}}^{3}}$, т.е. составленного из двух полупространств $\mathbb{R}_{ - }^{3}$ и $\mathbb{R}_{ + }^{3}$. Коэффициенты тригонометрического представления элементов ${{\tau }_{{lk}}}$ матрицы передачи $\mathcal{T}$ названы в работе вычислительными параметрами СДС (см. ниже). Оказывается, что именно через них аналитически выражаются многие спектральные свойства СДС, а их квадраты участвуют в описании ячеистой структуры пространства импедансов ${{\mathcal{P}}_{N}}$ $N$-слойных СДС.
Введены понятия порождающих и профилирующих функций $N$-слойных СДС, оценки которых в разных нормах позволяют получить оценки энергетических коэффициентов отражения и пропускания. Полученные результаты могут быть широко использованы при решении задач анализа и оптимизационных задач синтеза диэлектрических фильтров различного назначения.
При решении задач синтеза фильтров желаемое поведение энергетического коэффициента отражения или пропускания слоистой системы в заданной полосе волновых чисел $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ обычно задается спектральными характеристиками55 этого фильтра $\tilde {R}\left( \kappa \right)$ и $\tilde {T}\left( \kappa \right)$ (см. соответствующие рисунки в [2]). Математическая постановка задачи оптимального в смысле П.Л. Чебышева синтеза слоистого диэлектрического фильтра рассмотрена в [1]:
(1)
$\mathop {{\text{max}}}\limits_{{{\mathcal{K}}_{1}} \leqslant \kappa \leqslant {{\mathcal{K}}_{2}}} \left| {R\left( {\kappa ,\vec {p},\vec {\nu }} \right) - \tilde {R}\left( \kappa \right)} \right|\mathop \to \limits_{\vec {p},\vec {\nu }} {\text{min}},$В [2] мы рассмотрели математическую постановку задачи синтеза:
(2)
$\begin{gathered} \mathop {{\text{max}}}\limits_{{{\mathcal{K}}_{1}} \leqslant \kappa \leqslant {{\mathcal{K}}_{2}}} \left| {R\left( {\kappa ,\vec {p},\vec {\nu }} \right) - \tilde {R}\left( \kappa \right)} \right|\mathop \to \limits_{\vec {p},\vec {\nu }} {\text{min }} \hfill \\ {\text{при }}\vec {\nu } \subset {{\mathcal{N}}_{N}}{\text{ и }}\vec {p} \in {{{\mathbf{P}}}_{N}} \subset {{\mathcal{P}}_{N}}, \hfill \\ \end{gathered} $(3)
$\begin{gathered} \mathop {{\text{max}}}\limits_{{{\mathcal{K}}_{1}} \leqslant \kappa \leqslant {{\mathcal{K}}_{2}}} \left| {F\left( {\kappa ,\vec {p},\vec {\nu }} \right) - \tilde {F}\left( \kappa \right)} \right|\mathop \to \limits_{\vec {p},\vec {\nu }} {\text{min}} \\ {\text{при }}\vec {\nu } \subset {{\mathcal{N}}_{N}}{\text{ и }}\vec {p} \in {{{\mathbf{P}}}_{N}} \subset {{\mathcal{P}}_{N}}, \\ \end{gathered} $2. ПРЯМАЯ ЗАДАЧА И ЕЕ РЕШЕНИЕ. МАТРИЦА ПЕРЕДАЧИ СДС
Используя обозначения [1, 2] и [4–6], приведем основной результат. Элементы ${{\tau }_{{lm}}},{\text{\;\;}}l,m = 0,1$, матрицы $\mathcal{T}$ естественно назвать порождающими функциями СДС, так как при различных выборах “управляющих” векторов $\vec {\theta }$, $\vec {\nu }$ они представляют решение задачи анализа для любой СДС.
Экспоненциальное представление порождающих функций при $\vec {t} = k\vec {\nu }$ имеет вид
(4)
${{\tau }_{{lm}}}\left( {\vec {\theta },\vec {t}} \right) = \sum\limits_J {Q_{J}^{m}\left( {\vec {\theta }\left( \omega \right)} \right)\exp \left( { - i{{\Lambda }_{J}}\left( {\vec {t}} \right)} \right)} ,$(5)
$Q_{J}^{m}\left( {\vec {\theta }} \right) = \mathop \prod \limits_{k = 1}^{N + 1} 1{\text{/}}2\left[ {1 + {{{( - 1)}}^{{{{j}_{{k - 1}}} \oplus {{j}_{k}}}}}{{\theta }_{k}}} \right]$(6)
${{{{\Lambda }}}_{J}}\left( {\vec {t}} \right) = \mathop \sum \limits_{k = 1}^N {{( - 1)}^{{{{j}_{k}}}}}{{t}_{k}}$Замечание. Формулы (5) показывают, что при совпадении адмитансов соседних слоев pj – 1 = pj при каком-либо $j = 1, \ldots ,N + 1$, т.е. выполнении условия “вырождения”: ${{\theta }_{j}} = 1$, половина из всех коэффициентов Фурье (имеющих множитель 1 – θj) обратится в нуль, что превратит N-слойную СДС в (N – 1)-слойную. При выполнении двух условий вырождения для разных $j$ в нуль обратятся $3{\text{/}}4$ коэффициентов Фурье и СДС превратится в (N – 2)-слойную. При выполнении N условий “вырождения” N-СДС превратится в $0$-слойную – пространство ${{\mathbb{R}}^{3}}$, составленное из полупространств $\mathbb{R}_{ - }^{3}$ и $\mathbb{R}_{ + }^{3}$ (случай Френеля). Это явление влечет целую серию следствий, вскрывающих геометрическую структуру пространства адмитансов ${{\mathcal{P}}_{N}}N$-слойных СДС.
3. ГЕОМЕТРИЯ ПРОСТРАНСТВА АДМИТАНСОВ
Поскольку изображение ${{\mathcal{P}}_{N}}$ при $N \geqslant 3$ практически невозможно, графически проиллюстрируем соответствующие построения при N = 2. Они носят общий характер и справедливы при любом N.66 На рис. 1 и 2 показаны пространства ${{\mathcal{P}}_{2}}$ адмитансов двухслойных систем77. Различие между рисунками связано с использованием разных систем координат. На первом из них в качестве координат использованы исходные адмитансы ${{p}_{1}} > 0$, ${{p}_{2}} > 0$ и пространство ${{\mathcal{P}}_{2}}$ представляет собой четверть плоскости. На рис. 2 использованы “показательные координаты”, основанием которых служит базовый параметр рассматриваемых СДС: $\theta \mathop = \limits^{{\text{def}}} {{p}_{3}}{\text{/}}{{p}_{0}}$, а координаты ${{s}_{1}},{{s}_{2}}$ изменяются в пределах $ - \infty < {{s}_{1}} < + \infty ,~~ - \infty < {{s}_{2}} < + \infty $:
(7)
$\begin{gathered} {{\theta }_{1}}\mathop = \limits^{{\text{def}}} {{\theta }^{{{{s}_{1}} + 1/2}}},{\text{\;\;\;\;}}{{\theta }_{2}}\mathop = \limits^{{\text{def}}} {{\theta }^{{{{s}_{2}} - {{s}_{1}}}}},{\text{\;\;\;}} \\ {\text{\;}}{{\theta }_{3}}\mathop = \limits^{{\text{def}}} {{\theta }^{{ - {{s}_{2}} + 1/2}}},{\text{\;\;\;\;}}{{\theta }_{1}}{{\theta }_{2}}{{\theta }_{3}}\mathop = \limits^{{\text{def}}} \theta = \frac{{{{p}_{3}}}}{{{{p}_{0}}}}. \\ \end{gathered} $Рис. 1.
Пространство адмитансов ($N = 2$) в “исходных” координатах $\left( {{{p}_{1}},{{p}_{2}}} \right)$.

Рис. 2.
Пространство адмитансов ($N = 2$) в “показательных” координатах $\left( {{{s}_{1}},{{s}_{2}}} \right)$.

В пересечении линии вырождения образуют треугольник вырождения с вершинами ${\text{I'}},\,\,{\text{II'}},\,\,{\text{III'}}$. Также на рисунке есть три линии U1, …, U3, две из них, ${{U}_{1}},{{U}_{3}}$, параллельны вертикальной ${{V}_{1}}$ и горизонтальной ${{V}_{3}}$ линиям вырождения, двойственны к ним и описываются уравнениями соответственно:
Третья линия ${{U}_{2}}$ является двойственной по отношению к биссектрисе координатного угла ${{p}_{2}} = {{p}_{1}}$. Линия ${{U}_{2}}$ является лучом из начала координат через вершину прямого угла между ${{V}_{1}}$ и ${{V}_{3}}$ и имеет уравнение
На рис. 2 эта линия параллельна линии вырождения ${{V}_{2}}$. Двойственные линии в пересечении образуют “большой треугольник” с вершинами ${\text{I}},\,\,{\text{II}},\,\,{\text{III}}$.
Кроме того, на рис. 1 и 2 есть три линии ${{N}_{1}},\,\, \ldots ,\,\,~{{N}_{3}}$, две из них, ${{N}_{1}},~{{N}_{3}}$, параллельные вертикальной ${{V}_{1}}$ и горизонтальной ${{V}_{3}}$ линиям вырождения, будем называть линиями “нулей” с соответствующими индексами и даются уравнениями соответственно
Третья линия ${{N}_{2}}$ на рис. 1 имеет уравнение
а на рис. 2 эта линия параллельна линии вырождения ${{V}_{2}}$. Три линии “нулей” в пересечении образуют “малый треугольник” с вершинами 1, 2, 3, стороны которого параллельны сторонам большого треугольника ${\text{I}},\,\,{\text{II}},\,\,{\text{III}}$.Также на рис. 1 изображены три кривые второго порядка, М1, …, М3, две параболы и одна гипербола, уравнения которых получаются при подстановке координат ${{p}_{1}},\,\,{{p}_{2}}$ в уравнения линий в переменных Френеля соответственно:
Соответствующие линии на рис. 2 являются медианами всех трех треугольников, а потому они пересекаются в одной общей для них точке – центре всех этих треугольников, который мы будем обозначать символом $\square $ – стилизованным “римским” нулем. Названия медианы для этих линий мы будем использовать и для рис. 1.
Четыре области на рис. 1, заштрихованные светло-серым цветом, совпадают с диаграммой Шустера [7], указавшего те области в пространстве ${{\mathcal{P}}_{2}}$, внутри которых существуют нули коэффициентов отражения для соответсвующих СДС, а на рис. 2 области Шустера – внутренность малого треугольника и внутренности его внешних углов.
4. ВЫЧИСЛИТЕЛЬНЫЕ ПАРАМЕТРЫ
Формулы Эйлера переводят (6) в тригонометрическое представление порождающих функций:
(8)
$\begin{gathered} {{\tau }_{{lm}}}\left( {\vec {\theta },\vec {t}} \right) = {{u}_{m}} - i{{v}_{m}}, \\ {{u}_{m}} = \mathop \sum \limits_{L:\parallel {\mathbf{L}}\parallel = 2n + 1} {{\left( { - 1} \right)}^{n}}\alpha _{L}^{m}{{{{\Psi }}}_{L}}\left( {\vec {t}} \right), \\ {{v}_{m}} = \mathop \sum \limits_{L:\parallel {\mathbf{L}}\parallel = 2n} {{( - 1)}^{n}}\alpha _{L}^{m}{{{{\Psi }}}_{L}}\left( {\vec {t}} \right), \\ \end{gathered} $(9)
$\begin{gathered} {{p}_{j}} = \sqrt {{{\varepsilon }_{j}}{\text{/}}{{\mu }_{j}}} ,\,\,\,{\mathbf{L}} = \left( {{{l}_{1}}, \ldots ,{{l}_{N}}} \right),~\,\,\,{{l}_{k}} = 0,1,\,\,\,k = 1, \ldots ,N, \\ \left\| {\mathbf{L}} \right\| = \sum\limits_{k = 1}^N {{{l}_{k}},} \,\,\,\,{{{{\Psi }}}_{L}}\left( {\vec {t}} \right) = \mathop \prod \limits_{k = 1}^N x_{k}^{{{{{\bar {l}}}_{k}}}}y_{k}^{{{{l}_{k}}}}, \\ {{x}_{k}} = {\text{cos}}\left( {{{t}_{k}}} \right),\,\,\,\,{{y}_{k}} = \sin \left( {{{t}_{k}}} \right). \\ \end{gathered} $Преобразование $\vec {t} = \vec {\nu }\omega $ делает эти функции $2\pi $-периодическими функциями по переменным tk = $ = {{v}_{k}}\omega {\text{\;\;}}\left( {k = 1, \ldots ,N} \right)$. Коэффициенты ${{{\mathbf{\alpha }}}_{m}}\, = \,(\alpha _{0}^{m}, \ldots ,$ $\alpha _{{{{2}^{{N - 1}}}}}^{m})$, $\alpha _{L}^{m},\left( {m = 0,1} \right),\,\,{\mathbf{L}} = \left( {{{l}_{1}}, \ldots ,{{l}_{N}}} \right),\,\,\left( {{{l}_{k}} = 0,1} \right)$ представления (8) мы называем вычислительными параметрами СДС99. Обе серии вычислительных параметров ($m = 0,1$) преобразованием Адамара связаны с отвечающими им коэффициентами Фурье в (4):
(10)
${{{\mathbf{\alpha }}}_{m}} = \mathcal{H}{{{\mathbf{Q}}}_{m}},\,\,\,\,{{{\mathbf{Q}}}_{m}} = \left( {Q_{0}^{m}, \ldots ,Q_{{{{2}^{{N - 1}}}}}^{m}} \right),$Замечание. Указанные на рис. 1 и 2 линии: вырождения, двойственные к ним и медианы при переходе к пространствам ${{\mathcal{P}}_{N}}$ более высокой размерности, чем $N = 2$, заменяются на гиперплоскости, а в нужных местах рис. 1 – гиперповерхностями, не более второго порядка по каждой переменной ${{p}_{k}}{\text{\;}}\left( {k = 1, \ldots ,N} \right)$.
Переход к показательным координатам $\vec {s}\mathop = \limits^{{\text{def}}} \left( {{{s}_{1}}, \ldots ,{{s}_{N}}} \right)$ в пространствах ${{\mathcal{P}}_{N}}$ большей, чем $N = 2$ размерности, проводится с использованием параметров Френеля ${{\theta }_{k}}{\text{\;}}\left( {k = 1, \ldots ,N + 1} \right)$ по формулам, в которых координаты ${{s}_{k}}$ изменяются в пределах $ - \infty < {{s}_{k}} < + \infty $:
(11)
$\begin{gathered} {{\theta }_{1}}\mathop = \limits^{{\text{d}}ef} {{\theta }^{{{{s}_{1}} + \frac{1}{2}}}},{\text{\;\;}} \ldots ,{{\theta }_{N}}\mathop = \limits^{{\text{def}}} {{\theta }^{{{{s}_{N}} + \frac{1}{2}}}},{\text{\;}}\,\,\,\,{{\theta }_{{N + 1}}}\mathop = \limits^{{\text{def}}} {{\theta }^{{ - \,\left( {\sum\limits_{k = 1}^N {{{s}_{N}}} } \right)\, - \,\frac{N}{2} + 1}}}, \\ \mathop \prod \limits_{k = 1}^N {{\theta }_{k}}\mathop = \limits^{{\text{def}}} \theta = {{p}_{{N + 1}}}{{p}_{0}}. \\ \end{gathered} $5. ТОЖДЕСТВА СРАВНЕНИЯ
Запишем принципиальные тождества сравнения для квадратов вычислительных параметров $\alpha _{I}^{m}$ для случая $m = 1$, не указывая $m$ явно, так как при $m = 0$ они заменяются на аналогичные. Сначала выпишем эти тождества при $N = 2$ (в этом случае их ровно 6), чтобы их было удобно проинтерпретировать с использованием рис. 1 и 2:
(12)
$\begin{gathered} \alpha _{0}^{2} - \alpha _{1}^{2} = \left( {1 - \theta _{3}^{2}} \right)\left( {1 - \theta _{1}^{2}\theta _{2}^{2}} \right),\,\,\,\,\alpha _{1}^{2} - \alpha _{2}^{2} = \left( {\theta _{3}^{2} - \theta _{1}^{2}} \right)\left( {1 - \theta _{2}^{2}} \right), \hfill \\ \alpha _{0}^{2} - \alpha _{2}^{2} = \left( {1 - \theta _{1}^{2}} \right)\left( {1 - \theta _{2}^{2}\theta _{3}^{2}} \right),\,\,\,\,\alpha _{1}^{2} - \alpha _{3}^{2} = \left( {\theta _{3}^{2} - \theta _{2}^{2}} \right)\left( {1 - \theta _{1}^{2}} \right), \hfill \\ \alpha _{0}^{2} - \alpha _{3}^{2} = \left( {1 - \theta _{2}^{2}} \right)\left( {1 - \theta _{1}^{2}\theta _{3}^{2}} \right),\,\,\,\,\alpha _{2}^{2} - \alpha _{3}^{2} = \left( {\theta _{1}^{2} - \theta _{2}^{2}} \right)\left( {1 - \theta _{3}^{2}} \right). \hfill \\ \end{gathered} $В правых частях написанных формул стоят произведения двух сомножителей, зависящих от параметров Френеля, так, что при изменении знаков этих скобок будут выполняться определенные отношения “доминирования” между квадратами вычислительных параметров: $\alpha _{I}^{2}{\kern 1pt} > $ или $ < {\kern 1pt} \alpha _{J}^{2}$. Обращение же скобок в нуль указывает на равенство записанных слева величин. Отметим, что в правой части участвуют скобки, отвечающие уравнениям в переменных Френеля, введенных выше линий: вырождения ${{V}_{j}},j = 1,2,3$, двойственных к ним ${{U}_{j}},j = 1,2,3$, и медиан ${{M}_{j}},j = 1,2,3$.
На рис. 2 видно, что указанные линии разбивают все пространство параметров ${{\mathcal{P}}_{2}}$ на 24 треугольника, внутри каждого из которых (для всех его точек!) выполняется неравенство упорядочения:
(13)
$\alpha _{i}^{2} < \alpha _{j}^{2} < \alpha _{k}^{2} < \alpha _{l}^{2}{\text{\;\;}}\left( {i,j,k,l = 0,1,2,3} \right),$Группировка областей $\left( {ijkl} \right)$ по доминированию состоит в фиксации какого-либо числа из $0,1,2,3$ в “старшей” позиции $l$. При этом вся плоскость $\left( {{{s}_{1}},{{s}_{2}}} \right)$ будет разбита на четыре зоны, которым присвоены “римские” номера $l$, ${\text{I}},{\text{II}},{\text{III}},{\text{\;}}\square $. Справедливо разбиение пространства ${{\mathcal{P}}_{N}}$ на $\left( {{{2}^{N}}} \right)!$ непересекающихся класса точек, заключенных в гипертетраэдры, аналогичные $\left( {{{2}^{2}}} \right)! = 24$ треугольникам для ${{\mathcal{P}}_{2}}$.
6. СВЯЗЬ ВЫЧИСЛИТЕЛЬНЫХ ПАРАМЕТРОВ С ПАРАМЕТРАМИ ФРЕНЕЛЯ
Чтобы обосновать сказанное, получим новые формулы, выражающие вычислительные параметры αj (j = 0, 1, …, 2N – 1) через параметры Френеля. Для этого в формуле (5), определяющей коэффициенты Фурье, проведем перемножение биномов, воспользовавшись аддитивной формой обобщенного бинома:
(14)
$\begin{gathered} \alpha _{I}^{m} = 1{\text{/}}2\left( {{{\tau }_{{\mathbf{L}}}} + {{{( - 1)}}^{m}}{{\tau }_{{{\mathbf{\bar {L}}}}}}} \right),\,\,\,\,{\mathbf{I}} = \left( {{{i}_{1}}, \ldots ,{{i}_{N}}} \right), \\ {{i}_{k}} = 0,1,{\text{\;\;}}\left( {k = 1, \ldots ,N} \right), \\ \end{gathered} $Для векторов ${\mathbf{L}}$, имеющих только одну единицу, соответствующее ${{\tau }_{L}}$ будет иметь вид ${{\theta }_{s}}{\text{\;\;}}\left( {s = 2, \ldots ,N} \right)$, и мы получим $N - 1$ гиперплоскостей вырождения ${{V}_{s}}$ при ${{\theta }_{s}} = 1$ и столько же двойственных им гиперплоскостей ${{U}_{s}}$ при ${{\theta }_{s}} = \theta $. Еще одна гиперплоскость вырождения ${{V}_{1}}$ получится при θ1 = 1, а двойственная к ней гиперплоскость ${{U}_{1}}$ получится при ${{\theta }_{1}} = \theta $. Последние гиперплоскости вырождения ${{V}_{{N + 1}}}$ и двойственная к ней ${{U}_{{N + 1}}}$ соответствуют ${{\theta }_{{N + 1}}} = 1$ и ${{\theta }_{{N + 1}}} = \theta $. Ровно посредине между каждой плоскостью вырождения ${{V}_{s}}$ и двойственной к ней ${{U}_{s}}$ располагается нулевая плоскость ${{N}_{s}}$. Подобно (11) при $m = 1$ можно выписать ${{2}^{{N - 1}}}\left( {{{2}^{N}} - 1} \right)$ тождеств сравнения:
(15)
$\begin{gathered} \alpha _{I}^{2} - \alpha _{J}^{2} = 1{\text{/}}4\left[ {{{{\left( {{{\tau }_{{\mathbf{L}}}} - {{\tau }_{{{\mathbf{\bar {L}}}}}}} \right)}}^{2}} - {{{\left( {{{\tau }_{{\mathbf{M}}}} - {{\tau }_{{{\mathbf{\bar {M}}}}}}} \right)}}^{2}}} \right] = \\ = \,\,1{\text{/}}4\left( {{{\tau }_{{{\mathbf{LM}}}}} - {{\tau }_{{{\mathbf{\bar {L}\bar {M}}}}}}} \right) \cdot \left( {{{\tau }_{{{\mathbf{L\bar {M}}}}}} - {{\tau }_{{{\mathbf{\bar {L}M}}}}}} \right), \\ \end{gathered} $7. КВАЗИОКРУЖНОСТИ В ПРОСТРАНСТВЕ ${{\mathcal{P}}_{N}}$
Прежде всего отметим, что для элементов ${{\tau }_{{lm}}}$ матрицы передачи $\mathcal{T}$ – порождающих функций – справедливо равенство
(16)
$\mathop \sum \limits_J {{(Q_{J}^{m})}^{2}}\mathop = \limits^{{\text{def}}} \left\| {{{\tau }_{{lm}}}\left( {\vec {t}} \right)} \right\|_{{{{\mathcal{L}}_{2}}}}^{2} = 1{\text{/}}{{2}^{N}}\mathop \sum \limits_I {{(\alpha _{I}^{m})}^{2}},$На рис. 3 при $N = 2$ изображена серия “квазиевклидовых” “квазиокружностей”, отвечающих нескольким значениям их “квазирадиусов”: ${{\rho }_{k}} = {{d}_{k}}\alpha _{0}^{2}{\text{\;\;\;}}\left( {k = 1, \ldots ,5} \right)$. На рис. 4 при $N = 2$ представлена серия “квазичебышевских квазиокружностей”: ${{\rho }_{k}} = {{d}_{k}}\alpha _{0}^{2}{\text{\;\;}}\left( {k = 1, \ldots ,5} \right),$ одна из которых совпала со сторонами среднего треугольника ${\text{I}}{\kern 1pt} ',\,\,{\text{II}}{\kern 1pt} {\text{'}},\,\,{\text{III}}{\kern 1pt} {\text{'}}$. Смысл названия “квазичебышевские квазиокружности” тесно связан со следующей точной (в том смысле, что она достигается в некоторой вершине куба периодов ${{T}^{N}}$ порождающих функций) оценкой:
(17)
$\mathop {{\text{max}}}\limits_{{{{\mathbf{T}}}^{N}}} |{{\tau }_{{lm}}}\left( {\vec {t}} \right){{|}^{2}} \leqslant \mathop {{\text{max}}}\limits_{\mathbf{I}} {{(\alpha _{{\mathbf{I}}}^{m})}^{2}},$Рис. 3.
“Евклидовы квазиокружности”: $\sum\nolimits_{k = 1}^3 {\alpha _{k}^{2}} = \rho ,\,\,\left( {{{\rho }_{k}} = {{d}_{k}}\alpha _{0}^{2},\,\,k = 1, \ldots ,3} \right)$.
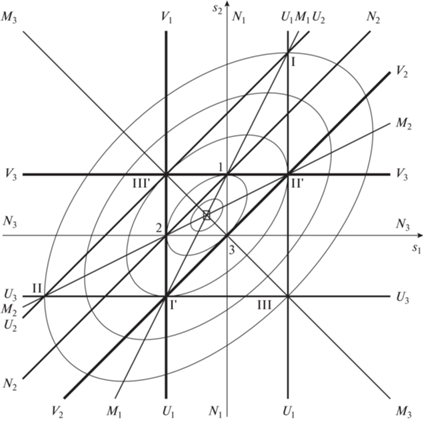
Рис. 4.
“Чебышевские квазиокружности”: $\mathop {{\text{max}}}\limits_{0 \leqslant I \leqslant {{2}^{N}} - 1} \alpha _{I}^{2} = \rho ,\,\,{{\rho }_{k}} = {{d}_{k}}\alpha _{0}^{2},\,\,k = 1, \ldots ,5)$.

С иcпользованием (17) получены эффективные, точные и неулучшаемые на классе СДС оценки энергетических коэффициентов отражения сверху и пропускания снизу:
(18)
$\begin{gathered} \mathop {{\text{max}}}\limits_{{{{\text{T}}}^{N}}} {{\left| {{\text{R}}\left( {\vec {t}} \right)} \right|}^{2}} \leqslant \mathop {{\text{max}}}\limits_{\mathbf{I}} \frac{{{{{(\alpha _{I}^{1})}}^{2}}}}{{{{{(\alpha _{I}^{0})}}^{2}}}},\,\, \\ \mathop {{\text{max}}}\limits_{{{{\text{T}}}^{N}}} {{\left| {{\text{T}}\left( {\vec {t}} \right)} \right|}^{2}} \leqslant 1 - \mathop {{\text{max}}}\limits_{\mathbf{I}} \frac{{{{{(\alpha _{I}^{1})}}^{2}}}}{{{{{(\alpha _{I}^{0})}}^{2}}}}. \\ \end{gathered} $С помощью неравенства Бернштейна эти оценки дают точные оценки производных указанных характеристик СДС.
8. ПРИМЕР СИНТЕЗА ПОЛОСОВОГО ФИЛЬТРА ПРИ N = 2
Рассмотрим пример синтеза полосового фильтра для заданного идеала $\tilde {F}\left( \kappa \right)$ ≡ 0 профилирующей функции, отвечающего такому же идеалу для коэффициента отражения $\tilde {R}\left( \kappa \right) \equiv 0$. Традиционно примем p0 = 1, а величину p3 – равной 1.52. Тогда получим ${{\theta }} = 1.52$, а $\sqrt {{{p}_{0}}{{p}_{3}}} \approx 1.233$. Размеры куба ${{K}_{N}}$ допустимых адмитансов выберем в соответствии с формулами (7) в условных единицах при значениях параметров ${{s}_{1}} = 0.125$, $~{{s}_{2}} = 0.875$.
При таком выборе параметров ${{s}_{1}}$ и ${{s}_{2}}$ в соответствии с работой [8] нули порождающей функции для части области пространства адмитансов, помеченной символом (2301) и лежащей внутри куба ограничений ${{K}_{2}}$, попадают на луч ${{\nu }_{2}} = 2{{\nu }_{1}}$, исходящий на плоскости ${{t}_{1}} = {{\nu }_{1}}\kappa $, ${{t}_{2}} = {{\nu }_{2}}\kappa $ из начала координат и определяющий оптимальную обмотку на торе, соответствующем порождающей функции. Профиль сечения порождающей функции вдоль указанного луча будет иметь вид фильтра квазичебышевского типа, если поместить середину интересующего нас интервала волновых чисел $\left[ {{{\mathcal{K}}_{1}},{{\mathcal{K}}_{2}}} \right]$ в точку ${{t}_{1}} = \pi {\text{/}}2$, ${{t}_{2}} = {\text{\;}}\pi $, выбрав величину $\nu = \sqrt {\nu _{1}^{2} + \nu _{2}^{2}} $. При этом в широком диапазоне волновых чисел отношение максимального значения профилирующей функции на луче к ее минимально допустимому уровню просветления $\alpha _{2}^{2} \approx 0.004167$ заведомо будет превосходить величину $(\alpha _{1}^{2} + ~\alpha _{3}^{2}){\text{/}}(2\alpha _{2}^{2}) \approx 27.6$, которая является важнейшей характеристикой построенного таким образом фильтра.
ЗАКЛЮЧЕНИЕ
Исследовано взаимодействие структур пространств электродинамических параметров адмитансов и электрических толщин слоев СДС. Объединение изложенных выше построений с полученными нами ранее результатами по детальному исследованию расположения нулей коэффициента отражения [8, 9] в зависимости от адмитансов материалов системы выводит математический аппарат решения задачи синтеза оптимальных полосовых фильтров на новый уровень.
Список литературы
Худак Ю.И., Парфенов Д.В., Музылев Н.В., Хачлаев Т.С. // Рос. технол. журн. 2020. Т. 8. № 5. С. 26.
Худак Ю.И., Парфенов Д.В. // РЭ. 2021. Т. 66. № 9. С. 845.
Кард П.Г. Анализ и синтез многослойных интерференционных пленок. Таллин: Валгус, 1971.
Худак Ю.И. // Докл. РАН. 2013. Т. 448. № 5. С. 1.
Худак Ю.И. // Докл. РАН. 2015. Т. 467. № 2. С. 149.
Худак Ю.И. // Рос. технол. журн. 2017. Т. 5. № 3. С. 3.
Schuster K. // Annalen der Physik (Folge 6). 1949. B. 4. H. 5. S. 352.
Худак Ю.И., Ахмедов И.А., Музылев Н.В., Парфенов Д.В. // Нелинейный мир. 2016. № 2. С. 38.
Худак Ю.И., Ахмедов И.А., Музылев Н.В., Парфенов Д.В. // Электромагнитные волны и электронные системы. 2016. № 2. С. 24.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


