Радиотехника и электроника, 2022, T. 67, № 2, стр. 117-129

ВВЕДЕНИЕ

В связи с влиянием ионосферы Земли на работу радиосистем различного назначения: систем радиолокации, радиосвязи и радионавигации (позиционирования), актуальной задачей является диагностика и контроль ионосферы, а также постоянный мониторинг экстремальных явлений в атмосфере [1–4]. Математическое моделирование распространения радиоволн в возмущенной ионосферной плазме [5], привязанное непосредственно к оперативным данным наклонного и вертикального зондирования [6–8], является перспективным методом решения указанной задачи.

В данной работе рассмотрен метод восстановления эффективной частоты соударений электронов в ионосферной плазме, основанный на измерении задержки отраженных от ионосферы сигналов и амплитудных характеристик линейно частотно-модулированных (ЛЧМ) сигналов ионозонда вертикального зондирования (ВЗ) [6, 7], так как ионозонды ВЗ являются одним из наиболее эффективных и апробированных средств диагностики ионосферы Земли [9].

1. РАСШИРЕННАЯ БИХАРАКТЕРИСТИЧЕСКАЯ СИСТЕМА

Рассмотрим подход к определению эффективной частоты соударений электронов в ионосферной плазме, основанный на решении расширенной бихарактеристической системы Лукина [10–12]:

В формулах (1)–(3) введены следующие обозначения: ω – круговая частота, $\omega = 2\pi f$ (f – рабочая частота); $\varepsilon (\vec {r},\vec {k},\omega )$ – эффективная диэлектрическая проницаемость среды распространения; $\vec {k}$(t) – волновой вектор; $\vec {r}$$ = (x,y,z)$ – декартовы координаты луча; t – время группового запаздывания сигнала; $(\eta ,\zeta )$ – углы выхода луча.

Первые шесть уравнений (1) определяют координаты луча и волновой вектор. Для их нахождения необходимо дополнить систему (1) начальными условиями:

В формулах (4) ${{\varepsilon }_{0}}$ – значение эффективной диэлектрической проницаемости среды в источнике, который расположен в начале координат. Для того чтобы избежать особенностей при вычислениях вертикального луча, нами выбрана параметризация волнового вектора, для которой вертикальному лучу соответствуют $\zeta = 0,\,\,\,\eta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ [13].

Для вертикального луча из (4) находим

Следующие 12 уравнений (см. (2), (3)) определяют скорости изменений производных координат и компонент волновых векторов по угловым координатам η и ζ. Для этой группы уравнений начальные условия имеют вид

В случае нормального падения получаем

Решение расширенной бихарактеристической системы позволяет найти расходимость D, которая вычисляется как корень из отношения якобианов ${{\hat {J}}_{0}}$ и $\hat {J}$ [12, 14]:

Если среда изотропная, т.е. ${{\partial \varepsilon } \mathord{\left/ {\vphantom {{\partial \varepsilon } {\partial{ \vec {k}}}}} \right. \kern-0em} {\partial{ \vec {k}}}} = 0$, то в системе (1) первая группа уравнений упрощается:

Известно, что в предположении изотропности среды (ионосферной плазмы) эффективную диэлектрическую проницаемость можно представить в виде

где e и ${{m}_{e}}$ – заряд и масса электрона, с – скорость света, ${{\omega }_{p}}$ – плазменная частота, а $N(\vec {r})$ – электронная концентрация. С учетом (10) формула (9) преобразуется и имеет вид

Тогда выражение для якобиана $\hat {J}$ принимает вид

Очевидно, что выражение для расходимости D теперь можно представить как

Предположим, что эффективная диэлектрическая проницаемость среды зависит только от высоты z, т.е. $\varepsilon (z,\omega )$. Тогда из системы (1) следует, что k_x и k_y вдоль траектории постоянны, а так как для вертикального луча начальные значения k_x и k_y равны нулю (см. (5)), то находим, что k_x = k_y = 0. Поэтому выражение для J можно переписать в следующем виде:

Из системы (1) находим, что $x(t) = y(t) = 0\,$, и остаются два уравнения относительно z(t) и k_z(t), образующие подсистему:

с начальными условиями

Численное решение системы (14) с учетом (5) позволяет найти $z(t)$ и ${{k}_{z}}(t)$.

Для вычисления якобиана J необходимо знать производные x и y по начальным углам выхода лучей ζ и η (14). Эти производные находятся как решения системы (2), (3):

с начальными условиями (6) или (7). В предположении, что горизонтальные градиенты отсутствуют, можно установить, что

2. МЕТОД ДИАГНОСТИКИ ЭФФЕКТИВНОЙ ЧАСТОТЫ СОУДАРЕНИЙ

Амплитуда A зондирующего сигнала связана с расходимостью D и поглощением ψ формулой [13, 14]

в которой величина E₀ – значение амплитуды поля вне ионосферы на расстоянии r₀ от источника излучения, расположенного в начале координат. В случае изотропного излучателя получаем

При необходимости в выражение (20) могут быть включены диаграмма направленности, коэффициент усиления и другие параметры. В формуле (20) W − мощность источника излучения, и если мощность выражена в киловаттах, а r₀ – в метрах, то размерность E₀ будет В/м. При вычислениях принято, что W = 1 кВт.

Предполагается, что из данных ВЗ можно получить зависимость задержки $2\,{{t}_{m}}$ отразившегося от ионосферы сигнала от частоты f, а также зависимость амплитуды A принятого сигнала от частоты зондирования f. Параметр t_m(f) – время прихода сигнала из излучателя в точку отражения от ионосферы.

Считая, что зависимость электронной концентрации N(z) от высоты z известна, т.е. уже восстановлена по зависимости задержки сигнала от частоты излучения, можно, опираясь на формулы разд. 1, определить расходимость D (13).

Тогда из (19) находим поглощение

Поглощение ψ можно найти по формуле [15, 16]

где ${{\varepsilon }_{2}}\,$ – мнимая часть диэлектрической проницаемости среды. Мнимую часть диэлектрической проницаемости среды можно приближенно представить в виде [9, 15]

где

а ν_e – эффективная частота соударений электронов.

Предполагая, что эффективная частота соударений на высотах выше 80 км не превышает 10⁶ с^–1, в знаменателе выражения (23) можно пренебречь величиной Z ² и считать, что

Приравняв (21) и (22) и исключив ψ, можно для определения ${{\nu }_{e}}(z)$ получить интегральное уравнение типа Вольтерра второго рода:

С учетом (24) и (25) уравнение (26) нетрудно переписать в виде

Для решения уравнения (27) применим метод итераций [13, 14] и найдем эффективную частоту соударений ν_e как функцию высоты z. Следует подчеркнуть, что высота z зависит от группового времени t и вычисляется вдоль лучевой траектории отдельно для каждой частоты. Поэтому функция z(t) также зависит от частоты.

Рассмотрим алгоритм решения уравнения (27). Так как ниже определенной высоты ионосферная плазма отсутствует, то электронная концентрация равна нулю. Следовательно, до некоторой частоты f₀, для которой время t_m равно t_m0, интеграл в левой части (27) равен нулю:

Рассмотрим частотный интервал (f₀, f_n), принадлежащий частотному интервалу (f_min, f_max), на котором осуществляется зондирование, причем f_min < < f₀ < f_n < f_max. Будем считать, что f_max совпадает с максимальной плазменной частотой ионосферного слоя. Разобъем интервал (f₀, f_n) на n частей: f₀, f₁, …, f_j, …, f_n. Предположим, что на каждом j-м интервале (f_{j – 1}, f_j) функция G постоянная и равна G_j. Пусть t_mj – время прихода сигнала с частотой f_j из передатчика в точку отражения от ионосферы. Они известны из решения бихарактеристической системы. Тогда из (27) нетрудно получить

Формулы (29) можно упростить и получить

После вычислений G_j, зная, что каждая из этих величин это произведение эффективной частоты соударений электронов N(z), электронной концентрации в точке отражения и константы ${{V}_{c}}$, можно легко найти зависимость эффективной частоты соударений ν_e от высоты z.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ. ОДНОСЛОЕВАЯ МОДЕЛЬ

Приведем примеры численной реализации рассмотренных выше алгоритмов. Далее на основе приведенных выше формул рассчитана амплитуда поля в точке приема, совпадающей с точкой излучения сигнала, для разных частот, восстановлена эффективная частота соударений электронов в плазме ν_e и выполнено сравнение модельных и расчетных значений.

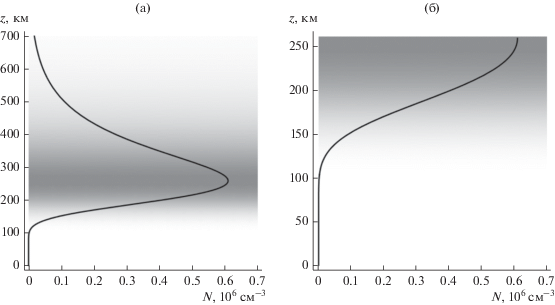
Рассмотрим однослоевую модель ионосферы. Зависимость электронной концентрации от высоты приведена на рис. 1 и показана как фоном, так и линией. Весь ионосферный слой представлен на рис. 1а, а та часть ионосферы, которая доступна сигналам станции ВЗ, – на рис. 1б.

Рис. 1.

Зависимость электронной концентрации N от высоты z: а – весь ионосферный слой, б – фрагмент.

Модель зависимости эффективной частоты соударений электронов ν_e. от высоты z, взятая из экспериментальных данных, показана на рис. 2а и 2б широкой белой линией [13]. Как и на рис. 1, плотность электронной концентрации показана фоном.

Рис. 2.

Моделирование зависимости lg ν_e от высоты: а – полный профиль, б – фрагмент, белая линия – экспериментальные данные, темная линия – результат моделирования.

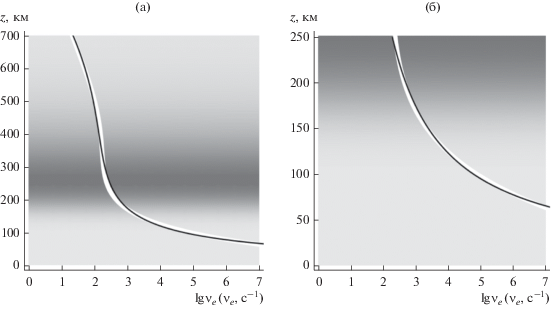
Аппроксимация эффективной частоты соударений ν_e, полученная методом наименьших квадратов, на рис. 2а показана тонкой линией. Она может быть описана выражением

в котором a₀ ≈ –1.02, b₁ ≈ 498.9, a₁ ≈ 0.0080, a₂ ≈ ≈ ‒8.04 × 10^–6. По данным ВЗ зависимость ν_e(z) может быть восстановлена не выше максимума слоя F2, т.е. только в нижней части ионосферы, показанной на рис. 2б. Зависимость эффективной частоты соударений от высоты в этой области проще. Аппроксимацию можно представить гиперболической функцией:

в которой a ≈ 0.617, b ≈ 416.18. В формулах (31) и (32) высота z выражена в километрах.

Рассмотрим численные решения системы бихарактеристических уравнений (15), (16) (рис. 3, 4). На рис. 3 показаны лучевые траектории. В плоскости (x, z) все лучевые траектории образуют вертикальную прямую линию (см. рис. 3а), а в координатах (t, z) каждая частота от 1 до 6.993 МГц имеет свою траекторию и показана своим оттенком серого цвета (рис. 3б). Из рисунка видно, что с возрастанием частоты растет время распространения сигнала.

Рис. 3.

Лучевые траектории для однослоевой модели: а – в плоскости (x, z), б – в плоскости (t, z) на частотах от 1 до 6.993 МГц (снизу вверх).

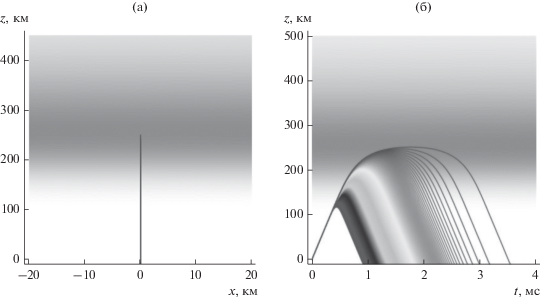
Рис. 4.

Зависимость ${{k}_{z}}$ от времени (а) и высоты (б) для однослоевой модели на частотах от 1 до 6.993 (а – слева направо, б – снизу вверх).

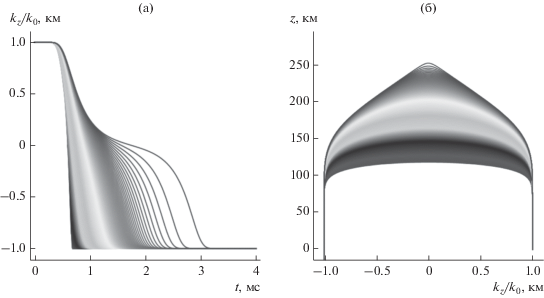
Зависимости вертикальной компоненты волнового вектора ${{k}_{z}}$ от времени t и высоты z показаны на рис. 4. Частота возрастает от 1 до 6.993 МГц на рис. 4а слева направо, а на рис. 4б – снизу вверх.

При построении рис. 4 волновой вектор ${{k}_{z}}$ нормирован на начальное значение волнового вектора ${{k}_{0}} = {{k}_{z}}(0)$. Отметим, что величина ${{k}_{0}}$ является функцией частоты (16). Из рис. 4 видно, что значение нормированного волнового вектора меняется при распространении в ионосфере, уменьшаясь до 0 в точке отражения, а после смены знака волнового вектора опять по модулю возрастает. Когда отношение ${{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$ становится равным 1, луч покидает ионосферу.

Рассмотрим теперь амплитудные характеристики, получаемые из решения расширенной бихарактеристической системы (18). Зависимости ослабления сигнала ${{A}_{m}}$ от времени и высоты

вдоль лучей, соответствующих различным частотам, приведены на рис. 5.

Рис. 5.

Зависимость амплитуды сигнала от времени (а) и высоты (б) для однослоевой модели.

При движении вдоль луча от источника ослабление сначала резко увеличивается (до 100 дБ). Далее ослабление резко уменьшается при приближении к точке отражения, соответствующей каустике [16–19], а потом опять возрастает, когда луч возвращается в источник излучения. На каустике (в точке отражения) в геометрооптическом приближении амплитуда сигнала обращается в бесконечность, хотя из рис. 5 это не очевидно. Однако более точные расчеты показывают, что при приближении к точке отражения, а также в источнике ${{A}_{m}} \to - \infty \,$.

Рассмотрим характеристики радиосигнала, отраженного от ионосферы, в точке приема. Зависимость высоты отражения сигнала ${{z}_{m}}$ от частоты, вычисленная по модельным данным, показана на рис. 6а, а зависимость времени прихода луча в точку отражения ${{t}_{m}}$ от частоты – на рис. 6б. Видно, что и время ${{t}_{m}}$, и высота отражения ${{z}_{m}}$ сигнала монотонно растут с ростом частоты f. При приближении частоты f к критической f_m (≈7 МГц) наблюдается особенно быстрый рост как высоты z_m, так и времени ${{t}_{m}}$.

Рис. 6.

Зависимость высоты отражения сигнала ${{z}_{m}}$ (а) и времени t_m (б) от частоты f для однослоевой модели.

Использую частоту f как параметр и опираясь на данные рис. 6а и 6б, можно построить зависимость высоты отражения сигнала ${{z}_{m}}$ от задержки ${{t}_{m}}$ (рис. 7). Для однослоевой модели эта кривая плавная и взаимно-однозначная.

Рис. 7.

Функция высоты отражения сигнала ${{z}_{m}}$ от времени t_m.

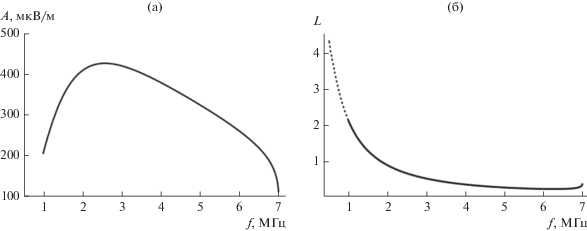
На рис. 8 приведена зависимость от частоты f поглощения ψ, найденная по формулам (22), (23), при условии, что зависимость логарифма эффективной частоты соударений ν_e от высоты z определяется графиком на рис. 2б. Видно, что поглощение убывает при увеличении частоты и начинает вновь увеличиваться при приближении частоты f к критической.

Рис. 8.

Зависимость поглощения ψ от частоты f.

Зависимости амплитуды сигнала в точке приема А (19) и функции L (21) от частоты f показаны на рис. 9. Амплитуда радиосигнала, отраженного от ионосферы, сначала растет при увеличении частоты (до ~2.5 МГц), а затем резко убывает (см. рис. 9а). Зависимость функции L (20) от частоты f более плавная (см. рис. 9б), поскольку она пропорциональна логарифму отношения амплитуды сигнала и лучевой расходимости, умноженной на постоянный коэффициент. Участок рис. 9б на частотах меньше 1 МГц получен с помощью экстраполяции (пунктирная линия) и важен для вычислений.

Рис. 9.

Зависимость амплитуды A (а) и логарифма амплитудной функции L (б) от частоты f.

Результаты моделирования зависимости эффективной частоты соударений электронов ν_e от высоты z показаны на рис. 10. Светлой широкой линией показана модельная зависимость эффективной частоты соударений ν_e от высоты, а тонкой – расчетные значения. Видно, что модельные и расчетные значения совпадают с хорошей точностью, а сама точность совпадений модельных и расчетных значений увеличивается с высотой. На рис. 10б помимо модельной зависимости ν_e приведены экстраполяционные кривые, построенные по формуле (32) (тонкая линия) и по формуле (34):

Рис. 10.

Частота соударений для однослоевой модели: а – сопоставление зависимости от высоты модельной (широкая белая линия) и расчетной (темная линия) частоты соударений, б – аппроксимация эффективной частоты соударений по формулам (32) (сплошная темная линия) и (34) (пунктир).

полученной по расчетным данным (пунктирная линия). Из рис. 10б следует, что совпадение удовлетворительное.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ. ДВУСЛОЕВАЯ МОДЕЛЬ

Проблемы с восстановлением эффективной частоты соударений возникают тогда, когда имеет место двуслоевая модель электронной концентрации или присутствуют локальные неоднородности. На рис. 11 показана используемая в расчетах зависимость электронной концентрации от высоты для двуслоевой модели со слоями F и E.

Рис. 11.

Зависимость электронной концентрации от высоты для двуслоевой модели.

На рис. 12 представлены лучевые траектории для двуслоевой модели. Как и на рис. 3б, каждая частота имеет свою траекторию и показана своим оттенком серого цвет: от 1 МГц (нижняя линия) до 6.993 МГц (верхняя). В отличие от рис. 3б, на рис. 12 хорошо видна группа лучей, отразившаяся от нижнего слоя E.

Рис. 12.

Лучевые траектории в плоскости (t, z) для двуслоевой модели на частотах от 1 до 6.993 МГц (снизу вверх).

Зависимости вертикальной компоненты волнового вектора ${{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$ от времени t и от высоты z показаны на рис. 13. Частота возрастает от 1 до 6.993 МГц на рис. 13а слева направо, а рис. 13б – снизу вверх. Сравнение рис. 4 и 13 позволяет оценить влияние слоя E на волновой вектор. Особенно следует отметить центральную область на рис. 13б, соответствующую волновому межслоевому каналу, в которую не проникают лучи.

Рис. 13.

Зависимость ${{{{k}_{z}}} \mathord{\left/ {\vphantom {{{{k}_{z}}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$ от времени (а) и высоты (б) для двуслоевой модели на частотах от 1 до 6.993 МГц (а – слева направо, б – снизу вверх).

Рассмотрим особенности характеристик радиосигнала, отраженного от ионосферы, в точке приема в двуслоевой модели. Зависимость высоты отражения сигнала от частоты показана на рис. 14. Видно, что, как и в случае однослоевой модели, высота отражения ${{z}_{m}}$ сигнала монотонно растет с ростом частоты f. В районе частоты порядка 3 МГц виден разрыв, обусловленный меж-слоевой долиной.

Рис. 14.

Зависимость высоты отражения сигнала ${{z}_{m}}$ (а) и времени t_m (б) от частоты f для двуслоевой модели.

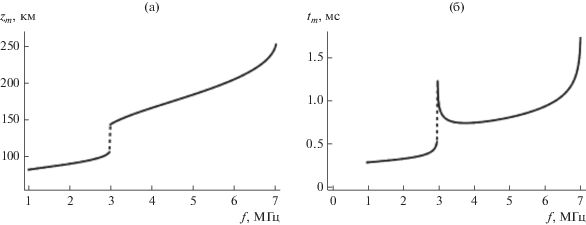
Однако зависимость времени ${{t}_{m}}$ прихода луча в точку отражения от частоты уже не является монотонной. Особенно резкий рост времени t_m наблюдается при приближении частоты f к критической частоте как слоя F f_m (≈7 МГц), так и слоя E (≈3 МГц). Резкий рост кривых на рис. 14 в районе межслоевой долины и максимума слоя F2 неизбежно приводит к неустойчивости итерационного процесса при восстановлении эффективной частоты соударений.

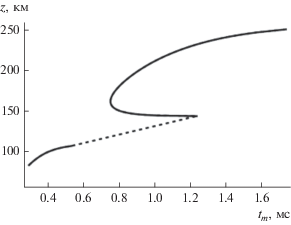
Как и в случае однослоевой модели, исключив частоту f, можно построить график зависимости высоты отражения ${{z}_{m}}$ от задержки t_m (рис. 15). Как и на рис. 14, пунктирная линия на рис. 15 связана с разрывом, обусловленным межслоевой долиной, и условно соединяет две части графика. Следует отметить неоднозначность: одному и тому же времени t_m могут соответствовать две различные высоты отражения, что связано с резким увеличением времени t_m при приближении к критическим частотам как слоя E, так и слоя F.

Рис. 15.

Зависимость высоты отражения сигнала ${{z}_{m}}$ от времени t_m.

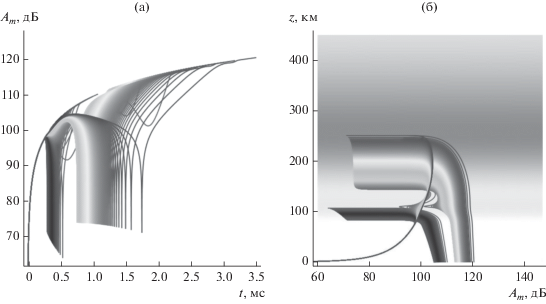
Зависимости ослабления сигнала ${{A}_{m}}$ от времени и от высоты для двуслоевой модели, рассчитанные по формуле (33) вдоль лучей, соответствующих различным частотам, приведены на рис. 16.

Рис. 16.

Зависимость амплитуды сигнала от времени (а) и от высоты (б) для двуслоевой модели.

Сравнивая рис. 5 для однослоевой модели и рис. 16 для двуслоевой, видим, что для двуслоевой модели кривые разделились на две группы. Первая группа кривых соответствует лучам, отразившимся от слоя E. Это левые кривые на рис. 16а и нижние кривые на рис. 16б. Вторая группа кривых соответствует лучам с более высокой частотой, отразившимся от слоя F (правые кривые на рис. 16а и верхние кривые на рис. 16б). Между ними прослеживаются линии, связанные с переходной областью.

Зависимость поглощения ψ от частоты f представлена на рис. 17. В отличие от однослоевой модели (см. рис. 8), функция имеет экстремум (максимум) в окрестности критической частоты слоя E и не является монотонной.

Рис. 17.

Зависимость поглощения ψ от частоты f для двуслоевой модели.

Перейдем теперь к восстановлению зависимости эффективной частоты соударений ν_e как функции высоты z. На рис. 18 показана частотная зависимость функции L, используемой для восстановления.

Рис. 18.

Зависимость функции L от частоты f для двуслоевой модели.

Она, разумеется, соответствует функции ψ, но имеет аналитическое продолжение в область малых частот, на которых измерения недоступны. Наличие слоя E, а главное, межслоевой долины препятствует прямому применению описанного выше алгоритма для восстановления ν_e как функции высоты z. Результат восстановления ν_e(z) на низких частотах (и малых высотах) представлен на рис. 19.

Рис. 19.

Сравнение зависимости модельной (широкая белая линия) и расчетной (темная линия) частот соударений электронов от высоты.

Для нижней ионосферы расчетные (сплошная черная линия) и модельные значения (белая широкая линия) совпадают с хорошей точностью. Петля на конце черной линии – это следствие приближения (28). Нижняя часть ионосферы является особенно важной областью, поскольку формирует основное поглощение радиоволны.

По данным, представленным на рис. 19, методом наименьших квадратов можно построить экстраполяционную модель:

которая, естественно, отличается и от аналогичной модели для однослоевой ионосферы (34) и от аппроксимации исходной зависимости (32). Однако результат экстраполяции оказывается вполне приемлемым.

На рис. 20 сопоставлена экстраполяционная модель (пунктирная линия), построенная по расчетным данным, и исходная зависимость.

Рис. 20.

Сравнение исходной зависимости (широкая белая линия) и экстраполяционной модели (пунктир).

Очевидно, что совпадение хорошее. На высоких частотах с помощью данных зондирования ЛЧМ возможна дополнительная коррекция.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе развит метод восстановления эффективной частоты соударений электронов в ионосферной плазме на основе данных об ослаблении и запаздывании частотно-модулированных радиосигналов при вертикальном зондировании ионосферы Земли. На основе метода расширенной бихарактеристической системы выполнено численное моделирование как в случае однослоевой, так и двуслоевой модели.

Рассчитаны и приведены графики лучевых траекторий частотно-модулированных сигналов в координатах время–высота на разных частотах, построены графики зависимостей поглощения сигналов в точке приема от частоты, графики максимальной высоты отражения и времени прихода сигналов в точку отражения от частоты, получены зависимости амплитуды сигнала от времени и высоты вдоль лучей, построены зависимости вертикальной компоненты волнового вектора от высоты и времени. Разработанная методика обработки экспериментальных данных позволяет получить зависимость эффективной частоты соударений от высоты с хорошей точностью.