Радиотехника и электроника, 2022, T. 67, № 3, стр. 303-312
Одномерные диоды с учетом собственного магнитного поля
М. А. Завьялов a, Т. М. Сапронова a, В. А. Сыровой a, *
a ВЭИ – филиал “РФЯЦ – ВНИИТФ им. акад. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 15.10.2020
После доработки 15.10.2020
Принята к публикации 24.01.2021
- EDN: TQRKWA
- DOI: 10.31857/S0033849422030202
Аннотация
Исследована справедливость модели одномерного движения релятивистских электронов при учете поперечных градиентов собственного магнитного поля в уравнениях Максвелла и пренебрежении эффектами пинча и релятивистского антипинча, приводящем при рассмотрении проблемы усиления электронного тока в плоском униполярном и биполярном диодах с ионным фонтаном к трехкратному увеличению мощности при том же ускоряющем напряжении в случае учета собственного магнитного поля пучка.
ВВЕДЕНИЕ
Вопрос о релятивистских потоках с прямолинейными траекториями, в том числе об одномерных релятивистских диодах, занимал исследователей, начиная с середины прошлого века. В работах [1, 2] показано, что моноэнергетические пучки при учете собственного магнитного поля не могут существовать в диодах с плоской, цилиндрической или сферической геометрией. Однако модели, в которых принимается во внимание только релятивистская форма интеграла энергии, из-за своей простоты успешно конкурировали с немногочисленными точными решениями со строгим учетом собственного магнитного поля и эмитирующими поверхностями в виде полуплоскости или спирального цилиндра [3]. Наиболее простая задача о плоском диоде привлекала наибольшее внимание. Распределение потенциала $\varphi = \varphi \left( z \right)$ в этом случае в релятивистской нормировке, исключающей из уравнений пучка все физические постоянные используемой системы единиц, описывается уравнением
(1)
$\frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = \frac{{J\left( {1 + {{\varphi }}} \right)}}{{\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }},$В работе [4] решение получено в параметрической форме с использованием интеграла Якоби, в [5] оно выражено через эллиптические интегралы. Расчет функции ${{\varphi }}\left( z \right)$ приведен в работе [6], а в более подробном виде – в [7], где релятивистский диод играл роль вспомогательной задачи при определении коэффициента усиления электронного тока в биполярном диоде с релятивистскими электронами. Ультрарелятивистское приближение с линейной зависимостью плотности тока от потенциала, приводимое во всех монографиях, имеющих отношение к интенсивным релятивистским пучкам, также основано на приближении (1).
Аналогичные (1) модели цилиндрического и сферического диодов описываются уравнениями
(2)
$\begin{gathered} \frac{d}{{dR}}\left( {R\frac{{d{{\varphi }}}}{{dR}}} \right) = \frac{{{{R}_{0}}J\left( {1 + {{\varphi }}} \right)}}{{\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }}, \\ \frac{d}{{dr}}\left( {{{r}^{2}}\frac{{d{{\varphi }}}}{{dr}}} \right) = \frac{{r_{0}^{2}J\left( {1 + {{\varphi }}} \right)}}{{\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }}, \\ \end{gathered} $Обзор ранних работ по этим задачам приведен в [8], причем решение в них строилось в виде рядов, в лучшем случае медленно сходящихся. Подробный численный анализ сферического диода выполнен в работе [9].
Предположение об отсутствии зависимости от координаты, изменяющейся в направлении движения, позволило описать течение очень общего вида [10] с одной компонентой скорости ${{v}_{z}} = {{v}_{z}}\left( {x,y} \right)$ при учете собственного магнитного поля
(3)
${{v}_{z}} = {\text{th}}{\kern 1pt} \Psi \left( f \right),\,\,\,\,f = f\left( {x,y} \right),\,\,\,\Delta f = 0,$Радиальное движение с прямолинейными траекториями в сферических координатах r, $\theta $, $\psi $, описывающее конический поток бриллюэновского типа с ${{v}_{r}} = {{v}_{r}}\left( \theta \right)$, исследовано в работах [12, 13]:
(4)
${{v}_{r}} = \frac{{{{T}^{2}} - 1}}{{{{T}^{2}} + 1}},\,\,\,T = b{{\left( {{\text{tg}}\frac{\theta }{2}} \right)}^{a}};\,\,\,a,b = {\text{const}}.$В монографии [14] этот электронный поток получил название парапотенциального.
Приближенный характер моделей (1), (2), и не только в релятивистском случае, ставил вопрос о противоречивости одномерной модели, ответом на который стала формулировка условий возможности пренебречь действием собственного магнитного поля. Обзор ранее известных результатов с их оценкой и предложением новых моделей (модель периферической частицы и параксиальная модель) приведен в работах [7, 15] для плоского диода. Критерий справедливости одномерного рассмотрения был сформулирован исходя из требования малого возмущения траектории электрона под действием собственного магнитного поля с учетом стабилизирующего эффекта внешнего продольного магнитного поля и сведен к ограничениям на относительные размеры пучка. В работах [9, 15] аналогичное исследование выполнено для сферического диода.
В работе [16] при рассмотрении электронных потоков, описываемых трехмерной параксиальной теорией В.Н. Данилова [17], обнаружено, что требование постоянства сечения пучка приводит к распределению потенциала на оси, отличному от (1), причем этот факт связан с учетом в [17] собственного магнитного поля:
(5)
$\frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = \frac{J}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }}.$Принимая во внимание приближенный характер параксиального подхода, интересно выяснить смысл этого результата. Во всяком случае ясно, что хотя бы частичный учет эффекта может привести к более обоснованным ограничениям, чем те, которые сформулированы в [7, 15] для модели (1). Имеет смысл распространить рассмотрение также на цилиндрический и сферический диоды.
1. АДЕКВАТНОСТЬ МОДЕЛИ ОДНОМЕРНОГО ДВИЖЕНИЯ С УЧЕТОМ СОБСТВЕННОГО МАГНИТНОГО ПОЛЯ
Аппаратом для решения этой задачи является геометризованная теория плотных электронных пучков [18], наиболее полное изложение которой содержат монографии [19, 20]. В отличие от параксиальной теории геометризованный подход позволяет построить точное соотношение на трубке тока для эмиссии, ограниченной пространственным зарядом или температурой, при произвольной ориентации магнитного поля $\vec {H}$ на катоде, причем член, содержащий плотность тока эмиссии, имеет ту же форму, что и в (5).
Классические параксиальные модели обеспечивают выполнение условий термоэмиссии в ${{\rho }}$-режиме только при специальной ориентации $\vec {H}$:
где L, M, N – компоненты напряженности магнитного поля в системе ${{x}^{1}}$, ${{x}^{2}}$, ${{x}^{3}}$, связанной с геометрией течения: ${{x}^{1}}$ – продольная координата на трубке тока ${{x}^{2}} = {\text{const}}$, ${{x}^{3}} = \psi $ – азимут или ${{x}^{3}} = x$ для плоских пучков; индекс ноль соответствует величинам на катоде ${{x}^{1}} = 0$. Произвольная ориентация магнитного поля обеспечивается благодаря локально неортогональной системе ${{x}^{1}}$, ${{x}^{2}}$ в меридиональной плоскости R, z (или y, z для плоских течений) с метрикой вида(7)
${{g}_{{11}}} = h_{1}^{2},\,\,\,{{g}_{{22}}} = h_{2}^{2},\,\,\,{{g}_{{12}}} = h_{1}^{{}}{{h}_{2}}\cos {{\theta }_{{12}}}.$(8)
$\begin{gathered} {{g}_{{12}}} = - {{h}_{{10}}}{{h}_{{20}}}{{{\bar {N}}}_{0}}{{{{\xi }}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\exp ( - a{{{{\xi }}}^{2}}),\,\,\,{{\xi }} \equiv {{h}_{{10}}}{{x}^{1}}, \\ a = {\text{const}}; \\ \bar {N} \equiv {N \mathord{\left/ {\vphantom {N {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}},\,\,\,\,{{V}_{2}} = {{\left( {{{9J} \mathord{\left/ {\vphantom {{9J} 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \\ \end{gathered} $Соотношение на трубке тока при отсутствии внешнего магнитного поля принимает вид
(9)
$\begin{gathered} \left( {1 + {{\varphi }}} \right){{u}^{2}}\left\{ {\frac{1}{{\sin {{\theta }_{{12}}}}}\frac{1}{{{{h}_{1}}}}{{{\left( {\frac{{{{h}_{{2,1}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}} - {{h}_{2}}\frac{{\theta _{{12,1}}^{2}}}{{h_{1}^{2}{{{\sin }}^{2}}{{\theta }_{{12}}}}}} \right. - \\ \left. { - \,\,\frac{{{\text{ctg}}{{\theta }_{{12}}}}}{{{{h}_{1}}}}{{{\left[ {\frac{1}{{{{h}_{1}}}}{{{\left( {\frac{{{{g}_{{12}}}}}{{{{h}_{1}}}}} \right)}}_{{,1}}}} \right]}}_{{,1}}}} \right\} = - \frac{1}{{{{h}_{1}}}}{{\left( {{{h}_{2}}\sin {{\theta }_{{12}}}} \right)}_{{,1}}}\frac{1}{{{{h}_{1}}}}{{{{\varphi }}}_{{,1}}} + \\ + \,\,{{h}_{2}}\sin {{\theta }_{{12}}}\left[ { - 2\left( {1 + {{\varphi }}} \right)k_{1}^{2}{{u}^{2}} + \left( {1 + {{\varphi }}} \right){{k}_{1}}{{k}_{2}}{{u}^{2}} + \begin{array}{*{20}{c}} {} \\ {} \end{array}} \right. \\ + \,\,{{k}_{2}}{\text{tg}}\theta \frac{1}{{{{h}_{1}}}}{{{{\varphi }}}_{{,1}}} - \frac{1}{{{{h}_{1}}}}{{\left( {\frac{1}{{{{h}_{1}}}}{{{{\varphi }}}_{{,1}}}} \right)}_{{,1}}} - 2{{k}_{1}}{\text{Nu}} - \\ \left. { - \,\,\frac{1}{{1 + {{\varphi }}}}{{N}^{2}} + \frac{1}{{1 + {{\varphi }}}}E_{\nu }^{2}} \right] + \frac{{{{h}_{{20}}}{{h}_{{30}}}J}}{{{{h}_{3}}{{{\left( {1 + {{\varphi }}} \right)}}^{2}}u}}; \\ {{u}^{2}} = \frac{{{{\varphi }}\left( {2 + {{\varphi }}} \right)}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{2}}}},\,\,\,\,{{E}_{\nu }} = \left( {1 + {{\varphi }}} \right){{k}_{1}}{{u}^{2}} + uN, \\ {{k}_{2}} = \frac{1}{{{{h}_{2}}\sin {{\theta }_{{12}}}}}\left( {\frac{{{{g}_{{12}}}}}{{h_{1}^{2}}}\frac{{{{h}_{{3,1}}}}}{{{{h}_{3}}}} - \frac{{{{h}_{{3,2}}}}}{{{{h}_{3}}}}} \right). \\ \end{gathered} $В формуле (9) величина θ определяет угол между осями ${{x}^{1}}$ и z; ${{k}_{1}}$, ${{k}_{2}}$ – главные кривизны поверхности ${{x}^{2}} = {\text{const}}$; u – скорость, ${{E}_{\nu }}$ – нормальное электрическое поле на трубке тока; ${{h}_{{20}}}$, ${{h}_{{30}}}$ – значения функций ${{h}_{2}}$, ${{h}_{3}}$ на катоде ${{x}^{1}}$= 0. Для частных производных по ${{x}^{1}}$, ${{x}^{2}}$ приняты следующие сокращенные обозначения:
(10)
${{\partial {{\varphi }}} \mathord{\left/ {\vphantom {{\partial {{\varphi }}} {\partial {{x}^{1}}}}} \right. \kern-0em} {\partial {{x}^{1}}}} \equiv {{{{\varphi }}}_{{,1}}},\,\,\,\,{{\partial {{h}_{3}}} \mathord{\left/ {\vphantom {{\partial {{h}_{3}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} \equiv {{h}_{{3,2}}}.$Слагаемое с плотностью тока J в (9) образовано разностью членов, описывающих действие пространственного заряда ${{\rho }}$ и учет собственного магнитного поля посредством уравнения ${\text{rot}}{\kern 1pt} \vec {H} = {{\rho }}\vec {v}$. Отношение второго члена к первому определено функцией [19, 20]
(11)
${{F}_{0}} = \frac{{{{\varphi }}\left( {2 + {{\varphi }}} \right)}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{2}}}}.$Слагаемое с ${{N}^{2}}$ существует и в нерелятивистском случае и обязано своим возникновением фрагменту силы Лоренца, в котором учтен “шир” продольной скорости, пропорциональный N. Член с $E_{\nu }^{2}$, порождающий слагаемое ${{u}^{2}}{{N}^{2}}$, имеет исключительно релятивистский характер и тот же знак в (9), что и член с пространственным зарядом, и описывает тем самым эффект релятивистского антипинча.
Таким образом, в дальнейшем будем говорить о возможности пренебрежения двумя последними эффектами (члены, содержащие квадрат собственного поля ${{N}^{2}}$) при учете поперечных градиентов в уравнении для ${\text{rot}}{\kern 1pt} \vec {H}$.
В случае сплошных осесимметричных и плоскосимметричных пучков соотношение на вырожденной трубке тока – оси $z$ – описывается формулой [19–21]
(12)
$\begin{gathered} \left( {1 + {{\varphi }}} \right){{u}^{2}}{{h}_{{2,11}}}{\text{ = }} - {{h}_{{2,1}}}{{{{\varphi }}}_{{,1}}} - {{\alpha }}{{h}_{2}}{{{{\varphi }}}_{{,11}}} + {{\beta }}\frac{{{{h}_{{20}}}J}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{2}}u}}; \\ {{\alpha }} = \left\{ {\begin{array}{*{20}{c}} {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \\ 1 \end{array}} \right.,\,\,\,\,{{\beta }} = \left\{ {\begin{array}{*{20}{c}} {{{{{h}_{{20}}}} \mathord{\left/ {\vphantom {{{{h}_{{20}}}} {2{{h}_{2}}}}} \right. \kern-0em} {2{{h}_{2}}}}} \\ 1 \end{array}} \right., \\ \end{gathered} $Уравнение (9) при заданных параметрах трубки тока (${{k}_{1}}$, ${{k}_{2}}$, $\theta $), пучка (${{\varphi }}$, N, J ) и способе отсчета продольной координаты (${{h}_{1}}$) позволяет рассчитать функцию ${{h}_{2}}({{x}^{1}})$; при заданной метрике (7) оно становится уравнением для потенциала φ.
Заранее неочевидная возможность существования периферической трубки тока с прямолинейной границей не противоречит точным уравнениям пучка. Уравнение (12) при распределении потенциала на оси (5) и аналогичном распределении для осесимметричных потоков имеет точное решение вида ${{h}_{2}} = {{c}_{1}}{{x}^{1}} + {{c}_{0}}$, для которого производная кривизны трубки тока на оси ${{k}_{{1,2}}} = {{h}_{{2,11}}} = 0$. В результате близкая к оси трубка тока ${{x}^{2}} = {\text{const}}$ также имеет нулевую кривизну.
Ленточный пучок рассматривается в декартовых координатах
(13)
$\begin{gathered} {{x}^{1}} = z,\,\,\,\,{{x}^{2}} = y,\,\,\,\,{{x}^{3}} = x;\,\,\,\,{{h}_{1}} = {{h}_{2}} = {{h}_{3}} = 1, \\ \theta = 0,\,\,\,\,{{k}_{1}} = {{k}_{2}} = 0. \\ \end{gathered} $Цилиндрической трубке тока соответствуют выражения
(14)
$\begin{gathered} {{x}^{1}} = z,\,\,\,\,{{x}^{2}} = R,\,\,\,\,{{x}^{3}} = \psi ;\,\,\,{{h}_{1}} = {{h}_{2}} = 1, \\ {{h}_{3}} = R,\,\,\,\theta = 0,\,\,\,\,{{k}_{1}} = 0,\,\,\,\,{{k}_{2}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}. \\ \end{gathered} $Клиновидная граница пучка определена формулами
(15)
$\begin{gathered} {{x}^{1}} = R,\,\,\,\,{{x}^{2}} = \psi ,\,\,\,\,{{x}^{3}} = z;\,\,\,\,{{h}_{1}} = {{h}_{3}} = 1, \\ {{h}_{2}} = R,\,\,\,\,\theta = {{\psi }_{0}},\,\,\,\,{{k}_{1}} = {{k}_{2}} = 0. \\ \end{gathered} $Для конической поверхности $\theta = {{\theta }_{0}}$ имеем
(16)
$\begin{gathered} {{x}^{1}} = r,\,\,\,\,{{x}^{2}} = \theta ,\,\,\,\,{{x}^{3}} = \psi ; \\ {{h}_{1}} = 1,\,\,\,\,{{h}_{2}} = r,\,\,\,\,{{h}_{3}} = r\sin \theta ;\,\,\,\,\theta = {{\theta }_{0}}, \\ \end{gathered} $Уравнение (9) для периферической трубки тока в случае ленточного и цилиндрического пучков принимает вид
(17)
$\begin{gathered} \left( {1 + {{\varphi }}} \right){{u}^{2}}\left[ { - \frac{{\theta _{{12,1}}^{2}}}{{\sin {{\theta }_{{12}}}}} - {\text{ctg}}{{\theta }_{{12}}}{{g}_{{12,11}}}} \right] = \\ = - {{\left( {\sin {{\theta }_{{12}}}} \right)}_{{,1}}}{{{{\varphi }}}_{{,1}}} - \sin {{\theta }_{{12}}}\left[ {{{{{\varphi }}}_{{,11}}} + \frac{{{{N}^{2}}}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{3}}}}} \right] + \\ + \,\,\frac{{{{h}_{{20}}}J}}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }},\,\,\,\,{{h}_{{20}}} = 1. \\ \end{gathered} $Для клиновидного потока получаем
(18)
$\begin{gathered} \left( {1 + {{\varphi }}} \right){{u}^{2}}\left[ { - \frac{{R\theta _{{12,1}}^{2}}}{{\sin {{\theta }_{{12}}}}} - {\text{ctg}}{{\theta }_{{12}}}{{g}_{{12,11}}}} \right] = \\ = - {{\left( {R\sin {{\theta }_{{12}}}} \right)}_{{,1}}}{{{{\varphi }}}_{{,1}}} - R\sin {{\theta }_{{12}}}\left[ {{{{{\varphi }}}_{{,11}}} + \frac{{{{N}^{2}}}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{3}}}}} \right] + \\ + \,\,\frac{{{{h}_{{20}}}J}}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }},\,\,\,\,{{h}_{{20}}} = {{R}_{0}}. \\ \end{gathered} $Граница конического пучка описывается уравнением
(19)
$\begin{gathered} \left( {1 + {{\varphi }}} \right){{u}^{2}}\left[ { - \frac{{r\theta _{{12,1}}^{2}}}{{\sin {{\theta }_{{12}}}}} - {\text{ctg}}{{\theta }_{{12}}}{{g}_{{12,11}}}} \right] = \\ = - {{\left( {r\sin {{\theta }_{{12}}}} \right)}_{{,1}}}{{{{\varphi }}}_{{,1}}} - \\ - \,\,r\sin {{\theta }_{{12}}}\left[ {\frac{1}{r}{{{{\varphi }}}_{{,1}}} + {{{{\varphi }}}_{{,11}}} + \frac{{{{N}^{2}}}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{3}}}}} \right] + \\ + \,\,\frac{{h_{{20}}^{2}J}}{{r\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }},\,\,\,\,{{h}_{{20}}} = {{r}_{0}}. \\ \end{gathered} $Уравнения (17)–(19) для периферической трубки тока совпадают с уравнением на оси пучка (12) и не отличаются от соотношений (1), (2) с модифицированной в соответствии с (5) правой частью, если можно пренебречь неортогональностью системы и слагаемым с квадратом собственного магнитного поля ${{N}^{2}}$.
Оценить первый фактор можно, используя прикатодные асимптотики входящих в уравнения (17)–(19) величин, ответственных за неортогональность системы [18–21]:
(20)
$\begin{gathered} {{g}_{{12}}} = - {{h}_{{20}}}{{{\bar {N}}}_{0}}{{{{\xi }}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},\,\,\,\cos {{\theta }_{{12}}} = - {{{\bar {N}}}_{0}}{{{{\xi }}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}, \\ \sin {{\theta }_{{12}}} = 1 - \frac{1}{2}\bar {N}_{0}^{2}{{{{\xi }}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}, \\ {{\theta }_{{12}}} = \frac{{{\pi }}}{2} + {{{\bar {N}}}_{0}}{{{{\xi }}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} + \frac{1}{6}\bar {N}_{0}^{3}{{{{\xi }}}^{{{3 \mathord{\left/ {\vphantom {3 3}} \right. \kern-0em} 3}}}}, \\ {{\varphi }} = \frac{1}{2}V_{2}^{2}{{{{\xi }}}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}},\,\,\,\,u = {{V}_{2}}{{{{\xi }}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Легко видеть, что неортогональные члены и слагаемое с магнитным полем вблизи катода имеют порядок ${{{{\xi }}}^{0}}$ и много меньше членов порядка ${{{{\xi }}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}$ со второй производной потенциала и члена с J.
Необходимыми условиями одномерного течения являются требования однородности плотности тока эмиссии J и постоянства кривизны ${{\kappa }_{1}}$ эмитирующей поверхности.
В работе [22] сформулированы выражения для производных ${{J}_{{,22}}}$, ${{J}_{{,2222}}}$ и ${{\kappa }_{{1,22}}}$ на оси z, определенные формулами
(21)
$\begin{gathered} {{h}_{2}} = {{b}_{0}}\left( {1 + {{{\bar {b}}}_{3}}x + {{{\bar {b}}}_{4}}{{x}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + {{{\bar {b}}}_{6}}{{x}^{2}} + {{{\bar {b}}}_{7}}{{x}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}} + ... + {{{\bar {b}}}_{{12}}}{{x}^{4}}} \right), \\ \frac{1}{J}\frac{{{{J}_{{,22}}}}}{{b_{0}^{2}}} = 10\overline {{{b}_{6}}} ,\,\,\,\,\frac{{{{\kappa }_{{1,22}}}}}{{b_{0}^{2}}} = 5{{{\bar {b}}}_{9}} + \frac{9}{2}{{{\bar {b}}}_{3}}{{{\bar {b}}}_{6}},\,\,\,x \equiv {{x}^{1}}. \\ \end{gathered} $Между коэффициентами разложения потенциала ${{\varphi }}$ (${{{{\varphi }}}_{{10}}}$, ${{{{\varphi }}}_{{13}}}$) и функции ${{h}_{2}}$ (${{\bar {b}}_{6}}$, ${{\bar {b}}_{9}}$) существуют связи, приведенные ниже для плоскосимметричных и осесимметричных потоков:
(22)
$\begin{gathered} {{{{{\bar {\varphi }}}}}_{{10}}} = - \frac{8}{9}{{{\bar {b}}}_{6}} + \frac{{83}}{{225}}\bar {b}_{3}^{2}, \\ {{{{{\bar {\varphi }}}}}_{{13}}} = \frac{{37}}{{33}}\left( { - {{{\bar {b}}}_{9}} + \frac{{1652}}{{1665}}\bar {b}_{3}^{{}}{{{\bar {b}}}_{6}} - \frac{{31\,463}}{{124\,875}}\bar {b}_{3}^{3}} \right); \\ {{{{{\bar {\varphi }}}}}_{{10}}} = - \frac{{16}}{9}{{{\bar {b}}}_{6}} + \frac{{163}}{{150}}\bar {b}_{3}^{2}, \\ {{{{{\bar {\varphi }}}}}_{{13}}} = \frac{{74}}{{33}}\left( { - {{{\bar {b}}}_{9}} + \frac{{2449}}{{1665}}\bar {b}_{3}^{{}}{{{\bar {b}}}_{6}} - \frac{{122\,029}}{{249\,750}}\bar {b}_{3}^{3}} \right). \\ \end{gathered} $Антипараксиальные разложения [19, 20] при эмиссии в ${{\rho }}$-режиме обладают тем свойством, что произвольно заданные коэффициенты осевого распределения потенциала ${{{{\varphi }}}_{4}}$, ${{{{\varphi }}}_{7}}$, ${{{{\varphi }}}_{{10}}}$, ${{{{\varphi }}}_{{13}}}$, ${{{{\varphi }}}_{{16}}}$ определяют соответственно следующие величины, описывающие характер физической задачи: J, ${{\kappa }_{1}}$, ${{J}_{{,22}}}$, ${{\kappa }_{{1,22}}}$, ${{J}_{{,2222}}}$. Коэффициенты ${{{{\varphi }}}_{{4 + k + 1}}}$, ${{{{\varphi }}}_{{4 + k + 2}}}$, k = 0, 1,…, расположенные между ${{{{\varphi }}}_{{4 + k}}}$ и ${{{{\varphi }}}_{{4 + k + 3}}}$, не могут быть заданы произвольно, но жестко определены и зависят от компонент магнитного поля на катоде, а при больших значениях индекса – еще и от ранее введенных произвольных элементов ${{{{\varphi }}}_{{4 + k}}}$. Из формул (22) видно, что регламентированные коэффициенты не входят в описание величин ${{\bar {b}}_{6}}$, ${{\bar {b}}_{9}}$, в то время как коэффициент ${{\bar {b}}_{{12}}}$ в выражении для ${{J}_{{,2222}}}$ в [22] от них зависит.
При рассмотрении точных уравнений пучка и приближенной модели типа (5) с одинаковыми значениями произвольно задаваемых параметров регламентированные коэффициенты разложений будут иметь разные значения.
Уравнение (5) для плоского диода вблизи стартовой поверхности $z = 0$ имеет следующее решение:
(23)
$\begin{gathered} {{{{\varphi }}}_{{ap}}} = {{{{\varphi }}}_{4}}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} \times \\ \times \,\,\left( {1 - 0.09524V_{2}^{2}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + 0.03789V_{2}^{4}{{z}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}} + ...} \right), \\ {{{{\varphi }}}_{7}} = {{{{\varphi }}}_{{10}}} = {{{{\varphi }}}_{{13}}} = 0. \\ \end{gathered} $Уравнение сферического диода, аналогичное уравнению (5), и его локальное решение при эмиссии со сферы $r = {{r}_{0}}$ определены формулами
(24)
$\begin{gathered} \frac{{{{d}^{2}}{{\varphi }}}}{{d{{r}^{2}}}} + \frac{2}{r}\frac{{d{{\varphi }}}}{{dr}} = \frac{{r_{0}^{2}J}}{{{{r}^{2}}{{{\left( {1 + {{\varphi }}} \right)}}^{2}}u}},\,\,\,\,\frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} - {{T}_{0}}\frac{1}{{1 + \bar {z}}}\frac{{d{{\varphi }}}}{{dz}} = \\ = \frac{J}{{{{{\left( {1 + \bar {z}} \right)}}^{2}}}}\frac{1}{{{{{\left( {1 + {{\bar {\varphi }}}} \right)}}^{2}}u}},\,\,\,z = r - {{r}_{0}}, \\ \bar {z} \equiv \frac{z}{{{{r}_{0}}}} = - \frac{1}{2}{{T}_{0}}z,\,\,\,\,{{T}_{0}} = - \frac{2}{{{{r}_{0}}}};\,\,\,{{{{\varphi }}}_{{ap}}} = \\ = {{{{\varphi }}}_{4}}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left( {1 + \frac{8}{{15}}{{T}_{0}}z - 0.09524V_{2}^{2}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + \frac{{163}}{{600}}T_{0}^{2}{{z}^{2}} - } \right. \\ - 0.038095V_{2}^{2}{{T}_{0}}{{z}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}} + \\ \left. { + \,\,0.06549V_{2}^{4}{{z}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}} + \frac{{122\,029}}{{891\,000}}T_{0}^{2}{{z}^{3}} + ...} \right). \\ \end{gathered} $Построение решения точных уравнений пучка [22] с коэффициентами ${{{{\varphi }}}_{7}}$, ${{{{\varphi }}}_{{10}}}$, ${{{{\varphi }}}_{{13}}}$ из (23), (24) приводит к следующему результату:
(25)
$\begin{gathered} {{{{\varphi }}}_{{ex}}} = {{{{\varphi }}}_{4}}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} \times \\ \times \,\,\left( {1 + 0.05159V_{2}^{2}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + 0.008997V_{2}^{4}{{z}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}} + ...} \right), \\ {{{{\varphi }}}_{{ex}}} = {{{{\varphi }}}_{4}}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left( {1 + \frac{8}{{15}}{{T}_{0}}z + 0.05159V_{2}^{2}{{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} + } \right. \\ + \,\,\frac{{163}}{{600}}T_{0}^{2}{{z}^{2}} + 0.04317V_{2}^{2}{{T}_{0}}{{z}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0em} 3}}}} - \\ \left. { - \,\,0.00001512V_{2}^{4}{{z}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}} + \frac{{122\,029}}{{891\,000}}T_{0}^{3}{{z}^{3}} + ...} \right). \\ \end{gathered} $Различие регламентированных коэффициентов при сравнении функций ${{{{\varphi }}}_{{ap}}}$, ${{{{\varphi }}}_{{ex}}}$ в (23)–(25) очевидно.
По изложенным причинам нет возможности воспользоваться результатами [22] и сформулировать условие малости члена $\left( {{1 \mathord{\left/ {\vphantom {1 {24}}} \right. \kern-0em} {24}}} \right){{\bar {J}}_{{,2222}}}{{\eta }^{4}}$, $\eta \equiv {{b}_{0}}{{x}^{2}}$ по сравнению с единицей, что привело бы к ограничению на величину ${{J}^{2}}{{\eta }^{4}}$.
Однако подстановка коэффициентов ${{{{\varphi }}}_{7}}$, ${{{{\varphi }}}_{{10}}}$, ${{{{\varphi }}}_{{13}}}$ из (23), (24) в формулы (21), (22) приводит к нулевым значениям производных плотности тока и кривизны катода на оси, и это результат, соответствующий точным уравнениям пучка:
Вдали от особенности можно пренебречь магнитным полем в уравнениях (17)–(19), если
(27)
$\frac{{{{N}^{2}}}}{{{{{\left( {1 + {{\varphi }}} \right)}}^{3}}}} \ll G\frac{J}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }},$Продолжение оценок основано на выражениях для собственного магнитного поля в предположении о прямолинейном движении зарядов:
(28)
$\begin{gathered} N = {{N}_{0}} = - Ja;\,\,\,\,N = {{N}_{0}} = \frac{1}{2}Ja; \\ N = {{N}_{0}} = J{{R}_{0}}{{\psi }_{0}}; \\ N = {{N}_{0}}\frac{{{{r}_{0}}}}{r},\,\,\,\,{{N}_{0}} = J{{r}_{0}}{\text{tg}}\frac{{{{\theta }_{0}}}}{2}, \\ \end{gathered} $В случае ленточного пучка условие (27) для плотности тока J и тока с “квадрата” ${{I}_{\square }} = J{{a}^{2}}$ принимает вид
(29)
$J \ll {1 \mathord{\left/ {\vphantom {1 {({{a}^{2}}F)}}} \right. \kern-0em} {({{a}^{2}}F)}},\,\,\,\,{{I}_{\square }} \ll {1 \mathord{\left/ {\vphantom {1 F}} \right. \kern-0em} F},\,\,\,\,F = \frac{{\sqrt {{{F}_{0}}} }}{{1 + {{\varphi }}}}.$Входящая в формулы (29) функция F достигает максимума ${{F}_{m}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ при ${{\varphi }} = \sqrt 2 - 1$ (рис. 1).
Для цилиндрического пучка аналогичные (29) формулы выглядят следующим образом:
(30)
$J \ll {4 \mathord{\left/ {\vphantom {4 {({{a}^{2}}F)}}} \right. \kern-0em} {({{a}^{2}}F)}},\,\,\,\,I \ll {{4{{\pi }}} \mathord{\left/ {\vphantom {{4{{\pi }}} F}} \right. \kern-0em} F}.$Параметры клиновидного пучка должны удовлетворять условиям
(31)
$J \ll \frac{1}{{{{{\left( {{{R}_{0}}{{\psi }_{0}}} \right)}}^{2}}}}\frac{1}{F}\frac{{{{R}_{0}}}}{R},\,\,\,\,{{I}_{\square }} \ll \frac{1}{F}\frac{{{{R}_{0}}}}{R}.$В случае конического пучка имеем
(32)
$J \ll \frac{1}{{{{{\left[ {{{r}_{0}}{\text{tg}}\left( {{{{{\theta }_{0}}} \mathord{\left/ {\vphantom {{{{\theta }_{0}}} 2}} \right. \kern-0em} 2}} \right)} \right]}}^{2}}}}\frac{1}{F},\,\,\,\,I \ll 4{{\pi }}{{\cos }^{2}}\frac{{{{\theta }_{0}}}}{2}\frac{1}{F}.$Для перехода к размерным величинам в формулах (28)–(32) необходимо провести следующие замены:
(33)
$J \to {{J}_{*}}J,\,\,\,\,I \to {{I}_{*}}I;\,\,\,\,{{J}_{*}} = \frac{{{{\varepsilon }_{0}}{{c}^{3}}}}{{\eta L_{{{\kern 1pt} *}}^{2}}},\,\,\,\,{{I}_{*}} = \frac{{{{\varepsilon }_{0}}{{c}^{3}}}}{\eta },$Приведем численные оценки критериев (29)–(32) при ${{L}_{{{\kern 1pt} *}}} = a = {{R}_{0}} = {{r}_{0}} = 1$ см. Характерные значения плотности тока и тока численно совпадают, ${{I}_{*}} = 1335$ А. Вдали от особенности, где в оценках присутствует функция F, заменим ${1 \mathord{\left/ {\vphantom {1 F}} \right. \kern-0em} F}$ ее минимальным значением (${1 \mathord{\left/ {\vphantom {1 F}} \right. \kern-0em} F}$ = 2), чтобы усилить неравенства. Для ленточного пучка критерий (29) принимает вид
(34)
${{I}_{{\square p}}} \ll {{{{I}_{*}}} \mathord{\left/ {\vphantom {{{{I}_{*}}} F}} \right. \kern-0em} F} = 2.67\,\,{\text{кА}}.$В случае цилиндрического пучка получаем
Клиновидному пучку с компрессией ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} R}} \right. \kern-0em} R} = 5$ и “квадратом” $R \times {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 3}} \right. \kern-0em} 3}$ соответствует неравенство
Для сферического диода при ${{\theta }_{0}} = 60^\circ $ ограничения (32) принимают вид
2. ПЛОСКИЕ ДИОДЫ С ИОННЫМ ФОНТАНОМ ПРИ УЧЕТЕ СОБСТВЕННОГО МАГНИТНОГО ПОЛЯ
Работа [23] посвящена исследованию эффекта увеличения коэффициента усиления электронного тока в униполярном и биполярном плоских диодах за счет использования ионного фонтана – ионов, инжектируемых через проницаемый термокатод. При этом плотность электронного тока с катода соответствовала модели (1). Анализ тех же задач на основании модели (5) с учетом собственного магнитного поля представляет очевидный интерес.
Отметим символами С, В, А катод, плоскость отражения ионов и анод. Потенциал ${{\varphi }}$ удовлетворяет уравнениям
(38)
$\begin{gathered} \frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = {{J}_{e}}\left[ {\frac{1}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }} - \frac{{{\beta }}}{{\sqrt {2\left( {{{{{\varphi }}}_{B}} - {{\varphi }}} \right)} }}} \right. - \\ \left. { - \,\,\frac{{{\alpha }}}{{\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} }}} \right],\,\,\,\,0 \leqslant z \leqslant {{z}_{B}}; \\ \frac{{{{d}^{2}}{{\varphi }}}}{{d{{z}^{2}}}} = {{J}_{e}}\left[ {\frac{1}{{\left( {1 + {{\varphi }}} \right)\sqrt {{{\varphi }}\left( {2 + {{\varphi }}} \right)} }} - \frac{{{\alpha }}}{{\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} }}} \right], \\ {{z}_{B}} \leqslant z \leqslant 1;\,\,\,\,{{\beta }} = \frac{{2{{J}_{{iB}}}}}{{{{J}_{e}}}}\sqrt {\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}}} ,\,\,\,\,{{\alpha }} = \frac{{{{J}_{i}}}}{{{{J}_{e}}}}\sqrt {\frac{{{{\eta }_{e}}}}{{{{\eta }_{i}}}}} , \\ \end{gathered} $Первые интегралы уравнений (38) при условии сопряжения по полю при $z = {{z}_{B}}$ описываются выражениями
(39)
$\begin{gathered} \frac{1}{2}{{\left( {\frac{{d{{\varphi }}}}{{dz}}} \right)}^{2}} = \\ = {{J}_{e}}\left[ {\arccos \frac{1}{{1 + {{\varphi }}}}} \right. + {{\beta }}\left( {\sqrt {2\left( {{{{{\varphi }}}_{B}} - {{\varphi }}} \right)} - \sqrt {2{{{{\varphi }}}_{B}}} } \right) + \\ \left. {\begin{array}{*{20}{c}} {} \\ {} \end{array} + \,\,{{\alpha }}\left( {\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} - \sqrt {2{{{{\varphi }}}_{A}}} } \right)} \right],\,\,\,\,0 \leqslant z \leqslant {{z}_{B}}; \\ \frac{1}{2}{{\left( {\frac{{d{{\varphi }}}}{{dz}}} \right)}^{2}} = {{J}_{e}}\left[ {\arccos \frac{1}{{1 + {{\varphi }}}}} \right. - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} + \\ \left. {\left. {\frac{{^{{}}}}{{}} + \,\,{{\alpha }}\left( {\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{\varphi }}} \right)} } \right. - \sqrt {2{{{{\varphi }}}_{A}}} } \right)} \right],\,\,\,\,{{z}_{B}} \leqslant z \leqslant 1. \\ \end{gathered} $Повторное интегрирование определяет неявную зависимость потенциала от координаты
Условия эмиссии в ${{\rho }}$-режиме выполнены в (39) на катоде, потребуем, чтобы они имели место и в плоскостях В, А:
(41)
$\begin{gathered} \arccos \frac{1}{{1 + {{{{\varphi }}}_{B}}}} - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} + \\ + \,\,{{\alpha }}\left[ {\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{{{\varphi }}}_{B}}} \right)} - \sqrt {2{{{{\varphi }}}_{A}}} } \right] = 0, \\ \arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}}} - {{\beta }}\sqrt {2{{{{\varphi }}}_{B}}} - {{\alpha }}\sqrt {2{{{{\varphi }}}_{A}}} = 0. \\ \end{gathered} $В результате величины ${{{{J}_{i}}} \mathord{\left/ {\vphantom {{{{J}_{i}}} {{{J}_{e}}}}} \right. \kern-0em} {{{J}_{e}}}}$, ${{{{J}_{{iB}}}} \mathord{\left/ {\vphantom {{{{J}_{{iB}}}} {{{J}_{e}}}}} \right. \kern-0em} {{{J}_{e}}}}$ выражаются через потенциалы ${{{{\varphi }}}_{B}}$, ${{{{\varphi }}}_{A}}$ следующим образом:
(42)
$\begin{gathered} {{\alpha }} = \frac{1}{{\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{{{\varphi }}}_{B}}} \right)} }}\left[ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}}} - \arccos \frac{1}{{1 + {{{{\varphi }}}_{B}}}}} \right], \\ {{\beta }} = \frac{1}{{\sqrt {2{{{{\varphi }}}_{B}}} }} \times \\ \times \,\,\left\{ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{B}}}} + {{\alpha }}\left[ {\sqrt {2\left( {{{{{\varphi }}}_{A}} - {{{{\varphi }}}_{B}}} \right)} - \sqrt {2{{{{\varphi }}}_{A}}} } \right]} \right\}. \\ \end{gathered} $Отнесем потенциал к значению на аноде
(43)
${{\bar {\varphi }}} = {{{\varphi }} \mathord{\left/ {\vphantom {{{\varphi }} {{{{{\varphi }}}_{A}}}}} \right. \kern-0em} {{{{{\varphi }}}_{A}}}}$и введем новые обозначения:
(44)
$\begin{gathered} {{\bar {\alpha }}} = {{\alpha }}\sqrt {2{{{{\varphi }}}_{A}}} = \frac{1}{{\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} }} \times \\ \times \,\,\left[ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}}} - \arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}}}} \right], \\ {{\bar {\beta }}} = {{\beta }}\sqrt {2{{{{\varphi }}}_{A}}} = \\ = \frac{1}{{\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} }}\left[ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}}} + {{\bar {\alpha }}}\left( {\sqrt {1 - {{{{{\bar {\varphi }}}}}_{B}}} - 1} \right)} \right]. \\ \end{gathered} $Интегралы в (40) в результате перенормировки примут вид
(45)
$\begin{gathered} {{I}_{1}} = {{{{\varphi }}}_{A}}\int\limits_0^{{{\bar {\varphi }}}} {\left[ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}}}} \right. + {{\bar {\beta }}}\left( {\sqrt {{{{{{\bar {\varphi }}}}}_{B}} - {{\bar {\varphi }}}} - \sqrt {{{{{{\bar {\varphi }}}}}_{B}}} } \right)} + \\ {{\left. {\begin{array}{*{20}{c}} {} \\ {} \end{array} + {{\bar {\alpha }}}\left( {\sqrt {1 - {{\bar {\varphi }}}} - 1} \right)} \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}d{\kern 1pt} {{\bar {\varphi }}},\,\,\,\,0 \leqslant z \leqslant {{z}_{B}}; \\ {{I}_{2}} = {{{{\varphi }}}_{A}} \times \\ \times \,\,\int\limits_{{{{{{\bar {\varphi }}}}}_{B}}}^{{{\bar {\varphi }}}} {{{{\left[ {\arccos \frac{1}{{1 + {{{{\varphi }}}_{A}}{{{{{\bar {\varphi }}}}}_{B}}}} - {{\bar {\beta }}}\sqrt {{{{{{\bar {\varphi }}}}}_{B}}} + {{\bar {\alpha }}}\left( {\sqrt {1 - {{\bar {\varphi }}}} - 1} \right)} \right]}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} d{\kern 1pt} {{\bar {\varphi },}} \\ {{{\bar {z}}}_{B}} \leqslant z \leqslant 1. \\ \end{gathered} $Запишем соотношения (40), (45) при $z = {{z}_{B}}$ и $z = 1$:
(46)
$\sqrt {2{{J}_{e}}} {{z}_{B}} = {{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right),\,\,\,\,\sqrt {2{{J}_{e}}} \left( {1 - {{z}_{B}}} \right) = {{I}_{2}}\left( 1 \right).$Плотность электронного тока, коэффициент усиления ${{K}_{e}}$ по отношению к току релятивистского диода по модели (1) и координата плоскости отражения ${{z}_{B}}$ ионного фонтана описываются формулами
(47)
$\begin{gathered} \sqrt {2{{J}_{e}}} = {{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right) + {{I}_{2}}\left( 1 \right),\,\,\,\,{{K}_{e}} = {{\left[ {\frac{{{{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right) + {{I}_{2}}\left( 1 \right)}}{{{{I}_{0}}}}} \right]}^{2}}, \\ {{z}_{B}} = \frac{{{{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right)}}{{{{I}_{1}}\left( {{{{{{\bar {\varphi }}}}}_{B}}} \right) + {{I}_{2}}\left( 1 \right)}};\,\,\,{{I}_{0}} = \int\limits_0^{{{{{\varphi }}}_{A}}} {\frac{{dt}}{{\sqrt[4]{{t\left( {2 + t} \right){\kern 1pt} }}}}} . \\ \end{gathered} $На рис. 2 приведены результаты расчетов для униполярного диода с ионным фонтаном при различных значениях потенциала анода в интервале (0.1,…,2). Аналогичные кривые для биполярного диода демонстрирует рис. 3. В табл. 1 представлены данные о коэффициенте усиления ${{K}_{e}}$ и координате плоскости отражения ионов ${{z}_{B}}$ в случае униполярного диода при нескольких значениях потенциала анода ${{{{\varphi }}}_{A}}$ и потенциала инжекции ионов ${{{{\varphi }}}_{B}}$. Таблица 2 содержит сравнение этих параметров при ${{{{\varphi }}}_{A}} = 2$ для моделей (1) [23] и (5). Таблицы 3, 4 соответствуют биполярному диоду, причем табл. 3 аналогична табл. 1, а в табл. 4 проведено сравнение максимального коэффициента усиления ${{K}_{{em}}}$ для нескольких значений ${{{{\varphi }}}_{A}}$ по моделям (1) [23] и (5) с указанием соответствующих величин ${{{{\varphi }}}_{B}}$, ${{z}_{B}}$.
Рис. 2.
Коэффициент усиления электронного тока ${{K}_{e}}$ (а) и координата плоскости отражения ионов фонтана ${{z}_{B}}$ (б) в зависимости от потенциала анода ${{{{\varphi }}}_{A}}$ и потенциала инжекции ионов ${{{{\varphi }}}_{B}}$ для униполярного диода при ${{{{\varphi }}}_{A}} = 2$ (1), 1 (2), 0.5 (3), 0.2 (4), 0.1 (5).
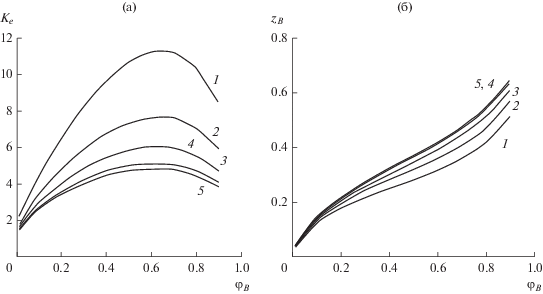
Рис. 3.
Коэффициент усиления электронного тока ${{K}_{e}}$ (а) и координата плоскости отражения ионов фонтана ${{z}_{B}}$ (б) в зависимости от потенциала анода ${{{{\varphi }}}_{A}}$ и потенциала инжекции ионов ${{{{\varphi }}}_{B}}$ для биполярного диода при ${{{{\varphi }}}_{A}} = 2$ (1), 1 (2), 0.5 (3), 0.2 (4), 0.1 (5).

Таблица 1.
Коэффициент усиления электронного тока ${{K}_{e}}$ и координата плоскости отражения ионов фонтана в зависимости от значений ${{{{\varphi }}}_{A}}$, ${{{{\varphi }}}_{B}}$ для униполярного диода
| ${{{{\varphi }}}_{B}}$ | ${{{{\varphi }}}_{A}}$ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.5 | 1.0 | 2.0 | ||||||
| ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | |
| 0.01 | 1.438 | 0.036 | 1.478 | 0.036 | 1.599 | 0.035 | 1.796 | 0.034 | 2.178 | 0.032 |
| 0.1 | 2.630 | 0.151 | 2.723 | 0.149 | 3.004 | 0.144 | 3.482 | 0.137 | 4.484 | 0.126 |
| 0.2 | 3.444 | 0.221 | 3.588 | 0.218 | 4.029 | 0.210 | 4.797 | 0.197 | 6.462 | 0.178 |
| 0.3 | 4.042 | 0.277 | 4.233 | 0.273 | 4.825 | 0.260 | 5.868 | 0.243 | 8.175 | 0.217 |
| 0.4 | 4.473 | 0.327 | 4.706 | 0.321 | 5.430 | 0.305 | 6.717 | 0.284 | 9.596 | 0.251 |
| 0.5 | 4.749 | 0.376 | 5.015 | 0.368 | 5.842 | 0.349 | 7.320 | 0.323 | 10.652 | 0.285 |
| 0.6 | 4.865 | 0.426 | 5.150 | 0.417 | 6.040 | 0.394 | 7.636 | 0.364 | 11.242 | 0.321 |
| 0.7 | 4.800 | 0.481 | 5.088 | 0.472 | 5.986 | 0.446 | 7.597 | 0.412 | 11.234 | 0.364 |
| 0.8 | 4.511 | 0.549 | 4.778 | 0.538 | 5.610 | 0.511 | 7.097 | 0.474 | 10.436 | 0.421 |
| 0.9 | 3.887 | 0.646 | 4.098 | 0.636 | 4.753 | 0.608 | 5.915 | 0.570 | 8.481 | 0.515 |
Таблица 2.
Сравнение значений параметров ${{K}_{e}}$, ${{z}_{B}}$ при ${{{{\varphi }}}_{A}} = 2$ для униполярного диода по моделям (1), (5)
| ${{{{\varphi }}}_{B}}$ | ${{{{\varphi }}}_{A}} = 2$ | |||
|---|---|---|---|---|
| Модель (1) | Модель (5) | |||
| ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | |
| 0.01 | 1.377 | 0.040 | 2.178 | 0.032 |
| 0.1 | 2.366 | 0.170 | 4.484 | 0.126 |
| 0.2 | 2.945 | 0.255 | 6.462 | 0.178 |
| 0.3 | 3.330 | 0.324 | 8.175 | 0.217 |
| 0.4 | 3.589 | 0.385 | 9.596 | 0.251 |
| 0.5 | 3.747 | 0.443 | 10.652 | 0.285 |
| 0.6 | 3.810 | 0.501 | 11.242 | 0.321 |
| 0.7 | 3.771 | 0.563 | 11.234 | 0.364 |
| 0.8 | 3.605 | 0.633 | 10.436 | 0.421 |
| 0.9 | 3.242 | 0.726 | 8.481 | 0.515 |
Таблица 3.
Коэффициент усиления электронного тока ${{K}_{e}}$ и координата плоскости отражения ионов фонтана в зависимости от значений ${{{{\varphi }}}_{A}}$, ${{{{\varphi }}}_{B}}$ для биполярного диода
| ${{{{\varphi }}}_{B}}$ | ${{{{\varphi }}}_{A}}$ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.5 | 1.0 | 2.0 | ||||||
| ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | ${{K}_{e}}$ | ${{z}_{B}}$ | |
| 0.01 | 2.602 | 0.027 | 2.659 | 0.027 | 2.834 | 0.027 | 3.137 | 0.026 | 3.756 | 0.024 |
| 0.1 | 4.661 | 0.116 | 4.791 | 0.115 | 5.186 | 0.112 | 5.902 | 0.107 | 7.486 | 0.099 |
| 0.2 | 6.082 | 0.172 | 6.280 | 0.170 | 6.919 | 0.164 | 8.099 | 0.155 | 10.741 | 0.140 |
| 0.3 | 7.106 | 0.217 | 7.382 | 0.214 | 8.268 | 0.205 | 9.899 | 0.191 | 13.625 | 0.171 |
| 0.4 | 7.805 | 0.257 | 8.156 | 0.253 | 9.278 | 0.240 | 11.345 | 0.223 | 16.094 | 0.197 |
| 0.5 | 8.186 | 0.296 | 8.602 | 0.291 | 9.927 | 0.275 | 12.363 | 0.254 | 17.980 | 0.222 |
| 0.6 | 8.231 | 0.338 | 8.692 | 0.331 | 10.158 | 0.312 | 12.848 | 0.286 | 19.057 | 0.250 |
| 0.7 | 7.895 | 0.386 | 8.372 | 0.378 | 9.883 | 0.355 | 12.647 | 0.325 | 19.019 | 0.283 |
| 0.8 | 7.097 | 0.448 | 7.544 | 0.438 | 8.955 | 0.411 | 11.525 | 0.377 | 17.422 | 0.329 |
| 0.9 | 5.646 | 0.544 | 5.993 | 0.533 | 7.080 | 0.503 | 9.042 | 0.465 | 13.486 | 0.411 |
Таблица 4.
Максимальное значение ${{K}_{{em}}}$ коэффициента усиления электронного тока и соответствующие значения параметров ${{z}_{B}}$, ${{{{\varphi }}}_{B}}$ для биполярного диода по моделям (1), (5)
| ${{{{\varphi }}}_{A}}$ | Модель (1) | Модель (5) | ||||
|---|---|---|---|---|---|---|
| ${{K}_{{em}}}$ | ${{z}_{B}}$ | ${{{{\varphi }}}_{B}}$ | ${{K}_{{em}}}$ | ${{z}_{B}}$ | ${{{{\varphi }}}_{B}}$ | |
| 0.1 | 7.589 | 0.326 | 0.540 | 8.231 | 0.338 | 0.6 |
| 0.5 | 7.256 | 0.329 | 0.517 | 10.158 | 0.312 | 0.6 |
| 1.0 | 6.973 | 0.334 | 0.499 | 12.848 | 0.286 | 0.6 |
| 2.0 | 6.620 | 0.346 | 0.480 | 19.057 | 0.250 | 0.6 |
Из сопоставления результатов видно, что коэффициент усиления ${{K}_{e}}$ при учете собственного магнитного поля растет по мере увеличения потенциала анода, а плоскость отражения ионов приближается к катоду. Максимальный коэффициент усиления примерно в три раза больше по сравнению со случаем, когда собственное магнитное поле не принимается во внимание. Сказанное справедливо как для униполярного, так и для биполярного потоков.
Отметим, что модель (5) не имеет ультрарелятивистского приближения, так как уравнение (5) при ${{\varphi }} \to \infty $ принимает вид
и не может быть привязано к катоду. Соотнесение с анодом вводит в формулы неизвестное значение поля на аноде и по этой причине представляется бесполезным. Впрочем, как отмечалось в работе [9], ультрарелятивистское приближение модели (1) не имеет практического смысла из-за чрезвычайно медленного стремления к пределу.
ЗАКЛЮЧЕНИЕ
Модели одномерных релятивистских диодов при учете поперечных градиентов собственного магнитного поля, описываемых уравнениями Максвелла, и принебрежении эффектами пинча и релятивистского антипинча приводят к распределению потенциала на оси пучка, которое обеспечивает равенство нулю вторых производных плотности тока эмиссии и кривизны катода и тем самым реализует в окрестности оси необходимое условие одномерного движения: $J = {\text{const}}$, ${{\kappa }_{1}} = {\text{const}}$. Сформулированы ограничения на ток пучка при различных конфигурациях потока, позволяющие пренебречь упомянутыми эффектами.
Решение задачи об усилении электронного тока в релятивистской области для плоских униполярного и биполярного диодов с ионным фонтаном показывает, что учет собственного магнитного поля приводит к трехкратному увеличению мощности при том же ускоряющем напряжении.
Список литературы
Lucas A.R. // J. Electr. Contr. 1958. V. 3. № 3. P. 245.
Buneman O. // J. Electr. Contr. 1958. V. 5. № 6. P. 561.
Вашковский А.В., Сыровой В.А., Цимринг Ш.Е. // РЭ. 1996. Т. 41. № 3. С. 350.
Gold L. // J. Electr. Contr. 1957. V. 3. № 6. P. 564.
Игнaтeнкo B.П. // PЭ. 1962. T. 7. № 7. C. 1175.
Acton E.V.W. // J. Electr. Contr. 1957. V. 3. № 2. P. 203.
Белкин В.М., Завьялов М.А., Сыровой В.А. // РЭ. 2011. Т. 56. № 2. С. 212.
Белов Н.Е. // ЖТФ. 1978. Т. 48. № 1. С. 119.
Белкин В.М., Завьялов М.А., Сыровой В.А. // РЭ. 2009. Т. 54. № 4. С. 493.
Данилов В.Н. // Журн. прикл. механики и техн. физики. 1968. № 1. С. 3.
Lomax R.J. // J. Electr. Contr. 1958. V. 5. № 6. P. 563.
Сыровой В.А. // Журн. прикл. механики и техн. физики. 1963. № 3. С. 26.
Сыровой В.А. // Журн. прикл. механики и техн. физики. 1965. № 6. С. 3.
Миллер Р. Введение в физику сильноточных пучков заряженных частиц. М.: Мир, 1984.
Завьялов М.А., Сыровой В.А. Биполярные пучки: эксперимент, теория, технические приложения. Снежинск: Изд-во РФЯЦ-ВНИИТФ, 2019.
Cыpoвoй B.A. // PЭ. 2018. T. 63. № 8. C. 871.
Данилов В.Н. // Журн. прикл. механики и техн. физики. 1968. № 5. С. 3.
Cыpoвoй B.A. // PЭ. 1996. T. 41. № 10. C. 1255.
Сыровой В.А. Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Syrovoy V.A. Theory of Intense Beams of Charged Particles. US: Elsevier, 2011.
Cыpoвoй B.A. // PЭ. 1997. T. 42. № 12. C. 1501.
Cыpoвoй B.A. // PЭ. 2021. T. 66. № 7. C. 703.
Завьялов М.А., Стальков П.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 8. С. 799.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника




