1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 67, № 4, 2022

Радиотехника и электроника, 2022, T. 67, № 4, стр. 391-403

Транспортировка электронных пучков с сечением, близким к прямоугольному

Т. М. Сапронова a, В. А. Сыровой a, *

a ВЭИ – филиал “РФЯЦ – ВНИИТФ им. акад. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация

* E-mail: red@cplire.ru

Поступила в редакцию 23.12.2020
После доработки 23.12.2020
Принята к публикации 19.10.2021

Полный текст (PDF)

Аннотация

Исследована задача о транспортировке плотного электронного пучка с “почти прямоугольным” сечением (частный случай – эллиптический контур) без изменения его формы и ориентации. Обсуждается возможность реализации начальных состояний потока на входе в тракт транспортировки, принимаемых обычно в численных моделях траекторного анализа.

1. РАЗЛИЧНЫЕ ПОДХОДЫ К ПРОБЛЕМЕ ТРАНСПОРТИРОВКИ

За последние десятилетия существенно возросло количество публикаций, посвященных ленточным электронным пучкам, в том числе проблеме их транспортировки, в которых, как правило, представлены результаты численного моделирования с использованием коммерческих программ траекторного анализа. В типичных для этого вида публикаций работах [1–4] под транспортировкой понимается исследование эволюции пучка с сечением, напоминающим прямоугольник (торцы обычно выполнены в виде полуокружностей) при инжекции в прямоугольный канал.

Дисбаланс между начальной формой сечения и конфигурацией тракта транспортировки в случае сильного магнитного поля приводит к диокотронной неустойчивости. Отказ от поиска сбалансированных состояний пучка ожидаемым образом не позволяет решить задачу о его распространении без деформации и поворотов начального сечения и в электростатическом случае. Именно в такой формулировке далее будем говорить о проблеме транспортировки, противопоставляя ее изучению распространения несбалансированного пучка в канале заданной формы.

В работах [5–7] численными методами исследованы равновесные конфигурации пучка с закругленными указанным выше способом краями в прямоугольном канале. В [5] это щель или полубесконечный прямоугольник, в [6, 7] – прямоугольное сечение с заданным отношением сторон. Визуально результаты производят впечатление тождественных.

Для подавления диокотронной неустойчивости обычно предлагается усилить магнитное поле, в работе [6] авторы сформулировали способ ослабления деформации сечения за счет стремления к эквипотенциальности контура.

Задача о формировании и транспортировке ленточного пучка относится к категории разномасштабных, как и задача о потоках с высокой компрессией. Изменение интенсивности квадруполя внешнего электрического поля на 1% (об этом будет сказано ниже) приводит к кардинальной перестройке потенциала в пучке. По этой причине все замечания к 3D-пакетам траекторного анализа, обсуждавшиеся в [9] в связи с проблемой теплового зазора и пучков с высокой компрессией, справедливы и по отношению к ленточным потокам.

Существующие расчеты трехмерных электронно-оптических систем носят эмпирический характер, не учитывающий теоретических результатов в этой области. Трудно представить практику расчетов, в которых значение пирсовского угла 67.5° всякий раз устанавливалось бы экспериментально, однако с 3D-оптикой ситуация напоминает указанную. Публикация в Physical Review работы [10], в которой решение задачи о формировании цилиндрического пучка с эллиптическим сечением дано в форме контурного интеграла в комплексной плоскости параметра р с интеграндом в виде бесконечного ряда из произведений радиальных и угловых функций Матье, свидетельствует об осведомленности англоязычного научного сообщества в области 3D-оптики плотных пучков: решение в случае произвольного сечения [11], описываемое определенным интегралом, и расчеты формирующих электродов для эллипса и прямоугольника [12–14] получены за 30–35 лет до [10]. Решение [10] вошло также в диссертацию одного из авторов [15].

Теория формирования произвольных трехмерных потоков в общем виде не существует, однако к настоящему времени известны: 1) локальное решение уравнений пучка вблизи произвольной стартовой поверхности в ${{\rho }}$- и Т-режимах эмиссии [16, 17]; 2) формирующие электроды для цилиндра и конуса с произвольными сечениями, локально справедливые для пучков с криволинейными траекториями при эмиссии с плоскости и сферы; 3) параксиальные решения внешней задачи для квазицилиндрических потоков, к которым при использовании криволинейных координат относятся практически все встречающиеся на практике варианты. Проблемы формирования подобных течений обсуждаются в обзорной статье [18].

Пакеты траекторного анализа обрабатывают любые постановки, в том числе и не имеющие физического смысла, и при отсутствии соответствующей теоретической подготовки у авторов и пользователей и некритическом отношении к результатам могут порождать абсурдные решения. Примеры подобных ситуаций обсуждаются в [9].

Существует несколько теоретических моделей, позволяющих исследовать трехмерные электронные течения, которые могут приводить к обоснованным начальным состояниям пучка на входе в канал транспортировки. Это трехмерная параксиальная теория релятивистских потоков с произвольным сечением [19], изложение которой можно найти в монографиях [20, 21]; теория потенциальных нерелятивистских пучков с эллиптическим сечением и экранированным катодом [22]; теория вихревых релятивистских эллиптических пучков [23–27], свободная от ограничений [22]; различные варианты теории ленточных пучков [28–34]; геометризованная теория электростатических пучков с произвольным сечением [35, 36]. Модели [19, 22–27, 35, 36] описывают трехмерные потоки, в то время как теория ленточных пучков [28–34] позволяет рассматривать вырезки произвольной конфигурации из двумерных течений. Работа [37] посвящена исследованию возможностей, которые предоставляет теория [19] для формирования и транспортировки “почти прямоугольных” пучков.

Наибольшую сложность при построении теоретических моделей потоков с близким к прямоугольному сечением представляет нахождение аналитического контура и связанной с ним системы криволинейных координат с конформной метрикой. Соотношения между криволинейными и декартовыми координатами должны быть взаимнооднозначными на удалениях от пучка, достаточных для эффективного расчета формирующих электродов. На практике можно рассчитывать только на аппарат аналитического продолжения при том или ином параметрическом задании контура, а не на конформное отображение соответствующих областей, которое автоматически решало бы упомянутые выше проблемы.

Примеры нарушения однозначности при аналитическом продолжении границы приводятся в монографиях [20, 21, 29, 38], причем в [38] чисто математическому факту придана неверная физическая интерпретация, то же самое в работах [39, 40]. Однако во всех этих случаях координатная сетка, хотя и неоднозначная в некоторых областях, заполняла всю плоскость.

Вполне приемлемый с точки зрения аппроксимации прямоугольного контура суперэллипс описывается уравнениями

(1)
${{x}_{e}} = a\sqrt {\cos u} ,\,\,\,\,{{y}_{e}} = b\sqrt {\sin u} $
и при аналитическом продолжении $u \to u + iv$ порождает сетку, определенную формулами

(2)
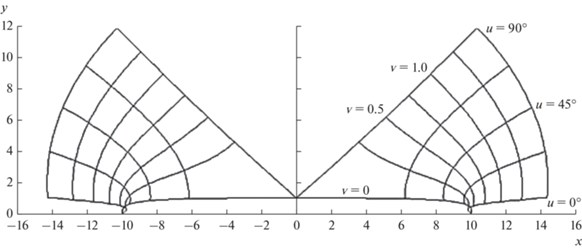
$\begin{gathered} x\left( {u,v} \right) = \frac{1}{{\sqrt 2 }}\left( {a\sqrt {{{m}_{c}} + {{R}_{c}}} - b\sqrt {{{m}_{s}} - {{R}_{s}}} } \right), \\ y\left( {u,v} \right) = \frac{1}{{\sqrt 2 }}\left( {a\sqrt {{{m}_{c}} - {{R}_{c}}} + b\sqrt {{{m}_{s}} + {{R}_{s}}} } \right); \\ {{R}_{c}} = \cos u{\kern 1pt} {\text{ch}}v,\,\,\,\,{{I}_{c}} = - \sin u{\kern 1pt} {\text{sh}}v,\,\,\,\,m_{c}^{2} = R_{c}^{2} + I_{c}^{2}; \\ {{R}_{s}} = \sin u{\kern 1pt} {\kern 1pt} {\text{ch}}v,\,\,\,{{I}_{s}} = \cos u{\kern 1pt} {\kern 1pt} {\text{sh}}v,\,\,\,\,m_{s}^{2} = R_{s}^{2} + I_{s}^{2}. \\ \end{gathered} $

На рис. 1 приведены контур $v = 0$ и сетка u, v, оставляющая незаполненной область между линиями $u = \pm {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$.

Рис. 1.

Координатная сетка u, v, полученная при аналитическом продолжении уравнений суперэллипса.

В работе [13] построена система координат, связанная с отображением “повышенной гладкости”, которое получается разложением в ряд Лорана функции, отображающей внешность прямоугольника на внешность единичного круга при удержании конечного числа членов:

(3)
$\begin{gathered} x + iy = c\left( {w + \sum\limits_{k = 1}^n {{{c}_{k}}{{w}^{{1 - 2k}}}} } \right), \\ w = \exp \left( { - v + iu} \right),\,\,\,\,v \leqslant 0; \\ {{c}_{1}} = \cos 2{{\gamma }},\,\,\,{{c}_{2}} = - \frac{1}{6}\left( {1 - c_{1}^{2}} \right), \\ {{c}_{3}} = - \frac{1}{{10}}{{c}_{1}}\left( {1 - c_{1}^{2}} \right),\,\,\,{{c}_{4}} = \frac{1}{{56}}\left( {1 - 6c_{1}^{2} + 5c_{1}^{4}} \right). \\ \end{gathered} $

Эта система, которой мы будем пользоваться ниже при проведении расчетов, в качестве границы пучка имеет контур $v = 0$ в виде скругленного прямоугольника (далее – прямоугольник); с – нормировочный множитель, обеспечивающий равенство $y\left( {{{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2},0} \right) = 1$ для выбранного n. Попытка использовать в качестве контура линию уровня $v = - \varepsilon $ самого конформного отображения, описываемого интегралом Кристоффеля–Шварца в задаче о формировании цилиндрического пучка, выделенного из плоского диода при эмиссии в ${{\rho }}$-режиме, не привела к успеху из-за возникновения вблизи скругленного угла эквипотенциалей с изломом, что в физическом плане приводит к необходимости реализации поверхностей с переменным потенциалом [13, 20, 21].

Отметим, что неаналитические контуры с разрывом второй производной, упоминавшиеся выше, приводят к таким же результатам, не замечаемым численными алгоритмами. Дискретизация может скрыть, но не устранить проблемы, существование которых вне зависимости от используемого аппарата обусловлено единственностью решения задачи.

Подходы, отличные от численных моделей, сводятся к двум вариантам. Первый удобно назвать моделью закрепленных зарядов [41–48], второй связан с определением параметров пучка при выходе на режим с прямолинейными образующими трубок тока на основании подходов [19, 22–36]. Завершающий этап – определение конфигурации сечения канала, обеспечивающего транспортировку пучка с сохранением его формы и ориентации. Эти же модели определяют характер распределения потенциала в поперечном сечении на входе в тракт транспортировки, назначаемого в программах анализа вне связи с историей формирования пучка.

Все формулы в дальнейшем представлены в нормировке (релятивистской или нерелятивистской), исключающей из уравнений пучка все физические постоянные используемой системы единиц [20, 29].

2. МОДЕЛЬ ЗАКРЕПЛЕННЫХ ЗАРЯДОВ

Выражение для потенциала в бесконечном цилиндре с эллиптическим сечением [41, 42], равномерно заполненном пространственным зарядом плотностью ${{\rho }}$, используется во многих работах, иногда после слов “как хорошо известно” [15, 44, 45, 48]:

(4)
${{{{\varphi }}}_{i}} = \frac{1}{4}{{\rho }}\left[ {\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{{a - b}}{{a + b}}\left( {{{x}^{2}} - {{y}^{2}}} \right)} \right].$

Квадруполь в (4) представляет собой внешнее поле, добавленное к полю пространственного заряда, исходя из желания иметь логарифмическую особенность потенциала вне цилиндра на бесконечности. В работе [46] показано, что в вопросах формирования и транспортировки плотного пучка беспокоиться об асимптотике на бесконечности из-за ограниченности области рассмотрения не имеет смысла, а поведение точного решения даже для осесимметричного цилиндрического пучка, выделенного из потока в плоском диоде, не описывается логарифмической функцией.

Модель неподвижных зарядов в оптике плотных пучков основывается на предположении о продольной скорости, значительно превышающей скорость поперечного расплывания пучка под действием сил пространственного заряда и поперечного внешнего поля. В работе [44] на основе дрейфовой теории показано, что фактором, обеспечивающим выполнение условия $\rho = {\text{const}}$, может быть сильное продольное магнитное поле. Для случая, когда ларморовский радиус не мал или при отсутствии магнитного поля, остается аргумент малого времени, в течение которого анализируется эволюция пучка.

Определение формы канала транспортировки для потенциала в пучке (4) в работе [15] при $\rho = {\text{const}}$ или в случае полиномиальной зависимости ${{\rho }}$ от эллиптической координаты [45] предсказуемым образом приводило к быстрой трансформации эквипотенциалей в окружности с малым коэффициентом заполнения сечения канала пучком.

В монографии [43] предложен отличный от [41] вариант внешнего квадруполя:

(5)
${{{{\varphi }}}_{i}} = \frac{1}{4}{{\rho }}\left[ {\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{{{{a}^{2}} - {{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}\left( {{{x}^{2}} - {{y}^{2}}} \right)} \right],$
обеспечивающий постоянство потенциала на контуре. В [43] распределение (5) квалифицировано как не представляющее интереса из-за того, что пучок должен был бы распространяться вплотную к стенке канала. В работе [44] показано, что модификация потенциала в пучке за счет новой интенсивности внешнего квадруполя приводит к образованию в лапласовской области сепаратрисы с находящимися под ней эквипотенциалями, которые могли бы определить форму канала транспортировки, однако все эти кривые находятся слишком близко к границе пучка.

В работе [47] отказ от эквипотенциальности контура за счет изменения интенсивности квадруполя на 1% приводит для случая ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 10$, $b = 1$ к почти равномерному расстоянию между каналом транспортировки и пучком (~0.3) при отношении значений потенциала в вершинах эллипса ${{{{{{\varphi }}}_{a}}} \mathord{\left/ {\vphantom {{{{{{\varphi }}}_{a}}} {{{{{\varphi }}}_{b}}}}} \right. \kern-0em} {{{{{\varphi }}}_{b}}}} = 1.52$ и коэффициенте заполнения канала 0.75.

Сохраняя сформулированные выше предположения о справедливости модели, перейдем к рассмотрению пучков с прямоугольным сечением (3). Учтем результаты, относящиеся к эллиптическому контуру, и введем внешнее поперечное электрическое поле, которое определяется содержащим высшие гармоники решением уравнения Лапласа:

(6)
$\begin{gathered} {{{{\varphi }}}_{i}} = \frac{1}{4}{{\rho }}\left( {{{x}^{2}} + {{y}^{2}}} \right) + {{K}_{2}}{{R}^{2}}\cos 2\psi + \\ + \,\,{{K}_{4}}{{R}^{4}}\cos 4\psi + {{K}_{6}}{{R}^{6}}\cos 6\psi + {{K}_{8}}{{R}^{8}}\cos 8\psi , \\ \end{gathered} $
где R, $\psi $ – полярные координаты. Контур пучка v = 0 в (3) описывается гармониками вплоть до седьмой включительно в отличие от эллипса с функциями $\cos u$, $\sin u$.

Точное решение задачи определено формулой

(7)
${{\varphi }} = {{{{\varphi }}}_{i}} + S,\,\,\,S = - {{\rho }}\operatorname{Re} \int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {{{h}^{2}}\left( {u + i{{\xi }},\eta } \right)} {\kern 1pt} d{{\xi }},$
где выражение для квадрата коэффициента Ляме ${{h}^{2}}$ системы (3) приведено в [37]. В развернутом виде функция S описывается выражением

$\begin{gathered} S = - {{\rho }}{{c}^{2}}\left\{ {\,\left[ {\frac{1}{4}c_{1}^{2}\left( {\exp \left( {2{v}} \right) - 1} \right) - \frac{1}{2}\left( {c_{1}^{2} - 1} \right)v + } \right.} \right. \\ \left. { + \,\,\frac{1}{4}\left( {\exp \left( { - 2v} \right) - 1} \right) + \frac{1}{2}{{c}_{1}}\left( {1 - {\text{ch}}2v} \right)\cos 2u} \right] + \\ + \,\,\left[ {\frac{1}{4}c_{1}^{2}\left( {\exp \left( {6v} \right) - 1} \right) - \frac{3}{2}c_{2}^{2}v - \frac{3}{4}{{c}_{1}}{{c}_{2}}\left( {{\text{sh}}2v + \begin{array}{*{20}{c}} {} \\ {} \end{array}} \right.} \right. \\ \left. { + \,\,\frac{1}{2}\exp \left( {2v} \right) - \frac{2}{3}\exp \left( {4v} \right) + \frac{1}{6}\exp \left( { - 2v} \right)} \right)\cos 2u + \\ \end{gathered} $
$\begin{gathered} + \,\,\frac{3}{4}{{c}_{2}}\left( {{\text{sh}}4v + \frac{2}{3}\exp \left( {2v} \right) - \exp \left( {4v} \right) + } \right. \\ \left. {\left. { + \frac{1}{3}\exp \left( { - 4v} \right)} \right)\cos 4u} \right] + \left[ {\frac{1}{4}c_{3}^{2}\left( {\exp \left( {10v} \right) - 1} \right)} \right. - \\ - \frac{5}{2}c_{3}^{2}v - \frac{{15}}{8}{{c}_{2}}{{c}_{3}}\left( {{\text{sh}}2v + \frac{1}{6}\exp \left( {2v} \right) - } \right. \\ \left. { - \,\,\frac{4}{{15}}\exp \left( {8v} \right) + \frac{1}{{10}}\exp \left( { - 2v} \right)} \right)\cos 2u - \frac{5}{{12}}{{c}_{1}}{{c}_{3}}\left( {{\text{sh}}4v + \begin{array}{*{20}{c}} {} \\ {} \end{array}} \right. \\ \end{gathered} $
(8)
$\begin{gathered} \left. {^{{^{{^{{^{{}}}}}}}} + \,\,\exp \left( {4v} \right) - \frac{6}{5}\exp \left( {6v} \right) + \frac{1}{5}\exp \left( { - 4v} \right)} \right)\cos 4u + \\ + \,\,\frac{5}{{12}}{{c}_{3}}\left( {{\text{sh}}6v + \frac{6}{5}\exp \left( {4v} \right) - \frac{3}{2}\exp \left( {6v} \right)} \right. + \\ \left. {\left. { + \,\,\frac{3}{{10}}\exp \left( { - 6v} \right)} \right)\cos 6u} \right] + \left[ {\frac{1}{4}c_{4}^{2}\left( {\exp \left( {14v} \right) - 1} \right)} \right. - \\ - \,\,\frac{7}{2}c_{4}^{2}v - \frac{{35}}{{12}}{{c}_{3}}{{c}_{4}}\left( {{\text{sh}}2v + \frac{1}{{10}}\exp \left( {2v} \right) - } \right. \\ \end{gathered} $
$\begin{gathered} \left. { - \,\,\frac{6}{{35}}\exp \left( {12{v}} \right) + \frac{1}{{14}}\exp \left( { - 2{v}} \right)} \right)\cos 2u - \frac{{21}}{{20}}{{c}_{2}}{{c}_{4}} \times \\ \times \,\,\left( {{\text{sh}}4v + \frac{1}{3}\exp \left( {4v} \right) - \frac{{10}}{{21}}\exp \left( {10v} \right) + \frac{1}{7}\exp \left( { - 4v} \right)} \right) \times \\ \times \,\,\cos 4u - \frac{7}{{24}}{{c}_{1}}{{c}_{4}}\left( {{\text{sh}}6{v} + \frac{3}{2}\exp \left( {6v} \right) - } \right. \\ \left. { - \,\,\frac{{12}}{7}\exp \left( {8v} \right) + \frac{3}{{14}}\exp \left( { - 6v} \right)} \right)\cos 6u + \frac{7}{{24}}{{c}_{4}}\left( {{\text{sh}}8v{{ + }^{{^{{}}}}}} \right. \\ + \,\,\left. {\left. {\left. {\frac{{12}}{7}\exp \left( {6v} \right) - 2\exp \left( {8v} \right) + \frac{2}{7}\exp \left( { - 8v} \right)} \right)\cos 8u} \right]\,} \right\}. \\ \end{gathered} $

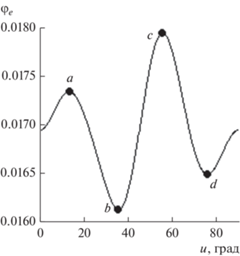
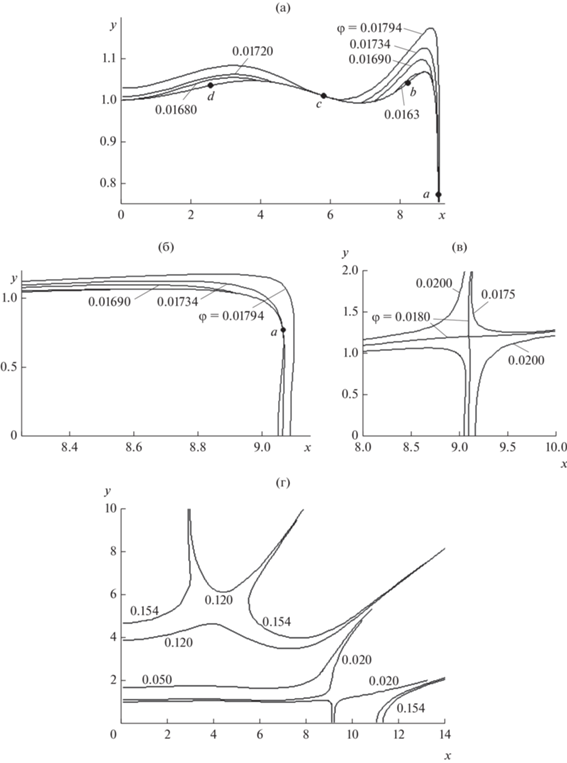
Имея в виду результаты, относящиеся к эллиптическому сечению, подберем коэффициенты в формуле (6) так, чтобы потенциал на границе $v = 0$ при $u = 0$, ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 8}} \right. \kern-0em} 8}$, ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 4}} \right. \kern-0em} 4}$, 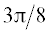, ${{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$ принимал одинаковые значения. На рис. 2 представлено распределение потенциала ${{{{\varphi }}}_{e}} = {{{{\varphi }}}_{i}}\left( {u,0} \right)$ на контуре с ${{\gamma }} = 20^\circ $, ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 9.05$, причем величина ${{{{\varphi }}}_{i}}$ осциллирует вблизи ${{{{\varphi }}}_{i}}\left( {0,0} \right)$ с вариацией порядка 6%. На рис. 3 изображены ход эквипотенциалей вблизи точек экстремумов (рис. 3а, 3б); вблизи образования сепаратрисы (рис. 3в) и структура решения на значительных расстояниях от границы пучка (рис. 3г). Как и в случае с эллипсом, огибающие контур эквипотенциали существуют, однако они слишком слабо удалены от границы.

Рис. 2.

Распределение потенциала φе(u) на контуре прямоугольника, γ = 20°.

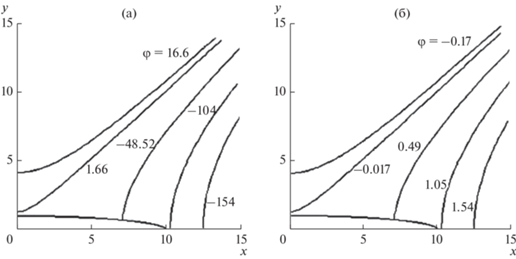
Рис. 3.

Эквипотенциали лапласовского поля для прямоугольника γ = 20° с равенством потенциала в пяти точках контура; а, б – картина поля вблизи контура(точки экстремумов и потенциал в них a – u = 13.5°, φ = 0.01734, b – u = 35.5°, φ = 0.01612, c – u = 55.25°, φ = 0.01794, d – u = 73.75°, φ = 0.01649); в – эквипотенциали в окрестности образования сепаратисты; г – картина поля на больших расстояниях от контура.

Для удаления сепаратрисы от контура сечения был принят убывающий закон изменения потенциала от $u = 0$ к $u = {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$:

(9)
${{{{\varphi }}}_{e}}\left( {{{u}_{k}}} \right) = \frac{{La - b + \left( {1 - L} \right){{R}_{k}}}}{{a - b}}{{{{\varphi }}}_{a}},\,\,\,\,{{R}_{k}} = R\left( {{{u}_{k}}} \right),$
где L имеет смысл отношения ${{{{{{\varphi }}}_{b}}} \mathord{\left/ {\vphantom {{{{{{\varphi }}}_{b}}} {{{{{\varphi }}}_{a}}}}} \right. \kern-0em} {{{{{\varphi }}}_{a}}}}$.

На рис. 4а приведено распределение потенциала на границе $v = 0$ при $L = 0.5$; рис. 4б демонстрирует картину кривых ${{\varphi }} = {\text{const}}$ в плоскости u, v, где не приходящие на ось u кривые определяют огибающие контур пучка эквипотенциали. При уменьшении L сепаратриса удаляется от контура; на рис. 4в представлены кривые ${{\varphi }} = {\text{const}}$ при $L = 0.3$, 0.5 вблизи скругленного угла и возле всего контура. Область образования сепаратрисы со значением потенциала ${{\varphi }} \approx 1.642$ в координатах u, v изображена на рис. 5а при $L = 0.3$; в плоскости x, y она представлена на рис. 5б. Просвет по осям x, y составляет $\Delta {\kern 1pt} x = 0.06$, $\Delta y = 1.27$.

Рис. 4.

Эквипотенциали вне прямоугольного контура при возрастании потенциала φa > φb; а – распределение потенциала φе(u) на контуре при L = 0.5; б – картина эквипотенциалей в плоскости u, v; в – конфигурация эквипотенциалей в плоскости x, y: 1 – L = 0.3, 2 – L = 0.5.

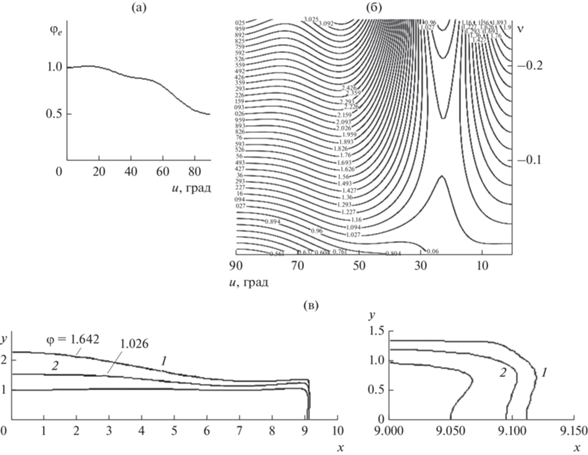
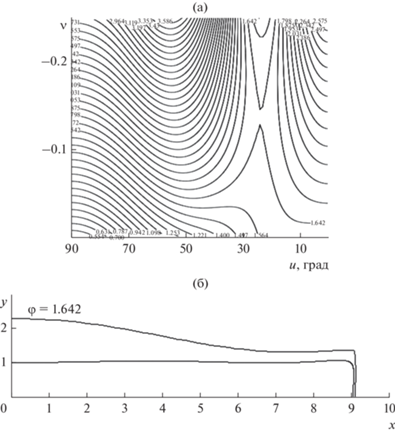
Рис. 5.

Параметры сепаратрисы для прямоугольника γ = 20°, L = 0.3; а – область образования сепаратрисы в координатах u, v; б – сепаратриса, просвет между сепаратрисой и контуром пучка по осям x, y: ∆x = 0.06, ∆y = 1.27 (a = 9.05, b = 1), координаты “угла сепаратрисы” по осям x, y: xs = 9.083, ys = 1.33.

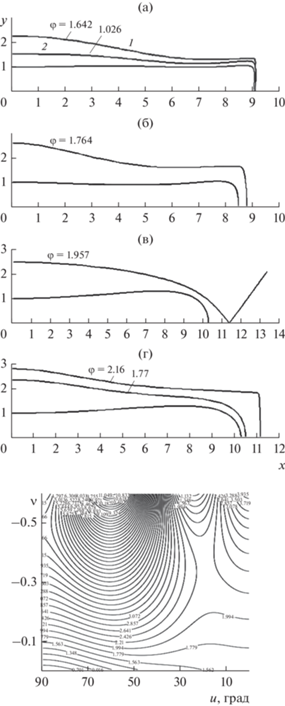
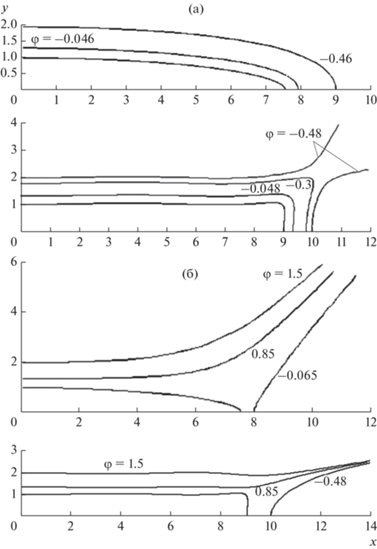
На рис. 6 приведена картина поля вблизи контуров, описываемых формулами (3) при уменьшении числа коэффициентов ${{c}_{k}}$, ${{K}_{n}}$.

Рис. 6.

Вариация контура и лапласовского поля в зависимости от числа сохраненных членов (ск) и фрагментов внешнего поперечного поля (Кn); а – с4 ≠ 0, К8 ≠ 0, 1 – L = 0.3, 2 – L = 0.5; б – с4 = 0, К8 = 0, L = 0.3; в – с3 = 0, К6 = 0, L = 0.3; г – с3 = 0, К6 ≠ 0, L = 0.3; эквипотенциали в плоскостях x, y и u, v.

Выше было сказано, что в численных моделях рассматривается распределение потенциала по сечению, пропорциональное либо ${{R}^{2}}$, либо ${{y}^{2}}$. Для эллиптического пучка в первом (см. (5)) и втором случаях условие ${{{{\varphi }}}_{i}} = {\text{const}}$ при $v = 0$ обеспечивается внешним квадруполем разной интенсивности (рис. 7):

(10)
${{K}_{2}} = - \frac{{{{a}^{2}} - {{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}};\,\,\,{{K}_{2}} = \frac{{{{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}.$
Рис. 7.

Внешние поперечные квадруполи для распределения потенциала в пучке: а – φ ~ R2; б – φ ~ у2.

В силу того, что для ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{y}^{2}}$ справедливо представление

(11)
$\frac{1}{2}{{y}^{2}} = \frac{1}{4}{{R}^{2}} - \frac{1}{4}{{R}^{2}}\cos 2\psi ,$
потенциал ${{{{\varphi }}}_{i}}$ из (6) для ${{K}_{2}}$ из (10) различается лишь сдвигом коэффициента ${{K}_{2}}$: ${{K}_{2}} \to {{K}_{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$.

3. УСЛОВИЯ ИНЖЕКЦИИ, ОПРЕДЕЛЕЯЕМЫЕ ФОРМИРОВАНИЕМ ЭЛЕКТРОННОГО ПОТОКА

Выше было сказано, что относящиеся к прямоугольному каналу как в несбалансированном варианте, так и при определении равновесных конфигураций результаты получены в отрыве от вопроса об источнике, гарантирующем принятое начальное состояние пучка на входе в тракт. Отсутствие подобной гарантии ставит под сомнение полученные выводы. При исследовании этого вопроса в качестве источника электронов естественно рассматривать термоэмиссионный катод.

Параксиальная теория. В работе [37] показано, что параксиальная теория [19] пространственных релятивистских пучков произвольной конфигурации во внешнем магнитном поле при условии сохранения формы сечения пучка требует его ускорения по закону одномерного движения, отличающегося от известного решения учетом поперечных градиентов собственного магнитного поля в уравнении ${\text{rot}}\vec {H} = {{\rho }}\vec {v}$ [49]. Таким образом, пучок, выведенный на этот режим, должен иметь постоянный потенциал не только на контуре, но и во всем сечении. К тому же результату приводит геометризованная модель [35, 36].

Плоскосимметричные пучки. Плоскосимметричные потоки [28–34], допускающие выделение из них фрагмента с произвольным сечением, в равновесном состоянии $f = {\text{const}}$ имеют плотность пространственного заряда и потенциал, определяемые формулами

(12)
$\begin{gathered} \frac{{{\rho }}}{{1 + \tilde {U}}} = \Omega _{z}^{2} + \Omega _{x}^{2} - \frac{{{{f}_{0}}}}{f}{{\Omega }_{{z0}}}{{\Omega }_{z}}, \\ {{{{\varphi }}}_{i}} = U + V{{\Omega }_{x}}y + \frac{1}{2}{{\rho }}{{y}^{2}}, \\ \end{gathered} $
где f – полуширина пучка; ось х направлена по нормали к плоскости течения (z, y); $\vec {\Omega }$ – напряженность магнитного поля; U, V – потенциал и скорость на оси; индекс нуль относит величины к катоду.

При отсутствии продольного поля ${{\Omega }_{z}}$ в нерелятивистском случае формулы (12) определяют плоский бриллюэновский поток. Вместе с тем в условия равновесия (12) входит релятивистская коррекция, не имеющая отношения к бриллюэновским режимам с учетом только релятивистского интеграла энергии или при учете собственного магнитного поля:

(13)
${{\rho }} = \Omega _{x}^{2}{{\left( {1 + \Omega _{x}^{2}{{y}^{2}}} \right)}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{\rho }} = {{\Omega }_{x}}{\text{ch}}\left( {{{\Omega }_{x}}y} \right).$

В выражении (12) присутствует магнитное поле на катоде, причем параметры равновесного режима связаны с плотностью тока эмиссии J соотношением

(14)
$J = \sqrt {U\left( {2 + \tilde {U}} \right)} \left[ {\frac{f}{{{{f}_{0}}}}\left( {\Omega _{z}^{2} + \Omega _{x}^{2}} \right) - {{\Omega }_{{z0}}}{{\Omega }_{z}}} \right].$

Сносовая скорость ${{v}_{x}}$ деформирует контур пучка на катоде по закону $x \to \bar {x}$

(15)
$\begin{gathered} {{v}_{x}} = \frac{1}{{1 + \tilde {U}}}\left( {\frac{{{{f}_{0}}}}{f}{{\Omega }_{{z0}}} - {{\Omega }_{z}}} \right),\,\,\,\,\bar {x} = x + k\left( z \right)y, \\ k\left( z \right) = \int {\frac{1}{{\sqrt {U\left( {2 + \tilde {U}} \right)} }}} \left( {\frac{{{{f}_{0}}}}{f}{{\Omega }_{{z0}}} - {{\Omega }_{z}}} \right)dz. \\ \end{gathered} $

В случае k(z) = 0 сечение не изменяется. При невыполнении этого равенства у начального эллипса не только изменяются полуоси, но и за счет поворота нарушается зависимость от y у ${{{{\varphi }}}_{i}}$ из (12). Прямоугольник переходит в параллелограмм, скругленное описание которого может быть получено по алгоритмам [13, 14].

На рис. 8а, 8б представлены эллиптический и прямоугольный пучки с параболическим распределением потенциала при $k\left( z \right) = 0$ и при постоянстве потенциала в сечении, свойственном одномерным потокам.

Рис. 8.

Поверхности φ = const вне эллиптического и прямоугольного контуров без внешних поперечных полей: а – для одномерного движения на входе в канал транспортировки; б – в случае плоского бриллюэновского равновесия.

Эллиптические трубки тока. Для пучка с эллиптическим сечением ${{\xi }} = {{{{\xi }}}_{e}}$, прямой осью, полуосями а, b и трубками тока ${{\xi }} = {\text{const}}$ связь криволинейных ${{\xi }}$, $\hat {\psi }$ и декартовых координат x, y в плоскости сечения определена следующими формулами [23–27]:

(16)
$x = \left( {a\cos \hat {\psi }} \right)\bar {\xi },\,\,\,y = \left( {b\sin \hat {\psi }} \right)\bar {\xi },\,\,\,\,\bar {\xi } = {\xi \mathord{\left/ {\vphantom {\xi {{{\xi }_{e}}}}} \right. \kern-0em} {{{\xi }_{e}}}}.$

Обратные соотношения описываются выражениями

(17)
$\begin{gathered} {{{{{\bar {\xi }}}}}^{2}} = \frac{{{{x}^{2}}}}{{{{a}^{2}}}} + \frac{{{{y}^{2}}}}{{{{b}^{2}}}},\,\,\,{\text{tg}}\hat {\psi } = \frac{a}{b}{\text{tg}}\psi = \frac{{ay}}{{bx}}; \\ \cos 2\hat {\psi } = \frac{{{{b}^{2}}{{x}^{2}} - {{a}^{2}}{{y}^{2}}}}{{{{b}^{2}}{{x}^{2}} + {{a}^{2}}{{y}^{2}}}},\,\,\,\sin 2\hat {\psi } = \frac{{abxy}}{{{{b}^{2}}{{x}^{2}} + {{a}^{2}}{{y}^{2}}}}. \\ \end{gathered} $

Для потенциала в пучке при $U,{\kern 1pt} \,V = {\text{const}}$, ${{\Omega }_{z}}$, ${{C}_{{21}}}$, ${{C}_{{22}}} = {\text{const}}$ имеем

(18)
$\begin{gathered} {{\varphi }_{i}} = U + \left( {{{\varphi }_{{20}}} + {{\varphi }_{{2c}}}\cos 2\hat {\psi } + {{\varphi }_{{2s}}}\sin 2\hat {\psi }} \right){{{\bar {\xi }}}^{2}}, \\ 2{{\varphi }_{{20}}} = {{a}_{0}}{{b}_{0}}{{\Omega }_{{z0}}}W + \frac{1}{2}\left( {1 + \tilde {U}} \right)\left( {{{a}^{2}} + {{b}^{2}}} \right){{W}^{2}} + \\ + \,\,\frac{1}{4}\left[ {\left( {{{a}^{2}} + {{b}^{2}}} \right)\rho \tilde {V} - \left( {{{a}^{2}} - {{b}^{2}}} \right){{C}_{{21}}}} \right], \\ 2{{{{\varphi }}}_{{2c}}} = - \frac{1}{2}\left( {1 + \tilde {U}} \right)\left( {{{a}^{2}} - {{b}^{2}}} \right){{W}^{2}} + \\ + \,\,\frac{1}{4}\left[ {\left( {{{a}^{2}} - {{b}^{2}}} \right){{\rho }}\tilde {V} - \left( {{{a}^{2}} + {{b}^{2}}} \right){{C}_{{21}}}} \right],\,\,\,\,2{{{{\varphi }}}_{{2s}}} = - \frac{1}{4}ab{{C}_{{22}}}, \\ \end{gathered} $
где ${{C}_{{21}}}$, ${{C}_{{22}}}$ – интенсивности квадруполей в формуле для векторного потенциала:

(19)
${{A}_{z}} = - \frac{1}{4}{{\rho }}\tilde {V}\left( {{{x}^{2}} + {{y}^{2}}} \right) + {{C}_{{21}}}\left( {{{x}^{2}} - {{y}^{2}}} \right) - 2{{C}_{{22}}}xy.$

Функция W представляет собой главный член контравариантной компоненты скорости ${{v}^{3}}$, соответствующей “эллиптическому азимуту” $\hat {\psi }$ (аналог угловой скорости в осесимметричном случае)

(20)
${{v}^{3}} = W = \frac{1}{{1 + \tilde {U}}}\frac{{ab{{\Omega }_{z}} - {{{\left( {ab{{\Omega }_{z}}} \right)}}_{0}}}}{{{{a}^{2}} + {{b}^{2}}}}.$
Условие равновесия пучка $a,\,{\kern 1pt} b = {\text{const}}$ определено из основного уравнения теории
(21)
$\begin{gathered} \frac{{ab{{\Omega }_{z}} - {{{\left( {ab{{\Omega }_{z}}} \right)}}_{0}}}}{{ab{{{\left( {{{a}^{2}} + {{b}^{2}}} \right)}}^{2}}}}\left[ {\left( {{{a}^{4}} + {{b}^{4}}} \right){{\Omega }_{z}} + 2ab{{{\left( {ab{{\Omega }_{z}}} \right)}}_{0}}} \right] = \\ = \frac{{{\rho }}}{{1 + \tilde {U}}} \\ \end{gathered} $
и в силу ${{\rho }} > 0$ по правилам нормировки имеет смысл при выполнении неравенства
(22)
$F = \frac{{{{a}_{0}}{{b}_{0}}}}{{ab}}\frac{{{{\Omega }_{{z0}}}}}{{{{\Omega }_{z}}}} < 1,$
где $\left( {{{{{a}_{0}}{{b}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}{{b}_{0}}} {ab}}} \right. \kern-0em} {ab}}} \right)$ – компрессия по площади.

Переходя в выражении (18) для ${{{{\varphi }}}_{i}}$ к декартовым координатам при помощи соотношений (16) и выражения для ${{\rho }}$ из (21), получаем

(23)
$\begin{gathered} {{{{\varphi }}}_{i}} = U + \frac{1}{4}{{\rho }}\left( {{{x}^{2}} + {{y}^{2}}} \right) + \\ + \,\,\frac{1}{2}\left( { - \frac{1}{2}\frac{{{{a}^{2}} - {{b}^{2}}}}{{ab}}W{{\Omega }_{z}} + V{{C}_{{21}}}} \right)\left( {{{x}^{2}} - {{y}^{2}}} \right) - \frac{1}{8}{{C}_{{22}}}xy. \\ \end{gathered} $

Таким образом, для состояния равновесия потенциал внутри пучка должен содержать внешние квадруполи вполне определенной интенсивности, в отличие от [41] не зависящей от ${{\rho }}$. Связь плотности пространственного заряда с плотностью тока эмиссии позволяет установить ее значение, соответствующее распределению (23):

(24)
$\begin{gathered} \rho = \frac{{{{a}_{0}}{{b}_{0}}J}}{{abV}},\,\,\,\,J = \sqrt {U\left( {2 + \tilde {U}} \right)} \frac{{ab}}{{{{a}_{0}}{{b}_{0}}}} \times \\ \times \,\,\frac{{{{a}^{2}}{{b}^{2}}}}{{{{{\left( {{{a}^{2}} + {{b}^{2}}} \right)}}^{2}}}}\left( {1 - F} \right)\left( {\frac{{{{a}^{4}} + {{b}^{4}}}}{{{{a}^{2}}{{b}^{2}}}} + 2F} \right). \\ \end{gathered} $

Рассмотрим различные специализации формул (21), (23). Для экранированного катода ${{\Omega }_{{z0}}} = 0$ и отсутствия квадруполей ${{C}_{{21}}} = {{C}_{{22}}} = 0$ получаем

(25)
$\begin{gathered} W = \frac{{ab{{\Omega }_{z}}}}{{\left( {1 + \tilde {U}} \right)\left( {{{a}^{2}} + {{b}^{2}}} \right)}},\,\,\,\,{{\rho }} = \left( {1 + \tilde {U}} \right)\frac{{{{a}^{4}} + {{b}^{4}}}}{{{{{\left( {{{a}^{2}} + {{b}^{2}}} \right)}}^{2}}}}\Omega _{z}^{2}, \\ {{{{\varphi }}}_{i}} = U + \frac{1}{4}{{\rho }}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \\ - \,\,\frac{1}{4}\frac{1}{{1 + \tilde {U}}}\frac{{{{a}^{2}} - {{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}\Omega _{z}^{2}\left( {{{x}^{2}} - {{y}^{2}}} \right). \\ \end{gathered} $

При наложении в нерелятивистском случае дополнительной связи

(26)
${{\Omega }_{z}} = \frac{{{{a}^{2}} + {{b}^{2}}}}{{{{a}^{2}}{{b}^{2}}}}$
выражения (25) определяют точное решение уравнений пучка, которое описывает обобщенный бриллюэновский поток [50–52]; подробное исследование этого решения с устранением неточностей первых работ приведено в [29, 53]. Таким образом, при выполнении (26) пучок с термокатода выходит на равновесное состояние, описывающее плоское потенциальное течение, рассматривавшееся в отрыве от возможности его реализации.

При полном погружении катода в магнитное поле ${{\Omega }_{{z0}}} = {{\Omega }_{z}}$, ${{C}_{{21}}} = {{C}_{{22}}} = 0$ имеем

(27)
$\begin{gathered} W = \frac{1}{{1 + \tilde {U}}}\frac{{ab}}{{{{a}^{2}} + {{b}^{2}}}}\left( {1 - F} \right){{\Omega }_{{z0}}},\,\,\,\,F = \frac{{{{a}_{0}}{{b}_{0}}}}{{ab}}, \\ {{\rho }} = \frac{{{{a}^{2}}{{b}^{2}}}}{{{{{\left( {{{a}^{2}} + {{b}^{2}}} \right)}}^{2}}}}\left( {\frac{{{{a}^{4}} + {{b}^{4}}}}{{{{a}^{2}}{{b}^{2}}}} + 2F} \right)\left( {1 - F} \right){{\Omega }_{{z0}}}, \\ {{{{\varphi }}}_{i}} = U + \frac{1}{4}{{\rho }}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{1}{4}\frac{1}{{1 + \tilde {U}}} \times \\ \times \,\,\frac{{{{a}^{2}} - {{b}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}\left( {1 - F} \right)\Omega _{{z0}}^{2}\left( {{{x}^{2}} - {{y}^{2}}} \right). \\ \end{gathered} $

Площадь сечения в этом случае может только увеличиваться, а отсутствие компрессии (декомпрессии в данном случае) соответствует нулевой плотности тока эмиссии.

В силу $U,\,\,\rho = {\text{const}}$ эти величины определяют начало отсчета потенциала и масштабный множитель для картины эквипотенциальных поверхностей. При ${{\Omega }_{{z0}}} = 0$ из формулы (25) получаем

(28)
$\begin{gathered} {{{{{\bar {\varphi }}}}}_{i}} = \frac{{{{{{\varphi }}}_{i}} - U}}{{{\rho }}} = \frac{1}{4}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \\ - \,\,\frac{1}{4}\frac{1}{{{{{\left( {1 + \tilde {U}} \right)}}^{2}}}}\frac{{{{a}^{4}} - {{b}^{4}}}}{{{{a}^{4}} + {{b}^{4}}}}\left( {{{x}^{2}} - {{y}^{2}}} \right). \\ \end{gathered} $

Переход $a \to \infty $ трансформирует формулу (28) в (12).

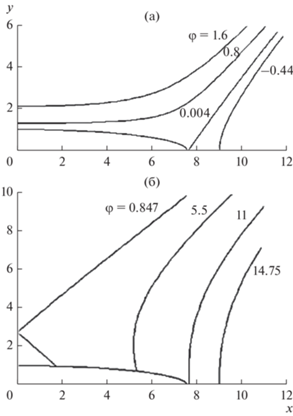
На рис. 9а, 9б приведена картина эквипотенциальных поверхностей ${{\bar {\varphi }}} = {\text{const}}$ в нерелятивистском случае и при $\tilde {U} = 1$ (511 кВ), рассчитанная по формуле (7).

Рис. 9.

Поверхности φ = const для эллиптического пучка без внешних поперечных полей в случае бриллюэновского равновесия на входе в канал транспортировки: а – нерелятивистский случай ($\tilde {U}$ = 0); б – релятивистские скорости ($\tilde {U}$ = 1).

Формула, аналогичная (28), при частичной экранировке катода, имеет вид

(29)
$\begin{gathered} {{{{{\bar {\varphi }}}}}_{i}} = \frac{1}{4}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{1}{4}\frac{{{{{{\alpha }}}^{4}} - 1}}{{{{{{\alpha }}}^{4}} + 1}} \times \\ \times \,\,{{\left( {1 + 2\frac{{{\alpha }}}{{{{{{\alpha }}}^{4}} + 1}}\frac{{{{a}_{0}}{{b}_{0}}}}{{{{b}^{2}}}}\frac{{{{\Omega }_{{z0}}}}}{{{{\Omega }_{z}}}}} \right)}^{{ - 1}}}\left( {{{x}^{2}} - {{y}^{2}}} \right),\,\,\,\,{{\alpha }} = \frac{a}{b}. \\ \end{gathered} $

Условие (22) накладывает ограничение на возможное значение ${{\Omega }_{{z0}}}$, величина которого оказывает заметное воздействие на распределение потенциала на границе пучка в случае трансформации вытянутого эллипса в приближающийся к окружности контур; при обратной деформации сечения (большие значения ${{\alpha }}$) влияние ${{\Omega }_{{z0}}}$ пренебрежимо мало.

Для пучка с параметрами

(30)
$\begin{gathered} {{a}_{0}} = 10,\,\,\,\,{{b}_{0}} = 1,\,\,\,a = {1 \mathord{\left/ {\vphantom {1 {30}}} \right. \kern-0em} {30}}, \\ b = {1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5},\,\,\,\,\left( {{{{{a}_{0}}{{b}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}{{b}_{0}}} {ab}}} \right. \kern-0em} {ab}}} \right) = 150 \\ \end{gathered} $
величина ${{{{\Omega }_{{z0}}}} \mathord{\left/ {\vphantom {{{{\Omega }_{{z0}}}} {{{\Omega }_{z}}}}} \right. \kern-0em} {{{\Omega }_{z}}}}$ не должна превышать 0.00666. При ${{{{\Omega }_{{z0}}}} \mathord{\left/ {\vphantom {{{{\Omega }_{{z0}}}} {{{\Omega }_{z}}}}} \right. \kern-0em} {{{\Omega }_{z}}}} = {1 \mathord{\left/ {\vphantom {1 {200}}} \right. \kern-0em} {200}}$ интенсивность квадруполя в (29) составляет (–0.1306) с отношением φa/φb = $ = 0.873$. При ${{\Omega }_{{z0}}} = 0$ коэффициент перед $\left( {{{x}^{2}} - {{y}^{2}}} \right)$ равен (–0.193) при ${{{{{{\varphi }}}_{a}}} \mathord{\left/ {\vphantom {{{{{{\varphi }}}_{a}}} {{{{{\varphi }}}_{b}}}}} \right. \kern-0em} {{{{{\varphi }}}_{b}}}} = 0.36$. При ${{\alpha }} = 10$ поправка за счет ${{\Omega }_{{z0}}}$ в (29) меньше ${{10}^{{ - 3}}}$.

ЗАКЛЮЧЕНИЕ

При решении задачи об эволюции пучка, сечение которого в разной степени приближено к прямоугольному, выполняемой численными методами, исходят из предположения, что в плоскости инжекции объект имеет однородную плотность, одномерное или двумерное распределение потенциала и скорость, направленную вдоль оси системы. Вопрос о возможности реализации принятых условий обычно не обсуждается.

Перечисленные требования на входе в тракт транспортировки могут быть выполнены для одномерных потоков или пучков в состоянии бриллюэновского равновесия. Существующие теоретические модели, отличающиеся от численных адекватным описанием сингулярной прикатодной зоны, позволяют сформировать релятивистский поток с изменяющимся прямоугольным сечением в присутствии неоднородного внешнего магнитного поля с выходом на режим одномерного движения или на бриллюэновское равновесие для эллиптических трубок тока. В первом случае потенциал постоянен по всему сечению пучка, во втором поле пространственного заряда однозначно связано с интенсивностью внешнего квадруполя.

Замкнутые эквипотенциальные каналы с достаточным удалением стенки от электронного потока при сохранении его формы и ориентации, как показывает проведенное исследование, возможны в модели закрепленных зарядов при умеренном скруглении угла (${{c}_{4}} = 0$) или в случае выхода на режим одномерного движения. Во всех прочих вариантах, включая бриллюэновское равновесие пучка на входе в тракт транспортировки, канал должен иметь вид квадрупольной линзы.

Численные модели расчета трехмерных электронно-оптических систем – область эмпирики. К их использованию в разномасштабных задачах с ленточными пучками могут быть высказаны те же претензии, что и в случае потоков с высокой компрессией [9]. Дополнительные проблемы связаны с тем, что с появлением поверхностей с изломами эквипотенциалей при расчете неаналитических контуров, которые не замечаются численными алгоритмами и неконтролируемыми флуктуациями плотности, обусловленными сущностью численной модели и упомянутыми в [6].

Поверхность инжекции не может быть плоскостью кроссовера из-за несбалансированности потока в этом сечении, хотя модели синтеза допускают обращение в нуль не только второй, но и третьей производных траекторной функции [53, 54].

Адекватность численного подхода не тождественна возможности перерабатывать любые постановки, в том числе и абсурдные [9], и прямо зависит от учета известных к настоящему времени сведений из теории формирования трехмерных электронных потоков. Экспериментальная доводка прибора элиминирует недостатки математического моделирования, количество которых желательно минимизировать.

Список литературы

  1. Ruan C., Wang S., Zhao D. et al. // Proc. Int. Vacuum Electronics Conf. (IVEC-2012). Monterey. 24–26 Apr. N.Y.: IEEE, 2012. P. 147.

  2. Ruan C., Wang S., Han Y. et al. // IEEE Trans. Electron Dev. 2014. V. 61. № 6. P. 1643.

  3. Tang X., Sha G., Duan Z. et al. // Proc. IEEE 14 th Int. Vacuum Electronics Conf. (IVEC-2013). Paris. 21–23 May. N.Y.: IEEE, 2013. P. 215.

  4. Бурцев А.А., Данилушкин А.В. // РЭ. 2019. Т. 64. № 10. С. 1002.

  5. Астрелин В.Т., Ерофеев В.И. // ЖТФ. 1989. Т. 59. № 2. С. 135.

  6. Nguyen K.T., Pasour J.A., Antonsen T.M. et al. // IEEE Trans. Electron Dev. 2009. V. 56. № 5. P. 744.

  7. Pasour J.A., Nguyen K.T., Antonsen T.M. et al. // Proc. 2009 IEEE Int. Vacuum Electronics Conf. (IVEC-2009). Rome. 28–30 Apr. N.Y.: IEEE, 2009. P. 300.

  8. Nguyen K.T., Pasour J.A., Wright E.L. et al. // Proc. 2008 IEEE Int. Vacuum Electronics Conf. (IVEC-2008). Monterey. 22–24 Apr. N.Y.: IEEE, 2008. P. 179.

  9. Акимов П.И., Никитин А.П., Сыровой В.А. // Электрон. техника. Сер. 1. СВЧ-техника. 2018. № 1. С. 32.

  10. Bhatt R., Chen C. // Phys. Rev. Accelerators and Beams. 2005. V. 8. № 1. P. 014201.

  11. Сыровой В.А. // Прикл. матем. механика. 1970. Т. 34. № 1. С. 4.

  12. Пегов С.А., Сыровой В.А. // РЭ. 1974. Т. 19. № 10. С. 2157.

  13. Данилов В.Н., Сыровой В.А. // РЭ. 1977. Т. 22. № 7. С. 1473.

  14. Данилов В.Н., Сыровой В.А. // Изв. вузов. Радиофизика. 1977. Т. 20. № 11. С. 1727.

  15. Bhatt R.J. Inverse Problems in Elliptic Charge-Particle Beams. Massachusetts Institute of Technology: 2006.

  16. Сыровой В.А. // Изв. вузов. Радиофизика. 1988. Т. 31. № 8. С. 984.

  17. Cыpoвoй B.A. // PЭ. 2017. T. 62. № 5. C. 493.

  18. Сыровой В.А. // Письма в ЭЧАЯ. 2020. Т. 17. № 2. С. 169.

  19. Данилов В.Н. // Журнал прикл. механики и техн. физики. 1968. № 5. С. 3.

  20. Сыровой В.А. Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.

  21. Syrovoy V.A. Theory of Intense Beams of Charged Particles. US: Elsevier, 2011.

  22. Пензяков В.В., Олейников В.И. // РЭ. 1975. Т. 20. № 5. С. 1049.

  23. Cыpoвoй B.A. // PЭ. 2008. T. 53. № 8. C. 999.

  24. Cыpoвoй B.A. // PЭ. 2011. T. 56. № 1. C. 111.

  25. Cыpoвoй B.A. // PЭ. 2016. T. 61. № 7. C. 692.

  26. Cыpoвoй B.A. // PЭ. 2018. T. 63. № 5. C. 472.

  27. Акимов П.И., Гаврилин А.А., Никитин А.П. и др. // РЭ. 2018. Т. 63. № 11. С. 1303.

  28. Oвчapoв B.T. // PЭ. 1962. T. 7. № 8. C. 1368.

  29. Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.

  30. Cыpoвoй B.A. // PЭ. 2017. T. 62. № 6. C. 584.

  31. Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1106.

  32. Cыpoвoй B.A. // PЭ. 2001. T. 46. № 5. C. 617.

  33. Cыpoвoй B.A. // PЭ. 2001. T. 46. № 9. C. 1139.

  34. Cыpoвoй B.A. // PЭ. 2016. T. 61. № 3. C. 263.

  35. Cыpoвoй B.A. // PЭ. 2002. T. 47. № 3. C. 372.

  36. Cыpoвoй B.A. // PЭ. 2014. T. 59. № 4. C. 358.

  37. Cыpoвoй B.A. // PЭ. 2018. T. 63. № 8. C. 871.

  38. Кирштейн П.Т., Кайно Г.С., Уотерс У.Е. Формирование электронных пучков. М.: Мир, 1970.

  39. Мануилов В.Н., Цимринг Ш.Е. // РЭ. 1978. Т. 23. № 7. С. 1486.

  40. Maнyилoв B.H. // PЭ. 1981. T. 26. № 11. C. 2425.

  41. Капчинский И.М. Теория линейных резонансных ускорителей. Динамика частиц. М.: Энергоатомиздат, 1982.

  42. Муратов М.З. Потенциалы эллипсоида. М.: Атомиздат, 1976.

  43. Лоусон Дж. Физика пучков заряженных частиц. М.: Мир, 1980.

  44. Лебедев В.А., Мешков И.Н., Шарапа А.Н. // ЖТФ. 1979. Т. 49. № 4. С. 726.

  45. Акимов П.И., Гаврилин А.А., Никитин А.П. и др. // Журн. Радиоэлектроники. 2015. № 11. http:// jre.cplire.ru/jre/nov15/4/text.pdf.

  46. Сыровой В.А. // Письма в ЭЧАЯ. 2018. Т. 15. № 3. С. 211.

  47. Сыровой В.А. // Письма в ЭЧАЯ. 2019. Т. 16. № 2. С. 121.

  48. Han Y., Ruan C. // Chin. Phys. B. 2012. V. 21. № 5. C. 0541103-1.

  49. Завьялов М.А., Сапронова Т.М., Сыровой В.А. // РЭ. 2022. Т. 67. № 3. С. 303.

  50. Walker L.R. // J. Appl. Phys. 1955. V. 26. № 6. P. 781.

  51. Kirstein P.T. // J. Electr. Contr. 1958. V. 4. № 5. P. 425.

  52. Pöschl K., Veith W. // J. Appl. Phys. 1962. V. 33. № 3. P. 1013.

  53. Cыpoвoй B.A. // PЭ. 1994. T. 39. № 3. C. 481.

  54. Гамаюнов Ю.Г., Патрушева Е.В., Тореев А.И., Шаталина С.А. // РЭ. 2008. Т. 53. № 3. С. 344.

  55. Гамаюнов Ю.Г., Патрушева Е.В. // РЭ. 2017. Т. 62. № 11. С. 1126.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал