Радиотехника и электроника, 2022, T. 67, № 5, стр. 509-513
О сингулярности решения уравнений плотного электронного пучка при эмиссии в Т-режиме
Т. М. Сапронова a, *, В. А. Сыровой a
a ВЭИ – филиал “РФЯЦ – ВНИИТФ им. академ. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 03.08.2021
После доработки 03.08.2021
Принята к публикации 16.09.2021
- EDN: GWQFUT
- DOI: 10.31857/S0033849422040088
Аннотация
Проанализировано поведение регулярных функций в двучленной формуле для потенциала с выделением особенности для одномерных диода и магнетрона при эмиссии в Т-режиме.
ВВЕДЕНИЕ
Предположение о нулевой начальной скорости электронов в гидродинамической модели плотного электронного пучка приводит к бесконечному значению плотности пространственного заряда ${{\rho }}$ на стартовой поверхности при эмиссии, ограниченной пространственным зарядом или температурой. Математическим следствием этого факта является появление особой точки на катоде, характер которой зависит от режима эмиссии и наличия магнитного поля $\vec {H}$. В работе [1] показано, что при эмиссии в ${{\rho }}$-режиме и $\vec {H} \ne 0$ структура особенности может быть представлена в виде трехчленной формулы, описывающей “линейную комбинацию” двух точек ветвления, коэффициентами в которой являются аналитические функции продольной координаты l, нормальной к катоду.
Для потенциала электрического поля ${{\varphi }}$ формула имеет вид
(1)
${{\varphi }} = {{l}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{\Phi }_{1}}\left( l \right) + {{l}^{{{6 \mathord{\left/ {\vphantom {6 3}} \right. \kern-0em} 3}}}}{{\Phi }_{2}}\left( l \right) + {{l}^{{{8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0em} 3}}}}{{\Phi }_{3}}\left( l \right).$Зависимости от тангенциальных к катоду координат у функций ${{\Phi }_{k}}$ для упрощения записи не приводим.
При эмиссии в Т-режиме структура особенности описывается более простым выражением
(2)
${{\varphi }} = {{l}^{{{2 \mathord{\left/ {\vphantom {2 2}} \right. \kern-0em} 2}}}}{{\Phi }_{1}}\left( l \right) + {{l}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\Phi }_{2}}\left( l \right).$Коэффициенты в зависимостях (1), (2) не могут быть выражены в элементарных функциях даже в случае одномерных течений, описываемых точными решениями.
Для электростатических пучков в ${{\rho }}$-режиме эмиссии особенность факторизуется:
(3)
${{\varphi }} = {{l}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\Phi \left( l \right).$Выделение особенности в одномерных задачах. Потенциал в плоском магнетроне при переходе от системы СИ к безразмерным переменным (символы с чертой), устраняющим из уравнений пучка все физические постоянные используемой системы единиц, описывается соотношением
(4)
$\frac{{{{d}^{2}}{{\bar {\varphi }}}}}{{d{\kern 1pt} {{{\bar {x}}}^{2}}}} = \frac{{\bar {J}}}{{\sqrt {2{{\bar {\varphi }}} - {{{\bar {H}}}^{2}}{{{\bar {x}}}^{2}}} }},\,\,\,\,{{\bar {\varphi }}} = \bar {x}{{\bar {\Phi }}_{1}}\left( {\bar {x}} \right) + {{\bar {x}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\bar {\Phi }}_{2}}\left( {\bar {x}} \right),$(5)
${{\bar {\varphi }}} = \frac{{{\varphi }}}{{{{{{\varphi }}}_{*}}}},\,\,\,\,\bar {E} = \frac{E}{{{{E}_{*}}}},\,\,\,\,\bar {H} = \frac{H}{{{{H}_{*}}}},\,\,\,\bar {J} = \frac{J}{{{{J}_{*}}}},\,\,\,\,\bar {x} = \frac{x}{{L{{{\kern 1pt} }_{*}}}};$Введем дополнительную нормировку искомых функций и аргумента в (4):
(6)
$\begin{gathered} {{{\bar {\Phi }}}_{1}} = \bar {E}{{{\hat {\Phi }}}_{1}},\,\,\,\,{{{\bar {\Phi }}}_{2}} = \frac{{\bar {J}}}{{2\sqrt {2\bar {E}} }}{{{\hat {\Phi }}}_{2}}, \\ {{\bar {\varphi }}} = \frac{{8{{{\bar {E}}}^{4}}}}{{{{{\bar {J}}}^{2}}}}{{\hat {\varphi },}}\,\,\,\,\bar {x} = \frac{{8{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}}\hat {x}, \\ \end{gathered} $В новых переменных соотношения (4) примут вид
(7)
$\frac{{{{d}^{2}}{{\hat {\varphi }}}}}{{d{{{\hat {x}}}^{2}}}} = \frac{2}{{\sqrt {{{\hat {\varphi }}} - 4{{{{\gamma }}}^{2}}{{{\hat {x}}}^{2}}} }},\,\,\,\,{{\hat {\varphi }}} = \hat {x}{{\hat {\Phi }}_{1}} + {{\hat {x}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\hat {\Phi }}_{2}};\,\,\,\,{{\gamma }} = \frac{{\bar {E}\bar {H}}}{{\bar {J}}}.$Возведем обе части дифференциального уравнения для ${{\hat {\varphi }}}$ в квадрат и будем искать решение в форме (7)
(8)
${{\left( {\frac{{{{d}^{2}}{{\hat {\varphi }}}}}{{d{{{\hat {x}}}^{2}}}}} \right)}^{2}}\left( {{{\hat {\varphi }}} - 4{{{{\gamma }}}^{2}}{{{\hat {x}}}^{2}}} \right) = 4.$Сепарация регулярных функций и функций с факторизованной особенностью, справедливая вблизи стартовой поверхности, приводит к системе уравнений
(9)
$\begin{gathered} \left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right)\left( {\hat {x}\Psi _{1}^{2} + \Psi _{2}^{2}} \right) + 2\hat {x}{{{\hat {\Phi }}}_{2}}{{\Psi }_{1}}{{\Psi }_{2}} = 4, \\ {{{\hat {\Phi }}}_{2}}\left( {\hat {x}\Psi _{1}^{2} + \Psi _{2}^{2}} \right) + 2\left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right){{\Psi }_{1}}{{\Psi }_{2}} = 0, \\ \end{gathered} $
Разрешая уравнения (9) относительно комбинаций ${{\left( {\sqrt {\hat {x}} {{\Psi }_{1}}} \right)}^{2}} + \Psi _{2}^{2}$, $\left( {\sqrt {\hat {x}} {{\Psi }_{1}}} \right){{\Psi }_{2}}$, имеем
(11)
$\begin{gathered} {{\left( {\sqrt {\hat {x}} {{\Psi }_{1}}} \right)}^{2}} + \Psi _{2}^{2} = \frac{4}{{{\delta }}}\left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right), \\ \left( {\sqrt {\hat {x}} {{\Psi }_{1}}} \right){{\Psi }_{2}} = - \frac{2}{{{\delta }}}\sqrt {\hat {x}} \,{{{\hat {\Phi }}}_{2}}; \\ {{\delta }} = {{\left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right)}^{2}} - \hat {x}\,\hat {\Phi }_{2}^{2}. \\ \end{gathered} $Дополним левую часть первого соотношения (11) до квадрата суммы функций $\sqrt {\hat {x}} {{\Psi }_{1}}$ и ${{\Psi }_{2}}$ и выразим первую из них через вторую при помощи второго соотношения$.$ Результатом будет квадратное уравнение относительно ${{\Psi }_{2}}$
(12)
$\begin{gathered} \left( {\sqrt {\hat {x}} \,{{\Psi }_{1}}} \right) + \Psi _{2}^{{}} = \frac{1}{{\sqrt {{\delta }} }}{{\left[ {\left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right) - \sqrt {\hat {x}} \,{{{\hat {\Phi }}}_{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \sqrt {\hat {x}} {{\Psi }_{1}} = - \frac{2}{{{\delta }}}\sqrt {\hat {x}} \frac{{{{{\hat {\Phi }}}_{2}}}}{{{{\Psi }_{2}}}}; \\ \Psi _{2}^{2} - \frac{1}{{\sqrt \delta }}{{\left[ {\left( {{{{\hat {\Phi }}}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x}} \right) - \sqrt {\hat {x}} \,{{{\hat {\Phi }}}_{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\Psi _{2}^{{}} - \frac{2}{{{\delta }}}\sqrt {\hat {x}} \,{{{\hat {\Phi }}}_{2}} = 0. \\ \end{gathered} $Регулярные фрагменты ${{\hat {\Phi }}_{1}}$, ${{\hat {\Phi }}_{2}}$ потенциала в форме (7) удовлетворяют следующей системе дифференциальных уравнений:
Обратим внимание на тот факт, что уравнения (13), определяющие в окрестности $\hat {x} = 0$ регулярные функции ${{\hat {\Phi }}_{1}}$, ${{\hat {\Phi }}_{2}}$, имеют правые части, образованные неаналитическими слагаемыми. Кроме того, выполнение равенства
(14)
$F = {{\hat {\Phi }}_{1}} - 4{{{{\gamma }}}^{2}}\hat {x} - \sqrt {\hat {x}} \,{{\hat {\Phi }}_{2}} = 0$Построение разложений для функций ${{\hat {\Phi }}_{1}}$, ${{\hat {\Phi }}_{2}}$ из (13) вблизи $x = 0$приводит к следующему результату:
(15)
$\begin{gathered} {{{\hat {\Phi }}}_{1}} = {{f}_{0}} + {{f}_{1}}\hat {x} + {{f}_{2}}{{{\hat {x}}}^{2}} + ..., \\ {{{\hat {\Phi }}}_{2}} = {{g}_{0}} + {{g}_{1}}\hat {x} + {{g}_{2}}{{{\hat {x}}}^{2}} + ...; \\ {{f}_{0}} = 1,\,\,\,\,{{f}_{1}} = - \frac{4}{3},\,\,\,\,{{g}_{0}} = \frac{8}{3}, \\ {{g}_{1}} = \frac{{16}}{9} + \frac{{16}}{{15}}{{{{\gamma }}}^{2}},\,\,\,\,{{f}_{2}} = - \frac{{256}}{{81}} - \frac{{128}}{{45}}{{{{\gamma }}}^{2}}, \\ {{g}_{2}} = \frac{{176}}{{27}} + \frac{{352}}{{45}}{{{{\gamma }}}^{2}} + \frac{{48}}{{35}}{{{{\gamma }}}^{4}}, \\ {{\hat {\varphi }}} = \hat {x}{{{\hat {\Phi }}}_{1}} + {{{\hat {x}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{{\hat {\Phi }}}_{2}}. \\ \end{gathered} $В дальнейшем при рассмотрении численных примеров в качестве базисных значений параметров пучка примем величины, близкие к указанным в работе [4], посвященной описанию электронно-оптической системы планарного гиротрона
(16)
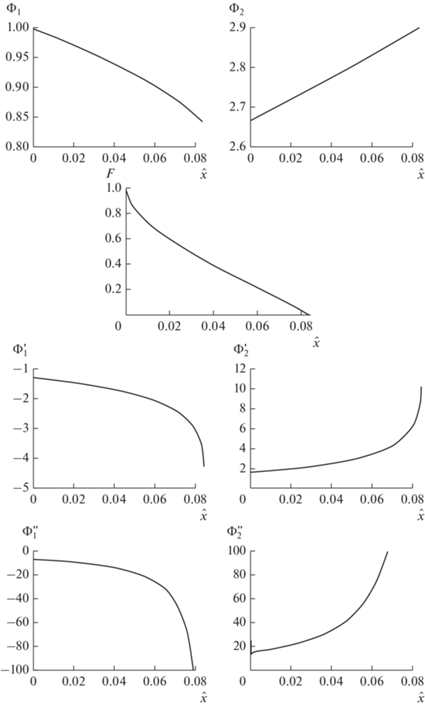
$\begin{gathered} {{{{\varphi }}}_{*}} = 50\,\,{\text{кВ}},\,\,\,\,{{V}_{*}} = 9.4 \times {{10}^{7}}\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{c}}}} \right. \kern-0em} {\text{c}}}, \\ {{H}_{*}} = 4.24 \times {{10}^{4}}\,\,{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {{\text{м,}}}}} \right. \kern-0em} {{\text{м,}}}}\,\,\,\,{{J}_{*}} = 41.5\,\,\,{{\text{А}} \mathord{\left/ {\vphantom {{\text{А}} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{;}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{;}}}} \\ \bar {E} = 0.6,\,\,\,\,\bar {H} = 2.9,\,\,\,\,\bar {J} = 0.1, \\ \end{gathered} $Плоский диод. На рис. 1 приведены функции ${{\hat {\Phi }}_{1}}$, $\hat {\Phi }_{1}^{'}$,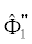 
; ${{\hat {\Phi }}_{2}}$, $\hat {\Phi }_{2}^{'}$, 
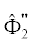и F, полученные при интегрировании уравнений (13). Значение ${{\hat {x}}_{*}}$ при этом составляет
Рис. 1.
Функции ${{\Phi }_{1}}$, ${{\Phi }_{2}}$ с первыми и вторыми производными и функция F для диода.
Для плоского диода в Т-режиме существует аналитическое решение в параметрической форме, описываемое не содержащими значений $\bar {J}$, $\bar {E}$ универсальными зависимостями от ${{\tau }}$:
(18)
$\begin{gathered} \frac{{{{{\bar {J}}}^{2}}}}{{{{{\bar {E}}}^{3}}}}{{{\bar {x}}}^{{{\text{ex}}}}} = {{{\hat {x}}}^{{{\text{ex}}}}} = \frac{1}{2}{{{{\tau }}}^{2}}\left( {\frac{1}{3}{{\tau }} + 1} \right), \\ \frac{{{{{\bar {J}}}^{2}}}}{{{{{\bar {E}}}^{4}}}}{{{{{\bar {\varphi }}}}}^{{{\text{ex}}}}} = {{{{{\hat {\varphi }}}}}^{{{\text{ex}}}}} = \frac{1}{2}{{{{\tau }}}^{2}}{{\left( {\frac{1}{2}{{\tau }} + 1} \right)}^{2}}, \\ \frac{1}{{\bar {E}}}\frac{{d{\kern 1pt} {{{{{\bar {\varphi }}}}}^{{{\text{ex}}}}}}}{{d{\kern 1pt} {{{\bar {x}}}^{{{\text{ex}}}}}}} = \frac{{{{{{\tau }}}^{2}} + 3{{\tau }} + 2}}{{{{\tau }} + 2}}. \\ \end{gathered} $Нормировав потенциал ${{\varphi }}$ на потенциал анода ${{{{\varphi }}}_{A}}$ (${{{{\bar {\varphi }}}}_{A}} = 1$), получим значения параметра ${{{{\tau }}}_{A}}$, расстояния $\bar {x}_{A}^{{{\text{ex}}}}$ между электродами и поля $\bar {E}_{A}^{{{\text{ex}}}}$ на аноде:
(19)
$\begin{gathered} \frac{{{{{\bar {J}}}^{2}}}}{{{{{\bar {E}}}^{4}}}} \times 1 = \frac{1}{2}{{\tau }}_{A}^{2}{{\left( {\frac{1}{2}{{{{\tau }}}_{A}} + 1} \right)}^{2}},\,\,\,\,{{{{\tau }}}_{A}} = \sqrt {1 + 2{{\alpha }}} - 1, \\ {{\alpha }} = \frac{{\bar {J}\sqrt 2 }}{{{{{\bar {E}}}^{2}}}},\,\,\,\,\bar {x}_{A}^{{{\text{ex}}}} = \frac{{{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}}\hat {x}_{A}^{{{\text{ex}}}}, \\ \hat {x}_{A}^{{{\text{ex}}}} = \frac{1}{3}\left[ {1 + \left( {{{\alpha }} - 1} \right)\sqrt {1 + 2{{\alpha }}} } \right], \\ \frac{1}{{\bar {E}}}\bar {E}_{A}^{{{\text{ex}}}} = \sqrt {1 + 2{{\alpha }}{\kern 1pt} } . \\ \end{gathered} $Нормировки (6) для решения в форме (7) с выделенной особенностью отличаются от нормировок точного решения (18) множителем 8 в знаменателе:
(20)
$\hat {x} = {{{{{\hat {x}}}^{{{\text{ex}}}}}} \mathord{\left/ {\vphantom {{{{{\hat {x}}}^{{{\text{ex}}}}}} 8}} \right. \kern-0em} 8},\,\,\,\,{{\hat {\varphi }}} = {{{{{{{\hat {\varphi }}}}}^{{{\text{ex}}}}}} \mathord{\left/ {\vphantom {{{{{{{\hat {\varphi }}}}}^{{{\text{ex}}}}}} 8}} \right. \kern-0em} 8}.$Выполнение условия (14) вводит ограничение на величину параметра ${{\alpha }}$ и связь составляющих его физических параметров $\bar {J}$, $\bar {E}$.
Значению ${{\hat {x}}_{*}}$ из (17) соответствует величина ${{{{\alpha }}}_{*}}$, удовлетворяющая уравнению
(21)
$\left( {{{{{\alpha }}}_{*}} - 1} \right)\sqrt {1 + 2{{{{\alpha }}}_{*}}} + 1 = 24{{\hat {x}}_{*}},\,\,\,\,{{{{\alpha }}}_{*}} = 1.5058.$Из формул (19) находим прочие параметры диода в этом случае:
(22)
$\begin{gathered} {{{{\tau }}}_{{A{\kern 1pt} *}}} = \sqrt {1 + 2{{{{\alpha }}}_{*}}} - 1 = 1.002898, \\ \hat {x}_{{A{\kern 1pt} *}}^{{{\text{ex}}}} = \frac{1}{3}\left[ {1 + \left( {{{{{\alpha }}}_{*}} - 1} \right)\sqrt {1 + 2{{{{\alpha }}}_{*}}} } \right] = 0.671022, \\ {{{\hat {x}}}_{*}} = {{\hat {x}_{{A{\kern 1pt} *}}^{{{\text{ex}}}}} \mathord{\left/ {\vphantom {{\hat {x}_{{A{\kern 1pt} *}}^{{{\text{ex}}}}} 8}} \right. \kern-0em} 8} = 0.083877, \\ {{\hat {\varphi }}}_{*}^{{{\text{ex}}}} = \frac{1}{2}{{\tau }}_{{A{\kern 1pt} *}}^{2}{{\left( {\frac{1}{2}{{{{\tau }}}_{{A{\kern 1pt} *}}} + 1} \right)}^{2}} = 1.133717, \\ \end{gathered} $Хотя соотношения (13) при $\hat {x} > {{\hat {x}}_{*}}$ не имеют смысла, однако ошибку ${{\delta }}$ их приближенного решения в этой области можно оценить, сравнивая величины ${{\hat {\varphi }}}$ из (15) и ${{{{\hat {\varphi }}}}^{{{\text{ex}}}}}$ из (18):
(23)
$\begin{gathered} {{\hat {\varphi }}} = \hat {x}\left( {{{f}_{0}} + {{f}_{1}}\hat {x} + {{f}_{2}}{{{\hat {x}}}^{2}}} \right) + {{{\hat {x}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {{{g}_{0}} + {{g}_{1}}\hat {x} + {{g}_{2}}{{{\hat {x}}}^{2}}} \right), \\ {{\hat {\varphi }}} = {{{{{{{\hat {\varphi }}}}}^{{ex}}}} \mathord{\left/ {\vphantom {{{{{{{\hat {\varphi }}}}}^{{ex}}}} 8}} \right. \kern-0em} 8},\,\,\,\,{{\delta }} = \left| {{{\left( {{{\hat {\varphi }}} - {{{{{\hat {\varphi }}}}}^{{ex}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\hat {\varphi }}} - {{{{{\hat {\varphi }}}}}^{{ex}}}} \right)} {{{{{{\hat {\varphi }}}}}^{{ex}}}}}} \right. \kern-0em} {{{{{{\hat {\varphi }}}}}^{{ex}}}}}} \right|. \\ \end{gathered} $Ниже приведены значения этой характеристики при разных величинах ${{\alpha }}$:
Для ${{\alpha }} = 2$ при ошибке порядка 1% межэлектродный интервал простирается до ${{\hat {x}}^{{{\text{ex}}}}} = 1.08$ вместо ${{\hat {x}}^{{{\text{ex}}}}} = 0.671022$ из (22). В табл. 1 приведены возможные значения величин $\bar {J}$, $\bar {E}$, $\bar {x}$ для этого случая в исходных нормировках (5), а также размерная плотность тока в ${{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}}$. Для вычисления $\bar {x}$ использованы соотношения
(24)
$\begin{gathered} \bar {x} = \frac{{{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}}{{{\hat {x}}}_{A}} = \frac{{{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}}\frac{1}{3}\left[ {1 + \left( {{{\alpha }} - 1} \right)\sqrt {1 + 2{{\alpha }}} } \right], \\ {{\alpha }} = 2,\,\,\,\,\bar {x} = \frac{{{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}} = \frac{{1 + \sqrt 5 }}{3},\,\,\,\,\bar {J} = \frac{{{{\alpha }}{{{\bar {E}}}^{2}}}}{{\sqrt 2 }}, \\ \frac{{{{{\bar {E}}}^{3}}}}{{{{{\bar {J}}}^{2}}}} = \frac{1}{{2\bar {E}}},\,\,\,\,\bar {x} = \frac{1}{6}\,\,\frac{{1 + \sqrt 5 }}{{\bar {E}}}. \\ \end{gathered} $Таблица 1.
Возможные параметры диода при ${{\alpha }}\,\,{\text{ = }}\,\,{\text{2}}$
| $\bar {E}$ | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.15 |
|---|---|---|---|---|---|---|
| $\bar {J}$ | 0.509 | 0.354 | 0.226 | 0.127 | 0.0566 | 0.0318 |
| $\bar {x}$ | 0.899 | 1.079 | 1.348 | 1.798 | 2.697 | 3.596 |
| $J,\,{{\,\,{\text{A}}} \mathord{\left/ {\vphantom {{\,\,{\text{A}}} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{2}}}}}}$ | 21 | 14.7 | 9.4 | 5.3 | 2.4 | 1.3 |
Малое значение ошибки ${{\delta }}$ при ${{\alpha }} = 1.5058$ (см. выше) позволяет вычислить величину ${{\hat {x}}_{*}}$ на основе асимптотик для функций ${{\hat {\Phi }}_{1}}$, ${{\hat {\Phi }}_{2}}$ из (15). Оно оказывается равным ${{\hat {x}}_{*}} = 0.0887$ и отличается от значения, полученного в результате интегрирования системы (13), на 5.75%.
Плоский магнетрон. Точное решение в параметрической форме приведено в [5] и содержит величину ${{\gamma }}$, образованную комбинацией физических параметров J, E, H задачи:
(25)
$\begin{gathered} {{{\hat {x}}}^{{{\text{ex}}}}} = 8{{{{\gamma }}}^{3}}\hat {x} = {{\tau }} - \sin {{\tau }} + {{\gamma }}\left( {1 - \cos {{\tau }}} \right),\,\,\,{{\gamma }} = {{\bar {E}\bar {H}} \mathord{\left/ {\vphantom {{\bar {E}\bar {H}} {\bar {J}}}} \right. \kern-0em} {\bar {J}}}, \\ {{{{{\hat {\varphi }}}}}^{{{\text{ex}}}}} = 16{{{{\gamma }}}^{4}}{{\hat {\varphi }}} = {{\left( {1 - \cos {{\tau }} + {{\gamma }}\sin {{\tau }}} \right)}^{2}} + {{({{{\hat {x}}}^{{{\text{ex}}}}})}^{2}}. \\ \end{gathered} $На рис. 2а, 2б представлено соотношение (значения ${{\delta }}$) точного решения (25) и приближенного решения
(26)
$\begin{gathered} {{\hat {\varphi }}}\,\,{\text{ = }}\,\,\hat {x}{{{\hat {\Phi }}}_{1}} + {{{\hat {x}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{{\hat {\Phi }}}_{2}},\,\,\,\,{{{\hat {\Phi }}}_{1}} = {{f}_{0}} + {{f}_{1}}\hat {x} + {{f}_{2}}{{{\hat {x}}}^{2}}, \\ {{{\hat {\Phi }}}_{2}} = {{g}_{0}} + {{g}_{1}}\hat {x} + {{g}_{2}}{{{\hat {x}}}^{2}} \\ \end{gathered} $Рис. 2.
Относительная ошибка δ приближенного решения для магнетрона при ${{\gamma }} = 1,\,2,\,3,\,4$ в диапазоне ${{\delta }} = 0...10\% $ (а) и ${{\delta }} = - 0.4...1\% $ (б).
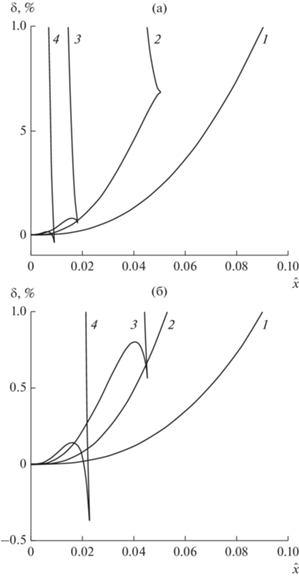
с параболической аппроксимацией функций ${{\hat {\Phi }}_{1}}$, ${{\hat {\Phi }}_{2}}$ при разных значениях ${{\gamma }}$. Ниже приведена оценка величины $\hat {x}$, при котором ошибка формы (26) не превышает 1%:
При наличии магнитного поля параболическая аппроксимация в форме (26) обеспечивает ошибку, не превышающую 1%, на незначительной части Δ межэлектродного пространства. Так, для ${{\gamma }} = 1$, $\bar {J} = 0.764$, $\bar {H} = 1.27$ при $\hat {x}_{A}^{{{\text{ex}}}} = 1.788$ эта часть составляет $\Delta = 5\,\% $; при ${{\gamma }} = 3$, $\bar {J} = 0.34$, $\bar {H} = 2.55$ величина $\Delta $ составляет 0.16%.
Список литературы
Cыpoвoй B.A. // PЭ. 2005. T. 50. № 7. C. 875.
Брауде С.Я. // ЖЭТФ. 1935. Т. 5. № 7. С. 621.
Брауде С.Я. // ЖТФ. 1940. Т. 10. № 3. С. 217.
Manuilov V.N., Zaslavsky V.Yu., Ginzburg N.S. et al. // Phys. of Plasmas. 2014. V. 21. № 2. P. 023106.
Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника
Пн.-пт.: 10.00-19.00