Радиотехника и электроника, 2022, T. 67, № 5, стр. 500-508

ВВЕДЕНИЕ

На современном этапе развития оптических технологий оптическое волокно (ОВ) нашло широкое применение не только в телекоммуникации, но и во многих других отраслях [1]. В зависимости от целевого приложения различаются необходимые масштабы производства требуемого типа ОВ – от крупносерийного до штучного производства специализированных ОВ.

Производство ОВ сложный и дорогостоящий процесс, поэтому на этапе его разработки требуется предварительное моделирование. В известных программных продуктах, позволяющих моделировать ОВ (например, Code V, ZEMAX, Opal, TracePro), преимущественно используются имитационные методы. Имитационные модели удобно применять при моделировании существующих объектов для определения их показателей в переменных условиях. Это требует проведения множества экспериментов, ограниченных точностью выходных данных, с последующей аппроксимацией и повторением. Для разработки новых типов специализированных ОВ требуются строгие методы моделирования, позволяющие находить оптимальное значения показателей волокна без проведения аппроксимационных этапов на физическом объекте. В данных методах используется аналитическое моделирование, ограниченное детерминированными процессами, требующее меньше вычислительной мощности, математически проверяемое в прямой и обратной постановке.

Методы аналитического моделирования в области связи хорошо проработаны положениями теории цепей, применяемой для расчетов фильтров, корректоров, трансформаторов, линий связи и т.п. в различных диапазонах частот – от сверхнизких до сверхвысоких.

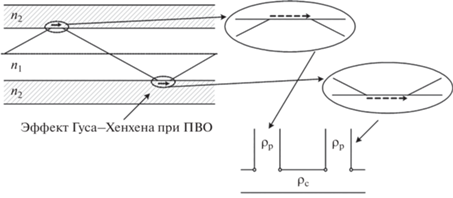
Наличие у ОВ избирательности волновой характеристики затухания, подобной имеющейся у оптических фильтров (ОФ), дает основания поиска модели ОВ в виде оптического фильтра, частотные характеристики которого полностью (или максимально приближенно) отображают частотные характеристики затухания ОВ. В основе распространения оптического сигнала (ОС) по ОВ лежит многократно повторяющееся явление полного внутреннего отражения (ПВО) (рис. 1) [1, 2]. При отражении ОС проникает во вторую среду, проходит там расстояние порядка длины волны распространяющегося ОС и возвращается в первую среду. Таким образом возникает сдвиг точки выхода сигнала относительно точки входа [3–5]. Данное явление получило название эффекта Гуса–Хенхена, а факт его существования дает основание для отнесения ОВ к оптическим гетероструктурам (ОГС) – направляющим системам, предназначенным для передачи сигналов оптического диапазона длин волн: инфракрасного, видимого, ультрафиолетового и рентгеновского [6]. Гетероструктуры как системы, составленные из чередующихся пар элементов с отличающимися значениями однотипных параметров, обладают спектральной избирательностью. В данной статье теория и расчет ОГС основаны на общем подходе к структурам как к цепям с распределенными параметрами, состоящими из отрезков передающих линий, исследуемых методами теории цепей.

Применение теории цепей было распространено и на оптический диапазон в части элементов с сосредоточенными элементами (оптических многослойных фильтров и корректоров) [6].

Цель данной работы – решить задачу распространения положений теории цепей на элементы с рассредоточенными элементами – ОВ, что позволит аналитически, с применением апробированных на практике научных методов и методик, рассчитывать параметры волокна в прямой и обратной постановке.

1. МОДЕЛИРОВАНИЕ ЗВЕНА ОПТИЧЕСКОГО ВОЛОКНА

В различных учебниках, научных изданиях и отчета приводится множество волновых характеристик затухания ОВ [7–9], которые имеют существенные отличия по форме и величине при прочих равных условиях. Производители ОВ и оптических кабелей (ОК) также, производя измерения волновой характеристики затухания одного и того же ОВ при различных условиях, получают существенно отличающиеся результаты, хотя типы ОВ стандартизованы и их характеристики производители приводят справочно. Этот факт объясняется тем, что при изменении радиуса изгиба ОВ изменяется и количество переотражений ОС и чем больше этих переотражений, тем больше затухание сигнала и у́же полоса пропускания.

Но сами по себе многократные переотражения не дали бы такого эффекта без распространения ОС во второй среде. В однородной среде сигнал практически не претерпевает затухания [10]. Отсюда следует, что именно нарастание количества сдвигов ОС и его суммарного пути распространения во второй среде при многократном ПВО определяет изменение волновой характеристики затухания ОВ, а также угол падения ОС и материалы, из которых изготовлены сердцевина и оболочка ОВ. Таким образом, явление сдвига Гуса–Хенхена дает основание для рассмотрения и расчета оптических направляющих систем с точки зрения теории цепей.

В данной статье это явление моделируется резонансным контуром (рис. 1), включенным в оптический путь прохождения сигнала. В этом случае ОВ, состоящее из сердцевины с показателем преломления n₁ и оболочки с n₂, моделируется схемой фильтра в виде длинной линии, с волновым сопротивлением ρ_с, с упорядоченно включенными в нее резонансными контурами с волновым сопротивлением ρ_р. Таким образом, задача расчета оптических характеристик ОВ сводится к расчету характеристик оптического многошлейфного фильтра (ОМШФ).

Для расчета параметров резонансного контура необходимо оценивать величину сдвига Гуса–Хенхена в различных средах распространения. Для оценки величины сдвига были проведены расчеты по формулам, полученным Ренардом в результате исследования эффекта Гуса–Хенхена [11].

Величина сдвига в случае s-поляризации с учетом того, что µ = 1, рассчитывается по формуле:

Величина сдвига в случае p-поляризации определяется по формуле где Θ₁ ∈ [Θ_кр; π/2], Θ_кр – критический угол ПВО.

Все параметры среды с большим показателем преломления (ПП) обозначаются нижним индексом 1, а с меньшим показателем – индексом 2; К – диэлектрическая постоянная. Из формул (1) и (2) видно, что величина сдвига Гуса–Хенхена прямо пропорциональна длине волны λ.

Для сравнительного анализа изменения сдвига при различных свойствах сред были взяты девять различных соотношений ПП сред (рис. 2, кривые 1–9 соответственно):

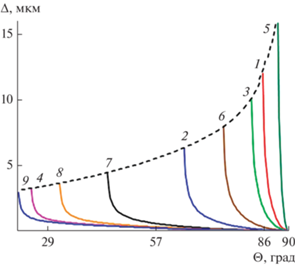
1) n₁ = 1.47, n₂ = 1.46 (стандартное кварцевое ОВ);

2) n₁ = 1.47, n₂ = 1.32 (ОВ с кварцевой сердцевиной и полимерной оболочкой);

3) n₁ = 1.47, n₂ = 1.45 (кварцевое ОВ с экспериментальным ПП оболочки);

4) n₁ = 3.22, n₂ = 1.32 (полимерное ОВ с экспериментальным ПП);

5) n₁ = 1.47, n₂ = 1.46 (кварцевое ОВ с экспериментальным ПП оболочки);

6) n₁ = 1.47, n₂ = 1.41 (кварцевое ОВ с экспериментальным ПП оболочки);

7) n₁ = 1.87, n₂ = 1.32 (кварцевое ОВ с экспериментальным ПП сердцевины);

8) n₁ = 2.47, n₂ = 1.32 (кварцевое ОВ с экспериментальным ПП сердцевины);

9) n₁ = 3.4, n₂ = 1.32 (полимерное ОВ с экспериментальным ПП).

Результаты расчетов сдвига Гуса–Хенхена для s-поляризации представлены на рис. 2.

Из полученных характеристик видно, что при увеличении отношения показателей преломления оптических сред:

‒ предельный угол ПВО уменьшается, а сектор ПВО увеличивается (закон Снеллиуса);

‒ максимум смещения (∆_max) убывает (см. рис. 2);

‒ избирательные свойства единицы длины ОВ усиливаются:

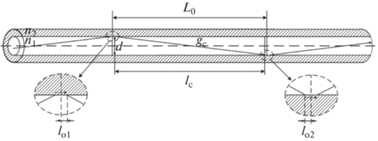
Для моделирования ОВ необходимо ввести новое понятие – звено ОВ (рис. 3). Звено оптического волокна – линейный участок ОВ длиной L₀, состоящий из трех участков.

1. Участка ОВ длиной l_о1, в котором ОС распространяется в оболочке ОВ при первом ПВО, составляющего половину сдвига Гуса–Хенхена.

2. Участка ОВ длиной l_с, в котором ОС прямолинейно распространяется в сердцевине ОВ между первой и второй точками отражения ОС от граничных противоположных слоев ОВ.

3. Линейного участка ОВ длиной l_о2, в котором ОС распространяется в оболочке ОВ при втором ПВО, составляющего половину сдвига Гуса–Хенхена.

При этом участки l_о1 = l_о2 = l_о имеют смысл наведенных лучом квантовых ям [12, 13], которые обладают ярко выраженными свойствами резонаторов с резонансными частотами f_р.

Количество звеньев N_зв на ОВ длиной 1 м исчисляется десятками тысяч. И при таком большом количестве звеньев затухание ОВ остается невысоким. Это объясняется, во-первых, высокой добротностью материала участка звена ОВ (кварцевое стекло), во-вторых, широкой полосой пропускания (ППр) звеньев ОВ и, в-третьих, тем, что все звенья ОВ имеют одинаковые конструктивные и материальные параметры, а это обеспечивает согласованное (без отражений) включение всех звеньев ОВ между собой.

Выделим на рис. 3 треугольник, размер одного катета которого – это диаметр сердцевины d, гипотенуза – длина пути ОС на участке звена g_c, второй катет – проекция гипотенузы на ось волокна l_c. Угол между первым катетом и гипотенузой изменяется в пределах

Выразим длину гипотенузы треугольника g_c через значения диаметра сердцевины ОВ d и угла Θ₁ в виде

Из (5) следует, что длина g_c изменяется от критической величины, соответствующей критическому углу ПВО ${{g}_{{\text{c}}}} = {{g}_{{{{c}_{{{\text{кр}}}}}}}} = {d \mathord{\left/ {\vphantom {d {{\text{cos}}{{\Theta }_{{{\text{кр}}}}}}}} \right. \kern-0em} {{\text{cos}}{{\Theta }_{{{\text{кр}}}}}}}$, до бесконечности. Последнее означает, что ОС свободно распространяется в сердцевине параллельно границам раздела двух сред, не касаясь граничных слоев. Из теории цепей известно, что в однородном участке линии без потерь могут распространяться сигналы с любыми длинами волн, при этом количество укладываемых четвертьволновых отрезков на участке звена зависит от длины волны сигнала

Необходимо особо выделить случай N_λ/4= 1, когда на длине g_c укладывается только один четвертьволновый отрезок с частотой, равной

В таком звене при N_λ/4= 1 длина участка в сотни (тысячи) раз длиннее средней длины волны полосы прозрачности звена ОВ и, следовательно, частота f_с будет во столько же раз меньше средней частоты звена ОВ.

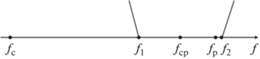
На рис. 4 показано расположение характерных частот звена ОВ: граничные частоты заданной ППр звена ОВ (f₁ и f₂), частота участка l_с ОВ f_с, частота наведенного резонатора f_р и средняя частота ППр f_ср. Указанное несимметричное расположение характерных частот является особенностью звена ОВ, и при построении его модели эта особенность должна быть учтена.

2. МОДЕЛИРОВАНИЕ ОПТИЧЕСКОГО ВОЛОКНА НА ОСНОВЕ ФАЗОКОНТУРНЫХ СХЕМ ЗАМЕЩЕНИЯ

В данной работе теория и расчет ОГС основаны на общем подходе к структурам, как к цепям с распределенными параметрами, состоящими из отрезков передающих линий. Так как для ОВ характерен шлейфный способ соединения резонатора со связкой, то оно относится к определенному типу ОГС – ОМШФ [6, 14].

Основой моделирования является установление условий, при которых существует подобие между оригиналом и моделью. Определенные явления оригинала и модели считаются подобными, если они описываются одинаковыми по форме уравнениями.

Рассмотрим уравнения передачи оригинала – отрезка электрической линии без потерь (рис. 5б) на оси частот распределенных систем f. Обобщенная матрица передачи для нее имеет вид [15–18]

где ω = βl = πf/2f₀ – волновая длина отрезка линии; β = 2π/λ = 2πf/v – коэффициент фазы отрезка линии; v – скорость распространения волны в линии; λ – длина волны в линии; f₀ – первая резонансная частота отрезка линии при длине l = λ₀/4; ρ – нормированное волновое сопротивление линии без потерь.

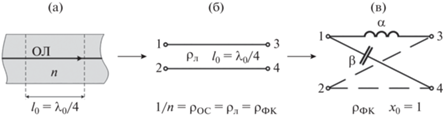
На резонансной частоте f₀ входное сопротивление четвертьволнового отрезка (λ/4-отрезка) линии при нагрузочном сопротивлении W_н = 0 (короткое замыкание отрезка) равно бесконечности, а при W_н = ∞ (холостой ход отрезка) – нулю.

Аналогичными свойствами на оси частот сосредоточенных систем x = f/f₀ обладает фазовый контур первого порядка – ФК1П (рис. 5в) [6, 19]. Коэффициенты обобщенной матрицы ФК1П выражаются через сопротивления его плеч Z_a и Z_b:

где Z_a = jxa – индуктивное сопротивление продольного плеча; Z_b = 1/jxβ – емкостное сопротивление поперечного плеча; α – нормированная индуктивность ФК1П; β – нормированная емкость ФК1П; x₀ = 1/(αβ)^1/2 – резонансная и антирезонансная частоты на оси частот x систем с сосредоточенными параметрами ФК1П при сопротивлениях нагрузки соответственно Z_H = ∞ и Z_H = 0; ρ' = = (αβ)^1/2 – нормированное волновое сопротивление ФК1П, без потерь. Из равенства матриц (8) и (9) [6, 19]

следуют соотношения

откуда определяются прямое и обратное преобразования частоты ФК1П и волновой длины отрезка линии:

Следовательно, при изменении частоты x от 0 до ∞ фазовый контур как модель повторяет частотные характеристики отрезка линии как оригинала, если переменная волновая длина ω изменяется при этом от 0 до π.

Рассмотрим оптический слой (рис. 5а). Его матрица передачи, матрица Абеля [6, 14], имеет вид

Сравнение матриц передачи отрезка линии, ФК1П и оптического слоя обнаруживает их идентичность, которая дает основание сделать вывод о том, что ОГС относятся к классу волновых аналоговых фильтров (ВАФ). Следовательно, оптический слой толщиной l = λ₀/4 может быть представлен моделью в виде четвертьволнового отрезка двухпроводной электрической линии с распределенными элементами и моделью в виде ФК1П с сосредоточенными элементами. Это означает, что дальнейшее рассмотрение принципов построения ОВ в виде ОГС можно заменить рассмотрением принципов построения фильтров на фазовых контурах (ФФК) или ВАФ. Все результаты исследований будут справедливы для всего класса ВАФ и для их общей модели ФФК.

Одними из основных расчетных параметров оригинала (отрезка линии) и его модели (ФК1П) являются текущие частоты оригинала f и нормированной модели x, связанные между собой соотношением

где x₀ = 1 – нормированная резонансная частота модели, f₀ – первая резонансная частота оригинала.

Вторым основным расчетным параметром является нормированное значение волнового сопротивления отрезка линии ρ_л и равное ему значение волнового сопротивления ФК1П ρ_ФК, т.е.

Так как в ОВ и слоях магнитная проницаемость равна единице (μ = 1), то в качестве волнового параметра в них принят показатель преломления, выражаемый через значение диэлектрической проницаемости материала ε или через нормированное значение волнового сопротивления линии ρ_л.

Таким образом, используя метод моделирования, можно перевести задачу синтеза ВАФ в области частот f (0 < f < 2f₀) в задачу синтеза его модели – ФФК в области частот x (0 < x < ∞). Решение задачи синтеза ФФК рассматривается в [6, 14, 19] для некоторых видов топологий ФФК, совпадающих с топологией ОМШФ. Там же показано, что с помощью определенных преобразований частоты требования к частотной характеристике затухания LC-ФФК пересчитываются в требования к низкочастотному (НЧ) αβ‑фильтру – НЧ-прототипу с текущей частотой η и резонансной частотой ${{{{\eta }}}_{0}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{\alpha \beta }}} }}} \right. \kern-0em} {\sqrt {{{\alpha \beta }}} }}$. В соответствии с алгоритмом

В современной теории и практике проектирования фильтров нижних частот существуют фундаментально разработанные многочисленные аналитические методы анализа, синтеза, преобразования и оптимизации схем НЧ-прототипов с различными частотными характеристиками: Чебышёва, Баттерворта, Лежандра, Бесселя и др. [15–18, 21]. Метод моделирования позволяет полностью использовать весь арсенал наработанных методов при решении задач синтеза ОМШФ и, таким образом, сложнейшие задачи синтеза ОМШФ могут быть точно решены методами общей теории фильтров и теории цепей. По найденным требованиям к частотным характеристикам НЧ-прототипа определяются количество элементов в схеме и их значения. Значения элементов НЧ-прототипа с применением обратных преобразований частоты пересчитываются в значения вторичных параметров ВАФ, знание которых позволяет перейти к конструктивному расчету элементов ВАФ с учетом используемых в них видов колебаний в соответствии с алгоритмом:

Таким образом, ФК1П является моделью оптического слоя толщиной l = λ₀/4. Теперь необходимо определить модель участка сдвига Гуса–Хенхена для режима ПВО. В случае превышения падающего на границу раздела сред ОС критического значения ПВО он разделяется на преломленный и отраженный. На границе двух сред три луча соединены в один узел. Заменим каждый участок лучей схемами многозвенных фазоконтурных цепочек для параллельного соединения (рис. 6а) и для последовательного соединения (рис. 6б). Вариант последовательного соединения выходов трех фазоконтурных четырехполюсников (ФЧП) представляет особый интерес для построения модели резонатора.

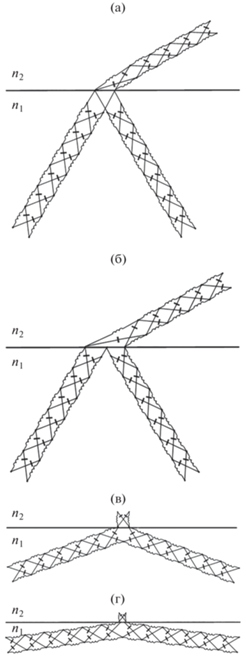
При Θ₁ = Θ₂ угол равен π/2, и тогда преломленный ФЧП заменяется двухполюсником с одним разомкнутым ФК1П, включенным только в одну ветвь. Необходимое соединение падающей и отраженной ФЧП происходит через неполный четырехполюсник с разомкнутым ФК1П в одной ветви, как это показано на рис. 6в. Таким образом, моделью сдвига Гуса–Хенхена является ФК1П в режиме двухполюсника с холостым ходом, который в цепи каскадно включенных ФЧП является резонатором.

Далее, при увеличении угла падения ОС на границу раздела сред величина сдвига Гуса–Хенхена уменьшается, что объясняется увеличением резонансной частоты ФК1П, которая в пределе переходит в частоту х = ∞, и уменьшением его волнового сопротивления (рис. 6г).

Для удобства моделирования ОВ при разбиении его на звенья необходимо иметь резонаторы по краям каждого из звеньев, поэтому модель сдвига Гуса–Хенхена, ФК1П в режиме двухполюсника с холостым ходом, необходимо разбить на два последовательно включенных ФК1П. При этом волновое сопротивление каждого из двух таких ФК1П будет в два раза меньше изначального. Порядок этого преобразования приведен на рис. 7.

Для удобства дальнейшего моделирования ОВ разделим резонатор на два последовательно включенных ФК1П. Каждый такой резонатор моделирует половину сдвига Гуса–Хенхена с волновым сопротивлением, равным половине волнового сопротивления модели полного сдвига Гуса–Хенхена. Тогда модель звена ОВ будет состоять из трехэлементного звена ФФК (рис. 8).

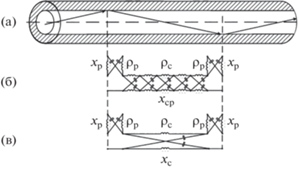
1. ФК1П в режиме холостого хода, т.е. четырехполюсник с разомкнутым выходом, включенный в последовательную ветвь каскадно включенных ФК1П – модели участка ОВ длиной l_о1, в котором ОС распространяется в оболочке ОВ при первом ПВО, составляющего половину сдвига Гуса–Хенхена, перед прямолинейным распространением оптического луча в сердцевине.

2. Цепи N_λ/4 каскадно-включенных ФК1П – модели участка ОВ, в котором ОС прямолинейно распространяется в сердцевине ОВ между первым и вторым явлениями ПВО (l_с).

3. ФК1П в режиме холостого хода, т.е. с разомкнутым выходом, включенный в последовательную ветвь каскадно-включенных ФК1П – модели участка ОВ длиной l_о2, в котором ОС распространяется в оболочке ОВ при втором ПВО, составляющего половину сдвига Гуса–Хенхена, после прямолинейного распространения ОС в сердцевине.

Модель следующего звена ОВ начинается снова неполным ФЧП‑резонатором, продолжается цепочкой ФЧП‑связкой и заканчивается неполным четырехполюсником-резонатором. Окончательная модель многозвенного ОВ представлена схемой многозвенного фильтра на фазовых контурах шлейфного типа со связками из N ФК1П (ФФК-N-Ш) (рис. 9).

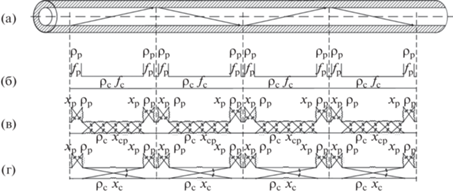
Для этих фильтров в [6, 14, 19, 20] предложена следующая терминология: резонатор (двухполюсник) с волновым сопротивлением ρ_р и резонансной частотой x_р, связка с количеством ФК1П, равным N, и волновым сопротивлением ρ_с, коэффициент отношения волновых сопротивлений соседних связки и резонатора

Фильтры на фазовых контурах относятся к классу электрических цепей с сосредоточенными элементами; цепи выполняют роль моста, соединяющего теорию и расчет фильтров на сосредоточенных элементах (ФСЭ) и ВАФ на отрезках передающих линий (см. рис. 9), к которым по признаку избирательности можно отнести и ОВ. Принадлежность ФФК к классу ФСЭ позволяет воспользоваться соответствующими преобразованиями частоты для пересчета его характеристик в характеристики фундаментально изученных типов LC-фильтров и свести, таким образом, задачу синтеза ВАФ к задаче аналитического синтеза соответствующего известного НЧ- или полосового LC-прототипа.

ЗАКЛЮЧЕНИЕ

Разработанная математическая модель волокна в отличие от известных построена на основе фазоконтурных схем замещения и позволяет установить взаимозависимости параметров материалов, геометрических параметров и параметров передачи ОВ. Представленный подход к моделированию ОВ за счет последовательных и обоснованных преобразований и формирования структуры модели позволяет сделать принципиальное обобщение: ОВ, по физической сущности модели, является распределенным фильтром на отрезках передающих линий и относится к классу волновых аналоговых гетероструктур. Таким образом, применение положений теории цепей получает расширение на моделирование оптических направляющих систем с рассредоточенными элементами, что позволяет аналитически, с применением апробированных на практике научных методов и методик, решать задачи расчета параметров волокна в прямой и обратной постановке.

Практическое применении представленного подхода требует решения ряда частных задач: определение типа ОМШФ, к которому относятся модель ОВ, и типа его характеристики затухания; апробация разработанной модели ОВ путем сравнения расчетных характеристик с характеристиками производимых волокон.