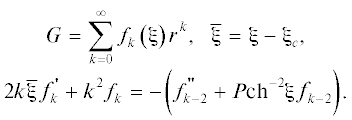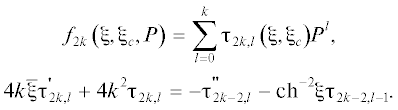Радиотехника и электроника, 2022, T. 67, № 7, стр. 693-703
Формирование плотных электронных пучков с прямой осью и произвольным сечением
В. А. Сыровой *
ВЭИ – филиал ФГУП “РФЯЦ – ВНИИТФ им. академ. Е.И. Забабахина”
111250 Москва, ул. Красноказарменная, 12, Российская Федерация
* E-mail: red@cplire.ru
Поступила в редакцию 27.10.2021
После доработки 27.10.2021
Принята к публикации 18.11.2021
- EDN: CQZQYR
- DOI: 10.31857/S0033849422070130
Аннотация
Рассмотрены алгоритмы решения трехмерных задач для пучков с прямой осью и произвольным сечением как в точной постановке, так и в рамках параксиального описания. Проанализированы варианты эллиптических сечений и сечений в виде скругленного прямоугольника.
ВВЕДЕНИЕ
Технические устройства с пучком прямоугольного сечения существовали задолго до того, как актуальным стал вопрос теоретического рассмотрения подобных проблем. Ряд диафрагм соответствующей формы решал эту задачу при малой мощности пучка и несущественного с практической точки зрения токоперехвата. В последние десятилетия потоки с прямоугольным или эллиптическим сечением широко используются в мощных приборах СВЧ, а стремление к более высокочастотному диапазону, связанному с миниатюризацией конструкций, требует проведения математического моделирования с высокой точностью. Лобовые численные методы исследования не обеспечивают адекватного описания сингулярных прикатодных зон при эмиссии в $\rho $- и Т-режимах. Существующие теоретические модели трехмерных пучков могут давать либо полное решение проблемы, либо поставлять локальную информацию о поведении формирующих электродов вблизи катода, либо, наконец, определять качественную картину электрического поля в более сложных случаях.
Цель работы – формулировка современного состояния теории формирования трехмерных электронных потоков в наиболее часто встречающемся варианте пучков с прямой осью.
1. МЕТОД РИМАНА
Решение проблемы формирования как в двумерном, так и в трехмерном случаях сводится к эллиптическому уравнению в частных производных второго порядка вида
(1)
$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{y}^{2}}}} + A\frac{{\partial \Phi }}{{\partial x}} + B\frac{{\partial \Phi }}{{\partial y}} + C\Phi = F$с коэффициентами, зависящими от x, y.
Метод Римана, разработанный для уравнений гиперболического типа с действительными характеристиками, модифицирован для эллиптических уравнений и излагается в монографии [1]. Если начальные условия ${{\Phi }_{e}}$ и ${{\left( {{{\partial \Phi } \mathord{\left/ {\vphantom {{\partial \Phi } {\partial n}}} \right. \kern-0em} {\partial n}}} \right)}_{e}}$ известны на линии $\Gamma $
и G – функция Римана, удовлетворяющая сопряженному уравнению и некоторым условиям на характеристиках, проходящих через точку наблюдения С, то решение задачи описывается выражением
(3)
$\begin{gathered} \Phi = \operatorname{Re} \left[ {{{{\left( {\Phi G} \right)}}_{P}} + \frac{{^{{}}}}{{_{{_{{}}}}}}} \right. \\ + \,\,\int\limits_0^v {{{{\left( {G\frac{{\partial \Phi }}{{\partial v}} - \Phi \frac{{\partial G}}{{\partial v}} + 4\Phi G\operatorname{Im} a} \right)}}_{e}}d{{\xi }}} + \\ \left. { + \,\,4\int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {Gfd{{\xi }}} } \right]. \\ \end{gathered} $Функции на Г во внеинтегральном члене и одинарном интеграле, зависящие от u, испытали аналитическое продолжение $u \to u + iv$, $u \to u + i{{\xi }}$ соответственно; в двойном интеграле функции от u, v подвергнуты следующей трансформации: $u \to u + i{{\xi }}$, $v \to \eta $. Двойной интеграл в (3) не вносит вклад в потенциал и нормальную производную на Г.
“Распрямляющее” отображение с однозначной сеткой ортогональных криволинейных координат u, v с равными коэффициентами Ляме ${{h}_{1}} = {{h}_{2}} = h$, переводящее контур Г в прямую $v = 0$, определено формулами
(4)
$\begin{gathered} x + iy = {{x}_{e}}\left( w \right) + i{{y}_{e}}\left( w \right),\,\,\,\,w = u + iv, \\ w* = u - iv;\,\,\,\,{{{{\alpha }}}_{e}} = {{d{{x}_{e}}} \mathord{\left/ {\vphantom {{d{{x}_{e}}} {du}}} \right. \kern-0em} {du}},\,\,\,\,{{{{\beta }}}_{e}} = {{d{{y}_{e}}} \mathord{\left/ {\vphantom {{d{{y}_{e}}} {du}}} \right. \kern-0em} {du}}. \\ \end{gathered} $Функции a, f в (3) связаны с коэффициентами уравнения (1) соотношениями
(5)
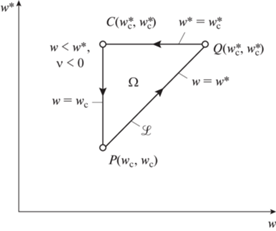
$\begin{gathered} a = \frac{1}{4}{{h}^{2}}\left( {A + iB} \right)\left( {\frac{{\partial u}}{{\partial x}} + i\frac{{\partial v}}{{\partial x}}} \right),\,\,\,\,f = \frac{1}{4}{{h}^{2}}F, \\ {{h}^{2}} = {{\left[ {{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {v}}}{{\partial x}}} \right)}}^{2}}} \right]}^{{ - 1}}} = {{\left( {\frac{{\partial x}}{{\partial u}}} \right)}^{2}} + {{\left( {\frac{{\partial y}}{{\partial u}}} \right)}^{2}}. \\ \end{gathered} $Решение строится в характеристическом треугольнике, изображенном на рис. 1. Для гиперболических уравнений он определяет ограниченную область, в то время как в случае уравнений с мнимыми характеристиками решение “выплескивается” в полупространство – внешность границы пучка.
2. ЦИЛИНДРИЧЕСКИЙ ПУЧОК С ПРОИЗВОЛЬНЫМ СЕЧЕНИЕМ
Эталонные задачи. Необходимо найти решение уравнения Лапласа
(6)
$\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{z}^{2}}}} = 0$для цилиндрического пучка с определяемым формулами (2) контуром Г поперечного сечения и условиями на границе вида
(7)
${{{{\varphi }}}_{e}} = {{z}^{\nu }},\,\,\,\,{{{{\varphi }}}_{{ve}}} \equiv {{\left( {{{\partial {{\varphi }}} \mathord{\left/ {\vphantom {{\partial {{\varphi }}} {\partial v}}} \right. \kern-0em} {\partial v}}} \right)}_{e}} = 0$с дробным показателем степени $\nu $.
Выполнение интегрального преобразования
(8)
${{\varphi }}\left( {x,y,z} \right) = \int\limits_{\left( 0 \right)}^\infty {\Phi \left( {x,y;p} \right)\exp \left( { - pz} \right)dp} $с контурным интегралом в комплексной плоскости параметра р (обход особенности в нуле обозначен символом (0)) приводит уравнения для функций Ф, G к уравнению Гельмгольца с соответствующими начальными данными для Ф:
(9)
$\begin{gathered} \frac{{{{\partial }^{2}}\Phi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{y}^{2}}}} + {{p}^{2}}\Phi = 0, \\ {{\Phi }_{e}} = {{{{p}^{{ - \nu - 1}}}} \mathord{\left/ {\vphantom {{{{p}^{{ - \nu - 1}}}} {\Gamma \left( { - \nu } \right)}}} \right. \kern-0em} {\Gamma \left( { - \nu } \right)}},\,\,\,\,{{\Phi }_{{ve}}} = 0, \\ \end{gathered} $где $\Gamma \left( { - \nu } \right)$ – гамма-функция.
Функцией Римана оказывается функция Бесселя нулевого порядка:
(10)
$G = {{J}_{0}}\left( {pr} \right),\,\,\,\,{{r}^{2}} = {{\left( {x - {{x}_{c}}} \right)}^{2}} + {{\left( {y - {{y}_{c}}} \right)}^{2}},$причем r имеет смысл расстояния от произвольной точки $\left( {x,y} \right)$ до точки наблюдения $\left( {{{x}_{c}},{{y}_{c}}} \right)$.
Применение формулы Римана (3) и использование известного контурного интеграла Липшица–Ганкеля дает решение задачи в форме, включающей определенный интеграл:
(11)
$\begin{gathered} {{\varphi }}\left( {x,y,z} \right) = {{z}^{\nu }} + \frac{{\nu \left( {1 - \nu } \right)}}{2} \times \\ \times \,\,{\text{Re}}\int\limits_0^v {\frac{{\left( {{{x}_{e}} - x} \right){{{{\beta }}}_{e}} - \left( {{{y}_{e}} - y} \right){{{{\alpha }}}_{e}}}}{{{{{({{z}^{2}} + r_{e}^{2})}}^{{1 - {\nu \mathord{\left/ {\vphantom {\nu 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,F\left( {\frac{{2 - \nu }}{2},\frac{{1 + \nu }}{2};2;\frac{{r_{e}^{2}}}{{{{z}^{2}} + r_{e}^{2}}}} \right)d{{\xi }}, \\ \end{gathered} $где F – гипергеометрическая функция Гаусса.
Описанный выше алгоритм не может быть использован при целочисленном значении $\nu = n$. Для условий на Г вида
решение имеет полиномиальную структуру
(13)
$\begin{gathered} {{\varphi }} = {{\Phi }_{0}} + {{\Phi }_{2}}{{z}^{2}} + ... + {{\Phi }_{{2k - 2}}}{{z}^{{2k - 2}}} + {{a}_{{2k}}}{{z}^{{2k}}}, \\ n = 2k; \\ {{\varphi }} = {{\Phi }_{1}} + {{\Phi }_{3}}{{z}^{3}} + ... + {{\Phi }_{{2k - 1}}}{{z}^{{2k - 1}}} + {{a}_{{2k + 1}}}{{z}^{{2k + 1}}}, \\ n = 2k + 1. \\ \end{gathered} $Функция Римана для этой задачи равна единице $\left( {G = 1} \right)$, а двойной интеграл в формуле Римана (3) удовлетворяет нужным условиям на Г:
(14)
$\begin{gathered} {{\Phi }_{{n - 2l}}} = - \left( {n - 2l + 2} \right)\left( {n - 2l + 1} \right) \times \\ \times \,\,\operatorname{Re} \int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {{{h}^{2}}{{\Phi }_{{n - 2l + 2}}}d{{\xi }}} . \\ \end{gathered} $Функции ${{\Phi }_{m}}$ вычисляются в порядке убывания индекса при ${{\Phi }_{n}} = {{a}_{n}}$.
Эмиссия в $\rho $-режиме. Решению Чайлда–Лэнгмюра для плоского диода соответствует значение $\nu = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$. В результате формула (11) принимает вид [2]
(15)
$\begin{gathered} {{\varphi }}\left( {x,y,z} \right) = {{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} - \\ - \,\,\frac{2}{9}{\text{Re}}\int\limits_0^v {\frac{{\left( {{{x}_{e}} - x} \right){{{{\beta }}}_{e}} - \left( {{{y}_{e}} - y} \right){{{{\alpha }}}_{e}}}}{{{{{\left( {{{z}^{2}} + r_{e}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \times \\ \times \,\,F\left( {\frac{1}{3},\frac{7}{6};2;\frac{{r_{e}^{2}}}{{{{z}^{2}} + r_{e}^{2}}}} \right)d{{\xi }}{\text{.}} \\ \end{gathered} $Выражение (15) удобно для изучения структуры решения и выполнения численных расчетов.
Локальное уравнение нулевой эквипотенциали в плоскости $\left( {X,z} \right)$ (Х – нормаль к Г), построенное на основе (15), описывается формулой
(16)
$\begin{gathered} X = \left( {{\text{tg}}\frac{{3{{\pi }}}}{8}} \right)z + \frac{9}{{56}}\left( {{{{\sin }}^{{ - 2}}}\frac{{{\pi }}}{8}} \right){{k}_{\Gamma }}{{z}^{2}} - \\ - \,\,\frac{{153}}{{6272\sqrt 2 }}\left( {{{{\sin }}^{{ - 4}}}\frac{{{\pi }}}{8}} \right)k_{\Gamma }^{2}{{z}^{3}}, \\ \end{gathered} $где ${{k}_{\Gamma }}$ – кривизна контура.
Эмиссия в Т-режиме. Потенциал в плоском диоде в соответствующих нормировках может быть представлен в универсальной параметрической форме [3]:
(17)
$z = \frac{1}{2}{{{{\tau }}}^{2}} + \frac{1}{6}{{{{\tau }}}^{3}},\,\,\,\,2{{\varphi }} = {{\left( {\tau + \frac{1}{2}{{{{\tau }}}^{2}}} \right)}^{2}}.$В явном виде функция ${{\varphi }}\left( z \right)$ определена рядом по полуцелым степеням z:
(18)
$\varphi = z + {{\varphi }_{3}}{{z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + {{\varphi }_{4}}{{z}^{2}} + {{\varphi }_{5}}{{z}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}} + ....$При сохранении коэффициента ${{{{\varphi }}}_{7}}$ в (18) и $z = 1$, ${{\tau }} = 1.196$ точное значение потенциала ${{{{\varphi }}}_{{{\text{ex}}}}} = 1.826$ из (17) отличается от приближенного ${{{{\varphi }}}_{{{\text{ap}}}}} = 1.813$ из (18) на 0.7%.
Дробные степени в формуле (18) допускают использование алгоритма (11), а для слагаемых с целочисленными степенями z справедливы соотношения (13). В результате суммирования на границе пучка воспроизводится ряд (18), который эквивалентен соотношениям (17) и может быть ими заменен, что приводит к выполнению точных условий на поверхности произвольного цилиндра.
Решение в виде двойного интеграла при эмиссии в $\rho $-режиме. Воспользуемся предложением, высказанным В.Т. Овчаровым в [5] для осесимметричных параксиальных пучков, и представим решение уравнения (6) в виде
(${{{{\varphi }}}_{i}}$ – потенциал в потоке), отказавшись от требования параксиальности. Функция S при этом удовлетворяет уравнению Пуассона
(20)
$\frac{{{{\partial }^{2}}S}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}S}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}S}}{{\partial {{z}^{2}}}} = - {\kern 1pt} \rho ,\,\,\,\,\rho = \frac{4}{9}{{z}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}$($\rho $ – плотность пространственного заряда) и однородным условиям на границе потока.
Двойной интеграл в (3) определяет новую форму решения для цилиндрической вырезки из плоского диода [6]:
(21)
$\begin{gathered} \varphi = {{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} - \frac{4}{9}\int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {\frac{{{{h}^{2}}\left( {\zeta ,\eta } \right)}}{{{{{\left( {{{z}^{2}} + {{r}^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}F\left( {\frac{1}{3},\frac{1}{6};1;\lambda } \right)} d\xi , \\ \lambda = {{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {\left( {{{z}^{2}} + {{r}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{z}^{2}} + {{r}^{2}}} \right)}},\,\,\,\,{{r}^{2}} = {{\left[ {x\left( {\zeta ,\eta } \right) - x\left( {u,v} \right)} \right]}^{2}} + \\ + \,\,{{\left[ {y\left( {\zeta ,\eta } \right) - y\left( {u,v} \right)} \right]}^{2}}, \\ x + iy = {{x}_{e}}\left( w \right) + i{{y}_{e}}\left( w \right),\,\,\,\,\zeta = u + i\xi . \\ \end{gathered} $3. КОНИЧЕСКИЙ ПУЧОК С ПРОИЗВОЛЬНЫМ СЕЧЕНИЕМ
Перейдем в уравнении Лапласа, записанного в сферических координатах r, $\theta $, $\psi $, к новым переменным ${{\xi }}$, $\eta $, $\psi $:
(22)
$\begin{gathered} \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{\psi }^{2}}}} + \frac{1}{{{\text{c}}{{{\text{h}}}^{2}}{{\xi }}}}\left( {\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{\eta }^{2}}}} + \frac{{\partial {{\varphi }}}}{{\partial \eta }}} \right) = 0, \\ {{\xi }} = \ln {\text{tg}}\frac{\theta }{2},\,\,\,\,\eta = \ln \frac{r}{{{{r}_{0}}}}, \\ \end{gathered} $где ${{r}_{0}}$ – радиус катода. В уравнении (22) на псевдоплоскости ${{\xi }}$, $\psi $ выделен двумерный лапласиан с декартовой метрикой.
Конус с произвольным сечением определен параметрическими уравнениями
(23)
$\begin{gathered} \xi = {{\xi }_{e}}\left( u \right),\,\,\,\,\psi = {{\psi }_{e}}\left( u \right); \\ \xi + i\psi = {{\xi }_{e}}\left( w \right) + i{{\psi }_{e}}\left( w \right),\,\,\,\,w = u + iv, \\ \alpha + i\beta = \xi _{e}^{'}\left( w \right) + i\psi _{e}^{'}\left( w \right),\,\,\,\,{{h}^{2}} = {{\alpha }^{2}} + {{\beta }^{2}}, \\ {{\alpha }_{e}} = \xi _{e}^{'}\left( u \right),\,\,\,\,\,{{\beta }_{e}} = \psi _{e}^{'}\left( u \right). \\ \end{gathered} $После выполнения интегрального преобразования, аналогичного (8), функции Ф, G удовлетворяют одному уравнению
(24)
$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{\psi }^{2}}}} + \frac{P}{{{\text{c}}{{{\text{h}}}^{2}}{{\xi }}}}\Phi = 0,\,\,\,\,P = p\left( {p - 1} \right),$однако выразить G через известные специальные функции не удается. В работе [7] построен асимптотический ряд для функции Римана, нулевое и первое приближение которого определены формулами
(25)
$\begin{gathered} G = {{J}_{0}}\left( \lambda \right) + \frac{1}{2}\left[ {\frac{1}{{{\text{ch}}{{\xi }_{c}}}}r + \lambda {\text{th}}{{\xi }_{c}}\left( {\xi - {{\xi }_{c}}} \right)} \right]{{J}_{1}}\left( \lambda \right) + ..., \\ {{\lambda }} = {{pr} \mathord{\left/ {\vphantom {{pr} {{\text{ch}}{{{{\xi }}}_{c}}}}} \right. \kern-0em} {{\text{ch}}{{{{\xi }}}_{c}}}},\,\,\,\,{{r}^{2}} = {{\left( {{{\xi }} - {{{{\xi }}}_{c}}} \right)}^{2}} + {{\left( {\psi - {{\psi }_{c}}} \right)}^{2}}. \\ \end{gathered} $Этапы построения сводятся к следующему. Будем искать решение в виде ряда
Требование конечности функции G при $r = 0$ выполняется для разложения по четным степеням r, причем функции ${{f}_{{2k}}}$ оказываются полиномами степени k по параметру Р:
Коэффициенты ${{{{\tau }}}_{{2k,l}}}$ представим в виде разложений
(28)
${{{{\tau }}}_{{2k,l}}}\left( {{{\xi }},{{{{\xi }}}_{c}}} \right) = \sum\limits_{s = 0}^\infty {{{{{\tau }}}_{{2k,l,s}}}\left( {{{{{\xi }}}_{c}}} \right){{{{{\bar {\xi }}}}}^{s}}} .$Подстановка (28) в уравнение (27) позволяет получить рекуррентные соотношения для коэффициентов бесконечных рядов, суммирование которых приводит к функциям Бесселя в выражении (25) для функции Римана. В результате появляется возможность использовать интеграл Липшица–Ганкеля для выполнения обратного интегрального преобразования, приводящего решение исходной задачи к виду, аналогичному (11).
Потенциал ${{{{\varphi }}}_{i}}$ в потоке описывается хорошо сходящимся рядом по $\eta = \ln r$ [8] с первым членом ${{\eta }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$. Как и в случае цилиндра при эмиссии в Т-режиме, первые слагаемые в формуле для ${{\varphi }}$ после суммирования могут быть заменены известным точным решением для сферического диода в параметрической форме с функциями Бесселя [9].
Кривизна нулевой эквипотенциали ${{\varphi }} = 0$ в плоскости, содержащей нормаль к контуру, определена формулой
(29)
$k = \frac{2}{{{{r}_{0}}}}\cos \frac{{{\pi }}}{8}\left[ {\frac{{17}}{{30}} + \left( {\frac{9}{{56}}{\text{tg}}\frac{{{\pi }}}{8} - \frac{1}{{2\sqrt 2 }}} \right){{k}_{\Gamma }}} \right].$Угол 67.5° наклона нулевой эквипотенциали к границе пучка оказывается универсальной величиной при эмиссии в $\rho $-режиме и связан вне зависимости от конфигурации и физических характеристик потока с аналитическим продолжением члена ${{\eta }^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$.
Решение задачи о формировании биполярных электронно-ионных потоков в виде цилиндра и конуса с произвольными сечениями представлено в работах [10, 11].
4. СЕЧЕНИЕ В ВИДЕ СКРУГЛЕННОГО ПРЯМОУГОЛЬНИКА
В работе [12] сформулирован способ построения сечения, которое представляет собой скругленный прямоугольник с гладким контуром, являющимся координатной линией $v = 0$ системы u, v конформного отображения “повышенной гладкости”. Алгоритм состоит в разложении в ряд Лорана подынтегрального выражения в интеграле Кристоффеля–Шварца, осуществляющего отображение внешности прямоугольника на внешность единичного круга, и почленном интегрировании полученного выражения с удержанием n членов:
(30)
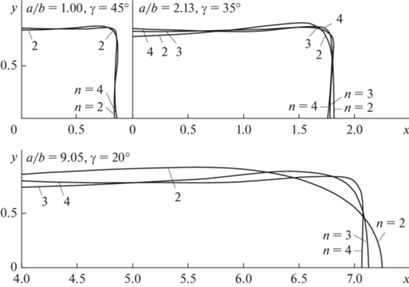
$\begin{gathered} x + iy = c\left( {t + \sum\limits_{k = 1}^n {{{c}_{k}}{{t}^{{1 - 2k}}}} } \right),\,\,\,\,t = \exp \left( { - v + iu} \right), \\ {{c}_{1}} = \cos 2{{\gamma }},\,\,\,\,{{c}_{2}} = - \frac{1}{6}\left( {1 - c_{1}^{2}} \right), \\ {{c}_{3}} = - \frac{1}{{10}}{{c}_{1}}\left( {1 - c_{1}^{2}} \right),\,\,\,\,{{c}_{4}} = \frac{1}{{56}}\left( {1 - 6c_{1}^{2} + 5c_{1}^{4}} \right). \\ \end{gathered} $Здесь с – масштабный множитель; ${{\gamma }}$ – параметр, определяющий отношение сторон ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ прямоугольника. Контур приемлемой конфигурации [12] с ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} = 1,\,{\kern 1pt} 2,\,{\kern 1pt} 10$ получается при n = 2, 3, 4 соответственно (рис. 2).
На рис. 3 представлена картина поля в диагональном сечении скругленного квадрата [12], рассчитанная по формуле (14). Поведение эквипотенциалей соответствует картине в плоской пушке Дж. Р. Пирса в области порядка радиуса скругления угла с последующим поворотом кривых к катоду. Рисунок 4 иллюстрирует конфигурацию кривых ${{\varphi }} = {\text{const}}$ в поперечных сечениях $z = {\text{const}}$, которая в качественном отношении остается той же при ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}\sim 10$. Исследование скругленных прямоугольных контуров на сфере выполнено в работе [13]. Поскольку уравнение (22) включает двумерный лапласиан по ${{\xi }}$, $\psi $ с декартовой метрикой, аппарат комплексных переменных и конформных отображений может быть использован и на псевдоплоскости ${{\xi }}$, $\psi $.
Рис. 3.
Эквипотенциальные кривые в диагональном сечении скругленного квадрата при n = 2 (сплошные кривые) и n = 4 (штриховые).
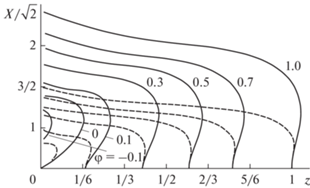
Рис. 4.
Эквипотенциальные кривые для скругленного квадрата γ = 45° при n = 2 в поперечных сечениях z = = const: z = 0.2 (а), 0.9 (б).
Для контура ${{\xi }} = {{{{\xi }}}_{e}}\left( u \right)$, $\psi = {{\psi }_{e}}\left( u \right)$ имеем
(31)
$\begin{gathered} {{\bar {\xi }}} + i\psi = c\left( {t + \sum\limits_{k = 1}^n {{{c}_{k}}{{t}^{{1 - 2k}}}} } \right),\,\,\,\,t = \exp \left( { - v + iu} \right), \\ {{\bar {\xi }}} = {{\xi }} - {{{{\xi }}}_{*}},\,\,\,\,{{{{\xi }}}_{*}} = \frac{1}{2}\left( {{{{{\xi }}}_{1}} + {{{{\xi }}}_{2}}} \right) \\ \end{gathered} $с теми же коэффициентами, что и в (30).
“Прямоугольник” на сфере единичного радиуса образован пересечением линий $\theta = {{\theta }_{1}}$, $\theta = {{\theta }_{2}}$, $\psi = \pm {{\psi }_{0}}$, причем переменные $\theta $, $\psi $ играют роль полярного радиуса и азимута. Длины сторон описываются формулами
На рис. 5 изображен “квадрат” ${{\theta }_{1}} = 30^\circ $, ${{\theta }_{2}} = 60^\circ $, ${{\psi }_{0}} = 22^\circ $, нулевая аппроксимация “кругом” ${{{{\bar {\xi }}}}^{2}} + $ $ + \,\,{{\psi }^{2}} = {\text{const}}$ и скорректированный вариант контура при n = 4. Истинная окружность диаметром, равным размеру сечения $\psi = 0$, проведена для сравнения с нулевым приближением. Растяжение контура 3 в 1.206 раз дает приемлемую аппроксимацию исходной кривой, соответствие с которой может быть увеличено при бòльших значениях n.
5. ЭЛЛИПТИЧЕСКОЕ СЕЧЕНИЕ
Эллипс является нулевой аппроксимацией прямоугольного контура. В фундаментальной работе теории формирования [14] метод разделения переменных использован в двумерных задачах с пучком в виде кругового цилиндра и конуса при эмиссии в ${{\rho }}$-режиме. Решение является точным только в формальном смысле, так как выражено через контурный интеграл в комплексной плоскости параметра р, допускающий исключительно асимптотические оценки [14].
В работе [15] подход [14] распространен на случай эллиптического сечения, причем эллиптическая цилиндрическая система ξ, η, z определена формулами
(33)
$x = \sqrt {{{b}^{2}} - {{a}^{2}}} {\text{sh}}{\kern 1pt} \xi \sin \eta {\kern 1pt} ,\,\,\,\,y = \sqrt {{{b}^{2}} - {{a}^{2}}} {\text{ch}}{\kern 1pt} \xi \cos \eta {\kern 1pt} .$Начальные данные (7) не зависят от $\eta $, поэтому автор искал решение ${{\varphi }} = {{\varphi }}\left( {{{\xi }},{\kern 1pt} \,z} \right)$ в форме контурного интеграла с интеграндом в виде бесконечного ряда по функциям Матье $\mathcal{M}_{{2m}}^{{\left( j \right)}}\left( {{\xi }} \right)$, описываемым бесконечными рядами из произведений функций Бесселя и Ганкеля. Отсутствие зависимости от $\eta $ привело к изменению угла наклона эквипотенциали ${{\varphi }} = 0$ на контуре вместо постоянного значения ${{3{{\pi }}} \mathord{\left/ {\vphantom {{3{{\pi }}} 8}} \right. \kern-0em} 8}$.
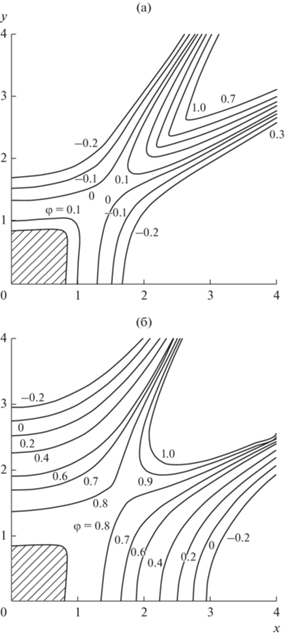
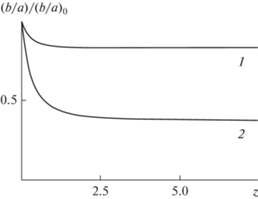
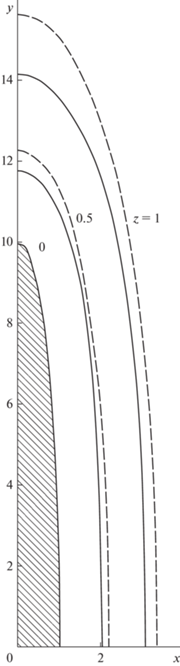
Формула (15) с решением в виде определенного интеграла использована для расчета электродов в случае эллиптического сечения [16]. В плоскостях $z = {\text{const}}$ эквипотенциали представляют собой эллипсоидальные овалы, близкие к эллипсу с соответствующими полуосями. На рис. 6 для ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a} = {\kern 1pt} \,\,10$ координаты эллипса отмечены кружочками. При удалении от границы пучка отношение полуосей ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ эквипотенциали ${{\varphi }} = 0$ быстро стремится к константе, зависящей от значения этого параметра ${{\left( {{b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}} \right)}_{0}}$ на Г и отличной от единицы (рис. 7).
Рис. 6.
Эквипотенциаль $\varphi = 0$ (b/a = 10) для эллиптического сечения в плоскостях z = const; координаты эллипса отмечены кружочками.

Рис. 7.
Отношение полуосей эквипотенциали $\varphi = 0$ для эллиптического цилиндра в зависимости от z при b/a = 1.5 (1) и 10 (2).
В 2005 г. в журнале “Physical Review. Accelerators and Beams” была опубликована статья [17] двух авторов, на 30 лет отставшая от развития теории. В ней исправлена ошибка работы [15] за счет включения в подынтегральное выражение контурного интеграла бесконечного ряда с произведениями радиальных и угловых функций Матье. Это же решение вошло в диссертацию одного из авторов [18].
Чрезвычайно громоздкое по сравнению с [2, 16] решение, как и результаты [14], имеет формальный характер, связанный с отсутствием точного выражения для соответствующих контурных интегралов.
6. ПАРАКСИАЛЬНАЯ МОДЕЛЬ РАСЧЕТА ФОРМИРУЮЩИХ ЭЛЕКТРОДОВ
Узкие пучки. Практические потребности не могут быть закрыты описанными выше электронно-оптическими системами с одномерными электронными потоками в плоском и сферическом диодах. Узкие пространственные пучки произвольного сечения, испытывающего деформацию с ростом продольной координаты z, являются предметом исследования трехмерной параксиальной теории релятивистских потоков во внешнем неоднородном магнитном поле В.Н. Данилова [19] или геометризованной модели электростатических потоков [20].
В работе [21] исследованы возможности, предоставляемые теорией [19] для поперечного сечения пучка, сохраняющего свою ориентацию и меняющегося по закону
Начальная конфигурация сечения ${{\xi }} = {{{{\xi }}}_{e}}\left( u \right)$, η = $ = {{\eta }_{e}}\left( u \right)$ в ${{\rho }}$- или Т-режиме эмиссии является скругленным прямоугольником или эллипсом.
Подобно тому как выше рассматривались фрагменты одномерных потоков с произвольным сечением, аналогичные вырезки могут быть выполнены для плоских течений, описываемых классической параксиальной теорией [3], теорией В.Т. Овчарова [22] или геометризованными моделями [23–28], которые имеют более широкие возможности (произвольная ориентация магнитного поля на катоде). Эволюция контролируемого сечения в этом случае определена формулами
Геометризованная теория основана на новой форме уравнений пучка, записанных в заранее неизвестной системе координат ${{x}^{i}}$, i = 1, 2, 3, которая связана с траекториями (координатные линии ${{x}^{1}}$) или трубками тока (поверхности ${{x}^{2}} = {\text{const}}$). Условия эвклидовости пространства (шесть тождеств Ляме – нелинейные дифференциальные уравнения в частных производных второго порядка относительно элементов метрического тензора ${{g}_{{ik}}}$) дополняют уравнения для физических параметров потока.
Система ${{x}^{i}}$ в общем случае является неортогональной. Для двумерных пучков выполнение условий термоэмиссии обеспечивается локальной неортогональностью системы вблизи сингулярной стартовой поверхности. Уравнения 2D геометризованной теории удалось подвергнуть декомпозиции. Они представлены в виде соотношения на трубке тока для элемента ${{g}_{{22}}}$, которое выглядит как обыкновенное уравнение второго порядка по продольной координате ${{x}^{1}}$ с поперечной координатой ${{x}^{2}}$ в качестве параметра, и системы эволюционных уравнений. Последняя описывает производные по ${{x}^{2}}$ от всех геометрических и физических параметров потока с правыми частями, определяемыми заданной информацией на базовой трубке тока ${{x}^{2}} = 0$:
(36)
${{\partial {{f}_{k}}} \mathord{\left/ {\vphantom {{\partial {{f}_{k}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}} = {{F}_{k}}({{x}^{1}}).$В качестве ${{x}^{1}}$ при ${{x}^{2}} = 0$ может быть использована произвольная функция l – длины дуги образующей трубки тока. Эту модель поэтому удобно называть l-представлением геометризованной теории. В работах [26, 27] построен вариант ${{\varphi }}$‑представления, когда в качестве продольной координаты во всем потоке используется потенциал электрического поля ${{x}^{1}} = {{\varphi }}$. Изменение статуса ${{\varphi }}$ – переход от искомой функции к независимой переменной – приводит к снижению порядка уравнения Пуассона со второго до первого. Соотношение на трубке тока становится нелинейным во всем поле течения в отличие от l-варианта теории, где нелинейность связана с локальной неортогональностью. Тестирование геометризованных моделей на известных точных решениях [30] показало, что использование ${{\varphi }}$-представления может приводить к большей точности приближенного решения.
Построение третьего варианта геометризованной теории (W-представление) [28] связано с потенциальными релятивистскими пучками (отсутствие нормальной компоненты магнитного поля на катоде, W – потенциал обобщенного импульса).
К геометризованной теории примыкают модели пучков с эллиптическим поперечным сечением, рассматриваемых в системе координат, связанной с эллиптическим трубками тока. В работе [31] это потенциальные нерелятивистские потоки с плоской криволинейной осью, а в [32–36] – релятивистские вихревые пучки, для исследования которых алгоритм [31] не пригоден. Модели этого типа представляют собой пример известного в механике жидкости “иррационального приближения” [37], основное свойство которого состоит в невозможности построения цепочки моделей все более высокого порядка. В моделях [31–36] потенциал квадратичен по поперечной координате, но нет возможности уточнения этой зависимости или перехода от эллипса к более сложному контуру.
Общий вид решения. Идею построения параксиального решения, сформулированную в [5] для осесимметричных потоков, которая выражается формулой (19) в предположении, что S является функцией второго порядка малости (${{\partial {{\varphi }}} \mathord{\left/ {\vphantom {{\partial {{\varphi }}} {\partial z}}} \right. \kern-0em} {\partial z}}\sim \varepsilon $), можно использовать при формировании трехмерных потоков. В силу принятых предположений S удовлетворяет двумерному уравнению Пуассона и описывается выражением
(37)
$\begin{gathered} \frac{{{{\partial }^{2}}S}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}S}}{{\partial {{y}^{2}}}} = - {\kern 1pt} {{\rho }}, \\ S = - \operatorname{Re} \int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {{{\rho }}\left( {z,u + i{{\xi }},\eta } \right){\kern 1pt} } {{h}^{2}}\left( {z,u + i{{\xi ,}}\eta } \right)d{{\xi }}. \\ \end{gathered} $Цилиндр и конус с произвольным сечением при эмиссии в ${{\rho }}$-режиме. Формула (37) в случае цилиндра принимает вид [38]
(38)
${{\varphi }} = {{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}} - \frac{4}{9}{{z}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}\operatorname{Re} \int\limits_0^v {d\eta } \int\limits_0^{v - \eta } {{{h}^{2}}\left( {u + i{{\xi }},\eta } \right)} {\kern 1pt} d{{\xi }}{\kern 1pt} .$Функция ${{h}^{2}}\left( {u,v} \right)$ для скругленного прямоугольника определена формулой
(39)
$\begin{gathered} {{c}^{{ - 2}}}{{h}^{2}}\left( {u,v} \right) = \exp \left( { - 2v} \right) - 2{{c}_{1}}\cos 2u + \\ + \,\,\exp \left( {2v} \right)\left( {c_{1}^{2} - 6{{c}_{2}}\cos 4u} \right) + ... \\ \end{gathered} $с сохранением членов с коэффициентом ${{c}_{4}}$.
Интегрирование в формуле (28) для ${{h}^{2}}$ из (39) может быть выполнено в элементарных функциях [38].
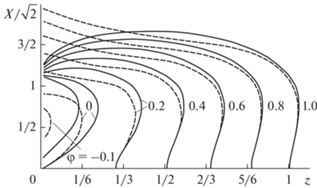
На рис. 8 приведено сравнение точного и параксиального решений для скругленного квадрата в диагональном сечении. Картины близки в качественном отношении, но приближенное решение характеризуется меньшими градиентами в очертании эквипотенциальных поверхностей при $z = {\text{const}}$.
Рис. 8.
Сравнение приближенного (сплошные кривые) и точного (штриховые) решений в диагональном сечении и = 45° скругленного квадрата γ = 45° при n = 2.
Рассмотрение окрестности катода на основании решения (38) приводит к следующему уравнению нулевой эквипотенциали:
(40)
$X = {{{{\alpha }}}_{3}}z + \frac{3}{4}{{k}_{\Gamma }}{{z}^{2}} + \frac{1}{4}{{{{\alpha }}}_{3}}k_{\Gamma }^{2}{{z}^{3}},\,\,\,\,{{{{\alpha }}}_{3}} = {\text{tg}}\vartheta = {3 \mathord{\left/ {\vphantom {3 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}.$Угол наклона $\vartheta \approx 64.76^\circ $ при параксиальном описании пучков в связанной с геометрией потока системе координат имеет столь же универсальный характер, как угол 67.5° в точном решении задачи. Вычисленные на основании (16), (40) значения кривизны и ее производной линии ${{\varphi }} = 0$ на границе пучка различаются на 5.7 и 19.5% соответственно.
Биполярный цилиндрический пучок с сечением в виде скругленного прямоугольника рассмотрен в работе [39].
Сравнение приближенного и точного решений для эллиптического контура приведено на рис. 9. Параксиальное решение для эллиптического цилиндра ранее построено в работе [31].
Рис. 9.
Сравнение приближенного (сплошные кривые) и точного (штриховые) решений в поперечных сечениях для эллиптического пучка b/a = 10, φ = 0.
Для конуса с произвольным сечением функция S определена формулой
(41)
$\begin{gathered} \frac{{{{\partial }^{2}}S}}{{\partial {{{{\xi }}}^{2}}}} + \frac{{{{\partial }^{2}}S}}{{\partial {{\psi }^{2}}}} = - \frac{{{{r}^{2}}{{\rho }}}}{{{\text{c}}{{{\text{h}}}^{2}}{{\xi }}}}, \\ S = - {{r}^{2}}{{\rho }}\left( r \right)\operatorname{Re} \int\limits_0^v {dt} \int\limits_0^{v - t} {\frac{{{{h}^{2}}\left( {u + i{{\tau }},t} \right)}}{{{\text{c}}{{{\text{h}}}^{2}}{{\xi }}\left( {u + i{{\tau ,}}t} \right)}}} d{{\tau }}. \\ \end{gathered} $Торцевая область планарного гиротрона. В работах [40, 41] при расчетах электронно-оптической системы прибора используются исключительно численные методы. Формирование торцов первоначально прямоугольного пучка, сечение которого под действием сносовой скорости трансформируется в параллелограмм, требует привлечения аппарата, которым не располагают численные модели. В работе [42] подход [38] распространен на новый вид сечения. Решение уравнения Лапласа в торцевой области в параксиальном приближении выражено через элементарные функции. Значение параметра γ, определяющего углы параллелограмма, следует из расчета электронного потока на основании параксиальной [43] или геометризованной [25] теории плоских течений и является функцией продольной координаты.
Асимптотический ряд с уменьшающимся порядком особенности. Параксиальное разложение существенно неравномерно: второй член в (38) имеет особенность более высокого порядка, чем первый. Этим объясняется максимальная ошибка приближенного решения в прикатодной области. Выше мы видели, что успех решения для произвольного цилиндра и конуса основан на выделении двумерного лапласиана с декартовой метрикой и построении функции Римана, выраженной через бесселевы функции.
Для трехмерных электростатических пучков и пучков в режиме магнитного сопровождения [44] подобный результат достигнут с использованием метода многих масштабов [37], адаптированного к задачам оптики плотных электронных потоков в работе [45]. При этом уравнение Лапласа записывается в системе деформированных координат ${{\zeta }}$, $\bar {x}$, $\bar {y}$, связанных с граничной трубкой тока $v = 0$ и катодом ${{\zeta }} = 0$:
(42)
$\begin{gathered} x = \bar {x} + \varepsilon {{x}_{1}}\left( {\bar {x},\bar {y},z} \right) + {{\varepsilon }^{2}}{{x}_{2}}\left( {\bar {x},\bar {y},z} \right), \\ y = \bar {y} + \varepsilon {{y}_{1}}\left( {\bar {x},\bar {y},z} \right) + {{\varepsilon }^{2}}{{y}_{2}}\left( {\bar {x},\bar {y},z} \right), \\ \bar {x} + i\bar {y} = {{x}_{e}}\left( {w,\varepsilon z} \right) + i{{y}_{e}}\left( {w,\varepsilon z} \right), \\ w = u + iv,\,\,\,\,{{\zeta }} = z + {{\varepsilon }^{2}}L\left( {u,\varepsilon z} \right). \\ \end{gathered} $Вместо продольной координаты ${{\zeta }}$ введем две координаты: быструю z и медленную Z для описания особенности и регулярных функций соответственно:
(43)
${{\zeta }} \to z + \varepsilon Z,\,\,\,\,{{{{\varphi }}}_{e}} = {{z}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}{{{{\bar {\varphi }}}}_{e}}\left( {u,Z} \right).$Вторые производные по z в уравнении Лапласа сохраняются, а эволюцию трубки тока будем считать медленной
Деформирующие функции ${{x}_{1}}$, ${{x}_{2}}$, ${{y}_{1}}$, ${{y}_{2}}$ в (42) подберем из условия равенства коэффициентов при ${{{{\partial }^{2}}{{\varphi }}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\varphi }}} {\partial {{u}^{2}}}}} \right. \kern-0em} {\partial {{u}^{2}}}}$, ${{{{\partial }^{2}}{{\varphi }}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\varphi }}} {\partial {{v}^{2}}}}} \right. \kern-0em} {\partial {{v}^{2}}}}$ и отсутствия перекрестной производной ${{{{\partial }^{2}}{{\varphi }}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\varphi }}} {\partial u\partial v}}} \right. \kern-0em} {\partial u\partial v}}$. На языке контравариантного метрического тензора ${{g}^{{ik}}}$ эти требования определены равенствами
В дальнейшем процесс построения решения аналогичен случаю произвольного конуса с тем отличием, что уравнения для двумерного потенциала Ф и функции Римана G содержат члены с первыми производными по u, v. В работе [44] решение построено с использованием одинарного интеграла в формуле Римана (3), в то время как в [46] при рассмотрении клиновидных пучков с произвольным сечением использована форма (37) с двойным интегралом.
Тепловой зазор. В работе [47] обсуждается принятая в пакетах траекторного анализа практика задания теплового зазора, не имеющего отношения к решению уравнений пучка и уравнения Лапласа вблизи кромки катода. Зазор обычно выполняется в виде горизонтальной щели, параллельной оси прибора. В двумерном случае существует точное решение локальной задачи на основе теории антипараксиальных разложений [1] о конфигурации поля в этой области, приводящее к профилированному зазору, образованному боковой поверхностью катода в третьем квадранте и отрицательной эквипотенциалью, расположенной между двумя асимптотами нулевой эквипотенциали $\vartheta = 67.5^\circ $ и ϑ = 180° + + 22.5°.
Практикуемый способ задания зазора можно уподобить предложению определять потенциал вблизи катода не степенью ${4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$ расстояния по нормали n, а любой произвольной функцией, например, $1 - \exp ( - {{n}^{2}})$. Достижение результата с ошибкой порядка 0.3%, необходимого при расчетах пучков с линейной компрессией 30, при таком способе действий представляется невероятным, тем более что оценить реальную ошибку в рамках пакетов, использующих вблизи катода гидродинамическое приближение (самый грубый вариант – локальный закон ${4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}$), невозможно.
В трехмерном случае решение соответствующей задачи отсутствует, но обсуждавшиеся выше результаты для произвольного цилиндра и конуса позволяют сформулировать некоторые разумные предложения. Формула (16) выражает локальный принцип независимости сечений, согласно которому конфигурация нулевой эквипотенциали зависит в данном сечении от локальной кривизны ${{k}_{\Gamma }}$ контура, а не от ее изменения вдоль Г. Решение для кругового цилиндра с радиусом, соответствующим ${{k}_{\Gamma }}$, известно и включает форму боковой поверхности катода и отрицательных эквипотенциалей. Таким образом, пользуясь решением двумерной задачи и обойдя контур трехмерного пучка, получим эквипотенциали, реализующие обоснованный ${\text{c}}$ точки зрения теории тепловой зазор. Для конического пучка с искривленным катодом принцип независимости сечений действует, включая квадратичные члены.
Описанный алгоритм формирования теплового зазора реализован в работе [36] для ленточного пучка с эллиптическим сечением, стартовавшим с цилиндрического катода и достигавшим линейной компрессии порядка 30.
ЗАКЛЮЧЕНИЕ
Пакеты траекторного анализа, широко используемые в последние десятилетия для расчета ленточных пучков с сечением, близким к прямоугольному, не прошли надлежащего тестирования на эталонных точных решениях, используют обычно весьма грубую модель прикатодной зоны (одномерные диоды без учета неоднородного токоотбора и наличия магнитного поля), абсурдную модель теплового зазора, не обеспеченную теоретическим базисом, и эмпирический учет торцевых эффектов. В результате в разномасштабных задачах (пучки с высокой компрессией, прямоугольные сечения с большим отношением сторон) достижение требуемой точности является проблематичным, а несовершенства математической модели должны компенсироваться экспериментальной доводкой прибора. По мере продвижения в сторону более высоких частот и миниатюризации конструкций значение перечисленных проблем будет возрастать.
Существующие результаты теории трехмерных потоков способны содействовать устранению перечисленных недостатков, а модели, основанные в конечном счете на решении обыкновенных дифференциальных уравнений, могут быть использованы для тех же электронно-оптических расчетов, что и пакеты анализа. Примером такого рода являются исследования, проведенные в работе [36].
Автор заявляет об отсутствии конфликта интересов.
Список литературы
Сыровой В.А. Теория интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Сыровой В.А. // Прикл. матем. и механика. 1970. Т. 34. № 1. С. 4.
Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.
Cыpoвoй B.A. // PЭ. 2005. T. 50. № 2. C. 1503.
Oвчapoв B.T. // PЭ. 1967. T. 12. № 12. C. 2156.
Cыpoвoй B.A. // PЭ. 2012. T. 57. № 7. C. 804.
Сыровой В.А. // ЖТФ. 1971. Т. 41. № 12. С. 2607.
Langmuir I., Blodgett K.B. // Phys. Rev. 1924. V. 24. № 1. P. 49.
Кан В.Л. // ЖТФ. 1948. Т. 18. № 4. С. 483.
Cыpoвoй B.A. // PЭ. 2005. T. 50. № 8. C. 1003.
Cыpoвoй B.A. // PЭ. 2007. T. 52. № 2. C. 231.
Данилов В.Н., Сыровой В.А. // РЭ. 1977. Т. 22. № 7. С. 1473.
Cыpoвoй B.A. // PЭ. 2013. T. 58. № 3. C. 284.
Radley D.E. // J. Electr. Contr. 1958. V. 4. № 12. P. 125.
Nakai A. // Nucl. Instrum. and Methods. 1967. V. 54. № 1. P. 57.
Пегов С.А., Сыровой В.А. // РЭ. 1974. Т. 19. № 10. С. 2157.
Bhatt R., Chen C. // Phys. Rev. Accelerators and Beams. 2005. V. 8. № 1. P. 014201-1.
Bhatt R. Inverse Problems in Elliptic Charged-Particle Beams. 2006. Massachusetts Inst. of Technology.
Данилов В.Н. // Журн. прикл. механики и техн. физики. 1968. № 5. С. 3.
Cыpoвoй B.A. // PЭ. 2014. T. 59. № 4. C. 358.
Cыpoвoй B.A. // PЭ. 2018. T. 63. № 8. C. 871.
Oвчapoв B.T. // PЭ. 1962. T. 7. № 8. C. 1367.
Cыpoвoй B.A. // PЭ. 2001. T. 46. № 5. C. 617.
Cыpoвoй B.A. // PЭ. 2001. T. 46. № 9. C. 1139.
Cыpoвoй B.A. // PЭ. 2016. T. 61. № 3. C. 263.
Cыpoвoй B.A. // PЭ. 2017. T. 62. № 5. C. 502.
Cыpoвoй B.A. // PЭ. 2019. T. 64. № 1. C. 82.
Cыpoвoй B.A. // PЭ. 2022. T. 67. № 6. C. 615.
Cыpoвoй B.A. // PЭ. 1999. T. 44. № 5. C. 615.
Сапронова Т.М., Сыровой В.А. // РЭ. 2010. Т. 35. № 6. С. 726.
Пензяков В.В., Олейников В.И. // РЭ. 1975. Т. 20. № 5. С. 1049.
Cыpoвoй B.A. // PЭ. 2008. T. 53. № 8. C. 999.
Cыpoвoй B.A. // PЭ. 2011. T. 56. № 1. C. 111.
Cыpoвoй B.A. // PЭ. 2016. T. 61. № 7. C. 692.
Cыpoвoй B.A. // PЭ. 2018. T. 63. № 5. C. 472.
Акимов П.И., Гаврилин А.А., Никитин А.П. и др. // РЭ. 2018. Т. 63. № 11. С. 1303.
Ван-Дайк М. Методы возмущений в механике жидкости. М.: Мир, 1967.
Данилов В.Н., Сыровой В.А. // Изв. вузов. Радиофизика. 1977. Т. 20. № 11. С. 1727.
Вашковский А.В., Завьялов М.А., Сыровой В.А. // РЭ. 1999. Т. 44. № 4. С. 485.
Manuilov V.N., Zaslavsky V.Yu., Ginzburg N.S. et al. // Phys. Plasmas. 2014. V. 21. P. 023106.
Кишко С.А., Кулешов А.Н., Глявин М.Ю. и др. // РЭ. 2014. Т. 59. № 7. С. 722.
Сапронова Т.М., Сыровой В.А. // РЭ. 2017. Т. 62. № 11. С. 1106.
Cыpoвoй B.A. // PЭ. 2017. T. 62. № 6. C. 584.
Cыpoвoй B.A. // PЭ. 2012. T. 57. № 2. C. 240.
Данилов В.Н., Сыровой В.А. // Прикл. матем. и механика. 1971. Т. 35. № 4. С. 656.
Cыpoвoй B.A. // PЭ. 2012. T. 57. № 11. C. 1221.
Акимов П.И., Никитин А.П., Сыровой В.А. // Электрон. техника. СВЧ-техника. 2018. № 1. С. 32.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника