Радиотехника и электроника, 2023, T. 68, № 2, стр. 131-137
Однопозиционная пассивная локация источника излучения с криволинейным движением и учетом эволюции периода сигнала в точке приема
Ю. Г. Булычев a, *, А. А. Мозоль b
a Всероссийский научно-исследовательский институт “Градиент”
344000 Ростов-на-Дону, просп. Соколова, 96, Российская Федерация
b Северо-Кавказский филиал Московского технического университета связи и информатики
344000 Ростов-на-Дону, ул. Серафимовича, 62, Российская Федерация
* E-mail: ProfBulychev@yandex.ru
Поступила в редакцию 27.06.2022
После доработки 18.08.2022
Принята к публикации 25.08.2022
- EDN: EPOXCI
- DOI: 10.31857/S0033849423010035
Аннотация
Развит однопозиционный метод беспеленговой пассивной локации с учетом периодичности излучаемого импульсного радиосигнала, когда источник излучения движется по криволинейной траектории. Метод не требует оценивания текущей частоты Доплера, а в качестве измеряемого параметра выступает временнáя невязка между периодами излучаемого и принимаемого сигналов, обусловленная движением источника. Рассмотрены вопросы, связанные с вычислительной корректностью и точностными характеристиками метода, а также практическими рекомендациями. Приведен численный пример.
ВВЕДЕНИЕ
Вопросы, связанные с однопозиционными методами пассивной локации источника излучения (ИИ), имеют давнюю историю и подробно отражены в известной литературе (см., например, [1–20]). Среди них наибольший интерес представляют беспеленговые методы, поскольку достижение требуемой точности в пеленгаторных системах (особенно мобильных и требующих осуществления специального маневра), как правило, сопряжено с существенными технико-технологическими сложностями, большими габаритами и экономическими затратами.
Известны доплеровско-временные беспеленговые методы, оперирующие с периодическими сигналами и ориентированные на возможность измерения непрерывного смещения доплеровской частоты или периода принимаемого сигнала в точке наблюдения, обусловленного движением ИИ (в работе [6, с. 169–173] представлен исчерпывающий список литературы по данному вопросу). Указанные методы основаны на идее “синтеза базы”, что приводит в конечном итоге к формированию нескольких точек наблюдения на траектории движения и возможности использования известных методов многопозиционной локации (например, триангуляционного, разностно-дальномерного, дальномерно-дальномерного и их комбинаций [21, 22]). При этом, как правило, рассматриваются такие траектории, которые на участке наблюдения либо известны (например, орбитальные с известными параметрами движения), либо с достаточной для практики точностью аппроксимируются моделью прямолинейного равномерного движения (как с известными, так и неизвестными параметрами движения). При этом принципиальным моментом является наличие априорной информации о скорости движения ИИ, что для практики зачастую является неприемлемым.
В [23] снимается ограничение, связанное с наличием априорной информации о величине скорости, однако решение задачи ограничивается моделью прямолинейного равномерного движения, не учитывающей возможный маневр ИИ. Однако предлагаемый в [23] беспеленговый метод однопозиционной локации предполагает предварительную текущую оценку доплеровской частоты, путем нахождения производной от временной невязки между периодами излучаемого и принимаемого сигналов. Известно, что даже незначительные флуктуационные ошибки измерений могут существенно влиять на результаты численного дифференцирования и точность решения задач, связанных с оценкой параметров движения ИИ.
Цель данной работы – устранить указанные недостатки и пробелы, для чего разработан беспеленговый метод, который по аналогии с [23] основан на вычислении временной невязки между периодами излученного и принятого сигнала, ориентирован на модель криволинейного движения ИИ и не требует промежуточных расчетов, связанных с дифференцированием и текущей оценкой частоты Доплера. Наблюдателя, который реализует данный метод, будем называть пассивным периодо-временным локатором (ППВЛ).
1. ПОСТАНОВКА ЗАДАЧИ
Пусть в прямоугольной декартовой системе координат $XYZ$ (в центре которой находится ППВЛ) движение ИИ описывается полиномиальной моделью (для упрощения выкладок и наглядности метода ограничимся полиномом второй степени с начальным условием ${{\vec {r}}_{0}} = \vec {r}\left( 0 \right)$)
(1)
$\vec {r}\left( t \right) = {{\vec {r}}_{0}} + {{\vec {v}}_{0}}t + {{2}^{{ - 1}}}\vec {a}{{t}^{2}},\,\,\,\,\,t \in \left[ {0,T} \right],$где $\vec {r}\left( t \right) = {{\left[ {x\left( t \right),y\left( t \right),z\left( t \right)} \right]}^{T}}$ – вектор положения ИИ, ${{\vec {v}}_{0}} = {{\left[ {{{v}_{{x0}}},{{v}_{{y0}}},{{v}_{{z0}}}} \right]}^{T}}$ – вектор начальной скорости, ${{v}_{0}} = \left\| {{{{\vec {v}}}_{0}}} \right\|$ – величина скорости, $\vec {a} = {{\left[ {{{a}_{x}},{{a}_{y}},{{a}_{z}}} \right]}^{T}}$ – вектор ускорения, $a = \left\| {\vec {a}} \right\|$ – величина ускорения, Т – знак транспонирования.) В общем случае вместо (1) можно рассматривать обобщенный линейный полином с произвольными базисными функциями.
Отрезок наблюдения $\left[ {0,T} \right]$ представим в виде
(2)
$\left[ {0,T} \right] = \bigcup\limits_{n = 1}^N {\left[ {{{t}_{{n - 1}}},{{t}_{n}}} \right]} ,\,\,\,\,{{t}_{n}} > {{t}_{{n - 1}}},\,\,\,{{t}_{0}} = 0,\,\,\,{{t}_{N}} = T.$В точке наблюдения для каждого узла ${{t}_{n}}$ подсчитывается число периодов ${{M}_{n}}$ принятого импульсного сигнала $S\left( t \right)$ (с периодом ${{T}_{S}}$), целиком укладывающихся в отрезок $\left[ {0,{{t}_{n}}} \right]$. Текущее приращение дальности до ИИ описывается как ${{\Delta }_{R}}(t) = R\left( t \right) - {{R}_{0}}$, а соответствующий ему временной набег
где $R\left( t \right) = \left\| {\vec {r}\left( t \right)} \right\|$ – наклонная дальность, $\left\| \cdot \right\|$ – символ нормы вектора, ${{R}_{0}} = \left\| {{{{\vec {r}}}_{0}}} \right\|$ – начальная дальность, $c$ – скорость света.
Если в качестве измеряемого параметра принять величину ${{\delta }_{n}} = \delta ({{t}_{n}})$, то можно воспользоваться следующим векторным уравнением периодо-временных измерений
где $\vec {h} = {{\left[ {{{h}_{n}},n = \overline {1,N} } \right]}^{T}}$, $\vec {\delta } = {{\left[ {{{\delta }_{n}},n = \overline {1,N} } \right]}^{T}}$, $\vec {\xi } = {{\left[ {{{\xi }_{n}},n = \overline {1,N} } \right]}^{T}}$, ${{h}_{n}} = h({{t}_{n}})$, ${{\xi }_{n}} = \xi \left( {{{t}_{n}}} \right)$, под $\vec {\xi } = {{\left[ {{{\xi }_{n}},n = \overline {1,N} } \right]}^{T}}$ понимается погрешность измерений, распределенная по нормальному закону с нулевым математическим ожиданием и корреляционной матрицей ${{{\mathbf{K}}}_{{\vec {\xi }}}}$, а измеряемый параметр ${{\delta }_{n}} = \delta ({{t}_{n}})$ связан с числом подсчитываемых периодов соотношением (полагая ${{R}_{n}} = R\left( {{{t}_{n}}} \right)$)
(5)
$\begin{gathered} {{\delta }_{n}} = {{t}_{n}} - {{M}_{n}}{{T}_{s}} = {{c}^{{ - 1}}}\left[ {{{R}_{n}} - {{R}_{0}}} \right], \\ {{M}_{n}} = \sum\limits_{p = 1}^n {\Delta {{M}_{p}}} , \\ \end{gathered} $$\Delta {{M}_{p}}$ – количество периодов, подсчитываемых на отрезке $\left[ {{{t}_{{p - 1}}},{{t}_{p}}} \right]$, ${{t}_{0}} = 0$.
Если расстояние между ИИ и ППВЛ уменьшается, то ${{\delta }_{n}} < 0$, в противном случае ${{\delta }_{n}} > 0$. Появление временной невязки ${{\delta }_{n}} = \delta ({{t}_{n}})$ обусловлено эффектом сжатия или растяжения исходного периодического импульсного сигнала в точке наблюдения за счет движения ИИ.
Требуется с учетом (1)–(5) разработать метод однопозиционной пассивной локации ИИ с криволинейным (полиномиальным) движением на базе ППВЛ, не требующий вычисления текущей частоты Доплера. Метод должен включать в себя решение следующих вопросов: формирование алгоритма оценивания наклонной дальности и ряда характерных параметров движения ИИ на точных данных (принимая $\vec {\xi } = 0$); определение условий вычислительной корректности метода на точных данных; учет случайных погрешностей измерений; решение задачи локации на избыточных данных с учетом погрешностей измерений (задача сглаживания на основе метода наименьших квадратов (МНК)) и получение соотношения для расчета корреляционной матрицы ошибок оценивания параметров движения ИИ; проведение вычислительного эксперимента на ЭВМ с целью демонстрации возможностей метода.
2. ПОСТРОЕНИЕ АЛГОРИТМА ПАССИВНОЙ ЛОКАЦИИ НА ТОЧНЫХ ДАННЫХ
С учетом (1) можно получить выражение
(6)
$\begin{gathered} {{R}^{2}}\left( t \right) = R_{0}^{2} + 2t\left\langle {{{{\vec {r}}}_{0}},{{{\vec {v}}}_{0}}} \right\rangle + \\ + \,\,{{t}^{2}}\left( {v_{0}^{2} + \left\langle {{{{\vec {r}}}_{0}},\vec {a}} \right\rangle } \right) + {{t}^{3}}\left\langle {{{{\vec {v}}}_{0}},\vec {a}} \right\rangle + {{4}^{{ - 1}}}{{t}^{4}}{{a}^{2}}. \\ \end{gathered} $где $\left\langle { \cdot \;, \cdot } \right\rangle $ – символ скалярного произведения двух векторов.
Формула (6) представляет собой первое базовое соотношение развиваемого метода. Второе базовое соотношение следует непосредственно из формулы (3):
(7)
${{R}^{2}}\left( t \right) = R_{0}^{2} + 2c{{R}_{0}}\delta \left( t \right) + {{c}^{2}}{{\delta }^{2}}\left( t \right).$Приравнивая правые части выражений (6) и (7), после несложных преобразований получаем уравнение
(8)
$\begin{gathered} - 2c\delta \left( t \right){{\chi }_{1}} + 2t{{\chi }_{2}} + {{t}^{2}}{{\chi }_{3}} + \\ + \,\,{{t}^{3}}{{\chi }_{4}} + {{4}^{{ - 1}}}{{t}^{4}}{{\chi }_{5}} = {{c}^{2}}{{\delta }^{2}}\left( t \right), \\ \end{gathered} $где ${{\chi }_{1}} = {{R}_{0}}$, ${{\chi }_{2}} = \left\langle {{{{\vec {r}}}_{0}},{{{\vec {v}}}_{0}}} \right\rangle $, ${{\chi }_{3}} = \left( {v_{0}^{2} + \left\langle {{{{\vec {r}}}_{0}},\vec {a}} \right\rangle } \right)$, ${{\chi }_{4}} = \left\langle {{{{\vec {v}}}_{0}},\vec {a}} \right\rangle $, ${{\chi }_{5}} = {{a}^{2}}$ – неизвестные коэффициенты, имеющие понятный физический смысл и подлежащие идентификации.
Введем набор (вектор) временных узлов
где $l \in \overline {1,L} $, ${{t}_{{\left[ l \right]d}}} \in \left\{ {{{t}_{1}},t{}_{2},...,{{t}_{N}}} \right\}$, ${{t}_{{\left[ l \right]d + 1}}} > {{t}_{{\left[ l \right]d}}}$.
Для фиксированного $l$ и ${{D}_{{\left[ l \right]}}} = 5$ сформируем следующую систему линейных алгебраических уравнений (СЛАУ):
где ${{\vec {b}}_{{\left[ l \right]}}} = {{\left[ {{{c}^{2}}\delta _{{\left[ l \right]d}}^{2},d = \overline {1,5} } \right]}^{T}}$, $\vec {\chi } = {{\left[ {{{\chi }_{i}},i = \overline {1,5} } \right]}^{T}}$, а матрица ${{{\mathbf{A}}}_{{\left[ l \right]}}}$ (размером 5 × 5) образована строками $\left( { - 2c{{\delta }_{{\left[ l \right]d}}},2{{t}_{{\left[ l \right]d}}},t_{{\left[ l \right]d}}^{2},t_{{\left[ l \right]d}}^{3},{{4}^{{ - 1}}}t_{{\left[ l \right]d}}^{4}} \right)$, $d = \overline {1,5} $.
Решение СЛАУ (9) позволяет определять параметры криволинейного движения ИИ на точных данных для каждого набора ${{\vec {t}}_{{\left[ l \right]}}} = {{\left[ {{{t}_{{\left[ l \right]d}}},d = \overline {1,{{D}_{{\left[ l \right]}}}} } \right]}^{T}}$.
Рассмотрим частный случай, когда ИИ движется прямолинейно и равномерно. Теперь вместо (8) имеем уравнение (в котором ${{\chi }_{3}} = v_{0}^{2}$)
(10)
$ - 2c\delta \left( t \right){{\chi }_{1}} + 2t{{\chi }_{2}} + {{t}^{2}}{{\chi }_{3}} = {{c}^{2}}{{\delta }^{2}}\left( t \right).$Аналогичная СЛАУ (с матрицей ${\mathbf{A}}$ размером 3 × 3) для рассматриваемого случая позволяет находить дальность ${{R}_{0}}$, величину скорости ${{v}_{0}}$ и косинус угла $\gamma $ между векторами ${{\vec {r}}_{0}}$ и ${{\vec {v}}_{0}}$ с учетом очевидных соотношений: ${{R}_{0}} = {{\chi }_{1}}$, ${{V}_{0}} = \sqrt {{{\chi }_{3}}} $, $\cos \gamma = {{\chi }_{2}}{{\left( {{{R}_{0}}{{v}_{0}}} \right)}^{{ - 1}}}$. Если векторы ${{\vec {v}}_{0}}$ и $\vec {a}$ коллинеарны (для прямолинейного равноускоренного движения ИИ), то ${{\chi }_{4}} = {{v}_{0}}a$, ${{\chi }_{5}} = {{a}^{2}}$. По найденным значениям ${{\chi }_{1}}$, …, ${{\chi }_{5}}$ вычисляем следующие параметры движения ИИ:
До сих пор в качестве измеряемого параметра рассматривалась величина ${{\delta }_{n}} = {{t}_{n}} - {{M}_{n}}{{T}_{s}}$, которая предполагает знание периода ${{T}_{s}}$ импульсного сигнала. Однако развиваемый метод можно обобщить на случай неизвестного периода, если уравнение (8) для дискретного времени представить в виде
(11)
$\begin{gathered} - 2c\left( {{{t}_{{\left[ l \right]d}}} - {{M}_{n}}{{T}_{S}}} \right){{\chi }_{1}} + 2{{t}_{{\left[ l \right]d}}}{{\chi }_{2}} + t_{{\left[ l \right]d}}^{2}{{\chi }_{3}} + \\ + \,\,t_{{\left[ l \right]d}}^{3}{{\chi }_{4}} + {{4}^{{ - 1}}}t_{{\left[ l \right]d}}^{4}{{\chi }_{5}} = {{c}^{2}}{{\left( {{{t}_{{\left[ l \right]d}}} - {{M}_{n}}{{T}_{S}}} \right)}^{2}}. \\ \end{gathered} $Принимая в качестве измеряемых величин ${{M}_{{\left[ l \right]d}}}$ и ${{t}_{{\left[ l \right]d}}}$, а период ${{T}_{S}}$ включая в число неизвестных параметров, на основе (11) можно получить базовое уравнение для решения задачи пассивной локации при неизвестном периоде сигнала (по аналогии с [23], где рассматривается прямолинейное равномерное движение ИИ с неизвестной скоростью). Однако указанное обобщение не приводится в статье ввиду громоздких выкладок, а результат требует отдельного исследования.
3. АНАЛИЗ УСЛОВИЙ НЕКОРРЕКТНОСТИ
Не снижая общности рассуждений, ограничимся плоским случаем (принимая $z = 0$) и сигналом с известным периодом. Очевидно, что для корректного применения развиваемого метода, связанного с решением СЛАУ (9), необходимо и достаточно выполнения условия $\det {{{\mathbf{A}}}_{{\left[ l \right]}}} \ne 0$, что приводит к искомому результату
Для выявления случаев, при которых это условие нарушается, запишем столбцы матрицы ${{{\mathbf{A}}}_{{\left[ l \right]}}}$ в виде векторов:
Несложно заметить, что столбцы ${{\vec {A}}_{{\left[ l \right]2}}}$,${{\vec {A}}_{{\left[ l \right]3}}}$ и ${{\vec {A}}_{{\left[ l \right]4}}}$ линейно независимы, следовательно, для проверки условия $\det {{{\mathbf{A}}}_{{\left[ l \right]}}} \ne 0$ достаточно показать, что ${{\vec {A}}_{{\left[ l \right]1}}}$ линейно независим с этими столбцами. Так как ${{R}_{{\left[ l \right]d}}} = {{[x_{{\left[ l \right]d}}^{2} + y_{{\left[ l \right]d}}^{2}]}^{{1/2}}}$, где $x_{{\left[ l \right]d}}^{2} = (x{}_{0}\, + {{v}_{{x\,0}}}{{t}_{{\left[ l \right]d}}} + $ $ + \,\,{{2}^{{ - 1}}}{{a}_{x}}t_{{\left[ l \right]d}}^{2}{{)}^{2}}$ и $y_{{\left[ l \right]d}}^{2} = {{(y{}_{0} + \,{{v}_{{y\,0}}}{{t}_{{\left[ l \right]d}}} + {{2}^{{ - 1}}}{{a}_{y}}t_{{\left[ l \right]d}}^{2})}^{2}}$, то нарушение условия $\det {{{\mathbf{A}}}_{{\left[ l \right]}}} \ne 0$ эквивалентно тому, что векторы ${{\vec {X}}_{{\left[ l \right]}}} = {{[x_{{\left[ l \right]d}}^{2},d = \overline {1,{{D}_{{\left[ l \right]}}}} ]}^{T}}$ и ${{\vec {Y}}_{{\left[ l \right]}}} = $ $ = {{[y_{{\left[ l \right]d}}^{2},d = \overline {1,{{D}_{{\left[ l \right]}}}} ]}^{T}}$ коллинеарны, т.е. ${{\vec {X}}_{{\left[ l \right]}}} = {{k}_{{\left[ l \right]}}}{{\vec {Y}}_{{\left[ l \right]}}}$, где ${{k}_{{\left[ l \right]}}}$ – коэффициент пропорциональности. В противном случае имеем
(12)
$\begin{gathered} {{R}_{{\left[ l \right]d}}} = {{\left[ {x_{{\left[ l \right]d}}^{2} + y_{{\left[ l \right]d}}^{2}} \right]}^{{1/2}}} = {{\left[ {{{{\left( {{{k}_{{\left[ l \right]}}}} \right)}}^{2}}y_{{\left[ l \right]d}}^{2} + y_{{\left[ l \right]d}}^{2}} \right]}^{{1/2}}} = \\ = {{\left[ {{{{\left( {{{k}_{{\left[ l \right]}}}} \right)}}^{2}} + 1} \right]}^{{1/2}}}\left| {{{y}_{{\left[ l \right]d}}}} \right| = {{q}_{{\left[ l \right]}}}\left| {{{y}_{{\left[ l \right]d}}}} \right|, \\ \end{gathered} $(13)
$ - 2c{{\delta }_{{\left[ l \right]d}}} = - 2\left[ {{{R}_{{\left[ l \right]d}}} - {{R}_{0}}} \right] = - 2\left[ {{{q}_{{\left[ l \right]}}}\left| {{{y}_{{\left[ l \right]d}}}} \right| - {{R}_{0}}} \right].$Из (12) и (13) следует, что координаты вектора ${{\vec {A}}_{{\left[ l \right]1}}}$ можно представить линейной комбинацией из координат векторов ${{\vec {A}}_{{\left[ l \right]2}}}$, ${{\vec {A}}_{{\left[ l \right]3}}}$ и ${{\vec {A}}_{{\left[ l \right]4}}}$. Физический смысл условия ${{\vec {X}}_{{\left[ l \right]}}} = {{k}_{{\left[ l \right]}}}{{\vec {Y}}_{{\left[ l \right]}}}$ (условие вычислительной некорректности метода) состоит в том, что ИИ движется по линии визирования ППВЛ.
Таким образом, для вычислительной корректности метода необходимо исключить случаи, когда ИИ движется вдоль линии визирования или в ее окрестности. Это накладывает определенные ограничения на условия наблюдения ИИ, что необходимо предусмотреть на практике.
4. УЧЕТ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Для учета влияния случайных погрешностей измерений $\vec {\xi }$ на точностные характеристики развиваемого метода с учетом СЛАУ (9) воспользуемся традиционной процедурой расчета элементов корреляционной матрицы ${{{\mathbf{K}}}_{{\vec {\chi }\left[ l \right]}}}$ ошибок оценивания координат вектора $\vec {\chi }$ в линейном приближении [24]. Для этого воспользуемся представлением $\vec {\chi } = {\mathbf{A}}_{{\left[ l \right]}}^{{ - 1}}{{\vec {b}}_{{\left[ l \right]}}} = {{\left[ {{{\chi }_{k}}\left( {{{{\vec {\delta }}}_{{\left[ l \right]}}}} \right),k = \overline {1,5} } \right]}^{T}}$ (где ${{\vec {\delta }}_{{\left[ l \right]}}} = {{\left[ {{{\delta }_{{\left[ l \right]d}}},d = \overline {1,5} } \right]}^{T}}$) и частными производными следующего вида: ${{\partial {{\chi }_{k}}\left( {{{{\vec {\delta }}}_{{\left[ l \right]}}}} \right)} \mathord{\left/ {\vphantom {{\partial {{\chi }_{k}}\left( {{{{\vec {\delta }}}_{{\left[ l \right]}}}} \right)} {\partial {{\delta }_{{\left[ l \right]d}}}}}} \right. \kern-0em} {\partial {{\delta }_{{\left[ l \right]d}}}}}$. С учетом этого искомая матрица находится так
(14)
${{{\mathbf{K}}}_{{\vec {\chi }\left[ l \right]}}} = {{{\mathbf{F}}}_{{\vec {\chi }\left[ l \right]}}}{{{\mathbf{K}}}_{{\vec {\xi }}}}{\mathbf{F}}_{{\vec {\chi }\left[ l \right]}}^{T},$где ${{{\mathbf{F}}}_{{\vec {\chi }\left[ l \right]}}} = \left[ {{{\partial {{\chi }_{k}}\left( {{{{\vec {\delta }}}_{{\left[ l \right]}}}} \right)} \mathord{\left/ {\vphantom {{\partial {{\chi }_{k}}\left( {{{{\vec {\delta }}}_{{\left[ l \right]}}}} \right)} {\partial {{\delta }_{{\left[ l \right]d}}}}}} \right. \kern-0em} {\partial {{\delta }_{{\left[ l \right]d}}}}},k = \overline {1,5} ,d = \overline {1,5} } \right]$.
Выражение (14) позволяет априорно на математических ожиданиях измеряемых параметров оценить потенциальные возможности развиваемого метода и выработать практические рекомендации для его наилучшего использования при конкретных условиях наблюдения ИИ, а также обоснованно подходить к выбору основных параметров метода (длины интервала наблюдения ($T$), количества узлов ($N$) и временных наборов (${{\vec {t}}_{{\left[ l \right]}}}$)). Так, номер $l* \in \left\{ {1,2,...,L} \right\}$ оптимального набора ${{\vec {\delta }}_{{\left[ {{{l}^{ * }}} \right]}}}$, обеспечивающего минимизацию ошибки оценивания, находится по правилу
(15)
$l* = \arg \mathop {\min }\limits_l \left\| {{{{\mathbf{K}}}_{{\vec {\chi }\left[ l \right]}}}} \right\|,$где $\left\| {{{{\mathbf{K}}}_{{\vec {\chi }\left[ l \right]}}}} \right\|$ – норма матрицы ${{{\mathbf{K}}}_{{\vec {\chi }\left[ l \right]}}}$.
5. УЧЕТ ИЗБЫТОЧНЫХ ИЗМЕРЕНИЙ
По аналогии с (9) на базе уравнения (8) строится СЛАУ, в которой для случая избыточных измерений матрица ${{{\mathbf{A}}}_{{\left[ l \right]}}}$ и вектор ${{\vec {b}}_{{\left[ l \right]}}}$ имеют произвольное число строк ${{D}_{{\left[ l \right]}}} \leqslant N$. Полагаем, что ${{D}_{{\left[ l \right]}}}$ превышает количество оцениваемых параметров. С учетом этого, по аналогии с (14), корреляционную матрицу ошибок измерений координат вектора ${{\vec {b}}_{{\left[ l \right]}}}$ можно представить так
(16)
${{{\mathbf{K}}}_{{\vec {b}\left[ l \right]}}} = {{{\mathbf{F}}}_{{\vec {\delta }\left[ l \right]}}}{{{\mathbf{K}}}_{{\vec {\xi }}}}{\mathbf{F}}_{{\vec {\delta }\left[ l \right]}}^{T}$.При условии достаточно малых ошибок измерений для построения сглаженной оценки $\vec {\chi }_{{\left[ l \right]}}^{ * }$ вектора $\vec {\chi }$ можно воспользоваться МНК
(17)
$\vec {\chi }_{{\left[ l \right]}}^{ * } = {{\left( {{\mathbf{A}}_{{\left[ l \right]}}^{T}{\mathbf{K}}_{{\vec {b}\left[ l \right]}}^{{ - 1}}{{{\mathbf{A}}}_{{\left[ l \right]}}}} \right)}^{{ - 1}}}{\mathbf{A}}_{{\left[ l \right]}}^{T}{\mathbf{K}}_{{\vec {b}\left[ l \right]}}^{{ - 1}}{{\vec {h}}_{{\vec {b}\left[ l \right]}}}{\kern 1pt} ,$где ${{\vec {h}}_{{\vec {b}\left[ l \right]}}} = {{[{{h}_{{\vec {b}\left[ l \right]d}}},d = \overline {1,{{D}_{{\left[ l \right]}}}} ]}^{T}}$ – вектор вторичных измерений.
Корреляционную матрицу ошибок оценивания находим так
(18)
${{{\mathbf{K}}}_{{\vec {\chi }_{{\left[ l \right]}}^{ * }}}} = {{\left( {{\mathbf{A}}_{{\left[ l \right]}}^{T}{\mathbf{K}}_{{\vec {b}\left[ l \right]}}^{{ - 1}}{{{\mathbf{A}}}_{{\left[ l \right]}}}} \right)}^{{ - 1}}},$при этом для выбора оптимального набора применяем критерий типа (15).
Следует отметить, что подход (16)–(18) не является строго оптимальным, поскольку элементы матрицы ${{{\mathbf{A}}}_{{\left[ l \right]}}}$ зависят от результатов наблюдений. Но при определенных ограничениях на погрешности измерений он дает вполне приемлемый результат. Для более точного сглаживания можно использовать известные процедуры нелинейного оптимального оценивания, которые приводят на практике к трудоемким рекуррентным алгоритмам, предполагающим задание достаточно точного начального условия (для обеспечения необходимой точности и скорости сходимости).
Другой способ построения оценки $\vec {\chi }{\text{*}}$ может состоять в предварительном сглаживании первичных измерений $h{}_{{\left[ l \right]1}},h{}_{{\left[ l \right]2}},...,h{}_{{\left[ l \right]{{D}_{{\left[ l \right]}}}}}$ соответствующим полиномом $\delta _{{\left[ l \right]}}^{ * }(t)$ и применении полученных результатов к решению построенной СЛАУ (однако эффективность реализации такого способа требует отдельного исследования). Кроме того, можно найти сглаженную оценку дальности для любого $t \in \left[ {0,T} \right]$, а именно:
(19)
${{R}_{{\left[ l \right]}}}\left( t \right) = R_{{0\left[ l \right]}}^{ * } + c\delta _{{\left[ l \right]}}^{ * }(t),$где в качестве оптимального принимаем набор с номером $l = l* \in \{ 1,2,...,L\} $.
6. НЕКОТОРЫЕ ОБОБЩЕНИЯ И ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
Выше рассматривался случай оценивания начальной дальности ${{R}_{0}} = R\left( 0 \right)$ для момента времени $t = 0$. Однако если ряд Тейлора, используемый для описания криволинейного движения ИИ, записать относительно не начального, а любого произвольного $t = t* \in \left[ {0,T} \right]$, то по аналогии с изложенным можно решить задачу пассивной локации именно для момента времени $t{\text{*}}$, в частности, найти дальность ${{R}_{ * }} = R\left( {t{\text{*}}} \right)$. Развитый метод несложно реализовать в виде следующих алгоритмов: по выборке нарастающего объема, на “скользящей” сетке или в виде фильтра Калмана [25]. При этом движение ИИ на интервале наблюдения можно рассматривать как кусочно-полиномиальное (в [23] оно рассматривалось как кусочно-линейное). При практической реализации метода возникают вопросы (например, выбор степени полинома, описывающего движение ИИ, или количества подсчитываемых импульсов), которые связаны с организацией измерительного процесса. В [25] даются практические рекомендации для решения этих вопросов в полном объеме. Очевидно, что развиваемый метод наиболее эффективен в случае, когда речь идет о больших пройденных расстояниях (т.е. “синтезируется база”, обеспечивающая необходимую точность оценивания), а это задает определенные ограничения на тип ИИ (в частности, его скорость, возможности маневра и т.д.), обоснованность используемого полинома на заданном интервале наблюдения и тактико-технические характеристики ППВЛ.
Для случаев, связанных с движением ИИ по линии визирования, можно предложить гибридный вариант использования развитого и известного энергетического метода [13]. Доказано, что этот метод, оперирующий с относительным уровнем принимаемого импульсного сигнала, наилучшим образом реализует свои потенциальные возможности при движении ИИ по линии визирования. В некотором смысле развитый и энергетический методы “ортогональны” в плане точности. Следовательно, комбинируя эти методы, можно обеспечить равномерную рабочую зону гибридного метода и достичь приемлемых точностных характеристик для различных условий наблюдения.
7. РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА
Предположим, что ИИ осуществляет плоскостное движение:
где ${{x}_{0}} = 7.5 \times {{10}^{3}}$, ${{y}_{0}} = {{10}^{2}}$, ${{{v}}_{{x0}}} = - {{{v}}_{{y0}}} = - 4 \times {{10}^{2}}$. Здесь и далее время и погрешности измерений временных интервалов задаются в секундах, координаты и дальность – в метрах, скорость – в м/с, ускорение – в м/с2, частота – в герцах.
Рассматриваются два варианта движения:
вариант 1 соответствует прямолинейному движению, когда ${{a}_{x}} = - {{a}_{y}} = - 7$ (угол между вектором начальной скорости ${{\vec {v}}_{0}}$ и $\vec {a}$ равен нулю),
вариант 2 – криволинейному движению, когда ${{a}_{x}} = - 7$, ${{a}_{y}} = 0$ (угол между векторами ${{\vec {v}}_{0}}$ и $\vec {a}$ равен 45°).
В обоих вариантах $\gamma = 135^\circ $.
Источник излучения формирует импульсный сигнал
где $T = 16$, ${{T}_{S}} = {{10}^{{ - 4}}}$, $\tau = {{10}^{{ - 5}}}$, ${{f}_{0}} = {{10}^{{10}}}.$ Параметры работы ППВЛ: $L = 3$, ${{D}_{{\left[ 1 \right]}}} = 6$, ${{D}_{{\left[ 2 \right]}}} = 5$, ${{D}_{{\left[ 3 \right]}}} = 9$, ${{\vec {t}}_{{\left[ 1 \right]}}} = {{\left[ {1,4,7,10,13,16} \right]}^{T}}$, ${{\vec {t}}_{{\left[ 2 \right]}}} = {{\left[ {1,5,9,13,16} \right]}^{T}}$, ${{\vec {t}}_{{\left[ 3 \right]}}} = [1,3,$ $5,7,9,11,13,15,16{{]}^{T}}$, $\Delta {{M}_{p}} = \Delta M = {{10}^{4}}$, ${{{\mathbf{K}}}_{{\vec {\xi }}}} = $ $ = {\text{diag}}\left[ {{{\sigma }^{2}},...,{{\sigma }^{2}}} \right]$, при этом погрешности измерений временного набега $\delta \left( t \right)$, обусловленные размытием фронтов импульсов, полагались некоррелированными и задавались по нормальному закону распределения с нулевым математическим ожиданием и значением среднеквадратического отклонения $\sigma \in \left\{ {{{{10}}^{{ - 10}}},{{{10}}^{{ - 9}}}} \right\}$. Сглаживание измерений (4) осуществлялось путем аппроксимации полиномом 14-й степени (высокая степень обусловлена широким спектральным составом функции $\delta \left( t \right)$ за счет участвующей в ее представлении иррациональности (корня), несмотря на то, что сама эта функция является достаточно гладкой).
Величина “синтезируемой базы” для варианта 1 составила 9.7475 × 103, а для варианта 2 – 9.1382 × 103 (разность длин баз равна 609.3, что соответствует 6.25%). Принятым исходным данным соответствуют следующие параметры: ${{\chi }_{1}} = 7.5 \times {{10}^{3}}$, ${{\chi }_{2}} = - 2.96 \times {{10}^{6}}$, ${{\chi }_{3}} = 2.68 \times {{10}^{5}}$ (для варианта 1), ${{\chi }_{3}} = 2.67 \times {{10}^{5}}$ (для варианта 2), ${{\chi }_{4}} = 5.6 \times {{10}^{3}}$ (для варианта 1), ${{\chi }_{4}} = 2.8 \times {{10}^{3}}$ (для варианта 2), ${{\chi }_{5}} = 9.9$. На основе трех наборов ${{\vec {t}}_{{\left[ l \right]}}} = {{\left[ {{{t}_{{\left[ l \right]d}}},d = \overline {1,{{D}_{{\left[ l \right]}}}} } \right]}^{T}}$ был реализован алгоритм (17) по выборке фиксированного объема, при этом оценки значений текущей дальности находились по формуле (19) и усреднялись на основе тысячи экспериментов (см. рис. 1). Результаты по абсолютным и относительным погрешностям приведены в табл. 1. Видим, что уменьшение размера “синтезируемой базы” на 6.25% (для варианта 2) приводит к увеличению погрешностей оценивания, однако выбором узлов временной сетки (с учетом наборов ${{\vec {t}}_{{\left[ 1 \right]}}}$, ${{\vec {t}}_{{\left[ 2 \right]}}}$ и ${{\vec {t}}_{{\left[ 3 \right]}}}$) можно добиться существенного повышения точности. Как видно из таблицы, в большинстве рассмотренных случаев относительные погрешности не превышают 5%, при этом наибольшая погрешность оценивания соответствует параметрам ${{\chi }_{4}}$ и ${{\chi }_{5}}$, которые в уравнении (8) стоят при старших степенных функциях (${{t}^{3}}$ и ${{t}^{4}}$ соответственно).
Рис. 1.
Относительная погрешность Потн оценивания дальности для $\sigma = {{10}^{{ - 10}}}$ (а) и $\sigma = {{10}^{{ - 9}}}$ (б): вариант 1 при ${{a}_{x}} = - {{a}_{y}} = - 7$ (кривые 1–3) и вариант 2 при ${{a}_{x}} = - 7$, ${{a}_{y}} = 0$ (кривые 4–6) для ${{\vec {t}}_{{\left[ 1 \right]}}}$ (1, 4), ${{\vec {t}}_{{\left[ 2 \right]}}}$ (2,5) и ${{\vec {t}}_{{\left[ 3 \right]}}}$ (3, 6).
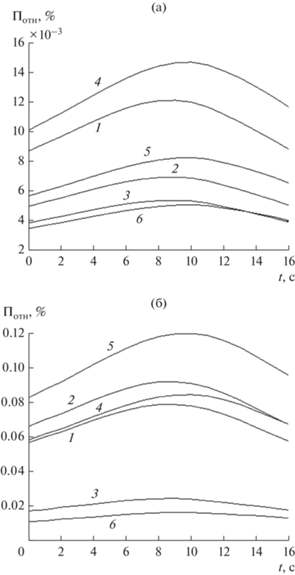
Таблица 1.
Сравнительный анализ
| Вид движения | Наборы узлов |
$\sigma $ | Значения погрешностей оценивания коэффициентов | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ${{\chi }_{1}}$ | ${{\chi }_{2}}$ | ${{\chi }_{3}}$ | ${{\chi }_{4}}$ | ${{\chi }_{5}}$ | ||||||||
| абс. | отн. | абс. | отн. | абс. | отн. | абс. | отн. | абс. | отн. | |||
| Прямолинейное | ${{\vec {t}}_{{\left[ 1 \right]}}}$ | 10–10 | 0.65 | 0.01 | 236.15 | 0.01 | 11.57 | 0.004 | 4.35 | 0.08 | 0.02 | 0.23 |
| 10–9 | 4.25 | 0.06 | 1.4 × 103 | 0.05 | 155.25 | 0.06 | 36.32 | 0.65 | 0.2 | 2.03 | ||
| ${{\vec {t}}_{{\left[ 2 \right]}}}$ | 10–10 | 0.38 | 0.005 | 129.81 | 0.004 | 10.19 | 0.004 | 2.83 | 0.05 | 0.02 | 0.15 | |
| 10–9 | 4.95 | 0.07 | 1.6 × 103 | 0.06 | 189.41 | 0.07 | 43.3 | 0.77 | 0.25 | 2.43 | ||
| ${{\vec {t}}_{{\left[ 3 \right]}}}$ | 10–10 | 0.29 | 0.004 | 99.42 | 0.003 | 9.26 | 0.003 | 2.38 | 0.04 | 0.013 | 0.13 | |
| 10–9 | 1.3 | 0.02 | 582.81 | 0.07 | 57.86 | 0.02 | 0.12 | 0.002 | 0.01 | 0.1 | ||
| Криволинейное | ${{\vec {t}}_{{\left[ 1 \right]}}}$ | 10–10 | 0.76 | 0.01 | 278.36 | 0.01 | 8.61 | 0.003 | 3.85 | 0.14 | 0.03 | 0.39 |
| 10–9 | 4.36 | 0.06 | 1.5 × 103 | 0.05 | 131.39 | 0.05 | 30.33 | 1.08 | 0.23 | 3.29 | ||
| ${{\vec {t}}_{{\left[ 2 \right]}}}$ | 10–10 | 0.43 | 0.006 | 150.64 | 0.005 | 8.60 | 0.003 | 2.52 | 0.09 | 0.02 | 0.26 | |
| 10–9 | 6.19 | 0.08 | 2.1 × 103 | 0.07 | 169.23 | 0.06 | 41.42 | 1.48 | 0.31 | 4.49 | ||
| ${{\vec {t}}_{{\left[ 3 \right]}}}$ | 10–10 | 0.26 | 0.005 | 90.03 | 0.003 | 7.44 | 0.003 | 1.8 | 0.06 | 0.01 | 0.19 | |
| 10–9 | 0.84 | 0.01 | 413.4 | 0.01 | 65.47 | 0.02 | 3.62 | 0.13 | 0.04 | 0.61 | ||
При решении СЛАУ следует привлекать известные методы регуляризации, поскольку для данного примера число обусловленности матрицы данной СЛАУ составляет $2.2 \times {{10}^{5}}$ для варианта 1 и $2.6 \times {{10}^{5}}$ для варианта 2.
Результаты численного эксперимента показывают, что чем больше расстояние между узлами используемой временной сетки, тем меньшее влияние оказывают случайные погрешности измерений на результирующую точность оценивания. Это расстояние должно быть согласовано с динамикой ИИ, а именно: чем меньше скорость движения ИИ, тем больше должен быть шаг этой сетки и длительность интервала наблюдения.
ЗАКЛЮЧЕНИЕ
Таким образом, разработан метод однопозиционной локации применительно к стационарному ППВЛ, позволяющему оценивать параметры криволинейного полиномиального движения ИИ по результатам вычислений временной невязки между периодами излученного импульсного радиосигнала и периодами, подсчитанными в точке наблюдения. Метод не требует оценки текущей частоты Доплера и знания каких-либо априорных данных о параметрах принятой модели движения ИИ. Исследованы основные ограничения метода и условия его наиболее эффективного применения. Также получены аналитические соотношения, позволяющие оценивать точностные характеристики метода для различных условий наблюдения ИИ.
Метод может быть реализован как самостоятельно, так и в составе гибридного метода, объединяющего другие известные подходы пассивной однопозиционной и многопозиционной локации ИИ. Поскольку развитый метод позволяет определять дальность, то он может быть использован в дальномерно-дальномерных системах многопозиционной локации при решении известной задачи трилатерации [21, 22].
При наличии в периодо-временных измерениях не только флуктуационных погрешностей, но и сингулярных ошибок целесообразно первоначально подвергать эти измерения процедуре обобщенного инвариантно-несмещенного оценивания [26], обеспечивающей компенсацию этих ошибок, достижение эффекта сглаживания и оптимальное оценивание различных числовых характеристик (линейных функционалов, например, производных, интегралов, спектральных коэффициентов и т.д.), полезных не только для повышения устойчивости метода, но и оценки его эффективности.
Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Основы маневрирования кораблей / под ред. М. Скворцова. М.: Воениздат, 1966.
Шебшаевич В.С. Введение в теорию космической навигации. М.: Сов. радио, 1971.
Громов Г.Н. Дифференциально-геометрический метод навигации. М.: Радио и связь, 1986.
Хвощ В.А. Тактика подводных лодок. М.: Воениздат, 1989.
Соловьев Ю.А. Спутниковая навигация и её приложения. М.: Экотрендз, 2003.
Мельников Ю.П., Попов С.В. Радиотехническая разведка. М.: Радиотехника, 2008.
Ярлыков М.С. Статистическая теория радионавигации. М.: Радио и связь, 1985.
Сосулин Ю.Г., Костров В.В., Паршин Ю.Н. Оценочно-корреляционная обработка сигналов и компенсация помех. М.: Радиотехника, 2014.
Булычев Ю.Г., Манин А.П. Математические аспекты определения движения летательных аппаратов. М.: Машиностроение, 2000.
Булычев Ю.Г., Васильев В.В., Джуган Р.В. и др. Информационно-измерительное обеспечение натурных испытаний сложных технических комплексов. М.: Машиностроение–Полет, 2016.
Гельцер А.А. Однопозиционный метод определения местоположения источника радиоизлучения с использованием отражений сигналов от множества элементов рельефа и местных предметов // Автореф. дис. канд. техн. наук. Томск: Гос. ун-т систем управления и радиоэлектроники, 2012. 22 с.
Сиренко И.Л., Донец И.В., Рейзенкинд Я.А. и др. // Радиотехника. 2019. № 10. С. 28.
Булычев Ю.Г., Ивакина С.С., Насенков И.Г. // Радиотехника. 2015. № 6. С.107.
Булычев Ю.Г., Мозоль А.А. // Успехи совр. радиоэлектроники. 2017. № 4. С. 58.
Булычев Ю.Г., Мозоль А.А., Насенков И.Г. // РЭ. 2018. Т. 63. № 6. С. 563.
Булычев Ю.Г., Булычев В.Ю., Ивакина С.С. и др. // РЭ. 2016. Т. 61. № 4. С. 344.
Дятлов А.П., Дятлов П.А. // Спец. техника. 2010. № 5. С. 16.
Aidala V.J., Nardone S.C. // IEEE Trans. 1982. V. AES-18. № 4. P. 432.
Amelin K.S., Miller A.B. // J. Commun. Technol. Electron. 2014. V. 59. № 6. P. 622.
Miller A. B. // Automation and Remote Control. 2015. V. 76. № 6. P. 1018.
Кондратьев В.С., Котов А.Ф., Марков Л.Н. Многопозиционные радиотехнические системы. М.: Радио и связь, 1986.
Черняк В.С. Многопозиционная радиолокация. М.: Радио и связь, 1993.
Булычев Ю.Г., Мозоль А.А. // РЭ. 2021. Т. 66. № 5. С. 468.
Вентцель Е.С. Теория вероятностей. М.: Высш. школа, 1999.
Жданюк Б.Ф. Основы статистической обработки траекторных измерений. М.: Сов. радио, 1978.
Булычев Ю.Г., Елисеев А.В. // Журн. вычислит. математики и матем. физики. 2008. Т. 48. № 4. С. 580.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника


