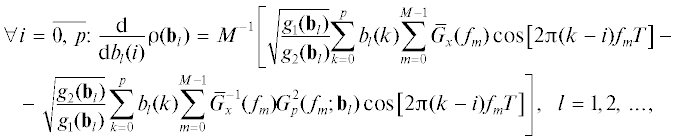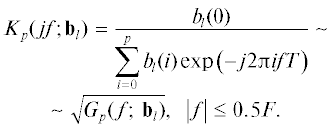Радиотехника и электроника, 2023, T. 68, № 2, стр. 138-145

ВВЕДЕНИЕ

На протяжении нескольких десятков лет авторегрессионная (АР) модель привлекает к себе внимание исследователей и практиков в качестве способа эффективного кодирования речевого сигнала с многократным сжатием данных в информационных системах и технологиях самого разного назначения: от передачи речи по цифровым каналам связи до речевой аналитики и голосового управления [1, 2]. Как следствие, построение АР-модели, или АР-моделирование давно стало классической задачей в области автоматической обработки речи (АОР) [3–5]. Неудивительно поэтому, что существует множество разных подходов к ее решению, в рамках которых предложено множество разных методов и алгоритмов. Среди них доминируют параметрические методы цифрового спектрального анализа [6]. Примером может служить метод Берга, в котором гарантируется устойчивость формируемой АР-модели речевого сигнала вне зависимости от его длительности и тонкой структуры [7]. Однако точность метода Берга далеко не всегда отвечает требованиям практики, в том числе из-за эффектов нелинейной обработки: смещения и расщепления спектральных мод в условиях малых выборок наблюдений [8].

Для преодоления недостатков параметрических методов был предложен [9] метод спектрального АР-моделирования речевого сигнала в режиме скользящего окна наблюдений конечной длительности τ. Благодаря использованию в этом методе дискретного преобразования Фурье (ДПФ), основанного на линейной обработке речевого сигнала, его авторам удалось существенно повысить точность АР-модели. Определенные сомнения при этом вызывает проблема устойчивости или стабильности [10] формируемой модели в смысле цифровой рекурсивной фильтрации [11]. Причем ее острота резко возрастает по мере увеличения требований пользователя к результатам итеративной вычислительной процедуры [9]. Решению указанной проблемы и посвящена, главным образом, данная статья.

Статья написана по результатам проведенного автором исследования в развитие результатов его предыдущих работ, опубликованных в соавторстве с сотрудниками Лаборатории алгоритмов и технологий анализа сетевых структур НИУ “Высшая школа экономики”, Нижний Новгород, Россия за период 2020–2022 гг. Цель исследования – разработка нового метода АР-моделирования речевого сигнала повышенной точности и устойчивости в условиях малых выборок.

1. ПОСТАНОВКА ЗАДАЧИ

Задача формулируется как оптимизационная в терминах дискретного спектрального моделирования (ДСМ) [12]. Пусть задан речевой фрейм {x(n)} конечной размерности N = τF, где F – частота дискретизации речевого сигнала. Отталкиваясь от общего выражения на выделенном наборе из M $ \gg $ 1 дискретных частот ${{f}_{m}}{\text{ }} = {{f}_{{m - 1}}} + \Delta f$, $\Delta f = {F \mathord{\left/ {\vphantom {F M}} \right. \kern-0em} M}$, спектральной плотности мощности (СПМ) АР-модели p-го порядка [8]

(T = 1/F, ${{\sigma }}_{0}^{2}\,\,{\text{ = }}\,\,{\text{const}}$), путем последовательных приближений (итераций)

с шагом γ₀ = const найдем оптимальный вектор весовых коэффициентов b_l = {b_l(i)} из условия минимизации модифицированной величины COSH-расстояния:

формируемой СПМ (1) относительно ее опорного образца {G₀(f_m)} в теоретико-информационном смысле [9, 13]. Ввиду широкого распространения АР-модели в области АОР [7, 8] задача в данной постановке представляет очевидный интерес. Кроме того, из справедливости тождества

для произвольной СПМ G*(f) > 0 и неотрицательной константы c > 0, в том числе при равенстве $c\,\,{\text{ = }}\,\,{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{{\sigma }}_{0}^{2}}}} \right. \kern-0em} {{{\sigma }}_{0}^{2}}}$, вытекает инвариантность меры (3) к масштабному множителю ${{\sigma }}_{0}^{2}$. Это исключает необходимость пошагового масштабирования АР-модели (1) в рамках итеративной вычислительной процедуры (2).

В работе [9] в качестве спектрального образца {G₀(f_m)} использовалась основанная на M-точечном (M ≥ N) ДПФ речевого сигнала ($j = \sqrt { - 1} $)

периодограмма Шустера общего вида [8]

Однако в этом случае не гарантируется устойчивость формируемой АР-модели (1), и это острая проблема для большинства известных методов ДСМ [10, 12].

Эффективным способом решения указанной проблемы представляется использование вместо периодограммы (5) ее огибающей{${{\bar {G}}_{x}}$(f_m)} [14]. Во-первых, этим учитывается известная нацеленность АР-модели на описание именно огибающей СПМ, если мы имеем в виду вокализованный речевой сигнал [7]. И, во-вторых, использование огибающей периодограммы Шустера сильно уменьшает степень изрезанности формы опорного спектрального образца {G₀(f_m)} как главного фактора неустойчивости АР-модели в задачах ДСМ [10]. Рассмотрим этот способ подробно в рамках общей формулировки (1)–(3) оптимизационной задачи.

2. СИНТЕЗ АЛГОРИТМА

Согласно акустической теории речеобразования [1, 7] СПМ вокализованных отрезков речевого сигнала имеет квазилинейчатую структуру и состоит из модулированных по амплитуде гармоник частоты основного тона F₀ [15]. Их огибающая содержит важную информацию о внутрипериодной (внутри периода основного тона) тонкой структуре речевого сигнала и именно в этом качестве представляет первостепенный интерес [16]. Аналогичную линейчатую структуру со сдвигом своих отсчетов в частотной области на $\Delta f = {F \mathord{\left/ {\vphantom {F M}} \right. \kern-0em} M}$ имеет и периодограмма (5). Причем в силу линейности ДПФ (4) ее огибающая {${{\bar {G}}_{x}}$(f_m)} по форме подобна огибающей истинной СПМ. Вместе с тем АР-модель (1) является наиболее распространенным способом ее математического описания в задачах АОР [1]. Желательно, разумеется, при этом использовать ее наиболее точный оптимальный вариант.

Однако здесь возникает серьезная проблема в отношении критерия оптимальности. Все сколько-нибудь известные на данный момент критерии – Акаике, Щварца и их разнообразные модификации [17] – рассчитаны исключительно на эргодические случайные процессы. Речевой сигнал, рассматриваемый в условиях малых выборок, к ним не относится. Выход подсказывает работа [15], в которой предложен алгоритм оптимизации порядка p < ∞ АР-модели (1) через решение обратной задачи речеобразования по принципу “от речевого сигнала к его голосовому источнику”.

Вокализованная речь имеет своим источником периодическую последовательность коротких (доли миллисекунды) импульсов возбуждения голосового тракта диктора [16]. Обозначим ее СПМ через {G_y(f_m)}. В предположении о линейности голосового тракта и заданной априори СПМ речевого сигнала {G*(f_m)} в идеале будем иметь [5]

Это известное уравнение выравнивающего [18] фильтра в частотной области.

Идеальная СПМ (6) отличается от истинной {G*(f_m)} только формой огибающей {${{\bar {G}}_{y}}$(f_m)}. В силу малой длительности импульсов возбуждения она имеет практически прямоугольный вид в полосе рабочих частот f_m ≤ 0.5F [11]. Для всех m < M при этом выполняется равенство

Отсюда в соответствии с (3) получим тождество

А это признак идеального выравнивающего фильтра (6). Правда, данное тождество не достижимо в строгом смысле в условиях априорной неопределенности в отношении истинного вида СПМ {G*(f_m)}. Однако его можно использовать в качестве критерия точности АР-модели (1). Для этого подставим в (6) вместо неизвестных в общем случае СПМ {G*(f_m)} и {$\bar {G}$*(f_m)} их текущие выборочные оценки: {$\hat {G}$*(f_m)} и {$\hat {\bar {G}}$*(f_m)} соответственно. В рамках формализации (1)–(5) в результате получим равенство

Уравнение выравнивающего фильтра в данном случае определяется через АР-модель (1). Отсюда в первом приближении по аналогии с равенством (6) можно записать

После подстановки выражения (8) в левую часть тождества (7) получим меру качества АР-модели (1) вида

на роль целевой функции (3) рассматриваемой оптимизационной задачи. В ней в качестве опорного спектрального образца {G₀(f_m)} используется огибающая $\left\{ {{{{\bar {G}}}_{х}}({{f}_{m}})} \right\}$ периодограммы Шустера. Задача переходит в практическую плоскость: демодуляция СПМ (5) или оценка спектральной огибающей. Один из перспективных вариантов ее решения основывается на применении рециркулятора последовательности отсчетов в частотной области.

3. ПРИМЕР ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ

По определению (5) периодограмма Шустера является неотрицательной функцией частоты. Поэтому ее демодуляция, или амплитудное детектирование в частотной области, не требует обычной нелинейной (диодной) обработки сигнала в целях выпрямления его полярности. Достаточно сгладить последовательность отсчетов речевого сигнала согласно разностному уравнению [11]

где β_x = const. Выражение (10) описывает работу стандартного рециркулятора в функции межпериодного накопителя последовательности отсчетов речевого сигнала в режиме скользящего окна наблюдений в частотной области. В определенном смысле это аналог периодограммы Даньелла со сглаживанием соседних отсчетов [8]. Размер (длина) окна, или инерционность рециркулятора, регулируется выбором значения его параметра β_x > 0. Показатель инерционности [11]

ограничен снизу величиной $\Delta {{f}_{0}}$ = F/N разрешающей способности ДПФ (4) по частоте. Однако выражение (8) накладывает на показатель θ естественные ограничения и сверху – в расчете на определенную степень гладкости формы АР-оценки СПМ {G_p(f_m; b_l)}. Поэтому ограничимся равенством ${{\theta = }}\Delta {{f}_{0}}$, откуда получим верхнюю границу

Выражения (10) и (11) в совокупности определяют огибающую периодограммы Шустера при ее использовании в (12) в качестве опорного спектрального образца. Например, при M = N = 128 будем иметь β_x ≤ 0.37.

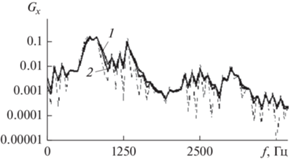
Наглядной иллюстрацией к этому примеру служит рис. 1, на котором представлены три графика: периодограммы (5) и ее огибающей (10) для двух значений параметра β_x. Графики получены в границах одного и того же фрейма гласного звука речи “а” при равенствах τ = 16 мс, F = 8 кГц и M = = 128. Как видим, варьируя значение коэффициента усиления β_x, мы можем в широких пределах регулировать форму спектральной огибающей $\left\{ {{{{\bar {G}}}_{х}}({{f}_{m}})} \right\}$ при сохранении достаточно высокой степени ее подобия форме исходной периодограммы (5). Система равенств

Рис. 1.

Графики периодограммы Шустера (штриховая кривая) и ее огибающей (сплошные кривые) в двух вариантах значений параметра β_x: 0.37 (1) и 0.25 (2).

и выражения (9)–(11) в совокупности определяют новый метод АР-моделирования речевого сигнала по данным его ДПФ на интервале наблюдений конечной длительности τ. Эффективность данного метода была исследована экспериментально.

4. ПРОГРАММА И МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

Объектом исследования служили сигналы шести русских гласных фонем из предыдущей работы автора [9]. Идея состояла в сравнительном анализе эффективности двух методов АР-моделирования речи: предложенного в данной работе – с использованием спектральной огибающей (12), и его прототипа, в котором в качестве опорного спектрального образца использовалась периодограмма Шустера (5). Напомним, что длительность каждого сигнала T_x = 2…3 с изначально предполагала его линейное членение на последовательность коротких (τ = 16 мс) фреймов при их частичном (по 3 мс в начале и в конце) взаимном перекрытии во времени. В результате для каждой фонемы была создана представительная речевая база данных объемом K = 1.6T_x/τ = 200…300 однородных фреймов {x(n)}. При частоте дискретизации речевого сигнала F = 8 кГц размерность каждого из них составила N = 128.

В дальнейшем по каждому фрейму с использованием 128-точечного ДПФ (M = 128) была получена периодограмма (5), а после этого – согласно выражениям (10)–(12) при равенстве β_x = 0.25 – ее огибающая $\left\{ {{{{\bar {G}}}_{х}}({{f}_{m}})} \right\}$ в качестве соответствующего спектрального образца {G₀(f_m)}. Его АР-модель (1) порядка p = 10 (типовое значение для систем АОР [1]) была получена согласно итеративной процедуре (2) при ее инициализации вектором параметров b₀ = = (1, –a_p), где a_p – вектор коэффициентов линейной авторегрессии p-го порядка. При этом было использовано выражение для градиента критериальной функции (9) общего вида [9]

где введены обозначения

Сходимость итераций (2) в точку b* минимума зависимости (9) гарантировалась выбором допустимого (ограниченного сверху) значения шага γ₀ = 0.1. Однако возникают вопросы принципиального характера: насколько гарантирована устойчивость итоговой АР-модели и какова ее точность?

Устойчивость формируемой модели (1) на нулевом шаге итераций обеспечивалась инициализацией вычислительной процедуры (2) с использованием выборочной оценки вектора коэффициентов a_p методом Берга. Устойчивость ее последующих приближений контролировалась наблюдателем визуально: по виду импульсной характеристики соответствующего формирующего фильтра с комплексным коэффициентом передачи

(13)

Рабочей характеристикой, или показателем эффективности предложенного метода служили значения функции (3), рассчитанные согласно выражению (9) для каждого отдельного фрейма данных {x(n)}. Впоследствии эти значения статистически усреднялись на множестве из K их практически независимых реализаций. При этом погрешность усредненных оценок в ее относительном выражении не вышла за пределы δ = 165/√K = 10…11% при доверительной вероятности, равной 0.9 [15, 19].

5. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Полученные результаты представлены на рисунках. На рис. 2а, 2б показаны кривые сходимости $V(l) = {{\rho }}({{{\mathbf{b}}}_{l}}),\,\,l\,{\text{ = }}\,{\text{1,2, }}...{\text{,}}$ двух разных методов АР-моделирования речи. Напомним, что различия между рассматриваемыми методами состоят в используемом опорном образце СПМ {G₀(f_m)}. Первоначально это была периодограмма Шустера (4), (5), а в новом методе – ее огибающая (10). Все остальные их элементы, включая итеративную градиентную процедуру (2), совпадают. Совпадают в данном случае и их начальные приближения вектора АР-параметров по методу Берга:

Рис. 2.

Кривые сходимости в метрике (3) двух методов АР-моделирования сигнала звука речи “а” (сплошные кривые): с использованием в качестве опорного спектрального образца периодограммы Шустера (а) и ее огибающей (б) в сопоставлении с кривыми сходимости их альтернатив (штриховые кривые): предложенного в статье метода и его прототипа соответственно.

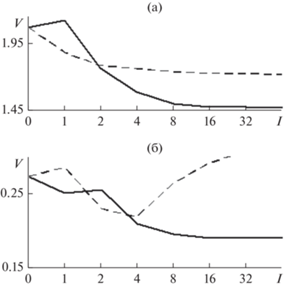
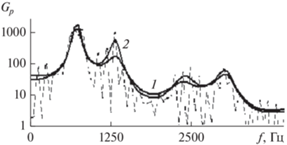
Как видим, обе кривые быстро сходятся в область оптимума l > l₀ = 4, где выполняется приближенное равенство b* ≈ b₈. В нормированном виде V₀(l) = V(l)/V(0), l = 1, 2, …, они практически не отличаются друг от друга по динамике (рис. 3). Правда, полученные результаты довольно сильно отличаются между собой по точности. Это хорошо видно из сравнения графиков двух СПМ на рис. 4. Кроме того, путем слежения за импульсной характеристикой формирующего фильтра (13) было установлено, что приближения вектора АР-параметров b_l, полученные новым методом (1)–(12), отвечают устойчивому варианту АР-модели (1) для всех l ≤ 64. Напротив, при применении метода-прототипа устойчивость АР-модели нарушается, начиная, по крайней мере, с восьмого шага приближений, для которого выполняется равенство

Рис. 3.

Нормированные кривые сходимости двух методов АР-моделирования: с использованием в качестве опорного спектрального образца периодограммы Шустера (кривая 1) и ее огибающей (кривая 2).

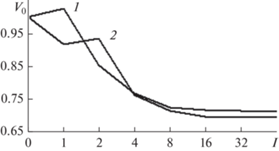
Рис. 4.

Семейство СПМ по результатам применения двух методов АР-моделирования: с использованием в качестве опорного спектрального образца периодограммы Шустера (кривая 1) и ее огибающей (кривая 2) в сопоставлении с графиком периодограммы Шустера (штриховая линия).

Отметим, что в рамках нового метода был получен качественно иной результат:

Наглядной иллюстрацией к сказанному служат штриховые кривые на рис. 2, которые отображают в метрике (3) динамику итераций (2) для альтернативного в каждом из двух случаев метода АР-моделирования. Так, начиная с точки l > 4 штриховая кривая на рис. 2б утрачивает все признаки сходимости к оптимуму. Это справедливо для метода-прототипа. Напротив, штриховая кривая на рис. 2а этими признаками определенно обладает. Это относится к новому методу. По-видимому, именно так проявляет себя проблема устойчивости АР-модели (1).

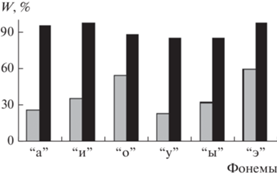
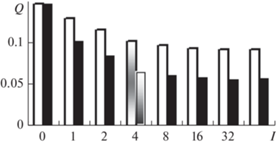
Отметим, что сделанные выводы распространяются и на другие гласные звуки речи контрольного диктора. Подтверждением служат две гистограммы распределений по гласным фонемам средней доли W(b_l) устойчивых результатов АР-моделирования на рис. 5, где серым фоном отмечены результаты работы [9]. При доверительной вероятности 0.95 погрешность измерений составила в данном случае величину порядка 196/√2000 ≈ 5% [19]. Таким образом, если в качестве опорного спектрального образца {G₀(f_m)} использовать не непосредственно периодограмму Шустера, а ее огибающей, то практически полностью исключается проблема устойчивости АР-модели в задачах ДСМ.

Рис. 5.

Гистограммы распределения по гласным фонемам контрольного диктора средней доли устойчивых АР-моделей (1) по результатам четырех итераций (2) при применении двух методов моделирования: с использованием в качестве опорного спектрального образца периодограммы Шустера (серые столбики [9]) и ее огибающей (черные столбики).

6. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Проведенное исследование было бы не полным без ответа на вопрос о сравнительной точности двух представленных на рис. 4 оценках СПМ. По существу, речь идет о критерии качества формируемой АР-модели. Ответом на этот вопрос могут служить результаты второй, заключительной стадии экспериментальных исследований. На этой стадии АР-модель (1) рассматривалась в качестве инверсии квадрата комплексного коэффициента передачи

выравнивающего фильтра (6). СПМ речевого сигнала на выходе этого фильтра

в идеале должна иметь прямоугольную огибающую {${{\bar {G}}_{y}}$(f_m; b_l)}, для которой в полосе рабочих частот выполняется тождество (7). В силу неидеальности АР-модели (1) оно приводит к следующему выражению для объективного показателя ее точности:

Он и служил в дальнейшем характеристикой сравнительной эффективности двух методов АР-моделирования. При этом для выделения спектральной огибающей $\left\{ {{{{\overline G }}_{y}}({{f}_{m}};{{{\mathbf{b}}}_{l}})} \right\}$ по аналогии с (10) использовали рециркулятор

Его коэффициент усиления в цепи обратной связи

рассчитывается из условия приблизительного равенства параметра инерционности $\theta = {{F}_{0}}$ частоте основного тона ${{F}_{0}}$ ≈ 130 Гц в речи контрольного диктора [15]. Для иллюстрации сказанного на рис. 6 представлены графики двух СПМ речевого сигнала на выходе выравнивающего фильтра (14), реализованного в двух вариантах оценки СПМ (см. рис. 4). Их огибающие, рассчитанные согласно (16), показаны на рисунке штриховыми кривыми. Даже визуально – по форме спектральной огибающей – метод-прототип проигрывает новому методу АР-моделирования. Полученные результаты отражены на рис. 7 в виде двух гистограмм показателя точности АР-моделирования (15) в зависимости от номера итерации l. Штриховкой здесь отмечены значения показателя для двух представленных на рис. 4 оценок СПМ. Как видим, и в отношении точности АР-модели (1) метод, предложенный в данной работе, выигрывает, причем существенно, у своего прототипа: примерно 36.5%. По сравнению с методом Берга (при l = 0 на рис. 7) выигрыш возрастает до 56%. Объяснением данного эффекта может служить сама идея АР-моделирования речевого сигнала на основе огибающей его линейчатого спектра мощности.

Рис. 6.

Графики СПМ сигнала гласного звука речи “а” на выходе выравнивающего фильтра (14) при применении двух методов АР-моделирования (сплошные кривые): метода-прототипа (а) и предложенного нового метода (б), в сопоставлении с графиками двух спектральных огибающих ${{\bar {G}}_{y}}({{f}_{m}})$ (штриховые кривые), рассчитанными согласно (16).

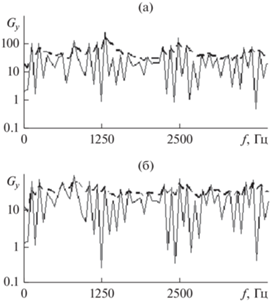
Рис. 7.

Гистограммы распределения показателя точности АР-модели (1) гласного звука речи “а” в зависимости от числа итераций (2) при применении двух методов моделирования: с использованием в качестве опорного спектрального образца периодограммы Шустера (светлые столбики) и ее огибающей (черные столбики).

ЗАКЛЮЧЕНИЕ

В результате проведенного исследования предложен новый метод АР-моделирования речевого сигнала в режиме скользящего окна наблюдений длительностью в один речевой фрейм. Его основополагающая идея состоит в использовании методологии ДСМ с огибающей периодограммы Шустера в качестве опорного спектрального образца. В результате удалось не только решить проблему устойчивости формируемой АР-модели речевого сигнала, но и существенно повысить ее точность в теоретико-информационном смысле.

Полученные результаты предназначены для использования в системах АОР различного назначения, включая речевую связь, прикладную акустику, техническую и медицинскую диагностику, анализ эмоционального состояния дикторов по голосу и др. [2, 20].