Радиотехника и электроника, 2023, T. 68, № 3, стр. 271-278

Идентификация сигналов на фоне помех трансформирующего типа со стиранием

В. В. Климов^*

Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация

^* E-mail: klimov47@list.ru

Поступила в редакцию 03.04.2022
После доработки 03.04.2022
Принята к публикации 18.04.2022

EDN: LCIWOI
DOI: 10.31857/S0033849423020092

Полный текст (PDF)

Аннотация

Рассмотрена задача идентификации двух источников бинарных сигналов на фоне помех трансформирующего типа со стиранием в условиях противодействия. Ситуация описывается антагонистической игрой, аналитическое решение которой дает оптимальные стратегии игроков и цену игры как функцию априорной вероятности появления одного из источников. Рассмотрены частные случаи.

ВВЕДЕНИЕ

Исследование окружающей среды дистанционными методами требует разработки математических моделей и методов принятия оптимальных решений в условиях априорной неопределенности [1–4]. В таких ситуациях для получения гарантированного результата приходится рассматривать внешнюю среду как активного игрока, настроенного антагонистически. Данная работа и посвящена исследованию такой ситуации. Подобная постановка задачи актуальна, например, в мониторинге воздушного пространства.

1. ПОСТАНОВКА ЗАДАЧИ

Пусть имеется два источника S₁ и S₂ бинарных сигналов. Каждый из источников может посылать два различных сигнала m₁ и m₂, причем на каждом следующим один за другим интервале времени происходит включение источников в канал связи случайным образом.

Вероятность включения источника S₁ равна Р, а источника S₂ – (1–Р). Сигналы поступают в систему наблюдения по каналу без памяти при действии нейтральных помех трансформирующего типа и помех стирания, где под помехой стирания понимается появление сигнала m₃, отличного от m₁ и m₂. Вероятность трансформации сигнала m₁ в m₂ или сигнала m₂ в m₁ равна Р₀, а вероятность стирания – S. При этом предполагается, что вероятность искажения сигнала не превосходит 1/2, т.е. выполняется неравенство

(1)

${{Р}_{0}} + S \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

На выходе канала связи имеется система наблюдения, в задачу которой входит обработка поступающих сигналов по определенному правилу и вынесение решения о наличии в данном дискретном интервале времени источника либо S₁, либо S₂. По условию задачи система наблюдения знает, какой из сигналов (m₁ или m₂) на данном интервале времени источник S₁ должен посылать. Тем не менее это не исключает ошибок при вынесении решений. Действительно, система наблюдения не знает, какой из источников был включен в канал связи; второй причиной ошибок является наличие помех трансформирующего типа и помех стирания.

Показателем качества работы системы наблюдения принимается средний выигрыш. Предполагается, что система наблюдения не имеет информации о том, какой из сигналов посылает источник S₂, более того, источник S₂ ведет себя наихудшим образом с точки зрения системы наблюдения. Таким образом, данную ситуацию можно описать антагонистической игрой, в которой первым игроком является система наблюдения в коалиции с источником S₁, вторым игроком является источник S₂.

Рис. 1.

Взаимодействие источников сигналов и системы наблюдения.

Пусть а – выигрыш системы наблюдения за правильное решение, b – за неверное решение, причем a ≥ b ≥ 0.

Первый игрок стремится увеличить свой средний выигрыш; второй игрок стремится уменьшить средний выигрыш. Схема взаимодействия источников сигналов и системы наблюдения представлена на рис. 2.

Рис. 2.

Выигрыш первого игрока при P ≥ P₁.

2. ПОСТРОЕНИЕ РЕШАЮЩЕГО ПРАВИЛА

Опишем теперь множество чистых стратегий игроков. Источник S₂ может посылать один из двух сигналом m₁ или m₂. Таким образом, у второго игрока имеется только две чистых стратегий. Чистыми стратегиями первого игрока являются решающие функции. Выпишем все чистые стратегии:

(2)

$\begin{gathered} {{{\mathbf{I}}}_{1}} = {\text{ }}\left[ {{{m}_{1}}:{{{{m}_{2}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{2}}{{m}_{3}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{2}} = {\text{ }}\left[ {{{m}_{2}}:{{{{m}_{1}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{1}}{{m}_{3}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{3}} = {\text{ }}\left[ {{{m}_{2}}{{m}_{3}}:{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{4}} = {\text{ }}\left[ {{{m}_{1}}{{m}_{3}}:{{{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{2}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{5}} = {\text{ }}\left[ {{{m}_{1}}:{{{{m}_{2}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{2}}{{m}_{3}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ {{{\mathbf{I}}}_{6}} = {\text{ }}\left[ {{{m}_{2}}:{{{{m}_{1}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{1}}{{m}_{3}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ {{{\mathbf{I}}}_{7}} = {\text{ }}\left[ {{{m}_{2}}{{m}_{3}}:{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ {{{\mathbf{I}}}_{8}} = {\text{ }}\left[ {{{m}_{1}}{{m}_{3}}:{{{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{2}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ {{{\mathbf{I}}}_{9}} = {\text{ }}\left[ {{{m}_{3}}:{{{{m}_{1}}{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{1}}{{m}_{2}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{{10}}} = {\text{ }}\left[ {{{m}_{1}}{{m}_{2}}:{{{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{3}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right], \\ {{{\mathbf{I}}}_{{11}}} = {\text{ }}\left[ {{{S}_{1}}} \right], \\ {{{\mathbf{I}}}_{{12}}} = {\text{ }}\left[ {{{S}_{2}}} \right], \\ {{{\mathbf{I}}}_{{13}}} = {\text{ }}\left[ {{{m}_{3}}:{{{{m}_{1}}{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{1}}{{m}_{2}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ {{{\mathbf{I}}}_{{14}}} = {\text{ }}\left[ {{{m}_{1}}{{m}_{2}}:{{{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{3}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right], \\ \end{gathered} $

(3)

${\mathbf{I}} = \left\{ {I_{i}^{j}} \right\},\,\,\,\,j = 1,\,\,2;\,\,\,\,i = 1,\,\,14,$

где элементы $I_{i}^{j}$ матрицы I имеют следующий вид:

$\begin{gathered} I_{1}^{1} = a\left[ {P(1 - {{P}_{0}} - S) + (1 - P)(1 - {{P}_{0}})} \right] + \\ + \,\,b\left[ {P({{P}_{0}} + S)(1 - P){{P}_{0}}} \right], \\ \end{gathered} $

$\begin{gathered} I_{2}^{1} = a\left[ {P{{P}_{0}} + (1 - P)({{P}_{0}} + S)} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}}) + (1 - P)(1 - {{P}_{0}} - S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{3}^{1} = a\left[ {P({{P}_{0}} + S) + (1 - P){{P}_{0}}} \right] + \\ + \,b\left[ {P(1 - {{P}_{0}} - S) + (1 - P)(1 - {{P}_{0}})} \right], \\ \end{gathered} $

$\begin{gathered} I_{4}^{1} = a\left[ {P(1 - {{P}_{0}}) + (1 - P)(1 - {{P}_{0}} - S)} \right] + \\ + \,\,b\left[ {P{{P}_{0}} + (1 - P)({{P}_{0}} + S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{5}^{1} = a\left[ {P{{P}_{0}} + (1 - P)(1 - {{P}_{0}})} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}}) + (1 - P){{P}_{0}}} \right], \\ \end{gathered} $

$\begin{gathered} I_{6}^{1} = a\left[ {P(1 - {{P}_{0}} - S) + (1 - P)({{P}_{0}} + S)} \right] + \\ + \,\,b\left[ {P({{P}_{0}} + S) + (1 - P)(1 - {{P}_{0}} - S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{7}^{1} = a\left[ {P(1 - {{P}_{0}}) + (1 - P){{P}_{0}}} \right] + \\ + \,\,b\left[ {P{{P}_{0}} + (1 - P)(1 - {{P}_{0}})} \right], \\ \end{gathered} $

$\begin{gathered} I_{8}^{1} = a\left[ {{{P}_{0}} + S) + (1 - P)(1 - {{P}_{0}} - S)} \right] + \\ {\text{ + }}\,\,b\left[ {P(1 - {{P}_{0}} - S) + (1 - P)({{P}_{0}} + S)} \right], \\ \end{gathered} $

(4)

$\begin{gathered} I_{9}^{1} = a\left[ {PS + (1 - P)(1 - S)} \right] + \\ {\text{ + }}\,\,b\left[ {P(1 - S) + (1 - P)S} \right], \\ \end{gathered} $

$\begin{gathered} I_{{10}}^{1} = a\left[ {P(1 - S) + (1 - P)S} \right] + \\ {\text{ + }}\,\,b\left[ {PS + (1 - P)(1 - S)} \right], \\ \end{gathered} $

$I_{{11}}^{1} = aP + b(1 - P),$

$I_{{12}}^{1} = a(1 - P) + bP,$

$\begin{gathered} I_{{13}}^{1} = a\left[ {PS + (1 - P)(1 - S)} \right] + \\ {\text{ + }}\,\,b\left[ {P(1 - S) + (1 - P)S} \right], \\ \end{gathered} $

$\begin{gathered} I_{{14}}^{1} = a\left[ {P(1 - S) + (1 - P)S} \right] + \\ {\text{ + }}\,\,b\left[ {PS + (1 - P)(1 - S)} \right]. \\ \end{gathered} $

Отметим, что

$I_{{13}}^{1} = I_{9}^{1},\,\,\,\,I_{{14}}^{1} = I_{{10}}^{1}.$

Элементы $I_{i}^{2}$ матрицы I имеют следующий вид:

$\begin{gathered} I_{1}^{2} = a\left[ {P(1 - {{P}_{0}} - S) + (1 - P)({{P}_{0}} + S)} \right] + \\ + \,\,b\left[ {P({{P}_{0}} + S) + (1 - P)(1 - {{P}_{0}} - S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{2}^{2} = a\left[ {P{{P}_{0}} + (1 - P)(1 - {{P}_{0}})} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}}) + (1 - P){{P}_{0}}} \right], \\ \end{gathered} $

$\begin{gathered} I_{3}^{2} = a\left[ {P({{P}_{0}} + S) + (1 - P)(1 - {{P}_{0}} - S)} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}} - S) + (1 - P)({{P}_{0}} + S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{4}^{2} = a\left[ {P(1 - {{P}_{0}}) + (1 - P){{P}_{0}}} \right] + \\ + \,\,b\left[ {P{{P}_{0}} + (1 - P)(1 - {{P}_{0}})} \right], \\ \end{gathered} $

$\begin{gathered} I_{5}^{2} = a\left[ {P{{P}_{0}} + (1 - P)({{P}_{0}} + S)} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}}) + (1 - P)(1 - {{P}_{0}} - S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{6}^{2} = a\left[ {P(1 - {{P}_{0}} - S) + (1 - P)(1 - {{P}_{0}})} \right] + \\ + \,\,b\left[ {P({{P}_{0}} + S) + (1 - P){{P}_{0}}} \right], \\ \end{gathered} $

$\begin{gathered} I_{7}^{2} = a\left[ {P(1 - {{P}_{0}}) + (1 - P)(1 - {{P}_{0}} - S)} \right] + \\ + \,\,b\left[ {P{{P}_{0}} + (1 - P)({{P}_{0}} + S)} \right], \\ \end{gathered} $

$\begin{gathered} I_{8}^{2} = a\left[ {P({{P}_{0}} + S) + (1 - P){{P}_{0}}} \right] + \\ + \,\,b\left[ {P(1 - {{P}_{0}} - S) + (1 - P)(1 - {{P}_{0}})} \right], \\ \end{gathered} $

$\begin{gathered} I_{9}^{2} = a\left[ {PS + (1 - P)(1 - S)} \right] + \\ + \,\,b\left[ {P(1 - S) + (1 - P)S} \right], \\ \end{gathered} $

(5)

$\begin{gathered} I_{{10}}^{2} = a\left[ {P(1 - S) + (1 - P)S} \right] + \\ + \,\,b\left[ {PS + (1 - P)(1 - S)} \right], \\ \end{gathered} $

$I_{{11}}^{2} = aP + b(1 - P),$

$I_{{12}}^{2} = a(1 - P) + bP,$

$\begin{gathered} I_{{13}}^{2} = a\left[ {PS + (1 - P)(1 - S)} \right] + \\ + \,\,b\left[ {P(1 - S) + (1 - P)S} \right], \\ \end{gathered} $

$\begin{gathered} I_{{14}}^{2} = a\left[ {P(1 - S) + (1 - P)S} \right] + \\ + \,\,b\left[ {PS + (1 - P)(1 - S)} \right]. \\ \end{gathered} $

Отметим, что, как и в случае $I_{i}^{1}$ , выполняется

$I_{{13}}^{2} = I_{9}^{2},\,\,\,\,I_{{14}}^{2} = I_{{10}}^{2}.$

Таким образом, стратегии I₁₃ и I₁₄ можно опустить.

Рассмотрим случай, когда включение источника S₁ в канал связи достаточно маловероятно, т.е. пусть Р ≤ 1/2.

Исследуем матрицу с элементами $I_{i}^{j}$ на наличие в ней доминируемых стратегий, учитывая соотношение

(6)

${{P}_{0}} + S \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

Сравнивая строки матрицы $I_{i}^{j}$, получим

$I_{1}^{j} \geqslant I_{4}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{2}^{j} \geqslant I_{3}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{5}^{j} \geqslant I_{8}^{j}\,\,{\text{при}}\,\,j = 1,2;$

(7)

$I_{6}^{j} \geqslant I_{7}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{9}^{j} \geqslant I_{{10}}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{{12}}^{j} \geqslant I_{{11}}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{1}^{j} \geqslant I_{5}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{6}^{j} \geqslant I_{2}^{j}\,\,{\text{при}}\,\,j = 1,2,$

$I_{{12}}^{j} \geqslant I_{9}^{j}\,\,{\text{при}}\,\,j = 1,2.$

Вычеркивая четвертую, третью, восьмую, седьмую, десятую, одиннадцатую, пятую, вторую, девятую стратегию (строку), получим в итоге три стратегии, I₁, I₆, I₁₂.

Таким образом, задача сводится к решению игры I размером (3 × 2), где матрица I им примет вид

(8)

${\mathbf{I}} = \begin{array}{*{20}{c}} {{{{\mathbf{I}}}_{1}}} \\ {{{{\mathbf{I}}}_{6}}} \\ {{{{\mathbf{I}}}_{{12}}}} \end{array}\left\| {\begin{array}{*{20}{c}} {{{m}_{1}}}&{{{m}_{2}}} \\ A&B \\ B&A \\ E&E \end{array}} \right\|,$

где

$A = a(1 - {{P}_{0}} - PS) + b({{P}_{0}} + PS),$

$\begin{gathered} B = a(P + {{P}_{0}} + S - 2P{{P}_{0}} - 2PS) + \\ + \,\,b(1 - {{P}_{0}} - P - S + 2P{{P}_{0}} + 2PS), \\ \end{gathered} $

$E = a(1 - P) + bP.$

Будем решать полученную игру графическим методом.

Пусть y – вероятность выбора вторым игроком первой стратегии, (1 – y) – вероятность выбора вторым игроком второй стратегии, а Z_i – выигрыш первого игрока при выборе им i-й чистой стратегии.

Очевидно,

$i = 1,\,\,{\text{когда}}\,\,{\text{выбрана}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{1}};$

$i = 2,\,\,{\text{когда}}\,\,{\text{выбрана}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{6}};$

$i = 3,\,\,{\text{когда}}\,\,{\text{выбрана}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{{12}}}.$

Имеем

(9)

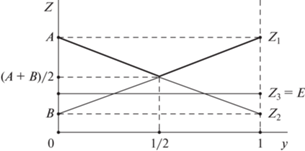
$\begin{array}{*{20}{c}} {{{Z}_{1}}} \\ {{{Z}_{2}}} \\ {{{Z}_{3}}} \end{array}\left\| {\begin{array}{*{20}{c}} y&{1 - y} \\ A&B \\ B&A \\ E&E \end{array}} \right\|,$

где

${{Z}_{1}} = Ay + B{\text{ }}(1 - y),$

${{Z}_{2}} = By + A(1 - y),$

${{Z}_{3}} = E.$

Таким образом, имеем

(10)

$\begin{gathered} {{Z}_{1}} = \left( {A - B} \right)y + B, \\ {{Z}_{2}} = \left( {B - A} \right)y + A, \\ {{Z}_{3}} = E. \\ \end{gathered} $

Очевидно, что

(11)

$\begin{gathered} A - B = (a - b)(1 - P)(1 - 2{{P}_{0}} - S) \geqslant \\ \geqslant (a - b){\text{ }}(1 - P)(1 - 2{{P}_{0}} - S) \geqslant 0. \\ \end{gathered} $

Таким образом, получили соотношение A ≥ B, которое понадобится нам в графическом методе. Рассмотрим два случая, которые соответствуют разным частям диапазона изменения параметра Р ∈ [0, 1/2].

I случай:

$\begin{gathered} E \leqslant {{\left( {A + B} \right)} \mathord{\left/ {\vphantom {{\left( {A + B} \right)} 2}} \right. \kern-0em} 2},\,\,{\text{т}}{\text{.е}}{\text{.}} \\ P \geqslant {{P}_{1}} = {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(3 - 3S - 2{{P}_{0}})}}} \right. \kern-0em} {(3 - 3S - 2{{P}_{0}})}}. \\ \end{gathered} $

Выигрыш первого игрока при P ≥ P₁ представлен на рис. 2.

Из курса по теории игр [5] известно, что

(12)

${v} = \mathop {\min }\limits_y \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

На рис. 2 жирной линией представлен график функции

(13)

$Z = \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y),$

Как следует из рис. 2, минимальное значение этой функции достигается при y = 1/2 и равно (A + B)/2.

Таким образом, цена игры равна

(14)

${v} = {{(A + B)} \mathord{\left/ {\vphantom {{(A + B)} 2}} \right. \kern-0em} 2}.$

Оптимальная стратегия второго игрока имеет вид

(15)

$\begin{gathered} y_{1}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \\ y_{2}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}. \\ \end{gathered} $

Оптимальная стратегия первого игрока находится в результате решения уравнения

(16)

$xA + (1--x)B = xB + (1--x){\text{ }}А\,.$

Итак, решая это уравнение относительно x, получим

(17)

$\begin{gathered} x_{1}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \\ x_{6}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}. \\ x_{{12}}^{*} = 0. \\ \end{gathered} $

По определению переменных имеем

(18)

$A - E = (a - b)(P - {{P}_{0}} - PS){\text{ }},$

(19)

$B - E = (a - b)(2P + {{P}_{0}} + S - 2P{{P}_{0}} - 2PS - 1).$

По предположению случая I имеем

(20)

$E \leqslant {{(A + B)} \mathord{\left/ {\vphantom {{(A + B)} 2}} \right. \kern-0em} 2}.$

Это неравенство эквивалентно другому неравенству

(21)

$A - E \geqslant E - B,$

из которого следует

(22)

$P \geqslant {{P}_{1}} = {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(3 - 3S - 2{{P}_{0}})}}} \right. \kern-0em} {(3 - 3S - 2{{P}_{0}})}}.$

Цена игры как функция входящих параметров имеет вид

(23)

${v} = {{(a + b)} \mathord{\left/ {\vphantom {{(a + b)} 2}} \right. \kern-0em} 2} + (a - b){{(P + S - 2P{{P}_{0}} - 3PS)} \mathord{\left/ {\vphantom {{(P + S - 2P{{P}_{0}} - 3PS)} 2}} \right. \kern-0em} 2}.$

Перейдем к оставшейся части диапазона параметра P.

II случай:

$\begin{gathered} E \geqslant {{(A + B)} \mathord{\left/ {\vphantom {{(A + B)} 2}} \right. \kern-0em} 2},\,\,{\text{т}}{\text{.е}}{\text{.}} \\ P \leqslant {{P}_{1}} = {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(3--3S{\text{ }}--2{{P}_{0}})}}} \right. \kern-0em} {(3--3S{\text{ }}--2{{P}_{0}})}}. \\ \end{gathered} $

Выигрыш первого игрока при P ≤ P₁ представлен на рис. 3.

Рис. 3.

Выигрыш первого игрока при P ≤ P₁.

Как это следует из теории игр [5], цена игры

${v} = \mathop {\min }\limits_y \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

На рис. 3 жирной линией представлен график функции

(24)

$Z(y) = \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y),$

Очевидно, минимум этой функции достигается на [y₀, y⁰].

Таким образом, оптимальная стратегия второго игрока имеет вид

(25)

$y_{1}^{*} \in \left[ {{{y}_{0}},{{y}^{0}}} \right]{\text{ }},$

(26)

$y_{2}^{*} = 1 - y_{1}^{*}.$

Из требования E ≤ A следует, что

(27)

$P \geqslant {{{{P}_{0}}} \mathord{\left/ {\vphantom {{{{P}_{0}}} {\left( {1 - S} \right)}}} \right. \kern-0em} {\left( {1 - S} \right)}} = {{P}_{{0S~}}}.$

Границы диапазона находятся решением уравнений

(28)

$\begin{gathered} {{y}_{0}} = {{(E - A)} \mathord{\left/ {\vphantom {{(E - A)} {(B - A)}}} \right. \kern-0em} {(B - A)}} = {{(A - E)} \mathord{\left/ {\vphantom {{(A - E)} {(A - B)}}} \right. \kern-0em} {(A - B)}} = \\ = {{(P - {{P}_{0}} - PS)} \mathord{\left/ {\vphantom {{(P - {{P}_{0}} - PS)} {(1 - P)}}} \right. \kern-0em} {(1 - P)}}(1 - 2{{P}_{0}} - S){\text{ }}. \\ \end{gathered} $

(29)

$\begin{gathered} {{y}^{0}} = {{(E - B)} \mathord{\left/ {\vphantom {{(E - B)} {(A - B)}}} \right. \kern-0em} {(A - B)}} = {{(1 - 2P - {{P}_{0}} - S + 2P{{P}_{0}} + 2PS)} \mathord{\left/ {\vphantom {{(1 - 2P - {{P}_{0}} - S + 2P{{P}_{0}} + 2PS)} {(1--P)(1--2{{P}_{0}}--S)}}} \right. \kern-0em} {(1--P)(1--2{{P}_{0}}--S)}} = \\ = {{(1 - 2P)(1 - S - {{P}_{0}})} \mathord{\left/ {\vphantom {{(1 - 2P)(1 - S - {{P}_{0}})} {(1 - P)}}} \right. \kern-0em} {(1 - P)}}(1 - 2{{P}_{0}} - S). \\ \end{gathered} $

Сравнивая значения y₀ и y⁰, легко заметить, что эти значения симметричны относительно точки y = 1/2, т.е.

(30)

${{y}^{0}} = 1 - {{y}_{0}}.$

Из предложения случая II следует, что

(31)

$E \geqslant {{(A + B)} \mathord{\left/ {\vphantom {{(A + B)} 2}} \right. \kern-0em} 2},$

из которого следует, что

(32)

$A - E \leqslant E - B$

и это приводит к неравенству

(33)

$P \leqslant {{P}_{1}} = {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(3 - 3S - 2{{P}_{0}})}}} \right. \kern-0em} {(3 - 3S - 2{{P}_{0}})}}.$

Оптимальная стратегия первого игрока имеет вид

(34)

$\begin{gathered} x_{1}^{*} = 0, \\ x_{6}^{*} = 0. \\ x_{{12}}^{*} = 1. \\ \end{gathered} $

Цена игры в этом случае равна

(35)

${v} = E = a(1 - P) + bP.$

Итак, оптимальная стратегия системы наблюдения при условии

(36)

$x* = {{I}_{{12}}} = [{{S}_{2}}]{\text{ }}.$

Рассмотрим теперь случай, когда включение источника S₁ в канал связи достаточно вероятно, т.е. пусть выполняется соотношение

$Р \geqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

Исследуем матрицу I на наличие в ней доминируемых стратегий, учитывая соотношение

(37)

${{P}_{0}} + S \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

Сравнивая элементы строк матрицы I, получим

$I_{1}^{j} \geqslant I_{3}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{6}^{j} \geqslant I_{8}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{4}^{j} \geqslant I_{2}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{7}^{j} \geqslant I_{5}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{{11}}^{j} \geqslant I_{{12}}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{{10}}^{j} \geqslant I_{9}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{4}^{j} \geqslant I_{1}^{j}\,\,{\text{при}}\,\,j = 1,2;$

$I_{7}^{j} \geqslant I_{6}^{j}\,\,{\text{при}}\,\,j = 1,2;$

(38)

$I_{{11}}^{j} \geqslant I_{{10}}^{j}\,\,{\text{при}}\,\,j = 1,2.$

Вычеркивая третью, восьмую, вторую, пятую, двенадцатую, девятую, первую, шестую, десятую стратегию (строку), получим в итоге три стратегии: I₄, I₇, I₁₁.

Таким образом, задача сводится к решению игры с платежной матрицей I размером (3 × 2), где элементы матрицы имеют следующий вид:

(39)

${\mathbf{I}} = \begin{array}{*{20}{c}} {{{{\mathbf{I}}}_{4}}} \\ {{{{\mathbf{I}}}_{7}}} \\ {{{{\mathbf{I}}}_{{11}}}} \end{array}\left\| {\begin{array}{*{20}{c}} {{{m}_{1}}}&{{{m}_{2}}} \\ C&D \\ D&C \\ F&F \end{array}} \right\|,$

где

$C = a{\text{ }}(1 - {{P}_{0}} - S + PS) + b({{P}_{0}} + S - PS),$

$D = a(P + {{P}_{0}} - 2P{{P}_{0}}) + b(1 - P - {{P}_{0}} + 2P{{P}_{0}}),$

$F = aP + b(1 - P).$

Будем решать полученную игру графическим методом. Пусть y – вероятность выбора вторым игроком первой стратегии, (1 – y) – вероятность выбора вторым игроком второй стратегии, а Z_i –выигрыш первого игрока при выборе им i-й чистой стратегии.

Очевидно, случаю

$i = 1,\,\,{\text{соответствует}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{4}},$

$i = 2,\,\,{\text{соответствует}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{7}},$

$i = 3,\,\,{\text{соответствует}}\,\,{\text{стратегия}}\,\,{{{\mathbf{I}}}_{{12}}}.$

Итак, имеем

(40)

$\begin{array}{*{20}{c}} {{{Z}_{1}}} \\ {{{Z}_{2}}} \\ {{{Z}_{3}}} \end{array}\left\| {\begin{array}{*{20}{c}} y&{1 - y} \\ C&D \\ D&C \\ F&F \end{array}} \right\|,$

где

${{Z}_{1}} = Cy + D(1 - y),$

${{Z}_{2}} = Dy + C(1 - y),$

${{Z}_{3}} = F.$

Приведя подобные члены, получим

${{Z}_{1}} = \left( {C - D} \right)y + D,$

(41)

${{Z}_{2}} = \left( {D - C} \right)y + C,$

${{Z}_{3}} = F.$

Сравнивая между собой значения C и D, получим

(42)

$\begin{gathered} C - D = a(1 - P - 2{{P}_{0}}(1 - P) - S + PS) + \\ + \,\,b(2{{P}_{0}} + S - PS - 1 + P - 2P{{P}_{0}}) = \\ = (a - b)(1 - P)(1 - 2{{P}_{0}} - S) \geqslant \\ \geqslant (a - b)(1 - P)(1 - 2{{P}_{0}} - 2S) \geqslant 0{\text{ }}. \\ \end{gathered} $

I случай: F ≤ (C + D)/2, или P ≤ (1 – S)/(1 – S) + + 2P₀) = P₂.

Выигрыш первого игрока при P ≤ P₂ представлен на рис. 4:

${v} = \mathop {\min }\limits_y \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

Рис. 4.

Выигрыш первого игрока при P ≤ P₂.

На рис. 4 жирной линией представлен график функции

$Z(y) = \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

Как следует из графика, минимальное значение функции Z(y) достигается при y = 1/2 и равно (C + + D)/2. Значит, цена игры

(43)

${v} = {{(C + D)} \mathord{\left/ {\vphantom {{(C + D)} 2}} \right. \kern-0em} 2}.$

Оптимальная стратегия второго игрока имеет вид

(44)

$\begin{gathered} y_{1}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \hfill \\ y_{2}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}. \hfill \\ \end{gathered} $

Оптимальная стратегия первого игрока находится в виде решения относительно x уравнения

(45)

$xC + (1 - x)D = xD + (1 - x)С.$

Итак, решение этого уравнения дает

(46)

$\begin{gathered} x_{4}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \\ x_{7}^{*} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}, \\ x_{{11}}^{*} = 0. \\ \end{gathered} $

Очевидно, неравенство F ≤ (C + D)/2 равносильно неравенству

(47)

$\left( {C - F} \right) + \left( {D - F} \right) \geqslant 0,$

(48)

$\begin{gathered} C - F = a(1 - {{P}_{0}} - S + PS - P) + \\ + \,\,b( - 1 + P + {{P}_{0}} + S--PS) = \\ = (a - b)(1 - P - {{P}_{0}} - S + P), \\ \end{gathered} $

(49)

$\begin{gathered} D - F = a({{P}_{0}} - 2P{{P}_{0}}) + \\ + \,\,b( - {{P}_{0}} + 2P{{P}_{0}}) = (a - b){{P}_{0}}(1 - 2P). \\ \end{gathered} $

Отсюда следует

(50)

$P \leqslant {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(1 - S + 2{{P}_{0}})}}} \right. \kern-0em} {(1 - S + 2{{P}_{0}})}} = {{P}_{2}}.$

Цена игры в этом случае

(51)

${v} = {{(a + b)} \mathord{\left/ {\vphantom {{(a + b)} 2}} \right. \kern-0em} 2} + (a - b){{(P - S - 2P{{P}_{0}} + PS)} \mathord{\left/ {\vphantom {{(P - S - 2P{{P}_{0}} + PS)} 2}} \right. \kern-0em} 2}.$

Перейдем к оставшейся части диапазона параметра Р.

$F \geqslant {{(C + D)} \mathord{\left/ {\vphantom {{(C + D)} 2}} \right. \kern-0em} 2},\,\,{\text{или}}\,\,P \geqslant {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(1--S + 2{{P}_{0}})}}} \right. \kern-0em} {(1--S + 2{{P}_{0}})}} = {{P}_{2}}.$

Выигрыш первого игрока при P ≥ P₂ представлен на рис. 5.

Рис. 5.

Выигрыш первого игрока при P ≥ P₂.

Из теории игр известно [5], что цена игры равна

${v} = \mathop {\min }\limits_y \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

На рис. 5 жирной линией представлен график функции

$Z(y) = \mathop {\max }\limits_{i = 1,3} {{Z}_{i}}(y).$

Минимум ее достигается на отрезке [y₀, y⁰].

Таким образом, оптимальная стратегия второго игрока имеет вид

$y_{1}^{*} \in \left[ {{{y}_{0}},{{y}^{0}}} \right]{\text{ }},$

$y_{2}^{*} = 1 - y_{1}^{*}.$

Границы данного диапазона имеют вид

(52)

$\begin{gathered} {{y}_{0}} = ~{{(F - C)} \mathord{\left/ {\vphantom {{(F - C)} {(D - C)}}} \right. \kern-0em} {(D - C)}} = {{(C - F)} \mathord{\left/ {\vphantom {{(C - F)} {(C--~D)}}} \right. \kern-0em} {(C--~D)}} = \\ = {{(1 - P - {{P}_{0}} - S + PS)} \mathord{\left/ {\vphantom {{(1 - P - {{P}_{0}} - S + PS)} {(1 - P)}}} \right. \kern-0em} {(1 - P)}}(1 - 2{{P}_{0}} - S), \\ \end{gathered} $

(53)

$\begin{gathered} {{y}^{0}} = {{(F - D)} \mathord{\left/ {\vphantom {{(F - D)} {(C - D)}}} \right. \kern-0em} {(C - D)}} = \\ = {{(2P{{P}_{0}} - {{P}_{0}})} \mathord{\left/ {\vphantom {{(2P{{P}_{0}} - {{P}_{0}})} {(1 - P)}}} \right. \kern-0em} {(1 - P)}}(1 - 2{{P}_{0}} - S). \\ \end{gathered} $

Легко видеть, что y₀ и y⁰ симметричны относительно y =1/2, т.е.

${{y}_{0}} = 1 - {{y}^{0}}.$

Оптимальная стратегия первого игрока имеет вид

(54)

$\begin{gathered} x_{4}^{*} = 0, \\ x_{7}^{*} = 0, \\ x_{{11}}^{*} = 1. \\ \end{gathered} $

Цена игры на этой части диапазона равна

(55)

${v} = aP + b(1 - P){\text{ }}.$

Итак, получим четыре интервала параметра Р:

$[0,{{P}_{1}}],\,\,[{{P}_{1}},{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}],\,\,[{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{{P}_{2}}],\,\,[{{P}_{2}},1].$

Зависимость цены игры от априорной вероятности представлена на рис. 6.

Рис. 6.

Зависимость цены игры от априорной вероятности.

На графике приведены также и частные случаи задачи: полное отсутствие помех (P₀= 0, S = 0), случай отсутствия стирания (S = 0), случай отсутствия помех трансформации (P₀= 0).

Значения параметров, отмеченных на графике, имеют вид

(56)

${{P}_{1}} = ~{{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(1 - 3S - 2{{P}_{0}})}}} \right. \kern-0em} {(1 - 3S - 2{{P}_{0}})}},$

(57)

${{P}_{2}} = {{(1 - S)} \mathord{\left/ {\vphantom {{(1 - S)} {(1 - S + 2{{P}_{0}})}}} \right. \kern-0em} {(1 - S + 2{{P}_{0}})}},$

(58)

$P_{1}^{0} = {1 \mathord{\left/ {\vphantom {1 {(3 - 2{{P}_{0}})}}} \right. \kern-0em} {(3 - 2{{P}_{0}})}},$

(59)

$P_{2}^{0} = {1 \mathord{\left/ {\vphantom {1 {(1 + 2{{P}_{0}})}}} \right. \kern-0em} {(1 + 2{{P}_{0}})}}.$

Итак, при P ≤ P₁ цена игры равна

(60)

${v} = a(1 - P) + bP,$

при P₁ ≤ P ≤ 1/2 цена игры –

(61)

при 1/2 ≤ P ≤ P₂ цена игры –

(62)

при P₂ ≤ P цена игры –

(63)

${v} = aP + b(1 - P).$

Оптимальная стратегия второго игрока представлена на рис. 7.

Рис. 7.

Оптимальная стратегия второго игрока.

Значения параметров имеют вид

(64)

${{P}_{{0S}}} = {{{{P}_{0}}} \mathord{\left/ {\vphantom {{{{P}_{0}}} {(1 - S)}}} \right. \kern-0em} {(1 - S)}},$

(65)

${{P}_{{1S}}} = {{(1 - {{P}_{0}} - S)} \mathord{\left/ {\vphantom {{(1 - {{P}_{0}} - S)} {(1 - S)}}} \right. \kern-0em} {(1 - S)}}.$

Очевидно, что P_0S и P_1S симметричны относительно P = 1/2,

(66)

${{P}_{{0S}}} = 1 - {{P}_{{1S}}}.$

3. ИТОГОВОЕ ПРАВИЛО

Решающее правило системы имеет вид:

на отрезке [0, P₁] принимается решение “S₂”

(67)

$\left. {{{m}_{1}}:{{{{m}_{2}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{2}}{{m}_{3}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right\}\,\,{\text{c}}\,\,{\text{вероятностью}}\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$

на отрезке [P₁, 1/2] – решение

(68)

$\left. {{{m}_{2}}:{{{{m}_{1}}{{m}_{3}}} \mathord{\left/ {\vphantom {{{{m}_{1}}{{m}_{3}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right\}\,\,{\text{c}}\,\,{\text{вероятностью}}\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$

или решение

(69)

$\left. {{{m}_{1}}{{m}_{3}}:{{{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{2}}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}}} \right\}\,\,{\text{c}}\,\,{\text{вероятностью}}\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$

на отрезке [1/2, P₂] – решение

(70)

$\left. {{{m}_{2}}{{m}_{3}}:{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right\}\,\,{\text{c}}\,\,{\text{вероятностью}}\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$

на отрезке [P₂, 1] принимается решение “S₁”.

Оптимальное решение можно представить при (i ≠ j) на рис. 8.

Рис. 8.

Оптимальная стратегия системы наблюдения.

Решающее правило системы наблюдения можно представить и в другой форме. Итоговое решающее правило системы наблюдения представлено на рис. 9.

Рис. 9.

Итоговое решающее правило системы наблюдения.

Список литературы

Климов В.В. // Вопросы математического моделирования. М. ИРЭ АН СССР, 1979. С.25.
Крапивин В.Ф. Теоретико-игровые методы синтеза сложных систем в конфликтных ситуациях. М.: Сов. радио, 1972.
Климов В.В. // Экологические системы и приборы. 2000. № 5. С. 2.
Вентцель Е.С. Исследование операций. М.: Сов. радио, 1972.
Дрешер М. Стратегические игры. Теория и приложения. М.: Сов. радио, 1964.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал