Расплавы, 2021, № 1, стр. 90-102
О статистической изменчивости измеримых объектов, возникающих при непрерывной разливке стали
a ООО “ОгнеупорТрейдГрупп”
Москва, Россия
b Национальный исследовательский технологический университет “МИСиС” (НИТУ МИСиС)
Москва, Россия
* E-mail: svildanov@mail.ru
Поступила в редакцию 03.08.2020
После доработки 13.08.2020
Принята к публикации 25.08.2020
Аннотация
Проанализированы выборки значений температуры жидкого металла в процессе непрерывной разливки стали. Выборки сформированы из измеренных термопарой значений температуры жидкого металла, находящегося в сталеразливочном ковше и данных при пяти последовательных измерениях температуры жидкого металла, находящегося в промежуточном ковше. Измерения в сталеразливочном ковше произведены после этапа вакуумирования стали, перед подачей металла на непрерывную разливку. Измерения температуры в промежуточном ковше выполнены на протяжении всего периода разливки, включающего все плавки, назначенные в серию. Выдвинута гипотеза о нормальном распределении совокупности значений температуры металла и в сталеразливочном ковше, и в промежуточном ковше. Проверку выдвинутой гипотезы проводили с помощью трех критериев согласия: критерия хи-квадрат χ2, критерия Колмогорова λ и критерия Шапиро–Уилка W. Показано, что гипотеза о нормальном распределении значений температуры в сталеразливочном ковше не противоречит экспериментальным данным по всем трем критериям согласия, и может быть принята. Гипотеза о нормальном распределении температуры при замерах в промежуточном ковше должна быть отклонена, как не согласующаяся с экспериментальными данными, при этом все три критерия согласия показывают необходимость отвергнуть указанную гипотезу. Основными факторами, приводящими к отклонению распределения температуры от нормального закона, являются: повышенная скорость охлаждения металла в промежуточном ковше, введение на поверхность металла шлакообразующих и теплоизолирующих смесей. С увеличением числа замеров температуры в промежуточном ковше, абсолютные значения статистик критериев согласия, хотя и остаются выше критической границы (критерии согласия Пирсона и Колмогорова) и ниже (критерий Шапиро–Уилка), распределение температуры в промежуточном ковше стремится к нормальному распределению.
ВВЕДЕНИЕ
На различных этапах исследовательского или производственного процесса получают и анализируют числовые данные об объектах, характеристики и свойства которых могут быть измерены. Такими данными являются, в частности, результаты измерений, например, температуры жидкого металла.
Результаты измерений можно охарактеризовать как объекты с ощутимой случайной изменчивостью. Вряд ли можно найти реальный процесс, в котором тот или иной измеряемый параметр не находился бы под воздействием набора факторов, влияющих на значение этого параметра, т.е. на результат измерения. Учет влияния всех факторов, по-видимому, невозможен, и здесь мы имеем дело со случайными реализациями измерений – событиями, являющимися и вероятностными объектами.
Поэтому, одним из эффективных средств интерпретации, а в дальнейшем и прогнозировании свойств измеримых объектов, является применение методов математической статистики к тем вероятностным моделям, которые описывают поведение измеримого объекта в различных условиях.
Существенное значение приобретает статистический анализ данных выборок, полученных на определенных временных отрезках процессов, растянутых во времени. Здесь, исходя из анализируемых данных, важно не только получить вид распределения совокупности, из которой взята выборка, но и по возможности установить факторы, влияющие на вид такого распределения. Желательно определить хотя бы качественно изменения выборочных данных во времени.
Одной из областей, где возникает такая статистическая задача, является непрерывная разливка стали [1–4]. Важнейшим объектом здесь выступает температура жидкого металла в сталеразливочном и в промежуточном ковшах. На данном этапе процесса разливки максимальный уровень температуры металла определяется температурой, полученной на завершающей стадии внепечной обработки. В дальнейшем, температура металла только снижается. Скорость охлаждения металла зависит от многих параметров: естественного охлаждения жидкого металла в сталеразливочном ковше, охлаждения в промежуточном ковше, скорости разливки, применения шлакообразующих и теплоизолирующих смесей в промежуточном ковше [5–7]. Основным источником информации в данном случае является выборка. Объем выборки ограничен ввиду и сложности измерений, и сравнительно небольшой длительности периода разливки. Поэтому весьма важным представляется получение эмпирических распределений. При этом основная задача состоит в том, чтобы сделать вывод о конкретном виде распределения совокупности, из которой извлечена выборка. Такой вывод является достаточно неопределенным. Данная неопределенность связана с влиянием многих факторов на уровень значений температуры, например ошибок, при измерении термопарой, теплопотерями и т.д. Выявление наиболее значимых факторов, приводящих к отклонению, например, от нормального распределения совокупности, является весьма актуальным.
Цель работы состоит в проверке правомерности гипотезы о нормальном распределении совокупности значений температуры в сталеразливочном и промежуточном ковшах, оценке влияния времени замера температуры в промежуточном ковше на закон ее распределения. Далее на основании выводов установить факторы, влияющие на отклонение температуры от нормального закона распределения.
МЕТОДЫ ИССЛЕДОВАНИЯ
Проверку гипотезы о нормальном распределении температуры можно осуществить с помощью критериев согласия. Применим три таких критерия – критерий χ-квадрат Пирсона, критерий Колмогорова λ и критерий Шапиро–Уилка W.
Проверку начнем с критерия χ-квадрат Пирсона [8, 9].
Функция плотности нормального закона зависит от двух параметров – математического ожидания μ и дисперсии σ.
(1)
$f(x) = \frac{1}{{\sigma \sqrt {2\pi } }}{{e}^{{\frac{{ - {{{\left( {x - \mu } \right)}}^{2}}}}{{2{{\sigma }^{2}}}}}}}.$(2)
$\mu {\kern 1pt} * = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}({{X}_{1}},...,{{X}_{n}}),$В качестве оценки σ возьмем несмещенную выборочную дисперсию ${{S}^{{*2}}}{\text{:}}$
Тогда для вероятности попадания случайной величины X в отрезок [${{x}_{{i - 1}}},$ ${{x}_{i}}$], имеем:(4)
$P({{x}_{{i - 1}}} \leqslant X \leqslant {{x}_{i}}) = \int\limits_{{{x}_{{i - 1}}}}^{{{x}_{i}}} {f\left( x \right)dx} .$Вероятности попадания выразятся:
При использовании критерия Пирсона в качестве статистики χ2 = χ2(${{x}_{1}},$ …, ${{x}_{n}}$) выбирают функцию выборочных данных χ2, которую вычисляют по формуле:
(5)
${{\chi }^{{\text{2}}}} = \sum\limits_{i = 1}^k {\frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}} ,$С неограниченным ростом n, случайную величину ${{{\chi }}^{2}}$ можно считать распределенной по закону хи-квадрат. Поскольку объемы выборок ограничены, надо иметь в виду, что вероятность ошибки отклонения верной гипотезы в общем случае не совпадает с уровнем значимости α.
Это распределение зависит от одного параметра r – числа степеней свободы. В нашем случае параметр r равен:
где k – число интервалов разбиения; S – число вычисленных по выборке параметров закона распределения, равное 2.Если наша гипотеза о нормальном распределении совокупности верна, то экспериментальное значение ${\chi }_{{{\text{эксп}}}}^{2},$ вычисленное на основании анализа выборки, не может превышать значения ${\chi }_{{{\text{кр}}}}^{2}.$
Задавая вероятность β, например 0.95, можно считать, что события с вероятностью α = 1 – β, маловероятны.
Применяя критерий согласия хи-квадрат, необходимо иметь в виду также, что основой для вычисления статистики критерия служат сгруппированные данные (гистограммы), а конкретное значение этой статистики оказывается существенным образом зависящим от выбора числа интервалов и его границ [10].
Нередко применение различных критериев к задаче на проверку “нормальности” распределения приводит к результату, показывающему, что данные, считающиеся распределенными нормально по одному критерию, не являются “нормальными” при использовании другого критерия [11–13].
Поэтому необходима дополнительная проверка гипотезы о нормальном распределении нашей совокупности.
Проверку гипотезы о нормальном распределении температуры осуществим с помощью критерия согласия Колмогорова (λ-критерия).
Как и прежде, F(x) – неизвестная функция распределения совокупности, а $F_{n}^{*}\left( x \right)$ – эмпирическая функция распределения, построенная по выборке (${{x}_{1}},$ …, ${{x}_{n}}$). Случайная величина:
(7)
${{\rho }_{n}} = \sqrt n \mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - F(x)} \right|$(8)
${{F}_{{{{\rho }_{n}}}}}\left( x \right) = P({{\rho }_{n}} < x)\mathop \to \limits_{n~ \to \infty } K(x),$По гипотезе полагаем, что F(x) = ${{F}_{0}}$(x), где функция ${{F}_{0}}$(x) распределена по нормальному закону, и выбираем статистику ${{\lambda }_{n}}$ = $\sqrt n \mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|.$
Если выдвинута гипотеза о нормальном распределении, то:
(9)
${{F}_{0}}(x) = 0.5 + \Phi \left( {\frac{{{{x}_{i}} - x{\kern 1pt} *}}{{S{\kern 1pt} *}}} \right),$Здесь мы также имеем в виду, что при подстановке оценок параметров, построенных по выборке вместо неизвестных параметров функции F(x), в статистику Колмогорова изменяется ее предельное распределение, а это означает, что вероятность ошибки отбросить верную гипотезу отличается от заданного значения α.
Согласно [14], когда приходится использовать лишь одну выборку, уровень значимости необходимо брать достаточно большим, например, α = 0.05–0.1, чтобы расширить критическую область.
Зададим уровень значимости α, а значения λкр найдем из соотношения P(λ ≥ λкр) = = 1 – P(λ < λкр) = 1 – K(λкр). При α = 0.1, λкр = 1.224. Сравнивая расчетное число λэксп, определенное по выборке, с числом λкр, найдем, что если λэксп > λкр, проверяемая гипотеза отвергается, если λэксп < λкр, то считаем, что предполагаемая функция распределения совокупности не противоречит экспериментальным данным.
Для повышения достоверности результатов проверки применим еще один критерий – критерий Шапиро–Уилка.
Согласно [15, 16], сравнение критерия ${{{\chi }}^{2}}$ с критерием Шапиро–Уилка (W) при проверке допущения о нормальном распределении генеральной совокупности показывает, что критерий W является более мощным, т.е. обеспечивает большую вероятность отбросить неправильную модель.
В [17, 18] показано, что проверка с помощью критерия W является эффективным методом оценки справедливости допущения о нормальности генеральной совокупности, даже если число наблюдений относительно невелико.
Чтобы использовать критерий для случайной выборки объемом n (при n ≤ 50) c наблюдаемыми значениями ${{x}_{1}},$ …, ${{x}_{n}},$ поступаем следующим образом.
Располагаем наблюдения таким образом, чтобы получить упорядоченную выборку значений ${{x}_{1}},$ …, ${{x}_{n}},$ где ${{x}_{{1~}}}$ ≤ ${{x}_{2}}$ ≤ … ≤ ${{x}_{n}}.$
Вычисляем выборочную дисперсию:
(10)
${{S}^{2}} = \sum\limits_{i = 1}^n {{{{\left( {{{x}_{i}} - x{\kern 1pt} *} \right)}}^{2}}} = \sum\limits_{i = 1}^n {x_{i}^{2}} - \frac{{{{{\left( {\sum\limits_{i = 1}^n {{{x}_{i}}} } \right)}}^{2}}}}{n},$Если n – четное число, принимаем k = n/2; если n – нечетное число, принимаем k = = (n – 1)/2. Затем вычисляем коэффициент:
(11)
$b = {{a}_{n}}({{x}_{n}} - {{x}_{1}}) + {{a}_{{n - 1}}}({{x}_{{n - 1}}} - {{x}_{2}}) + ... + {{a}_{{n - k + 1}}}({{x}_{{n - k + 1}}} - {{x}_{k}}) = \sum\limits_{i = 1}^k {{{a}_{{n - i + 1}}}} ({{x}_{{n - i + 1}}} - {{x}_{i}}),$Далее вычисляем критерий Шапиро–Уилка:
Сравниваем вычисленное значение W с процентилями распределения этого критерия, показанными в соответствующей табл. 1. Эта таблица дает минимальные значения W, которые мы получили бы для вероятностей 1, 2, 5, 10 и 50% при различных значениях n, если бы данные действительно имели нормальное распределение.
Таблица 1.
Характеристики выборок и значения выборочных статистик
| Вид статистики | Выборочное среднее, $x{\kern 1pt} *$ | Выборочная дисперсия, $S{\kern 1pt} *$ | Уровень значимости, α | Критич. значение статистики | Эксперим. значение статистики |
|---|---|---|---|---|---|
| Измерение в сталеразливочном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1549 | 1.71 | 0.05 | 7.8 | 0.75 |
| ${{\lambda }_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1549 | 1.71 | 0.1 | 1.358 | 1.330 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1549 | 1.71 | 0.05 | 0.952 | 0.957 |
| Первое измерение в промежуточном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1514 | 4.09 | 0.05 | 11.1 | 22.78 |
| ${{\lambda }_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1514 | 4.09 | 0.1 | 1.358 | 1.56 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1514 | 4.09 | 0.05 | 0.952 | 0.879 |
| Второе измерение в промежуточном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1515 | 3.89 | 0.05 | 9.5 | 20.75 |
| ${{\lambda }_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1515 | 3.89 | 0.1 | 1.358 | 1.275 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1515 | 3.89 | 0.05 | 0.952 | 0.890 |
| Третье измерение в промежуточном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1515 | 2.6 | 0.05 | 6.00 | 6.65 |
| ${{\lambda }_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1515 | 2.6 | 0.1 | 1.358 | 1.02 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1515 | 2.6 | 0.05 | 0.952 | 0.920 |
| Четвертое измерение в промежуточном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1513 | 1.87 | 0.05 | 9.5 | 10.21 |
| ${{\lambda }_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1513 | 1.87 | 0.1 | 1.358 | 0.765 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1513 | 1.87 | 0.05 | 0.952 | 0.850 |
| Пятое измерение в промежуточном ковше | |||||
| χ2 = $\mathop \sum \limits_{i = 1}^k \frac{{{{{({{n}_{i}} - n{{p}_{i}})}}^{2}}}}{{n{{p}_{i}}}}$ | 1512 | 3.03 | 0.05 | 7.8 | 12.33 |
| ${{{\lambda }}_{n}}$ = $\sqrt n $$\mathop {\max }\limits_x \left| {F_{n}^{*}\left( x \right) - {{F}_{0}}(x)} \right|$ | 1512 | 3.03 | 0.1 | 1.358 | 0.595 |
| W = $\frac{{{{b}^{2}}}}{{{{S}^{2}}}}$ | 1512 | 3.03 | 0.05 | 0.952 | 0.925 |
Таким образом, малые значения W указывают на отсутствие нормальности. Например, если значение W, вычисленное по формуле (12), меньше 5%-го табличного значения, то вероятность того, что выборка взята из совокупности, распределенной по нормальному закону, не превышает 0.05. В этом случае можно сделать вывод о том, что допущение о нормальном распределении не приемлемо.
Проверочным шагом можно назвать оценку приближенной вероятности получения вычисленного значения W при допущении о нормальном распределении случайной величины по формуле:
Значения γ, η и ε для соответствующего размера выборки берутся из табл. 1. Затем также с помощью табл. 1 определяется вероятность получить значение нормированной нормальной случайной величины, равное или меньшее z. Полученная величина и есть приближенная вероятность того, что такая выборка могла быть взята из нормально распределенной генеральной совокупности.ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
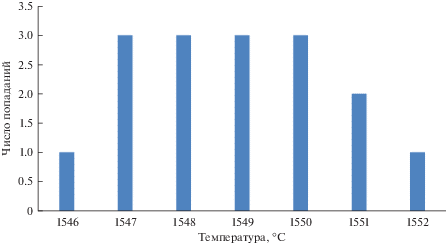
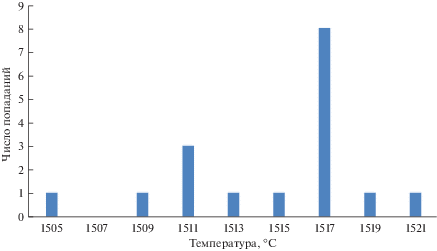
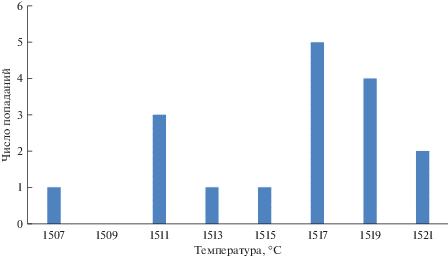
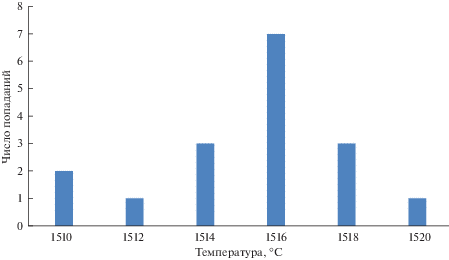
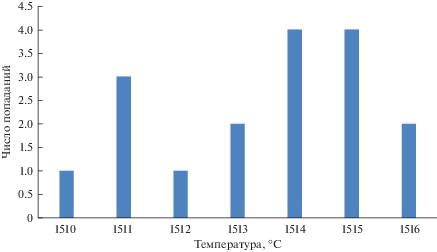
Проанализированы выборки значений температуры при разливке стали марки 38Г2СФА. На рис. 1–6 представлены гистограммы попадания экспериментальных значений температуры в соответствующие интервалы. Рисунок 1 – значения температуры в сталеразливочном ковше после внепечной обработки перед началом разливки. Рисунок 2 – значения температуры в промежуточном ковше при первом замере в начале разливки. Рисунки 3–5 – значения температуры в промежуточном ковше в процессе разливки. Рисунок 6 – значения температуры в промежуточном ковше на завершающей стадии разливки.
По виду гистограмм нельзя однозначно сделать вывод о том, какое распределение имеет совокупность значений температуры. В них можно увидеть признаки нормального распределения, выраженные в том, что на рис. 1 имеется симметричный, хотя и тупой максимум, симметричные “хвосты”. На рис. 4 отчетливо виден максимум, но “хвосты” при этом ассиметричны, причем левый “хвост” более тяжелый. На рис. 6 имеется ассиметричный максимум, а правый “хвост” тяжелее левого, более пологого. Гистограммы, изображенные на рис. 2, 3 и 5, имеют признаки смесей различных распределений. Анализ указанных смешанных распределений выходит за рамки данной работы.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Результаты проверки гипотезы о нормальном распределении температуры сведены в табл. 1.
Из данных табл. 1 видно, что при измерении температуры в сталеразливочном ковше экспериментальные значения статистик, соответствующие критериям согласия Пирсона ${{{\chi }}^{2}}$ и Колмогорова λ, оказываются меньше, чем критические значения, а экспериментальное значение критерия Шапиро–Уилка ${{W}_{{{\text{эксп}}}}}$ превышает табличное 50%-ное значение W = 0.952, полученное из соответствующей таблицы для n = 17. Используя табличные данные, для γ = –4.713, η = 1.739, ε = 0.2622 можем рассчитать приближенную вероятность получения вычисленного значения W = 0.957 при допущении о нормальном распределении температуры: z = –4.713 + 1.739 ln$\left( {\frac{{0.957 - 0.2622}}{{1 - 0.957}}} \right)$ = 0.126, P(z ≤ 0.126) = 0.549. Поскольку полученная вероятность высока, а экспериментальные значения статистик Пирсона и Колмогорова меньше соответствующих критических значений, можно сделать вывод о том, что гипотеза о нормальном распределении температуры в сталеразливочном ковше не противоречит экспериментальным данным, к которым применены все три критерия согласия.
При первом измерении температуры в промежуточном ковше экспериментальные значения статистик ${{{\chi }}^{2}}$ и λ превышают соответствующие критические значения, а экспериментальное значение статистики Шапиро–Уилка W меньше табличного, из чего следует вывод о том, что в данном случае гипотезу о нормальном распределении температуры нужно отклонить.
При втором измерении температуры в промежуточном ковше критерий ${{{\chi }}^{2}}$ и критерий W предписывают отклонить гипотезу о нормальном распределении температуры как противоречащей экспериментальным данным, но наименее мощный критерий λ показывает, что нулевая гипотеза не противоречит экспериментальным данным.
При третьем, четвертом и пятом измерении температуры в промежуточном ковше ситуация аналогична предыдущему случаю.
При переходе от измерений температуры в сталеразливочном ковше к измерениям температуры в промежуточном ковше происходит значительное изменение абсолютных значений экспериментальных статистик критериев. Это свидетельствует о существенном отклонении от нормального закона распределения, характерного для значений температуры в сталеразливочном ковше.
Далее, в зависимости от времени разливки или (что то же самое) числа измерений температуры в промежуточном ковше, значения критериев ${{{\chi }}^{2}}$ и λ снижаются, а значение критерия W – увеличивается, все более сближаясь с критическими значениями. Таким образом, распределения значений температуры стремятся к нормальному распределению.
Полученные результаты согласуются с физической картиной разливки стали. Металл в сталеразливочном ковше после внепечной обработки перед разливкой находится в наиболее стабильном спокойном состоянии. На него не воздействуют никакие внешние возмущения, например, нагрев, перемешивание, дегазация, добавки легирующих элементов. Металл подвержен только естественному охлаждению через огнеупорную футеровку, крышку и корпус ковша.
В этом смысле нормальное распределение и является наилучшим приближением, поскольку почти все внешние возмущающие факторы оказываются либо скомпенсированными, либо минимизированными.
Другая ситуация наблюдается в промежуточном ковше. Металл непрерывно поступает в промежуточный ковш из сталеразливочного ковша. Скорость поступления является не постоянной и зависит от требуемой скорости разливки. Наблюдается значительная турбулентность при перемещении жидкого металла в промежуточном ковше. Скорость охлаждения металла в промежуточном ковше возрастает и меняется в широких пределах от начального момента его заполнения до некоторого значения после подачи в промежуточный ковш шлакообразующих и теплоизолирующих смесей. Именно по этой причине температура жидкой стали в промежуточном ковше, по крайней мере, при первом и последующих замерах, не описывается нормальным распределением. Лишь на заключительном этапе разливки, когда жидкий металл в системе “сталеразливочный ковш–промежуточный ковш” приближается к стационарному состоянию со стабильной скоростью разливки, наблюдается тенденция приближения температурной выборки к нормальному распределению.
Таким образом, наиболее значимыми факторами, влияющими на отклонение распределения значений температуры от нормального закона, являются резкое охлаждение металла при переходе из сталеразливочного ковша в промежуточный ковш, более высокая скорость охлаждения металла в промежуточном ковше, возникновение в промежуточном ковше дополнительных факторов воздействия на температуру металла при подаче шлакообразующих и теплоизолирующих смесей.
ЗАКЛЮЧЕНИЕ
Проанализированы выборки, представляющие собой значения температур, измеренных при непрерывной разливке стали в системе “сталеразливочный ковш–промежуточный ковш”. Выборки взяты из совокупности значений температуры в сталеразливочном ковше и при пяти последовательных измерениях температуры в промежуточном ковше. Выполнена проверка допущения о виде распределения совокупности значений температуры с помощью различных критериев согласия.
Установлено, что гипотеза о нормальном распределении совокупности значений температуры в сталеразливочном ковше не противоречит экспериментальным данным. Для стали, находящейся в промежуточном ковше, выборки температуры порождены совокупностями, распределения которых отличны от нормальных. С увеличением длительности разливки и приближения процесса разливки к стационарному состоянию распределения температур в промежуточном ковше приближаются к нормальному закону распределения.
Список литературы
Ботников С.А., Хлыбов О.С., Костычев А.Н. Разработка прогнозирования температуры металла в сталеразливочном и промежуточном ковшах в литейно-прокатном комплексе // Сталь. 2019. № 10. С. 7–12.
Эльдарханов А.С., Нурадинов А.С., Баранова В.Н. Некоторые аспекты применения внешних воздействий при непрерывной разливке стали // Сталь. 2015. № 10. С. 17–20.
Климанчук В.В., Бочек А.П., Лавринишин С.А. и др. Эффективность защиты металла, разливаемого непрерывном способом // Сталь. 2007. № 1. С. 20–22.
Тимошпольский В.И., Трусова И.А. Совершенствование технологии непрерывной разливки сортовых заготовок. Способы измерения температур при затвердевании и охлаждении. Сообщение 1 // Сталь. 2019. № 11. С. 14–18.
Вильданов С.К., Лиходиевский А.В. МПК Теплоизолирующая и защитная смесь для зеркала металла в промежуточном ковше МНЛЗ. Пат. 2 334 587 РФ. Опубл. 27.09.2008. Бюл. № 27.
Вильданов С.К. Разработка и внедрение теплоизолирующих и шлакообразующих материалав серии “Изотерм-1600” // Сталь. 2018. № 9. С. 17–22.
Вильданов С.К., Рогалева Л.В., Пыриков А.Н. О некоторых критериях эффективности комплексных теплоизолирующих и шлакообразующих смесей // Новые огнеупоры. 2020. № 5. С. 17–23.
Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: Высшая школа, 1984.
Бочаров П.П., Печинкин А.В. Математическая статистика. М.: Издательства российского университета Дружбы народов, 1994.
Королев В.Ю. Теория вероятностей и математическая статистика. М.: Проспект, 2006.
Кокс Д., Хинкли Д. Теоретическая статистика. М.: Мир, 1978.
Леман Э. Проверка статистических гипотез. М.: Наука, 1979.
Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы обработки данных. М.: Мир, 1980.
Хальд А. Математическая статистика с техническими приложениями. М.: Иностранная литература, 1956.
Cochran W.G. The ${{{\chi }}^{2}}$ Test of Goodness of Fit // Ann. Math. Statist. 1952. 23. P. 315.
Williams C.A. On the Choice of the Number and Width of Classes for the Chi-square Test Goodness of Fit // J. Am. Stat. Assn. 1950. 45. P. 77.
Shapiro S.S., Wilk M.B. An analysis of Variance Test for Normality (complete samples) // Biometrika. 1965. 52. P. 591.
Hahn G.J, Shapiro S.S. Statistical Models in Engineering. Wiley N.Y., 1967.
Дополнительные материалы отсутствуют.