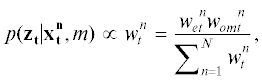Сенсорные системы, 2019, T. 33, № 1, стр. 30-43
Система позиционирования внутри зданий мобильной робототехнической платформы на основе детекции краев
М. П. Абрамов 1, 3, *, О. С. Шипитько 1, А. С. Лукоянов 1, 3, Е. И. Панфилова 2, 3, И. А. Кунина 1, 2, 3, А. С. Григорьев 1
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д.19, Россия
2 Институт системного анализа Федерального исследовательского центра “Информатика и управление”
Российской академии наук, ИСА ФИЦ ИУ РАН
117312 Москва, проспект 60-летия Октября, д. 9, Россия
3 Московский физико-технический институт (государственный университет)
141701 Московская обл., Долгопрудный, Институтский пер., д. 9, Россия
* E-mail: abramov@visillect.com
Поступила в редакцию 17.09.2018
Аннотация
Необходимой предпосылкой для решения задачи навигации является точное знание собственного положения в пространстве. В работе предлагается метод высокоточного позиционирования мобильной робототехнической платформы внутри зданий. Предсказание положения строится на основе данных бортовых датчиков движения (датчик скорости вращения колес и датчик угловых скоростей платформы). В качестве априорной информации используется план здания, хранимый в виде цифровой многоканальной растровой карты. Оценка правдоподобия положения вычисляется путем сопоставления краев, задетектированных на изображениях, получаемых от монокулярной камеры видимого диапазона, с априорно известной картой. Таким образом, предложенный метод использует особенности, присущие любым помещениям (стыки между стенами и полом), и не требует дополнительной подготовки рабочей среды. Для объединения разнородных наблюдений применяется фильтр частиц, учитывающий мультимодальное распределение вероятностей оценки собственного положения. Так как оценка правдоподобия положения фильтром частиц основана на вероятностной модели измерений сенсоров, точное моделирование ошибок измерений является ключом к улучшению качества позиционирования. В работе предложена модель измерений детектора краев, учитывающая геометрические ошибки детекции и ложные срабатывания детектора. Предложенная система позиционирования была экспериментально протестирована на роботе-макете легкового автомобиля. Результаты экспериментов демонстрируют, что предложенный метод позволяет определять собственное положение робототехнического комплекса с ошибкой, в среднем не превышающей 0.1 м на каждом из 100 тестовых запусков.
ВВЕДЕНИЕ
Локализация (позиционирование) – определение позиции и ориентации робота в фиксированной системе координат (Wang, 1988). Совокупность позиции и ориентации робота будем называть его положением. Точная оценка собственного положения в пространстве необходима для точного управления движением, планирования маршрута и избежания столкновений. В этой работе рассматривается задача позиционирования внутри зданий. В связи с тем, что количество робототехнических систем, оперирующих в рассчитанной на человека среде, постепенно растет, задача внутреннего позиционирования приобретает большую значимость. К особенностям локализации внутри зданий относятся ограниченность территории, на которой функционирует робот, а также неприменимость систем глобальной навигации (ГЛОНАСС, GPS) из-за ослабления сигнала при прохождении через стены.
За последнее десятилетие были получены значительные достижения в области разработки алгоритмов одновременной локализации и построения карты (Simultaneous Localization and Mapping, SLAM) (Valencia, Andrade-Cetto, 2018; Mur-Artal, Tard’os, 2017), позволяющих одновременно с оценкой положения проводить картирование территории. Однако на практике нередки ситуации, когда карта местности может быть легко получена заранее и использована для позиционирования. Так, при локализации внутри здания схематический план здания зачастую доступен, может быть оцифрован и использован в качестве априорной информации. Априорное знание карты увеличивает точность алгоритмов определения собственного положения по сравнению с алгоритмами одновременной локализации и построения карты, что может быть важно, когда робот выполняет свои функции в пространстве, разделяемом с людьми.
Известно множество подходов к задаче локализации внутри помещений, основанных на обработке информации от различных сенсоров: внутренних сенсоров движения (датчика скорости вращения колес, гиростабилизатора и других), маяков (англ. beacon) – фиксированных в пространстве источников сигнала различной природы (радиочастотной (Perez-Grau et al., 2016), ультразвуковой (Nagy et al., 2016)), лидаров (LIDAR – Light Identification Detection and Ranging) (Yang et al., 2017), оптических (Kim et al., 2015b) и RGB-D (Heredia et al., 2015) камер. От выбора сенсорной базы зависит как качество локализации, так и стоимость робототехнического решения. К тому же каждая разновидность сенсоров обладает собственными преимуществами и недостатками. Так, активные сенсоры (ультразвуковые датчики расстояния, лидары и радиомаячки) способны обеспечить точную оценку позы, но подвержены интерференции с другими источниками сигнала схожей природы (Kim et al., 2015a). Стоимость некоторых сенсоров (например, лидаров) достаточно высока и может быть лимитирующим фактором в некоторых приложениях.
Визуальная локализация – локализация, основанная на обработке данных, полученных с оптических камер – широко применяется в робототехнике (Konovalenko et al., 2015; Piciarelli, 2016; Chen, Jia, 2014). Использование визуальных данных имеет ряд преимуществ. Во-первых, благодаря развитию потребительской электроники, мобильных телефонов и фотоаппаратов наблюдается существенное снижение средней стоимости оптических камер, что увеличивает интерес к ним со стороны научного и инженерного сообществ и, как следствие, ускоряет развитие новых алгоритмов обработки визуальной информации. Во вторых, будучи пассивным сенсором, камера лишена недостатков активных сенсоров (интерференция, высокое энергопотребление). Современные методы визуальной локализации чаще всего основаны на детекции особых точек с целью восстановления соответствия между изображениями и определения текущей позы камеры (Fedorenko et al., 2017; Konovalenko et al., 2015; Charmette et al., 2016). Однако следует заметить, что типовые помещения, в особенности коридоры, часто слабо текстурированы, что приводит к недостаточному количеству особенностей или к их некорректному сопоставлению и негативно сказывается на точности локализации. Альтернативой особым точкам являются линейные особенности (края и линии), свойственные структурам, сделанным руками человека. В литературе предложено несколько методов локализации на основе распознавания краев. Так, в статье (Röfer, Jüngel, 2003) локализация на основе распознавания краев применяется для оценки положения робота на соревновательном поле RoboCup. Пеленг наблюдаемых краев используется как источник локализационных данных для фильтра частиц. В статье (Vlassis et al., 2001) авторы предлагают и экспериментально подтверждают эффективность метода на основе выделения линейных особенностей на изображениях кругового обзора для использования в локализации и навигации робота. Визуальная локализация в городском окружении по одной камере с использованием фильтра частиц представлена в работе (Leung, 2007), в которой источником данных для локализации являются направления линейных особенностей, полученных при помощи анализа точки схода на оптическом изображении. Выделенные особенности сопоставляются с картой для оценки текущей позы робота.
В этой работе предлагается метод высокоточного позиционирования мобильной робототехнической платформы внутри зданий. Предсказание положения строится на основе данных от бортовых датчиков движения (датчик скорости вращения колес и датчик угловых скоростей платформы). В качестве априорной информации используется план здания, хранимый в виде цифровой многоканальной растровой карты. Оценка правдоподобия положения вычисляется путем сопоставления краев, задетектированных на изображениях, получаемых от монокулярной камеры видимого диапазона, с априорно известной картой. Таким образом, предложенный метод основывается на особенностях, присущих любым помещениям (стыках между стенами и полом), и не требует дополнительной подготовки рабочей среды. Для объединения разнородных наблюдений применяется фильтр частиц (Dellaert et al., 1999), позволяющий учесть мультимодальное распределение вероятностей оценки собственного положения. Так как для оценки правдоподобия положения фильтром частиц используется вероятностная модель измерений сенсоров, точное моделирование ошибок измерений является ключом к улучшению качества позиционирования. В работе также предложена модель измерений детектора краев, учитывающая несколько источников ошибок: геометрические ошибки детекции и ложные срабатывания детектора. Предложенная система позиционирования была экспериментально протестирована на роботе-макете легкового автомобиля.
ЛОКАЛИЗАЦИЯ НА ОСНОВЕ ВИЗУАЛЬНОГО РАСПОЗНАВАНИЯ КРАЕВ
В данном разделе подробно рассмотрен предлагаемый метод локализации, его теоретические основы и отдельные подсистемы.
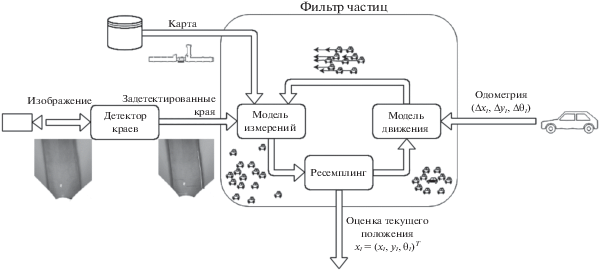
Упрощенная схема работы предлагаемого алгоритма локализации представлена на рис. 1. Основным источником локализационных данных являются задетектированные на оптическом изображении края. Края, образованные стенами и полом, а также края статических объектов – устойчивые особенности, позволяющие надежно определять собственное положение в пространстве. Другой важный источник информации – система бортовых датчиков движения (датчик скорости вращения колес и датчик скорости поворота), позволяющая оценить относительные передвижения робота. Задетектированные края, оценка относительного передвижения, а также априорно известная цифровая карта здания поступают на вход фильтра частиц. Он позволяет представить апостериорное состояние системы (положение робота в пространстве относительно системы координат, связанной с картой) в виде набора гипотез и соответствующих им оценок правдоподобия. Последующие разделы подробно описывают отдельные компоненты системы позиционирования.
Цифровая карта здания. Необходимая для алгоритма локализации априорная информация – цифровая карта здания. Она содержит горизонтальные проекции стыков стен и пола, которые используются для сопоставления с краями, распознаваемыми на изображениях, получаемых в режиме реального времени от оптической камеры. Для увеличения точности позиционирования, помимо краев, образуемых стенами и полом, на карту могут быть дополнительно нанесены края стационарных объектов, различимых детектором краев.
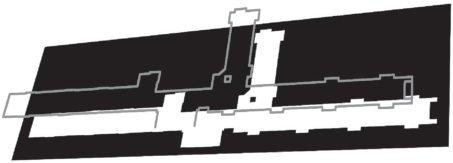
Другая важная априорная информация, содержащаяся на плане здания, – информация о проходимости того или иного участка (рис. 2). Она позволяет фильтру частиц отбрасывать маловероятные гипотезы о положении робота, уменьшая тем самым количество рассматриваемых гипотез и, как следствие, требования к вычислительным ресурсам.
Рис. 2.
Цифровая карта-план здания. Серыми линиями обозначены края, черные области – области непроходимые для робота.
Цифровая карта хранится в памяти робота в виде растрового многоканального изображения. Такой способ хранения позволяет получить информацию о любой локации на карте за постоянное время O(1), при условии ограниченности территории, свойственной задаче локализации внутри зданий. Кроме того, при таком способе хранения новая априорная информация может быть легко добавлена на карту в виде дополнительных слоев.
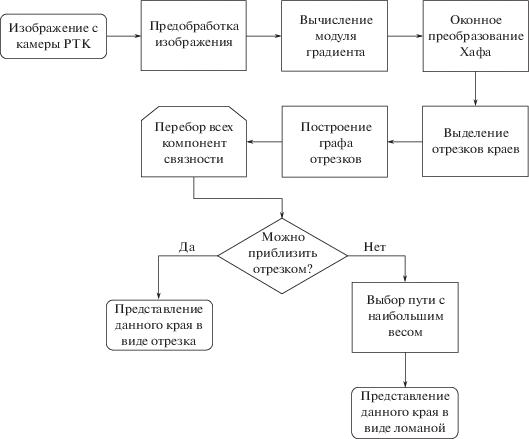
Алгоритм распознавания краев. Детально описан предлагаемый алгоритм распознавания краев, схожий по структуре с алгоритмом распознавания дорожной разметки, предложенным в работе (Панфилова, 2017). Блок-схема алгоритма представлена на рис. 3. Краем будем называть такой участок изображения, профиль яркости которого представляет собой одномерную “ступень”. Подробнее этот тип краев описан в работе (Canny, 1986).
Входом алгоритма является изображение, полученное с одной из оптических камер робота, а выходом – множество ломаных линий краев, заданных точками в координатах входного изображения. Для выделения таких ломаных линий входное изображение сначала подвергается исправлению радиальной дисторсии и проективно преобразуется к виду сверху (birds eye view). Параметры проективного преобразования могут быть найдены из априорных знаний о расположении сенсора в системе координат, связанной с роботом. Далее для каждого пикселя исходного изображения вычисляется модуль градиента, а вычисленные значения представляются в виде нового изображения – карты градиентов.
Для поиска множества отрезков краев на исходном изображении полученная карта градиентов разбивается на пересекающиеся области (окна), в каждом из которых вычисляется быстрое преобразование Хафа (Ershov et al., 2015). Размер и шаг окна – настраиваемые параметры, но важным условием является их взаимное пересечение. В каждой строке полученного Хаф-образа содержатся суммы вдоль всех отрезков с наклоном, соответствующим данной строке. Для поиска контрастного отрезка, соответствующего границе, необходимо выделить такую строку Хаф-образа, дисперсия которой была бы наибольшей и при этом превышала некоторое заданное пороговое значение. Тогда точка из этой строки с максимальным значением интегральной яркости и будет соответствовать наиболее контрастному отрезку края на исходном изображении. В каждом окне выделяется до одного отрезка края.
На следующем шаге алгоритма отрезки группируются в края. Для этого рассмотрим найденные отрезки как вершины некоторого неориентированного графа. При этом между двумя вершинами есть ребро тогда и только тогда, когда выполняется “критерий взаимного расположения отрезков”, т.е. следующие два пункта выполняются одновременно:
• Расстояние d между двумя ближайшими точками отрезков меньше заданного порога;
• Величина угла α, образованного отрезками, лежит в заданном диапазоне.
Чтобы объединить найденные отрезки в ломаные линии, соответствующие краям на исходном изображении, в составленном графе выделяются компоненты связности. Далее проверяется, насколько хорошо каждая компонента связности (или что то же самое – множество отрезков) может быть приближена одним отрезком, т.е. ломаной с одним звеном. Для этого набор отрезков, соответствующих данному краю, представляется в виде множества точек, и пара наиболее удаленных друг от друга точек соединяется отрезком (U, V). Если количество точек, достаточно близких к (U, V), превосходит одну треть от общего числа точек, то считается, что край хорошо приближается отрезком (точка считается достаточно близкой к отрезку, если расстояние от нее до ближайшей точки отрезка меньше s пикселей). Если же это условие не выполняется и край плохо приближается отрезком, то каждому ребру $(u,v)$ в описанном ранее графе (а точнее его компоненте связности, отвечающей рассматриваемому краю) присваивается вес, равный расстоянию между наиболее удаленными точками отрезков u и $v$. При помощи алгоритма Флойда (Floyd, 1962) вычисляется кратчайшее расстояние между каждой парой вершин. Из всех полученных путей выбирается тот, который имеет наибольший вес и при этом среди всех таких проходит через наименьшее количество вершин. Полученный путь представляем в виде ломаной, точки излома которой – это либо концы отрезков, либо точки их пересечения.
Параметры детектора краев, которые использовались как при оценке качества алгоритма, так и при использовании в составе системы локализации, представлены в табл. 1.
Таблица 1.
Параметры детектора краев
| Параметр | Значение |
|---|---|
| Размер окна Хафа | 50 пикселей |
| Ширина области пересечения окон | 10 пикселей |
| Минимальное значение дисперсии | 5000 |
| Порог расстояния s | 3 пикселя |
| Порог на расстояние d | 10 пикселей |
| Диапазон угла α | [160°; 180°] |
| Масштаб изображения, преобразованного к виду сверху | 75 пикселей/м |
Фильтр частиц. Для объединения разнородных данных и оценки текущего положения робота используется алгоритм локализации Монте-Карло (фильтр частиц) (Dellaert et al., 1999). Он позволяет оценить вектор состояния системы ${{{\mathbf{x}}}_{{\mathbf{t}}}}$ в момент времени t при помощи множества гипотез (так называемых частиц) и ассоциированных с ними весов (численных оценок вероятности гипотез) – $\left\{ {\left\langle {{\mathbf{x}}_{{\mathbf{t}}}^{{\mathbf{n}}},w_{t}^{n}} \right\rangle } \right\}$, где $n = 1,\;...,\;N$ – порядковый индекс частицы, N – количество частиц. В применении к задаче локализации каждая частица представляет собой гипотезу о положении транспортного средства в пространстве ${{{\mathbf{x}}}_{{\mathbf{t}}}} = {{({{x}_{t}},{{y}_{t}},{{\theta }_{t}})}^{T}}$, где ${{x}_{t}}$ и ${{y}_{t}}$ – двумерные координаты робота в системе координат, связанной с картой в момент времени t, и ${{\theta }_{t}}$ – соответствующий угол рысканья. Вектор состояния ${{{\mathbf{x}}}_{{\mathbf{t}}}}$ зависит от предыдущего состояния системы ${{{\mathbf{x}}}_{{{\mathbf{t}} - 1}}}$ в соответствии с вероятностным законом движения $p({{{\mathbf{x}}}_{{\mathbf{t}}}}{\text{|}}{{{\mathbf{u}}}_{{\mathbf{t}}}},{{{\mathbf{x}}}_{{{\mathbf{t}} - 1}}})$, где ${{{\mathbf{u}}}_{{\mathbf{t}}}}$ – вектор управляющих сигналов, примененных к системе в момент времени $t - 1$. Вероятностный закон $p({{{\mathbf{z}}}_{{\mathbf{t}}}}{\text{|}}{{{\mathbf{x}}}_{{\mathbf{t}}}},m)$, называемый моделью измерений, позволяет оценить вероятность измерения ${{{\mathbf{z}}}_{{\mathbf{t}}}}$ при условии заданного положения робота ${{{\mathbf{x}}}_{{\mathbf{t}}}}$ и известной карты m. Проблема, решаемая с применением фильтра частиц, может быть сформулирована следующим образом: имея все последовательные измерения сенсоров ${{{\mathbf{z}}}^{{\mathbf{t}}}} = {{{\mathbf{z}}}_{0}},\;...,\;{{{\mathbf{z}}}_{{\mathbf{t}}}}$, и управляющие сигналы ${{{\mathbf{u}}}^{{\mathbf{t}}}} = {{{\mathbf{u}}}_{0}},\;...,\;{{{\mathbf{u}}}_{{\mathbf{t}}}}$ необходимо восстановить апостериорное состояние системы ${{{\mathbf{x}}}_{{\mathbf{t}}}}$ в любой заданный момент времени t (Thrun, 2002). Классический алгоритм локализации Монте-Карло:
Алгоритм 1. Алгоритм локализации Монте-Карло
Используемые модели движения и измерений схожи с моделями, предложенными в работах (Shipitko, Grigoryev, 2018; Jo et al., 2015). Основное отличие состоит в том, что в указанных работах рассматривается сценарий локализации вне зданий на основе детекции дорожной разметки, в то время как в этой работе схожие модели применяются для локализации внутри зданий по задетектированным краям. Рассмотрим структуру используемых моделей подробнее.
Модель движения. На каждой итерации алгоритма частицы перемещаются в соответствии с измерениями бортовых датчиков движения. Аддитивный Гауссов шум с нулевым средним применяется к позиции и ориентации каждой частицы для учета шума измерений. С учетом разницы двух последовательных измерений бортовых датчиков движения:
(1)
$\left\{ {\begin{array}{*{20}{l}} {{\Delta }{{x}_{t}} = x_{t}^{{odom}} - x_{{t - 1}}^{{odom}},} \\ {{\Delta }{{y}_{t}} = y_{t}^{{odom}} - y_{{t - 1}}^{{odom}},} \\ {{\Delta }{{\theta }_{t}} = \theta _{t}^{{odom}} - \theta _{{t - 1}}^{{odom}},} \end{array}} \right.$(2)
$\left\{ {\begin{array}{*{20}{l}} {x_{t}^{n} = x_{{t - 1}}^{n} + d_{t}^{n}{\text{cos}}\left( {\theta _{{t - 1}}^{n} + {\Delta }{{\theta }^{n}} + \delta _{t}^{n}} \right),} \\ {y_{t}^{n} = y_{{t - 1}}^{n} + d_{t}^{n}{\text{sin}}\left( {\theta _{{t - 1}}^{n} + {\Delta }{{\theta }^{n}} + \delta _{t}^{n}} \right),} \\ {\theta _{t}^{n} = \theta _{{t - 1}}^{n} + {\Delta }{{\theta }^{n}} + \delta _{t}^{n},} \end{array}} \right.$Набор бортовых датчиков движения, использующихся для оценки движения робота в этой работе, включает в себя датчики скорости вращения колес и датчик скорости изменения угла рысканья. Важно отметить, что данный набор сенсоров не может обеспечить точное позиционирование без дополнительной коррекции, так как измерения обоих видов датчиков подвержены существенному дрейфу во времени. По этой причине абсолютная оценка положения бортовых датчиков движения не используется для локализации, а во внимание принимаются лишь относительные измерения $\left( {{\Delta }{{x}_{t}},{\Delta }{{y}_{t}},{\Delta }{{\theta }_{t}}} \right)$.
Модель измерений. На следующем шаге алгоритма для расчета веса каждой гипотезы используется модель измерений. Она позволяет вычислить, насколько хорошо каждая частица соотносится с показаниями сенсоров в данный момент времени. В этом разделе описывается модель измерений, представляющая собой комбинацию двух функций правдоподобия:
где ${{w}_{e}}$ и ${{w}_{{om}}}$ – оценки правдоподобия положения робота на основе задетектированных краев и карты проходимости соответственно.Главный источник локализационных данных – детектор краев, работающий с изображениями оптической монокулярной камеры. Края на изображении аппроксимируются ломаными. Ломаные затем преобразуются из системы координат, связанной с оптическим центром камеры, в систему координат, жестко связанную с картой. Вес частицы, сформированный на основе распознанных краев, пропорционален пересечению краев, нанесенных на карту, и краев, преобразованных к системе координат карты с учетом текущего положения частицы (рис. 4).
Рис. 4.
Сопоставление распознанных краев (красная пунктирная линия) и краев, нанесенных на карту (черная сплошная линия). Распознанные края представлены ломаными. Положительный вклад в вес частицы вносят только точки ломаных, лежащие на краях карты.

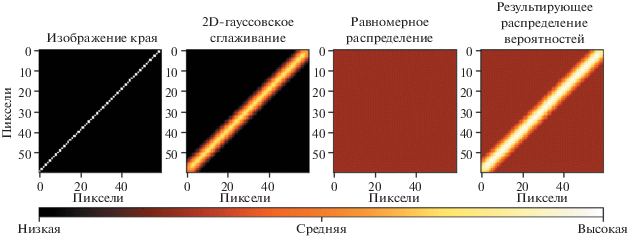
Модель ошибки детекции краев напрямую закодирована в карту на предварительном шаге подготовки карты. Мы предполагаем, что ошибка детекции имеет Гауссово распределение с нулевым средним по обеим координатам. Для ее учета к карте краев применяется Гауссово размытие. Среднеквадратичное отклонение σ при этом выражает величину ожидаемой ошибки и должно быть экспериментально определено для разных алгоритмов детектирования краев (рис. 5). Существует также вероятность ложной детекции края – детекции в области изображения, не содержащей образа края. Для учета ложных срабатываний детектора краев в модель шума добавлено второе слагаемое, описывающее равномерное распределение вероятности ложного срабатывания.
Рис. 5.
Модель измерения детектора краев. Модель шума измерения является комбинацией двумерного гауссова шума и равномерного распределения, отвечающего за ложные срабатывания детектора краев. Первые два изображения демонстрируют край на карте (белая линия) и соответствующее ему двумерное нормальное распределение. Третье изображение показывает равномерное распределение, учитывающее ложные срабатывания детектора краев. На четвертом изображении показано результирующее распределение вероятности измерения, являющееся комбинацией описанных ранее распределений.
Таким образом, модель измерения детектора краев может быть записана как:
(4)
${{w}_{e}}_{t}^{n} = \mathop \sum \limits_{i = 1}^I \,\mathop \sum \limits_{j = 1}^J \frac{1}{{2\pi \sigma _{d}^{2}}}{{e}^{{ - \left( {\frac{{{{I}_{x}}{{{(x_{{i,j}}^{{map}})}}^{2}} + {{I}_{y}}{{{(y_{{i,j}}^{{map}})}}^{2}}}}{{2\sigma _{d}^{2}}}} \right)}}} + \frac{1}{{wh}},$Кроме того, для увеличения точности позиционирования используется априорная информация об окружении – карта проходимости. Она ограничивает область, в которой возможно нахождение частиц, и позволяет исключить из рассмотрения маловероятные гипотезы, что в свою очередь увеличивает точность локализации и уменьшает вычислительную сложность алгоритма. Функция правдоподобия для карты проходимости может быть выражена следующим образом:
(5)
$w_{{o{{m}_{t}}}}^{n} = \left\{ {\begin{array}{*{20}{l}} {1,\quad\quad {е с л и \;}\;{п о л о ж е н и е \;}\;{\text{п р о х о д и м о }},} \\ {0,\quad\quad {в \;}\;{\text{п р о т и в н о м }}\;{\;с л у ч а е }.} \end{array}} \right.$Числовые параметры фильтра частиц, используемые в этой работе, представлены в табл. 2.
Таблица 2.
Параметры фильтра частиц
| Параметр | Значение |
|---|---|
| Количество частиц N | 200 |
| Частота запуска | 2 Гц |
| Гауссов шум линейной составляющей оценки перемещения бортовых датчиков движения | |
| ${{\mu }_{l}}$ | 0.0 |
| ${{\sigma }_{l}}$ | 0.5 |
| Гауссов шум угловой составляющей оценки перемещения бортовых датчиков движения | |
| ${{\mu }_{a}}$ | 0.0 |
| ${{\sigma }_{a}}$ | 0.05 |
| Гауссов шум детектора краев | |
| ${{\mu }_{d}}$ | 0.0 |
| ${{\sigma }_{d}}$ | 0.07 |
МЕТОДОЛОГИЯ ЭКСПЕРИМЕНТА
В данном разделе описывается методология проведения экспериментов, включающих тестирование детектора краев и системы локализации. Приведены параметры алгоритмов, описаны тестовые данные и используемые метрики качества.
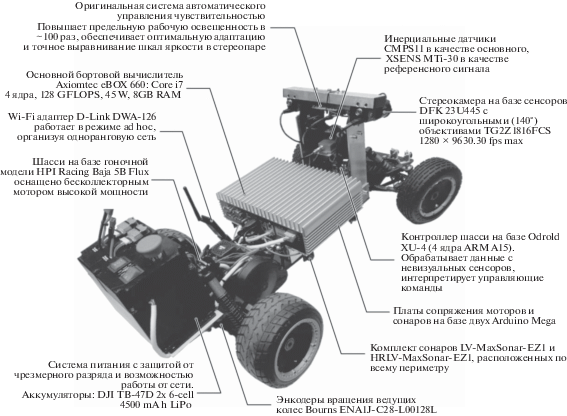
Предложенный алгоритм позиционирования был реализован и протестирован на роботе-макете легкового автомобиля (рис. 6).
Робот-макет. Система бортовых датчиков движения робота представлена энкодерами, оценивающими мгновенную скорость робота, и датчиком скорости рыскания, измеряющим угол поворота робота. На роботе располагаются два связанных локальной сетью вычислителя. Первый – компактный встраиваемый компьютер серии eBox с 4-ядерным процессором, тактовой частотой процессора 2.3 ГГц и 8ГБ оперативной памяти. Второй – одноплатный компьютер ODROID-XU4 с 4-ядерным процессором, тактовой частотой процессора 2.0 ГГц и 2 ГБ оперативной памяти. На роботе установлены две монокулярные камеры на базе сенсоров DFK 23U445 с широкоугольными (140°) объективами TG2Z1816FCS. Они закреплены на высоте 0.4 м над уровнем земли, под углом 22° к горизонтали.
Референсная траектория. Для оценки точности разработанного метода позиционирования необходимо знание референсной траектории. Для восстановления референсной траектории использовался следующий подход. Во время работы алгоритма локализации на каждом шаге сохранялись индексы, показывающие соответствие частиц из апостериорного распределения частицам из априорного распределения с предыдущего шага. Вместе эти данные образуют граф перехода частиц. Построение референсной траектории происходит путем обхода графа назад во времени, референсные позы вычисляются путем усреднения частиц, о которых заведомо известно, что они выживут на последующих шагах алгоритма, вплоть до окончания его работы. Далее фильтр частиц инициализируется заново с набором частиц, начальные позы которых соответствуют положениям частиц, которые выжили на предыдущем запуске. Процесс запуска фильтра частиц и восстановление референсной траектории повторяются до тех пор, пока среднее Евклидово расстояние между точками траекторий последовательных итераций больше заданного порога.
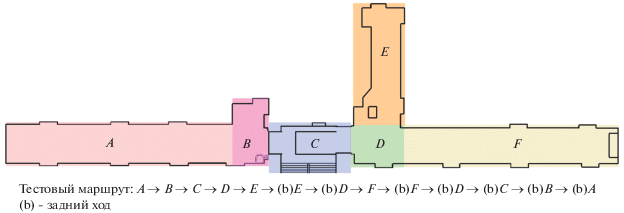
Тестирование системы локализации. Эксперимент проводили на тестовом маршруте, представленном на рис. 7. Цифровая карта здания задавалась двухканальным растровым изображением размером 4676 × 1372 пикселей, в котором первый канал содержал карту горизонтальных проекций стыков стен и пола, второй – карту проходимости. Для учета различных сценариев движения тестовый маршрут содержал развороты на 90° и участки движения задним ходом. Целевая скорость движения робота составляла 1 м/c на протяжении всего маршрута.
Тестирование детектора краев. Качество детектора краев оценивалось на тестовом наборе данных, который представляет из себя набор изображений коридора, полученных с фронтальной камеры робота во время тестового запуска (рис. 8). Тестовый набор данных содержит 118 изображений размера 1920 × 1080 пикселей.
Для оценки качества детектора краев использовались точность и полнота, для вычисления которых необходимо подсчитать количество истинноположительных (TP), ложноположительных (FP) и ложноотрицательных (FN) срабатываний детектора. Рассмотрим ломаную линию L, состоящую из N звеньев $\left( {{{x}_{i}},{{y}_{i}}} \right),$ $i \in \left[ {0,N - 1} \right]$. Введем понятие региона точности (Region of Precision, ROP):
(6)
$\begin{gathered} RO{{P}_{L}}\left( \omega \right) = \\ = \;\left\{ {\left( {x,y} \right){\text{|}}\left( {x,y} \right) \in {\Omega },x \in {{{\Omega }}_{i}},\;i \in \left[ {0,N - 1} \right]} \right\}, \\ \end{gathered} $Для определения, является ли ответ детектора TP, FP или FN, вычислим следующие значения (рис. 9):
Рис. 9.
Сопоставление истинной ломаной с экспериментальной (${{g}_{{{{r}_{j}}}}}$, слева) и cопоставление экспериментальной ломаной с истинной (${{g}_{{{{e}_{i}}}}}$, справа).
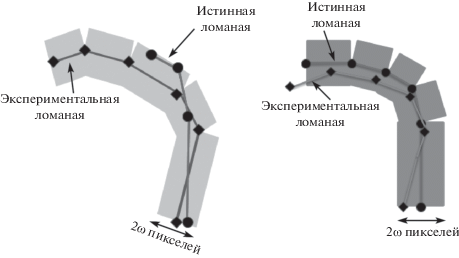
• ${{g}_{{{{r}_{j}}}}} = RO{{P}_{{{{L}_{{{{e}_{i}}}}}}}}\left( \omega \right) \cap RO{{P}_{{{{L}_{{{{r}_{j}}}}}}}}\left( 0 \right)$ – насколько хорошо j-я истинная ломаная соотнеслась c i-й экспериментальной, ${{g}_{{{{r}_{j}}}}} = 0\forall i \Rightarrow FN$;
• ${{g}_{{{{e}_{i}}}}} = RO{{P}_{{{{L}_{{{{r}_{j}}}}}}}}\left( \omega \right) \cap RO{{P}_{{{{L}_{{{{e}_{i}}}}}}}}\left( 0 \right)$ – насколько хорошо i-я экспериментальная ломаная соотнеслась c j-й истинной, ${{g}_{{{{e}_{i}}}}} = 0\forall j \Rightarrow FP$;
• иначе $g = \min \left( {{{g}_{{{{r}_{j}}}}},{{g}_{{{{e}_{i}}}}}} \right) > 0 \Rightarrow TP$.
РЕЗУЛЬТАТЫ
В разделе описываются экспериментальные результаты тестирования детектора краев и системы локализации. Делается вывод о точности и надежности предложенной системы определения собственного положения.
Детектор краев. Качество работы детектора на тестовом наборе данных представлено в табл. 3.
Таблица 3.
Результаты тестирования детектора краев
| Метрика | Значение |
|---|---|
| TP | 0.35 |
| FP | 0.50 |
| FN | 0.16 |
| Точность | 0.41 |
| Полнота | 0.69 |
Результаты демонстрируют, что велико значение ложноположительных (FP) срабатываний. Другими словами, детектируется большое количество краев, не содержащихся в экспертной разметке тестового набора данных. Это обусловлено тем, что при разметке отмечались только края, соответствующие стыкам между стенами и полом, в то время как детектор краев детектирует и другие края на изображении: стыки напольного покрытия, неровности пола и другое. Кроме того, отметим, что низкое качество детекции краев на отдельных изображениях компенсируется за счет высокой частоты поступления и обработки визуальных данных и, как следствие, многократного наблюдения одного и того же участка сцены во время движения.
Система локализации. Результаты тестирования системы позиционирования представлены на рис. 10. Для оценки увеличения точности оценки собственного положения было произведено экспериментальное сравнение предложенной системы позиционирования с позиционированием, основанным только на показаниях бортовых датчиков движения. Таблица 4 демонстрирует численные результаты экспериментов.
Рис. 10.
Ошибки локализации при использовании фильтра частиц в качестве системы позиционирования на одном тестовом запуске.
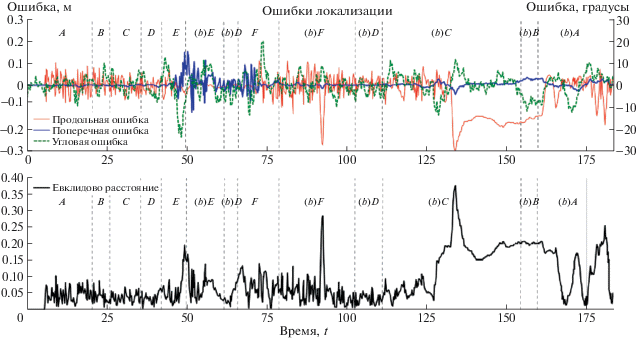
Таблица 4.
Численные результаты экспериментов
| Метод позиционирования | Метрика | Результаты | |||
|---|---|---|---|---|---|
| Продольная ошибка, м | Поперечная ошибка, м | θ(°) | Евклидово расстояние, м | ||
| Бортовые датчики движения | Максимальный модуль ошибки | 0.43 | 2.04 | 70.90 | 3.35 |
| Средняя ошибка | –0.12 | 0.11 | 3.78 | 1.43 | |
| Средний модуль ошибки | 0.15 | 0.24 | 9.73 | 1.43 | |
| Среднеквадратичное отклонение | 0.19 | 0.42 | 13.80 | 1.64 | |
| Фильтр частиц | Максимальный модуль ошибки | 0.30 | 0.15 | 23.58 | 0.37 |
| Средняя ошибка | –0.02 | 0.003 | –0.06 | 0.08 | |
| Средний модуль ошибки | 0.05 | 0.01 | 4.10 | 0.08 | |
| Среднеквадратичное отклонение | 0.07 | 0.02 | 5.34 | 0.10 | |
Таким образом, предложенная система позиционирования внутри зданий позволяет определять собственное положение робота с погрешностью, в среднем не превышающей 0.1 м в обоих направлениях. Несмотря на низкое качество предложенной системы детекции краев, фильтр частиц способен надежно локализировать робота в сложном окружении. Можно заметить, что на некоторых участках движения наблюдается существенная ошибка мгновенной оценки угла рысканья θ, однако она успешно корректируется фильтром по прошествии времени (рис. 10). Максимальная ошибка позиционирования (0.37 м) наблюдается при движении задним ходом в сложном окружении ((b)C) (рис. 7 и 10), где наблюдалось множество ложных срабатываний детектора краев. Более того, особенности автомобильной кинематики влекут большую нестабильность положения при движении задним ходом, что также ведет к увеличению ошибки локализации. Важно отметить, что во время экспериментального тестирования предложенная система локализации продемонстрировала $0{\% }$ вероятности отказа (невозможности восстановить траекторию движения робота) на 100 тестовых запусков.
Сравнение с позиционированием на основе датчиков движения (строка “Бортовые датчики движения” в табл. 4) показывает, что предложенная система локализации дает существенный прирост точности, о чем можно судить по таким показателям, как средний модуль продольной ошибки (уменьшение на 67%), поперечной ошибки ( 96%), уменьшение среднеквадратичных отклонений ошибок на 30 и 93% соответственно.
К недостаткам предложенного метода позиционирования можно отнести необходимость априорного знания карты территории, которая не всегда доступна. Необходимо также отметить, что наличие в рабочей зоне протяженных однородных участков (например, длинный прямой коридор без ответвлений) может увеличить продольную ошибку позиционирования, так как отдельные части такой зоны сложно различимы для предложенной системы локализации.
ЗАКЛЮЧЕНИЕ
В работе предложена система позиционирования мобильной робототехнической платформы внутри зданий, основанная на детекции краев на оптическом изображении. Для сопоставления задетектированных краев с цифровой картой здания и оценки положения робота в системе координат, связанной с картой, был использован фильтр частиц. Предложенный метод прост в реализации и вычислительно эффективен, что позволяет использовать его в системах с жестким ограничением на вычислительные ресурсы.
В работе использован способ хранения карты здания в виде растрового многоканального изображения. Каждый слой такой карты может содержать информацию о различных особенностях окружающей среды (карта проходимости, карта краев), а также в явном виде хранить предпосчитанные модели шумов сенсоров, что было продемонстрировано для шума измерения детектора краев. Существующая карта может быть легко расширена новыми слоями, а способ хранения в качестве цифрового изображения позволяет получить информацию о любой локации на карте за постоянное время O(1), при условии ограниченности рабочей зоны робота, характерной для задачи позиционирования внутри зданий.
Тестирование системы на реальных данных продемонстрировало, что средняя точность позиционирования достигает 0.08 м. Кроме того, было показано, что система позиционирования на основе детекции краев дает существенный прирост точности по сравнению с позиционированием на основе бортовых датчиков движения, средняя точность которого составила 1.43 м.
Дальнейшим улучшением предложенного метода локализации может стать расширение набора визуальных детекторов, например, детекция особых точек, или объектов, часто встречающихся в зданиях – дверные проемы. Другим очевидным усовершенствованием может стать разработка более точных моделей шумов использующихся датчиков для более точного расчета функции правдоподобия текущей оценки положения робота.
Исследование выполнено за счет гранта Российского научного фонда (проект № 14-50-00150).
Список литературы
Панфилова Е.И., Кунина И.А. Детектирование линий разметки в задаче распознавания дорожной разметки. Труды 60-й Всероссийской научной конференции МФТИ. МФТИ, 2017. С. 271–273.
Canny J. A computational approach to edge detection. IEEE Transactions on pattern analysis and machine intelligence. 1986. P. 679–698.
Charmette B., Royer E., Chausse F. Vision-based robot localization based on the efficient matching of planar features. Machine Vision and Applications. 2016. V. 27 (4). P. 415–436.
Chen X., Jia Y. Indoor localization for mobile robots using lampshade corners as landmarks: Visual system calibration, feature extraction and experiments. International Journal of Control, Automation and Systems. 2014. V. 12 (6). P. 1313–1322.
Dellaert F., Fox F., Burgard W., Thrun S. Monte carlo localization for mobile robots. Robotics and Automation, 1999. Proceedings. 1999 IEEE International Conference on. IEEE, 1999. V. 2. P. 1322–1328.
Ershov E., Terekhin A., Nikolaev D., Postnikov V., Karpenko S. Fast hough transform analysis: pattern deviation from line segment. Eighth International Conference on Machine Vision (ICMV 2015). International Society for Optics and Photonics, 2015. V. 9875. P. 987509.
Fedorenko F.A., Ivanova A.A., Limonova E.E., Konovalenko I.A. Trainable siamese keypoint descriptors for real-time applications. 2016 International Conference on Robotics and Machine Vision. International Society for Optics and Photonics, 2017. V. 10253. P. 1025306.
Floyd R.W. Algorithm 97: shortest path. Communications of the ACM. 1962. V. 5 (6). P. 345.
Heredia M., Endres F., Burgard W., Sanz R. Fast and robust feature matching for rgb-d based localization. arXiv preprint arXiv:1502.00500. 2015.
Jo K., Jo Y., Suhr J.K., Jung H.G., Sunwoo M. Precise localization of an autonomous car based on probabilistic noise models of road surface marker features using multiple cameras. IEEE Trans. Intelligent Transportation Systems. 2015. V. 16 (6). P. 3377–3392.
Kim G., Eom J., Park Y. Investigation on the occurrence of mutual interference between pulsed terrestrial lidar scanners. Intelligent Vehicles Symposium (IV), 2015 IEEE. IEEE, 2015a. P. 437–442. (a)
Kim H., Lee D., Oh T., Choi H., Myung H. A probabilistic feature map-based localization system using a monocular camera. Sensors. 2015b. V. 15 (9). P. 21636–21659. (b)
Konovalenko I.A., Miller A.B., Miller B.M., Nikolaev D.P. Uav navigation on the basis of the feature points detection on underlying surface. ECMS. 2015. P. 499–505.
Leung K.Y.K. Monocular vision based particle filter localization in urban environments. Master’s thesis. University of Waterloo, 2007. P. 10.
Mur-Artal R., Tardós J.D. Visual-inertial monocular slam with map reuse. IEEE Robotics and Automation Letters. 2017. V. 2 (2). P. 796–803.
Nagy C., Biró-Ambrus Z., Lőrinc Márton. Ultrasound-based indoor robot localization using ambient temperature compensation. Acta Universitatis Sapientiae Electrical and Mechanical Engineering. 2016. V. 8 (1). P. 19–28.
Perez-Grau F.J., Fabresse F.R., Caballero F., Viguria A., Ollero A. Long-term aerial robot localization based on visual odometry and radio-based ranging. Unmanned Aircraft Systems (ICUAS), 2016 International Conference on. IEEE, 2016. P. 608–614.
Piciarelli C. Visual indoor localization in known environments. IEEE Signal Processing Letters. 2016. V. 23 (10). P. 1330–1334.
Röfer T., Jüngel M. Fast and robust edge-based localization in the sony four-legged robot league. Robot Soccer World Cup. Springer, 2003. P. 262–273.
Shipitko O., Grigoryev A. Ground vehicle localization with particle filter based on simulated road marking image. European Conference on Modelling and Simulation. Wilhelmshaven, Germany. 2018. P. 341–347.
Thrun S. Particle filters in robotics. Proceedings of the Eighteenth conference on Uncertainty in artificial intelligence. Morgan Kaufmann Publishers Inc. 2002. P. 511–518.
Valencia R., Andrade-Cetto J. Active pose slam. Mapping, Planning and Exploration with Pose SLAM. Springer, 2018. P. 89–108.
Vlassis N., Motomura Y., Hara I., Asoh H., Matsui T. Edge-based features from omnidirectional images for robot localization. Proceedings of the 2001 IEEE International Conference on Robotics and Automation. 2001. V. 2. P. 1579–1584.
Wang C.M. Location estimation and uncertainty analysis for mobile robots. Proceedings of the 1988 IEEE International Conference on Robotics and Automation. 1988. P. 1231–1235.
Yang Y., Yang G., Zheng T., Tian Y., Li L. Feature extraction method based on 2.5-dimensions lidar platform for indoor mobile robots localization. Proceedings of the 2017 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM). 2017. P. 736–741.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы