Сенсорные системы, 2019, T. 33, № 1, стр. 44-51
Робастный критерий поиска точки схода проекций прямолинейных траекторий движения детектированных в видеопотоке транспортных средств
Д. А. Бочаров 1, 2, *, К. А. Аксенов 3, Ю. А. Шемякина 4, 5, И. А. Коноваленко 1, 2, 4, 6
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д. 19, Россия
2 ООО “Визиллект”
127521 Москва, Шереметьевская улица, д. 25, Россия
3 Национальный исследовательский университет Высшая школа экономики – НИУ ВШЭ
101000 Москва, Мясницкая улица, д. 20, Россия
4 Smart Engines Ltd.
117312 Москва, проспект 60-летия Октября, д. 9, Россия
5 Институт системного анализа Федерального исследовательского центра “Информатика и управление”
Российской академии наук – ИСА ФИЦ ИУ РАН,
117312 Москва, проспект 60-летия Октября, д. 9, Россия
6 Московский физико-технический институт (государственный университет) – МФТИ (ГУ)
141701 Московская область, Долгопрудный, Институтский переулок, д. 9, Россия
* E-mail: bocharov.mitry@gmail.com
Поступила в редакцию 17.09.2018
Аннотация
Одним из подходов к самокалибровке камер для транспортной видеоаналитики является анализ траекторий наблюдаемого движения. В данной работе рассматривается задача поиска точки схода траекторий движения автомобилей на изображении в предположении о прямолинейности и параллельности их движения. Алгоритм оценки точки схода по наблюдаемым трекам движения, предложенный Tuan Hue Thi, устойчив к наличию посторонних траекторий, однако не устойчив к выбросовому шуму точек на траекториях. В данной работе обсуждаются возможные причины возникновения такого шума и предлагается устойчивый к нему алгоритм. На данных, созданных при помощи имитационного моделирования, численно оценивается зависимость точностей референтного и предлагаемого алгоритмов в зависимости от уровня шума. Приведены примеры работы предлагаемого алгоритма на реальных данных, полученных с использованием системы распознавания автомобильных номеров в видеопотоке.
ВВЕДЕНИЕ
Технологии анализа изображений и распознавания образов находят широкое применение в интеллектуальных транспортных системах (Cucchiara et al., 1999; Ohja, Sakhare, 2015). Они обеспечивают, в частности, функциональность распознавания номерных знаков автомобилей (Du et al., 2013), оценки скорости движения автомобилей (Konovalenko, Kuznetsova, 2015; Cathey, Dailey, 2005) и их классификации (Grigoryev et al., 2015а; 2015б). Входные данные в этих приложениях, как правило, поставляются видеокамерами видимого диапазона.
При монтаже и настройке видеокамер интеллектуальных транспортных систем возникает задача геометрической калибровки, т.е. определения параметров ориентации камеры в пространстве (Kanhere et al., 2010). Поскольку калибровка каждой камеры при помощи калибровочных объектов требует квалифицированного персонала, времени и специального оборудования, наличие методов автоматической калибровки (самокалибровки или автокалибровки) камер существенно способствует масштабируемости систем (Alvarez et al., 2014; Ovchinkin, Ershov, 2018). Известны и продолжают развиваться методы самокалибровки, основанные на поиске точек схода прямых на изображении, прообразы которых параллельны в исходном пространстве (Kanhere et al., 2010; Caprile, Torre, 1990). В качестве прообразов прямых линий используют границы дорожного полотна (Song, Tai, 2006), его разметку (Dong et al., 2009; Fung et al., 2003) или траектории движения автомобилей (Dubska et al., 2015; Thi et al., 2008) в предположении о прямолинейном и параллельном движении.
В данной работе мы будем рассматривать задачу определения координат точки схода траекторий движения транспортных средств в предположении о прямолинейности и параллельности их движения. Будем считать, что траектории даны в виде срабатываний детектора автомобиля, где одно срабатывание детектора на кадре соответствует точке на плоскости изображения. Предполагается, что каждой такой точке детектором присваивается уникальный идентификатор, определяющий соответствие срабатывания одному и тому же транспортному средству. Таким образом, срабатывания с одинаковым идентификатором формируют множество результатов детекции одного и того же объекта. Данное множество точек в работе мы будем называть треком. Пусть $\mathbb{D}$ – набор из N треков
где ${{T}_{i}}$ – i-трек, представленный набором из ${{m}_{i}}$ точек ${{\vec {p}}_{{i,j}}} \in {{\mathbb{R}}^{2}}$ на плоскости изображенияЗадача оценки точки схода траекторий движения автомобилей по наблюдаемым трекам в предположении о прямолинейном и параллельном движении уже решалась в работе Туана Хюэ Тхи (Thi et al., 2008). Согласно предложенному алгоритму, каждый трек независимо аппроксимируется прямой, а результирующая точка выбирается среди пересечений двух таких прямых по критерию максимума пересечений, попавших в область фиксированного радиуса. Благодаря такой голосующей схеме алгоритм устойчив к посторонним траекториям – траекториям, которые не принадлежат пучку параллельных траекторий в исходном пространстве.
Треки, соответствующие посторонним траекториям, мы будем называть треками-выбросами, а остальные – треками, удовлетворяющими модель. Будем считать, что координатный шум точек трека описывается нормальным распределением с нулевым средним. Также будем учитывать, что в системах прослеживания транспортных средств среди точек трека могут возникать выбросы – точки, которые не соответствуют предполагаемой модели трека с аддитивным нормальным шумом. Появление выбросов может быть следствием ошибок присваивания срабатываниям детектора уникальных идентификаторов при одновременном прослеживании нескольких автомобилей, из-за чего среди точек трека могут быть точки, которые в действительности соответствуют срабатываниям на автомобилях, движущихся по другим траекториям. Также в треках могут возникать выбросы в случаях, когда видеокамера установлена над прямолинейным участком дороги перед перекрестком или поворотом. В этом случае выбросами в треке будут точки, которые соответствуют срабатываниям на автомобилях вне прямолинейного участка. В связи с тем, что в предложенном в работе (Thi et al., 2008) алгоритме треки аппроксимируются прямыми неробастным методом, этот алгоритм не устойчив в случае большой вероятности выброса (порядка единиц выбросов на трек) даже при отсутствии треков-выбросов.
В данной работе предлагается новый алгоритм поиска точки схода траекторий по трекам движения. Этот алгоритм устойчив как к наличию посторонних траекторий, так и к наличию выбросовых точек в треках. На данных, полученных при помощи имитационного моделирования, проведено сравнение зависимостей точности предложенного алгоритма и алгоритма, описанного в работе (Thi et al., 2008) от уровня выбросового шума. Приведены примеры работы обоих алгоритмов на реальных данных.
КРИТЕРИЙ ПОИСКА ТОЧКИ СХОДА
Задачу поиска точки схода будем формулировать как задачу поиска координат минимума критерия
Критерий $S(\vec {v},\mathbb{D})$ будем определять как сумму ошибок аппроксимации каждого трека наилучшей прямой, проходящей через оцениваемую точку схода. Для устойчивости к наличию выбросов внутри трека аппроксимацию трека будем рассчитывать как стандартную М-оценку, используемую в алгоритмах RANSAC (Fischler, Billes, 1981):
(1)
${{\hat {\vec {l}}}_{i}} = \mathop {\arg \min }\limits_{\vec {l}} \sum\limits_{j = 1}^{{{m}_{i}}} \rho ({{\vec {p}}_{{i,j}}},\vec {l}),$Тогда ошибка $s(\vec {v},{{T}_{i}})$ аппроксимации i-го трека наилучшей прямой ${{\hat {\vec {l}}}_{i}}$, проходящей через оцениваемою точку схода $\vec {v}$, будет равна
(2)
$s(\vec {v},{{T}_{i}}) = \sum\limits_{j = 1}^{{{m}_{i}}} \rho ({{\vec {p}}_{{i,j}}},{{\hat {\vec {l}}}_{i}}),$(3)
$S(\vec {v},\mathbb{D}) = \sum\limits_{i = 1}^N \,\sum\limits_{j = 1}^{{{m}_{i}}} \rho ({{\vec {p}}_{{i,j}}},{{\hat {\vec {l}}}_{i}}).$Таким образом, задача определения координат точки схода $\hat {\vec {v}}$ сводится к следующей оптимизационной задаче:
(4)
$\hat {\vec {v}} = \mathop {\arg \min }\limits_{\vec {v} \in {{\mathbb{R}}^{2}}} \sum\limits_{i = 1}^N \,\sum\limits_{j = 1}^{{{m}_{i}}} \rho ({{\vec {p}}_{{i,j}}},{{\hat {\vec {l}}}_{i}}).$На рис. 1 приведен пример набора из семи треков $\mathbb{D}$ и точки схода $\hat {\vec {v}}$, для которых значение критерия $S(\vec {v},\mathbb{D})$ минимально.
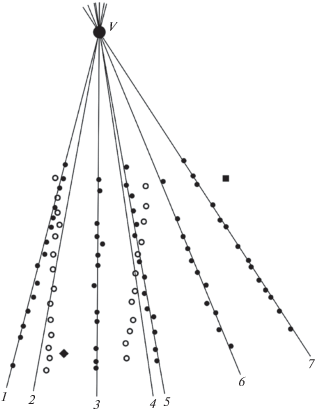
Рис. 1.
Пример входных данных и оптимальной для них точки схода.
Точками с заливкой изображены треки, удовлетворяющие модель (1, 3, 5, 6 и 7), точками без заливки – треки-выбросы (2 и 4). Для каждого трека изображена аппроксимация наилучшей прямой, проходящей через $\vec {v}$. Ромбом и квадратом изображены точки-выбросы внутри 3-го и 7-го треков соответственно. Точка $\vec {v}$ соответствует найденной точке схода.
АЛГОРИТМ ВЫЧИСЛЕНИЯ ТОЧКИ СХОДА
Поскольку функция (3) невыпуклая, для решения оптимизационной задачи предлагается алгоритм, основанный на схеме RANSAC. Прямую ${{\hat {\vec {l}}}_{i}}$, наилучшим образом аппроксимирующую трек ${{T}_{i}}$ и вычисляемую по формуле (1), приблизим прямой $\hat {\vec {l}}_{i}^{'}$, которую будем выбирать среди набора прямых $L(\vec {v},{{T}_{i}})$, где каждая прямая проходит через фиксированную точку $\vec {v}$ и одну из ${{m}_{i}}$ точек трека:
Для вычисления ошибки аппроксимации трека ${{T}_{i}}$ заменим в формуле (2) наилучшую прямую ${{\hat {\vec {l}}}_{i}}$ на ее приближение ${{\hat {\vec {l}}}_{i}}^{\prime }$:
(5)
$s'(\vec {v},{{T}_{i}}) = \sum\limits_{j = 1}^{{{m}_{i}}} \rho \left( {{{{\vec {p}}}_{{i,j}}},\hat {\vec {l}}_{i}^{'}} \right).$Тогда критерий $S'(\vec {v},\mathbb{D})$, приближающий $S(\vec {v},\mathbb{D})$, можно записать в виде
Приведем алгоритм вычисления точки схода, оптимизирующий критерий (6), за K итераций:
1. Инициализировать начальные значения критерия $S_{{\min }}^{'}: = + \infty $ и наилучшей точки схода $\hat {\vec {v}}: = (0;0)$.
2. Для каждого $k = 1,2,\; \ldots ,\;K$:
2.1. Получить гипотезу точки схода ${{\vec {v}}_{k}}$.
2.1.1. Выбрать случайную пару треков ${{T}_{i}},\;{{T}_{j}},\;i \ne j$.
2.1.2. Выбрать из трека ${{T}_{i}}$ случайную пару точек ${{\vec {p}}_{{i,a}}},\;{{\vec {p}}_{{i,b}}},\;a \ne b$.
2.1.3. Выбрать из трека ${{T}_{j}}$ случайную пару точек ${{\vec {p}}_{{j,c}}},\;{{\vec {p}}_{{j,d}}},\;c \ne d$.
2.1.4. Точку пересечения прямых, проведенных через ${{\vec {p}}_{{i,a}}},\;{{\vec {p}}_{{i,b}}}$ и ${{\vec {p}}_{{j,c}}},\;{{\vec {p}}_{{j,d}}}$, объявить гипотезой точки схода ${{\vec {v}}_{k}}$.
2.2. Вычислить по формуле (6) значение критерия $S_{k}^{'}({{\vec {v}}_{k}},\mathbb{D})$ для гипотезы ${{\vec {v}}_{k}}$ и набора треков $\mathbb{D}$.
2.3. Если $S_{k}^{'}({{\vec {v}}_{k}},\mathbb{D}) < S_{{\min }}^{'}$, то обновить значения наилучшей точки схода $\hat {\vec {v}}: = {{\vec {v}}_{k}}$ и минимального значения критерия $S_{{\min }}^{'}: = S_{k}^{'}({{\vec {v}}_{k}},\mathbb{D})$.
3. Вернуть значение $\hat {\vec {v}}$.
Оценка количества итераций
Оценим количество итераций K, за которые с заданной вероятностью q мы получим хотя бы одну надежную гипотезу, основанную на треках и точках, не являющихся выбросами. Пусть ${{w}_{t}}$ и ${{w}_{p}}$ – доли треков и точек трека, соответствующих модели. Оценим вероятность выбора ненадежной гипотезы точки схода. Она состоит из двух слагаемых: из вероятности выбрать два трека так, что по крайней мере один из них будет выбросом, стремящейся при росте числа треков к $1 - w_{t}^{2}$, и из вероятности выбрать по две точки в двух соответствующих модели треках, так, что в наборе будет хотя бы одна точка-выброс, стремящейся к $w_{t}^{2}(1 - w_{p}^{4})$. Вероятность выбрать K ненадежных гипотез составляет ${{(1 - w_{t}^{2} + w_{t}^{2}(1 - w_{p}^{4}))}^{K}} = (1 - w_{t}^{2}w_{p}^{4}{{)}^{K}}$. Приравняем это выражение к $1 - q$ (заданной вероятности не выбрать надежный набор точек) и выразим K:
Асимптотическая вычислительная сложность алгоритма
Асимптотическая вычислительная сложность вычисления наилучшей прямой для одного трека и ошибки его аппроксимации по формуле (5) составляет $O({{m}^{2}})$, где m – число точек в треке. Сложность вычисления критерия $S'(\vec {v},\mathbb{D})$ по формуле (6) для одной итерации и N треков равна $O(N{{m}^{2}})$, а соответственно, для K итераций – $O(KN{{m}^{2}})$.
ЭКСПЕРИМЕНТЫ
В рамках экспериментов исследовалась зависимость долей правильных ответов предложенного алгоритма и алгоритма, описанного в работе Туана Хюэ Тхи (Thi et al., 2008) (далее – референтного) от ${{w}_{p}}$ – доли точек трека, удовлетворяющих модель.
Создание выборки имитационных данных
Выборка данных, на которых проводился эксперимент, состояла из d наборов треков. Опишем процесс создания i-го элемента выборки. В ограниченной области плоскости выбирается случайная точка $\vec {v}_{{ref}}^{i}$ из двумерного нормального распределения с вектором математических ожиданий ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\mu } }_{v}} = (320;440)$ и дисперсией $\sigma _{v}^{2} = 20$. Пусть ${{N}_{i}}$ – число траекторий, среди которых $N_{i}^{'}$ посторонних. Генерируется ${{N}_{i}} - N_{i}^{'}$ прямых (траекторий), проходящих через точку $\vec {v}_{{ref}}^{i}$, углы наклона которых из нормального распределения $N\left( {\frac{\pi }{2},\frac{\pi }{8}} \right)$. Для имитации посторонних траекторий генерируется $N_{i}^{'}$ прямых, каждая из которых задается парой точек $a = (0;U(0,200))$ и $b = (640;U(0,200))$, где U – равномерное распределение. Вдоль k-й прямой генерируется набор точек $\{ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {p} }_{{k,j}}},\;j = 1,2,\; \ldots ,\;{{m}_{k}}\} $, равномерно распределенных на отрезке прямой, ограниченном прямоугольной областью $A\left( {(0;0),\left( {640;\frac{{{{v}_{y}}}}{2}} \right)} \right)$, которая задана левой нижней и правой верхней вершинами, ${{v}_{y}}$ – y координата точки $\vec {v}_{{ref}}^{i}$. Координаты каждой точки зашумляются значениями из нормального распределения
Пусть $m_{k}^{'}$– число выбросов в треке. Для имитации выбросов случайно выбираются $m_{k}^{'}$ точек, которые смещаются на случайное расстояние, взятое из равномерного распределения
Среднее число треков в элементе выборки – 70, среднее количество точек – 30.
Оценка зависимости доли правильных ответов от уровня выбросового шума
Зафиксируем следующие параметры: долю удовлетворяющих модель треков ${{w}_{t}}$, дисперсию аддитивного шума ${{\sigma }^{2}}$, параметры предложенного и референтного алгоритмов. Будем вычислять на наборе из d синтезированных треков среднее количество правильно найденных точек схода для референтного и предложенного алгоритмов в зависимости от значения ${{w}_{p}}$. Будем считать точку схода оцененной ошибочно, если расстояние между оценкой ${{\hat {\vec {v}}}_{i}}$ и ее моделью $\vec {v}_{{ref}}^{i}$ превышает фиксированное пороговое значение $thresh = 50$.
На рис. 2 и 3 приведена зависимость доли правильных ответов алгоритмов для ${{w}_{p}} \in [0.5,1.0]$ при ${{\sigma }^{2}} = 0$ и ${{\sigma }^{2}} = 0.3$. Доля удовлетворяющих модель треков ${{w}_{t}} = 0.9$, объем выборки $d = 250$. Как видно из графиков, доля правильных ответов для референтного алгоритма падает при росте количества выбросов среди точек трека и достигает 0 в окрестности ${{w}_{p}} = 0.7$. В то же время для предложенного алгоритма доля правильных ответов неизменна на всем рассматриваемом интервале ${{w}_{p}} = [0.5,1.0]$.
Рис. 2.
Зависимость точности предложенного и референтного алгоритмов от доли соответствующих модели точек трека при ${{\sigma }^{2}} = 0$.
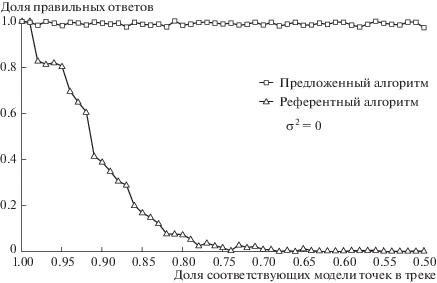
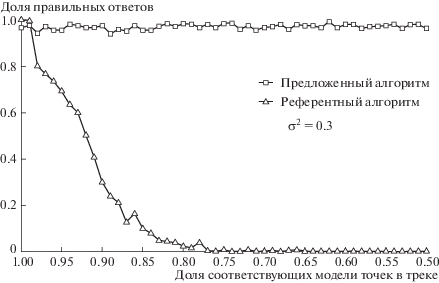
Рис. 3.
Зависимость точности предложенного и референтного алгоритмов от доли соответствующих модели точек трека при ${{\sigma }^{2}} = 0.3$.
Важно заметить, что средняя доля правильных ответов при нулевой дисперсии аддитивного шума точек колеблется рядом с заданной вероятностью $q = 0.99$, а при ненулевой дисперсии несколько снижается. Этот эффект объясняется тем, что в некоторых случаях наилучшая (и единственная) надежная гипотеза строится на основе двух прямых, каждая из которых вычислена по двум зашумленным, лежащим рядом точкам, соответствующим модели, вследствие чего точность такой гипотезы может быть значительно снижена.
Пример работы предложенного алгоритма на реальных данных
В качестве реальных данных взяты результаты слежения за номерными знаками автомобилей в видеопотоке, полученные системой распознавания номеров “МАРИНА” (Povolotskiy et al., 2017). Данная система включает в себя модуль обнаружения и распознавания номеров на одном кадре, а также модуль интеграции между кадрами, поддерживающий идентификатор номера на разных кадрах. Исходные видео получены с двух камер, установленных над участками многополосных дорог, при этом в поле зрения одной из них – дорога перед перекрестком.
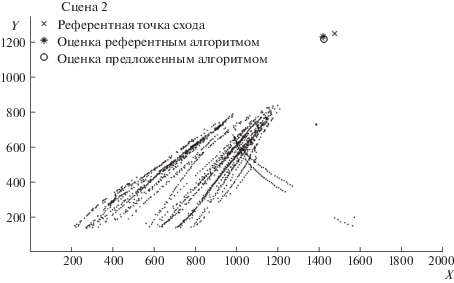
На рис. 4 и 5 приведена визуализация треков движения распознанных номерных знаков для двух разных наблюдаемых сцен (далее – сцена 1 и сцена 2). В качестве референтной точки на рисунках отображена точка схода границ дороги и дорожной разметки. Как можно видеть из примера на рис. 5, алгоритмы дают схожие оценки, близкие к референтной точке, а на рис. 4 предложенный алгоритм дает более точную оценку.
Рис. 4.
Визуализация треков движения распознанных номеров и результатов работы предложенного и референтного алгоритмов для сцены 1.
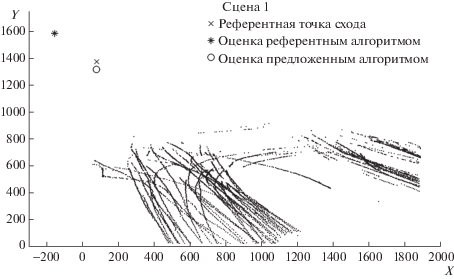
Рис. 5.
Визуализация треков движения распознанных номеров и результатов работы предложенного и референтного алгоритмов для сцены 2.
Следует заметить, что референтный алгоритм параметризован значением радиуса области вокруг гипотезы точки схода, который используется на этапе выбора наилучшей точки. Следовательно, алгоритм требует настройки данного параметра для конкретной сцены, что может оказаться затруднительным при массовой эксплуатации.
ЗАКЛЮЧЕНИЕ
В работе рассмотрена задача поиска точки схода траекторий движения транспортных средств в видеопотоке по трекам в предположении о прямолинейном и параллельном движении. Предложен новый, основанный на схеме RANSAC, алгоритм поиска точки схода, учитывающий возможные выбросы как среди траекторий, так и среди точек трека. При помощи имитационного моделирования создана выборка данных, на которой оценена зависимость доли правильных ответов предложенного алгоритма от доли выбросов среди точек трека. Эксперименты показали, что предложенный алгоритм (в отличие от референтного) устойчив к выбросовому шуму среди точек трека, доля которого лежит в диапазоне $[0,0.5]$. Асимптотическая вычислительная сложность алгоритма составляет $O(KN{{m}^{2}})$, где N – количество треков, m – число точек в треке и K – количество итераций. Планируется развитие экспериментальных исследований предложенного алгоритма на реальных данных.
Обзор литературы, создание ПО для проведения вычислительных экспериментов, а также разработка и исследование предложенного в работе алгоритма выполнены за счет средств гранта РНФ (Проект № 14-50-00150).
Список литературы отсутствует.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы


