Сенсорные системы, 2019, T. 33, № 1, стр. 15-29

ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Данная работа, продолжая тему исследований проективно инвариантных свойств фигур семейства овалов, возвращает внимание читателей (теперь уже с учетом данных теоретического плана, полученных нами в последние годы) к идее построения системы универсальных процедур обработки плоских геометрических объектов, представляющих собой композицию овальной кривой с линейным элементом (ЛЭ) общей им плоскости, – с точкой P либо прямой L, причем в любом их взаимном расположении и комплектации. Для данной жесткой конфигурации не оговаривается ограничений, предписывающих P или же L находиться в поле овала, на его границе либо снаружи фигуры. В зависимости от того, какова исходная композиция вида “Овал + ЛЭ”, предлагается применить ту или иную процедуру предварительной цифровой обработки (в соответствии с заданным видом входной сцены), трансформирующую объект в комплекс “Овал + intP + extL + T-поляра”, объявляемый стандартным, для проективно инвариантного описания которого требуется задействовать финальную численную схему обработки, при том, что формируемый с ее помощью выходной продукт представляет собой плоскую кривую вурф-отображения сцены “Овал + ЛЭ”. Поясним, что рассматриваемые далее методы предлагаемой нами стандартизации сцены (как схемы ее предобработки) подразумевают, что по отношению к полю овала ЛЭ могут быть внутреннего (“int”) или же внешнего (“ext”) расположения, но итогом предобработки должна оказаться сцена с однозначно задаваемыми внутренней P (будем именовать ее тестовым полюсом; именно наличие intP и позволяет вычислить кривую T-поляры, привлекаемую для получения вурф-отображения) и внешней прямой L, поскольку для каждого из этих ЛЭ (intP и extL) доказаны теоремы о связанных с ними инвариантных точках плоскости композиции. Оба эти положения природы необходимых, т.е. заявляют обязательность наличия неких проективно инвариантных свойств (теоремы существования), присущих композиции “овал + intP” (теорема 1; Савчик, Николаев, 2016) либо сценам вида “овал + extL” (теорема 2; Балицкий и др., 2017), но не ограничивают их “комплектации” (количества предельно допустимых проявлений этих свойств, поскольку, не имея характера достаточных, не принадлежат к теоремам единственности).

В Теореме 1 говорится о том, что овал общего вида с заданным в его поле тестовым полюсом P (в произвольной “int” позиции, не принадлежащей границе контура) порождает вовне его (в местах взаимопересечения криволинейных H-поляры и T-поляры; эти инструменты проективно инвариантного анализа гладких выпуклых кривых введены в работе (Николаев, 2011 а)) не менее трех стабильных точек, названных эллиптическими (ЭТ). Каждая ЭТ E детерминирует на контуре фигуры квартет инвариантных позиций, а сам набор E1, E2, E3, … обладает свойством квазиколлинеарности (т.е. имеет диспозицию приблизительно прямолинейную; и эта “качественная особенность”, формулируемая на основании проведенных нами многочисленных модельных экспериментов, не снабжает структурными оценками отклонений от прямолинейности). Описаны конкретные случаи, когда овал, обладая свойством скрытой осевой симметрии и имея позицию тестового полюса P, принадлежащую оси, мог образовывать сеты ЭТ в три, пять или семь точек, при том, что это была либо точно коллинеарная триада, либо структура в виде проективного пучка двух или трех прямолинейных носителей (по триаде ЭТ на каждом) с общим центром пучка в точке E, являющейся плюккеровым полюсом для поляры (Акимова и др., 2014), тождественной неявной оси симметрии овала (Николаев, 2011 б; 2012). Поскольку целью докладываемой работы в ситуации с наличием intP является попытка однозначно и проективно инвариантно связать фиксированную позицию intP с ее детерминируемым положением extL, то для решения этой задачи окажутся непригодными, как приемы некой “линеаризации” совокупного сета ЭТ (например, методом наименьших квадратов), так и признаки “некоторой уникальной пары Ek, Em”, оцениваемые по “оптимальной их диспозиции” и привлекаемой в качестве задающей прямую extL (типа “крайние в ряду”, “наиближайшие к овалу” и тому подобные критерии выбора пары), по причине их проективной неинвариантности. Таким образом, новым приемом этапа предварительной обработки должен стать подход к выбору пары ЭТ, приводящий для любых ракурсов регистрации сцены “овал + intP” к идентичному результату, что предопределяет опору на фундаментальный проективный инвариант – вурф (гораздо чаще его именуют “сложным отношением координат коллинеарного квартета точек”), с весьма обширным списком возможностей привлечения свойств экстремумов вурф-функций, формируемых при его посредстве (Глаголев, 1963). Необходимый критерий задания extL – через экстремальные характеристики вурф-функций, включающих аргументом полный сет ЭТ (как проективно замкнутую ломаную, соединяющую цепочку соседних ЭТ), – будет рассмотрен нами в следующем разделе, а в этом перейдем к описанию дуального метода опоры на теорему 2, когда в сцене вида “овал + extL” требуется проективно однозачно оценить позицию intP.

Теорема 2 декларирует наличие у композиции “овал + extL” минимального набора проективно стабильных точек, инцидентных прямой L (их должно быть не менее четырех) и контуру самого овала (на овальной кривой удается детектировать как минимум октет таковых). При воссоздании этой конструкции, в минимальном виде включающем на L и на контуре дюжину опорных позиций (а сама эта конфигурация из 12 точек и соединяющих их прямых воспроизводит на языке плюккеровых полюсов и поляр удвоенную диспозицию известной для коник теоремы взаимности (Моденов, 1969; Акимова и др., 2014)), на пересечении дуальных поляр во внутреннем поле овала появляются инвариантные точки C, классифицируемые как сет {intP}. И, поскольку заранее не известно, сколько таких {C} детерминирует входная композиция “овал + extL”, но описана численная схема быстрого поиска всех полюсов C, то для решения этой альтернативной частной задачи требуется сформулировать критерий проективно инвариантного вычисления уникальной позиции intP, не зависящей от количества членов в сете {C}, т.е. разработать алгоритм подобной позиционной оценки intP, детерминируемой сетом{C} и относительным расположением extL. Такая численная схема была разработана (она названа “итерационным фрактальным методом”) и успешно испытана нами в тестовых модельных экспериментах, о чем будет сообщено далее в соответствующем разделе (с иллюстрациями). Подчеркнем, что нам в модельных экспериментах с объектом “овал + extL” пока не удалось построить примера, когда число полюсов {C} больше двух, хотя при том же гарантированном ансамбле в 12 точек на контуре и на extL изучены условия, при которых пара внутренних полюсов C сближается до полного слияния (это происходит у овалов скрытой радиальной симметрии при сближении extL с линией горизонта), что снимает в данном случае проблему выбора intP по {C}. Рассмотрим кратко оставшиеся варианты организации входной сцены.

Допустим, что внешнее и внутреннее положения L и P взаимно заменены, и сцена обрела атрибуты intL и extP. Нетрудно понять, что и совместное их наличие, и вхождение порознь представляют собой один и тот же случай, поскольку intL и extP однозначно (и проективно инвариантно) связаны отношениями плюккеровых поляры и полюса: две “ext” касательные из полюса extP к овалу точками касания задают поляру intL (и наоборот, – по касательным в концевых точках хорды=поляры корректно восстанавливается позиция P). Если сцена представляет собой композицию с одним ЛЭ (“овал + intL” или “овал + extP”), то после оценки позиции “парного” атрибута доопределенный объект “овал + intL + extP” надо подвергнуть предобработке, описанной в работе (Николаев, Николаев, 2009): луч из extP, сканируя хорду intL, фиксирует на ней экстремальную точку intP, удовлетворяющую условию гармоничности для коллинеарного квартета extP, A, intP, B (т.е. осуществляет поиск по критерию W(extP, A, intP, B) = 1, где A и B – точки пересечения контура лучом).

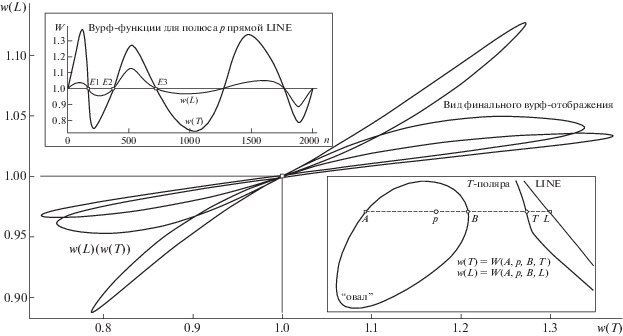
Несколько более громоздкая (вычислительно) схема предобработки требуется для композиций вида “овал + точка контура” либо “овал + касательная к контуру” (это не альтернативные случаи; для стоящей задачи они эквивалентны, поскольку “касательную” и “точку касания” в вычислительном плане можно связать взаимно однозначно). Ее мы обсудим в разд. 3 статьи, а в завершающей части Введения коснемся идеи финального этапа обработки сцены, описав, каким образом для композиции “Овал + intP + extL” можно сформировать ее инвариантно характеризующее вурф-отображение. Рисунок 1 на модельном примере показывает всю цепочку трансформаций, происходящих при проективно стабильной репрезентации сцены. Для того, чтобы сформировать финальное 2D вурф-отображение, необходимо вычислить пару независимых вурф-функций (их вид приведен на врезке слева вверху), привлекая хорду, совершающую по ходу “дискретного вращения” вокруг P последовательный круговой обход вершин аппроксимации овальной кривой. При этом на прямой, пересекающей extL (на врезке справа внизу она помечена как LINE), вычисляются позиции L(n) (где n – текущий номер вершины A либо B контура), что совместно с полюсом intP и парой A, B пересечений с контуром образует коллинеарный квартет A, P, B, L, позволяющий для каждого текущего положения n хорды вычислить вурф-функцию w(L(n)) = = W(A(n), P(n), B(n), L(n)). Получение проективно инвариантного отображения на плоскость вурфов требует оценки еще одной вурф-функции, независимой от w(L). Такую дополнительную оценку, привязанную к общему индексу n, обеспечивает вычисление T-поляры (это кривая, задаваемая цепью пересечений касательных в A и B; ее вычисление производится за любые пол-оборота хорды вокруг P (Николаев, 2011 б)). При замене в квартете позиции L(n) на T(n) появляется возможность вычисления второй вурф-функции w(T(n)) = W(A(n), P(n), B(n), T(n)), что и предопределяет на числовой плоскости (w(T), w(L)) вид искомого вурф-отображения w(L)(w(T)) (рис. 1). Перейдем к обсуждению задачи однозначного (проективно инвариантного) выбора позиции extL по координатным оценкам сета ЭТ {E}, детерминируемого на T-поляре фиксированным полюсом intP.

Рис. 1.

Идея описания композиции “овал + intP”. Прямая extL (LINE), найденная по триаде ЭТ (E1, E2, E3), и T-поляра, вычисленная по intP (p на рис.), позволяют оценить функции w(T) и w(L) (схема – на врезке справа внизу, вид – слева вверху), привлекаемые для формирования W-отображения w(L)(w(T)). Остальные пояснения в тексте.

1. О КРИТЕРИЯХ ЗАДАНИЯ extL ПО ДАННЫМ ПОЛНОГО СЕТА ЭТ

Нетрудно заметить, что вурф-функции w(T) и w(L), вид которых приведен на врезке рис. 1, имеют синфазную особенность – совместно пересекать плато единичного уровня, принимая гармонические значения вурфа при общем индексе n. Такое поведение является прямым следствием отнюдь не случайного расположения extL относительно овала с его фиксированным intP: с методической целью избранная для показа связей между w(T) и w(L), прямая LINE интерполирует коллинеарную триаду ЭТ. В ситуациях, когда полный набор {E} не достаточно точно интерполируем единой прямой (как это может произойти с осесимметричным овалом, особенность структуры {E} которого обсуждалась выше), не все из {E} будут принадлежать LINE при любых вариантах интерполяции, что усложняет задачу совместного анализа кривых w(T) и w(L), если критерий в выборе “наилучшего” интервала между соседними ЭТ (в качестве пары точек, детерминирующих расположение LINE) связать с поведением экстремумов на обеих. Можно ориентироваться на “динамику экстремумов” лишь одной w(T) (эти особенности – амплитуды минимумов и максимумов – обладают проективной устойчивостью), однако нет гарантии, что для некоторой пары интервалов (между соседними ЭТ) карта экстремумов не окажется сходной (с точностью дискретной аппроксимации кривой w(n)). На вспомогательном рис. 2 показано, что фигура “ОВАЛ” при перепроецировании к виду “овал” сохраняет свои “коллинеарные” свойства триады ЭТ (при этом позиция тестового полюса P смещается в положение p, изменяется и форма T-поляры), однако реальные погрешности свойства коллинеарности, по картине минимума w1 = w(T) на интервале E1-E2 не привносят “нюансов” (в сравнении с ходом к минимуму на интервале E2-E3, что и отражает врезка рис. 2), позволяющих стабильно отдавать предпочтение одному из интервалов в роли “задающего extL”. Для увеличения надежности критерия выбора был избран подход совместного анализа функций w(T) и w(L) при отказе от процедуры интерполяции, что реализовалось трансформацией искомой LINE в ломаную, где все соседствующие ЭТ соединялись отрезками. Этот прием создавал возможность анализа кривых w(T) и w(L) с обязательно совпадающими границами между гармоническими значениями в ЭТ. Был забракован (как недостаточно надежный; рис. 3) критерий выбора “уникального интервала ЭТ” по максимальной амплитуде экстремума вурф-функции (“max” либо “min”). По итогам серии испытаний аттестован приемлемым метод привлечения вурф-оценки max(W(Ei, mL, mT, Ek)), где в роли координат квартета вурфа фигурируют соответствующие значения n позиций окаймляющих гармонических Ei и Ek, а внутренняя пара метризует на этом интервале положения экстремумов w(T) и w(L). На врезке рис. 3 показано, как для сцены, изображенной на рис. 2, оценка интервала E2-E3 (равная 11.5) уверенно доминирует среди показателей по другим интервалам, выражая особенность согласованного поведения экстремумов w(T) и w(L) на данном интервале. Для демонстрации симметрии кривых относительно гармонического значения в ЭТ на рис. 3 они изображены с единичным сдвигом по W. С целью придания большей убедительности в эффективности избранного критерия max(W) приведем в заключительной части раздела модельный иллюстративный пример сцены, где полный сет {E} образуют пять ЭТ (что в согласии с нашими ранними численными экспериментами реализуется на модели овала, обладающего осевой симметрией, при условии, что тестовый полюс P инцидентен образу оси). Сводный рис. 4 на фрагменте а (слева) изображает вид овала совместно с участком пересекающихся T-поляры и H-поляры, ЭТ которых образуют структуру коллинеарных троек {E1, E2, E5} и {E1, E3, E4} с их общей ЭТ E1 (в роли вершины пучка для прямых=носителей триад и по сути – плюккерова полюса симметрии PS для поляры=оси). В этом случае опираться на свойства квази-коллинеарности сета {E} уже не имеет смысла, и приходится оценить целесообразность анализа интервалов в парах ЭТ, не являющихся непосредственными соседями в цепи {E}. Тогда “необременительное” расширение поиска парных комбинаций ЭТ могло бы выявить “истинно коллинеарные” интервалы E1-E5 и E1-E4 (дав заодно и способ оценки положения оси симметрии согласно свойствам вурфов W(PS, E2, c2, E5) и W(PS, E3, c3, E4) быть гармоническими, что показано на врезке рис. 4, а), только и этот подход нельзя назвать продуктивным: малые изменения формы овала и незначительные сдвиги P с оси симметрии разрушают коллинеарную структуру пучка ЭТ, и мы получаем неколлинеарную цепочку пяти ЭТ, т.е. возвращаемся к “общему случаю”. Эти ясные доводы дают дополнительную аргументацию в пользу разбиения цепи ЭТ на последовательность отрезков, где любой интервал F(n) содержит все необходимые данные для вычисления вурфа W(Ei, mL, mT, Ek), позволяющего (для сравниваемых участков функций w(T) и w(F)) по критерию наилучшей согласованности функций избрать отрезок, задающий положение extL. На врезке рис. 4, б приведены численные значения этих оценок (рейтинг интервалов {E3-E4, E1-E2, E5-E1, E2-E3, E4-E5} стал итогом упорядоченной цепи оценок {34, 18, 10, .55, .53}, дав лидерство интервалу E3-E4). Рис. 4, б демонстрирует вид вурф-функций, вычислявшихся в процедуре отбора, где помимо сравниваемых wT(n) и “кусочной” wF(n) (для большей ясности в отношении позиций ее экстремумов показана с удвоенной амплитудой, т.е. следует формуле 2wF(n) – 1) приводится финальный вид функции wL(n), уже не проходящей через все гармонические узлы ЭТ (что свойственно поведению функции wF(n)). На рис. 4, в приведены кривые W-отображений wL(n)(wT(n)) и wF(n)(wT(n)) (вторая – лишь для сравнения, поскольку она не удовлетворяет установке – быть результатом привлечения “единой” extL – единственной “LINE”). Следствием того, что фрагментарная коллинеарность ЭТ была присуща избранной сцене, вычисленное W-отображение wL(n)(wT(n)) незначительно отличается от кривой многократного покрытия (что и произошло бы, имей пятерка ЭТ реально коллинеарную структуру). Этим выводом закончим обсуждение задачи локализации extL по фиксированному полюсу intP, переходя к рассмотрению вопросов выбора intP для композиции “овал + extL”.

Рис. 2.

Схема предобработки сцены “овал + intP” с инвариантными свойствами T-поляры. Проекция фигуры “ОВАЛ” к виду “овал” переносит тестовый полюс P в позицию p, а ЭТ E1, E2, E3 – в e1, e2, e3, сохраняя свойства функций w1, w2. Остальные пояснения в тексте.

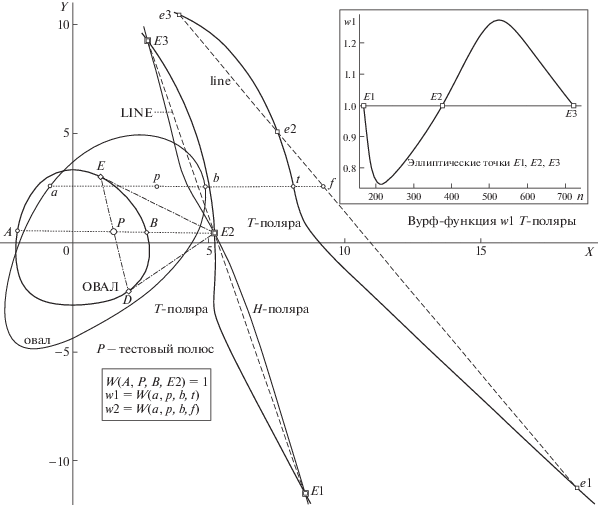
Рис. 3.

Идея критериев локализации LINE в сцене “овал + intP” согласно схеме max(w1(T)) и по оценке max(W(Ei, mL, mT, Ek)), реализуемой вычислением вурфа от границ интервала ЭТ Ei-Ek и позиций экстремумов mT у w1(T) и mL у w2(L). Остальные пояснения в тексте.

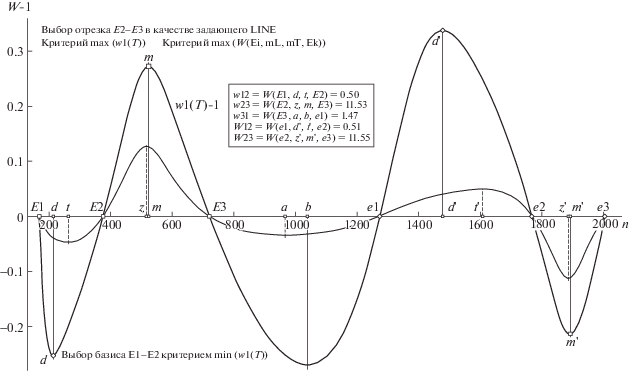
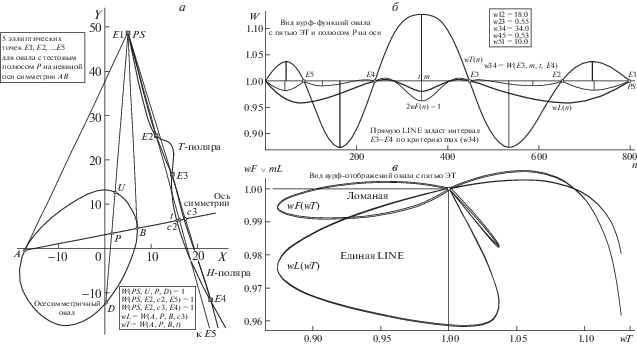
Рис. 4.

Сводная карта обработки сцены с пятью ЭТ, детерминируемыми полюсом P на оси симметрии овала. Вид сцены с осью A-B овала, полюсом симметрии PS и правилами (на врезке внизу) вычисления базисных вурфов (а), ход вурф-функций wT(n), wF(n) и wL(n) с показом (на врезке вверху) рейтинга оценок по критерию max(W(Ei-Ek)) (б) и финальный вид вурф-отображений wL(wT) и wF(wT) (в). Остальные пояснения в тексте.

2. ДУАЛЬНЫЕ СВОЙСТВА T-ПОЛЯРЫ И КРИТЕРИЙ ВЫБОРА intP

В теореме 2 сформулирована оценка снизу для числа проективно инвариантных позиций на extL (не менее четырех), порождающих октет стабильных точек контура овала (Балицкий и др., 2017). Эти восемь точек не исчерпывают характерную структуру связей между внешней прямой и овалом: в “int” поле фигуры появляется пара инвариантных точек c1, c2 (рис. 5) – в местах пересечения дуальных плюккеровых поляр (связывающих каждую из пар позиций F, S и J, G на extL, обозначенной на рис. 5 как “LINE”). Дуальная пара F, S детерминирует на контуре квартет {L, R, K, M} (с пересечением c2 в поле овала), паре J, G соответствует четверка {A, B, O, I} (с полюсом связи c1). Можно доказать, что ни одна из позиций первого квартета не может совпасть с координатами второго (на контуре они всегда чередуются), именно поэтому найденные вершины объединенного 8-точечника удобно использовать для получения более компактного описания сцены (чем вурф-отображение), строя граф ее инвариантного дескриптора по скользящему фрейму в пять соседних вершин. Имея преимуществом скорость обработки, описание такого вида имеет свой минус: малые гладкие деформации контура овала, произшедшие вдали от окрестностей вершин октета, могут оставить неизменным дескриптор – при том, что правило принадлежности овала данному классу проективной эквивалентности (требуемое для распознавания, инвариантного к смене ракурса регистрации объекта) может оказаться нарушенным. В рамках стоящей перед нами задачи описанная выше малая деформация фигуры так же может оставить неизменными координатные оценки пары полюсов c1, c2 (их может быть и больше двух, теорема 2 не ограничивает сверху их количества), однако в форме W-отображения, являющегося интегральным описанием объекта, происшедшие изменения его облика “должны отразиться”. Вернемся к вопросу однозначной локализции intP по оценкам диспозиции сета {c} произвольной размерности, предварительно затронув ранее не обсуждавшиеся (в предшествующих публикациях данного цикла исследований) аспекты связи положений теоремы 2 с дуальными свойствами T-поляры.

Рис. 5.

Связь позиций инвариантных ЭТ {e1, e2, e3} и квартета F, J, S, G на прямой LINE, фиксированной при “овале” с его int-полюсами p, c1, c2, опосредованная T-полярами T(p), T(c1) и T(c2). На врезке вверху в 16-кратном увеличении показан локус сцены с полюсами, в рамочках внизу – формулы и значения базисных вурфов. Остальные пояснения в тексте.

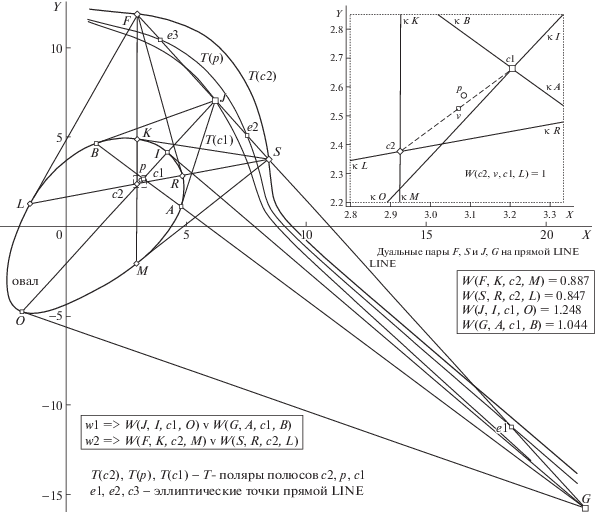
На рис. 5 фигура “овал” задана такой аналитической моделью, в которой позиция тестового полюса p, специальным образом подобранная, детерминирует (с подпороговой погрешностью) коллинеарную триаду ЭТ (помечены литерами e1, e2, e3 и локализованы меткой “малый квадрат”), принадлежащую T-поляре, изображенной на рис. 5 под именем “T(p)”. Триада {e} и задала положение прямой LINE, для которой были вычислены две ее проективно инвариантные пары F, S и J, G. Пару J, G дуально связывает полюс c1; по его координатам (в роли тестового полюса) сформирована T-поляра “T(c1)”. Аналогичным образом, полюс c2 пары F, S использован в качестве тестового для вычисления третьей поляры “T(c2)”. Этот прием позволил наглядным образом показать вновь обнаруженные свойства T-поляры (связывающие ее геометрию с “extL” инвариантами теоремы 2):

“Поляра T(c2) включает пару F, S, тогда как J и G принадлежат поляре T(c1)”!

Интуитивно возникшая гипотеза относительно позиционной связи пары c1, c2 с породившим всю структуру тестовым полюсом p подтверждений не получила. На врезке рис. 5 (справа вверху) с 16-кратным увеличением показан локус сцены, включивший все три полюса. Принадлежность p отрезку c1-c2 была экспериментально опровергнута. Так что острую актуальность в разработке критерия для позиционирования intP по базе {c} не удалось “разрядить” подбором формулы координатной зависимости p от c1 и c2 (да она и не помогла бы в случае не запрещаемого теоремой 2 сета {c} с числом полюсов, большим двух). Предстояла разработка подхода универсального (не предполагающего исключений) и пригодного для любой размерности {c}. Плодотворной оказалась идея включить одним из аргументов критерия позицию прямой extL. Первым шагом на этом пути был избран прием, инвариантно детерминирующий intP по паре c1, c2. Искомая позиция $v$ должна удовлетворять уравнению W(c1, $v$, c2, cL) = 1, где cL – пересечение прямых c1-c2 и extL, что всегда реализуемо, определяя положение для $v$ во внутренней части отрезка c1-c2 по законам гармонического расширения триады c1, c2, cL (при сдвиге extL в несобственную область проективный инвариант сменяется аффинным, и $v$ размещается в середине c1-c2). Не менее отрадным выглядит и тот факт, что в схеме поиска $v$ (и в обобщенном методе оценки intP для сцен, где полюсов {c} больше двух) нет необходимости в привлечении координат пересечений луча c1-c2 с контуром овала. Обобщить полученный одномерный вариант критерия применительно к ситуации сета {c} в виде выпуклого m-вершинника оказалось делом несложным. Развитый подход реализует итерационная процедура.

На врезке рис. 6 (справа внизу) показана схема численной обработки для “условной” композиции в виде тройки полюсов {C1, C2, C3} и заданной при них прямой “LINE”. На первом шаге итерации каждая из сторон треугольника C1-C2-C3 подвергается обработке, аналогичной рассмотренной для отрезка c1-c2, т.е. трижды решается задача гармонического расширения соответствующих коллинеарных триад, в результате чего появляется треугольник “a-b-c” позиционных оценок, вписанный в исходный (на той же врезке в качестве примера для стороны C1-C2 выписано уравненение W(C1, a, C2, e) = 1, решение которого фиксирует позицию точки “a”). В итоге второго шага итерации на поле внутри фигуры “a-b-c” появляется треугольник “c1-c2-c3”. Продолжение итеративного процесса (за 6-7 шагов) обеспечивает финальную оценку (с желаемой точностью) искомой позиции “C”. Но и упомянутые “6-7 шагов” не обязательны для процедуры получения “C”, так как возможна ее оптимизация: решается линейная система восьми уравнений (для восьми коэффициентов проективного преобразования плоскости в декартовом 3D пространстве), преобразующая треугольник C1-C2-C3 в правильный, вслед за чем матрица обратного преобразования переводит центр правильной фигуры в искомую позицию “C”. Рассмотренный выше пример с треугольной конфигурацией {c} без труда обобщается до случая выпуклого m-вершинника (что мы оставляем без пояснительного комментария).

Рис. 6.

Вид W-отображения w(T)(w(L)) сцены “овал + extL” (рис. 5), полученного согласно итерационному критерию, задающему полюс intv по {c} (схема вычисления C на примере трехвершинного сета {C1, C2, C3} дана на врезке справа внизу), и вурф-функций w(L), w(T), найденных по этому критерию (врезка слева вверху). Остальные пояснения в тексте.

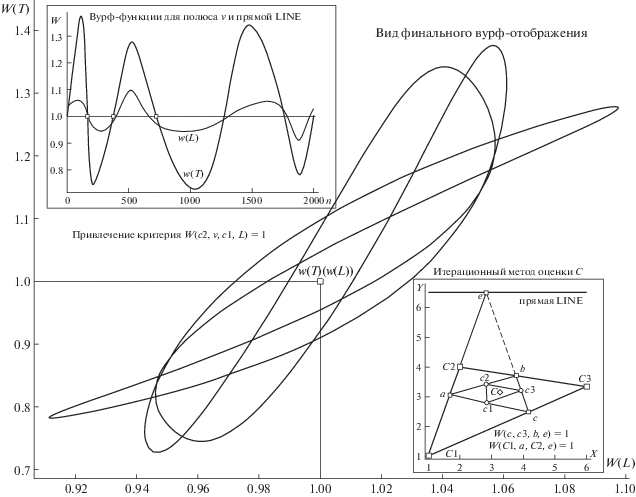
Вновь отсылая читателя к рис. 6, завершим тему данного раздела демонстрацией вида вурф-функций (врезка вверху слева) для сцены с модельной композицией рис. 5, где кривые w(L) и w(T) подчиняются поведению T-поляры, вычисляемой уже для нового тестового полюса $v$ (задаваемого в соответствии с описанной выше итерационной схемой по диспозиции c1, c2 и extL), каковая, будучи не связанной ни с триадой ЭТ (e1, e2, e3), ни с позициями инвариантного квартета {F, J, S, G} на “LINE”, обеспечивает ход функций w(L), w(T), не коррелируемый в совместном прохождении гармонических значений вурфа (как это было для сцены рис. 1–рис. 3). Это обстоятельство отражается на характерной форме W-отображения w(T)(w(L)), не имеющего узла многочисленных самопересечений в точке с координатами (1, 1) (на плоскости вурфов), как это показано на рис. 1, при том, что радиальная “квазисимметрия” относительно этой гармонической точки сохраняется.

3. О МЕТОДАХ ПРЕДВАРИТЕЛЬНОЙ ОБРАБОТКИ В СЦЕНАХ С ФИКСИРОВАННОЙ КАСАТЕЛЬНОЙ

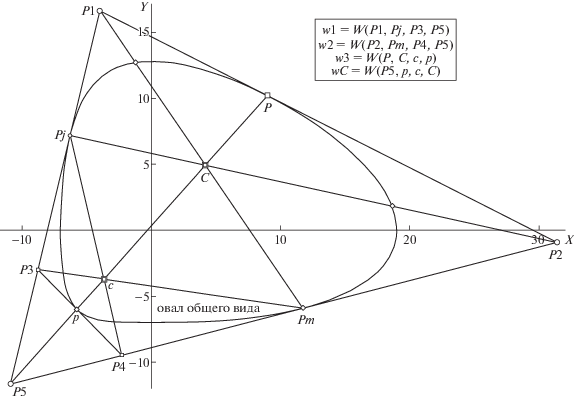
Рассмотрим последний случай организации сцен, когда в композицию с овалом (в роли ЛЭ) входит касательная, фиксируемая на его контуре в заданной точке касания. По причине вычислительной взаимообусловленности эквивалентны дефиниции ЛЭ и в виде прямой L (касательная), и в типизации позицией P (точка касания). Не углубляясь в детали двух работ, экспериментально вычислительной (на модели овала с фиксированной точкой на контуре (Николаев, 2017)) и чисто теоретической (с доказательством теоремы об овале с двумя особыми точками (Савчик, Николаев, 2018)), где описано привлечение свойств так называемых чевиан (название внутренних отрезков в треугольнике, общее для его медиан, высот, биссектрис) с критерием K их пересечения в общей точке C. Схема с тремя касательными изображена на рис. 7, где касательная в P фиксирована, a пара к ней прилежащих (в Pj и Pm) локализуется в переборном численном процессе, формируя цепь решений {C} (названную M-трек), на которой по второму критерию фиксируется целевая позиция intP. В проиллюстрированном случае для каждой последовательно перебираемой Pj(n) находится ей симметричная Pm(n) по условию K (пересечения чевиан P1-Pm, P2-Pj и P-P5 в C). При этом должно выполняться проверочное условие w1 = w2 (на врезке рис. 7 w1 = W(P1, Pj, P3, P5), w2 = W(P2, Pm, P4, P5)). Искомая intP выбирается на M-треке по априори выбранному условию k равенства w3 либо wC некоторой константе (например, wC ≡ 5/4). Теория подтверждает осуществимость такой переборной процедуры поиска intP с использованием критериев K (формирование M-трека) и k (выбор на нем позиции intP). Во второй из двух доказанных в теоретической работе теорем утверждается: “Для овала и точек $A$ и $B$ на нем существует, в общем (невырожденном) случае, не менее двух точек C, дополняющих $A$ и $B$ до тройки, обладающей свойством пересечения чевиан”. Успех в локализации intP сводит ситуацию к случаю “овал + intP”, рассмотренному в разд. 1.

Рис. 7.

Переборная схема получения проективно инвариантной позиции C (как текущей вершины проективно стабильного M-трека) в сцене с фиксированной точкой P на контуре овала и варьируемыми касательными в Pm и Pj (по критерию пересечения в C трех чевиан Pm-P1, Pj-P2 и P-P5) с показом (вверху в рамке) структурных правил вычисления вурфов (проверочных w1, w2 c критерием w1 = w2 и задающего тестовый полюс intC на M-треке решений {C} согласно априорному критерию wC ≡ const). Остальные пояснения в тексте.

4. ВАРИАНТЫ РЕШЕНИЯ ЗАДАЧИ, СВЯЗАННЫЕ С ДУАЛЬНОСТЬЮ T-ПОЛЯРЫ

Изложенные в разд. 2 соображения об “открывшихся на экспериментальном уровне дуальных свойствах T-поляры” логически подводят к возможности ее использования в качестве источника данных об альтернативных вариантах задания extL (для композиций вида “овал + intP”) в условиях, когда применение критерия “наилучшей согласованности” экстремумов w(T) и w(L) на интервалах между соседними ЭТ (см. рис. 3 в разд. 1) удается перенести уже не на межпозиционные интервалы сета {E}, а на отрезки, соответствующие парам проективно инвариантных точек c1, c2 поля овала, связывающих дуальную пару на extL и на пересекающей ее T-поляре (что проиллюстрировано на рис. 5 поведением поляр T(c1) и T(c2)). Развернем эту идею подробнее. В доказательстве теоремы 2 (Балицкий и др., 2017) применена параметризация extL овалом. Коллеги, анализировавшие свойство дуальности двух инвариантных пар (M, N) на extL (“для отображения f, не имеющего неподвижных точек, f(M) = N и f(N) = M”), сделали вывод о правдоподобности такой гипотезы: свойством дуальности f(M) = N, f(N) = M, может обладать не только прямая L, фиксированная извне при овале, но и кривая S, обладающая свойством – “всякая прямая, пересекающая овал, пересекает extS ровно в одной точке”. Нетрудно показать, что этому ограничению для extS удовлетворяет любая T-поляра, порождаемая полюсом intP (так как она имеет асимптоту, проходящую через P, и лежит по одну сторону от нее, к тому же не содержа петель). Не имея на сегодня корректно доказанного положения о T-поляре как универсальном носителе квартета стабильных позиций (т.е. аналог теоремы 2 для нее пока не доказан; при том, что не получено и модельных примеров его опровержения) тезисы процедур, излагаемые далее в этой связи, охарактеризуем эвристическими схемами.

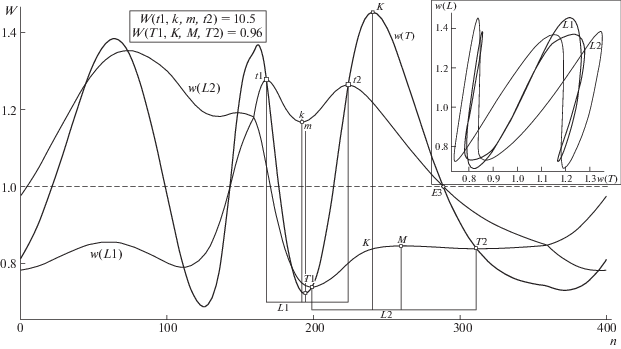
На рис. 8 изображен “ОВАЛ” в композиции с тестовым полюсом P и T-поляра, чье положение детерминировано этим intP. Модельный эксперимент фиксирует на поляре две пары дуально сопряженных инвариантных точек: t1, t2 и T1, T2 (на рис. показана также и триада ЭТ E1, E2, E3 – в пересечениях с H-полярой; при том, что на контуре овала им соответствуют тройка гармонических пар h1/H1, h2/H2 и h3/H3). Выявленные процедурой (поиска стабильных точек T-поляры) положения отрезков t1-t2 и T1-T2 – конкуренты на роль задающих extL; а оценку рейтинга по критерию согласованности экстремумов вурф-функций для них (а также вид функций w(T), w(L1), w(L2), где L1 ≡ t1-t2 и L2 ≡ T1-T2, и отображений w(L1)(w(T)), w(L2)(w(T)) на врезке) демонстрирует (в рамочке вверху) рис. 9. Данный модельный пример позволяет яснее выразить значительную экономию ресурса вычислений (в связи с утерей необходимости в детекции сета ЭТ и с уменьшением на W-функциях количества интервалов = претендентов задания extL), каковая проявляется при использовании эмпирически выявленных дуальных свойств T-поляры.

Рис. 8.

К идее привлечения T-поляры в сцене “овал + intP”, способной заменить extL для нее – с таким же наличием у поляры двух пар (T1, T2 и t1, t2) проективно инвариантных позиций (добавление к сету ЭТ E1, E2, E3). Структурные свойства и правила вычисления базисных вурфов (в рамках на поле рис.), позволяющих найти на контуре ОВАЛА пару сетов упорядоченных стабильных точек {A, B, C, D, a, b, c, d} и {H1, H2, H3, h1, h2, h3}, иcпользуемых для оценки двух дескрипторов сцены. Остальные пояснения в тексте.

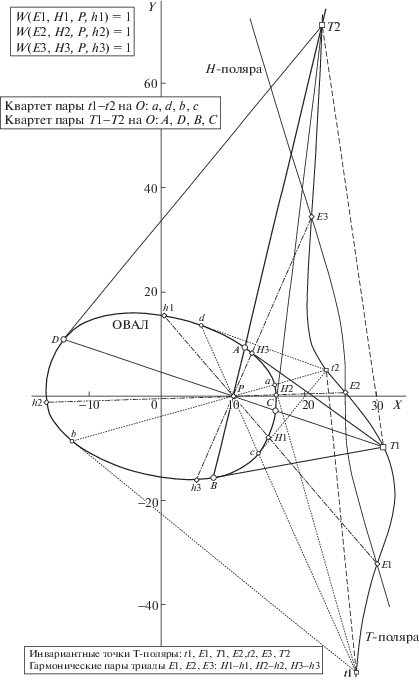
Рис. 9.

Вид вурф-функций w(T), w(L1) и w(L2) в ситуации привлечения T-поляры для сцен “овал + intP” с выбором из двух интервалов T1-T2 и t1-t2 (рис. 8) оптимального по оценке значений вурфов (с наилучшим согласованием экстремумов функций на этих интервалах) – с целью задания положения extL, инцидентного позиции “интервала=лидера”. На врезке справа показана карта W-отображений w(L1)(w(T)) и w(L2)(w(T)). Комментарии в тексте.

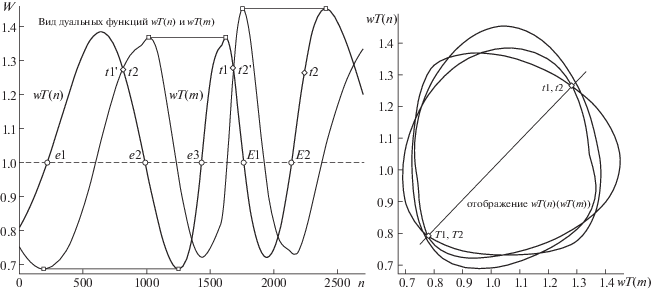
Пристальное внимание к особенностям дуального характера T-поляры в конечном итоге привело (для задачи получения W-отображения сцены “овал + intP) к пересмотру тезиса об обязательном привлечении ЛЭ extL. Действительно, вычисление W-отображения требует наличия двух независимых вурф-функций, связанных с общей для них вершиной аппроксимации овальной кривой. T-поляра позволяет любой такой вершине n поставить в однозначное соответствие ей дуальную m (ибо плюккеровы поляры пересекающихся хорд имеют своими полюсами точки T-поляры). В позициях двух инвариантных дуальных пар t1, t2 и T1, T2 эта связь усиливается, становясь взаимно однозначной, откуда следует, что w1(n)=w2(m) и w2(n)=w1(m), а потому W-отображение должно иметь два самопересечения на биссектрисе (положительного квадранта) плоскости вурфов, что и показывает рис. 10 справа (слева метки “кружок” локализуют на вурф-функциях позиции инвариантной пары t1', t2', дуальной паре t1, t2). Метки “квадрат”, соединенные тонкими прямыми, дают возможность убедиться, что амплитуды экстремумов функций wT(n) (утолщенная линия) и ей дуальной wT(m) (тонкая линия) совпадают. Ограничимся сделанным комментарием.

Рис. 10.

T-поляра в сцене “овал + intP” как самодостаточный источник данных для формирования вурф-отображения wT(n)(wT(m)) (справа) с использованием вурф-функции wT(m) (показана слева тонкой линией), дуально связанной с функцией wT(n) (утолщенная линия; инвариантные точки t1', t2' дуальны паре t1, t2). Остальные пояснения в тексте.

ЗАКЛЮЧЕНИЕ

Подведем главные итоги доложенной работы. Концепция, заявленная во Введении, является обобщенной постановкой задачи проективно инвариантного описания гладких выпуклых фигур, регистрируемых (оптика камер задана плоской центральной проекцией) совместно с ЛЭ (точкой либо прямой) в произвольной фиксированной композиции. Такая постановка мотивирует разбиение процедуры обработки на два этапа: первая фаза должна обеспечить (для варьируемой ЛЭ входной композиции) приведение сцены к эталонному виду “овал + intP + extL + T-поляра” (трансформируя исходный произвол задания “овал + ЛЭ” привлечением алгоритма, требуемого именно для этой сцены), тогда как стандартный процесс в финале формирует проективно инвариантное описание входного объекта в виде вурф-отображения (интерес к вурфу, по сути ключевому элементу производной Шварца, описанной более века назад, до сих пор не угас у математиков (Овсиенко, Табачников, 2008)). Обе вычислительные стадии быстрые (наиболее сложный случай – предобработка сцен с заданной касательной к овалу; с ссылкой на теорему 3 она рассмотрена в разд. 3).

Двухстадийный процесс получения W-отображения входной композиции (дающего возможность решать задачи распознавания овалов по схеме Фреше (Alt, Godau, 1995) на базе методов оптимизации (Гилл, Мюррей, 1985)), включивший все варианты задания объекта “овал + ЛЭ”, предложенный и успешно испытанный нами на численных моделях, не единственный в пуле новых результатов работы. Найдены (итогом включения в схемы обработки выдвинутых критериев) универсально применимые методы, исходной основой имевшие теорию рода необходимых признаков (теоремы), а потому потребовавшие для кластеров ЭТ и {c} найти проективно однозначную замену. Описаны перспективные (для технических систем) методы привлечения выявленных нами дуальных свойств T-поляры, следствиями чего могут стать: отказ от опоры на ЭТ (теорема 1) в роли источника данных для оценки extL по сету ЭТ и вычислительно более оптимальные приемы формирования W-отображений, не требующие extL (теорема 2) для оценки второй вурф-функции к нему.

В завершение темы не один год идущего исследования свойств кривых семейства овалов (и инструментов проективного их анализа, к числу которых относится T-поляра) следует упомянуть, что классические дифференциальные методы оценки инвариантов для них (Картан, 1933; Faugeras, 1993) не приложимы в рамках задач технического зрения (по причинам практически нереализуемых требований к точности вычисления производных высокого порядка на дискретных сетках для гладкой кривой). Но растущая актуальность подобного класса задач автоматического распознавания побуждает искать компромиссные подходы (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009; Николаев, 2017).

Работа выполнена при поддержке РФФИ (грант № 16-07-00836).