Сенсорные системы, 2019, T. 33, № 3, стр. 197-203

ВВЕДЕНИЕ

Сигналы с гребенчатыми частотными спектрами характеризуются периодически чередующимися максимумами и минимумами спектральной амплитуды (гребни). Такие сигналы находят широкое применение для тестирования разрешающей способности слуха – способности различать и опознавать звуковые сигналы со сложной спектрально-временной структурой. Этот способ тестирования слуха используется для диагностики у пациентов с частичной потерей слуха и у носителей кохлеарных имплантов (Summers, Leek, 1994; Pick et al., 1977; Henry, Turner, 2003; Henry et al., 2005; Won et al., 2007, 2014; Saoji et al., 2009; Anderson et al., 2011; Aronoff, Landsberger, 2013; Jeon et al., 2015; Narne et al., 2016). Применение тест-сигналов со сложными спектрами, но при этом со строго контролируемыми параметрами позволяет объективно оценивать эффективность слуховых аппаратов и кохлеарных имплантов. Однако основные принципы оценки остроты слуха при помощи “гребенчатых” тест-сигналов отрабатываются на нормально слышащих испытуемых.

Различение сигналов с гребенчатыми спектрами оценивали по двум основным параметрам: по максимальной плотности гребней и по минимальной глубине модуляции спектра (глубине гребней). Пороги по этим двум параметрам считались характеристиками разных процессов. Минимальная глубина гребней, при которой гребенчатый спектр отличался от “плоского” (без гребенчатого рисунка) спектра принималась за порог обнаружения гребенчатого рисунка; максимальная плотность гребней (количество циклов гребенчатого рисунка на единицу частоты), при которой гребенчатый спектр отличался от плоского, принималась за предел различения гребенчатых рисунков (Anderson et al., 2012). Такое разделение может быть принято лишь как условное, поскольку пороги глубины гребней измеряли как функцию плотности гребней. С равным успехом те же данные могут рассматриваться как функция плотности гребней от их глубины. Плотность и глубина гребней должны рассматриваться как единый рисунок гребенчатого спектра, и способность к различению таких рисунков может характеризовать разрешающую способность слуха.

Имеющиеся в литературе данные о пороговом соотношении глубины и плотности гребней спектра различаются, поскольку получены в разных схемах эксперимента. Одна из схем состояла в том, что пороги глубины гребней измеряли в экспериментах, когда задачей испытуемого было различение тест-сигналов с периодически изменяющейся фазой гребней спектра от референтных сигналов с той же глубиной и плотностью гребней, но с постоянной фазой гребней (Supin et al., 1999). Плотность гребней определялась как их количество на октавный диапазон частот (цикл/окт), а глубина гребней спектра – как отклонение спектральных максимумов и минимумов от среднего уровня. Этот показатель (безразмерная величина) мог принимать значения от нуля (спектр не имеет гребенчатой структуры) до единицы (максимально возможная глубина гребней, когда в “провалах” гребенчатого рисунка амплитуда спектральных составляющих падает до нуля). Пороговая глубина гребней спектра зависела от плотности гребней: при плотности 3–3.5 цикл/окт порог глубины гребней составлял около 0.2, а при плотности 5–10 цикл/окт (в зависимости от частотной полосы сигнала) порог достигал максимально возможной величины 1.0.

При сходной схеме эксперимента (как тестовый, так и референтный сигналы имели гребенчатые спектры с одинаковой плотностью гребней) были получены сходные значения порогов глубины гребней: максимально возможной величины (единица) пороговая глубина гребней достигала при плотности гребней около 10 цикл/окт. Если референтный сигнал имел спектр без гребенчатой структуры (“плоский” спектр), то различение между ним и тест-сигналом с гребенчатым спектром было возможно при плотностях более 20 цикл/окт (Anderson et al., 2012).

Предполагалось, что различие между данными, полученными в экспериментах с гребенчатыми и “плоскими” референтными сигналами, обусловлено вовлечением разных механизмов частотного анализа в слуховой системе (Nechaev et al., 2019). Если и тестовый и референтный сигналы имеют гребенчатые спектры, которые различаются только фазой гребней, то это различие эффективнее выявляется “спектральным” механизмом, который основан на тонотопическом представительстве в слуховой улитке и нервных центрах. Профили возбуждения, создаваемые сигналами с разными фазами гребенчатого спектра, различаются. Согласно экспериментальным данным, этот механизм способен обеспечивать различение спектров с плотностью гребней приблизительно до 10 цикл/окт. Если же один из сигналов имеет гребенчатый, а другой – “плоский” спектр, то оказывается существенно различной их временная организация, проявляющаяся в автокорреляционной функции (АКФ), что создает благоприятные условия для механизма временного анализа. С участием этого механизма, различение между гребенчатым и “плоским” спектрами возможно при плотностях гребней более 20 цикл/окт.

Если принять, что от схемы эксперимента (характера референтного сигнала, с которым сравнивается тест-сигнал) зависит участие спектрального и временного механизмов частотного анализа, то можно ожидать разную степень участия этих механизмов также и в различении глубины гребней спектра. Чтобы проверить это предположение, в данной работе измерены пороги глубины гребней гребенчатых спектров в двух схемах эксперимента: одна – с применением референтных сигналов с гребенчатыми спектрами, другая – с применением референтных сигналов с негребенчатыми, “плоскими” спектрами.

МЕТОДИКА

Испытуемые. В исследовании принимали участие шесть испытуемых (четверо мужчин и две женщины в возрасте от 23 до 49 лет). На частоте 2 кГц (частота применяемых сигналов) у всех испытуемых слуховые пороги были не хуже 5 дБ. Все испытуемые имели опыт участия в психоакустических измерениях.

Сигналы. Для тестирования разрешающей способности слуха применяли сигналы с гребенчатой структурой спектра (тест-сигналы). Их спектры характеризовались периодическим чередованием спектральных пиков и провалов (“гребни”). Референтные сигналы (сигналы сравнения) могли иметь гребенчатый или плоский спектр. Термин “плоский” здесь и ниже применяется только для обозначения спектров без гребенчатой структуры и не означает одинаковой амплитуды спектральных составляющих во всей частотной полосе сигнала.

Как тест-сигналы, так и референтные сигналы имели ограниченную спектральную полосу. Огибающая их спектра имела вид одного периода косинусоиды от логарифма частоты. Период косинусоиды составлял 2 окт, максимум был на частоте 2 кГц. Таким образом, весь спектр занимал частотную полосу от 1 до 4 кГц, и его ширина на уровне 0.5 от максимума составляла 1 окт (от 1.4 до 2.8 кГц) (рис. 1). Время нарастания и спада всех сигналов было одинаковым и составляло 10 мс. Сигналы подавали диотически (одинаково на оба уха) через головные телефоны. Интенсивность сигналов соответствовала 70 дБ уровня звукового давления (УЗД)

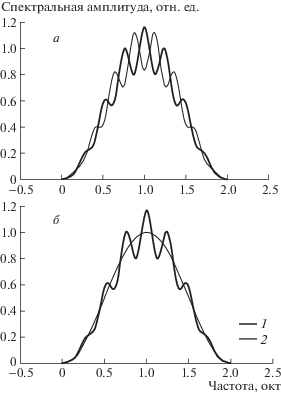
В пределах огибающей спектр тест-сигнала имел периодически чередующиеся максимумы и минимумы спектральной амплитуды – спектральные гребни. Гребенчатый рисунок задавался функцией косинуса от логарифма частоты, т.е. интервалы между гребнями были частотно-пропорциональными, и плотность гребней задавалась в цикл/окт. В процессе тестирования плотность гребней варьировали ступенчато, задавая значения 2, 3, 5, 7, 10, 15, 20 или 30 цикл/окт (псевдологарифмическая шкала, шесть ступеней на логарифмическую единицу). Глубина гребней характеризовалась индексом модуляции, который определялся формулой

где m – индекс модуляции (безразмерная величина), A_max и A_min – спектральная амплитуда соответственно в пиках и провалах гребенчатого рисунка. Этот индекс мог принимать значение от нуля (A_max = A_min, спектр не имеет гребенчатой структуры) до единицы (A_min = 0, максимально возможная глубина модуляции спектра). В процессе измерений индекс модуляции варьировали ступенчато, задавая значения 0.05, 0.07, 0.1, 0.15, 0.2, 0.3, 0.5, 0.7, 1.

В тест-сигнале каждые 400 мс происходила реверсия фазы гребней (пики и провалы спектрального рисунка менялись местами на шкале частот) (рис. 1,а). Сигнал содержал шесть сегментов с противоположными фазами гребней спектра, т.е. общая длительность сигнала составляла 2400 мс. Периодические реверсии фазы гребней были признаком, отличающим тест-сигнал от референтных сигналов.

Применяли два типа референтных сигналов: с гребенчатым и плоским спектром (рис. 1,б). В обоих случаях референтный сигнал имел ту же частотную полосу, тот же УЗД и ту же длительность, что и тест-сигнал. Если референтный сигнал имел гребенчатый спектр, то плотность и глубина гребней были те же, что у тест-сигнала. В этом случае различие между тестовым и референтным сигналами состояло в том, что фаза гребней референтного сигнала была постоянной.

Генерация сигналов. Все сигналы генерировали цифровым способом при частоте стробирования 32 кГц. Программа генерации включала следующие шаги. Белый шум генерировали как Гауссову последовательность случайных чисел. Эта последовательность чисел пропускалась через цифровой фильтр, который задавал как спектральную полосу сигнала, так и (при необходимости) гребенчатую структуру спектра. Результатом фильтрации был “розовый” шум с заданной полосой и гребенчатой структурой.

Для генерации тест-сигнала с периодическими реверсиями фазы гребней использовали два фильтра с противоположными фазами гребней. Каждые 400 мс белый шум переключался с входа одного фильтра на вход другого и обратно; выходы фильтров суммировали. Для генерации референтного сигнала с постоянной фазой гребней или с плоским спектром использовали один фильтр с соответствующей частотной характеристикой.

Полученные сигналы длительностью 2400 мс модулировали по амплитуде для получения нарастаний и спадов длительностью 10 мс. Все сигналы синтезировали непосредственно в ходе эксперимента с применением независимо генерируемых гауссовых последовательностей чисел (белого шума), поэтому сигналы с одними и теми же параметрами не были точной копией друг друга, а отличались друг от друга за счет случайных флуктуаций шума.

Процедура эксперимента. Для измерений применена трехальтернативная процедура с принудительным выбором. В каждой пробе испытуемому предъявляли три сигнала, следующих друг за другом: один тест-сигнал и два референтных сигнала. Порядок следования сигналов (тест-сигнал следовал первым, вторым или третьим) менялся от пробы к пробе в случайном порядке. Задача испытуемого состояла в том, чтобы определить, какой из трех сигналов – первый, второй или третий – отличался от двух других наличием периодических изменений тембра, т.е. какой из трех сигналов был тестовым.

В процессе одного эксперимента плотность гребней спектра тест-сигнала оставалась постоянной, а глубину гребней меняли от пробы к пробе по адаптивному правилу “один – вверх, два – вниз”. В соответствии с этим правилом, если испытуемый в двух пробах подряд правильно определял тест-сигнал, то в следующей пробе глубину гребней спектра снижали на один шаг; после каждой ошибки глубину гребней увеличивали на один шаг. Такая процедура приводила варьируемый параметр (глубину гребней) к значению, которое обеспечивает вероятность правильных ответов, равную 0.5^0.5 = 0.71 (Levitt, 1971). Эту глубину гребней принимали за порог, поскольку при ней вероятность правильных ответов (71%) близка к среднему значению (67%) между безошибочным обнаружением тест-сигнала (100%) и случайным угадыванием при невозможности обнаружения (33%). Процедуру продолжали до получения десяти точек перегиба – переходов от увеличения глубины гребней к ее уменьшению и обратно. Среднее значение глубины гребней для этих десяти точек принимали за оценку порога в данном эксперименте, т.е. при установленной плотности гребней. Повторяя процедуру при различных плотностях гребней, получали функцию порога глубины от плотности. Каждое измерение проводили трижды на каждом испытуемом. Результаты всех измерений усредняли для получения окончательной оценки порога со стандартным отклонением.

РЕЗУЛЬТАТЫ

Референтные сигналы с гребенчатыми спектрами. Пороги глубины гребней как функция от плотности гребней, полученные с использованием референтных сигналов с гребенчатыми спектрами, приведены на рис. 2. Пороги зависели от плотности гребней. При низкой плотности (2–3 цикл/окт) пороги были минимальны и составляли, в среднем по всем измерениям, 0.11 при 2 цикл/окт и 0.12 при 3 цикл/окт. С повышением плотности гребней пороги круто возрастали. Максимально возможной величины, равной 1.0, пороги достигали при плотности гребней 8.9 цикл/окт.

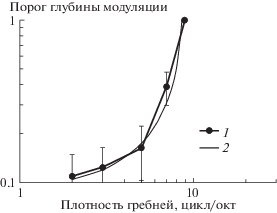
Подбор аналитической функции, аппроксимирующей эту зависимость, показал, что величина, обратная порогу, практически линейно (с негативным наклоном) зависит от плотности гребней, т.е. зависимость определяется простой формулой

где T – порог, D – плотность гребней, a и b – параметры. Параметры подбирали итерационным способом до получения наилучшего соответствия экспериментальным данным по критерию среднеквадратичного отклонения (СКО). Такое соответствие было получено при a = 12.6 и b = 1.28 (СКО = 0.14, R² = 0.989).

Референтные сигналы с плоскими спектрами. Пороги глубины гребней как функция от плотности гребней, полученные с использованием референтных сигналов с плоскими спектрами, приведены на рис. 3. Как и в предыдущем случае, пороги зависели от плотности гребней. Однако характер этой зависимости был существенно иным. При низких плотностях (до 7 цикл/окт включительно) пороги зависели от плотности гребней практически так же, как при референтных сигналах с гребенчатыми спектрами: пороги повышались от 0.13 при плотности 2 цикл/окт до 0.39 при плотности 7 цикл/окт. В этом диапазоне различия между порогами, полученными с разными референтными сигналами, не были статистически достоверными по результатам t-теста (t = 0.21, P = 0.84). Однако при дальнейшем повышении плотности гребней (10 цикл/окт и выше) зависимость порогов от плотности изменялась. Пороги продолжали возрастать, но возрастание замедлялось, так что пороги можно было измерить при плотностях гребней более 20 цикл/окт. Максимально возможной величины, равной 1.0, пороги достигали при плотности гребней 26 цикл/окт.

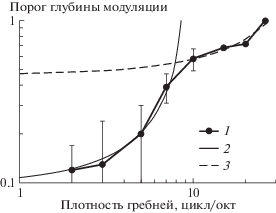
Таким образом, имело место принципиальное отличие от данных, полученных при референтных сигналах с гребенчатыми спектрами, когда пороги вообще не определялись при плотностях гребней от 10 цикл/окт и выше.

Ввиду наличия точки перелома между значениями 7 и 10 цикл/окт аппроксимация экспериментальных данных по формуле (2) не могла дать хорошего соответствия. Однако хорошее соответствие с экспериментальными данными достигалось при применении той же формулы, но при раздельной аппроксимации данных для диапазонов ниже 7 и выше 10 цикл/окт и с разными значениями параметров a и b для этих диапазонов. Наилучшее соответствие по критерию СКО было получено:

− для диапазона 2–7 цикл/окт: a = 10.38, b = = 1.09 (СКО = 0.015, R² = 0.997);

− для диапазона 10–26 цикл/окт: a = 2.16, b = = 0.043 (СКО = 0.033, R² = 0.979).

ОБСУЖДЕНИЕ

Измерение дискриминативных свойств сенсорной системы основано на выявлении различий между тест-сигналом и некоторым стандартным (референтным) сигналом. Успешность различения может зависеть не только от параметров тест-сигнала, но и от свойств референтного сигнала.

В описанных выше экспериментах пороги глубины гребней спектра также измеряли путем сравнения тест-сигналов с референтными сигналами. Основным наблюдением, сделанным в процессе этих измерений, можно считать тот факт, что зависимость порогов от плотности гребней спектра существенно различна при разных формах референтного сигнала (с гребенчатым или с плоским спектром). Если референтный сигнал имел гребенчатый спектр и отличался от тест-сигнала только фазой гребней, то зависимость порогов глубины от плотности гребней описывалась одной простой формулой. Если референтный сигнал имел плоский спектр, аналогичная зависимость описывалась разными формулами для низких и высоких плотностей гребней.

Из этих данных следует, что в первом случае зависимость определялась одним процессом, во втором – двумя процессами, каждый из которых проявлялся в определенном диапазоне плотности гребней.

При этом данные, полученные в диапазоне низких плотностей гребней, практически совпадали при обоих типах референтного сигнала. Естественно допустить, что в этом диапазоне плотностей (до 7 цикл/окт) действовал один и тот же процесс. Альтернативный процесс проявлялся при референтном сигнале с плоским спектром и в диапазоне плотности гребней от 10 цикл/окт.

Ранее было высказано предположение (Nechaev et al., 2019), что эти два процесса соответствуют двум известным механизмам частотного анализа в слуховой системе: спектральному и временному анализу. Спектральный механизм основан на частотно-избирательных свойствах слуховой улитки: колебания базилярной мембраны достигают максимума в том участке, который избирателен к данной частоте. Временной механизм основан на структуре потока нервных импульсов, поступающих от слуховой улитки в слуховые нервные центры: поток нервных импульсов модулирован звуковыми колебаниями и передает в слуховые нервные центры информацию о частоте колебаний. В различении сигналов с гребенчатым спектром могут участвовать как спектральный, так и временной механизмы анализа. Сигналы с гребенчатыми спектрами не имеют четкой временной структуры, однако имеют скрытую временную структуру, которая проявляется в их автокорреляционной функции (АКФ). АКФ сигналов, различающихся только фазой гребней спектра, имеют значительное сходство: они имеют сегмент, задержанный на величину, численно равную количеству гребней на единицу частоты. В этом случае временной механизм малоэффективен, а различение тестового и референтного сигнала происходит на основе спектрального анализа. АКФ сигналов с гребенчатыми и плоскими спектрами принципиально различаются: последние не имеют задержанного сегмента. Поэтому при референтном сигнале с плоским спектром эффективен временной анализ.

Представленные выше результаты уточняют эту схему. При невысоких плотностях гребней (до 7 цикл/окт) различение тест-сигнала и от “гребенчатого”, и от “плоского” референтного сигналов происходит одинаково, очевидно, на основе одного и того же спектрального механизма. Этот механизм обеспечивает низкие пороги глубины гребней (около 0.1 и менее) при низкой плотности гребней, но при повышении плотности гребней пороги резко возрастают, так что различение становится невозможным при плотностях, приближающихся к 10 цикл/окт. Временной механизм различения при низкой плотности гребней обеспечивает пороги глубины гребней около 0.5. С повышением плотности гребней пороги возрастают медленно, благодаря чему возможно различение гребенчатых и плоских спектров при плотностях гребней, приближающихся к 25–30 цикл/окт.

Таким образом, применение разных типов референтных сигналов (с гребенчатым или плоским спектром) позволяет дифференцированно оценить разрешающую способность спектрального и временного механизмов частотного анализа. При этом наиболее полные сведения могут быть получены при оценке разрешающей способности по комплексному амплитудно-частотному рисунку тест-сигналов.

Работа поддержана РФФИ (грант № 17-04-00096).