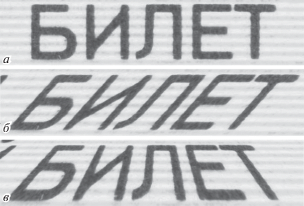Сенсорные системы, 2020, T. 34, № 2, стр. 131-146
Максимальная невязка направлений как критерий точности проективной нормализации изображения при оптическом распознавании текста
И. А. Коноваленко 1, 2, *, Д. В. Полевой 2, 3, 4, 5, Д. П. Николаев 1, 2
1 Институт проблем передачи информации РАН
127051 Москва, Большой Каретный переулок, д. 19, Россия
2 ООО Смарт Энджинс Сервис
117312 Москва, проспект 60-летия Октября, д. 9, Россия
3 Федеральный исследовательский центр “Информатика и управление” РАН
117312 Москва, проспект 60-летия Октября, д. 9, Россия
4 Национальный исследовательский технологический университет “МИСиС”
119049 Москва, Ленинский проспект, д. 4, Россия
5 Московский физико-технический институт
141701 г. Долгопрудный, Институтский переулок, д. 9, Россия
* E-mail: konovalenko@iitp.ru
Поступила в редакцию 08.10.2019
После доработки 27.10.2019
Принята к публикации 17.12.2019
Аннотация
Общепринято применение проективной нормализации (частный случай ортокоррекции) к фотографиям документов для их дальнейшего оптического распознавания. На сегодняшний день известен ряд критериев точности проективной нормализации. Почти все они характеризуют только невязку координат. Однако текстовые поля документов обычно имеют вытянутую форму, так что даже при небольших невязках координат возможны большие невязки направлений, которые значительно влияют на качество сегментации поля и распознавания отдельных символов в нем. Проблема точной коррекции невязок направлений стоит и в задачах томографии, если для измерения используется спиральная схема сканирования или проекции регистрируются в схемах томосинтеза. Для описания точности проективной нормализации изображения в точке предлагается поточечная максимальная невязка направлений. В качестве критерия точности проективной нормализации всего изображения предлагается максимальная невязка направлений, равная максимальной по области интереса поточечной максимальной невязке направлений. Получено аналитическое решение задачи вычисления поточечной максимальной невязки направлений. Выдвинута и численно подтверждена гипотеза о том, что поточечная максимальная невязка направлений – квазивыпуклая функция. Доказана теорема о том, что супремум квазивыпуклой функции на ограниченном замкнутом множестве равен супремуму на крайних точках его выпуклой оболочки. На основании гипотезы и теоремы предложено аналитическое решение задачи вычисления максимальной невязки направлений на полиэдральной области интереса.
ВВЕДЕНИЕ
Проективная нормализация изображений
Путем устранения радиальной дисторсии (Kunina et al., 2017) практически любая изображающая оптическая система может быть сведена к ортоскопической оптической системе, т.е. к такой изображающей оптической системе, которая описывается проективной моделью камеры (Шапиро и др., 2013). В рамках проективной модели камеры произвольная плоскость сцены оказывается связана с плоскостью изображения проективным преобразованием.
Ракурс съемки относительно плоской сцены называется нормальным, если изображающая оптическая система (далее – камера) ориентирована по нормали к сцене. Имитация сделанного с виртуального нормального ракурса съемки изображения на основе изображения, сделанного с произвольного ракурса, обеспечивается проективным преобразованием последнего. На основе работы (Путятин и др., 1998) будем называть такую имитацию проективной нормализацией изображения (ПНИ). Полученное в результате ПНИ изображение называется нормализованным. Нормализованное изображение является ортоскопическим, т.е. образ плоской сцены на нем подобен самой сцене, что принципиально упрощает ее дальнейший анализ. Как правило, при ПНИ от виртуального ракурса съемки требуют не только нормальности, но и фиксации тех или иных оставшихся степеней свободы камеры (твердого тела), которые проявляются как изотропное масштабирование, сдвиг и ориентация нормализованного изображения.
Проективная нормализация активно используется в качестве этапа предобработки изображений при решении различных задач технического зрения, таких как распознавание текстового содержания документов (Зейналов и др., 2009; Болотова и др., 2017; Шемякина и др., 2017; Skoryukina et al., 2018); распознавание автомобильных номеров (Povolotskiy et al., 2017); автоматическое узнавание телевизионной передачи по фотографии экрана телевизора (Skoryukina et al., 2017); детектирование шахматной доски с целью калибровки камеры (Xie Y et al., 2018); детектирование искусственной неровности на дорогах (Arvind et al., 2018); сопоставление контура представленного на изображении объекта с объектом в базе данных (Dubuisson, Jain, 1994; Sim et al., 1999; Orrite, Herrero, 2004; Николаев, 2016; Балицкий и др., 2017; Савчик, Николаев, 2018); томографическая реконструкция: при предобработке томографических проекций перед применением алгоритма реконструкции при использовании спиральной, конусной схемы сканирования (Бузмаков, 2019), спутниковый мониторинг (оценка временной изменчивости температуры поверхности океана, определение скорости передвижения облачных масс и многое другое) (Катаманов, 2007), составление планов и карт местности по результатам аэрофотосъемки (Karpenko et al., 2015; Холопов, 2017) и многих других. Кроме того, проективная нормализация фотографии документа применима для облегчения восприятия ее человеком (Legge et al., 1985).
Обзор геометрических критериев точности проективной нормализации изображений
Как было показано выше, ПНИ используется в качестве этапа предобработки изображений при решении многих задач технического зрения. Данный раздел посвящен обзору существующих в литературе геометрических критериев точности ПНИ.
Начнем с введения используемых далее определений и обозначений:
${{I}_{{input}}}$ – входное изображение (рис. 1). Обычно им является фотография.
Рис. 1.
Общая схема преобразований. Iinput – сделанная с произвольного ракурса фотография документа, Iideal – идеально нормализованное изображение, Ipract – практически нормализованное изображение.

H – проективное преобразование, задающее идеальную нормализацию изображения ${{I}_{{input}}}$. Далее будем рассматривать только случаи, когда H – единственное. На практике ${\text{H}}$ не известно, но считается известным при тестировании методов ПНИ.
${\hat {H}}$ – проективное преобразование, получаемое методом ПНИ и оценивающее H.
${{I}_{{ideal}}}$ – идеально нормализованное изображение. Формируется в результате применения ${\text{H}}$ к ${{I}_{{input}}}$.
${{I}_{{pract}}}$ – практически нормализованное изображение. Формируется в результате применения ${\hat {H}}$ к ${{I}_{{input}}}$.
${\mathbf{x}}\;\mathop = \limits^{{\text{def}}} \;{{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{2}}} \end{array}} \right]}^{T}}$– декартовы координаты пикселей на плоскости изображения ${{I}_{{ideal}}}$.
${\mathbf{y}}\;\mathop = \limits^{{\text{def}}} \;{{\left[ {\begin{array}{*{20}{c}} {{{y}_{1}}}&{{{y}_{2}}} \end{array}} \right]}^{T}}$– декартовы координаты пикселей на плоскости изображения ${{I}_{{pract}}}$.
${\text{V}}\;\mathop = \limits^{{\text{def}}} \;{\hat {H}}{{{\text{H}}}^{{ - 1}}}$– остаточное проективное преобразование, для каждой точки сцены переводящее координаты ее образа на изображении ${{I}_{{ideal}}}$ в координаты ее образа на изображении ${{I}_{{pract}}}$: ${\mathbf{y}} = {\text{V}}({\mathbf{x}}).$
${\text{d}}({\mathbf{x}}\,|\,{\text{V}})\;\mathop = \limits^{{\text{def}}} \;{{\left\| {{\mathbf{x}} - {\text{V}}({\mathbf{x}})} \right\|}_{2}}$– невязка координат (Kunina et al., 2016), поточечно характеризующая ошибку ПНИ.
$R \subset {{\mathbb{R}}^{2}}$ – занятое образом целевого объекта сцены (документа, автомобильного номера, здания и другое) множество точек изображения ${{I}_{{ideal}}}$, называемое областью интереса.
$Q\;\mathop = \limits^{{\text{def}}} \;{\text{V}}[R]\;\mathop = \limits^{{\text{def}}} \;\{ {\text{V}}({\mathbf{x}}):{\mathbf{x}} \in R\} $– образ области интереса R на изображении ${{I}_{{pract}}}$.
Перейдем непосредственно к обзору геометрических критериев точности ПНИ:
1. На конкурсе “Smartphone document capture” конференции ICDAR (Zhukovsky et al., 2017) в качестве критерия выбран коэффициент Жаккарда (Jaccard, 1901), который равен площади пересечения множеств Q и R, отнесенной к площади их объединения: ${{K}_{{Jaccard}}}(Q,R)\mathop = \limits^{{\text{def}}} \frac{{S(Q \cap R)}}{{S(Q \cup R)}}.$
2. В работе (Sim et al., 1999) для проективного сопоставления объектов используется метрика Хаус-дорфа, равная наибольшему расстоянию от точек одного множества до соответствующих им ближайших точек второго множества: ${{d}_{{Hausdorff}}}(Q,R)\;\mathop = \limits^{{\text{def}}} $ $\mathop = \limits^{{\text{def}}} \;\max \left\{ {\mathop {\max }\limits_{{\mathbf{y}} \in Q} \mathop {\min }\limits_{{\mathbf{x}} \in R} {{{\left\| {{\mathbf{y}} - {\mathbf{x}}} \right\|}}_{2}},\;\mathop {\max }\limits_{{\mathbf{x}} \in R} \mathop {\min }\limits_{{\mathbf{y}} \in Q} {{{\left\| {{\mathbf{x}} - {\mathbf{y}}} \right\|}}_{2}}} \right\}.$
В статье (Orrite, Herrero, 2004) она используется для проективного выравнивания частично заслоненных контуров, в статье (Jesorsky et al., 2001) – для робастной детекции лиц, в работе (Huttenlocher et al., 1993) – для вычисления близости двух изображений. В ряде работ опубликованы ее модификации (Dubuisson, Jain, 1994; Ефимов, Новиков, 2016).
3. В статье (Притула и др., 2014) для измерения близости двух контуров после проективного выравнивания в задаче проективно-инвариантного распознавания плоских замкнутых контуров применяется расстояние Фреше (Fréchet, 1906), которое определяется следующим образом: $F(Q,R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\inf }\limits_{a,b} \;\mathop {\max }\limits_{t \in [0,1)} \;{{\left\| {\delta Q(a(t)),\delta R(b(t))} \right\|}_{2}},$ где $\delta Q$ и $\delta R$ – непрерывные отображения отрезка [0, 1] в границы множеств Q и R соответственно, $a,\;b$ – непрерывные неубывающие сюръекции отрезка $[0,1]$ в себя (репараметризация). От метрики Хаусдорфа расстояние Фреше отличается тем, что накладывает ограничения на повторное использование точек из Q и R. Этот критерий используется также для вычисления точности сегментации изображений (Березский, Березская, 2015) и точности сопоставления карт (Wei et al., 2013).
4. В задаче автоматической коррекции дисторсии, вызванной кривизной линзы и движением камеры (Hsu, Sawhney, 1998), используется среднеквадратичный критерий: ${{L}_{2}}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\sqrt {\frac{1}{{S(R)}}\int_R {{{{\text{d}}}^{2}}({\mathbf{x}}\,|\,{\text{V}})d{\mathbf{x}}} } ,$ где $S(R)$ – площадь области интереса R. Он же используется для вычисления точности формирования единого изображения при помощи матрицы проекторов (Chen et al., 2002).
5. В работе (Катаманов, 2007) для вычисления точности автоматической привязки, полученной с геостационарного спутника изображений, использовался минимаксный критерий, равный максимальному значению невязки координат на области интереса R: ${{L}_{\infty }}({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\max }\limits_{{\mathbf{x}} \in R} {\text{ d}}({\mathbf{x}}\,|\,{\text{V}}).$
6. Некоторые критерии предназначены только для случая, когда область интереса R является прямоугольником. Тогда ее искаженный образ Q является четырехугольником. Например, в работах (Rodríguez-Piñeiro et al., 2011; Zhang, He, 2007; Takezawa et al., 2016; Awal et al., 2017) для оценки точности ПНИ используется ошибка в соотношении сторон четырехугольника Q. В работе (Calore et al., 2012) для оценки точности устранения проективных искажений используется угол между противоположными сторонами четырехугольника Q, а в работе (Холопов, 2017) – критерий, равный отношению минимального и максимального углов четырехугольника Q.
Заметим, что все найденные в литературе геометрические критерии точности зависят от
${\hat {H}}$ и H только через 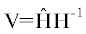 . Поэтому точность оценки ${\hat {H}}$ преобразования H можно понимать как близость остаточного преобразования V к тождественному
преобразованию I.
. Поэтому точность оценки ${\hat {H}}$ преобразования H можно понимать как близость остаточного преобразования V к тождественному
преобразованию I.
ЗАДАЧА РАСПОЗНАВАНИЯ ДОКУМЕНТА ПО СДЕЛАННОЙ С ПРОИЗВОЛЬНОГО РАКУРСА ФОТОГРАФИИ
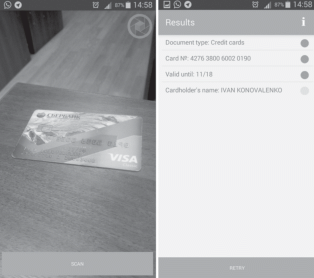
Рассмотрим следующую задачу компьютерного зрения. Пусть дана сделанная с произвольного ракурса фотография физически плоского документа. Требуется распознать текстовое содержание документа (Arlazarov et al.,2018). Для краткости в рамках данной работы назовем эту задачу “задачей распознавания”. Решающую задачу распознавания системы назовем “системой распознавания”. Пример работы системы распознавания приведен на рис. 2.
Рис. 2.
Пример работы системы распознавания. Слева направо: фотография документа, распознанное текстовое содержание документа.
Будем считать, что система распознавания декомпозирована на следующие два модуля (рис. 3) (Zhukovsky et al., 2017; Шемякина и др., 2017; Skoryukina et al., 2018).
$ \bullet $ Модуль ПНИ изображения, который на основе входного изображения ${{I}_{{input}}}$ вычисляет оценку ${\hat {H}}$ идеальной нормализации H, и, применяя ее к изображению ${{I}_{{input}}}$, формирует практически нормализованное изображение ${{I}_{{pract}}}$.
$ \bullet $ Модуль распознавания, который принимает на вход практически нормализованное изображение ${{I}_{{pract}}}$ и возвращает текстовое содержание документа.
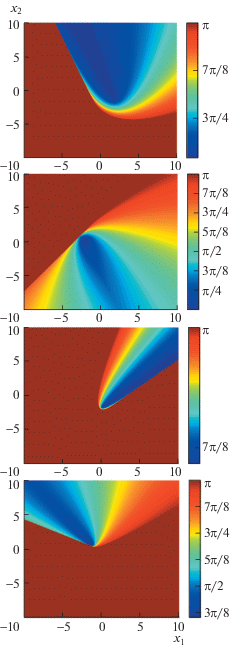
Пользуясь вышеприведенными данными, проанализируем известные критерии точности ПНИ на предмет их соответствия качеству последующего решения задачи распознавания. Большинство из них характеризуют только невязку координат. Однако текстовые поля документов обычно имеют вытянутую форму, так что даже при небольших невязках координат возможны большие невязки направлений (рис. 4), которые значительно влияют на качество сегментации поля и распознавания отдельных символов в нем (Bezmaternykh et al., 2018). Критерии точности, характеризующие невязку направлений, также встречаются в литературе (пункт 6), однако, их связь с качеством распознавания представляется недостаточной или, по крайней мере, недостаточно ясной. В следующем разделе мы предлагаем новый критерий на основе невязок направлений, специально построенный для описания точности ПНИ в задаче распознавания.
МАКСИМАЛЬНАЯ НЕВЯЗКА НАПРАВЛЕНИЙ ПРОЕКТИВНОЙ НОРМАЛИЗАЦИИ ИЗОБРАЖЕНИЯ
Угловой модуль
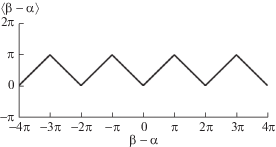
Для описания абсолютной разницы между углами α и β введем угловой модуль, равный углу между векторами $\left[ {\begin{array}{*{20}{c}} {\cos (\alpha )} \\ {\sin (\alpha )} \end{array}} \right]$ и $\left[ {\begin{array}{*{20}{c}} {\cos (\beta )} \\ {\sin (\beta )} \end{array}} \right]$:
(1)
$\begin{gathered} \langle \beta - \alpha \rangle \;\mathop = \limits^{{\text{def}}} \;\arccos (\cos (\beta - \alpha )) = \\ \, = \left| {((\beta - \alpha + \pi )\bmod 2\pi ) - \pi } \right|. \\ \end{gathered} $Угловой модуль отличается от обычного модуля тем, что учитывает периодичность углов (рис. 5).
Невязка направлений
Напомним, что остаточное проективное преобразование V для каждой точки сцены переводит координаты ее образа на изображении ${{I}_{{ideal}}}$ в координаты ее образа на изображении ${{I}_{{pract}}}$: ${\mathbf{y}} = {\text{V}}({\mathbf{x}}).$ Сперва рассмотрим случай общего положения, который заключается в том, что матрица Якоби $J({\mathbf{x}})$ преобразования V существует и невырождена в каждой точке выпуклой оболочки области интереса ${\mathbf{x}} \in {\text{Conv}}(R)$. Тогда бесконечно малый вектор, исходящий из точки ${\mathbf{x}} \in {\text{Conv}}(R)$ по направлению α, после преобразования V перейдет в бесконечно малый вектор, исходящий из точки ${\text{V}}({\mathbf{x}})$ по направлению β, которое можно рассчитать по формуле
(2)
$\begin{gathered} \beta ({\mathbf{x}},\alpha \,|\,{\text{V}}) = \\ \, = \mathop {\lim }\limits_{R \to + 0} {\text{ arctg2}}\left[ {{\text{V}}\left( {{\mathbf{x}} + R\left[ {\begin{array}{*{20}{c}} {\cos (\alpha )} \\ {\sin (\alpha )} \end{array}} \right]} \right) - {\text{V}}({\mathbf{x}})} \right], \\ \end{gathered} $(3)
$\beta ({\mathbf{x}},\alpha \,|\,{\text{V}}) = {\text{arctg2}}\left[ {J({\mathbf{x}})\left[ {\begin{array}{*{20}{c}} {\cos (\alpha )} \\ {\sin (\alpha )} \end{array}} \right]} \right].$Проективное преобразование по определению сохраняет прямые, поэтому вместо бесконечно малых векторов c тем же результатом можно рассматривать произвольные. Таким образом, радиус R в формуле (2) можно не устремлять к нулю, а выбирать его произвольно положительным (рис. 6, г):
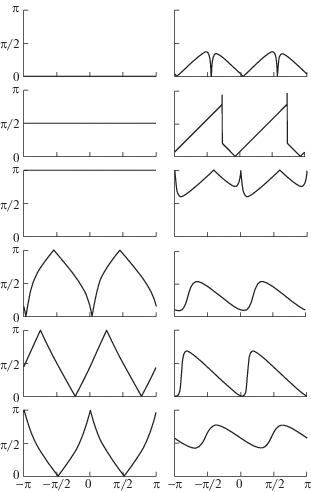
Рис. 6.
Геометрические искажения изображений, не дающие невязок направлений во всех точках: а – тождественное преобразование; б – сдвиг; в – изотропное масштабирование; г – проективное преобразование (не дает невязок направлений в одной точке); рамками показано идеальное положение изображения символа; д – соответствующий вышеуказанным случаям график невязки направлений.
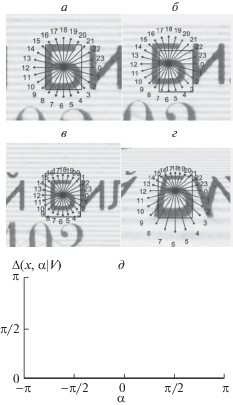
Невязкой направлений назовем функцию, которая в каждой точке ${\mathbf{x}} \in {\text{Conv}}(R)$ равняется искажению каждого направления α остаточным преобразованием V:
Примеры графиков Δ для различных x и V можно видеть на рис. 6, 7 и 8. Так как проективное преобразование сохраняет прямые, невязка направлений, как функция от x, не меняется по направлению α. В силу дифференцируемости проективного преобразования невязка направлений имеет период, равный π.
Поточечная максимальная невязка направлений
Известно, что невязки направлений различных типов (скос, поворот) создают сложности при сегментации и распознавании текста (Bezmaternykh et al., 2018). При этом неизвестно случая, чтобы большая невязка по какому-то из направлений не создавала таковых сложностей. Более того, невязки направлений $\Delta ({\mathbf{x}},\alpha \,|\,{\text{V}})$ – функции не произвольные, а всего лишь трехпараметрические – по числу элементов матрицы Якоби (3) без учета масштаба, и большое значение невязки по одному направлению влечет за собой сопоставимые значения по большой части оставшихся направлений. Таким образом, для возникновения сложностей при сегментации и распознавании текста достаточно большой невязки хотя бы по одному из направлений. Поэтому в качестве критерия точности ПНИ в точке мы предлагаем поточечную максимальную невязку направлений:
(4)
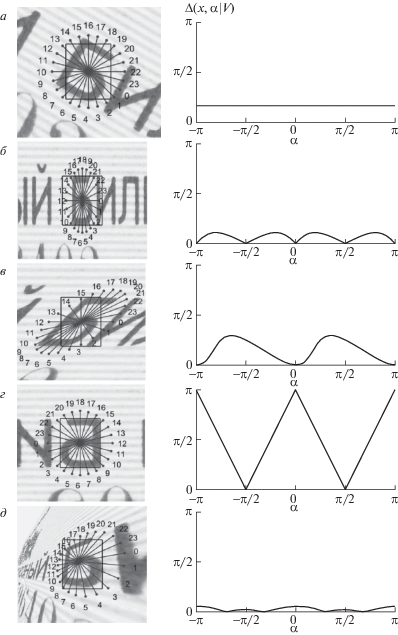
${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})\;\mathop = \limits^{{\text{def}}} \;\mathop {\max }\limits_\alpha {\text{ }}\Delta ({\mathbf{x}},\alpha \,|\,{\text{V}}).$Примеры графиков ${{\Delta }_{\infty }}$ для различных V можно видеть на рис. 9 и 10.
Рис. 9.
Невязки остаточного преобразования V: a – практически нормализованное изображение Ipract; зеленая рамка ограничивает идеальное положение образа документа; б – невязка координат ${\text{d}}({\mathbf{x}}\,|\,{\text{V}}) = {{\left\| {{\mathbf{x}} - {\text{V}}({\mathbf{x}})} \right\|}_{2}}$, измеренная в пикселях; в – поточечная максимальная невязка направлений ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$, измеренная в градусах; цвет соответствует значениям невязок; cтрелочками показано векторное поле преобразования ${\text{V}}({\mathbf{x}}) - {\mathbf{x}}$.
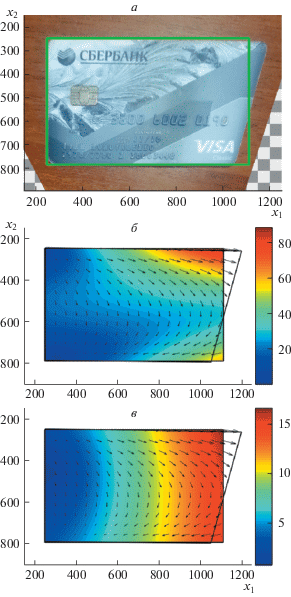
Максимальная невязка направлений
В качестве скалярного интегрального критерия точности проективной нормализации изображения ${{I}_{{pract}}}$ предлагается максимальная невязка направлений, равная максимальной по области интереса R поточечной максимальной невязке направлений:
(5)
$\Delta _{\infty }^{\infty }({\text{V}};R)\;\mathop = \limits^{{\text{def}}} \;\mathop {\max }\limits_{{\mathbf{x}} \in R} {\text{ }}{{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}) = \mathop {\max }\limits_{{\mathbf{x}} \in R} \;\mathop {\max }\limits_\alpha {\text{ }}\Delta ({\mathbf{x}},\alpha \,|\,{\text{V}}).$Остаточное преобразование V – проективное, а значит, преобразует прямые в прямые. Следовательно, критерий $\Delta _{\infty }^{\infty }$ равняется наибольшему среди углов, на которые преобразование V поворачивает всевозможные прямые ${\mathbf{l}}$, пересекающие область интереса R:
Таким образом, мы построили критерий точности ПНИ, “максимально” чувствительный к невязкам направлений. Напомним, что мотивацией для построения такого критерия послужила недостаточная чувствительность к невязкам направлений критериев, основанных на невязках координат. Однако критерий $\Delta _{\infty }^{\infty }$ сам по себе тем более не может претендовать на связь с качеством последующего распознавания нормализованного изображения, так как равняется строго нулю при сколь угодно большом сдвиге и изотропном масштабировании (рис. 6). Решение этой проблемы авторы видят в комбинированном использовании критерия максимальной невязки направлений $\Delta _{\infty }^{\infty }$ и критерия максимальной невязки координат
ранее исследованного в работе (Konovalenko, Shemiakina, 2018).Вырожденные случаи
Выше мы рассматривали только случай общего положения, когда матрица Якоби $J({\mathbf{x}})$ преобразования V существует и невырождена в каждой точке x выпуклой оболочки области интереса ${\text{Conv}}(R)$. В этом разделе рассмотрим остальные случаи, которые будем называть вырожденными.
$ \bullet $ Пусть существуют точки ${\text{Conv}}(R)$, в которых не существует матрицы Якоби. Выясним, что это за точки. Параметризуем преобразование V однородной матрицей $V\;\mathop = \limits^{{\text{def}}} \;({{{v}}_{{ij}}}) \in {{\mathbb{R}}^{{3 \times 3}}}$ следующим образом:
(6)
${\text{V}}({\mathbf{x}})\;\mathop = \limits^{{\text{def}}} \;\frac{{\left[ {\begin{array}{*{20}{c}} {{{{v}}_{{11}}}{{x}_{1}} + {{{v}}_{{12}}}{{x}_{2}} + {{{v}}_{{13}}}} \\ {{{{v}}_{{21}}}{{x}_{1}} + {{{v}}_{{22}}}{{x}_{2}} + {{{v}}_{{23}}}} \end{array}} \right]}}{{{{{v}}_{{31}}}{{x}_{1}} + {{{v}}_{{32}}}{{x}_{2}} + {{{v}}_{{33}}}}}.$Прямую с уравнением ${{{v}}_{{31}}}{{x}_{1}} + {{{v}}_{{32}}}{{x}_{2}} + {{{v}}_{{33}}} = 0$, на которой знаменатель преобразования ${\text{V}}$ обращается в ноль, будем называть горизонтом и обозначать ${{{\mathbf{l}}}_{\infty }} \subset {{\mathbb{R}}^{2}}$. Легко видеть, что матрица Якоби преобразования V существует во всех точках евклидовой плоскости за исключением горизонта: ${{\mathbb{R}}^{2}}{\backslash }{{{\mathbf{l}}}_{\infty }}$. Соответственно поточечная максимальная невязка направлений ${{\Delta }_{\infty }}$ для ${\mathbf{x}} \in {{{\mathbf{l}}}_{\infty }}$ формулой (4) не определяется. Однако оказывается, что ${{\Delta }_{\infty }}$ равняется π всюду по одну из сторон от горизонта. Это объясняется тем, что по “ту” сторону горизонта происходит отражение изображения, а значит, всегда найдется направление, противоположное исходному. Поэтому поточечная максимальная невязка направлений естественно доопределяется:
(7)
${\mathbf{x}} \in {{{\mathbf{l}}}_{\infty }} \Rightarrow {{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})\;\mathop = \limits^{{\text{def}}} \;\pi .$$ \bullet $ Пусть существуют точки ${\text{Conv}}(R)$, в которых матрица Якоби вырождена. Для проективного преобразования, как и для линейного, вырожденность матрицы Якоби в одной точке влечет ее вырожденность во всех точках. При этом плоскость изображения ${{I}_{{ideal}}}$ схлопывается в прямую или точку. Поточечная максимальная невязка направлений ${{\Delta }_{\infty }}$ в таком случае формулой (4) не определяется и смысла не имеет.
ВЫЧИСЛЕНИЕ МАКСИМАЛЬНОЙ НЕВЯЗКИ НАПРАВЛЕНИЙ ПРОЕКТИВНОЙ НОРМАЛИЗАЦИИ ИЗОБРАЖЕНИЯ
В данном разделе мы построим аналитическое решение задачи вычисления максимальной невязки направлений (5) на полиэдре.
Вычисление поточечной максимальной невязки направлений
Начнем с подзадачи вычисления поточечной максимальной невязки направлений (4):
Если ${\mathbf{x}} \in {{{\mathbf{l}}}_{\infty }}$, то ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}) = \pi $ по формуле (7). Далее рассмотрим случай ${\mathbf{x}} \notin {{{\mathbf{l}}}_{\infty }}$. Запишем задачу с использованием формулы (3):
(8)
${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}) = \mathop {\max }\limits_\alpha \left\langle {\left( {{\text{arctg}}2\left[ {J({\mathbf{x}})\left[ {\begin{array}{*{20}{c}} {\cos (\alpha )} \\ {\sin (\alpha )} \end{array}} \right]} \right]} \right) - \alpha } \right\rangle .$Матрица Якоби – константа, обозначим ее $J\;\mathop = \limits^{{\text{def}}} \;J({\mathbf{x}})$. Переменный единичный вектор обозначим ${\mathbf{a}}(\alpha )\;\mathop = \limits^{{\text{def}}} \;\left[ {\begin{array}{*{20}{c}} {\cos (\alpha )} \\ {\sin (\alpha )} \end{array}} \right]$. Кроме того, обозначим ${\mathbf{b}}({\mathbf{a}})\;\mathop = \limits^{{\text{def}}} \;J{\mathbf{a}}$ и $\beta ({\mathbf{b}}){\kern 1pt} \mathop = \limits^{{\text{def}}} {\kern 1pt} {\text{arctg2}}\left[ {\mathbf{b}} \right]$, тогда ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}){\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \mathop {\max }\limits_\alpha \langle \beta ({\mathbf{b}}({\mathbf{a}}(\alpha )))\, - \,\alpha \rangle .$
Функция $\langle \beta ({\mathbf{b}}({\mathbf{a}}(\alpha ))) - \alpha \rangle $ может достигать максимума только в двух случаях: если недифференцируемая функция $\langle \bullet \rangle $ (1) равна своему локальному и глобальному максимуму π и если равняется нулю производная ее аргумента. Найдем α, соответствующие каждому из этих случаев.
$ \bullet $ Пусть $\langle \beta ({\mathbf{b}}({\mathbf{a}}(\alpha ))) - \alpha \rangle = \pi .$ Тогда в соответствии с определением $\langle \bullet \rangle $ или рис. 5: $\beta ({\mathbf{b}}({\mathbf{a}}(\alpha ))) - \alpha = \pi + 2\pi n$, $n \in \mathbb{Z}$. Значит, вектор ${\mathbf{b}} = J{\mathbf{a}}$ противонаправлен вектору a: $J{\mathbf{a}} = \lambda {\mathbf{a}}$, $\lambda < 0$. В нашем случае a – это собственные векторы матрицы J, соответствующие ее вещественным отрицательным собственным числам λ. Тогда искомые $\alpha = {\text{arctg2}}\left[ {\mathbf{a}} \right]$ – ориентации таких векторов.
$ \bullet $ Пусть
(9)
$(\beta ({\mathbf{b}}({\mathbf{a}}(\alpha ))) - \alpha )_{\alpha }^{'} = 0 \Rightarrow \beta _{{\mathbf{b}}}^{'}{\mathbf{b}}_{{\mathbf{a}}}^{'}{\mathbf{a}}_{\alpha }^{'} = 1.$Возьмем производные:
Обозначим $K\;\mathop = \limits^{{\text{def}}} \;({{k}_{{ij}}})\;\mathop = \limits^{{\text{def}}} \;{{J}^{T}}{{M}^{T}}JM - {{J}^{T}}J$, тогда
Решая это квадратное уравнение в вещественных числах, находим значения ${\text{tg}}(\alpha )$, из которых получаем искомые α.
Тогда искомый максимум (8) достигается на одном из значений α, вычисленных выше. Таким образом, получено аналитическое решение задачи вычисления поточечной максимальной невязки направлений ${{\Delta }_{\infty }}$. Сформулируем алгоритм вычисления поточечной максимальной невязки направлений.
Вход: Точка ${\mathbf{x}} = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{2}}} \end{array}} \right]}^{T}}$ изображения ${{I}_{{ideal}}}$ и однородная матрица $({{{v}}_{{ij}}}) \in {{\mathbb{R}}^{{3 \times 3}}}$, определяющая (6) остаточное проективное преобразование V.
Выход: поточечная максимальная невязка направлений ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$.
– Если ${{{v}}_{{31}}}{{x}_{1}} + {{{v}}_{{32}}}{{x}_{2}} + {{{v}}_{{33}}} = 0$, то ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}) = \pi $. Иначе далее.
– Рассчитаем матрицу Якоби J проективного преобразования V в точке x.
– Найдем все собственные векторы $\{ {{{\mathbf{a}}}_{j}}\} _{{j = 1}}^{m}$ матрицы J, соответствующие ее вещественным отрицательным собственным числам.
– Рассчитаем углы ${{\alpha }_{j}} = {\text{arctg2}}[{{{\mathbf{a}}}_{j}}]$.
– Рассчитаем матрицу $({{k}_{{ij}}}) = {{J}^{T}}{{M}^{T}}JM - {{J}^{T}}J$, где $M = \left[ {\begin{array}{*{20}{c}} 0&{ - 1} \\ 1&0 \end{array}} \right]$.
– Найдем все вещественные корни $\{ {{t}_{i}}\} _{{i = 1}}^{n}$ квадратного уравнения
– Рассчитаем углы $\alpha _{i}^{'} = {\text{arctg}}[{{t}_{i}}]$.
– Сформируем набор углов $A = \{ \{ {{\alpha }_{j}}\} _{{j = 1}}^{m},\{ {{\alpha '}_{i}}\} _{{i = 1}}^{n}\} $.
– Рассчитаем поточечную максимальную невязку направлений:
Вычисление максимальной невязки направлений
Теперь перейдем непосредственно к задаче вычисления максимальной невязки направлений (5): $\Delta _{\infty }^{\infty }({\text{V}};R) = \mathop {\max }\limits_{{\mathbf{x}} \in R} {\text{ }}{{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}).$
Проведенные авторами численные эксперименты позволяют выдвинуть гипотезу о том, что поточечная максимальная невязка направлений ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$ проективного преобразования – квазивыпуклая функция (рис. 9 и 10). Примем эту гипотезу и допустим, что область интереса R – ограниченное и замкнутое множество. Тогда, в соответствии с теоремой 2 (Приложение), супремум ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$ на R равен супремуму на крайних точках выпуклой оболочки R:
Легко видеть, что функция ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$ непрерывна, поэтому по теореме Вейерштрасса имеем $\mathop {\max }\limits_{{\mathbf{x}} \in R} {\text{ }}{{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}) = \mathop {\max }\limits_{{\mathbf{x}} \in {\text{E}}({\text{Conv}}(R))} {{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}),$ тогда $\Delta _{\infty }^{\infty }({\text{V}};R) = \mathop {\max }\limits_{{\mathbf{x}} \in {\text{E}}({\text{Conv}}(R))} {{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}}),$ что во многих случаях существенно упрощает вычисление $\Delta _{\infty }^{\infty }$. Рассмотрим основной для нашего практического приложения частный случай, когда область интереса R состоит из многоугольников, т.е. является полиэдром. Выпуклая оболочка полиэдра – выпуклый многогранник, а в нашем плоском случае – выпуклый многоугольник. Крайние точки выпуклого многоугольника – его вершины. Значит, максимальную невязку направлений достаточно искать среди вершин $\{ {{{\mathbf{x}}}_{i}}\} _{{i = 1}}^{n}$ многоугольника, являющегося выпуклой оболочкой R (рис. 11):
(10)
$\Delta _{\infty }^{\infty }({\text{V}};R) = \mathop {\max }\limits_i {{\Delta }_{\infty }}({{{\mathbf{x}}}_{i}}\,|\,{\text{V}}).$Рис. 11.
Вычисление максимальной невязки направлений: белыми контурами ограничена полиэдральная область интереса R; черный контур – многоугольник ${\text{Conv}}(R)$; черные точки – его вершины ${\text{E}}({\text{Conv}}(R))$, на которых достигается максимальная невязка направлений $\Delta _{\infty }^{\infty }({\text{V}};R)$.

Таким образом, имеем следующий алгоритм вычисления максимальной невязки направлений на полиэдре.
Вход: остаточное проективное преобразование V, полиэдральная область интереса R.
Выход: максимальная невязка направлений $\Delta _{\infty }^{\infty }({\text{V}};R)$.
– Найдем вершины многоугольника, являющегося выпуклой оболочкой R: $\{ {{{\mathbf{x}}}_{i}}\} _{{i = 1}}^{n} = {\text{E}}({\text{Conv}}(R)).$
– Используя алгоритм вычисления ${{\Delta }_{\infty }}({\mathbf{x}}\,|\,{\text{V}})$, вычислим максимальную невязку направлений: $\Delta _{\infty }^{\infty }({\text{V}};R) = \mathop {\max }\limits_i {{\Delta }_{\infty }}({{{\mathbf{x}}}_{i}}\,|\,{\text{V}}).$
ЗАКЛЮЧЕНИЕ
В работе приведен ряд известных в литературе геометрических критериев точности проективной нормализации изображений (ПНИ) и проанализирована целесообразность их использования для оценки качества последующего распознавания текста на нормализованном изображении. Показано, что известные критерии имеют недостаточную чувствительность к невязкам направлений, возникающих вследствие неточности ПНИ, тогда как таковые невязки оказывают сильное негативное воздействие на качество сегментации поля и распознавания отдельных символов в нем. Для устранения этого недостатка построен вспомогательный критерий точности ПНИ, “максимально” чувствительный именно к невязкам направлений: для описания точности ПНИ в точке выбрана поточечная максимальная невязка направлений, в качестве критерия точности проективной нормализации всего изображения предложена максимальная невязка направлений, равная максимальной по области интереса поточечной максимальной невязке направлений. Получено аналитическое решение задачи вычисления поточечной максимальной невязки направлений. Выдвинута и численно подтверждена гипотеза о том, что поточечная максимальная невязка направлений – квазивыпуклая функция. Доказана теорема о том, что супремум квазивыпуклой функции на ограниченном замкнутом множестве равен супремуму на крайних точках его выпуклой оболочки. На основании гипотезы и теоремы предложено аналитическое решение задачи вычисления максимальной невязки направлений на полиэдральной области интереса.
Полученные результаты могут быть использованы как для построения методов ПНИ, так и для дальнейшего развития критериев точности ПНИ.
Работа выполнена при частичной финансовой поддержке РФФИ (проекты № 18-29-26022, 18-29-26035).
Список литературы
Балицкий А.М., Савчик А.В., Гафаров Р.Ф., Коноваленко И.А. О проективно инвариантных точках овала с выделенной внешней прямой. Проблемы передачи информации. 2017. Т. 53. № 3. С. 84–89.
Березский О.Н., Березская К.М. Количественная оценка качества сегментации изображений на основе метрик. Управляющие системы и машины. 2015. № 6. С. 59–65.
Болотова Ю.А., Спицын В.Г., Осина П.М. Обзор алгоритмов детектирования текстовых областей на изображениях и видеозаписях. Компьютерная оптика. 2017. Т. 41. № 3. С. 441–452.
Бузмаков А.В., Асадчиков В.Е., Золотов Д.А., Чукалина М.В., Ингачева А.С., Кривоносов Ю.С. Лабораторные рентгеновские микротомографы: методы предобработки экспериментальных данных. Известия РАН. Серия физическая. 2019. Т. 83 (2). С. 194–197. https://doi.org/10.1134/S0367676519020066
Ефимов А.И., Новиков А.И. Алгоритм поэтапного уточнения проективного преобразования для совмещения изображений. Компьютерная оптика. 2016. Т. 40. № 2. С. 258–265. https://doi.org/10.18287/2412-6179-2016-40-2-258-265
Зейналов Р., Велижев А., Конушин А. Восстановление формы страницы текста для коррекции геометрических искажений. Международная конференция Графикон. М.: 2009. С. 125–128.
Катаманов С.Н. Автоматическая привязка изображений геостационарного спутника MTSAT-1R. Современные проблемы дистанционного зондирования Земли из космоса. 2007. Т. 1. № 4. С. 63–68.
Николаев П.П. Проективно инвариантное описание неплоских гладких фигур. 1. Предварительный анализ задачи. Сенсорные системы. 2016. Т. 30. № 4. С. 290–311.
Притула Н.Е., Николаев П.П., Шешкус А.В. Сравнение двух алгоритмов проективно-инвариантного распознавания плоских замкнутых контуров с единственной вогнутостью. Сборник трудов ИТИС-14. 2014. С. 367–373.
Путятин Е.П., Прокопенко Д.О., Печеная Е.М. Вопросы нормализации изображений при проективных преобразованиях. Радиоэлектроника и информатика. 1998. № 2 (3). С. 82–86.
Рокафеллар Р. Выпуклый анализ. М.: Мир, 1973. Т. 472. С. 34–39.
Савчик А.В., Николаев П.П. Метод проективного сопоставления для овалов с двумя отмеченными точками. Информационные технологии и вычислительные системы. 2018. № 1. С. 60–67.
Холопов И.С. Алгоритм коррекции проективных искажений при маловысотной съемке. Компьютерная оптика. 2017. Т. 41. № 2. С. 284–290.
Шапиро Л., Стокман Д., Богуславский А.А., Соколов С.М. Компьютерное зрение. М.: БИНОМ, 2013. 763 с.
Шемякина Ю.А., Жуковский А.Е., Фараджев И.А. Исследование алгоритмов вычисления проективного преобразования в задаче наведения на планарный объект по особым точкам. Искусственный интеллект и принятие решений. 2017. № 1. С. 43–49.
Юдин Д.Б. Математические методы управления в условиях неполной информации. Издательская группа URSS, М. 2010. 400 с.
Arlazarov V.V., Slavin O.A.E., Uskov A.V.E., Janiszewski I.M. Modelling the flow of character recognition results in video stream. Bulletin of the South Ural State University. Ser. Mathematical Modelling, Programming and Computer Software. 2018. V. 11. № 2. P. 14–28. https://doi.org/10.14529/mmp180202
Arvind C.S., Mishra R., Vishal K., Gundimeda V. Vision based speed breaker detection for autonomous vehicle. Tenth International Conference on Machine Vision (ICMV): International Society for Optics and Photonics. 2018. V. 106960E. P. 1–9. https://doi.org/10.1117/12.2311315.
Awal A.M., Ghanmi N., Sicre R., Furon T. Complex document classification and localization application on identity document images. 14th IAPR International Conference on Document Analysis and Recognition (ICDAR). IEEE. 2017. V. 1. P. 426–431. https://doi.org/10.1109/ICDAR.2017.77.
Bezmaternykh P.V., Nikolaev D.P., Arlazarov V.L. Textual blocks rectification method based on fast Hough transform analysis in identity documents recognition. Tenth International Conference on Machine Vision (ICMV): International Society for Optics and Photonics. 2018. V. 1069606. P. 1–6. https://doi.org/10.1117/12.23 10162.
Calore E., Pedersini F., Frosio I. Accelerometer based horizon and keystone perspective correction. 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings. 2012. P. 205–209. https://doi.org/10.1109/I2MTC.2012.6229434.
Chen H., Sukthankar R., Wallace G., Li K. Scalable alignment of large-format multi-projector displays using camera homography trees. Proceedings of the conference on Visualization'02. IEEE Computer Society. 2002. P. 339–346.
Dubuisson M.P., Jain A.K. A modified Hausdorff distance for object matching. Proceedings of 12th international conference on pattern recognition. IEEE. 1994. V. 1. P. 566–568. https://doi.org/10.1109/ICPR.1994.576361.
Fréchet M.M. Sur quelques points du calcul fonctionnel. Rendiconti del Circolo Matematico di Palermo (1884–1940). 1906. V. 22. № 1. P. 1–72.
Hsu S.C., Sawhney H.S. Influence of global constraints and lens distortion on pose and appearance recovery from a purely rotating camera. Proceedings Fourth IEEE Workshop on Applications of Computer Vision. WACV'98 (Cat. No. 98EX201). 1998. P. 154–159. https://doi.org/10.1109/ACV.1998.732873.
Huttenlocher D.P., Klanderman G.A., Rucklidge W.J. Comparing images using the Hausdorff distance. IEEE Transactions on pattern analysis and machine intelligence. 1993. V. 15. № 9. P. 850–863. https://doi.org/10.1109/34.232073
Jaccard P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull Soc Vaudoise Sci Nat. 1901. V. 37. P. 547–579.
Jesorsky O., Kirchberg K.J., Frischholz R.W. Robust face detection using the hausdorff distance. International conference on audio-and video-based biometric person authentication. 2001. P. 90–95.
Karpenko S., Konovalenko I., Miller A., Miller B., Nikolaev D. UAV control on the basis of 3D landmark bearing-only observations. Sensors. 2015. V. 15. № 12. P. 29802–29820. https://doi.org/10.3390/s151229768
Konovalenko I.A., Shemiakina J.A. Error values analysis for inaccurate projective transformation of a quadrangle. Journal of Physics: Conference Series. – IOP Publishing. 2018. V. 1096. № 1. P. 1–9. https://doi.org/10.1088/1742-6596/1096/1/012038
Kunina I.A., Gladilin S.A., Nikolaev D.P. Blind radial distortion compensation in a single image using fast Hough transform. Computer optics. 2016. V. 40. P. 395–403. https://doi.org/10.18287/2412-6179-2016-40-3-395-403
Kunina I.A., Terekhin A.P., Gladilin S.A., Nikolaev D.P. Blind radial distortion compensation from video using fast Hough transform. International Conference on Robotics and Machine Vision. 2017. V. 10253. № 1025308. P. 1–7. https://doi.org/10.1117/12.2254867.
Legge G.E., Pelli D.G., Rubin G.S., Schleske M.M. Psychophysics of reading–I. Normal vision. Vision research. 1985. V. 25. № 2. P. 239–252. https://doi.org/10.1016/0042-6989(85)90117-8
Povolotskiy M.A., Kuznetsova E.G., Khanipov T.M. Russian license plate segmentation based on dynamic time warping. European Conference on Modelling and Simulation. 2017. P. 285–291.
Rodríguez-Piñeiro J., Comesaña-Alfaro P., Pérez-González F., Malvido-García A. A new method for perspective correction of document images. Document Recognition and Retrieval XVIII. International Society for Optics and Photonics. 2011. V. 787410. P. 1–12.
Sim D.G., Kwon O.K., Park R.H. Object matching algorithms using robust Hausdorff distance measures. IEEE Transactions on image processing. 1999. V. 8. № 3. P. 425–429. https://doi.org/10.1109/83.748897
Orrite C., Herrero J.E. Shape matching of partially occluded curves invariant under projective transformation. Computer Vision and Image Understanding. 2004. V. 93. № 1. P. 34–64. https://doi.org/10.1016/j.cviu.2003.09.005
Skoryukina N., Chernov T., Bulatov K., Nikolaev D.P., Arlazarov V. Snapscreen: TV-stream frame search with projectively distorted and noisy query. Ninth International Conference on Machine Vision (ICMV): International Society for Optics and Photonics. 2017. V. 103410Y. P. 1–5. https://doi.org/10.1117/12.2268735.
Skoryukina N., Shemiakina J., Arlazarov V.L., Faradjev I. Document localization algorithms based on feature points and straight lines. International Society for Optics and Photonics. 2018. V. 106961H. P. 1–5. https://doi.org/10.1117/12.2311478
Takezawa Y., Hasegawa M., Tabbone S. Camera-captured document image perspective distortion correction using vanishing point detection based on Radon transform. 23rd International Conference on Pattern Recognition (ICPR). IEEE. 2016. P. 3968–3974. https://doi.org/10.1109/ICPR.2016.7900254.
Wei H., Wang Y., Forman G., Zhu Y. Map matching by Fréchet distance and global weight optimization. Technical Paper, Departement of Computer Science and Engineering. 2013. P. 19–30.
Xie Y., Tang G., Hoff W. Geometry-based populated chessboard recognition. Tenth International Conference on Machine Vision (ICMV): International Society for Optics and Photonics. 2018. V. 1069603. P. 1–5.
Zhang Z., He L.W. Whiteboard scanning and image enhancement. Digital Signal Processing. 2007. V. 17. № 2. P. 414–432. https://doi.org/10.1016/j.dsp.2006.05.006
Zhukovsky A., Nikolaev D., Arlazarov V., Postnikov V., Polevoy D., Skoryukina N., Chernov T., Shemiakina J., Mukovozov A., Konovalenko I. Segments graph-based approach for document capture in a smartphone video stream. IAPR International Conference on Document Analysis and Recognition (ICDAR). 2017. №1. P. 337–342. https://doi.org/10.1109/ICDAR.2017.63.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы