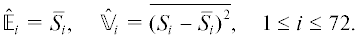Сенсорные системы, 2020, T. 34, № 4, стр. 307-328
ProLab: психофизически равномерная проективная система цветовых координат
И. А. Коноваленко 1, 2, *, А. А. Смагина 1, Д. П. Николаев 1, 2, П. П. Николаев 1, 3
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, д. 19, Россия
2 ООО “Смарт Энджинс Сервис”
117312 Москва, проспект 60-летия Октября, д. 9, Россия
3 Московский физико-технический институт
141701 г. Долгопрудный, Институтский переулок, д. 9, Россия
* E-mail: konovalenko@smartengines.com
Поступила в редакцию 17.06.2020
После доработки 06.07.2020
Принята к публикации 29.07.2020
Аннотация
В работе предлагается ввести новое пространство цветовых координат proLab, связанное с CIE XYZ трехмерным проективным преобразованием. В статье показывается, что по психофизической равномерности, оцениваемой при помощи метрики STRESS по отношению к формуле цветовых различий CIEDE2000, предлагаемое пространство значительно опережает широко используемую систему координат CIELAB, хотя и уступает современной CAM16-UCS. Угловые метрики ошибок определения цветности, обычно используемые в линейных цветовых пространствах, могут использоваться и в proLab, поскольку проективное преобразование сохраняет линейность многообразий. При этом, в отличие от линейных пространств, угловые ошибки, различные по цветовому тону, в proLab нормированы в соответствии с порогами цветоразличения человека. В работе также показывается, что гетероскедастичность дробового шума в proLab оказывается меньшей, чем в CAM16-UCS и стандартных цветовых пространствах. Это делает proLab удобной координатной системой для линейного цветового анализа – решения задач линейной регрессии в цветовом пространстве.
1. ВВЕДЕНИЕ
Целью данной работы является разработка новой системы цветовых координат для применения в алгоритмах анализа цветных изображений, полученных с цифровых камер видимого диапазона. Некоторые из алгоритмов цветового анализа опираются на линейные свойства цветовых распределений и почти все – на понятие расстояния в цветовом пространстве. При этом метрика цветового пространства, как правило, выводится не из физических предпосылок: создатели моделей метризации цветового пространства апеллируют к свойствам цветового восприятия человека и используют данные психофизиологии. Предлагаемая в данной работе система координат опирается как на модели цветового восприятия, так и на физические модели формирования цифровых изображений, поэтому для аккуратной постановки задачи нам понадобится довольно подробное введение. Следующие два параграфа введения посвящены цветовым моделям в психофизике, третий и четвертый параграф – особенностям формирования цветных цифровых изображений и алгоритмов их обработки. Затем формулируется основная проблема, на решение которой направлена данная работа, и предлагается метод ее решения. В шестом параграфе рассматриваются наиболее близкие работы других исследователей, в седьмом – формулируются свойства, которыми должна обладать разрабатываемая система.
Цветовые пространства и системы цветовых координат
Цветовые ощущения человека зависят от пространственного распределения спектральной освещенности сетчатки и внутреннего состояния его зрительной системы. В фотопических условиях наблюдения у человека-трихромата активны колбочки трех типов, а их реакции можно считать непрерывно зависящими от освещенности. В приближении равномерно распределенных пренебрежимо малых фоторецепторов можно считать, что в каждой точке сетчатки в ответ на освещенность возникает набор из трех скалярных реакций. Прочие элементы зрительной системы оперируют уже не произвольными параметрами спектральной освещенности, а исключительно этими реакциями. В такой модели цветовые ощущения от равномерно освещенного участка сетчатки при неизменном внутреннем состоянии будут принадлежать тому или иному многообразию, но его размерность не может быть выше трех вне зависимости от сложности зрительной системы и ее внутреннего состояния. Это многообразие мы и будем называть цветовым пространством, а его элементы – цветами.
Для картирования цветов используются различные координатные системы. В любой из них трехмерные координаты цветового вектора c связаны со спектральной освещенностью F некоторым вектор-функционалом Ψ, который может дополнительно зависеть от параметров θ зрительного контекста и внутреннего состояния зрительной системы:
где λ – длина волны света. Пространство цветовых координат называется линейным, если таковым является ${{\Psi }_{\theta }}$ при фиксированном векторе θ.В 1853 г. Грассман показал (Grassmann, 1853), что при колориметрическом зрительном контексте линейную трехмерную систему цветовых координат человека можно построить, причем в этих условиях внутренним состоянием можно пренебречь. Это позволило свести задачу определения цветового пространства человека в колориметрических условиях к установлению трехмерного базиса линейных цветовых координат в пространстве спектральных освещенностей. Элементы этого базиса получили название функций цветового соответствия стандартного наблюдателя, а соответствующая система цветовых координат получила наименование CIE XYZ (Smith, Guild, 1931). В этой системе связь между спектральной освещенностью сетчатки и цветовыми координатами записывается аналитически
(2)
${{{\mathbf{c}}}_{{\mathbf{x}}}}\;\mathop = \limits^{{\text{def}}} \;\int\limits_0^\infty {{\text{F}}(\lambda ){\mathbf{X}}(\lambda )d\lambda } ,$На сегодняшний день предложено множество цветовых координатных систем для стандартного наблюдателя, отличающихся удобством при тех или иных применениях. Некоторые из них подразумевают колориметрические условия, другие связаны с различными моделями цветового восприятия, тем или иным образом параметризующими θ. В предположении, что зрительный контекст и внутреннее состояние не меняют спектрального распределения чувствительности фоторецепторов, цветовой вектор ${{{\mathbf{c}}}_{\phi }}$ любой из этих координатных систем может быть выражен через координаты CIE XYZ без использования ${\text{F}}(\lambda )$:
(3)
${{{\mathbf{c}}}_{\phi }} = {{\Psi }_{{\Phi ,\theta }}}[{\text{F}}(\lambda )] = {{\Phi }_{\theta }}({{{\mathbf{c}}}_{{\mathbf{x}}}}),$Обычно модели цветового восприятия, как минимум, учитывают в θ адаптацию зрительной системы к цветовым параметрам доминирующего освещения сцены (Fairchild, 2013). В упрощенной модели фон Криса, используемой в системе CIELAB (Luo, 2014), адаптация моделируется как покомпонентное деление координат входного вектора ${{{\mathbf{c}}}_{{\mathbf{x}}}}$ в преобразовании ${{\Phi }_{\theta }}$ на вектор ${\mathbf{c}}_{{\mathbf{x}}}^{*}(\theta )$ цветовых координат источника света в системе CIE XYZ:
(4)
${{\Phi }_{\theta }}({{{\mathbf{c}}}_{{\mathbf{x}}}}) = {{\Phi }_{{\mathbf{0}}}}\left( {{\text{diag}}{{{\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}\left( \theta \right)} \right)}}^{{ - 1}}}{{{\mathbf{c}}}_{{\mathbf{x}}}}} \right),$Прямое (минуя CIE XYZ) преобразование координат между системами с одинаковой моделью адаптации не требует информации о параметрах освещения:
(5)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{{\mathbf{c}}}_{{\mathbf{a}}}} = {{{\text{A}}}_{\theta }}({{{\mathbf{c}}}_{{\mathbf{x}}}})\;\mathop = \limits^{{\text{def}}} \;{{{\text{A}}}_{0}}\left( {{\text{diag}}{{{\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}\left( \theta \right)} \right)}}^{{ - 1}}}{{{\mathbf{c}}}_{{\mathbf{x}}}}} \right)} \\ {{{{\mathbf{c}}}_{{\mathbf{b}}}} = {{{\text{B}}}_{\theta }}({{{\mathbf{c}}}_{{\mathbf{x}}}})\;\mathop = \limits^{{\text{def}}} \;{{{\text{B}}}_{0}}\left( {{\text{diag}}{{{\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}\left( \theta \right)} \right)}}^{{ - 1}}}{{{\mathbf{c}}}_{{\mathbf{x}}}}} \right)} \end{array}} \right. \Rightarrow \hfill \\ \Rightarrow {{{\mathbf{c}}}_{{\mathbf{b}}}} = {{{\text{B}}}_{0}}\left( {{\text{A}}_{0}^{{ - 1}}({{{\mathbf{c}}}_{{\mathbf{a}}}})} \right), \hfill \\ \end{gathered} $Метрика и психофизическая равномерность
Психофизические эксперименты позволяют не только установить спектральный базис цветового пространства человека, но и определить его метрические параметры. Это можно делать, например, измеряя пороговые для человека изменения спектральных стимулов в разных точках цветового пространства. Пространство цветовых координат называется психофизически равномерным (далее – равномерным), если евклидово расстояние в нем соответствует ощущаемой человеком разнице между соответствующими цветами. При этом длины векторов пороговых изменений во всех точках и во всех направлениях такого пространства равны. Базовая линейная система координат CIE XYZ дает цветовому пространству естественное евклидово представление, однако является существенно неравномерной в этом смысле.
Попытки создания равномерных пространств цветовых координат имеют длинную историю. Первое пространство, претендующее на равномерность, – Hunter Lab – было предложено Ричардом Хантером (Hunter, 1948). Позднее Дэвидом Макадамом на основании исследований Дина Джадда было предложено пространство, стандартизованное в 1960 г. международной комиссией по освещению (фр. Commission internationale de l’éclairage, CIE) как равномерное пространство цветности (CIE 1960 UCS) (International Commission, 1960). Термин “цветность”, использованный в названии, подчеркивает, что эта система координат не включает яркостной компоненты. Вскоре на ее основе Гюнтером Вышецки (Wyszecki, 1963) было предложено пространство, которое было принято как CIE 1964 (U*, V*, W*) Color Space (или CIEUVW). Оно уже позволяло рассчитывать цветовые различия и при несовпадающей яркости. Наконец, в 1976 г. на основе Hunter Lab было разработано пространство CIELAB (McLaren, 1976), которое до сих пор является наиболее употребимым в качестве равномерной системы цветовых координат при анализе сложных стимулов (изображений).
При этом пространство CIELAB все же является равномерным лишь приближенно, поэтому с момента его появления продолжались попытки построить более равномерные системы координат (Kuehni, 1999). Параллельно предлагались формулы моделирования цветовых различий, не являющиеся евклидовыми расстояниями в известных цветовых координатах, но при этом гораздо точнее описывающие результаты психофизических экспериментов. Венцом этих усилий стала формула CIEDE2000 (Alman et al., 2001; Luo et al., 2001), до последнего времени считающаяся наиболее точной среди известных (Wang et al., 2012). Тем не менее пространства цветовых координат с равномерной метрикой для некоторых приложений являются предпочтительными (например, в них можно строить эффективные поисковые структуры). Поэтому разработка равномерных пространств продолжается, и стандартом точности среди них на данный момент считается разработанное в 2016 г. пространство CAM16-UCS (Li et al., 2017).
Цветовые пространства камер видимого диапазона
Все вышесказанное с некоторыми оговорками можно соотнести и с техническими зрительными системами. Разумеется, говорить об “ощущениях” в этом случае бессмысленно, и под цветом при рассмотрении таких систем обычно понимается трехмерный вектор, передаваемый ими для дальнейшей обработки. Кроме того, внутренним состоянием θ в случае технической системы обычно можно пренебречь, или, по крайней мере, считать его известным. Однако наиболее существенно то, что спектральный базис цветового пространства камеры почти всегда значительно отличается от базиса стандартного наблюдателя. Более того, камеры разных производителей, как правило, имеют несовпадающие цветовые пространства.
Для обеспечения цветопередачи, т.е. для воспроизведения цвета на том или ином носителе так, чтобы у зрителя возникло цветовое ощущение, которое возникло бы у него на месте регистрирующего устройства, необходимо построить отображение из цветового пространства камеры в цветовое пространство стандартного наблюдателя. В общем случае это некорректная операция: элементу любого цветового пространства соответствует бесконечное множество метамерных спектральных освещенностей, и это множество может отображаться в значимый объем цветового пространства стандартного наблюдателя.
От выбора отображения зависит адекватность цветопередачи в различных условиях, и для его построения предлагаются различные методики и математические модели. Наиболее известной моделью является линейное отображение (Karaimer, Brown, 2018). Известны и нелинейные модели цветового соответствия: полиномиальная (Hong et al., 2001) и дробно-степенная (Finlayson et al., 2015). В экспериментах они показывают большую точность, при этом последняя модель отличается инвариантностью к изменению яркости, подобно линейной. Интересный подход рассматривается в работе (Bianco et al., 2013): параметры линейного отображения ставятся в зависимость от оценки доминирующего освещения, полученной некоторым алгоритмом на основе анализа входного изображения (появляется зависимость от $\theta $). Помимо модели соответствия, обсуждаются возможные уточнения экспериментальной методики (Kordecki, 2019), а также выбор функционала, оптимизируемого для определения параметров модели (Vazquez-Corral et al., 2014).
При работе с бытовыми камерами видимого диапазона калибровочное преобразование в цветовое пространство стандартного наблюдателя считается известным, что позволяет приписывать цветам, регистрируемым устройством, координаты цветового пространства человека. При этом метод получения его параметров, а иногда – и модель, остаются, как правило, неизвестными для пользователя.
Роль линейных многообразий в анализе цветных изображений
Алгоритмы анализа и обработки цветных изображений, используемые в технических системах, опираются не только на данные психофизики, но и на физические модели формирования изображений. Пожалуй, наиболее известной такой моделью является так называемая дихроматическая модель отражения, предложенная Шефером (Shafer, 1985). Эта модель утверждает, что цветовое распределение от однородно окрашенного глянцевого объекта, освещенного одним источником, целиком лежит в некоторой плоскости линейного пространства цветовых координат. Утверждение о линейном вырождении цветового распределения формулировалось и ранее, как минимум, в 1975 г. (Nikolaev, 1975), но модель Шефера уточняла и форму распределения внутри плоскости. Эта модель впоследствии развивалась и обобщалась, уточняя условия, в которых цветовые распределения однородно окрашенного объекта являются линейными многообразиями различной размерности (Brill, 1990; Nikolaev, Nikolayev, 2004). Все модели этого семейства мы будем называть линейными моделями формирования цветных изображений.
Линейные модели используются, например, в цветовой сегментации (Klinker et al., 1988; Cheng et al., 2001; Nikolaev, Nikolayev, 2004; Vinogradova и др., 2015), а также при решении задач вычислительной цветовой константности. Основной проблемой цветовой константности является необходимость определения цветности освещения сцены. Один из методов ее решения состоит в нахождении пересечения двух дихроматических плоскостей в линейном пространстве цветовых координат. Направляющий вектор прямой, по которой пересекаются плоскости, согласно линейной модели имеет цветность, совпадающую с цветностью доминирующего источника (Lee, 1986). Этот прием использовался во многих алгоритмах цветовой константности (Toro, Funt, 2007; Toro, 2008).
Хотя сначала в работах по этой теме рассматривались только случаи, когда цветовое распределение лежит в двумерном линейном подпространстве, впоследствии алгоритмы уже учитывали более реалистическую модель с наличием рассеянного света, где рассматриваемые многообразия уже не проходят через начало координат (Woo et al., 2018). Обобщения этого подхода используются и при анализе сцен с несколькими источниками света (Nikolaev, Nikolayev, 2004; Zickler et al., 2008), а также при обработке мультиспектральных изображений (Nikonorov, 2014).
Предположение о линейности взаимодействия света с веществом имеет и более простое и фундаментальное следствие: изменение интегральной яркости освещения не меняет цветности пикселей изображения, вне зависимости от числа переотражений в сцене, а также от окрасок объектов и цветности источника. На этом основываются используемые в вычислительной цветовой константности угловые метрики ошибки, такие как так называемая угловая ошибка восстановления (Finlayson et al., 1995; Gijsenij et al., 2011; Hemrit et al., 2018), которая представляет собой угол между истинным цветовым вектором освещения и его оценкой, и так называемая угловая ошибка репродукции (Finlayson, Zakizadeh, 2014). Последняя представляет собой угол между цветовым вектором белой поверхности под эквиэнергетическим источником (“истинной белой точкой”) и цветовым вектором, полученным в результате поканальной коррекции цвета белой поверхности под иным освещением, произведенной по оценке этого освещения.
Алгоритмы цветовой константности, основанные на инцидентности линейных многообразий, и угловые метрики точности применяются к данным в линейных пространствах цветовых координат, поскольку ключевые для них геометрические объекты в общем случае не сохраняются в нелинейных пространствах.
Постановка задачи
Линейный анализ цветовых распределений подразумевает решение двух задач. Первая задача заключается в оценивании параметров линейных кластеров в цветовом пространстве при помощи тех или иных методов регрессии, и здесь ключевую роль играет толерантность к цветовым различиям, вызываемым шумом. Вторая задача – анализ взаимного расположения найденных геометрических объектов в цветовом пространстве. В ней цветовые различия уже несут важную информацию, и в тех приложениях, в которых поведение алгоритма должно соответствовать человеческому восприятию, метрику цветовых различий желательно согласовывать с человеческой.
Применение стандартных методов статистического анализа к цветовой гистограмме изображения подразумевает, что цветовой шум является гомоскедастичным: аддитивное отклонение аппроксимируется случайной величиной с нулевым средним, распределение которой не зависит от цветовых координат измеряемой величины и инвариантно к вращениям. Очевидно, что даже аффинные преобразования цветовых координат могут влиять на анизотропию аддитивного шума, а нелинейные – и на зависимость параметров распределения от цветовых координат, т.е. адекватность применения стандартных статистических методов существенно зависит от координатной системы, в которой анализируется цветовое распределение.
Ситуация осложняется тем, что шум на изображении не является гомоскедастичным и в пространстве линейных откликов сенсора (Bernd, 2005). Это означает, что стандартные методы регрессии будут давать неоптимальные оценки положения носителей цветовых распределений даже в линейных пространствах цветовых координат.
В результате использование любого из известных пространств цветовых координат оказывается необоснованным: в психофизически равномерных усложняются представления линейных физических моделей, а шум является гетероскедастичным (Liang et al., 2019), тогда как в линейных пространствах метрики фактически произвольны, причем гомоскедастичность шума не гарантирована и здесь.
Ситуация с угловыми ошибками аналогична: в линейных цветовых пространствах не гарантируется воспринимаемое равенство различий при цветовых отклонениях на одинаковый угол в разных направлениях, а в равномерных пространствах линии постоянной цветности не являются прямыми, и понятие угловой ошибки не имеет в них естественного определения.
Теперь мы можем сформулировать нашу цель: построить психофизически равномерное пространство цветовых координат, сохраняющее линейность подпространств и многообразий, причем желательно, чтобы сенсорный шум был в нем как можно более гомоскедастичным.
Проективное преобразование трехмерных цветовых координат
Если бы для сохранения линейности многообразий требовалась линейность преобразования, вряд ли у поставленной задачи существовало бы решение с приемлемой равномерностью. Во-первых, линейное преобразование не может гетеро-скедастичный шум сделать гомоскедастичным, поскольку якобиан линейного преобразования постоянен по пространству. (При этом анизотропия шума все же может быть исправлена.) Во-вторых, линейные преобразования не могут существенно улучшить психофизическую равномерность пространства. Действительно, цвета, расположенные на ахроматической оси и равноотстоящие в координатах CIE XYZ, не являются психофизически равномерными, а линейные преобразования сохраняют отношение длин отрезков, расположенных на одной прямой.
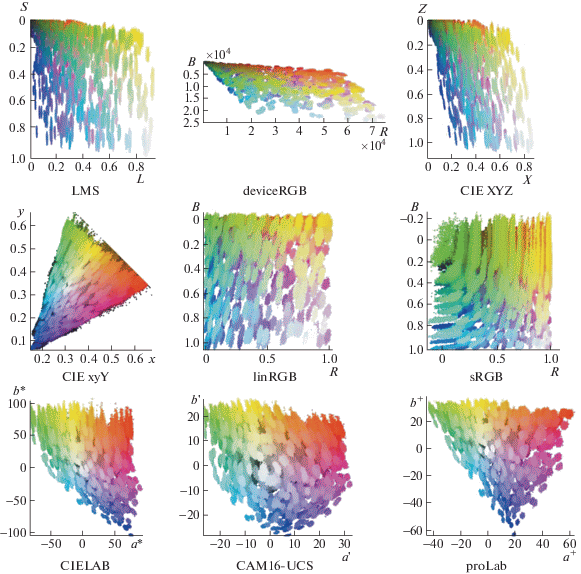
В действительности класс преобразований, сохраняющих линейность многообразий, шире: это любые проективные преобразования. В отличие от линейных, проективные преобразования могут по-разному изменять элементы объема в разных точках пространства. На рис. 1 показано, как проективное преобразование, сохраняя все прямые, может сжимать пространство в одной точке и растягивать в другой. Это позволяет надеяться, что систему координат с приемлемой равномерностью все же можно найти.
Рис. 1.
Плоскость XZ системы цветовых координат CIE XYZ в пространстве проективных цветовых координат. Символом W обозначена проекция белой точки.
Следует отметить, что проективные преобразования цветовых координат уже достаточно широко используются в различных приложениях (Finlayson et al., 2019), но при этом, как правило, преобразуется только плоскость цветности. Идея использования проективного преобразования именно для построения равномерного цветового пространства принадлежит, по-видимому, МакАдаму (MacAdam, 1937), но и в этой пионерской работе 1937 г. и в более поздних рассматривались двумерные преобразования.
Можно отметить несколько работ, где проективно преобразуется все пространство. Первой, по-видимому, является работа (Wallace et al., 2003). В ней трехмерное проективное преобразование использовалось для сопоставления цветовых тел различных проекционных аппаратов. Позже этот же подход был применен для фотореалистичного переноса цветовой палитры между изображениями (Gong et al., 2019). В обоих случаях речь идет о взаимной калибровке двух изображений, а не о переходе в некоторое эталонное пространство. В работе (Smagina et al., 2019) проективное преобразование использовалось уже именно для перехода в пространство с другой метрикой. В этой работе было показано, что фиксированное трехмерное проективное преобразование цветовых координат может улучшить результаты цветовой сегментации.
Что же мы предлагаем?
В данной работе мы предлагаем новую равномерную систему цветовых координат стандартного наблюдателя, основанную на трехмерном проективном преобразовании координат CIE XYZ, – proLab. Как будет показано ниже, она обладает следующими достоинствами:
• по психофизической равномерности proLab превосходит широко распространенную равномерную систему CIELAB (хотя и уступает CAM16-UCS);
• дробовой шум на изображении в proLab лучше соответствует гомоскедастической модели, чем в других равномерных пространствах;
• единственная среди равномерных систем proLab сохраняет линейность цветовых многообразий, что позволяет корректно использовать в ней угловые оценки точности цветопередачи, а также проводить линейный цветовой анализ в согласии с метрикой цветоразличения человека;
• преобразование из CIE XYZ в proLab обладает аналитической элегантностью и простотой вычисления в сравнении с CAM16-UCS и даже с более примитивной CIELAB.
Впервые идея построения системы координат proLab была представлена нами на симпозиуме Международного общества цветового зрения в 2019 г. (Konovalenko, 2019), но методика ее построения и численное исследование ее свойств публикуются впервые. Кроме того, с момента сообщения на симпозиуме параметры модели были уточнены.
План изложения основных результатов
Основная часть статьи организована следующим образом. Четыре раздела посвящены построению системы координат proLab. В разд. 2 вводятся необходимые обозначения, задается общий вид преобразования из CIE XYZ в proLab, а также обсуждается, как определять те параметры искомого преобразования, которые не влияют на метрику. В разд. 3 рассматриваются априорные ограничения на метрические параметры proLab. В разд. 4 вводится функционал, количественно оценивающий психофизическую равномерность цветовых координат. В разд. 5 излагается методика определения оптимальных параметров proLab и приводятся их значения.
Далее описываются свойства полученной системы цветовых координат. В разд. 6 предлагается функционал, оценивающий отклонение параметров шума цветовых координат от гомоскедастичных. В разд. 7 строится модель шума цветовых реакций сенсора и определяются ее параметры на необработанном сенсорном изображении, взятом из открытого набора данных. В разд. 8 приводится численное сравнение свойств proLab и ранее предложенных координатных систем по равномерности и гомоскедастичности шума. В обсуждении (разд. 9) рассматриваются некоторые качественные свойства предлагаемого координатного пространства, а также излагаются соображения о дальнейшей возможной оптимизации его параметров. Наконец, в заключение (разд. 10) кратко излагаются основные результаты работы.
2. ОБЩАЯ ЦВЕТОВАЯ МОДЕЛЬ PROLAB
Итак, мы будем строить пространство координат цветов стандартного наблюдателя такое, что линейные в CIE XYZ многообразия цветов сохранят в нем линейность. Дополнительно поставим целью, чтобы евклидово расстояние в этом пространстве аппроксимировало цветовые различия, определяемые некоторым фиксированным образом.
Введем необходимые обозначения. Пространство цветовых координат CIE XYZ обозначим ${{C}_{x}}$, пространство координат CIELAB – ${{C}_{l}}$, а искомое пространство – ${{C}_{p}}$. Преобразование из ${{C}_{x}}$ в ${{C}_{l}}$ обозначим ${\text{L}}$, а из ${{C}_{x}}$ в ${{C}_{p}}$ – P.
Из требования сохранения линейности многообразий следует, что P – проективное преобразование трехмерного пространства. Будем параметризовать все проективные преобразования в стандартной матричной форме, обозначая матрицу курсивом. В частности, зададим преобразование P матрицей гомографии $P\;\mathop = \limits^{{\text{def}}} \;({{p}_{{ij}}}) \in {{\mathbb{R}}^{{4 \times 4}}}$.
Введем функции ${{{\text{T}}}_{{\text{h}}}}$ и ${{{\text{T}}}_{{\text{c}}}}$ перехода из декартовых координат в однородные и обратно:
(6)
$\begin{gathered} {{{\text{T}}}_{{\text{h}}}}({\mathbf{c}})\;\mathop = \limits^{{\text{def}}} \;\left[ {\begin{array}{*{20}{c}} {\mathbf{c}} \\ 1 \end{array}} \right],\quad {\mathbf{c}} \in {{\mathbb{R}}^{3}}, \\ {{{\text{T}}}_{{\text{c}}}}({\mathbf{h}})\;\mathop = \limits^{{\text{def}}} \;\left[ {\begin{array}{*{20}{c}} {{{I}_{3}}}&{\mathbf{0}} \end{array}} \right]\frac{{\mathbf{h}}}{{{{h}_{4}}}},\quad {\mathbf{h}} \in {{\mathbb{R}}^{4}},\quad {{h}_{4}} \ne 0, \\ \end{gathered} $(7)
${\text{P}}({{{\mathbf{c}}}_{{\mathbf{x}}}})\;\mathop = \limits^{{\text{def}}} \;{{{\text{T}}}_{{\text{c}}}}(P{{{\text{T}}}_{{\text{h}}}}({{{\mathbf{c}}}_{{\mathbf{x}}}})),\quad {{{\mathbf{c}}}_{{\mathbf{x}}}} \in {{C}_{x}},\quad {\text{P}}({{{\mathbf{c}}}_{{\mathbf{x}}}}) \in {{C}_{p}}.$Требования к метрике над ${{C}_{p}}$ задают P с точностью до подобия в ${{C}_{p}}$. Действительно преобразование движения является проективным и не изменяет расстояний, а изотропное масштабирование эквивалентно выбору единиц измерения расстояния. Доопределим преобразование ${\text{P}}$.
Будем строить систему цветовых координат, которая может заменить CIELAB в его применениях. Тогда, во-первых, расстояние в ${{C}_{p}}$ должно моделировать и адаптацию к доминирующему освещению. По аналогии с CIELAB воспользуемся упрощенной моделью фон Криса (Luo, 2014): будем покомпонентно делить координаты входного вектора ${{{\mathbf{c}}}_{{\mathbf{x}}}}$ на цветовые координаты ${\mathbf{c}}_{{\mathbf{x}}}^{*} \in {{C}_{x}}$ источника света. Обозначим это преобразование как N. Оно проективно, а соответствующая ему матрица N записывается следующим образом:
(8)
$N\;\mathop = \limits^{{\text{def}}} \;{\text{diag}}{{\left( {{{{\text{T}}}_{{\text{h}}}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right)} \right)}^{{ - 1}}}.$Теперь P можно декомпозировать на преобразование адаптации N и преобразование Q, не зависящее от доминирующего источника:
(9)
${\text{P}} = {\text{Q}} \circ {\text{N}},\quad P = QN,\quad Q\;\mathop = \limits^{{\text{def}}} \;({{q}_{{ij}}}) \in {{\mathbb{R}}^{{4 \times 4}}},$Во-вторых, дополнительно потребуем, чтобы черная точка 0 после преобразования осталась в начале координат:
Тогда Q можно записать в следующем виде:
(11)
$Q(\varphi ,\rho ,\mu ) = {{R}_{1}}({{\varphi }_{1}}){{R}_{2}}({{\varphi }_{2}}){{R}_{3}}({{\varphi }_{3}})Z(\rho )M(\mu ),$(12)
$M(\mu )\;\mathop = \limits^{{\text{def}}} \;\left[ {\begin{array}{*{20}{c}} {{{\mu }_{1}}}&{{{\mu }_{2}}}&{{{\mu }_{3}}}&0 \\ 0&{{{\mu }_{4}}}&{{{\mu }_{5}}}&0 \\ 0&0&1&0 \\ {{{\mu }_{6}}}&{{{\mu }_{7}}}&{{{\mu }_{8}}}&1 \end{array}} \right],\quad {\text{|}}M{\text{|}} > 0,$Пусть метрические параметры $\mu $ выбраны. Зафиксируем теперь остальные параметры. Зададим направление и общий масштаб оси светлоты аналогично CIELAB:
(14)
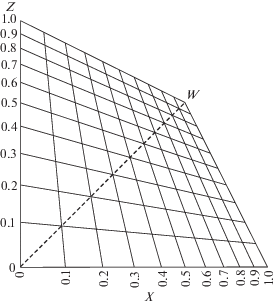
${\text{P}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right) = {{\left[ {\begin{array}{*{20}{c}} {100}&0&0 \end{array}} \right]}^{T}}.$Это условие однозначно задает параметры ${{\varphi }_{2}}$, ${{\varphi }_{3}}$ и ρ, оставляя произвольным угол поворота ${{\varphi }_{1}}$ вокруг оси светлоты. Чтобы зафиксировать и его, потребуем, чтобы расположение тонов насыщенных цветов примерно соответствовало CIELAB. Для определенности возьмем в пространстве CIELAB четверку точек $C_{l}^{{key}} \subset {{C}_{l}}$ с половинной светлотой, с одной нулевой координатой цветности, имеющие равные насыщенности и не выходящие за пределы цветового тела источника D65 (рис. 2):
(15)
$C_{l}^{{key}}\;\mathop = \limits^{{\text{def}}} \;\left\{ {\left[ {\begin{array}{*{20}{c}} {50} \\ { - 80} \\ 0 \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {50} \\ {80} \\ 0 \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {50} \\ 0 \\ { - 80} \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {50} \\ 0 \\ {80} \end{array}} \right]} \right\}.$Рис. 2.
Проекция четырех выбранных точек привязки цветового тона на плоскость $(a{\kern 1pt} *,b{\kern 1pt} *)$. Светло-серая область соответствует проекции цветового тела D65, темно-серая – его сечению плоскостью $L{\kern 1pt} * = 50$, содержащей выбранные точки, а радужная – такому же сечению цветового тела sRGB.
Теперь выберем такое ${{\varphi }_{1}}$, чтобы координаты в ${{C}_{p}}$ у выбранных точек как можно меньше отличались от исходных в ${{C}_{l}}$:
(16)
$\begin{gathered} \varphi _{1}^{{opt}} = \\ = {\text{arg}}\,{\text{mi}}{{{\text{n}}}_{{{{\varphi }_{1}}}}}\sum\limits_{{{{\mathbf{c}}}_{{\mathbf{l}}}} \in C_{l}^{{key}}} \left\| {{{{\mathbf{c}}}_{{\mathbf{l}}}} - {{{\text{T}}}_{c}}(P(\varphi ,\rho ,\mu ){{{\text{T}}}_{h}}({{{\text{L}}}^{{ - {\text{1}}}}}({{{\mathbf{c}}}_{{\mathbf{l}}}})))} \right\|_{2}^{2}. \\ \end{gathered} $Эта задача может быть решена аналитически с использованием метода поиска оптимального поворота (Besl, McKay, 1992).
Система координат proLab полностью определяется преобразованием P. Искомое преобразование будем строить следующим образом: найдем параметры μ матрицы M, оптимальные, исходя из требований к метрике, после чего приведем масштаб и ориентацию оси светлот к стандартному положению (14), определим ориентацию осей цветности, согласно (16), и, наконец, учтем нормировку (9).
3. ДОПОЛНИТЕЛЬНЫЕ ОГРАНИЧЕНИЯ НА ПАРАМЕТРЫ PROLAB
Найдем теперь область в пространстве метрических параметров μ, в которой цветовая модель proLab может быть осмысленно интерпретируема. Начнем с того, что не всякое проективное преобразование отобразит исходное цветовое тело в ограниченную область. Потребуем наличия этого естественного свойства.
Плоскость пространства ${{C}_{x}}$ с ее уравнением
(17)
$\left[ {\begin{array}{*{20}{c}} {{{p}_{{41}}}}&{{{p}_{{42}}}}&{{{p}_{{43}}}} \end{array}} \right]{{{\mathbf{c}}}_{{\mathbf{x}}}} + {{p}_{{44}}} = 0$Сформулируем теперь простое достаточное условие ограниченности цветового тела в ${{C}_{p}}$, не требующее знания формы цветового тела. Заметим, что для произвольного источника света его цветовое тело не выходит в ${{C}_{x}}$ за пределы ортотропного прямоугольного параллелепипеда с главной диагональю, соединяющей вершины 0 и ${\mathbf{c}}_{{\mathbf{x}}}^{*}$. Все восемь вершин этого параллелепипеда можно перечислить следующим образом:
(18)
${\text{diag}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right){\mathbf{b}},\quad {\mathbf{b}} \in {{\{ 0,1\} }^{3}}.$Учитывая нормировку (13), условие ограниченности цветового тела в ${{C}_{p}}$ можно записать как условие расположения всех этих вершин по одну сторону от горизонта (17):
(19)
$\left[ {\begin{array}{*{20}{c}} {{{p}_{{41}}}}&{{{p}_{{42}}}}&{{{p}_{{43}}}} \end{array}} \right]{\text{diag}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right){\mathbf{b}} + 1 \geqslant 0,\quad {\mathbf{b}} \in {{\{ 0,1\} }^{3}}.$Теперь выясним, при каких μ выполняется это условие. Из (8), (9) и (11) следует, что
(20)
$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{\mu }_{6}}}&{{{\mu }_{7}}}&{{{\mu }_{8}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{q}_{{41}}}}&{{{q}_{{42}}}}&{{{q}_{{43}}}} \end{array}} \right] = \\ = \left[ {\begin{array}{*{20}{c}} {{{p}_{{41}}}}&{{{p}_{{42}}}}&{{{p}_{{43}}}} \end{array}} \right]{\text{diag}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right), \\ \end{gathered} $(21)
$\left[ {\begin{array}{*{20}{c}} {{{\mu }_{6}}}&{{{\mu }_{7}}}&{{{\mu }_{8}}} \end{array}} \right]{\mathbf{b}} + 1 \geqslant 0,\quad {\mathbf{b}} \in {{\{ 0,1\} }^{3}}.$Заметим, что при ${\mathbf{b}} = {\mathbf{0}}$ это условие верно для любых μ, т.е. является избыточным.
Теперь введем еще одно ограничение. Как известно, координата L* пространства CIELAB имеет смысл светлоты или яркости, и желательно, чтобы первая координата proLab также имела этот смысл. Поэтому потребуем следующее:
(22)
$\begin{gathered} {\mathbf{0}} \leqslant {{{\mathbf{c}}}_{{\mathbf{0}}}},\quad {{{\mathbf{c}}}_{{\mathbf{1}}}} \leqslant {\mathbf{c}}_{{\mathbf{x}}}^{*}, \\ {{{\mathbf{c}}}_{{\mathbf{1}}}} - {{{\mathbf{c}}}_{{\mathbf{0}}}} \in \mathbb{R}_{{ \geqslant 0}}^{3} \Rightarrow {{\left( {{\text{P}}({{{\mathbf{c}}}_{{\mathbf{1}}}}) - {\text{P}}({{{\mathbf{c}}}_{{\mathbf{0}}}})} \right)}^{T}}{{{{\mathbf{\hat {e}}}}}_{{\mathbf{L}}}} \geqslant 0, \\ \end{gathered} $Упростим требование (22). Для этого рассмотрим множество плоскостей равной “светлоты” (первой координаты) proLab. В ${{C}_{p}}$ их уравнения имеют вид
(23)
${{L}^{ + }} = L_{s}^{ + },\quad {{L}^{ + }}\;\mathop = \limits^{{\text{def}}} \;{\mathbf{\hat {e}}}_{{\mathbf{L}}}^{T}{{{\mathbf{c}}}_{{\mathbf{p}}}}.$В силу проективности P прообразами этих плоскостей в ${{C}_{x}}$ являются плоскости, образующие пучок. При $0 \leqslant L_{s}^{ + } \leqslant 100$ прообразы в ${{C}_{x}}$ пересекают параллелепипед (18). Поскольку мы уже потребовали выполнения условия (19), можно утверждать, что в этом диапазоне угол поворота прообраза вокруг оси пучка является монотонной и непрерывной функцией аргумента $L_{s}^{ + }$. Тогда условие (22) эквивалентно требованию, чтобы координаты нормалей ко всем этим плоскостям имели одинаковый знак. Поскольку знак координаты нормали не может поменяться дважды, то это эквивалентно требованию неотрицательности всех координат нормалей для крайних плоскостей с уравнениями ${{L}^{ + }} = 0$ и ${{L}^{ + }} = 100$.
Определим, при каких ограничениях на μ это требование выполняется. Для этого введем еще одно координатное пространство ${{C}_{b}}$, задаваемое проективным преобразованием из ${{C}_{x}}$ с матрицей $B\mathop = \limits^{{\text{def}}} MN$:
(24)
${\text{B}}({{{\mathbf{c}}}_{{\mathbf{x}}}})\;\mathop = \limits^{{\text{def}}} \;{{{\text{T}}}_{c}}(MN{{{\text{T}}}_{{\text{h}}}}({{{\mathbf{c}}}_{{\mathbf{x}}}})),\quad {{{\mathbf{c}}}_{{\mathbf{x}}}} \in {{C}_{x}},\quad {\text{B}}({{{\mathbf{c}}}_{{\mathbf{x}}}}) \in {{C}_{b}}.$Из (9) и (11) следует
т.е. пространство ${{C}_{b}}$ связано с пространством ${{C}_{p}}$ подобием.Параметрами плоскости с уравнением ${{{\mathbf{l}}}_{\Phi }}{{{\text{T}}}_{{\text{h}}}}({{{\mathbf{c}}}_{\Phi }}) = 0$ в произвольном пространстве цветовых координат ${{C}_{\Phi }}$ (${{{\mathbf{c}}}_{\Phi }} \in {{C}_{\Phi }}$) будем называть вектор ${{{\mathbf{l}}}_{\Phi }}$. Тогда в соответствии с определением (24) имеем следующую связь между параметрами ${{{\mathbf{l}}}_{{\mathbf{x}}}}$ плоскостей в пространстве ${{C}_{x}}$ и ${{{\mathbf{l}}}_{{\mathbf{b}}}}$ – их образов в пространстве ${{C}_{b}}$:
Поэтому ограничение на параметры прямой в пространстве ${{C}_{b}}$, влекущее неотрицательность координат нормали ее образа в пространстве ${{C}_{x}}$, можно записать так:
(27)
${{{\mathbf{l}}}_{{\mathbf{b}}}}MN \geqslant \left[ {\begin{array}{*{20}{c}} 0&0&0&{ - \infty } \end{array}} \right].$Матрица N диагональна, при этом ее диагональные элементы положительны, поэтому неравенство можно упростить следующим образом:
(28)
${{{\mathbf{l}}}_{{\mathbf{b}}}}M \geqslant \left[ {\begin{array}{*{20}{c}} 0&0&0&{ - \infty } \end{array}} \right].$Наложим теперь это ограничение на плоскости ${{L}^{ + }} = 0$ и ${{L}^{ + }} = 100$ пространства ${{C}_{p}}$. Для этого рассмотрим образ белой точки в пространстве ${{C}_{b}}$. Обозначим его ${\mathbf{c}}_{{\mathbf{b}}}^{*}$:
(29)
${\mathbf{c}}_{{\mathbf{b}}}^{*}\;\mathop = \limits^{{\text{def}}} \;{\text{B}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right).$Поскольку плоскости пучка ${{L}^{ + }} = L_{s}^{ + }$ пространства ${{C}_{p}}$ ортогональны направлению на белую точку этого пространства ${\mathbf{c}}_{{\mathbf{p}}}^{*}$, то это же верно для их прообразов в ${{C}_{b}}$. Значит, параметры плоскостей этого пучка в ${{C}_{b}}$ имеют вид
(30)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{c}}{{{_{{\mathbf{b}}}^{*}}}^{T}}}&{{{l}_{4}}\left( {L_{s}^{ + }} \right)} \end{array}} \right],$Подставим эти параметры в условие (28) и раскроем M по определению (12):
(31)
$\left[ {\begin{array}{*{20}{c}} {{\mathbf{c}}{{{_{{\mathbf{b}}}^{*}}}^{T}}}&0 \\ {{\mathbf{c}}{{{_{{\mathbf{b}}}^{*}}}^{T}}}&{ - {\mathbf{c}}{{{_{{\mathbf{b}}}^{*}}}^{T}}{\mathbf{c}}_{{\mathbf{b}}}^{*}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mu }_{1}}}&{{{\mu }_{2}}}&{{{\mu }_{3}}} \\ 0&{{{\mu }_{4}}}&{{{\mu }_{5}}} \\ 0&0&1 \\ {{{\mu }_{6}}}&{{{\mu }_{7}}}&{{{\mu }_{8}}} \end{array}} \right] \geqslant {{0}_{{2,3}}}.$Из определения (8) следует, что $N{{{\text{T}}}_{{\text{h}}}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right) = {\mathbf{1}}$, откуда
(32)
${\mathbf{c}}_{{\mathbf{b}}}^{*} = {{{\text{T}}}_{{\text{c}}}}\left( {MN{{{\text{T}}}_{{\text{h}}}}\left( {{\mathbf{c}}_{{\mathbf{x}}}^{*}} \right)} \right) = {{{\text{T}}}_{{\text{c}}}}(M{\mathbf{1}}).$С учетом (12) окончательно получим:
(33)
$\begin{gathered} {\mathbf{c}}_{{\mathbf{b}}}^{*} = {\mathbf{m}}{\text{/}}m,\quad {\mathbf{m}} = \left[ {\begin{array}{*{20}{c}} {{{\mu }_{1}} + {{\mu }_{2}} + {{\mu }_{3}}} \\ {{{\mu }_{4}} + {{\mu }_{5}}} \\ 1 \end{array}} \right], \\ m = {{\mu }_{6}} + {{\mu }_{7}} + {{\mu }_{8}} + 1. \\ \end{gathered} $Поскольку $m \geqslant 0$ в силу условия (21), то (31) эквивалентно
(34)
$\left[ {\begin{array}{*{20}{c}} {m{{{\mathbf{m}}}^{T}}}&0 \\ {m{{{\mathbf{m}}}^{T}}}&{ - {{{\mathbf{m}}}^{T}}{\mathbf{m}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mu }_{1}}}&{{{\mu }_{2}}}&{{{\mu }_{3}}} \\ 0&{{{\mu }_{4}}}&{{{\mu }_{5}}} \\ 0&0&1 \\ {{{\mu }_{6}}}&{{{\mu }_{7}}}&{{{\mu }_{8}}} \end{array}} \right] \geqslant {{0}_{{2,3}}}.$Итак, с учетом семи ограничений на μ, полученных ранее (19) и шести ограничений (34), мы получили 13 дополнительных ограничений вида
где ${{{\text{f}}}_{i}}(\mu )$ – многочлены степени не выше трех.4. КРИТЕРИЙ ПСИХОФИЗИЧЕСКОЙ НЕРАВНОМЕРНОСТИ
В области, ограниченной введенными выше условиями, будем искать вектор μ, максимизирующий психофизическую равномерность. Под психофизической равномерностью пространства цветовых координат подразумевают точность моделирования психофизических цветовых различий евклидовым расстоянием в этом пространстве. Для количественной оценки неравномерности обычно используется критерий STRESS (standardised residual sum of squares): чем больше его значение, тем хуже равномерность (Kruskal, 1964; García et al., 2007; Wang et al., 2012; Pan, Westland, 2018).
Пусть a – вектор цветовых различий, оцененных в одном приближении, а b – вектор других оценок тех же цветовых различий, причем ${\text{||}}{\mathbf{a}}{\text{||}} \ne 0$ и ${\text{||}}{\mathbf{b}}{\text{||}} \ne 0$. Тогда критерий STRESS определяется для них следующим образом:
(36)
${\text{STRESS}}\left( {{\mathbf{a}},{\mathbf{b}}} \right)\;\mathop = \limits^{{\text{def}}} \;\frac{{{\text{||}}k{\mathbf{a}} - {\mathbf{b}}{\text{|}}{{{\text{|}}}_{2}}}}{{{\text{||}}{\mathbf{b}}{\text{|}}{{{\text{|}}}_{2}}}},\quad k = \frac{{({\mathbf{a}},{\mathbf{b}})}}{{{\text{||}}{\mathbf{a}}{\text{||}}_{2}^{2}}},$(37)
${\text{STRESS}}\left( {{\mathbf{a}},{\mathbf{b}}} \right) = \sqrt {1 - \frac{{{{{({\mathbf{a}},{\mathbf{b}})}}^{2}}}}{{{\text{||}}{\mathbf{a}}{\text{||}}_{2}^{2}{\text{||}}{\mathbf{b}}{\text{||}}_{2}^{2}}}} = \left| {\sin \widehat {{\mathbf{ab}}}} \right|.$Этот критерий симметричен и инвариантен к масштабированию любой из двух сравниваемых оценок:
(38)
${\text{STRESS}}\left( {k{\mathbf{a}},{\mathbf{b}}} \right) = {\text{STRESS}}\left( {{\mathbf{b}},{\mathbf{a}}} \right),\quad k \ne 0.$Отсюда следует, что априорная фиксация масштаба цветовых координат, задаваемая условием (14), не повлияет на оценки соответствия по критерию STRESS.
Также этот критерий инвариантен к согласованным перестановкам компонент векторов различий:
(39)
${\text{STRESS}}\left( {{{M}_{\pi }}{\mathbf{a}},{{M}_{\pi }}{\mathbf{b}}} \right) = {\text{STRESS}}\left( {{\mathbf{a}},{\mathbf{b}}} \right),$(40)
${\text{STRESS}}\left( \omega \right)\;\mathop = \limits^{{\text{def}}} \;{\text{STRESS}}\left( {{\mathbf{a}},{\mathbf{b}}} \right).$Значение STRESS может существенно зависеть от распределения, которому подчиняется выборка, использованная для его подсчета. В качестве эталона цветовых различий могут выбираться как непосредственно измеренные в психофизических экспериментах величины (Woo et al., 2018), так и формулы цветового различия (Thomsen, 2000; Urban et al., 2007). Недостатками первого подхода являются фиксированность и ограниченность выборки (3657 пар цветов в сумме по всем наборам данных по состоянию на 2001 г. (Luo et al., 2001)), что ставит под сомнение как полноту покрытия пространства пар, так и отсутствие нежелательных “перекосов” в распределении выборки. Недостатком второго подхода является дополнительная ошибка аппроксимации. В настоящей работе используется второй подход с эталоном в виде формулы CIEDE2000 (Alman et al., 2001; Luo et al., 2001).
По аналогии с работой (Urban et al., 2007) будем строить пары из цветовых векторов, равномерно распределенных в пространстве CIELAB в границах цветового тела доминирующего источника света, но, в отличие от (Urban et al., 2007), не будем ограничивать сверху цветовое различие в паре, поскольку нас интересуют не только малые различия.
Обозначим $G \subset {{C}_{l}}$ цветовое тело источника D65, а ${{G}_{n}}$ – равномерную выборку из него (${{G}_{n}} \subset G,$ ${\text{|}}{{G}_{n}}{\text{|}} = n$). Аналогично равномерную выборку цветовых пар из цветового тела обозначим $G_{n}^{2}$ ($G_{n}^{2} \subset {{G}^{2}} \subset C_{l}^{2},$ ${\text{|}}G_{n}^{2}{\text{|}} = n$). Наконец, обозначим Φ преобразование в исследуемое пространство ${{C}_{\phi }}$ из ${{C}_{x}}$, ${{\Phi }_{{\text{L}}}}$ – из ${{C}_{l}}$ (${{\Phi }_{{\text{L}}}} = \Phi \circ {{{\text{L}}}^{{ - {\text{1}}}}}$), где $ \circ $ – операция композиции преобразований, а $\Delta E_{{{\text{00}}}}^{*}(p)$ – эталонное цветовое различие CIEDE2000 на паре цветов $p \in C_{l}^{2}$. Тогда критерий неравномерности восприятия пространства цветовых координат ${{C}_{\phi }}$ на выборке $G_{n}^{2}$ будет записываться следующим образом:
(41)
$\begin{gathered} {\text{U}}[\Phi ,G_{n}^{2}]\;\mathop = \limits^{{\text{def}}} \;{\text{STRESS}}(\omega ),\quad {\text{где}} \\ \omega = \left\{ {(\left\| {{{\Phi }_{{\text{L}}}}({{{\mathbf{c}}}_{{\mathbf{a}}}}) - {{\Phi }_{{\text{L}}}}({{{\mathbf{c}}}_{{\mathbf{b}}}})} \right\|_{2}^{{}}} \right., \\ \left. {\Delta {\text{E}}_{{{\text{00}}}}^{*}(p))\,{\text{|}}\,p = \left( {{{{\mathbf{c}}}_{{\mathbf{a}}}},{{{\mathbf{c}}}_{{\mathbf{b}}}}} \right) \in G_{n}^{2}} \right\}. \\ \end{gathered} $5. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ PROLAB
Предлагаемые в данной работе параметры proLab были получены следующим образом:
– Методом, изложенным в монографии В. Максимова (Maximov, 1984), была вычислена сетка точек, лежащих на границе цветового тела G источника D65. Для этих точек была построена двумерная триангуляция, что позволило приблизить G многогранником с числом граней около 20 000. Поскольку G выпукло, для проверки принадлежности точки телу G в дальнейшем использовалась система линейных неравенств, каждое из которых проверяет положение точки относительно одной из граней.
– Была сгенерирована выборка ${{G}_{{2{{n}_{1}}}}}$, состоящая из $2{{n}_{1}}$ независимо и равномерно распределенных в CIELAB цветов, принадлежащих цветовому телу G, где ${{n}_{1}} = 10\;000$. Разбиением выборки ${{G}_{{2{{n}_{1}}}}}$ на ${{n}_{1}}$ пар была сформирована выборка пар $G_{{{{n}_{1}}}}^{2}$.
– Для нахождения вектора метрических параметров ${{\mu }^{{opt}}}$ решалась оптимизационная задача со штрафными функциями (Bäck et al., 1997):
(42)
$\begin{gathered} {{\mu }^{{opt}}} = \\ = \mathop {{\text{arg}}\,{\text{min}}}\limits_{\mu \in {{\mathbb{R}}^{8}}} U[{{C}_{m}}(\mu ),G_{{{{n}_{1}}}}^{2}] + \sigma \sum\limits_{i = 1}^{14} \max {{(0, - {{{\text{f}}}_{i}}(\mu ))}^{2}}, \\ \end{gathered} $(43)
$M = \left[ {\begin{array}{*{20}{c}} {{\text{2}}{\text{.1591}}}&{ - {\text{1}}{\text{.7823}}}&{ - {\text{0}}{\text{.0713}}}&0 \\ 0&{{\text{2}}{\text{.0866}}}&{{\text{0}}{\text{.2103}}}&0 \\ 0&0&1&0 \\ {{\text{0}}{\text{.7554}}}&{{\text{3}}{\text{.8666}}}&{{\text{1}}{\text{.6739}}}&1 \end{array}} \right].$– Параметры выбора системы координат φ и ρ, необходимые для доопределения матрицы Q (11), были найдены аналитически методом, изложенным в разд. 2. В результате получилась следующая матрица Q:
(44)
$Q = \left[ {\begin{array}{*{20}{c}} {75.5362}&{486.661}&{167.387}&0 \\ {617.7141}&{ - 595.4477}&{ - 22.2664}&0 \\ {48.3433}&{194.9377}&{ - 243.281}&0 \\ {0.7554}&{3.8666}&{1.6739}&1 \end{array}} \right].$Для источника света D65 с координатами ${\mathbf{c}}_{{\mathbf{x}}}^{ \divideontimes } = {{\left[ {\begin{array}{*{20}{c}} {0.9505}&1&{1.0888} \end{array}} \right]}^{T}}$ (Ohta, Robertson, 2006) окончательно были получены следующие параметры координатной системы proLab:
6. КРИТЕРИЙ ГЕТЕРОСКЕДАСТИЧНОСТИ ШУМА ЦВЕТОВЫХ КООРДИНАТ
Как было сказано во введении, измеряемые камерой цветовые координаты всегда зашумлены, а многие статистические методы, применяемые для анализа цветовых распределений, обоснованы для гомоскедастичных моделей шума. Построим критерий, позволяющий количественно оценить гетероскедастичность шума цветовых векторов в том или ином пространстве цветовых координат.
Рассмотрим пространство цветовых координат ${{C}_{\phi }}$, для которого известно преобразование $\Phi {\kern 1pt} :\;{{C}_{x}} \to {{C}_{\phi }}$. Будем считать, что шум в каждой точке ${{{\mathbf{c}}}_{{\mathbf{x}}}} \in {{C}_{x}}$ можно приблизить в пространстве ${{C}_{x}}$ аддитивным шумом с нулевым средним и известной матрицей ковариации ${{\Sigma }_{x}}({{{\mathbf{c}}}_{{\mathbf{x}}}})$. Тогда в первом приближении ковариацию шума в пространстве ${{C}_{\phi }}$ можно выразить следующим образом:
(46)
${{\Sigma }_{\phi }}({{{\mathbf{c}}}_{\phi }}) = {{J}_{\Phi }}({{{\mathbf{c}}}_{{\mathbf{x}}}})\;{{\Sigma }_{x}}\left( {{{{\mathbf{c}}}_{{\mathbf{x}}}}} \right)\;J_{\Phi }^{T}({{{\mathbf{c}}}_{{\mathbf{x}}}}),\quad {{{\mathbf{c}}}_{{\mathbf{x}}}} = {{\Phi }^{{ - {\text{1}}}}}\left( {{{{\mathbf{c}}}_{\phi }}} \right),$Будем считать шум гомоскедастичным, если все три собственных числа его ковариационной матрицы равны друг другу на всем цветовом теле. Тогда на выборке цветов ${{G}_{n}}$ можно оценить гетероскедастичность аппаратного шума в пространстве ${{C}_{\phi }}$ следующим образом:
(47)
$\begin{gathered} H[\Phi ,{{G}_{n}}]\;\mathop = \limits^{{\text{def}}} \;{\text{STRESS}}(\omega ), \\ \omega = \left\{ {(\lambda _{i}^{{1/2}}[{{\Sigma }_{\phi }}({{\Phi }_{{\text{L}}}}({{{\mathbf{c}}}_{{\mathbf{l}}}}))],1)\,{\text{|}}\,{{{\mathbf{c}}}_{{\mathbf{l}}}} \in {{G}_{n}},1 \leqslant i \leqslant 3} \right\}, \\ \end{gathered} $7. ПАРАМЕТРЫ ШУМА В ЦВЕТОВОМ ПРОСТРАНСТВЕ СЕНСОРА И ДРУГИХ ПРОСТРАНСТВАХ
Построим теперь модель шума для исходного цветового пространства сенсора. В работе (Bernd, 2005) приводится достаточно простая модель значений одноканального изображения, хорошо согласующаяся с экспериментальными данными:
(48)
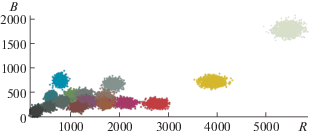
$s = g{\kern 1pt} n + \varepsilon ,\quad n \sim {\text{Pois}}({{s}_{0}}),\quad \mathbb{E}(\varepsilon ) = 0,$Верифицируем эту модель на датасете MLSDCR (Multiple Light Source Dataset for Colour Research) (Smagina et al., 2020), данные которого получены с фотоаппарата Canon 5D Mark III. Среди прочего, в MLSDCR есть необработанные (“raw”) изображения цветовой таблицы (рис. 3), а также приведены параметры калибровочного преобразования из цветового пространства камеры в цветовое пространство стандартного наблюдателя (в координатах sRGB).
Рис. 3.
Фотография цветовой таблицы, сделанная фотоаппаратом Canon 5D Mark III. Фиолетовыми рамками ограничены области, по которым оценивались средние и дисперсии откликов сенсора.

Будем оценивать параметры шума в каждой равномерно окрашенной области цветовой таблицы. Известно, что в экспериментах по цветовой калибровке точность измерений может оказаться ограниченной неравномерностью освещения (Kordecki, 2019). В нашем случае критическим является только возможная неравномерность внутри одной области. Чтобы уменьшить влияние этого фактора, в каждой области рассмотрим по небольшому центральному участку размером 42 × 42 пикселя мозаичного изображения (рис. 3). Также учтем, что разные элементы мозаики могут иметь различные параметры шума. В фотоаппарате Canon 5D Mark III используется стандартная (RGGB) мозаика Байера, поэтому для набора из 18 областей сформируем выборку ${{S}_{i}}$ ($1 \leqslant i \leqslant 72$) откликов сенсора на его равномерное освещение, разделяя значения по четырем возможным положениям в мозаике. Построение совместных гистограмм цветовых координат элементов выборки демонстрирует существенную гетероскедастичность шума (рис. 4).
Теперь по выборкам ${{S}_{i}}$ оценим средние и соответствующие им дисперсии откликов сенсора:
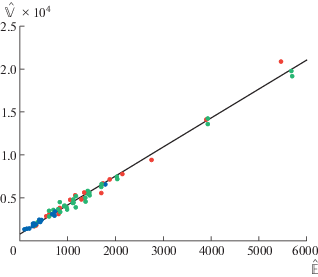
Используя метод главных компонент, оценим параметры модели (49):
Соответствующая линейная зависимость, приведенная на рис. 5, хорошо приближает выборочные оценки $\hat {\mathbb{E}}(s)$ и $\hat {\mathbb{V}}(s)$ для всех типов пикселей. Таким образом, мы получили следующую оценку дисперсии для значений необработанного мозаичного изображения фотоаппарата Canon 5D Mark III в режиме, использованном для получения нашего изображения:
Рис. 5.
Линейная зависимость дисперсии откликов сенсора от их выборочного среднего. Цвета точек условно соответствуют различным каналам сенсора.
Перейдем теперь в пространство ${{C}_{x}}$. Для этого воспользуемся преобразованием, приведенном в работе (Smagina et al., 2020), откуда мы взяли экспериментальные данные. Для корректного перехода в ${{C}_{x}}$ необходимо учесть влияние процедуры дебайеринга. Простейший дебайеринг заключается в усреднении двух G-элементов мозаики и агрегации результата с одним R- и одним B-элементом. Пространство полученных таким образом цветовых координат будем называть deviceRGB и обозначать ${{C}_{d}}$. С учетом ранее полученной модели (52) запишем ковариационную матрицу шума в ${{C}_{d}}$:
(53)
$\begin{gathered} {{\Sigma }_{d}}({{{\mathbf{c}}}_{{\mathbf{d}}}}) = {\text{diag}}\left( {\left[ {\begin{array}{*{20}{c}} 1&{1{\text{/}}2}&1 \end{array}} \right]} \right)\left( {3.38\,{\text{diag}}({{{\mathbf{c}}}_{{\mathbf{d}}}}) + 744{\kern 1pt} {{I}_{3}}} \right), \\ {{{\mathbf{c}}}_{{\mathbf{d}}}} \in {{C}_{d}}. \\ \end{gathered} $В работе (Smagina et al., 2020) приведена следующая матрица перехода из deviceRGB в linRGB стандартного наблюдателя:
(54)
${{D}_{1}} = \frac{{0.03}}{{{{2}^{{16}}}}}\left[ {\begin{array}{*{20}{c}} {41.93}&{ - 2.08}&{ - 37.24} \\ { - 14.32}&{39.13}&{10.79} \\ { - 0.02}&{ - 35.39}&{185.52} \end{array}} \right].$Учитывая, что переход из linRGB в СIE XYZ по определению линеен (Stokes et al., 1996) и задается матрицей
(55)
${{D}_{2}}\;\mathop = \limits^{{\text{def}}} \;\left[ {\begin{array}{*{20}{c}} {0.4125}&{0.3576}&{0.1804} \\ {0.2127}&{0.7152}&{0.0722} \\ {0.0193}&{0.1192}&{0.9503} \end{array}} \right],$(56)
$\begin{gathered} {{D}^{{ - 1}}} = {{D}_{2}}{\kern 1pt} {{D}_{1}} = \\ \, = {{10}^{{ - 6}}}\left[ {\begin{array}{*{20}{c}} {5.5711}&{3.0892}&{10.0585} \\ { - 0.6066}&{11.4383}&{6.0363} \\ { - 0.4189}&{ - 13.2786}&{80.9631} \end{array}} \right]. \\ \end{gathered} $При этом матрица ковариации сенсорного шума в пространстве CIE XYZ будет равна
(57)
${{\Sigma }_{x}}({{{\mathbf{c}}}_{{\mathbf{x}}}}) = {{D}^{{ - 1}}}{{\Sigma }_{d}}(D{{{\mathbf{c}}}_{{\mathbf{x}}}}){{D}^{{ - T}}},\quad {{{\mathbf{c}}}_{{\mathbf{x}}}} \in {{C}_{x}}.$Подставляя в (57) значения параметров из (53) и (56), получим модель цветового шума нашей камеры в пространстве ${{C}_{x}}$.
8. СРАВНЕНИЕ ЦВЕТОВЫХ КООРДИНАТ ПО ПСИХОФИЗИЧЕСКОЙ НЕРАВНОМЕРНОСТИ И ГЕТЕРОСКЕДАСТИЧНОСТИ ШУМА
Для оценивания психофизической неравномерности сформируем независимую тестовую выборку пар цветов $G_{{{{n}_{2}}}}^{2}$ размером ${{n}_{2}} = 100\;000$ пар по методике, описанной в разд. 5. В дальнейшем на этой выборке для каждой системы цветовых координат, задаваемой преобразованием Φ, будем оценивать психофизическую неравномерность по критерию (41): ${{{\text{U}}}_{{\text{T}}}}[\Phi ]\;\mathop = \limits^{{\text{def}}} \;{\text{U}}[\Phi ,G_{{{{n}_{2}}}}^{2}]$.
Также сформируем выборку цветов ${{G}_{{{{n}_{2}}}}}$, на которой будем оценивать гетероскедастичность шума. При этом потребуем не только принадлежности цветовых векторов цветовому телу источника D65, но и реализуемости всех рассматриваемых цветов камерой, т.е. их покомпонентной неотрицательности в пространстве deviceRGB:
(58)
${{{\mathbf{c}}}_{{\mathbf{l}}}} \in {{G}_{{{{n}_{2}}}}} \Rightarrow D{{{\text{L}}}^{{ - {\text{1}}}}}({{{\mathbf{c}}}_{{\mathbf{l}}}}) \geqslant 0.$На реализуемой подобласти цветового тела сделаем выборку ${{G}_{{{{n}_{2}}}}}$ равномерной и оценим гетероскедастичность согласно критерию (47): ${{{\text{H}}}_{{\text{T}}}}[\Phi ]\;\mathop = \limits^{{\text{def}}} \;{\text{H}}[\Phi ,{{G}_{{{{n}_{2}}}}}]$. Для вычисления ${{{\text{H}}}_{{\text{T}}}}[\Phi ]$ требуется матрица ковариации шума ${{\Sigma }_{\phi }}({{{\mathbf{c}}}_{\phi }})$, для ее получения используем приближение (46), а также модель (57) цветового шума в пространстве ${{C}_{x}}$.
Для сравнения будем использовать следующие широко используемые системы координат цветового пространства человека:
• CIE XYZ (Smith, Guild, 1931) – базовую систему цветовых координат стандартного наблюдателя;
• CIE xyY (Smith, Guild, 1931) – систему с явно выделенными координатами цветности;
• LMS (Fairchild, 2013) – систему координат, моделирующую линеаризованные отклики колбочек человека;
• sRGB (Stokes et al., 1996) – цветовые координаты, используемые при воспроизведении цветов на дисплеях и принтерах (большинство фото- и видеофайлов содержат информацию о цветах в этих координатах);
• linRGB (Stokes et al., 1996) – промежуточное (без гамма-коррекции ) представление воспроизводимых цветов, линейно связанное с CIE XYZ;
• CIELAB (McLaren, 1976) – широко распространенную систему психофизически равномерных цветовых координат;
• CAM16-UCS (Li et al., 2017) – систему координат, считающуюся на данный момент наиболее психофизически равномерной.
Будем сравнивать proLab с ними, а также с линейными цветовыми координатами сенсора камеры по критериям${{{\text{U}}}_{{\text{T}}}}$ и ${{{\text{H}}}_{{\text{T}}}}$, а также укажем, какие из них сохраняют линейность цветовых многообразий (табл. 1). Среди цветовых координат только CIE xyY имеет нетривиальную классификацию по коллинеации, поскольку сохраняет форму прямых, проходящих через начало координат CIE XYZ. ProLab, как и линейные системы координат, обладает свойством по построению сохранять прямые, остальные системы цветовых координат не сохраняют даже центральный пучок. По психофизической равномерности proLab значимо превосходит общепринятое равномерное пространство CIELAB, хотя и уступает CAM16-UCS – последней и наиболее успешной на сегодняшний день попытке построения психофизически равномерного пространства цветовых координат. По гомоскедастичности шума proLab уступило в нашем эксперименте только пространству deviceRGB, свойства которого существенно меняются от камеры к камере.
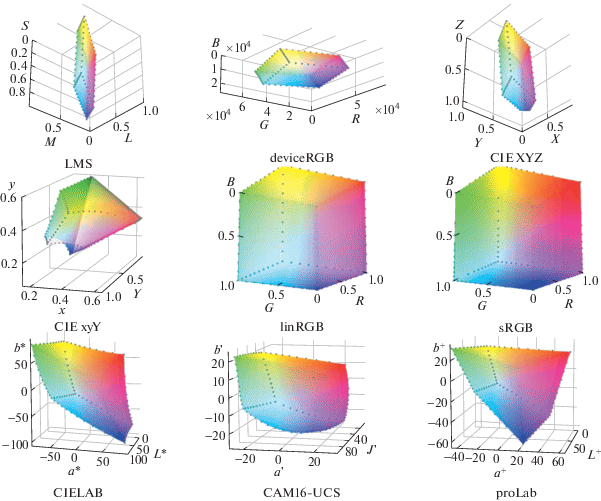
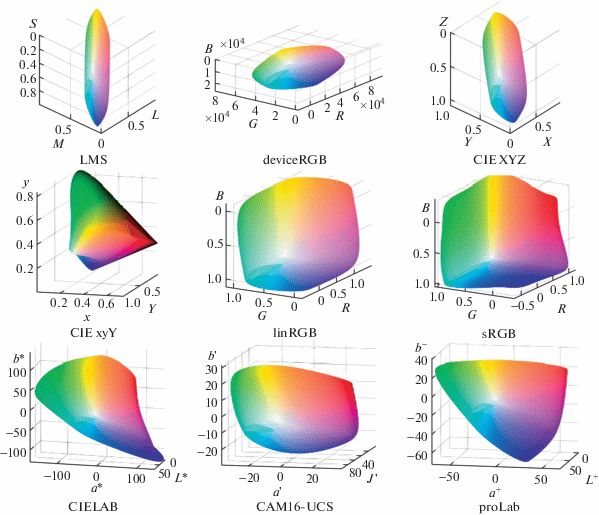
Рассмотрим теперь различия между пространствами цветовых координат более наглядно, используя различные визуализации. На рис. 6 изображено цветовое тело sRGB-дисплея в различных пространствах цветовых координат. Можно видеть, что в пространстве proLab цветовое тело sRGB сохраняет форму гексаэдра. Аналогичные диаграммы для цветового тела источника света D65 представлены на рис. 7. Из-за ограничений на цветовой охват насыщенность цветов, использованых для визуализации, на этой иллюстрации существенно занижена. На этих двух рисунках видно еще одно достоинство proLab: в отличие от CIELAB, эта координатная система сохраняет выпуклость цветовых тел.
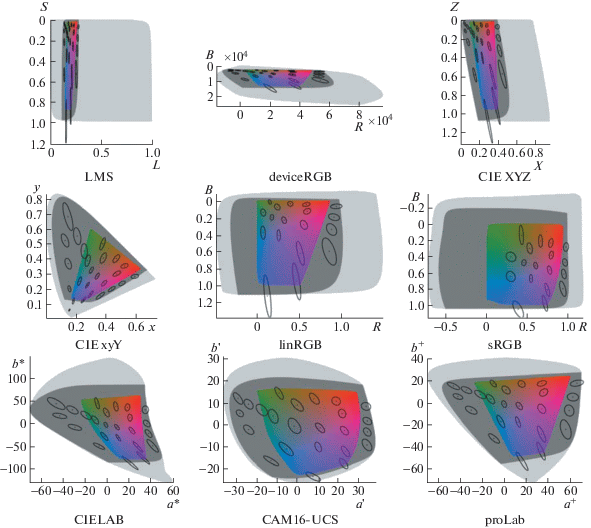
На рис. 8 при помощи эллипсов МакАдама (MacAdam, 1942) проиллюстрирована неравномерность рассматриваемых пространств цветовых координат по цветности. Эллипсы МакАдама представляют собой увеличенные в 10 раз эллипсы погранично-различимых цветовых различий (JND – just noticeable difference) и исходно определены в пространстве CIE xyY. Для их построения в произвольном пространстве ${{C}_{\Phi }}$ нами использовалось линейное приближение преобразования Φ в центрах эллипсов. Для каждого пространства цветовых координат изображена одна из его координатных плоскостей, на которую спроецированы эллипсы МакАдама для светлоты CIELAB $L{\kern 1pt} * = 50$, цветовое тело источника света D65 (светло-серый), а также сечения эквисветлотной поверхностью $L{\kern 1pt} * = 50$ цветовых тел источника (темно-серый) и sRGB-дисплея (радужный).
Рис. 8.
Неравномерность цветности: эллипсы МакАдама для $L{\kern 1pt} * = 50$ на фоне проекций цветового тела источника света D65 (светло-серый), его сечения (темно-серый) и сечения цветового тела sRGB-дисплея (радужный) в различных пространствах цветовых координат.
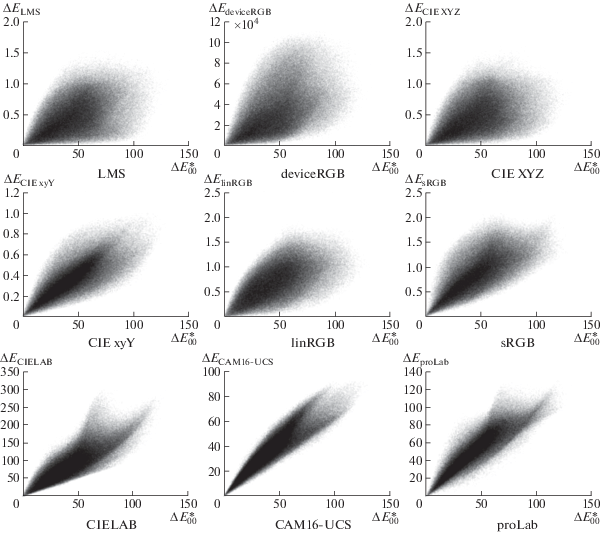
Другой способ визуально оценить психофизическую неравномерность использован на рис. 9. На нем для каждого пространства цветовых координат изображено совместное распределение его евклидова расстояния $\Delta {{{\text{E}}}_{\Phi }}$ и цветового различия CIEDE2000 $\Delta {\text{E}}_{{00}}^{*}$ на тестовой выборке $G_{{{{n}_{2}}}}^{2}$. Чем равномернее пространство цветовых координат, тем больше распределение на диаграмме должно концентрироваться вдоль прямой, проходящей через 0. Видно, что диаграммы CAM16-UCS и proLab имеют существенно лучшую форму, чем у конкурирующих пространств цветовых координат, но proLab проигрывает лидеру в области средних расстояний. Интересно, что CAM16-UCS имеет два явно различающихся локуса в районе больших расстояний, что означает существенную неравномерность в этом диапазоне. В свою очередь на диаграммах proLab и CIELAB видны сильно декоррелированные области, похожие между собой по расположению и форме, но у CIELAB эта область крупнее и дальше отклоняется от основного локуса.
Рис. 9.
Совместные распределения цветовых различий CIEDE2000 $\Delta E_{{{\text{00}}}}^{*}$ и евклидовых расстояний $G_{{{{n}_{2}}}}^{2}$ для различных систем цветовых координат.
Для детальной визуализации гетероскедастичности были построены диаграммы, подобные эллипсам МакАдама (рис. 10). Для набора цветов из цветового тела sRGB-дисплея с использованием параметров модели (52) были промоделированы распределения зашумленных измерений в пространстве deviceRGB. Каждое из распределений было спроецировано в тестируемое пространство цветовых координат и отображено на координатной плоскости своим усредненным цветом. Порядок отрисовки распределений, при котором светлые цвета накладываются на темные и заслоняют их, позволяет увидеть трехмерную структуру параметров шума.
9. ОБСУЖДЕНИЕ
Основным отличием proLab от других равномерных пространств цветовых координат является его проективность. Поскольку переход в proLab не смещает начало координат, то центральная проекция на любую плоскость, не проходящую через 0, в этом пространстве является корректной диаграммой цветности: все цвета, отличающиеся в исходном спектральном пространстве только яркостью, будут отображены в одну точку.
Другое интересное свойство proLab касается дробового шума на изображениях. Оценивание цвета по зашумленному изображению арифметическим усреднением корректно только в линейных пространствах цветовых координат. Однако оценивание цветности линейной регрессией некорректно даже в линейном пространстве, поскольку амплитуда дробового шума цветовых координат зависит от их значения. Поскольку гетероскедастичность шума в proLab меньше, чем в стандартных линейных пространствах, линейная регрессия в нем, по-видимому, является более корректной процедурой.
В данной работе система proLab строилась для источника D65, и естественным является вопрос о том, как ее следует использовать в условиях освещения источником света другого типа. Для достижения максимальной точности в таком случае следует формировать выборку пар цветов $G_{{{{n}_{1}}}}^{2}$ на цветовом теле используемого источника и оптимизировать на этой выборке матрицу Q. Такая процедура неудобна и трудоемка, поэтому мы предлагаем использовать подход, аналогичный CIELAB: при использовании этой системы с различными источниками света применяемые преобразования различаются только в части адаптации, а “ядро преобразования” остается прежним. Данный подход выглядит разумным и для CIELAB, и для proLab, поскольку обе эти системы имеют значимые погрешности в равномерности, и их дополнительная оптимизация вряд ли может существенно повлиять на конечный результат. Поэтому при использовании proLab с источниками, отличными от D65, мы рекомендуем сохранять значения элементов матрицы Q, приведенные в выражении (44).
При использовании любого из двух изложенных подходов матрица P окончательно определяется согласно упрощенной модели адаптации фон Криса (9). Это упрощение часто критикуется за свою низкую точность, и его использование в данной работе продиктовано исключительно соображениями совместимости с уже используемыми системами координат. Известен ряд более точных моделей адаптации, также носящих имя фон Криса, и выражаемых при этом линейным преобразованием цветовых координат (Bianco, Schettini, 2010). Все они могут быть использованы с proLab, поскольку замена модели адаптации на другую линейную (и даже проективную) не приводит к изменению матрицы Q, а требует только изменения определения (8) матрицы N.
В принципе, сохраняя общий вид proLab, можно модифицировать и ее метрические параметры, в зависимости от конкретной задачи. В частности, не очевидно, что при решении оптимизационной задачи пары с различной цветовой разностью $\Delta E_{{00}}^{*}$ должны иметь одинаковый вес. Можно себе представить приложения, в которых большие цветовые различия (или, напротив, малые) не существенны. В таких случаях следует оптимизировать параметры proLab тем же методом, но на иной выборке $G_{{{{n}_{1}}}}^{2}$. Кроме того, ограничение на “светлотный смысл” оси ${{L}^{ + }}$ можно ослаблять для увеличения психофизической равномерности результата, либо, напротив, ужесточать. В частности, можно дополнительно потребовать выполнения условия (22) и для цветовых координат LMS. Нетрудно заметить, что из выполнения условия (22) автоматически следует выполнение аналогичных условий для координат в linRGB. Действительно, все элементы матрицы перехода из linRGB в CIE XYZ неотрицательны (Stokes et al., 1996), а
(59)
${\mathbf{x}} \in \mathbb{R}_{{ \geqslant 0}}^{n},\quad A \in \mathbb{R}_{{ \geqslant 0}}^{{n \times n}} \Rightarrow A{\mathbf{x}} \in \mathbb{R}_{{ \geqslant 0}}^{n},$Важным представляется также дальнейшее исследование параметров шума в различных пространствах, включая proLab. Интересны как новые экспериментальные данные по различным камерам и режимам их работы, так и аналитические модели оценивания гетероскедастичности в тех или иных условиях. Помимо дробового шума, в модель может быть добавлен учет дискретизации сигнала сенсором. Влияние дискретизации на пороги цветоразличения технических систем исследовалось ранее (Palchikova et al., 2018), но вне контекста построения равномерных систем цветовых координат.
С одной стороны, наличие побочного локуса в совместной диаграмме расстояний на рис. 9 позволяет ставить вопрос о локализации участков цветового тела, где цветовые различия существенно непроективны. С другой стороны, строгое требование проективности было введено нами формально. Дополнительные погрешности регрессии при отклонении модели от проективности могут оказаться незначительными на фоне шума. Поэтому дальнейшее развитие предложенной системы координат могло бы заключаться в построении малопараметрической и вычислительно простой цветовой модели, близкой к проективной, и при этом обладающей большей психофизической равномерностью и меньшей гетероскедастичностью шума в ней.
10. ЗАКЛЮЧЕНИЕ
Предложена новая система цветовых координат proLab, которая по психофизической равномерности превосходит CIELAB и сохраняет при этом линейность цветовых многообразий. Последним свойством не обладают ни CIELAB, ни CAM16-UCS. В proLab, подобно линейным пространствам, можно использовать угловые метрики ошибок цветовой репродукции. При этом в отличие от них угловые отклонения в направлении различных цветовых тонов психофизически выравнены за счет привязки к CIEDE2000. Нами также показано, что, по крайней мере в некоторых случаях, шум в proLab оказывается более гомоскедастичным, чем в стандартных пространствах, включая линейные.
Все это делает proLab предпочтительной системой координат для анализа структуры цветовых гистограмм: инцидентность линейных многообразий в ней сохранена (например, в proLab можно определять направление на источник по пересечению плоскостей, определяющих цветовые распределения глянцевых поверхностей); координаты линейных многообразий в такой системе можно определять довольно точно без дополнительного учета гетероскедастичности шума (как обычно и поступают); взаимное расположение линейных элементов (в том числе углы между прямыми) выражается в единицах, связанных с человеческим восприятием цветовых различий.
Работа выполнена при частичной финансовой поддержке РФФИ в рамках научных проектов 17-29-03370 и 19-29-09075.
Список литературы отсутствует.
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы