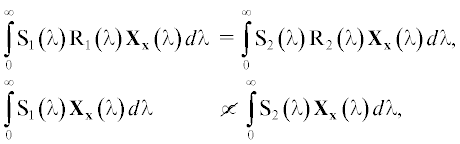Сенсорные системы, 2022, T. 36, № 2, стр. 153-182
Мультипликативно замкнутые спектральные модели в задачах цветового анализа
Д. П. Николаев 1, *, И. А. Коноваленко 1, П. П. Николаев 1
1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный переулок, 19, Россия
* E-mail: dimonstr@iitp.ru
Поступила в редакцию 11.01.2022
После доработки 25.01.2022
Принята к публикации 08.02.2022
- EDN: WRAZZO
- DOI: 10.31857/S0235009222020056
Аннотация
Работа посвящена методам и инструментам решения проблем цветовосприятия, реализующих в акте зрения объективное описание наблюдаемого. В статье рассмотрен ряд содержательных примеров задания малопараметрических спектральных описаний, обеспечивающих формальную связь пространств излучений и реакций сенсора. Эти структуры называются спектральными моделями. Описаны и объяснены на конкретных примерах (с анализом достоинств и недостатков) их принципиальные разновидности и внутритиповые модификации. Приведены с соответствующими мотивировками ограничения на физоптические характеристики сцены, регистрируемой сенсором, и варианты аппроксимации спектральных описаний ее элементов, обеспечивающие разрешимость упрощаемой таким образом обратной задачи, в общем случае не имеющей решения. В контексте требований к спектральным моделям рассмотрены проблемы, возникающие при моделировании феноменов цветовой константности, а также при постановках задачи калибровки камер. Обсуждены преимущества использования гауссовской спектральной модели (как нелинейной и мультипликативно замкнутой) в ее сопоставлении с оптимальными линейными моделями, а также описаны три ее модификации, расширяющие цветовой охват, в исходном варианте не воспроизводящей цветов пурпурного сегмента. На языке гауссовской модели – с переходом к оптимизирующим свойствам фонмизесовской модели – описан и показан итогом численных экспериментов (с привлечением “реальных” спектральных данных) метод оценки цветности источника по цветовой картине внутренних переотражений (интеррефлексов) в наборе разноокрашенных складчатых образцов. Текст сочетает анализ теоретических положений с обсуждением результатов компьютерного моделирования и физического эксперимента.
ВВЕДЕНИЕ
В предлагаемой статье авторы поставили для себя цель изложить (вместе с кратким историческим экскурсом) эволюцию подходов к решению одной из основных проблем восприятия наблюдаемого мира – проблемы спектрального описания цветных объектов. На протяжении последних десятилетий исследователями феноменов цветовосприятия и разработчиками систем зрительного распознавания были предприняты значительные усилия, чтобы выяснить, как (и насколько хорошо) спектры излучений и характеристики окраски могут быть восстановлены по трем компонентам цветового сигнала, регистрируемого цветовым сенсором, включая зрительную систему человека.
Проблема спектрального описания цветных объектов реального мира была исходно связана с проблемой цветоконстантности (ЦК). Явление ЦК, как способность зрительной системы человека и животных оценивать отражательные свойства поверхностей (их окраску) в условиях меняющейся цветности освещения наблюдаемой сцены, достаточно подробно изучено и описано, но в плане его формализации, как практической задачи зрительной объектной интерпретации, проблема ЦК не решена ввиду того, что является в общем случае некорректной обратной задачей (в силу неизбежного оптического и спектрального вырождения предмета анализа – картины, полученной сенсором).
Для того чтобы задача построения вычислительной схемы ЦК стала реализуемой, требуется введение тех или иных априорных ограничений на оптические свойства среды, в которой функционирует сенсорная система, при этом язык описания спектральных свойств тел и первичных источников освещения необходимо согласовать с их “цветовой” размерностью, что предполагает введение малопараметрических приближений в описании всех спектральных функций, фигурирующих в акте цветовосприятия. Именно они (целенаправленно вводимые ограничения и аппроксимации) делают задачу разрешимой, позволяя построить математическую модель ЦК (Brill, West, 1986; Maloney, Wandell, 1986б; Nikolaev, 1989; Macleod, Golz, 2003; Nikolaev , Nikolaev, 2005; Николаев 2007а; Logvinenko, 2013).
Следует заметить, что вопрос аппроксимации спектральных характеристик возникает и в существенно более широком классе задач обработки цветных изображений. Варианты таких аппроксимаций, позволяющие с допустимыми погрешностями связывать спектральные характеристики тел, излучателей и сенсоров на языке трехпараметрических описаний, получили в цветовой теории название “спектральные модели”.
Алгоритмы обработки изображений в биоинформатике, как правило, создают для трихроматических систем, что диктуется размерностью цветового пространства человека-трихромата. При этом надо понимать, что для решения технических задач, когда отсутствует необходимость в ограничениях на размерность цветового пространства специализированного сенсора, уже “не обязанного” следовать законам трихроматичности человеческого цветовосприятия, могут привлекаться многопараметричекие спектральные аппроксимации, при помощи которых описания функций процесса становятся существенно более реалистичными. Это направление, не связанное с визуализацией результатов обработки изображений для человека-трихромата, заслуживает отдельного рассмотрения, здесь же основные продвижения в совершенствовании спектральных моделей обсуждаются в рамках трехканальных систем, поскольку именно они в состоянии обеспечить высокое качество цветовоспроизведения на экранах мониторов и мобильных телефонов, а также и реалистичную цветопередачу печатных иллюстраций.
Как в отечественной, так и зарубежной литературе не имеется обзорных работ, в которых рассматриваются общие принципы построения спектральных моделей, пригодных для использования в алгоритмах технического зрения, и проводится их сравнительный анализ. Как правило, такого рода материал обсуждается в связи с конкретными задачами цветового зрения (Brill, West, 1986; Nikolaev et al., 2006; Mizokami, Webster, 2012). Вместе с тем в последнее время появляются публикации с описанием новых семейств спектральных моделей, которые предлагаются в качестве более адекватных гипотез о малопараметрической репрезентации спектральных стимулов. В связи с расширением списка подобных предложений, цель настоящей статьи – представить по возможности детализированный анализ различных вариантов спектральных моделей, включая те, которые предложены самими авторами, и провести их сравнение друг с другом по точности работы и оценкам полноты цветового охвата (границ цветовоспроизведения).
Статья структурирована следующим образом. В первом разделе описываются задачи цветового анализа, формально неразрешимые в общем случае, а именно: некоторые проблемы цветовой константности и аналитические задачи оптимальной калибровки сенсора. На материале этих (столь различных по своим целям) постановок демонстрируется необходимость введения спектральных моделей. Показывается, что с их помощью задачу оценки спектра отражения окрашенных тел – по наблюдаемому их цвету и известной цветности доминирующего источника освещения, как и задачу цветовой калибровки сенсора, удается сделать корректными. Далее рассматриваются различные типы спектральных моделей, как классических, так и относительно новых. Кратко изложена история создания самых старых и наиболее исследованных линейных спектральных моделей (ЛСМ), приведено несколько наиболее интересных их вариантов и обсуждены причины недостаточно точной работы схем с ЛСМ. В качестве альтернативы подходу с ЛСМ описаны варианты нелинейной гауссовской спектральной модели (ГСМ). На теоретическом уровне рассмотрены достоинства ГСМ (относительно принципиальных возможностей семейства ЛСМ) и проведено сравнение трех ее версий (сопоставление в границах ГСМ) по цветовому охвату в пурпурной области, критичной для всех видов спектральных моделей.
Во втором разделе статьи произведен анализ точности спектральных моделей при использовании в конкретных задачах цветного зрения: в оценке наблюдаемого спектра по его цвету (т.е. в задаче перехода из цветового пространства в спектральное); в оценке спектра отражения по наблюдаемому цвету при известной цветности источника (т.е. в задаче “поправки на спектр освещения”). Представляется, что для первой задачи ГСМ оказывается не менее удобной, чем ЛСМ, а для второй – ГСМ и удобнее и точнее, чем лучшие трехпараметрические ЛСМ.
В третьем разделе формально вводится понятие семейства мультипликативно замкнутых спектральных моделей (МЗСМ), в качестве замкнутых относительно операции умножения. Рассматривается его представитель – фонмизесовская спектральная модель (ФСМ). Обсуждаются свойства ФСМ на примере задачи оценки цветности источника по картине изменений цветовых характеристик излучения, регистрируемого в складке/лунке окрашенной поверхности. Показывается, что ФСМ имеет лучшую среди прочих МЗСМ цветопередачу и охват в пространстве тристимулов, а оценка цветности источника – в приближении учета интеррефлексов в вогнутостях объектов – выполняется с хорошей точностью в практических реализациях.
1. СПЕКТРАЛЬНЫЕ ЦВЕТОВЫЕ МОДЕЛИ И ИХ РОЛЬ В ЦВЕТОВОМ АНАЛИЗЕ
Задача цветовой константности состоит в оценивании свойств окраски тел, регистрируемых сенсором (глазом наблюдателя либо камерой цветораспознающей системы), но как проверить, что цель достигнута и оценки адекватны свойствам объектов сцены? Можно считать, что свойства окраски наблюдаемых тел известны некой системе цветового анализа, если для любого освещения она может предсказать цвет объекта, регистрируемого ее сенсором. Пусть сенсор линеен и функции его спектральной чувствительности ${\mathbf{X}}(\lambda )$ известны. Положим также, что источник света простой и известен относительный спектральный состав ${\text{S}}(\lambda )$ испускаемого им света; и, наконец, пусть объект имеет унихроматическую окраску и в сцене, его содержащей, нет переотражений (что выполняется для плоских ее участков). В такой максимально простой сцене пространственное распределение ${\mathbf{c}}(x,y)$ цвета объекта будет подчиняться следующему соотношению:
(1)
${\mathbf{c}}\left( {x,y} \right) = {\text{g}}\left( {x,y} \right)\int\limits_0^\infty {{\text{S}}\left( \lambda \right){\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } ,$Цвет изображения объекта является функцией не только параметров окраски объекта, но и параметров его освещения. Разумно считать, что параметры освещения существенно менее вариабельны в пределах одного изображения, чем параметры окрасок. Поэтому подавляющее большинство методов цветовой константности включают оценку параметров освещения как ключевую подзадачу (Gijsenij et al., 2011). Предположим, что эта задача тем или иным образом решена. Пусть известен цвет ${{{\mathbf{c}}}_{{\mathbf{s}}}}$ источника, определяемый следующим образом:
(2)
${{{\mathbf{c}}}_{{\mathbf{s}}}} = \int\limits_0^\infty {{\text{S}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } .$Пусть нам также известен цвет ${{{\mathbf{c}}}_{{{\mathbf{sr}}}}}$ окраски под этим освещением, определяемый как
(3)
${{{\mathbf{c}}}_{{{\mathbf{sr}}}}} = \int\limits_0^\infty {{\text{S}}\left( \lambda \right){\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } .$Для полного решения задачи цветовой константности требуется оценить ${\text{R}}(\lambda )$ при известном ${\mathbf{X}}(\lambda )$. Очевидно, что поставленная задача неразрешима без дополнительных априорных ограничений, даже несмотря на вынесение за скобки проблемы верного оценивания параметров освещения.
Рассмотрим теперь другой вопрос, связанный с проблемой цветовой калибровки сенсора для реализации точной цветопередачи. Пусть нам известна реакция с технического сенсора с чувствительностями ${\mathbf{X}}(\lambda )$ на освещенность ${\text{F}}(\lambda )$, создаваемую некоторой точкой сцены
(4)
${\mathbf{c}} = \int\limits_0^\infty {{\text{F}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } .$В линейной модели реакция ${{{\mathbf{c}}}_{{\mathbf{x}}}}$ человека (стандартного наблюдателя) на тот же стимул записывается аналогично
(5)
${{{\mathbf{c}}}_{{\mathbf{x}}}} = \int\limits_0^\infty {{\text{F}}\left( \lambda \right){{{\mathbf{X}}}_{{\mathbf{x}}}}\left( \lambda \right)d\lambda } .$Как определить ${{{\mathbf{c}}}_{{\mathbf{x}}}}$, зная с? Этот вопрос, строго говоря, выходит за рамки проблематики цветовой константности, но при этом весьма актуален в широком круге задач технического зрения, – в последние годы по теме цветовой калибровки опубликованы десятки статей (Bianco et al., 2013; Vazquez-Corral et al., 2014; Finlayson et al., 2015; Can Karaimer, Brown, 2018; Kordecki, 2019).
Нетрудно показать, что задача цветовой калибровки имеет решение, если выполнено так называемое условие Максвелла–Лютера–Айвза: ${{{\mathbf{X}}}_{{\mathbf{x}}}}(\lambda ) = M{\mathbf{X}}(\lambda )$, где M – матрица линейного преобразования. В таком случае верно следующее простое выражение: ${{{\mathbf{c}}}_{{\mathbf{x}}}} = M{\mathbf{c}}$. Если же условие не выполнено, то между цветами сенсоров нет однозначного соответствия, поскольку в этом случае существуют такие ${\text{F}}(\lambda )$, для которых ${\mathbf{c}}$ совпадают, а ${{{\mathbf{c}}}_{{\mathbf{x}}}}$ – нет. Задачу цветовой калибровки в таком случае приходится решать приближенно.
Проблему калибровки можно переформулировать следующим образом: требуется решить уравнение (4) относительно ${\text{F}}(\lambda )$. После этого ${{{\mathbf{c}}}_{{\mathbf{x}}}}$ находится подстановкой в (5). Удается показать, что любая калибровка, выражаемая однозначным отображением из $\{ {\mathbf{c}}\} $ в $\{ {{{\mathbf{c}}}_{{\mathbf{x}}}}\} $, может быть переформулирована указанным образом.
В обоих рассмотренных случаях ставится задача оценки спектра по его цвету. Потребовались серьезные теоретические усилия и объемные экспериментально вычислительные проверки, чтобы выяснить, каким образом – и насколько хорошо – спектры излучений и компонент окраски могут быть восстановлены по трем координатам цветового сигнала, регистрируемого цветовым сенсором. Если бы спектры освещения и окрасок варьировались случайным и произвольным образом, тогда поставленная задача вряд ли была разрешима. Оказалось, что спектры компонент окрасок природных материалов, как правило, не имеют большого числа резких перепадов в видимой области (рис. 1), что создает предпосылки их описания функциями с небольшим числом параметров. При постулировании принадлежности спектральных функций (участвующих в акте зрения) достаточно “хорошему” трехпараметрическому семейству сформулированная выше задача оказывается разрешимой в общем случае. Варианты таких (как правило, но не обязательно трехпараметрических) семейств получили в цветовой теории название “спектральные модели”.
До последнего времени большинство исследователей, занимающихся проблемами цветного зрения и цветовой константности, для их разрешения привлекали так называемые линейные спектральные модели (ЛСМ) (Yilmaz, 1962; Brill, 1978; Maloney, 1986а, Marimont, Wandell, 1992). В ЛСМ пространство спектральных функций ограничивается некоторым линейным подпространством:
(6)
${\text{M}}_{{\mathbf{B}}}^{ \pm }\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} {\mathbf{p}} \cdot {\mathbf{B}}\left( \lambda \right),$При $\dim {\mathbf{p}} = 3$ задача цветовой калибровки сенсора становится разрешимой в общем случае, причем решение линейно, аналогично случаю с выполненным условием Максвелла–Лютера–Айвза. Довольно очевидно, что решение, использующее ЛСМ, при выполнении этого условия даст верный ответ. Во всех прочих случаях точность ответа будет зависеть от того, насколько хорошо та или иная ЛСМ описывает реальное (для среды функционирования) распределение спектральных функций.
Кратко изложим историю создания ЛСМ и отметим несколько наиболее интересных ее вариантов. Илмаз первым в 1962 г. применил разложение в усеченный ряд Фурье для моделирования источников света и отражательной способности объектов. Салстром, по-видимому, первым сформулировал проблему оценивания спектральных функций в терминах разложений с использованием произвольных базисных функций (Sällström, 1973). В работах Брилла (Brill, 1978; 1979), Боксбаума (Buchsbaum, 1980), Мейлони (Maloney, 1986а), а также Мейлони и Вандела (Maloney, Wandell, 1986б) представление о базисных спектральных функциях было использовано для теоретического описания цветоконстантного трихроматического светочувствительного устройства (как модели цветовой константности человеческого восприятия). Именно Мейлони и Вандел назвали разложения спектров по базисным функциям линейными спектральными моделями.
В ряду известных линейных моделей следует отметить несколько наиболее интересных. В зональной спектральной модели (ЗСМ) ${\text{M}}_{{\text{Z}}}^{ \pm }$ базисом являются функции-ступеньки:
(7)
$\begin{gathered} {\text{M}}_{{\text{Z}}}^{ \pm }\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} {\mathbf{p}} \cdot {{{\mathbf{B}}}^{{\mathbf{Z}}}}\left( \lambda \right), \\ {\text{B}}_{{\text{i}}}^{{\text{Z}}}\left( \lambda \right)\mathop = \limits^{{\text{def}}} \left[ {\lambda \in {{\Lambda }_{i}}} \right],\quad i \ne j \Rightarrow {{\Lambda }_{i}} \cap {{\Lambda }_{j}} = \emptyset , \\ 1 \leqslant i,j \leqslant 3, \\ \end{gathered} $(8)
$\begin{gathered} {\text{M}}_{{\text{Y}}}^{ \pm }(\lambda ,{\mathbf{p}})\mathop = \limits^{{\text{def}}} {\mathbf{p}} \cdot {{{\mathbf{B}}}^{{\mathbf{Y}}}}\left( \lambda \right), \\ \left\{ {\begin{array}{*{20}{c}} {{\text{B}}_{{\text{1}}}^{{\text{Y}}}(\lambda )\mathop = \limits^{{\text{def}}} 1} \\ {{\text{B}}_{{\text{2}}}^{{\text{Y}}}(\lambda )\mathop = \limits^{{\text{def}}} \sin \phi } \\ {{\text{B}}_{{\text{3}}}^{{\text{Y}}}(\lambda )\mathop = \limits^{{\text{def}}} \cos \phi } \end{array}} \right.,\quad \phi \mathop = \limits^{{\text{def}}} 2\pi \frac{{\lambda - {{\lambda }_{V}}}}{{{{\lambda }_{R}} - {{\lambda }_{V}}}}, \\ \end{gathered} $(9)
${\text{M}}_{{\text{L}}}^{ \pm }(\lambda ,{\mathbf{p}})\mathop = \limits^{{\text{def}}} {\mathbf{p}} \cdot {{{\mathbf{B}}}^{{\mathbf{L}}}}(\lambda ),\quad {{{\mathbf{B}}}^{{\mathbf{L}}}}(\lambda )\mathop = \limits^{{\text{def}}} {\mathbf{X}}(\lambda ).$Коэн был, вероятно, первым, кто построил линейную модель не аналитически, а численно – по набору доступных реальных спектральных данных (Cohen, 1964). Методом главных компонент он вычислил трехпараметрическую модель для спектров отражения 150 образцов цветового атласа Манселла, оцифрованных с шагом 10 нм, и показал, что она объясняет 99.18% их вариации.
Здесь следует заметить, что ценность спектральной модели для решения задач цветового анализа существенно зависит от ее размерности. В классическую обработку цветных цифровых изображений вовлекается три цветовых канала, в согласии с трихроматическим устройством зрительной системы человека. В таких конвейерах обработки изображений наибольшую ценность имеют модели с $\dim {\mathbf{p}} \leqslant 3$ (хотя для автоматических цветовых систем опознания, где в участии человека-эксперта нет необходимости, подобное ограничение размерности может стать препятствием их эффективности). По этой причине работа Коэна вызвала большой резонанс в профессиональном сообществе.
Впоследствии его данные были перепроверены несколькими авторами, увеличившими размер выборки (Maloney, Wandell, 1986б), уменьшившими шаг дискретизации (Parkkinen et al., 1989) и расширившими набор спектров за счет других атласов цветов (Vrhel et al., 1994). Их вывод оказался иным: число параметров линейной модели, обеспечивающее приемлемую точность аппроксимации расширенного набора атласов, составляет не три, а пять-семь, в зависимости от варианта постановки (Maloney, 1999).
Здесь следует отметить, что во всех упомянутых работах ставился вопрос о точности аппроксимации в спектральном пространстве. Очевидно, что если бы малопараметрическая спектральная модель была достаточно точной в этом смысле, то ее можно было бы использовать в алгоритмах цветовой константности; обратное же неверно. Приведем пример: если малопараметрическая модель обеспечивает большую ошибку аппроксимации в спектральном пространстве, но эта ошибка сосредоточена на краях видимого диапазона, то в цветовом пространстве подобная ошибка практически не окажет влияния ввиду низкой чувствительности сенсора в этих областях. Таким образом, вопрос практической адекватности трехпараметрических линейных моделей остается открытым.
Одним из главных недостатков трехпараметрических ЛСМ является принципиальная невозможность моделировать с приемлемой точностью спектры насыщенных цветов более чем трех цветовых тонов спектрального локуса стандартного наблюдателя. Это связано с тем, что цвета предельной насыщенности, лежащие на спектральном локусе, порождаются исключительно монохроматическими излучениями (и их парными комбинациями), каковые линейно независимы. В том числе по этой причине некоторые исследователи начали предлагать и изучать обстоятельства приемлемости и преимущества нелинейных спектральных моделей.
Наиболее известной среди них является гауссовская спектральная модель (ГСМ):
(10)
${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})\mathop = \limits^{{\text{def}}} {{p}_{1}}\exp \left( { - \frac{{{{{\left( {\lambda - {{p}_{3}}} \right)}}^{2}}}}{{2p_{2}^{2}}}} \right).$Гауссианы в качестве альтернативы линейным моделям были предложены, по-видимому, независимо Вайнбергом (Weinberg, 1976), П.П. Николаевым (Николаев, 1985), а также МакЛеодом и Гольцем (Macleod, Golz, 2003). При ${{p}_{2}} \to 0$ излучения со спектрами ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$ приближаются к монохроматическим с произвольной длиной волны, задаваемой ${{p}_{3}}$, что недостижимо для ЛСМ. Кроме того, ГСМ обеспечивает наглядную связь между параметрами модели и естественными характеристиками цвета. Параметры ${{p}_{1}}$, $1{\kern 1pt} {\text{/}}{{p}_{2}}$ и ${{p}_{3}}$ довольно хорошо характеризуют соответственно яркость, насыщенность и цветовой тон цветового отклика стандартного наблюдателя на гауссовский стимул (Николаев, 1985).
На рис. 2 изображена серия представителей модели ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$, отличающихся только параметром ${{p}_{1}}$ (“параметром яркости”), значения которого пробегают отрезок [0.05; 0.95] с шагом 0, 1. Остальные параметры неизменны: ${{p}_{2}} = 55$, ${{p}_{3}} = 510$. Цветности излучений с такими спектрами совпадают.
Рис. 2.
Примеры представителей гауссовской спектральной модели ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{1}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б − их цветность в этом базисе.
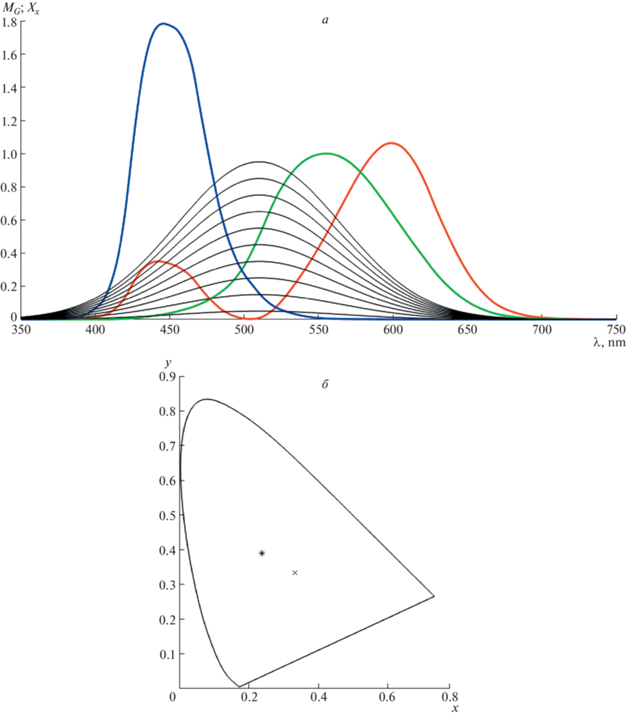
На фрагменте б рис. 2 звездочкой отмечен их образ на стандартной диаграмме цветности. Крестиком отмечена нейтральная (серая) точка.
На рис. 3 изображена серия представителей той же модели, отличающихся параметром ${{p}_{2}}$ (“параметром обратной насыщенности”), значения которого пробегают отрезок [5; 95] с шагом 10.
Рис. 3.
Примеры представителей гауссовской спектральной модели ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{2}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б – их цветность в этом базисе.
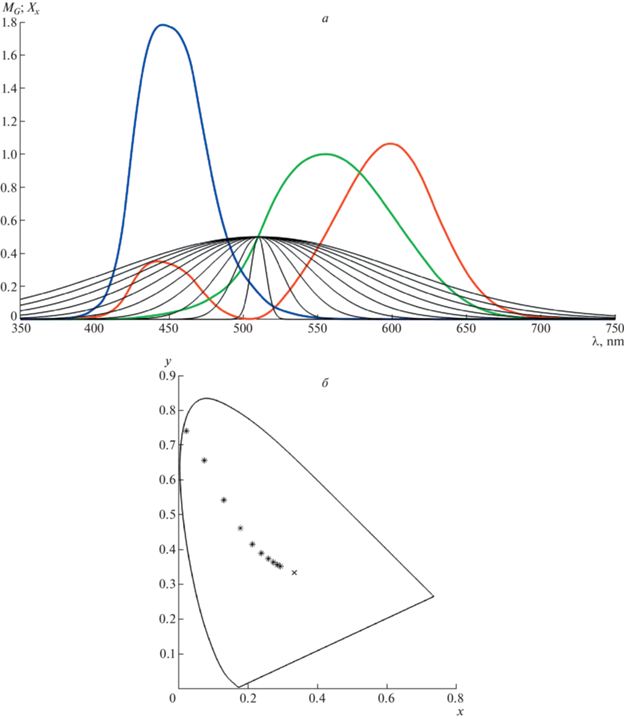
Остальные параметры фиксированы: ${{p}_{1}} = 0,5$, ${{p}_{3}} = 510$. На фрагменте б звездочками отмечены образы спектров серии на стандартной диаграмме цветности. По мере роста ${{p}_{2}}$ насыщенность цвета падает, а цветность спектра приближается к нейтральной точке (при этом изменение уменьшается с каждым шагом). Цветовой тон при этом изменяется незначительно: последовательность точек не сильно уклоняется от луча с началом в нейтральной точке.
На рис. 4 представлена заключительная серия спектров ГСМ. В этом случае параметр ${{p}_{3}}$ (“параметр тона”) принимает значения из отрезка [460; 640] с шагом 20. Оставшиеся параметры имеют следующие значения: ${{p}_{1}} = 0,5$, ${{p}_{2}} = 5$.
Рис. 4.
Примеры представителей гауссовской спектральной модели ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{3}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б − их цветность в этом базисе.

На фрагменте б звездочками отмечены образы спектров серии на стандартной диаграмме цветности. Видно, что цветности спектров близки к максимально насыщенным и покрывают практически весь спектральный локус.
Итак, одним из достоинств ГСМ является то, что модель адекватно аппроксимирует узкополосные спектры, тогда как никакая ЛСМ таким свойством не обладает. Но возможность аппроксимации сколь угодно узкополосных спектров еще не обеспечивает описание всевозможных цветов предельной насыщенности. Действительно, насыщенно пурпурные цвета могут быть реакцией только на излучения с мультимодальным спектральным распределением, т.е. никакой гауссовский спектр не моделирует излучение пурпурного цвета. На рис. 5 в различных цветовых координатах изображен цветовой охват модели ${{{\text{M}}}_{{\text{G}}}}$.
Рис. 5.
Хроматические диаграммы цветового тела базовой ГСМ в стандартной (CIE xyY) и равномерной (proLab) системах цветовых координат. Цветами показан цветовой охват sRGB, серый фон соответствует остальным цветам цветового конуса. Черным контуром ограничен цветовой охват всевозможных спектров из ${{{\text{M}}}_{{\text{G}}}}$.
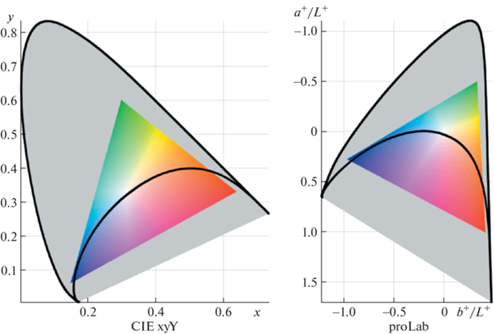
По диаграмме в равномерных цветовых координатах proLab (Konovalenko et al., 2021) можно судить, что значительная доля площади цветового треугольника недостижима для базовой ГСМ.
Для преодоления этого недостатка исследователи, включая авторов ГСМ, предложили несколько модификаций базовой модели. Так, Вейнберг (Weinberg, 1976), Николаевы (Николаев, Николаев, 1997), а также МакЛеод и Гольц (Macleod, Golz, 2003) предложили использовать выражение, являющееся в зависимости от знака ${{p}_{2}}$ члена либо гауссианой, либо обратной к ней функцией. Предложенную ими модель можно параметризовать, например, так
(11)
${{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} {{p}_{1}} + \exp \left( { - {{p}_{2}}{{{\left( {\lambda - {{p}_{3}}} \right)}}^{2}}} \right).$П.П. Николаев (Николаев, 2007б), а также Мизоками и Вебстер (Mizokami, Webster, 2012) предложили также “субтрактивную” модель ${{{\text{M}}}_{{{\text{G}} \updownarrow }}}$, в которую помимо гауссовских спектров ${{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$ входят спектры вида ${{p}_{1}} - {{{\text{M}}}_{{\text{G}}}}(\lambda ,{\mathbf{p}})$:
(12)
$\begin{gathered} {{{\text{M}}}_{{{\text{G}} \updownarrow }}}\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} \left[ {{{p}_{2}} < 0} \right]{{p}_{1}} + \\ \; + \left( {2\left[ {{{p}_{2}} \geqslant 0} \right] - 1} \right){{p}_{1}}\exp \left( { - {\text{|}}{{p}_{2}}{\text{|}}{{{\left( {\lambda - {{p}_{3}}} \right)}}^{2}}} \right), \\ \end{gathered} $(13)
$\begin{gathered} {{{\text{M}}}_{{{\text{G}} \circ }}}\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} \\ \; = {{p}_{1}}\exp \left( { - {{p}_{2}}{{{\left( {\left( {\lambda - {{p}_{3}} + {{\Delta }_{\lambda }}{\text{/}}2} \right)mod{{\Delta }_{\lambda }} - {{\Delta }_{\lambda }}{\text{/}}2} \right)}}^{2}}} \right), \\ \end{gathered} $На рис. 6 приведены представители всех трех упомянутых выше расширений ГСМ (${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$, ${{{\text{M}}}_{{{\text{G}} \updownarrow }}}$, и ${{{\text{M}}}_{{{\text{G}} \circ }}}$), соответствующие практически неразличимым между собой оттенкам пурпурного цвета.
Рис. 6.
Представители трех расширений ГСМ, использующихся для моделирования пурпурных цветов
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б – их цветность в этом базисе. Звездами обозначена модель ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$, ромбами – ${{{\text{M}}}_{{{\text{G}} \updownarrow }}}$, кружками – ${{{\text{M}}}_{{{\text{G}} \circ }}}$.
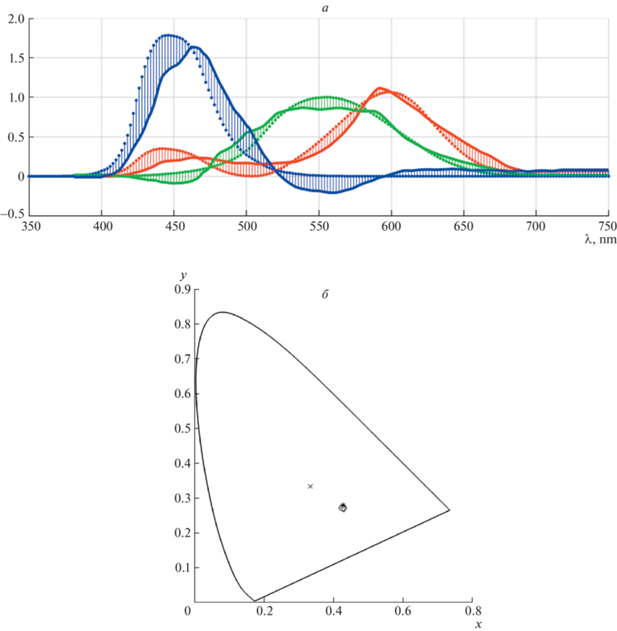
Вектора их параметров при этом равны ${{\left[ {\begin{array}{*{20}{c}} {0.15}&{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{{{95}}^{2}}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${{{{95}}^{2}}}$}}}&{520} \end{array}} \right]}^{T}}$, ${{\left[ {\begin{array}{*{20}{c}} {0.6}&{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{{{70}}^{2}}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${{{{70}}^{2}}}$}}}&{510} \end{array}} \right]}^{T}}$ и ${{\left[ {\begin{array}{*{20}{c}} 1&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{{{120}}^{2}}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${{{{120}}^{2}}}$}}}&{715} \end{array}} \right]}^{T}}$ соответственно.
Мизоками и Вебстер исследовали вопрос, является ли в сравнении с ЛСМ расширенная субтрактивная ГСМ ${{{\text{M}}}_{{{\text{G}} \updownarrow }}}$ достаточно хорошей аппроксимацией спектров отражения природных объектов (Mizokami, Webster, 2012). Для этого использовались распределения коэффициента отражения большого числа натуральных объектов, опубликованных к тому моменту в открытых базах данных. Количество достаточно точных гауссовских аппроксимаций оказалось сопоставимо с числом таковых в линейных моделях: в среднем на них приходилось 56% несоответствий по сравнению с 60% для протестированных линейных моделей. Значимым классом “плохих” для ГСМ оказались, что было довольно очевидно изначально, спектры с мультимодальным распределением.
В 2014 г. Мирзай и Фант сравнили цветовой охват всех трех обсуждаемых обобщений гауссиан на плоскости цветности стандартного наблюдателя (для излучений) и в цветовом теле стандартного источника света CIE D65 (для окрасок) (Mirzaei, Funt, 2014) и пришли к выводу, что наибольший охват демонстрируют “периодизованные” гауссианы ${{{\text{M}}}_{{{\text{G}} \circ }}}$. Кроме того, авторы заявили, что впервые предложили метод предсказания цвета неизвестной окраски под одним известным освещением по цвету, наблюдаемому под другим источником, основанный на гауссовской оценке окраски. Их исследование показало, что использование гауссовской модели в варианте ${{{\text{M}}}_{{{\text{G}} \circ }}}$ для спектров отражения ${\text{R}}(\lambda )$ при решении уравнения (3) дает в среднем более точные оценки, чем использование предложенных ранее линейных методов.
2. ИСПОЛЬЗОВАНИЕ ГАУССОВСКОЙ МОДЕЛИ В ЗАДАЧАХ ЦВЕТОВОГО АНАЛИЗА
Подход, в котором ценность спектральной модели определяется ее точностью при использовании в конкретных задачах цветового анализа, представляется, как минимум, разумным дополнением к теоретическим оценкам цветового охвата (в качестве репрезентативной оценки качества модели).
Рассмотрим общую часть рассмотренных в разд. 1 задач цветового анализа – оценить спектр ${\text{F}}(\lambda )$ наблюдаемого излучения по его цвету ${\mathbf{c}}$:
(14)
$\int\limits_0^\infty {{\text{F}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda = {\mathbf{c}}} ,$(15)
$\begin{gathered} {\text{F}}\left( \lambda \right) = {\mathbf{p}} \cdot {\mathbf{B}}\left( \lambda \right),\quad {\mathbf{p}} = {{A}_{{{\mathbf{BX}}}}}^{{ - 1}}{\mathbf{c}}, \\ {{A}_{{{\mathbf{BX}}}}}\mathop = \limits^{{\text{def}}} \int\limits_0^\infty {{{{\mathbf{B}}}^{T}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } . \\ \end{gathered} $Для ${\text{F}} \in \{ {{{\text{M}}}_{{{\text{G}} \divideontimes }}}\} $ аналитическое решение этой задачи в общем случае неизвестно. Построим приближенное решение и оценим его точность. Рассмотрим линейный сенсор со следующими функциями чувствительности:
(16)
$\begin{gathered} {{{\text{X}}}_{{\text{G}}}}_{{\text{i}}}\left( {\lambda ,\sigma ,\mu } \right)\mathop = \limits^{{\text{def}}} {{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{i}}}}} \right),\quad {{p}_{i}}_{1} = 1, \\ {{p}_{i}}_{2} = \sigma > 0,\quad {{p}_{i}}_{3} = {{\mu }_{i}}. \\ \end{gathered} $Будем называть его равноселективным гауссовским сенсором. Для такого сенсора задача определения параметров спектра из ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$ по реакциям на него имеет аналитическое решение. Пусть известен цвет ${\mathbf{c}}$ гауссовского спектра, регистрируемого равноселективным гауссовским сенсором
(17)
${\mathbf{c}} = \int\limits_0^\infty {{{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\left[ {\begin{array}{*{20}{c}} l&s&h \end{array}} \right]}}^{T}}} \right){{{\mathbf{X}}}_{{\mathbf{G}}}}(\lambda ,\sigma ,\mu )d\lambda } ,$(18)
$\left\{ {\begin{array}{*{20}{c}} {\frac{1}{s} = \frac{{\sum\limits_{i = 1}^3 {{\mu }_{i}}{{\mu }_{{\left( {i + 1} \right)mod3}}}({{\mu }_{i}} - {{\mu }_{{(i + 1)\;mod\;3}}})}}{{\left( {{{\mu }_{1}} - {{\mu }_{2}}} \right)\ln \left( {\frac{{{{c}_{3}}}}{{{{c}_{2}}}}} \right) + \left( {{{\mu }_{2}} - {{\mu }_{3}}} \right)\ln \left( {\frac{{{{c}_{1}}}}{{{{c}_{2}}}}} \right)}} - \frac{1}{\sigma }} \\ {h = \frac{{\left( {{{c}_{1}} - {{c}_{2}}} \right)\left( {s + \sigma } \right) + 2{{\mu }_{1}} + 2{{\mu }_{2}}}}{{2s\sigma \left( {{{\mu }_{1}} - {{\mu }_{2}}} \right)}}} \\ {l = \frac{{\sqrt {s + \sigma } \sum\limits_{i = 1}^3 {{c}_{i}}\exp \left( {\frac{{ - s\sigma {{{\left( {h - {{\mu }_{i}}} \right)}}^{2}}}}{{s + \sigma }}} \right)}}{{\sqrt \pi \sum\limits_{i = 1}^3 \exp \left( {\frac{{ - 2s\sigma {{{\left( {h - {{\mu }_{i}}} \right)}}^{2}}}}{{s + \sigma }}} \right)}}} \end{array}} \right..$Как стандартный наблюдатель, так и современные технические цветовые сенсоры не могут быть с достаточной точностью аппроксимированы моделью равноселективного гауссовского сенсора, однако хорошо приближаются моделью сенсора, связанного линейным преобразованием с равноселективным гауссовским.
Для оценки характеристик “улучшенного” сенсора решим такую оптимизационную задачу:
(19)
$\left\langle {{{A}_{x}},{{\sigma }_{x}},{{\mu }_{{\mathbf{x}}}}} \right\rangle = \mathop {arg{\kern 1pt} min}\limits_{\left\langle {A,\sigma ,\mu } \right\rangle } \parallel {\kern 1pt} A{{{\mathbf{X}}}_{{\mathbf{G}}}}\left( {\lambda ,\sigma ,\mu } \right) - {{{\mathbf{X}}}_{{\mathbf{x}}}}(\lambda ){\kern 1pt} {{\parallel }_{2}}.$Применим прямой метод оптимизации Нелдера–Мида (Nelder, Mead, 1965) по кортежу параметров $\langle \sigma ,\mu \rangle $, а оптимальную матрицу ${{A}_{i}}$ будем на каждой итерации $i$ искать аналитически методом наименьших квадратов. В качестве начального приближения возьмем $\sigma = 30$ и $\mu = {{\left[ {\begin{array}{*{20}{c}} {600}&{550}&{450} \end{array}} \right]}^{T}}$. За 1000 итераций получим следующее решение:
(20)
$\left\{ \begin{gathered} \begin{array}{*{20}{c}} {{{A}_{x}}}& = &{\left[ {\begin{array}{*{20}{c}} {1.1353}&{0.233}&{0.3116} \\ {0.5711}&{1.029}&{0.0655} \\ { - 0.0045}&{0.0226}&{1.7698} \end{array}} \right]} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{\sigma }_{x}}}& = &{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,24.94} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{\mu }_{x}}}& = &{{{{\left[ {\begin{array}{*{20}{c}} {600.4}&{544.4}&{451.0} \end{array}} \right]}}^{T}}} \end{array} \hfill \\ \end{gathered} \right.,$Решим ту же задачу для сенсора фотоаппарата Canon 5D Mark III с опубликованными значениями функции чувствительности ${{{\mathbf{X}}}_{{\mathbf{c}}}}(\lambda )$ (Smagina et al., 2020):
(21)
$\langle {{A}_{c}},{{\sigma }_{c}},{{\mu }_{{\mathbf{c}}}}\rangle = \mathop {arg{\kern 1pt} min}\limits_{\left\langle {A,\sigma ,\mu } \right\rangle } \parallel {\kern 1pt} A{{{\mathbf{X}}}_{{\mathbf{G}}}}(\lambda ,\sigma ,\mu ) - {{{\mathbf{X}}}_{{\mathbf{c}}}}(\lambda ){\kern 1pt} {{\parallel }_{2}}.$При тех же параметрах алгоритма получим следующее решение:
(22)
$\left\{ {\begin{array}{*{20}{c}} {{{A}_{c}}}& = &{\left[ {\begin{array}{*{20}{c}} {0.6311}&{0.0148}&{0.0168} \\ {0.1175}&{0.9962}&{0.1161} \\ {0.0576}&{ - 0.0232}&{0.6983} \end{array}} \right]} \\ {{{\sigma }_{c}}}& = &{35.06} \\ {{{\mu }_{c}}}& = &{{{{\left[ {\begin{array}{*{20}{c}} {601.2}&{535.7}&{471.6} \end{array}} \right]}}^{T}}} \end{array}} \right.$Чтобы качественно оценить величину погрешности, полученной в этих численных экспериментах, воспользуемся следующим соображением. Сенсоры фотоаппаратов изготавливаются так, чтобы функции чувствительности были как можно ближе к колориметрическим, т.е. линейно связанным с функциями стандартного наблюдателя ${{{\mathbf{X}}}_{{\mathbf{x}}}}(\lambda )$.
Найдем наилучшую линейную аппроксимацию ${{{\mathbf{X}}}_{{\mathbf{x}}}}(\lambda )$, используя функции чувствительности фотоаппарата в качестве базиса:
(23)
$A_{c}^{x} = \mathop {arg{\kern 1pt} min}\limits_A \parallel {\kern 1pt} A{{{\mathbf{X}}}_{{\mathbf{c}}}}\left( \lambda \right) - {{{\mathbf{X}}}_{{\mathbf{x}}}}\left( \lambda \right){\kern 1pt} {{\parallel }_{2}}.$Методом наименьших квадратов получим следующее решение:
(24)
$A_{c}^{x} = \left[ {\begin{array}{*{20}{c}} {1.6048}&{ - 0.0545}&{0.2997} \\ {0.6047}&{0.8246}&{ - 0.2531} \\ {0.1326}&{ - 0.4697}&{2.2337} \end{array}} \right],$Итак, реальный сенсор фотоаппарата можно считать эквивалентным равноселективному гауссовскому с точностью, почти в 4 раза превосходящей точность, с которой он может считаться колориметрическим (что необходимо для корректной цветопередачи). На рис. 7 результаты численных экспериментов представлены графически.
Рис. 7.
Линейная аппроксимация (а, в) функций чувствительности стандартного наблюдателя и (б) камеры Canon 5D Mark III, при использовании в качестве базиса (а, б) равноселективной гауссовской модели или (в) базиса камеры Canon 5D Mark III. Целевая функция отмечена точками, результат аппроксимации – сплошной линией. Красным, зеленым и синими цветами обозначены первая, вторая и третья компоненты вектора ${\mathbf{X}}(\lambda )$ соответственно.

Из иллюстрации ясно, что при гауссовской аппроксимации (а, б) в сравнении с колориметрической аппроксимацией сенсора камеры (в) не только выше точность, но и практически отсутствуют участки отрицательной чувствительности, т.е. гауссовская аппроксимация в рассмотренных случаях является физически адекватной.
Рассмотрим теперь задачу предсказания цветности окраски под эквиэнергетическим освещением по цвету, наблюдаемому под другим источником. Пусть известен цвет ${{{\mathbf{c}}}_{{\mathbf{s}}}}$ источника, определяемый следующим образом:
(25)
${{{\mathbf{c}}}_{{\mathbf{s}}}} = \int\limits_0^\infty {{\text{S}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } .$Положим также известным цвет ${{{\mathbf{c}}}_{{{\mathbf{sr}}}}}$ окраски под этим освещением, задаваемый согласно такому определению:
(26)
${{{\mathbf{c}}}_{{{\mathbf{sr}}}}} = \int\limits_0^\infty {{\text{S}}\left( \lambda \right){\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } .$Требуется оценить цветность ${{{\mathbf{c}}}_{{\mathbf{r}}}}$ этой окраски под эквиэнергетическим освещением:
(27)
${{{\mathbf{c}}}_{{\mathbf{r}}}} = \frac{{\int\limits_0^\infty {{\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } }}{{{{{\left\| {\int\limits_0^\infty {{\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda } } \right\|}}_{2}}}}.$Сформулируем алгоритм гауссовской оценки окраски по цвету (ГООЦ) для предсказания цветности окраски ${{{\mathbf{c}}}_{{\mathbf{r}}}}$ (выражение (27)) под эквиэнергетическим освещением по цвету ${{{\mathbf{c}}}_{{{\mathbf{sr}}}}}$ (выражение (26)), наблюдаемому под другим источником, при известном цвете ${{{\mathbf{c}}}_{{\mathbf{s}}}}$ источника (выражение (25)). Параметры $\langle {{A}_{c}},{{\sigma }_{c}},{{\mu }_{{\mathbf{c}}}}\rangle $ оптимальной гауссовской аппроксимации чувствительности сенсора считаем вычисленными заранее.
1. Аппроксимация спектральных стимулов в гауссовской модели. Зная $\langle {{\sigma }_{c}},{{\mu }_{{\mathbf{c}}}}\rangle $, подставим ${{A}_{c}}^{{ - 1}}{{{\mathbf{c}}}_{{\mathbf{s}}}}$ в (18) и получим параметры ${{{\mathbf{p}}}_{{\mathbf{s}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{l}_{s}}}&{{{s}_{s}}}&{{{h}_{s}}} \end{array}} \right]}^{T}}$ спектра ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}(\lambda ,{{{\mathbf{p}}}_{{\mathbf{s}}}})$, аппроксимирующего спектр ${\text{S}}(\lambda )$. Аналогично получим параметры ${{{\mathbf{p}}}_{{{\mathbf{sr}}}}} = {{\left[ {\begin{array}{*{20}{c}} {{{l}_{{sr}}}}&{{{s}_{{sr}}}}&{{{h}_{{sr}}}} \end{array}} \right]}^{T}}$ спектра ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}(\lambda ,{{{\mathbf{p}}}_{{{\mathbf{sr}}}}})$, аппроксимирующего спектр ${\text{S}}(\lambda )\;{\text{R}}(\lambda )$.
2. Оценивание спектральной компоненты окраски. Найдем параметры ${{{\mathbf{p}}}_{{\mathbf{r}}}}$ гауссовского спектра такие, что ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{r}}}}} \right) \propto \frac{{{{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\mathbf{p}}}_{{{\mathbf{sr}}}}}} \right)}}{{{{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{s}}}}} \right)}}$. (Здесь знак $ \propto $ обозначает пропорциональность.) Для этого положим ${{{\mathbf{p}}}_{{\mathbf{r}}}} = {{\left[ {\begin{array}{*{20}{c}} 1&{{{s}_{{sr}}} - {{s}_{s}}}&{\frac{{{{h}_{{sr}}}\;{{s}_{{sr}}} - {{h}_{s}}\;{{s}_{s}}}}{{{{s}_{{sr}}} - {{s}_{s}}}}} \end{array}} \right]}^{T}}$.
3. Оценивание цветности окраски под эквиэнергетическим освещением. Подставим ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{r}}}}} \right)$ в качестве ${\text{R}}(\lambda )$ в (27) и вычислим оценку ${{{\mathbf{c}}}_{{\mathbf{r}}}}$ численным интегрированием.
Для сравнения возьмем алгоритм, решающий ту же задачу, но в варианте использования ЛСМ. Алгоритм состоит из тех же трех шагов, что и алгоритм ГООЦ:
1. Аппроксимация спектральных стимулов в ЛСМ. Вычислим параметры ${{{\mathbf{p}}}_{{\mathbf{s}}}}$ спектра ${\text{M}}_{{\mathbf{B}}}^{ \pm }(\lambda ,{{{\mathbf{p}}}_{{\mathbf{s}}}})$, аппроксимирующего спектр ${\text{S}}(\lambda )$, пользуясь соотношением (15). Аналогично вычислим параметры ${{{\mathbf{p}}}_{{{\mathbf{sr}}}}}$ спектра ${\text{M}}_{{\mathbf{B}}}^{ \pm }(\lambda ,{{{\mathbf{p}}}_{{{\mathbf{sr}}}}})$, аппроксимирующего спектр ${\text{S}}(\lambda )\;{\text{R}}(\lambda )$.
2. Оценивание спектральной компоненты окраски. Оценим ${\text{R}}(\lambda )$ численным делением ${\text{R}}(\lambda ) = \frac{{{\text{M}}_{{\mathbf{B}}}^{ \pm }\left( {\lambda ,{{{\mathbf{p}}}_{{{\mathbf{sr}}}}}} \right)}}{{{\text{M}}_{{\mathbf{B}}}^{ \pm }\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{s}}}}} \right)}}$ (${\text{R}}\left( \lambda \right) \notin \left\{ {{\text{M}}_{{\mathbf{B}}}^{ \pm }} \right\}$).
3. Оценивание цветности окраски под эквиэнергетическим освещением. Получим ${{{\mathbf{c}}}_{{\mathbf{r}}}}$ согласно (27) численным интегрированием.
В качестве оценки точности алгоритма, испытанного на множестве пар $\langle {{{\text{S}}}_{i}}(\lambda ),{{{\text{R}}}_{i}}(\lambda )\rangle $, будем вычислять отношение средней ошибки оценки цветности тривиального алгоритма к средней ошибке оценки цветности испытываемого алгоритма. Под результатом тривиального алгоритма станем понимать цвет, совпадающий по цветности с наблюдаемым под освещением ${{{\text{S}}}_{i}}(\lambda )$ (так называемая аконстантная оценка), а координаты цветности $(\alpha ,\beta )$ определим следующим образом:
(28)
$\left[ {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right]\mathop = \limits^{{\text{def}}} \left[ {\begin{array}{*{20}{c}} {\frac{{ - 1}}{{3\sqrt 2 }}}&{\frac{{ - 1}}{{3\sqrt 2 }}}&{\frac{{\sqrt 2 }}{3}} \\ {\frac{1}{{\sqrt 6 }}}&{\frac{{ - 1}}{{\sqrt 6 }}}&0 \end{array}} \right]{\mathbf{c}}.$Для численных экспериментов были взяты 170 спектров отражения “естественных окрасок” (natural colorants) и 355 спектров отражения “окрасок Кринова” (Krinov colorants) из базы Лаборатории вычислительного зрения Университета им. С. Фрезера, Канада (http://www.cs.sfu.ca/colour). Дополнительный набор данных был любезно предоставлен В.В. Максимовым (Институт проблем передачи информации им. А.А. Харкевича РАН). Он состоял из 27 спектров отражения бумаги с нанесенной типографской краской различных цветов. Для моделирования источников света из базы Лаборатории вычислительного зрения были выбраны четыре спектра “естественных источников” с максимально различающихся цветностью. Дополнительно были смоделированы 11 планковских источников с цветовой температурой от 20 до 300 тысяч градусов Кельвина.
Результаты измерения точности рассматриваемых алгоритмов на различных комбинациях наборов данных сведены в табл. 1.
Таблица 1.
Результаты сравнения точности спектральных моделей в задаче оценки окраски по цвету. Жирным шрифтом выделены значения метрики, меньшие единицы
| $\{ {\text{S}}(\lambda )\} $ | $\{ {\text{R}}(\lambda )\} $ | ${\mathbf{X}}(\lambda )$ | Модель | ||
|---|---|---|---|---|---|
| ${\text{M}}_{{\text{L}}}^{ \pm }$ | ${\text{M}}_{{\text{Z}}}^{ \pm }$ | ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$ | |||
| P | K | H | 0.23 | 0.078 | 5.1 |
| C | 5.0 | 9.1 | 7.3 | ||
| M | H | 0.37 | 0.33 | 3.4 | |
| C | 5.1 | 10.0 | 8.0 | ||
| N | H | 0.080 | 0.18 | 5.7 | |
| C | 3.7 | 7.2 | 13.0 | ||
| N | K | H | 1.6 | 4.2 | 3.3 |
| C | 3.5 | 6.5 | 3.2 | ||
| M | H | 1.4 | 2.5 | 2.5 | |
| C | 4.0 | 6.5 | 4.3 | ||
| N | H | 0.41 | 4.0 | 4.7 | |
| C | 3.1 | 5.5 | 5.6 | ||
Алгоритм, использующий ЛСМ, был протестирован с двумя моделями, рассмотренными в разд. 1: зональной ${\text{M}}_{{\text{Z}}}^{ \pm }$ и моделью Ли ${\text{M}}_{{\text{L}}}^{ \pm }$. В первой колонке таблицы символ “P” обозначает набор планковских, а “N” – естественных источников света. Во второй колонке символ “K” обозначает набор Кринова, “М” – Максимова, а “N” – “естественных” окрасок. В третьей колонке символ “H” обозначает зрительную систему человека, а “C” – фотокамеру. Вывод очевиден: только ГСМ дала улучшение оценки (метрика больше единицы) в каждом из экспериментов.
На рис. 8 проиллюстрирован разброс оценок цветности при использовании каждой из трех сравниваемых спектральных моделей в эксперименте с естественными источниками света, “естественными” окрасками и фотокамерой.
Рис. 8.
Сравнение точности решения задачи цветовой константности при известной цветности источника в зависимости от используемой спектральной модели
а – модели Ли; б – зональной; в – гауссовской.

Красным цветом обозначены координаты ошибки цветности при применении алгоритма, черным – ошибки при использовании аконстантной оценки в качестве ответа (“наивный” подход).
3. ИСПОЛЬЗОВАНИЕ СКЛАДОК ДЛЯ ОЦЕНКИ ЦВЕТНОСТИ ОСВЕЩЕНИЯ И ФОНМИЗЕСОВСКАЯ СПЕКТРАЛЬНАЯ МОДЕЛЬ
Рассмотрим следующий класс спектральных моделей:
(29)
${\text{M}}_{{\mathbf{B}}}^{ \divideontimes }(\lambda ,{\mathbf{p}})\mathop = \limits^{{\text{def}}} \exp \left( { - {\mathbf{p}} \cdot {\mathbf{B}}\left( \lambda \right)} \right),\quad {{{\text{B}}}_{{\text{1}}}}(\lambda ) = 1,$Любая модель, представленная в виде (29), замкнута относительно перемножения элементов и умножения на неотрицательное число. Назовем представителей этого класса мультипликативно замкнутыми спектральными моделями (МЗСМ). Для любой МЗСМ в параметризации (29) выполняется следующее свойство:
(30)
${\text{M}}_{{\mathbf{B}}}^{ \divideontimes }\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{1}}}}} \right){\text{M}}_{{\mathbf{B}}}^{ \divideontimes }\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{2}}}}} \right) = {\text{M}}_{{\mathbf{B}}}^{ \divideontimes }\left( {\lambda ,{{{\mathbf{p}}}_{{\mathbf{1}}}} + {{{\mathbf{p}}}_{{\mathbf{2}}}}} \right),$Еще одним замечательным свойством семейства МЗСМ является то, что все их элементы – спектры (т.е. неотрицательные функции). Кроме того, у МЗСМ с неотрицательным базисом ${\mathbf{B}}(\lambda ) \geqslant 0$ конус неотрицательных параметров ${\mathbf{p}} \geqslant 0$ соответствует физически осмысленным окраскам $\left( {0 \leqslant {\text{M}}_{{\mathbf{B}}}^{ \divideontimes }\left( {\lambda ,{\mathbf{p}}} \right) \leqslant 1} \right)$.
Модель ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$ можно переписать как МЗСМ с полиномиальным базисом, при этом изменится параметризация модели, но никак не множество ее спектральных элементов (${{p}_{1}} > 0$). Будем обозначать такую параметризацию ${\text{M}}_{{\text{G}}}^{ \divideontimes }$:
(31)
$\begin{gathered} {\text{M}}_{{\text{G}}}^{ \divideontimes }\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} \exp \left( { - {\mathbf{p}} \cdot {{{\mathbf{B}}}^{{\mathbf{G}}}}\left( \lambda \right)} \right), \\ {\text{B}}_{i}^{{\text{G}}}\left( \lambda \right) = {{\lambda }^{{i - 1}}},\quad 1 \leqslant i \leqslant 3. \\ \end{gathered} $Ни ${{{\text{M}}}_{{{\text{G}} \updownarrow }}}$, ни ${{{\text{M}}}_{{{\text{G}} \circ }}}$ подобным свойством не обладают.
Из рассмотренных выше спектральных моделей перепараметризацию в виде МЗСМ допускает также линейная ЗСМ ${\text{M}}_{{\text{Z}}}^{ \pm }$ при условии, что ее базисные множества покрывают всю полупрямую длин волн. Ее мультипликативно замкнутый вариант обозначим ${\text{M}}_{{\text{Z}}}^{ \divideontimes }$:
(32)
$\begin{gathered} {\text{M}}_{{\text{Z}}}^{ \divideontimes }\left( {\lambda ,p} \right)\mathop = \limits^{{\text{def}}} \exp \left( { - p \cdot {{B}^{Z}}(\lambda )} \right), \\ \left\{ {\begin{array}{*{20}{c}} {B_{1}^{Z}(\lambda )}&{\mathop = \limits^{{\text{def}}} }&1 \\ {B_{2}^{Z}(\lambda )}&{\mathop = \limits^{{\text{def}}} }&{[\lambda \in {{\Lambda }_{2}}],\quad {{\Lambda }_{2}} \cap {{\Lambda }_{3}} = \emptyset } \\ {B_{3}^{Z}(\lambda )}&{\mathop = \limits^{{\text{def}}} }&{[\lambda \in {{\Lambda }_{3}}]} \end{array}} \right., \\ \end{gathered} $Заметим, что в эксперименте по оцениванию окраски по цвету, описанному в разд. 2, ЗСМ отстала от ГСМ незначительно, а линейная модель, не сводимая к МЗСМ, показала существенно менее стабильный результат. Можно предположить, что часть выбросов в оценках связаны с операцией деления неточно известных спектров. При численном делении, неизбежном при использовании ЛСМ, могут возникать большие ошибки в тех областях спектра, где деноминатор мал. Отношение же двух элементов МЗСМ вычисляется аналитически и является в некотором смысле регуляризованным.
Вернемся теперь к первой части задачи цветовой константности, а именно – к оценке цветности источника. Одним из возможных способов решения этой задачи является использование эффекта переотражения света, возникающего в складках. Описать его можно на примере, приведенном в пионерской работе 1971 г. (Нюберг и др., 1971а). В ней рассматривалась объемная сцена, освещенная единственным источником, а конфигурация поверхности тестового объекта была складчатой, и в освещение отдельных ее точек существенный вклад вносили рефлексы от других участков той же поверхности. Экспериментально было показано, что наличие складок на наблюдаемой поверхности дает человеку достаточные признаки реальной цветности освещения даже в отсутствие всех других (не исключая и вполне достаточных признаков, получаемых от бликующих объектов, что методически достигалось отсутствием зеркальных отражений в направлении наблюдателя). Благодаря возникающим в результате переотражений в глубине складок более насыщенным цветам испытуемые уверенно отличали красную гофрированную поверхность, освещенную белым светом, от белой поверхности, освещенной красным светом. Пары спектров были подобраны таким образом, что при однократном отражении цвет тестовых объектов колориметрически совпадал:
где обозначает отсутствие пропорциональности, ${{{\text{S}}}_{i}}(\lambda )$ – спектральный состав освещения в i-м варианте предъявления, а ${{{\text{R}}}_{i}}(\lambda )$ – спектральное распределение коэффициента отражения поверхности в нем же. Подбор
колориметрического совпадения цветов тестовых объектов подтверждался контрольным экспериментом,
в котором испытуемые не могли различить те же два варианта сцены – при условии ровной
(плоской и гладкой) поверхности объектов. Покажем возможность построения алгоритма
технического зрения, обеспечивающего численную оценку цветности источника, основываясь
на этом эффекте.
обозначает отсутствие пропорциональности, ${{{\text{S}}}_{i}}(\lambda )$ – спектральный состав освещения в i-м варианте предъявления, а ${{{\text{R}}}_{i}}(\lambda )$ – спектральное распределение коэффициента отражения поверхности в нем же. Подбор
колориметрического совпадения цветов тестовых объектов подтверждался контрольным экспериментом,
в котором испытуемые не могли различить те же два варианта сцены – при условии ровной
(плоской и гладкой) поверхности объектов. Покажем возможность построения алгоритма
технического зрения, обеспечивающего численную оценку цветности источника, основываясь
на этом эффекте.
Известно (Nikolaev, Nikolaev, 2004), что оптическое изображение однородно окрашенного объекта с учетом конечного числа переотражений можно записать следующим образом:
(34)
$\begin{gathered} {\text{F}}\left( {\lambda ,x,y} \right) = \sum\limits_{i = 1}^n {{{\text{g}}}_{i}}\left( {x,y} \right){{{\text{S}}}_{{{{z}_{i}}}}}\left( \lambda \right){{{\text{R}}}_{{1,{{r}_{i}}}}}\left( \lambda \right) \times \\ \times \;\prod\limits_{j = 1}^{{{m}_{i}}} {{{\text{R}}}_{{{{p}_{{i,j}}},{{q}_{{i,j}}}}}}\left( \lambda \right), \\ \end{gathered} $Будем рассматривать однородно окрашенную унихроматическую складку. Последнее уточнение имеет своей целью не упрощение задачи, а сосредоточение на наиболее интересном случае. Действительно, наличие в сцене дихроматических (глянцевых, бликующих) поверхностей позволяет установить цветность источника вне зависимости от наличия складок. Пусть также в сцене присутствует только один доминирующий источник света со спектральным составом ${\text{S}}(\lambda )$, цветность которого и требуется установить. При таких ограничениях выражение (34) упростится до следующего:
(35)
${\text{F}}\left( {\lambda ,x,y} \right) = \sum\limits_{i = 1}^n {{{\text{g}}}_{i}}\left( {x,y} \right){\text{S}}\left( \lambda \right){{{\text{R}}}^{i}}\left( \lambda \right),$Пусть R – элемент МЗСМ. Тогда ${{{\text{R}}}^{i}}(\lambda )$ при $i \in {\mathbf{N}}$ – элементы той же МЗСМ, причем векторы их параметров ${{\left[ {\begin{array}{*{20}{c}} {{{p}_{2}}}&{{{p}_{3}}} \end{array}} \right]}^{T}}$ в параметризации (29) лежат на одной прямой, проходящей через 0. Предположим дополнительно, что ${{{\text{g}}}_{i}}(x,y)$ и ${\text{R}}(\lambda )$ таковы, что практически приемлемым является следующее приближение:
(36)
$\begin{gathered} \tilde {R}\left( \lambda \right) = \sum\limits_{i = 1}^n {{{\text{g}}}_{i}}\left( {x,y} \right){{{\text{R}}}^{i}}\left( \lambda \right) \approx \\ \approx {\text{g}}\left( {x,y} \right){{{\text{R}}}^{{\alpha (x,y)}}}\left( \lambda \right) = \hat {R}\left( \lambda \right), \\ \end{gathered} $Чем ценно приближение (36)? Если оно адекватно, то будет работоспособен следующий алгоритм (Nikolaev, Nikolaev, 2007): зафиксируем МЗСМ; найдем на изображении сцены две складки разной окраски; для цвета каждого пикселя каждой из них оценим спектр и его параметры $\langle {{p}_{2}},{{p}_{3}}\rangle $; аппроксимируем получившиеся две выборки прямыми; построим спектр с параметрами, соответствующими точке пересечения этих прямых (${{p}_{1}}$ при этом положим равным 1); цветность излучения с получившимся спектром примем в качестве оценки точности источника.
Оценим, насколько приближение (36) неточно при использовании ГСМ. В качестве метрики ошибки будем использовать относительную ошибку e по норме ${{L}_{2}}$:
(37)
$e = \frac{{\int\limits_0^\infty {{{{(\tilde {R}\left( \lambda \right) - \hat {R})}}^{2}}d\lambda } }}{{\int\limits_0^\infty {{{{\tilde {R}}}^{2}}\left( \lambda \right)d\lambda } }},$Очевидно, что приближение (36) будет иметь высокую точность, если ряд коэффициентов g спадает достаточно быстро. Рассмотрим более интересный вариант. Пусть ${{{\text{g}}}_{i}}(x,y) = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{{2}^{{i - 1}}}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${{{2}^{{i - 1}}}}$}}$. В этом случае половина освещенности в наблюдаемой точке создается вторичными источниками – сторонами складки. Воспользуемся параметризацией ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$ (согласно определению (11)). Пусть параметры гауссианы R равны ${{\left[ {\begin{array}{*{20}{c}} 1&{1 \times {{{10}}^{{ - 4}}}}&{510} \end{array}} \right]}^{T}}$. При этом наилучшая по e аппроксимация $\hat {R}$ имеет параметры ${{\left[ {\begin{array}{*{20}{c}} {1.937}&{1.506 \times {{{10}}^{{ - 4}}}}&{510} \end{array}} \right]}^{T}}$, а относительная ошибка e составляет менее 4%. На рис. 9 изображены соответствующие спектры $\tilde {R}$ и $\hat {R}$, а также их разность.
Рис. 9.
Пример аппроксимации суммы степенного ряда гауссиан одной гауссианой. Пунктиром обозначен спектр $\tilde {R}$, сплошной линией – его аппроксимация $\hat {R}$, штриховой линией – их разность. Цветными линиями для сравнения обозначены функции чувствительностей ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя.
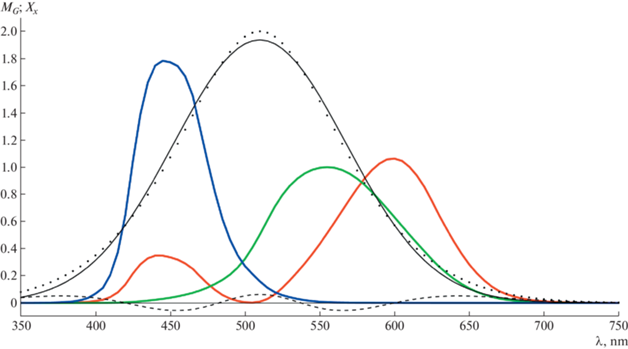
Как видно из рисунка и по значению $e$, исследуемая аппроксимация имеет высокую точность при выбранных параметрах, что является аргументом для использования ГСМ в алгоритмах оценивания цветности источника по изменению цвета в складках. Однако в разд. 1 обсуждалось, что модель ${{{\text{M}}}_{{{\text{G}} \divideontimes }}}$ существенно уступает по цветовому охвату другим спектральным гауссоподобным моделям, не являющимся МЗСМ. Возникает вопрос: существует ли МЗСМ, имеющая параметры цветового охвата, сопоставимые с ${{{\text{M}}}_{{{\text{G}} \circ }}}$, и при этом удовлетворяющая приближению (36)?
Рассмотрим МЗСМ ${\text{M}}_{{\text{M}}}^{ \divideontimes }$ с базисом, совпадающим с ЛСМ Илмаза:
(38)
$\begin{gathered} {\text{M}}_{{\text{M}}}^{ \divideontimes }(\lambda ,{\mathbf{p}})\mathop = \limits^{{\text{def}}} \exp \left( { - {\mathbf{p}} \cdot {{{\mathbf{B}}}^{{\mathbf{M}}}}(\lambda )} \right), \\ \left\{ \begin{gathered} {\text{B}}_{{\text{1}}}^{{\text{M}}}(\lambda )\mathop = \limits^{{\text{def}}} 1 \hfill \\ {\text{B}}_{{\text{2}}}^{{\text{M}}}(\lambda )\mathop = \limits^{{\text{def}}} \sin \phi , \hfill \\ {\text{B}}_{{\text{3}}}^{{\text{M}}}(\lambda )\mathop = \limits^{{\text{def}}} \cos \phi \hfill \\ \end{gathered} \right.\quad \phi \mathop = \limits^{{\text{def}}} 2\pi \frac{{\lambda - {{\lambda }_{V}}}}{{{{\lambda }_{R}} - {{\lambda }_{V}}}}, \\ \end{gathered} $(39)
$\begin{gathered} {{{\text{M}}}_{{\text{M}}}}\left( {\lambda ,{\mathbf{p}}} \right)\mathop = \limits^{{\text{def}}} {{p}_{1}}\exp \left( {{{p}_{2}}\;\cos (\phi - {{p}_{3}}) - {{p}_{2}}} \right), \\ \;\phi \mathop = \limits^{{\text{def}}} 2\pi \frac{{\lambda - {{\lambda }_{V}}}}{{{{\lambda }_{R}} - {{\lambda }_{V}}}}. \\ \end{gathered} $На рис. 10 изображена серия представителей модели ${{{\text{M}}}_{{\text{M}}}}(\lambda ,{\mathbf{p}})$, отличающихся только параметром ${{p}_{1}}$ (“параметром яркости”), значения которого пробегают отрезок [0.05; 0.95] с шагом 0.1.
Рис. 10.
Элементы ФСМ в натуральной параметризации ${{{\text{M}}}_{{\text{M}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{1}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б – их цветность в этом базисе.
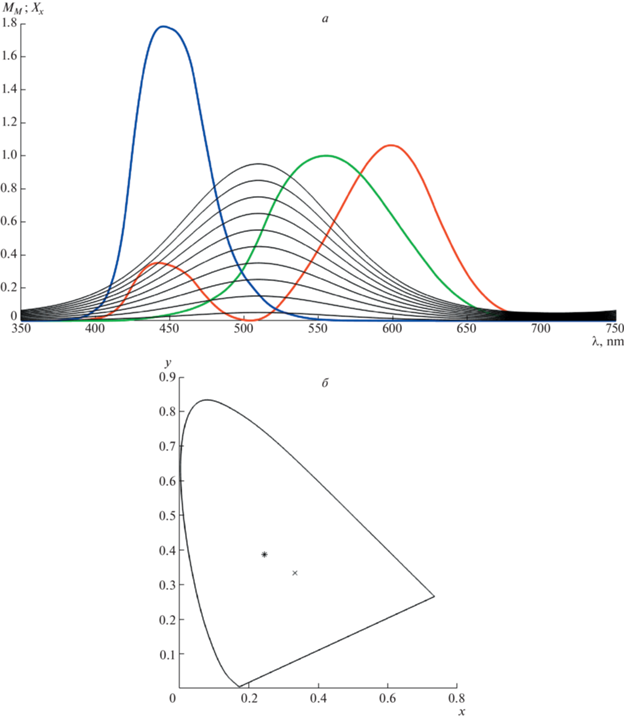
Остальные параметры неизменны: ${{p}_{2}} = 1.5$, ${{p}_{3}} = 2.5$. Цветности излучений с такими спектрами, очевидно, совпадают. На фрагменте б рис. 11 звездочкой отмечен их образ на стандартной диаграмме цветности. Крестиком отмечена нейтральная (серая) точка.
На рис. 11 изображена серия представителей той же модели, отличающихся параметром ${{p}_{2}}$ (“параметром насыщенности”).
Рис. 11.
Элементы ФСМ в натуральной параметризации ${{{\text{M}}}_{{\text{M}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{2}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б − их цветность в этом базисе.
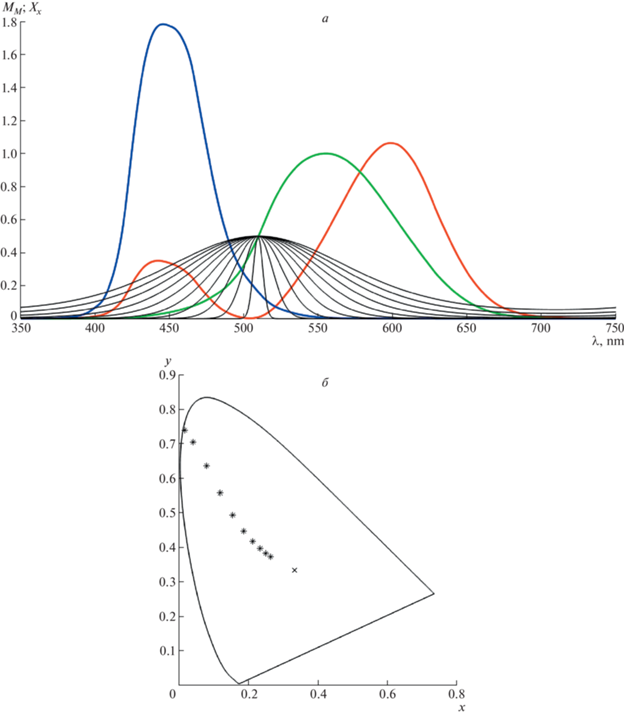
Величина ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {p_{2}^{2}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${p_{2}^{2}}$}}$ пробегает здесь отрезок $[0.05;\;0.95]$ с шагом 0, 1. Остальные параметры фиксированы: ${{p}_{1}} = 0.5$, ${{p}_{3}} = 2.5$. На фрагменте б рис.11 звездочками отмечены образы спектров серии на стандартной диаграмме цветности. По мере уменьшения ${{p}_{2}}$ насыщенность цвета падает, а цветность спектра приближается к нейтральной точке (при этом изменение уменьшается с каждым шагом). Цветовой тон в серии изменяется незначительно: последовательность точек не сильно уклоняется от луча с началом в нейтральной точке.
На рис. 12 представлена заключительная серия спектров ФСМ. В этом случае параметр ${{p}_{3}}$ (“параметр тона”) принимает значения из отрезка [0; 1.8π] с шагом $0.2{\kern 1pt} \pi $.
Рис. 12.
Элементы ФСМ в натуральной параметризации ${{{\text{M}}}_{{\text{M}}}}(\lambda ,{\mathbf{p}})$, отличающиеся только параметром ${{p}_{3}}$
а – спектральные функции на фоне базиса ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя, б − их цветность в этом базисе.

Оставшиеся параметры имеют следующие значения: ${{p}_{1}} = 0.5$, ${{p}_{2}} = 50$. На фрагменте б рис. 12 звездочками отмечены образы спектров серии на стандартной диаграмме цветности. Нетрудно заметить, что цветности спектров близки к максимально насыщенным и покрывают не только спектральный локус, но и отрезок, замыкающий локус пурпурных цветов. Таким образом, ФСМ можно считать еще одним приближенным расширением ГСМ на область пурпурных цветов. Из рассмотренных ранее расширений ${\text{M}}_{{\text{M}}}^{ \divideontimes }$ ближе всего к ${{{\text{M}}}_{{{\text{G}} \circ }}}$. Они обе построены на “замыкании” видимого диапазона в кольцо и обе не в точности совпадают с ГСМ на области ее определения. При этом ${{{\text{M}}}_{{{\text{G}} \circ }}}$ не является МЗСМ и для нее не существует способа аналитического пересчета спектров при учете параметров освещения.
Вернемся к анализу мультипликативного приближения эффективного спектра отражения в складке (36). Как и при использовании ГСМ, положим ${{{\text{g}}}_{i}}(x,y) = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{{2}^{{i - 1}}}}}}\right.\kern-0em} \!\lower0.7ex\hbox{${{{2}^{{i - 1}}}}$}}$. В отличие от ГСМ, для ФСМ ошибка (37) инвариантна только относительно изменения ${{p}_{1}}$ и ${{p}_{3}}$, но никак не ${{p}_{2}}$. Рассмотрим поэтому худший случай. Параметры R, максимизирующие ошибку e, для ФСМ в натуральной параметризации равны ${{\left[ {\begin{array}{*{20}{c}} 1&{1.1428}&{2.5133} \end{array}} \right]}^{T}}$. Для такого R наилучшая по e аппроксимация $\hat {R}$ имеет параметры ${{\left[ {\begin{array}{*{20}{c}} {1.925}&{1.6767}&{2.5133} \end{array}} \right]}^{T}}$, а относительная ошибка e составляет немногим более 4.6%. На рис. 13 изображены соответствующие спектры $\tilde {R}$ и $\hat {R}$, а также их разность.
Рис. 13.
Пример аппроксимации суммы ряда элементов ФСМ одним распределением фон Мизеса. Пунктиром обозначен спектр $\tilde {R}$, сплошной линией – его аппроксимация $\hat {R}$, штриховой линией – их разность. Цветными линиями для сравнения обозначены функции чувствительностей ${{{\mathbf{X}}}_{{\mathbf{x}}}}$ стандартного наблюдателя.

Вполне наглядно, что поведение остаточной ошибки у ГСМ и ФСМ схожи, а величина ошибки у ФСМ незначительно выше.
Приведем здесь еще одно подтверждение тому, что аппроксимация (36) имеет практическое значение. В работе (Gusamutdinova et al., 2017) были измерены спектральные яркости набора тканевых складок. Для каждой точки складки были рассчитаны цвета CIE XYZ стандартного наблюдателя. Для каждого цвета были найдены параметры $\left\langle {q1{\kern 1pt} ',q2{\kern 1pt} ',q3{\kern 1pt} '} \right\rangle $ спектра ФСМ, имеющего такой же цвет. (Использованная в работе (Gusamutdinova et al., 2017) параметризация ФСМ аффинно подобна введенной выше натуральной параметризации.) На рис. 14 приведены полученные (численной оценкой) распределения.
Рис. 14.
Экспериментальная проверка точности выполнения основного предположения алгоритма оценивания цветности источника с опорой на складки. На плоскости параметров $\langle q2{\kern 1pt} ',q3{\kern 1pt} '\rangle $ ФСМ отрезками отмечены линейные модели цветовых распределений реальных складок тканей различных окрасок. Звездой отмечена точка, соответствующая цветности источника. Иллюстрация взята из работы (Gusamutdinova et al., 2017).

Нетрудно заметить, что при использовании ФСМ основное предположение алгоритма оценивания цветности источника с опорой на складки выполнено: цветовые распределения достаточно точно оцениваются отрезками прямых, проходящих через точку, соответствующую цветности источника.
Сравним теперь ФСМ с ранее известными моделями по цветовому охвату. Ограничимся моделями ${\text{M}}_{{\text{Z}}}^{ \divideontimes }$, ${\text{M}}_{{\text{G}}}^{ \divideontimes }$, ${\text{M}}_{{\text{M}}}^{ \divideontimes }$ и ${{{\text{M}}}_{{{\text{G}} \circ }}}$ и будем исследовать два вопроса. Во-первых, оценим, какая область цветового треугольника достижима спектрами, удовлетворяющими той или иной модели. Излучения с цветностью, лежащей вне этой области, не могут быть адекватно промоделированы соответствующей спектральной моделью. Во-вторых, вслед за Мирзаем и Фантом введем понятие цветового тела спектральной модели.
Цветовые векторы c, составляющие цветовое тело Лютера–Нюберга, представимы в следующем виде:
(40)
${\mathbf{c}} = \alpha \int\limits_0^\infty {{\text{S}}\left( \lambda \right){\text{R}}\left( \lambda \right){\mathbf{X}}\left( \lambda \right)d\lambda ,\quad 0 \leqslant {\text{R}}\left( \lambda \right) \leqslant 1} ,$Будем считать освещение эквиэнергетическим (${\text{S}}(\lambda ) = 1$), а сенсор – удовлетворяющим модели стандартного наблюдателя (${\text{X}}(\lambda ) = {{{\text{X}}}_{{\text{x}}}}(\lambda )$). Границы видимого диапазона $[{{\lambda }_{V}};{{\lambda }_{R}}]$ для моделей ${\text{M}}_{{\text{M}}}^{ \divideontimes }$ и ${{{\text{M}}}_{{{\text{G}} \circ }}}$ примем равными [360; 830]. Базис модели ${\text{M}}_{{\text{Z}}}^{ \divideontimes }$ выберем среди трехступенчатых так, чтобы ее цветовое тело было максимальным. Под трехступенчатой ЗСМ здесь понимается модель с базисными множествами в виде тройки непересекающихся отрезков, покрывающих видимый диапазон. При фиксированном видимом диапазоне трехступенчатая ЗСМ определяется двумя параметрами – границами ${{\lambda }_{{BG}}}$ и ${{\lambda }_{{GR}}}$ между тремя базисными отрезками.
Цветовые тела всех выбранных спектральных моделей звездчатые, т.е. любой отрезок, соединяющий точку цветового тела и начало координат, лежит в цветовом теле. При этом максимальная светлота окраски достигается при ${{\max }_{\lambda }}{\text{R}}(\lambda ) = 1$. Воспользуемся этим фактом для определения объема цветового тела. Введем сетку 1000 × 1000 на диаграмме цветности. Для каждого узла сетки либо найдем параметры модели, соответствующие данной цветности, либо убедимся, что решение отсутствует. Максимизируем светлоту окраски. Вычислим объем как сумму объемов тетраэдров, три вершины которых являются узлами сетки, а четвертая – началом координат.
В табл. 2 приведены результаты численной оценки цветового охвата для МЗСМ (зональной, гауссовской и фонмизесовской), а также, для сравнения – и модели Логвиненко ${{{\text{M}}}_{{{\text{G}} \circ }}}$.
Таблица 2.
Результаты сравнения спектральных моделей по цветовому охвату
| Ограничение | Объем цветового тела | Площадь достижимой цветности | ||
|---|---|---|---|---|
| CIE XYZ | proLab, ×105 | CIE XYZ | proLab | |
| $0 \leqslant {\text{R}}(\lambda ) \leqslant 1$ | 0.418 | 4.54 | 0.334 | 2.69 |
| ${\text{R}} \in \{ {\text{M}}_{{\text{Z}}}^{ \divideontimes }\} $ | 0.272 (65%) | 2.5 (56%) | 0.138 (41%) | 1.09 (41%) |
| ${\text{R}} \in \{ {\text{M}}_{{\text{G}}}^{ \divideontimes }\} $ | 0.142 (34%) | 1.79 (39%) | 0.334 (100%) | 2.69 (100%) |
| ${\text{R}} \in \{ {\text{M}}_{{\text{M}}}^{ \divideontimes }\} $ | 0.162 (39%) | 2.26 (50%) | 0.334 (100%) | 2.69 (100%) |
| ${\text{R}} \in \{ {{{\text{M}}}_{{{\text{G}} \circ }}}\} $ | 0.181 (43%) | 2.58 (57%) | 0.334 (100%) | 2.69 (100%) |
Оцененные меры приведены как в системе координат CIE XYZ (для возможного сравнения с классическими работами), так и в равномерной системе цветовых координат proLab, понятие меры в которой согласовано со свойствами цветоразличения человека (Konovalenko et al., 2021). Оптимальный объем в proLab для зональной модели был достигнут при трехступенчатом базисе с параметрами ${{\lambda }_{{BG}}} = 489$ и ${{\lambda }_{{GR}}} = 572$. Модель Логвиненко показала лучшие результаты по цветовому охвату для окрасок (доля объема цветового тела), но она не является мультипликативно замкнутой.
Незначительно отстающая от ${{{\text{M}}}_{{{\text{G}} \circ }}}$ зональная модель, оптимизированная по объему цветового тела, обеспечивает очень плохой цветовой охват для излучений. На рис. 15 видно, что область цветового треугольника, доступная для модели ${\text{M}}_{{\text{Z}}}^{ \divideontimes }$, почти совпадает с проекцией цветового тела sRGB-дисплея.
Рис. 15.
Цветовой охват ЗСМ, оптимизированной по объему цветового тела, на диаграмме цветности в системе координат proLab. Цветами показан цветовой охват стандарта sRGB, черным контуром – исследуемой зональной модели.

При этом стандарт sRGB (Stokes et al., 1996) на сегодняшний день считается устаревшим именно из-за недостаточного цветового охвата. Все остальные рассмотренные модели не имеют проблем с передачей насыщенных цветов излучений, причем ФСМ показывает наилучший среди оставшихся МЗСМ цветовой охват для окрасок, что делает эту модель наиболее перспективной при разработке методов цветового анализа, опирающихся на мультипликативную замкнутость. Дополнительно заметим, что задача оптимального выбора спектральных моделей применительно к организации цветоконстантных схем рассмотрена в работе (Николаев и др., 2008).
На рис. 16 показана форма цветовых тел исследованных моделей в системе координат proLab.
Рис. 16.
Цветовые тела моделей а – ${\text{M}}_{{\text{G}}}^{ \divideontimes }$; б – ${\text{M}}_{{\text{M}}}^{ \divideontimes }$; в – ${{{\text{M}}}_{{{\text{G}} \circ }}}$ для эквиэнергетического источника света в системе координат proLab. Для сравнения приведено также г – полное цветовое тело Лютера–Нюберга.

Очевидно, что натуральное расширение ГСМ практически не справляется с цветопередачей светлых пурпурных окрасок. При этом ФСМ, хоть и уступает модели Логвиненко, справляется с этим значительно лучше.
ЗАКЛЮЧЕНИЕ
Текст, предложенный вниманию читателей, достаточно разнороден в отношении обсуждавшихся в нем формальных проблем и актуальных технических задач цветовой тематики. Вопросы корректных физоптических постановок, позволяющих успешно моделировать психофизически изученные феномены человеческого цветовосприятия с целью разработки путей решения этой в общем виде некорректной обратной задачи зрения, равно как и не связанные с цветоконстантной проблематикой задачи создания устройств, обеспечивающих для “трихромата-пользователя” максимально комфортные условия получения цветовой информации об излучениях и окрасках, связывает здесь в логическое целое фундаментальная роль той общей части описания спектральных категорий, что принято именовать спектральной моделью (что можно понимать и как ключевой фрагмент математического языка, связывающего мир излучений с массивом реакций на них сенсора, и в качестве совокупности теоретических упрощений и ограничений, “заложенных в конструкцию модели” и позволяющих реализовать цели поставленной цветовой задачи). Знание биоинформатических законов зрительного процесса – при разработке эффективной вычислительной его модели – позволяет обеспечить в свою очередь и совершенствование процедур цветовоспроизведения (в полиграфии и технологии дисплеев). Действительно, в технических схемах оптического распознавания моделирование визуального процесса (как пример подхода к решению обратной задачи) предполагает опору на изученные особенности человеческого зрения, требуя привлечения формального языка для описания его фаз и физических атрибутов. В нашем случае акценты теории связаны со спектральными свойствами излучения, доносящего информацию о наблюдаемой сцене, и с цветометрическим характером сенсора, передающего эти данные в сильно обедненном виде “блоку цветовых оценок и гипотез об окраске тел в поле зрения”.
Компьютерный бум середины прошлого века, породивший, в том числе, лавину технических задач зрительного интеллекта, вызвал к жизни необходимость “освоения в практических целях” ранее накопленных знаний о психофизике цветовосприятия. Законы Грассмана и открытый Гельмгольцем феномен цветовой константности побудили исследователей найти подходы к “автоматизации объектного цветовосприятия”, каковые и выразились в предложениях использовать в этих целях язык упомянутых выше линейных моделей. Просуммируем теперь основные тезисы и декларации данной работы. Хотя ЛСМ и весьма удобны математически для регуляризации некорректных задач цветового анализа, невозможность в трехканальной ЛСМ описать семейство насыщенных окрасок произвольного цветового тона, ограничивает их применение в обработке изображений, предназначенных для предъявления человеку. Этот существенный недостаток ЛСМ стимулировал разработку ряда нелинейных спектральных моделей, среди которых самыми перспективными на сегодняшний день представляются ГСМ (гауссовская, в различных модификациях) и ФСМ (фонмизесовская). Обе эти модели имеют два замечательных преимущества. Выходные тристимулы описываются в них непосредственно через три структурных параметра кривой, а сами эти параметры естественным образом коррелируют с независимыми цветовыми качествами у человека-трихромата: тоном (hue), насыщенностью (saturation) и светлотой/яркостью (lightness/brightness). Обе модели обладают свойством замкнутости при перемножении произвольного числа членов этого семейства и при возведении кривой в степень с любым положительным показателем, что создает возможность производить оценку цветовых параметров излучения (первичного от источника или отраженного телом) аналитически – и при вычислении цветности источника, и при оценивании триады цветовых характеристик тела. Кроме того, для ГСМ авторы показали, что она, подобно ЛСМ, позволяет аналитически оценивать характеристики спектра по реакциям сенсора. В отличие от ЛСМ речь идет о приближенном решении, но численные эксперименты показали, что ошибка такой аппроксимации в 4 раза меньше, чем ошибка цветовоспроизведения, обеспечиваемая сенсором реальной камеры (фотоаппарата Canon).
Полученные для ГСМ результаты стимулировали произвести сравнительный численный анализ ее поведения в задаче предсказания цветности окраски под эквиэнергетическим освещением (при известном цвете источника) по цвету, наблюдаемому под другим источником, причем сравнение проводилось с двумя ЛСМ (трехзональной и Ли) для репрезентативной (552 образца) базы окрасок и двух семейств их освещения (“натурального” и планковского). Выведенные в таблицу 1 итоги моделирования по предложенным авторами алгоритмам демонстрируют лидерство ГСМ по всем вариантам испытаний: только у ГСМ не было зафиксировано ни одной серии экспериментов, где метрика оценки точности (в сравнении с “наивным аконстантным” алгоритмом) была бы меньше единицы, что говорит о практической перспективности использования ГСМ (“улучшенной” версии) для решения задач цветовой константности.
Наряду с перечисленными достоинствами, у ГСМ есть существенный недостаток: невозможность представительства излучений пурпурного сектора (семейства бимодальных спектров вида линейной смеси излучений насыщенного синего и красного цветов). Попытки разрешить проблемы ГСМ с описанием пурпурных излучений завершились созданием трех модификаций исходного ее базиса, где одна из версий – модель так называемой “периодизованной” ГСМ Логвиненко – оценена наилучшей в категории “объем цветового охвата”, от нее весьма незначительно отстала модель ФСМ, мультипликативно замкнутая (МЗСМ). ГСМ в варианте Логвиненко не принадлежит числу МЗСМ, не фигурировала в качестве конкурента для ФСМ, перспективные для технического внедрения свойства которой продемонстрированы в последнем разделе статьи, где рассматривается работоспособность ФСМ в задаче оценки цветности доминирующего освещения по картине цветовых изменений (оценка параметра насыщенности) излучения, отражаемого из разных точек окрашенной складчатой поверхности. Компьютерный эксперимент, основанный на реальных спектрометрических данных для семи “гофрированных” разноокрашенных тканей, показал, что авторский (2007 г.) алгоритм оценки цветности источника с учетом переотражений в складках (аппроксимация суммы степенного ряда кривых отражательной способности одним членом в степени n интервала n > 1) можно охарактеризовать рекомендуемым в качестве схемы решения задачи ЦК для сцен, где в качестве единственно возможного ее ключа (признака цветности источника) в наличии только карта рефлексов в неплоской сцене.
В силу двух этих независимых требований – полноты представительства излучений, отраженных фиксированным источником для стандартного наблюдателя, – в цветовом теле Лютера–Нюберга, в сочетании с не ставшим стандартным для разработчиков процедур ЦК одним из ключевых признаков в гетерархических ее схемах (где системой проверок – в зависимости от свойств сцены – выбирается максимально подходящий признак цветности доминирующего источника) из числа предложенных МЗСМ именно фонмизесовская спектральная модель может быть рекомендована для практического внедрения.
Работа выполнена при поддержке РФФИ (грант № 19-29-09075).
Список литературы
Николаев П.П. Гауссовская модель и процедуры цветовой константности для сцен двойного освещения. I. Цветность и светлота. Сенсорные системы. 2007а. Т. 21 № 3. С. 195–214.
Николаев П.П. Модель константности цветовосприятия для случая непрерывных спектральных функций. Биофизика. 1985. Т. 30. № 1. С. 112–117.
Николаев П.П. О новых методах оценки цветности освещения в алгоритмах цветовой константности. Сенсорные системы. 2007б. Т. 21. № 1. С. 29–44.
Николаев П.П. Трихроматическая модель константности восприятия окраски объектов. Биофизика. 1989. Т. 34. № 2. С. 287–294.
Николаев П.П., Карпенко С.М., Николаев Д.П. Спектральные модели цветовой константности: правила отбора. Труды Института системного анализа Российской академии наук (ИСА РАН). 2008. Т. 38. С. 322–335.
Николаев П.П., Николаев Д.П. Модели константного зрительного восприятия. III. Спектральные и перцептивные инварианты в процедурах зрительной обработки. Сенсорные системы. 1997. Т. 11. № 2. С. 181–204.
Нюберг Н.Д., Бонгард М.М., Николаев П.П. О константности восприятия окраски I. Биофизика. 1971а. Т 16. № 2. С. 285–293.
Нюберг Н.Д., Николаев П.П., Бонгард М.М. О константности восприятия окраски II. Биофизика. 1971б. Т. 16. № 6. С. 1052–1063.
Bianco S., Bruna A.R., Naccari F., Schettini R. Color correction pipeline optimization for digital cameras. Journal of Electronic Imaging. 2013. V. 22 (2). P. 1–11. https://doi.org/10.1117/1.JEI.22.2.023014
Brill M.H. A device performing illuminant-invariant assessment of chromatic relations. Journal of Theoretical Biology. 1978. V. 71 (3). P. 473–478. https://doi.org/10.1016/0022-5193(78)90175-3
Brill M.H. Further features of the illuminant-invariant trichromatic photosensor. Journal of Theoretical Biology. 1979. V. 78 (2). P. 305–308. https://doi.org/10.1016/0022-5193(79)90271-6
Brill M.H. The relation between the color of the illuminant and the color of the illuminated object. Color Research & Application. 1995. V. 20 (1). P. 70–76. https://doi.org/10.1002/col.5080200112
Brill M.H., West G. Chromatic adaptation and color constancy: A possible dichotomy. Color Research & Application. 1986. V. 11 (3). P. 196–204. https://doi.org/10.1002/col.5080110306
Buchsbaum G. A spatial processor model for object colour perception. Journal of the Franklin Institute. 1980. V. 310 (1). P. 1–26. https://doi.org/10.1016/0016-0032(80)90058-7
Can Karaimer H., Brown M.S. Improving color reproduction accuracy on cameras. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. 2018. P. 6440–6449. https://doi.org/10.1109/CVPR.2018.00674
Cohen J. Dependency of the spectral reflectance curves of the munsell color chips. Psychonomic Science. 1964. V. 1 (1). P. 369–370. https://doi.org/10.3758/BF03342963
Finlayson G.D., Mackiewicz M., Hurlbert A. Color correction using root-polynomial regression. IEEE Transactions on Image Processing. 2015. V. 24 (5). P. 1460–1470. https://doi.org/10.1109/TIP.2015.2405336
Gijsenij A., Gevers T., Van De Weijer J. Computational color constancy: Survey and experiments. IEEE Transactions on Image Processing. 2011. V. 20 (9). P. 2475–2489. https://doi.org/10.1109/TIP.2011.2118224
Gusamutdinova N., Ershov E., Gladilin S., Nikolaev D. Verification of applicability two multiplicative closed spectral models for multiple reflection effect description. Proc. SPIE 10253, 2016 International Conference on Robotics and Machine Vision. 2017. V. 10253. P. 16–20. https://doi.org/10.1117/12.2266404
Ives H.E. The relation between the color of the illuminant and the color of the illuminated object. Transactions of the Illuminating Engineering Society. 1912. V. 7. P. 62–72.
Konovalenko I.A., Smagina A.A., Nikolaev D.P., Nikolaev P.P. Prolab: perceptually uniform projective colour coordinates system. IEEE Access. 2021. V. 9. P. 133023–133042. https://doi.org/10.1109/ACCESS.2021.3115425
Kordecki A. Practical testing of irradiance-independent camera color calibration. Proc. SPIE 11041, Eleventh International Conference on Machine Vision (ICMV 2018). 2019. V. 11041. P. 340–345. https://doi.org/10.1117/12.2522907
Krinov E.L. Spectral reflectance properties of natural formations. Technical report. National Research Council of Canada. 1953. 268 p.
Land E.H., McCann J.J. Lightness and retinex theory. J. Opt. Soc. Am. 1971. V. 61 (1). P. 1–11. https://doi.org/10.1364/JOSA.61.000001
Lee S.D., Kim C.Y., Seo Y.S. Linear model of surface and scanner characterization method. Proc. SPIE 2414, Device-Independent Color Imaging II. 1995. V. 2414. P. 84–93. https://doi.org/10.1117/12.206536
Logvinenko A.D. Object-colour manifold. International Journal of Computer Vision. 2013. V. 101 (1). P. 143–160. https://doi.org/10.1007/s11263-012-0555-2
Macleod D.I., Golz J.A. Computational Analysis of Colour Constancy. In Rainer Mausfeld & Dieter Heyer (eds.), Colour Perception: Mind and the Physical World. Oxford University Press, 2003. P. 205–246. https://doi.org/10.1093/acprof:oso/9780198505006.001.0001
Maloney L.T. Evaluation of linear models of surface spectral reflectance with small numbers of parameters. J. Opt. Soc. Am. A. 1986a. V. 3 (10). P. 1673–1683. https://doi.org/10.1364/JOSAA.3.001673
Maloney L.T., Wandell B.A. Color constancy: a method for recovering surface spectral reflectance. J. Opt. Soc. Am. A. 1986б. V. 3 (1). P. 29–33. https://doi.org/10.1364/JOSAA.3.000029
Maloney L.T. Physics-based approaches to modeling surface color perception. In K. R. Gegenfurtner, & L. T. Sharpe (Eds.), Color vision: From genes to perception. Cambridge University Press, 1999. P. 387–422.
Marimont D.H., Wandell B.A. Linear models of surface and illuminant spectra. J. Opt. Soc. Am. A. 1992. V. 9 (11). P. 1905–1913. https://doi.org/10.1364/JOSAA.9.001905
Mirzaei H., Funt B. Object-color-signal prediction using wraparound gaussian metamers. J. Opt. Soc. Am. A. 2014. V. 31 (7). P. 1680–1687. https://doi.org/10.1364/JOSAA.31.001680
Mizokami Y., Webster M.A. Are gaussian spectra a viable perceptual assumption in color appearance? J. Opt. Soc. Am. A. 2012. V. 29 (2). P. A10–A18. https://doi.org/10.1364/JOSAA.29.000A10
Nelder J.A., Mead R.A simplex method for function minimization. The Computer Journal. 1965. V. 7 (4). P. 308–313. https://doi.org/10.1093/comjnl/7.4.308
Nikolaev D.P., Nikolayev P.P. Comparative analysis of gaussian and linear spectral models for colour constancy. Proceedings of 19th European Conference on Modelling and Simulation. 2005. P. 300–305.
Nikolaev D.P., Nikolaev P.P. On spectral models and colour constancy clues. Proceedings of 21st European Conference on Modelling and Simulation. 2007. P. 318–323.
Nikolaev D.P., Nikolayev P.P. Linear color segmentation and its implementation. Computer Vision and Image Understanding. Special Issue: Colour for Image Indexing and Retrieval. 2004. V. 94 (1). P. 115–139. https://doi.org/10.1016/j.cviu.2003.10.012
Nikolaev D.P., Nikolayev P.P., Bozhkova V.P. Efficiency comparison of analytical gaussian and linear spectral models in the same colour constancy framework. Int. J. Simul. Syst. Sci. Technol. 2006. V. 7 (3). P. 21–36.
Parkkinen J.P.S., Hallikainen J., Jaaskelainen T. Characteristic spectra of munsell colors. J. Opt. Soc. Am. A. 1989. V. 6 (2). P. 318–322. https://doi.org/10.1364/JOSAA.6.000318
Sällström P. Color and physics: Some remarks concerning the physical aspects of human colour vision. Technical Report 9. Un. Stockholm Inst. of Phys. 1973.
Smagina A., Ershov E., Grigoryev A. Multiple light source dataset for colour research. Proc. SPIE 11433, Twelfth International Conference on Machine Vision (ICMV 2019). 2020. V. 11433. P. 635–642. https://doi.org/10.1117/12.2559491
Stiles W.S., Wyszecki G.W. Counting metameric object colors. J. Opt. Soc. Am. 1962. V. 52 (3). P. 313–328. https://doi.org/10.1364/JOSA.52.000313
Stokes M., Anderson M., Chandrasekar S., Motta R. A standard default color space for the internet – srgb, version 1.10. Technical report. International Color Consortium. 1996.
Vazquez-Corral J., Connah D., Bertalmío M. Perceptual color characterization of cameras. Sensors. 2014. V. 14 (12). P. 23205–23229. https://doi.org/10.3390/s141223205
Vrhel M.J., Gershon R., Iwan L.S. Measurement and analysis of object reflectance spectra. Color Research & Application. 1994. V. 19 (1). P. 4–9. https://doi.org/10.1111/j.1520-6378.1994.tb00053.x
Weinberg J.W. The geometry of colors. General Relativity and Gravitation. 1976. V. 7 (1). P. 135–169. https://doi.org/10.1007/BF00762021
Yilmaz H. Color Vision and a New Approach to General Perception. In Bernard E.E., Kare M.R. (eds)Biological Prototypes and Synthetic Systems. Springer, Boston, MA., 1962. P. 126–141. https://doi.org/10.1007/978-1-4684-1716-6_22
Дополнительные материалы отсутствуют.
Инструменты
Сенсорные системы