Известия РАН. Теория и системы управления, 2019, № 1, стр. 98-108

ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЕ В ОДНОЙ НЕЛИНЕЙНОЙ ЗАДАЧЕ ПОСЛЕДОВАТЕЛЬНОГО СБЛИЖЕНИЯ

Ю. И. Бердышев^*

ИММ УрО РАН
Екатеринбург, Россия

Поступила в редакцию 27.07.2017
После доработки 24.09.2018

DOI: 10.1134/S0002338819010037

Аннотация

Предлагается алгоритм построения оптимального по быстродействию управления в задаче о последовательном сближении нелинейной системы четвертого порядка с двумя неподвижными точками в заданной очередности. Система описывает модель движения автомобиля, самолета в горизонтальной плоскости с переменной управляемой величиной скорости и управляемым углом разворота.

Введение. Используемая система отличается от автомобиля Айзекса [1] и машины Дубинса [2] дополнительным (четвертым) дифференциальным уравнением, описывающим изменение величины скорости, и дополнительным управляющим параметром [3, 4]. Сам автомобиль здесь отождествляется с точкой, движущейся по горизонтальной плоскости. Состояние автомобиля однозначно определяется двумя его координатами на плоскости, а также величиной и направлением его вектора скорости. Начальное состояние автомобиля предполагается заданным. На горизонтальной плоскости отмечены две точки, с которыми автомобиль должен сблизиться в определенной последовательности за наименьшее время.

Оказывается, что для оптимального решения этой задачи нельзя использовать классический принцип максимума Л.С. Понтрягина [5]. Это связано с тем, что он сформулирован для “двухточечных задач”, в которых целевая точка единственна. Поэтому этот принцип можно применить только после декомпозиции рассматриваемой задачи на две последовательно решаемые “двухточечные задачи”. А именно вначале надо определить оптимальный по быстродействию переход из начального состояния в первую точку и зафиксировать значения величины и направления вектора скорости в этой точке. Затем найденное состояние автомобиля в этой точке принять за начальное при определении оптимальной траектории, связывающей первую и вторую точки.

Однако полученная указанным способом траектория обхода двух точек, склеенная из двух кусков, не будет оптимальной, так как при переходе из начального состояния в первую целевую точку не учитывалось положение на плоскости второй целевой точки. Этот учет позволяет осуществить используемые здесь принцип максимума и условия выравнивания [6, теорема 7.1]. В результате их применения время перехода из начального состояния в первую точку увеличивается, но при этом изменяются величина и направление вектора скорости автомобиля в первой точке, которые позволяют уменьшить не только время перехода из первой точки во вторую, но и уменьшить общее время перехода обхода двух целей.

Факт преимущества использования необходимых условий оптимальности [6, теорема 7.1] над классическим принципом максимума [5] при определении оптимального обхода двух точек, заданных в горизонтальной плоскости, проиллюстрирован на модельном примере [6, c. 48] с автомобилем Айзекса, имеющим постоянную скорость движения. В примере наглядно проведено сравнение двух траекторий обхода [6, рис. 2], полученных на основе перечисленных необходимых условий оптимальности [5, 6]. Принцип максимума [6] позволил определить вид оптимальной траектории, а условие выравнивания вычислить направление вектора скорости автомобиля в первой точке. При этом использовался тот факт, что при постоянной скорости движения автомобиля время сближения с целями пропорционально длине траектории, по которой осуществляется сближение. На приведенном там рисунке видно, что за счет потери некоторого времени на первом участке были улучшены начальные условия для прохождения второго участка. Эти улучшения позволили уменьшить длину всей траектории сближения, что и подтверждено простыми вычислениями.

Заметим, что при определении оптимальной траектории сближения с двумя точками применим принцип максимума Л.С. Понтрягина [5] только в том случае, если кроме геометрических координат первой цели заданы также величина и направление вектора скорости в этой цели. Тогда рассматриваемую задачу можно декомпозировать на две последовательно решаемые “двухточечные задачи”.

Данная статья является продолжением работы [7], в которой предложен метод построения управления, имеющего вторую компоненту ${{u}_{2}}(t)$, тождественно равную единице, и реализующего обход двух заданных точек. Там же приведены достаточные условия [7, теорема 1] оптимальности указанного управления. В настоящей работе при построении управления не требуется выполнения условий указанной теоремы.

1. Постановка задач. Пусть движение точки в горизонтальной плоскости $xy$ описывается системой нелинейных дифференциальных уравнений [3, 4]

(1.1)

$\dot {x} = \text{v}cos\theta ,\quad \dot {y} = \text{v}sin\theta ,\quad \dot {\theta } = \frac{{{{K}_{1}}}}{\text{v}}{{u}_{1}},\quad \dot {v} = {{K}_{2}}{{u}_{2}},$

где $\theta $ – угол между осью x и направлением вектора скорости $\vec {v} \triangleq (\dot {x},\dot {y})$ ($ \triangleq $ – равно по определению); ${{K}_{1}} > 0$, ${{K}_{2}} \geqslant 0$ – заданные постоянные; $\text{v}$ – величина скорости движения точки; ${{u}_{1}}$, ${{u}_{2}}$ – управляющие параметры, удовлетворяющие ограничениям

(1.2)

$\left| {{{u}_{1}}} \right| \leqslant 1,\quad \left| {{{u}_{2}}} \right| \leqslant 1.$

Значение $\text{v} = 0$ является особым для системы (1.1). Поэтому целесообразно [4, c. 114; 6] в знаменателе правой части третьего уравнения вместо величины $\text{v}$ подставить непрерывно дифференцируемую функцию $f(\text{v})$, которая ограничена снизу величиной $(2 - \sqrt 2 ){{\text{v}}_{{5\pi }}}$, а на промежутках $( - \infty ,0)$, $[0,{{\text{v}}_{{5\pi }}})$, $[{{\text{v}}_{{5\pi }}},\infty )$ принимает соответственно значения $(2 - \sqrt 2 ){{v}_{{5\pi }}}$, $2{{\text{v}}_{{5\pi }}} - \sqrt {2{{{({{\text{v}}_{{5\pi }}})}}^{2}} - {{\text{v}}^{2}}} $, $\text{v}$. Здесь ${{\text{v}}_{{5\pi }}}$ – величина скорости, которая получается в результате разворота вектора скорости движущейся точки на угол $5\pi $ при начальном значении $\text{v}(0) = {{\text{v}}_{0}}$, ${{\text{v}}_{0}} > 0$, и управлении ${{u}_{1}}(t) = 1$, ${{u}_{2}}(t) = - 1$, $t \geqslant 0$.

Система (1.1) описывает простейшую модель движения автомобиля, самолета в горизонтальной плоскости xy с переменной управляемой скоростью и управляемым углом разворота.

Объект (1.1), (1.2) функционирует на конечном достаточно большом промежутке времени $T = [0,{{t}^{0}}]$. Его начальное состояние задано

(1.3)

$x(0) = {{x}_{0}},\quad y(0) = {{y}_{0}},\quad \theta (0) = {{\theta }_{0}},\quad \text{v}(0) = {{\text{v}}_{0}},\quad {{\text{v}}_{0}} > 0$

В качестве множества допустимых управлений преследователя выберем U – множество всех измеримых по Борелю двумерных функций $U = ({{u}_{1}},{{u}_{2}})$, ${{u}_{i}}{\text{:}}\;T \to [ - 1,1]$, $i = 1,2$. Каждое управление $U \in {\mathbf{U}}$ порождает движение, исходящее из начальной позиции (1.3), которое будем обозначать через $\left( {{{x}_{U}},{{y}_{U}},{{\theta }_{U}},{{\text{v}}_{U}}} \right) = \left\{ {\left( {{{x}_{U}}(t),{{y}_{U}}(t),{{\theta }_{U}}(t),{{\text{v}}_{U}}(t)} \right),t \in T} \right\}$. Под траекторией системы (1.1), порожденной управлением $U \in {\mathbf{U}}$, целесообразно понимать проекцию ее фазовой траектории $\left( {{{x}_{U}},{{y}_{U}},{{\theta }_{U}},{{\text{v}}_{U}}} \right)$ на плоскость xy. Точку с координатами ${{x}_{0}}$, ${{y}_{0}}$ обозначим через M₀.

Пусть ${{x}_{i}}$, ${{y}_{i}}$ – координаты заданной точки W_i, $i \in \overline {1,2} $. Будем говорить, что управление $U \in {\mathbf{U}}$ обеспечивает сближение (встречу) системы (1.1) с точкой W_i, если найдется такой момент времени t_i, при котором будут выполнены соотношения

${{x}_{U}}({{t}_{i}}) = {{x}_{i}},\quad {{y}_{U}}({{t}_{i}}) = {{y}_{i}}.$

Задача состоит в определении моментов времени t_i, $i \in \overline {1,2} $, и управления $U \in {\mathbf{U}}$, обеспечивающего последовательное сближение объекта (1.1), (1.2) с двумя заданными неподвижными точками ${{W}_{i}} = ({{x}_{i}},{{y}_{i}})$, $i \in \overline {1,2} $, в порядке возрастания их номеров в соответствующие моменты времени t_i и при котором общее время сближения t₂ является наименьшим.

Использование функции $f(\text{v})$ позволяет обеспечить выполнение всех условий теоремы существования оптимального управления [8].

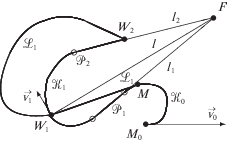
На взаимное расположение точек M₀, W₁, W₂ накладываем ограничение. А именно полагаем, что если решить двухточечную задачу об оптимальном переводе системы (1.1) из начального состояния в точку W₁ без учета положения точки W₂ по правилу (3.2)–(3.4) из [7], зафиксировать состояние системы в точке W₁, а затем решить задачу об оптимальном по быстродействию переводе из этого состояния в точку W₂, то траектории ${{\mathcal{L}}_{1}}$ и ${{\mathcal{L}}_{2}}$ (рис. 1), полученные в результате решения этих задач, будут состоять из криволинейного и прямолинейного участков. Заметим, что склейка ${{\mathcal{L}}_{1}} \cup {{\mathcal{L}}_{2}}$ не является оптимальной траекторией. Поскольку, потеряв некоторое время на участке между точками M₀, W₁, можно создать такие начальные условия для прохождения заключительного участка, которые позволят уменьшить суммарное время прохождения по обоим участкам [6, c. 48–50]. Оптимальная траектория $\mathcal{L}$ представима в виде склейки участков ${{\mathcal{K}}_{0}}$, ${{\mathcal{P}}_{1}}$, ${{\mathcal{K}}_{1}}$, ${{\mathcal{P}}_{2}}$ (рис. 1).

Рис. 1.

Вид оптимальных траекторий ${{\mathcal{L}}_{1}}$, ${{\mathcal{L}}_{2}}$, полученных при последовательном решении двухточечных задач

2. Принцип максимума и условие выравнивания. Известно [7], что при $\text{v} \geqslant 5\pi $ оптимальное управление $U = \left( {({{u}_{1}}(t),{{u}_{2}}(t)),\;t \in T} \right)$ удовлетворяет принципу максимума

(2.1)

${{u}_{1}}(t) = {\text{sign}}\mathop {\bar {\psi }}\nolimits_{k3} (t),\quad \mathop {\bar {\psi }}\nolimits_{k3} (t) \ne 0,\quad {{u}_{2}}(t) = {\text{sign}}\mathop {\bar {\psi }}\nolimits_{k4} (t),\quad \mathop {\bar {\psi }}\nolimits_{k4} (t) \ne 0,$

$t \in [{{t}_{{k - 1}}},{{t}_{k}}],\quad k = 1,2,$

и условию выравнивания

(2.2)

${{\Lambda }_{{11}}}cos{{\theta }_{{_{U}}}}({{t}_{1}}) + {{\Lambda }_{{12}}}sin{{\theta }_{{_{U}}}}({{t}_{1}}) = 0,$

где функции $\mathop {\bar {\psi }}\nolimits_{k3} (t)$, $\mathop {\bar {\psi }}\nolimits_{k4} (t)$ – решения систем уравнений

(2.3)

${{\psi }_{{21}}} = {{\Lambda }_{{21}}},{{\psi }_{{22}}} = {{\Lambda }_{{22}}},\quad {{\psi }_{{23}}} = {{\Lambda }_{{21}}}(y - {{y}_{2}}) - {{\Lambda }_{{22}}}(x - {{x}_{2}})$

$\mathop {\dot {\psi }}\nolimits_{24} = - {{\Lambda }_{{21}}}cos\theta - {{\Lambda }_{{22}}}sin\theta + \frac{{{{K}_{1}}}}{{{{\text{v}}^{2}}}}{{\psi }_{{23}}}{{u}_{1}},$

${{\psi }_{{11}}} = {{\Lambda }_{{11}}},\quad {{\psi }_{{12}}} = {{\Lambda }_{{12}}},\quad {{\psi }_{{13}}} = {{\Lambda }_{{11}}}(y - {{y}_{1}}) - {{\Lambda }_{{12}}}(x - {{x}_{1}}),$

(2.4)

$\mathop {\dot {\psi }}\nolimits_{14} = - {{\Lambda }_{{11}}}cos\theta - {{\Lambda }_{{12}}}sin\theta + \frac{{{{K}_{1}}}}{{{{\text{v}}^{2}}}}{{\psi }_{{13}}}{{u}_{1}}$

(2.5)

$\mathop {\bar {\psi }}\nolimits_{2i} \triangleq {{\psi }_{{2i}}},\quad \mathop {\bar {\psi }}\nolimits_{1i} \triangleq {{\psi }_{{1i}}} + {{\psi }_{{2i}}},\quad i \in \overline {1,4} ,$

с краевыми условиями

${{\psi }_{{13}}}({{t}_{1}}) = {{\psi }_{{23}}}({{t}_{2}}) = 0,\quad {{\psi }_{{14}}}({{t}_{1}}) = {{\psi }_{{24}}}({{t}_{2}}) = 0$

$({{\Lambda }_{{i1}}}$, ${{\Lambda }_{{i2}}}$, $i = 1,2$, – постоянные, подлежащие определению; ${{t}_{0}} = 0).$ Нетрудно показать, что дифференциальное уравнение для $\mathop {\bar {\psi }}\nolimits_{14} $ имеет вид

(2.6)

$\mathop {\dot {\bar {\psi }}}\nolimits_{14} = - ({{\Lambda }_{{11}}} + {{\Lambda }_{{21}}})cos\theta - ({{\Lambda }_{{12}}} + {{\Lambda }_{{22}}})sin\theta + \frac{{{{K}_{1}}}}{{{{\text{v}}^{2}}}}\mathop {\bar {\psi }}\nolimits_{13} {{u}_{1}}.$

Соотношения

$\mathop {\bar {\psi }}\nolimits_{13} \triangleq ({{\Lambda }_{{11}}} + {{\Lambda }_{{21}}})y - ({{\Lambda }_{{12}}} + {{\Lambda }_{{22}}})x - ({{\Lambda }_{{11}}}{{y}_{1}} + {{\Lambda }_{{21}}}{{y}_{2}} - {{\Lambda }_{{12}}}{{x}_{1}} - {{\Lambda }_{{22}}}{{x}_{2}}) = 0,$

$\mathop {\bar {\psi }}\nolimits_{23} \triangleq {{\Lambda }_{{21}}}(y - {{y}_{2}}) - {{\Lambda }_{{22}}}(x - {{x}_{2}}) = 0$

являются уравнениями прямых. Согласно (2.1), (2.5), при их пересечении управляющая функция ${{u}_{1}}(t)$ меняет знак. Поэтому их будем называть прямыми переключения.

Замена в знаменателе третьего уравнения системы (1.1), (1.2) величины $\text{v}$ на функцию $f(\text{v})$ влечет за собой изменение лишь функций $\mathop {\bar {\psi }}\nolimits_{14} $, $\mathop {\bar {\psi }}\nolimits_{24} $, а остальные вспомогательные функции остаются неизменными. Используя первое соотношение в (2.1), вид $\mathop {\bar {\psi }}\nolimits_{13} $, $\mathop {\bar {\psi }}\nolimits_{23} $ и ограничения на взаимное расположение точек M₀, W₁, W₂, можно показать, что любая траектория $\mathcal{L}$, претендующая на оптимальность, может состоять только из двух криволинейных участков ${{\mathcal{K}}_{0}}$, ${{\mathcal{K}}_{1}}$ и двух прямолинейных участков ${{\mathcal{P}}_{1}}$, ${{\mathcal{P}}_{2}}$, первый из которых соединяет ${{\mathcal{K}}_{0}}$ с ${{\mathcal{K}}_{1}}$, а второй соединяет ${{\mathcal{K}}_{1}}$ с ${{W}_{2}}$ (рис. 1). Кроме того, при движении по траектории $\mathcal{L}$ величина скорости всегда превосходит значение ${{\text{v}}_{{5\pi }}}.$ Поэтому для определения функций $\mathop {\bar {\psi }}\nolimits_{14} $, $\mathop {\bar {\psi }}\nolimits_{24} $ можно использовать уравнения (2.3)–(2.6). Заметим, что структура траектории $\mathcal{L}$ изображенной на рис. 1, удовлетворяет первому соотношению в (2.1) и условию выравнивания (2.2). Действительно, части траектории $\mathcal{L}$ от точки M₀ до точки W₁, лежащие по разные стороны от прямой l₁, которая содержит ${{\mathcal{P}}_{1}}$, имеют разный знак кривизны. Поэтому l₁ – прямая переключения. Очевидно, прямая l₂, содержащая участок ${{\mathcal{P}}_{2}}$, также является прямой переключения для части траектории от точки W₁ до точки W₂. Кроме того, прямые l, l₁, l₂, где l – прямая, ортогональная вектору скорости в точке W₁ и проходящая через нее, пересекаются в точке $F'$, что необходимо для выполнения условия (2.2).

3. Построение траектории сближения. Будем использовать ранее установленное правило построения оптимального управления при наличии одной цели. Смысл его состоит в следующем. Плоскость xy разбивается на три области: ${{\Gamma }_{{10}}}$, ${{\Gamma }_{{50}}}$, ${{\Gamma }_{{60}}}$. Управление движением выбирается в зависимости от того, в какой из этих областей находится цель [3, правило 6.1; 7, формулы (3.2)–(3.4)]. При определении оптимального управления в рассматриваемой задаче будем использовать принцип Беллмана, который здесь можно сформулировать следующим образом.

Если система (1.1), двигаясь по траектории $\mathcal{L}$, в некоторый момент времени t₁ попадает в точку ${{W}_{1}} = ({{x}_{1}},{{y}_{1}})$ с вектором скорости ${{\vec {v}}_{1}} = ({{\theta }_{1}},{{\text{v}}_{1}})$, то для оптимальности траектории $\mathcal{L}$ необходимо, чтобы на заключительном отрезке времени $[{{t}_{1}},{{t}_{2}}]$ управление определялось правилом (3.2)–(3.4) из [7], где ${{\Gamma }_{{10}}}$, ${{\Gamma }_{{50}}}$, ${{\Gamma }_{{60}}}$ заменены областями ${{\Gamma }_{{1{{t}_{1}}}}}$, ${{\Gamma }_{{5{{t}_{1}}}}}$, ${{\Gamma }_{{6{{t}_{1}}}}}$, при построении которых состояние $({{x}_{1}},{{y}_{1}},{{\theta }_{1}},{{\text{v}}_{1}})$ использовано в качестве начального. Пусть далее ${{\mathcal{L}}_{ * }}$ – первая часть траектории $\mathcal{L}$ расположенная между точками ${{M}_{0}}$, W₁, которую собственно и надо определить; $\mathcal{L}{\text{*}}$ – заключительная часть траектории, находящаяся между точками W₁, W₂, построенная по правилу [3, 7] при начальной позиции $({{x}_{1}},{{y}_{1}},{{\theta }_{1}},{{\text{v}}_{1}})$, реализуемой в точке W₁ в результате движения по траектории ${{\mathcal{L}}_{ * }}$.

Данная работа является продолжением [7], где предполагалось, что расстояния между точками ${{M}_{0}}$, W₁ и W₁, W₂ настолько велики, что траектория $\mathcal{L}$, претендующая на оптимальность, должна состоять из двух криволинейных участков ${{\mathcal{K}}_{0}}$, ${{\mathcal{K}}_{1}}$ и двух прямолинейных участков ${{\mathcal{P}}_{1}}$, ${{\mathcal{P}}_{2}}$ ненулевой длины, первый из которых соединяет ${{\mathcal{K}}_{0}}$ с ${{\mathcal{K}}_{1}}$, а второй соединяет ${{\mathcal{K}}_{1}}$ с W₂. Там же были исследованы функции $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$, определяющие управление скоростью и принимающие одинаковые значения в момент ${{t}_{1}}$ сближения с точкой W₁. Согласно [6], через $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ обозначено решение уравнения (2.3) при условии $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{2}}) = 0$, а через $\mathop {\bar {\psi }}\nolimits_{14} (t)$ – решение уравнения (2.6) при условии $\mathop {\bar {\psi }}\nolimits_{14} ({{t}_{1}}) = \mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{1}})$. Здесь t₁, t₁ – моменты попадания соответственно в точки W₁, W₂; ${{\tau }_{2}} \in ({{t}_{1}},{{t}_{2}})$ – первый момент, в который на траектории $\mathcal{L}{\text{*}}$ вектор скорости направлен в точку W₂.

Рис. 2.

Четыре возможных вида склейки графиков функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$

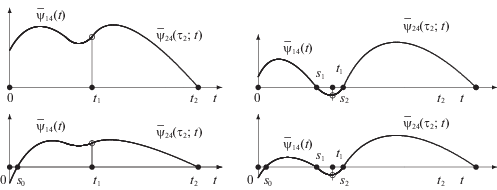
В [7] показано, что торможение на оптимальной траектории возможно только на двух отрезках времени, содержащих моменты t₁, ${{t}_{0}} = 0$, а склейка функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ может принимать лишь один из видов, изображенных на рис. 2, где кружком отмечены точки их стыковки; s₀, s₁, s₂ – моменты переключения управляющей функции ${{u}_{2}}(t)$; t₁, t₂ – моменты сближения объекта (2.1) с целевыми точками ${{W}_{1}}$, ${{W}_{2}}$. Там же определены условия [7, теорема 1], при которых склейка функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ на интервале $(0,{{t}_{2}})$ принимает только положительные значения (см. верхний левый график на рис. 2), т.е. вторая компонента ${{u}_{2}}(t)$ оптимального управления, согласно (2.1), тождественно равна единице. Эта теорема имеет следующий физический смысл. Если точки M₀, W₁, W₂ достаточно далеко удалены друг от друга, а при движении по траектории $\mathcal{L}$ в окрестностях точек M₀, W₁ объект разворачивается на небольшой угол, то траектория $\mathcal{L}$, удовлетворяющая обобщенному принципу максимума (2.1), условию выравнивания (2.2), по которой объект все время максимально разгоняется, является оптимальной. Если же разворот около точки W₁ настолько велик, что, например, нарушается первое условие: ${{W}_{2}} \in {{\Gamma }_{{1{{t}_{1}}}}}$ [7, теорема 1], то в окрестности этой точки необходимо торможение для более быстрого разворота.

В данной статье полагаем, что условия из [7, теорема 1] не выполнены. Тем не менее, в настоящей работе оптимальная траектория имеет такую же структуру как и в [7], т.е. состоит из двух криволинейных ${{\mathcal{K}}_{0}}$, ${{\mathcal{K}}_{1}}$ и двух прямолинейных участков ${{\mathcal{P}}_{1}}$, ${{\mathcal{P}}_{2}}$ (рис. 1). Разница состоит лишь в том, что любой прямолинейный участок может стягиваться в точку, а на криволинейных участках возможно торможение. При этом в случае, когда участок ${{\mathcal{P}}_{2}}$ имеет не нулевую длину, склейка функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ может принимать лишь один из видов, изображенных на рис. 2. Если участок ${{\mathcal{P}}_{2}}$ отсутствует, то, кроме того, на всем интервале $({{t}_{1}},{{t}_{2}})$ функция $\mathop {\bar {\psi }}\nolimits_{24} (t)$, являющаяся решением уравнения (2.3) при условии $\mathop {\bar {\psi }}\nolimits_{24} ({{t}_{2}}) = 0$, может быть отрицательной. Следовательно, искомое управление на отрезке $[{{t}_{1}},{{t}_{2}}]$ может имеет вид (${{u}_{1}}(t) = - 1$, ${{u}_{2}}(t) = - 1$). В этом случае прямой переключения l₂ должна быть прямая линия, проведенная через точку W₂ перпендикулярно вектору скорости движущегося объекта в этой точке [5, с. 126].

В зависимости от того, в одном либо в разных направлениях происходит разворот объекта на участках ${{\mathcal{K}}_{0}}$, ${{\mathcal{K}}_{1}}$, оптимальное управление $({{u}_{1}}(t),\;{{u}_{2}}(t))$ будет иметь один из следующих видов:

(3.1)

${{u}_{1}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad t \in [0,{{\tau }_{1}}),} \\ {0,\quad t \in [{{\tau }_{1}},\delta ),} \\ { - 1,\quad t \in [\delta ,{{\tau }_{2}}),} \\ {0,\quad t \in [{{\tau }_{2}},{{t}_{2}}],} \end{array}} \right.\quad {{u}_{2}}(t) = \left\{ {\begin{array}{*{20}{c}} { - 1,\quad t \in [0,{{s}_{0}}),} \\ {1,\quad t \in [{{s}_{0}},{{s}_{1}}),} \\ { - 1,\quad t \in [{{s}_{1}},{{s}_{2}}),} \\ {1,\quad t \in [{{s}_{2}},{{t}_{2}}],} \end{array}} \right.$

(3.2)

${{u}_{1}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad t \in [0,{{\tau }_{1}}),} \\ {0,\quad t \in [{{\tau }_{1}},\delta ),} \\ {1,\quad t \in [\delta ,{{\tau }_{2}}),} \\ {0,\quad t \in [{{\tau }_{2}},{{t}_{2}}],} \end{array}} \right.\quad {{u}_{2}}(t) = \left\{ {\begin{array}{*{20}{c}} { - 1,\quad t \in [0,{{s}_{0}}),} \\ {1,\quad t \in [{{s}_{0}},{{s}_{1}}),} \\ { - 1,\quad t \in [{{s}_{1}},{{s}_{2}}),} \\ {1,\quad t \in [{{s}_{2}},{{t}_{2}}].} \end{array}} \right.$

Здесь моменты ${{\tau }_{1}}$, δ, ${{\tau }_{2}}$, ${{s}_{0}}$, ${{s}_{1}}$, ${{s}_{2}}$ совместно с t₁ подлежат определению. Длины некоторых полуинтервалов, фигурирующих в (3.1), (3.2), могут стягиваться к нулю. Например, при выполнении условий из [7, теоремы 1] на интервале $(0,{{t}_{2}})$ склейка функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ принимает положительные значения. Поэтому из (2.1) следует, что управляющая функция ${{u}_{2}}(t)$ (3.1) на отрезке $[0,{{t}_{2}}]$ не имеет переключений и тождественно равна единице. Кроме того, при некоторых местоположениях точек W₁, W₂ могут отсутствовать прямолинейные участки траектории $\mathcal{L}$. Тогда возможны равенства ${{\tau }_{1}} = \delta $, ${{\tau }_{2}} = {{t}_{2}},$ уменьшающие число неизвестных параметров.

Какой из видов имеет место в действительности, зависит от знака α – угла между векторами ${{\vec {v}}_{{12}}}$, ${{\vec {v}}_{*}}$, где ${{\vec {v}}_{*}}$ – вектор скорости объекта (1.1) в точке W₁ на траектории ${{\mathcal{L}}_{1}}$, ${{\vec {v}}_{{12}}}$ – вектор, началом и концом которого являются точки W₁, W₂. Если угол α положительный, то выбираем вид (3.1). Если же $\alpha < 0,$ то используем (3.2). При $\alpha = 0$ траектория $\mathcal{L}{\text{*}}$ будет отрезком прямой, а при $\alpha = \pi $ выбираем (3.1). В настоящей работе более подробно рассматривается случай $0 < \alpha < \pi .$

Необходимо подобрать моменты переключения управления (3.1) так, чтобы кроме условия выравнивания (2.2) и первого соотношения в (2.1) было выполнено и второе равенство в (2.1). Сложность определения моментов переключения управления (3.1) состоит в том, что траекторию $\mathcal{L}$ исходящую из начальной позиции (1.3), надо строить в прямом времени, а склейку функций $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ вычислять в попятную, исходя из равенства $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{2}}) = 0$.

Благодаря использованию принципа Беллмана фактически требуется определить лишь четыре момента ${{\tau }_{1}}$, $\delta $, ${{s}_{0}}$, ${{s}_{1}}$ в формуле (3.1), а остальные моменты t₁, ${{\tau }_{2}}$, ${{s}_{2}}$, ${{t}_{2}}$ зависят от них. Действительно, траектория ${{\mathcal{L}}_{ * }}$, порожденная управлением

(3.3)

${{u}_{1}}(t) = \left\{ \begin{gathered} 1,\quad t \in [0,{{\tau }_{1}}), \hfill \\ 0,\quad t \in [{{\tau }_{1}},\delta ), \hfill \\ - 1,\quad t \geqslant \delta , \hfill \\ \end{gathered} \right.\quad {{u}_{2}}(t) = \left\{ \begin{gathered} - 1,\quad t \in [0,{{s}_{0}}), \hfill \\ 1,\quad t \in [{{s}_{0}},{{s}_{1}}), \hfill \\ - 1,\quad t \geqslant {{s}_{1}}, \hfill \\ \end{gathered} \right.$

в некоторый момент времени t₁ должна попадать в точку W₁. Поэтому момент t₁ и состояние $({{x}_{1}},{{y}_{1}},{{\theta }_{1}},{{\text{v}}_{1}})$ системы (1.1) в точке W₁ полностью вычисляются по параметрам ${{\tau }_{1}}$, $\delta $, ${{s}_{0}}$, ${{s}_{1}}$. Но состояние $({{x}_{1}},{{y}_{1}},{{\theta }_{1}},{{\text{v}}_{1}})$ однозначно определяет заключительную часть $\mathcal{L}{\text{*}}$ траектории $\mathcal{L}$.

Введем следующие обозначения: l₁, l₂ – прямые переключения соответственно для траекторий ${{\mathcal{L}}_{ * }}$, $\mathcal{L}{\text{*}}$; $F'$ – точка пересечения прямых ${{l}_{1}}$, ${{l}_{2}}$; ${{\vec {v}}_{1}}$ – вектор скорости объекта (1.1) в точке W₁ в момент t₁ на траектории ${{\mathcal{L}}_{ * }}$; ${{\text{v}}_{1}}$, ${{\theta }_{1}}$ – его координаты; l – прямая, ортогональная вектору скорости ${{\vec {v}}_{1}}$ и проходящая через точку W₁; F – точка пересечения прямых l, l₂; $d({{\mathcal{P}}_{i}})$ – длина отрезка ${{\mathcal{P}}_{i}}$, $i = 1,2$; $\tau $ – первый момент времени, в который вектор скорости на траектории ${{\mathcal{L}}_{1}}$ направлен в точку ${{W}_{1}};$ $s > 0$ – момент переключения с “–1” на “1” управляющей функции ${{u}_{2}}(t)$ при ${{W}_{1}}\not { \in }{{\Gamma }_{{10}}}$ (см. правило в [3, 7]) и s = 0 при ${{W}_{1}} \in {{\Gamma }_{{10}}}.$

4. Алгоритм построения управления.

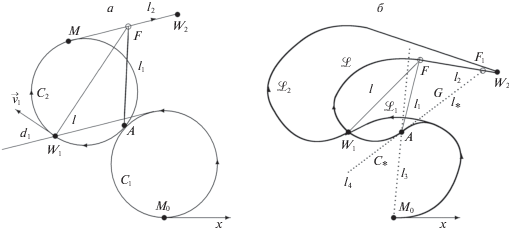
1. Используя правило из [3, 7] определения управления в задаче о переводе системы (1.1) из начального состояния (1.3) в точку ${{W}_{1}}$ за наименьшее время, находим моменты $\tau $, $s$ его переключения и строим траекторию ${{\mathcal{L}}_{1}}$ (рис. 3), которую выбираем в качестве нулевого приближения для ${{\mathcal{L}}_{ * }}$ – первой части траектории $\mathcal{L}$. Полагаем ${{s}_{0}} = s.$

Рис. 3.

${{\mathcal{L}}_{ * }}$ – нулевое приближение первой части оптимальной траектории (a); $\mathcal{L}{\text{*}}$ – вид оптимальной траектории, l₁, l₂ – ее прямые переключения (б)

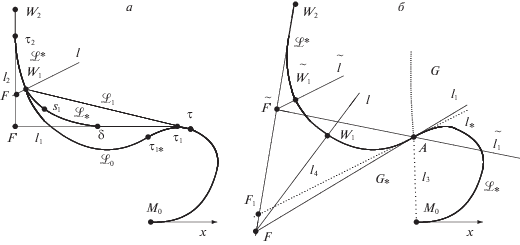
2. Найдем интервал изменения параметра ${{\tau }_{1}}$. Для этого вычислим значение ${{\tau }_{{1 * }}}$ из условия, что траектория ${{\mathcal{L}}_{0}}$, порожденная управлением

${{u}_{1}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad t \in [0,{{\tau }_{{1 * }}}),} \\ { - 1,\quad t \geqslant {{\tau }_{{1 * }}},} \end{array}} \right.\quad {{u}_{2}}(t) = \left\{ {\begin{array}{*{20}{c}} { - 1,\quad t \in [0,{{s}_{0}}),} \\ {1,\quad t \geqslant {{s}_{0}},} \end{array}} \right.$

проходит через точку W₁ (рис. 3a). Момент ${{\tau }_{1}}$ стыковки криволинейного и прямолинейного участков будем выбирать из промежутка $[\tau ,{{\tau }_{{1 * }}}]$. Если ${{\tau }_{1}} < {{\tau }_{{1 * }}}$, то момент ${{\tau }_{1}}$ однозначно определяет прямую переключения l₁ (рис. 3a).

3. При каждом параметре ${{\tau }_{1}} \in [\tau ,{{\tau }_{{1 * }}}]$ выберем число ${{\delta }_{1}}$ из условий, что траектория, порожденная управлением

${{u}_{1}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad t \in [0,{{\tau }_{1}}),} \\ {0,\quad t \in [{{\tau }_{1}},{{\delta }_{1}}),} \\ { - 1,\quad t \geqslant {{\delta }_{1}},} \end{array}} \right.\quad {{u}_{2}}(t) = \left\{ {\begin{array}{*{20}{c}} { - 1,\quad t \in [0,{{s}_{0}}),} \\ {1,\quad t \geqslant {{s}_{0}},} \end{array}} \right.$

проходит через точку W₁.

Начиная с величины ${{\delta }_{1}}$ будем увеличивать в (3.3) значение $\delta $ и ставить ему в соответствие момент времени s₁ (рис. 3a), при котором траектория ${{\mathcal{L}}_{ * }}$, порожденная управлением (3.3), проходит через точку W₁ в некоторый момент времени ${{t}_{1}}.$ Обозначим через ${{\delta }_{2}}$ наибольшее значение δ, при котором это возможно сделать. Таким образом, каждому параметру $\delta \in [{{\delta }_{1}},{{\delta }_{2}}]$ ставим в соответствие свой момент s₁ переключения управляющей функции ${{u}_{2}}(t)$. Заметим, что при $\delta = {{\delta }_{1}}$ момент ${{s}_{1}} = {{t}_{1}}$.

4. При фиксированных параметрах s₀, ${{\tau }_{1}}$, $\delta $ и соответствующем им моменте s₁ вычислим координаты ${{\text{v}}_{1}}$, ${{\theta }_{1}}$ вектора скорости ${{\vec {v}}_{1}}$ объекта (1.1) в момент t₁ (${{\text{v}}_{1}}$, ${{\theta }_{1}}$ – величина и направляющий угол вектора ${{\vec {v}}_{1}}$). Построим прямую l, проходящую через точку W₁ ортогонально вектору скорости ${{\vec {v}}_{1}}$.

5. Пусть x₁, y₁ – координаты точки W₁. Используем правило из [3, 7] построения оптимальной траектории $\mathcal{L}{\text{*}}$, доставляющей систему (1.1) из позиции $({{x}_{1}},{{y}_{1}},{{\theta }_{1}},{{\text{v}}_{1}})$ в точку ${{W}_{2}}$ за наименьшее время.

Если $d({{\mathcal{P}}_{2}}) \ne 0$, то траектория $\mathcal{L}{\text{*}}$ порождена управлением

${{u}_{1}}(t) = \left\{ {\begin{array}{*{20}{c}} {1,\quad t \in [{{t}_{1}},{{\tau }_{2}}),} \\ {0,\quad t \in [{{\tau }_{2}},{{t}_{2}}],} \end{array}} \right.\quad {{u}_{2}}(t) = \left\{ {\begin{array}{*{20}{c}} { - 1,\quad t \in [{{t}_{1}},{{s}_{2}}),} \\ {1,\quad t \in [{{s}_{2}},{{t}_{2}}]} \end{array}} \right.$

и ${{\tau }_{2}} < {{t}_{2}}$. Момент s₂ будет отсутствовать при ${{W}_{2}} \in {{\Gamma }_{{1{{t}_{1}}}}}$. В случае ${{W}_{2}}\not { \in }{{\Gamma }_{{1{{t}_{1}}}}}$ найдется момент ${{s}_{2}} \in ({{t}_{1}},{{\tau }_{2}}),$ при котором

$\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{s}_{2}}) = 0,\mathop {\quad \bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t) < 0,\quad t \in ({{t}_{1}},{{s}_{2}});\mathop {\quad \bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t) > 0,\quad t \in ({{s}_{2}},{{t}_{2}}),$

где функция $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ – решение уравнения (2.3) при условии $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{2}}) = 0$. Последнее неравенство является следствием выпуклости вверх функции $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ на интервале $({{s}_{2}},{{t}_{2}})$. Если же ${{W}_{2}} \in {{\Gamma }_{{1{{t}_{1}}}}}$, то на всем интервале $({{t}_{1}},{{t}_{2}})$ функция $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$ будет положительной.

Пусть $d({{\mathcal{P}}_{2}}) = 0$, т.е. ${{u}_{1}}(t) = - 1$, $t \in [{{t}_{1}},{{t}_{2}}]$. Тогда функция $\mathop {\bar {\psi }}\nolimits_{24} (t)$ на интервале $({{t}_{1}},{{t}_{2}})$ либо а) всюду положительна и ${{u}_{2}}(t) = 1$, $t \in [{{t}_{1}},{{t}_{2}}]$, либо б) всюду отрицательна и ${{u}_{2}}(t) = - 1$, $t \in [{{t}_{1}},{{t}_{2}}]$, либо в) в некоторый момент ${{s}_{2}}$ меняет знак с минуса на плюс, а управляющая функция ${{u}_{2}}(t)$ переключается с “–1” на “1”. Проходящая через точку W₂ прямая переключения l₂ в случае б) ортогональна вектору скорости в точке W₂, в случае в) определяется из условия $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{s}_{2}}) = 0$, в случае а) не определена однозначно, а лишь известен сектор, которому она принадлежит [5, c. 126]. В частности, она может быть параллельной вектору скорости в точке W₂. Заметим, что от коэффициентов прямой l₂ зависит функция $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{s}_{2}})$, по которой, согласно (2.1), вычисляется ${{u}_{2}}(t)$.

6. При фиксированных параметрах ${{s}_{0}}$, ${{\tau }_{1}}$, $\delta $ и соответствующему им значению s₁ определим область ${{\Gamma }_{{1{{t}_{1}}}}}$. Если ${{W}_{2}} \in {{\Gamma }_{{1{{t}_{1}}}}}$, то параметр $\delta $ будем уменьшать. Его вариация приведет к изменению момента s₁ и, как следствие, состояния системы (1.1) в точке W₁, области ${{\Gamma }_{{1{{t}_{1}}}}}$, граничного условия

(4.1)

$\mathop {\bar {\psi }}\nolimits_{14} ({{t}_{1}}) = \mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{1}}),\quad \mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};{{t}_{2}}) = 0$

для функции $\mathop {\bar {\psi }}\nolimits_{14} (t)$. Если при достижении параметра $\delta $ величины ${{\delta }_{1}}$ точка W₂ так и не выйдет из области ${{\Gamma }_{{1{{t}_{1}}}}}$, то функции $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{24} ({{\tau }_{2}};t)$, удовлетворяющие соотношениям (4.1), будут положительными в окрестности точки W₁ (см. два левых графика на рис. 2). В этом случае в соответствии с принципом максимума (2.1) не должно быть торможения в окрестности точки ${{W}_{1}}$ и ${{u}_{2}}(t) = 1$, $t \in [0,{{t}_{2}}]$, либо ${{u}_{2}}(t) = 1$, $t \in [{{s}_{0}},{{t}_{2}}]$.

Пусть ${{W}_{2}}\not { \in }{{\Gamma }_{{1{{t}_{1}}}}}$. Определим множество $\Delta $ параметров $\delta $, при которых это включение имеет место. Во множестве $\Delta $ найдем то $\delta $, при котором выполняется равенство $\mathop {\bar {\psi }}\nolimits_{14} ({{s}_{1}}) = 0$, где момент ${{s}_{1}}$ определен в п. 3.

7. Поскольку у траектории ${{\mathcal{L}}_{2}}$ в силу ограничения на выбор местоположения точек M₀, W₁, W₂ есть прямолинейный участок, то при малой величине ${{\tau }_{1}} - \tau $ имеет место соотношение $d({{\mathcal{P}}_{2}}) \ne 0$. В этом случае отрезок ${{\mathcal{P}}_{2}}$ однозначно определяет прямую переключения ${{l}_{2}}$ (${{\mathcal{P}}_{2}} \subset {{l}_{2}}$). Найдем точку $F$ пересечения прямых ${{l}_{2}}$, $l$ (рис. 3a).

Пусть $d({{\mathcal{P}}_{1}}) \ne 0$. Тогда известна прямая l₁, содержащая отрезок ${{\mathcal{P}}_{1}}$. Если точка $F$ лежит на прямой ${{l}_{1}}$, то выполняется условие выравнивания (2.2) и построенная траектория $\mathcal{L} = {{\mathcal{L}}_{ * }} \cup \mathcal{L}{\text{*}}$ является подозрительной на оптимальность. В противном случае следует увеличивать параметр ${{\tau }_{1}}$ и при измененном параметре ${{\tau }_{1}}$ вновь определять параметр $\delta $ до тех пор, пока прямые $l$, ${{l}_{1}}$, ${{l}_{2}}$ не пересекутся в одной точке.

Пусть $d({{\mathcal{P}}_{1}}) = 0$. Тогда траектория ${{\mathcal{L}}_{ * }}$ состоит из двух дуг ${{M}_{0}}A$, $A{{W}_{1}}$ разного знака кривизны (A – точка перегиба), а прямая l₁ в силу условия выравнивания (2.2) должна проходить через точки A, F (рис. 3б). Если при этом прямая l₁ не пересекает дугу ${{M}_{0}}A$, то траектория $\mathcal{L}$ претендует на оптимальность. Иначе необходима вариация параметра ${{\tau }_{1}}$.

8. При выполнении соотношения $\mathop {\bar {\psi }}\nolimits_{14} ({{s}_{0}}) = 0$ траектория $\mathcal{L}$ будет искомой. В противном случае необходимо изменить момент ${{s}_{0}}$ в (3.1) и вновь по п. 2–7 пересчитать параметры ${{\tau }_{1}}$, $\delta $, ${{s}_{1}}$.

Среди всех траекторий, имеющих два прямолинейных участка не нулевой длины, траектория $\mathcal{L}$, построенная по указанному алгоритму, будет единственной удовлетворяющей необходимым условиям оптимальности (2.1), (2.2). Это связано с тем, что прямолинейные участки ${{\mathcal{P}}_{1}}$, ${{\mathcal{P}}_{2}}$ однозначно определяют их содержащие прямые переключения l₁, l₂, а следовательно, и функции $\mathop {\bar {\psi }}\nolimits_{13} (t)$, $\mathop {\bar {\psi }}\nolimits_{23} (t)$, $\mathop {\bar {\psi }}\nolimits_{14} (t)$, $\mathop {\bar {\psi }}\nolimits_{14} (t)$, фигурирующие в соотношениях (2.1), (2.2). Поэтому в данном случае траектория $\mathcal{L}$ будет оптимальной. Этого нельзя утверждать при отсутствии хотя бы одного прямолинейного участка, так как тогда положение соответствующей прямой (l₁ или l₂) становится неопределенным.

5. Об условии существования прямолинейного участка ${{\mathcal{P}}_{1}}$. Вначале разберем более простой случай.

5.1. Частный случай ${{K}_{2}} = 0$. Здесь величина $\text{v}$ скорости объекта (1.1) постоянна, а оптимальная траектория последовательного обхода двух точек W₁, W₂ состоит из дуг окружностей радиуса $R = \text{v}{\text{/}}{{K}_{1}}$ и отрезков прямых. Пусть в начальный момент времени объект находится в точке ${{M}_{0}}$, а его вектор скорости направлен по оси x (рис. 4). Обозначим через C₁, C₂ окружности радиуса $R$, касающиеся оси x в точке M₀ и лежащие соответственно выше или ниже этой оси. В силу симметрии достаточно рассмотреть случай, когда точка ${{W}_{1}}$ находится выше оси x. Предполагается, что точка W₁ лежит вне круга, ограниченного окружностью C₁, т.е. расстояние $\rho $ между центром окружности C₁ и точкой W₁ больше величины $R$. В этом случае траектория ${{\mathcal{L}}_{1}}$ будет состоять из дуги окружности C₁ и отрезка ${{d}_{1}}$, касательной к C₁ прямой. На рис. 4a отрезок ${{d}_{1}}$ отмечен пунктирной линией. Указанная прямая разбивает геометрическую плоскость на две части. В зависимости от того, в какой из этих частей находится точка W₂, разворот по криволинейным участкам будет происходить в одном или в разных направлениях.

Рис. 4.

Виды оптимальных траекторий при ${{K}_{2}} = 0$: a, б – в случае $\rho > 3R$; в, г – в случае $R < \rho \leqslant 3R$

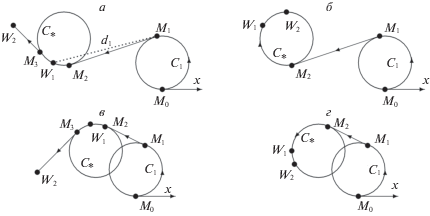
Предположим, что разворот по криволинейным участкам траектории осуществляется в одном направлении (рис. 4в, г). Тогда оптимальная траектория будет иметь либо два прямолинейных участка, дугу ${{\mathcal{K}}_{0}}$ окружности ${{C}_{1}}$ и дугу ${{\mathcal{K}}_{1}}$ окружности ${{C}_{ * }}$, которая расположена так, что ${{\mathcal{K}}_{1}}$ делится точкой ${{W}_{1}}$ пополам (рис. 4в), либо второй прямолинейный участок будет отсутствовать (рис. 4г).

Пусть имеет место случай, когда разворот по криволинейным участкам происходит в разных направлениях. Можно показать, что если $\rho > 3R$, то $d({{\mathcal{P}}_{1}}) \ne 0$, а участок ${{\mathcal{P}}_{2}}$ не будет стягиваться в точку только тогда, когда найдется такое расположение окружности ${{C}_{ * }}$ радиуса R, содержащей ${{\mathcal{K}}_{1}}$, при котором точка ${{W}_{1}}$ будет серединой дуги ${{\mathcal{K}}_{1}}$ (рис. 4а). В противном случае концом этой дуги будет точка ${{W}_{2}}$ (рис. 4б).

Если $R < \rho \leqslant 3R$, то будем катить окружность ${{C}_{2}}$ по ${{C}_{1}}$ до момента попадания точки ${{W}_{1}}$ на окружность ${{C}_{2}}$. Фиксируем ${{C}_{2}}$ в этом положении. Возможны два случая: а) ${{W}_{2}}\not { \in }C_{2}^{0}$, б) ${{W}_{2}} \in C_{2}^{0}$, где $C_{2}^{0}$ – круг, ограниченный окружностью ${{C}_{2}}$. В случае а) на ${{C}_{2}}$ отметим точку M, в которой вектор скорости направлен в точку W₂, и точку A касания ${{C}_{2}}$ с ${{C}_{1}}$ (рис. 5a). Если дуга ${{W}_{1}}M$ окажется меньше дуги $A{{W}_{1}}$, то найдется окружность ${{C}_{ * }}$ радиуса R, которой будет принадлежать участок ${{\mathcal{K}}_{1}}$, делящийся точкой ${{W}_{1}}$ пополам, при этом $d({{\mathcal{P}}_{1}}) \ne 0$ и вся траектория $\mathcal{L}$ будет иметь вид, изображенный на рис. 4a. Иначе участок ${{\mathcal{P}}_{1}}$ будет отсутствовать (рис. 5a). Здесь для выполнения условия выравнивания прямую переключения l₁ надо выбрать так, чтобы она проходила через точки A, F, где F – точка пересечения прямой l₂, содержащей участок ${{\mathcal{P}}_{2}}$, с прямой l, проходящей через точку W₁ ортогонально вектору ${{\vec {v}}_{1}}$. Можно показать, что в случае б) участок ${{\mathcal{K}}_{1}}$ будет находиться на окружности ${{C}_{ * }}$, которая проходит через точки W₁, W₂ и не пересекается с окружностью C₁. При этом будут иметь место соотношения $d({{\mathcal{P}}_{2}}) = 0$, $d({{\mathcal{P}}_{1}}) \ne 0$.

Рис. 5.

Оптимальная траектория ${{M}_{0}}A{{W}_{1}}M{{W}_{2}}$ обхода двух точек ${{W}_{1}}$, ${{W}_{2}}$ при ${{K}_{2}} = 0$ (а). Вид оптимальной траектории $\mathcal{L}$ и траекторий ${{\mathcal{L}}_{1}}$, ${{\mathcal{L}}_{2}}$ в случае ${{K}_{2}} \ne 0$ (б)

Заметим, что для обеспечения выполнения условия $d({{\mathcal{P}}_{2}}) \ne 0$ достаточно потребовать, чтобы расстояние r между точками W₁, W₂ было больше, чем 2R. Таким образом, справедливо следующее утверждение.

Утверждение 1. В случае ${{K}_{2}} = 0$ при выполнении неравенств $\rho > 3R$, $r > 2R$ у оптимальной траектории $\mathcal{L}$ будут существовать прямолинейные участки ${{\mathcal{P}}_{1}}$, ${{\mathcal{P}}_{2}}$. Участок ${{\mathcal{P}}_{1}}$ будет отсутствовать лишь тогда, когда имеют место соотношения $R < \rho \leqslant 3R$, ${{W}_{2}}\not { \in }C_{2}^{0}$ и длина дуги $A{{W}_{1}}$ меньше длины дуги ${{W}_{1}}M$ (рис. 5a).

5.2. Общий случай ${{K}_{2}} \ne 0$. Здесь также просто определить условия, при которых отсутствует участок ${{\mathcal{P}}_{1}}$, не представляется возможным. Это связано с наличием параметра u₂ и необходимостью выполнения второго соотношения в (2.1). Параметр u₂ влияет на изменение величины скорости, и при выполнении крутых разворотов необходимо эту величину уменьшать. Поэтому при движении по оптимальной траектории управляющая функция ${{u}_{2}}(t)$ может принимать как положительные, так и отрицательные значения по модулю, равные единице. Используя результаты исследования частного случая ${{K}_{2}} = 0$ и необходимость выполнения условия выравнивания, установим свойство оптимальной траектории, при котором ее прямолинейный участок ${{\mathcal{P}}_{1}}$ может отсутствовать.

При построении участка $\mathcal{L}{\text{*}}$ определим прямую переключения ${{l}_{2}}$. Предположим, что имеет место равенство $d({{\mathcal{P}}_{1}}) = 0$, т.е. участок ${{\mathcal{L}}_{ * }}$ траектории $\mathcal{L}$ между точками ${{M}_{0}}$, ${{W}_{1}}$ состоит из двух дуг ${{M}_{0}}A$ и $A{{W}_{1}}$ разного знака кривизны, где A – точка перегиба (рис. 3б, 5б). Используем обозначения: ${{l}_{3}}$ – прямая, проходящая через точки A и ${{M}_{0}}$; ${{\vec {v}}_{a}}$ – вектор скорости объекта (1.1) в точке $A$; ${{l}_{ * }}$ – луч, исходящий из точки A в направлении, противоположном вектору ${{\vec {v}}_{a}}$; l₄ – прямая, содержащая ${{l}_{ * }}$ (прямые l₃, l₄ изображены на рис. 3б, 5б пунктирными линиями); G – сектор, ограниченный прямой l₃ и лучом ${{l}_{ * }}$; ${{G}_{ * }}$ – сектор, симметричный G относительно точки $A$; F – точка пересечения прямой l₂, содержащей участок ${{\mathcal{P}}_{2}}$, с прямой l, проходящей через точку ${{W}_{1}}$ ортогонально вектору ${{\vec {v}}_{1}}$. Для выполнения условия выравнивания прямую l₁ будем проводить через точки A, F.

Утверждение 2. Для оптимальности траектории $\mathcal{L}$, не имеющей прямолинейного участка ${{\mathcal{P}}_{1}}$, необходимо, чтобы прямая l₁ принадлежала области $G \cup {{G}_{ * }}$.

Действительно, в противном случае прямая l₁ будет пересекать участок ${{\mathcal{L}}_{ * }}$ траектории $\mathcal{L}$, что противоречит первому соотношению в (2.1).

Следствие. Если точка F не находится в области $G \cup {{G}_{ * }}$, то траектория $\mathcal{L}$ не может быть оптимальной.

На рис. 3б иллюстрированы два случая местоположения первой цели на траектории $\mathcal{L}$ в точках W₁, ${{\tilde {W}}_{1}}$. В первом случае точка $F \in G \cup {{G}_{ * }}$, а прямая переключения l₁ не пересекает траекторию ${{\mathcal{L}}_{ * }}$; во втором случае точка $\tilde {F}\not { \in }G \cup {{G}_{ * }}$. Поэтому соответствующая ей ${{\tilde {l}}_{1}}$ пересекает ${{\mathcal{L}}_{ * }}$ и, следовательно, не может быть прямой переключения.

Заключение. В задаче о последовательном сближении автомобиля с несколькими целями (точками) за наименьшее время ранее использовалась модель его движения с постоянной скоростью, что существенно упрощало определение оптимальной траектории, состоящей из дуг окружностей минимального радиуса и отрезков прямых. Но у водителя естественно имеются не только руль для смены направления движения автомобиля, но и педали тормоза, газа. Это обстоятельство здесь учитывается за счет введения дополнительного уравнения, описывающего изменение величины скорости, и дополнительного управляющего параметра.

В настоящей работе на основе ранее полученных необходимых условий оптимальности для задач последовательного сближения с группой целей, правила построения оптимального управления в случае одной цели и принципа Беллмана разработан алгоритм определения моментов переключения управляющих параметров. Этот алгоритм учитывает положение второй цели при движении из начального состояния к первой цели. Результаты исследования рассматриваемой задачи подтверждают понятное для автолюбителей правило быстродействия: при осуществлении крутых разворотов надо скорость уменьшать и наоборот увеличивать при движении по пологим траекториям.

Список литературы

Айзекс Р. Дифференциальные игры. М.: Мир, 1967.
Dubins L.E. On Curves of Minimal Length with a Constraint on Average Curvature and with Prescribed Initial and Terminal Positions and Tangents // Amer. J. Math. 1957. V. 79. P. 497–516.
Berdyshev Iu.I. Time-optimal Control Synthesis for a Fourth-order Nonlinear System // J. Appl. Math. Mech. 1975. V. 39. № 6. P. 948–956.
Хамза М.Х., Колас И., Рунгальдер В. Оптимальные по быстродействию траектории полета в задаче преследования // Управление космическими аппаратами и кораблями. М.: Наука, 1971. С. 410–418.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Физматгиз, 1961.
Бердышев Ю.И. Нелинейные задачи последовательного управления и их приложение. Екатеринбург: УрО РАН, 2015.
Бердышев Ю.И. Об оптимальном по быстродействию управлении обобщенной машиной Дубинса // Тр. ИММ УрО РАН. 2016. Т. 22. № 1. С. 26–35.
Ли Э.Б., Маркус Л. Основы теории оптимального управления. М.: Наука, 1972.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал