Известия РАН. Теория и системы управления, 2019, № 2, стр. 133-144
ВОССТАНОВЛЕНИЕ УГЛОВОГО ДВИЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА ПО ДАННЫМ О ТОКОСЪЕМЕ С ПАНЕЛЕЙ СОЛНЕЧНЫХ БАТАРЕЙ
И. В. Белоконов 1, А. В. Крамлих 1, И. А. Ломака 1, *, П. Н. Николаев 1
1 Самарский ун-т
Самара, Россия
* E-mail: igorlomaka63@gmail.com
Поступила в редакцию 11.05.2018
После доработки 25.11.2018
Принята к публикации 26.11.2018
Аннотация
Рассмотрена задача восстановления углового движения космического аппарата по измерениям тока с панелей солнечных батарей с использованием алгоритма дифференциальной эволюции, причем модель измерений учитывает световой поток, отраженный от Земли. Обоснована возможность применения алгоритма дифференциальной эволюции и модели измерений в задаче восстановления углового движения на примере космического аппарата Аист. Использование данного алгоритма значительно упрощает традиционную методику восстановления углового движения.
Введение. Угловое движение космического аппарата (КА) традиционно определяется системой управления движением, которая получает информацию от датчиков угловой скорости, звездных датчиков, датчиков местной вертикали, датчиков направления на Солнце и т.д. Во время полета КА на его борту могут возникнуть различные нештатные ситуации, например полный или частичный отказ измерительных датчиков системы управления движением, при этом КА будет совершать неуправляемое вращение вокруг центра масс. В таких случаях угловое движение КА восстанавливается по информации от одного/двух работоспособных измерительных средств, например, по измерениям магнитного поля Земли [1], по измерениям угловой скорости [2], по информации звездного датчика [3], по токосъему с панелей солнечных батарей (СБ) [4]. Большой вклад в изучение вопросов, связанных с восстановлением углового движения КА, внес В.В. Сазонов [1–6].
В данной работе также рассматривается восстановление движения КА по показаниям токосъема с панелей СБ. Однако в отличие от [4] применяется усложненная модель измерений, учитывающая световой поток, отраженный Землей, для повышения адекватности модели измерений. Важным отличием данной работы также является применение алгоритма дифференциальной эволюции (АДЭ), требующего только задания области нахождения решения для оцениваемых параметров, вместо традиционно применяемых алгоритмов первого порядка (например, алгоритм Гаусса–Ньютона [5] и алгоритм Левенберга–Марквардта [6]), чувствительных к заданию начального приближения и часто приводящих к возникновению проблем со сходимостью решения.
С момента своего создания в 1995 г. АДЭ [7] заработал репутацию эффективного алгоритма глобальной оптимизации и нашел свое приложение в различных задачах, таких, как задача N тел [8], обратные задачи [9, 10]. Существуют работы, сравнивающие эффективность АДЭ с более традиционными методами, такими, как методы Пауэлла и Нелдера–Мида [9], алгоритм имитации отжига [8] и простой генетический алгоритм [11].
С помощью АДЭ решались задачи в космической отрасли, например, в [12] с помощью него выполнялся поиск оптимальной траектории полета КА, а в [13] с помощью АДЭ выполнялся поиск оптимальных траекторий движения роботизированного манипулятора для захвата космического мусора. В [14] АДЭ использован для определения моментов инерции КА в полете при приложении к КА управляющих воздействий с помощью маховиков и двигателей ориентации. Решения задачи с помощью АДЭ в меньшей степени зависит от начальных условий, чем у аналогичных алгоритмов. При этом по утверждению авторов достигается более точный результат, особенно при широком диапазоне возможного значения начального вектора состояния [9].
Преимуществами использования АДЭ по сравнению с приведенными алгоритмами являются, во-первых, отсутствие необходимости поиска начального приближения для искомых параметров. Во-вторых, отсутствие необходимости вычисления частных производных минимизируемой функции, что позволяет избавиться от трудоемких математических преобразований и дает возможность использования более сложных математических моделей углового движения и моделей измерений. В-третьих, достигается повышение точности решения из-за отсутствия необходимости численного нахождения частных производных и обеспечивается поиск глобального экстремума в отличие от методов первого и второго порядка, которые зачастую отыскивают локальные экстремумы.
Недостатком использования АДЭ является длительное время вычислений вследствие большого числа обращений к минимизируемой функции.
В настоящей работе представлены результаты решения задачи восстановления углового движения КА на реальных данных о токосъеме, полученных с борта малого КА (МКА) Аист-1, использующего для стабилизации движения магнитные катушки (эксперимент Магком) [15] во время его полета в мае 2013 г. Данный промежуток времени выбран для сравнения результатов восстановления, полученных при помощи предложенного подхода, с результатами из [5].
Решение задачи восстановления углового движения состоит из следующих этапов:
1) определение параметров движения центра масс КА на требуемом промежутке времени (например, с использованием GNSS, обработки TLE файлов [16, 17] или по информации из ЦУПа) путем интегрирования уравнений движения центра масс КА с учетом второй и четвертой зональных гармоник разложения потенциала поля притяжения Земли;
2) вычисление вектора направления на Солнце [18] и определение затененных/освещенных участков орбиты [19];
3) применение АДЭ для оценки вектора состояния КА на начальный момент времени.
1. Модифицированная модель измерений. Вследствие сложности учета процессов, происходящих в солнечных панелях, примем, что СБ представляет собой плоскую поверхность, ориентация которой задается единичным вектором нормали n в связанной системе координат (ССК). Ток, генерируемый СБ (${{I}_{{{\text{п р }}}}}$ – ток от прямого солнечного излучения, Imax – максимальное значение тока с панелей, определяется из телеметрии, в данной работе Imax = 0.95 Å), принимается пропорциональным косинусу угла падения солнечных лучей на их светочувствительную поверхность:
где S – единичный вектор направления на Солнце, cos(n, S) – косинус угла между соответствующими векторами.Для солнечных лучей Земля представляет собой оптически весьма неоднородную и изменчивую поверхность. На фотографии нашей планеты с большого расстояния можно видеть вечно изменяющийся облачный покров, почти полностью скрывающий за собой поверхность материков и морей. Визуальная яркость различных участков земного шара меняется в широком диапазоне, причем как в видимом, так и в невидимом участках спектра. Отраженное солнечное излучение складывается из излучения, отраженного от облачного покрова, излучения, отраженного от подстилающей поверхности, а также излучения, рассеянного атмосферой.
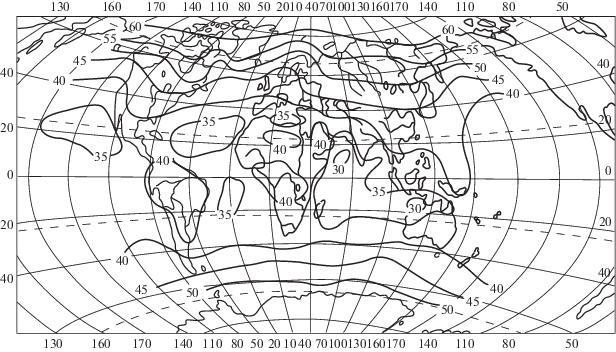
Двигаясь по низким орбитам над поверхностью Земли, КА облучается в каждый момент времени лишь от какой-то ее небольшой области, для которой местное альбедо может отличаться от среднего планетарного сферического альбедо (рис. 1).
Причина отличия местного альбедо от среднего сферического заключается не только в том, что разные участки Земли обладают разными отражательными способностями, но и в том, что коэффициенты отражения большинства участков земной поверхности зависят от угла падения солнечных лучей. Под большими углами бликующие и зеркалящие поверхности отражают лучи совсем иначе, чем диффузно рассеивающие поверхности, даже если при нормальном облучении их коэффициенты отражения оказываются близкими. Экспериментальные исследования отражательной способности снега, песка, земли, воды и т.д. показали, что диапазон изменения альбедо разных участков земной поверхности весьма широк от 0.03 для леса до 0.9 для свежевыпавшего снега [20].
Поэтому в отличие от [6] помимо учета генерации тока от прямого солнечного излучения, описываемого моделью (1.1), в данной работе также учитывается ток Iотр, генерируемый отраженным от Земли солнечным излучением:
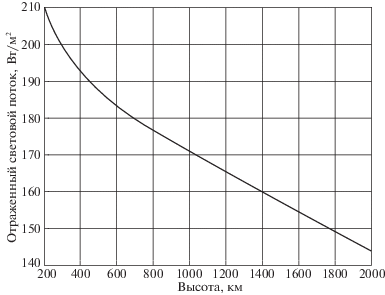
где Aср – усредненное значение альбедо Земли, φ2 – комбинированный угловой коэффициент [20]. Таким образом, модель измерений в данной работе имеет видИзвестны работы по исследованию зависимости величины отраженного Землей солнечного излучения от высоты орбиты, данная зависимость приведена в работе [21] (рис. 2).
Из рис. 2 видно, что доля отраженного излучения от общего светового потока, излучаемого Солнцем (1400 Вт/м2), составляет в среднем от 10 до 15%.
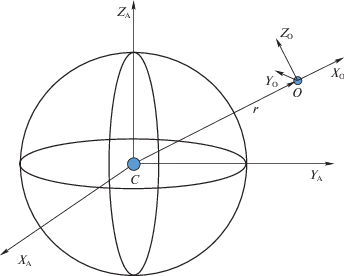
2. Постановка задачи идентификации углового движения КА по информации о токосъеме с панелей. Для записи уравнений движения КА вокруг центра масс (точка O) (рис. 3), а также соотношений, используемых при обработке данных, вводятся три правые декартовые системы координат.
Связанная с КА система координат (ССК) образована главными центральными осями инерции и имеет обозначение OXcYcZc. Абсолютная геоцентрическая система координат (АСК) имеет обозначение CXAYAZA с началом в центре масс Земли (точка C). Ось XA направлена в точку весеннего равноденствия. Ось ZA направлена в северный полюс мира. Ось YA дополняет систему до правой. Орбитальная система координат (ОСК) имеет обозначение OXoYoZo. Начало системы находится в центре масс КА. Ось Xo направлена по радиус-вектору КА. Ось Zo перпендикулярна плоскости орбиты. Ось Yo дополняет систему до правой.
ОСК получается из АСК тремя последовательными поворотами на угол долготы восходящего
узла Ω вокруг оси ZA, на угол наклонения орбиты i вокруг новой оси ${{X}_{{\text{A}}}}'$ на аргумент широты u вокруг новой оси 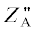 . Положение ССК относительно ОСК задается тремя последовательными поворотами на угол
прецессии ψ вокруг оси Yo, угол атаки α вокруг новой оси ${{Z}_{{\text{o}}}}'$ и на угол собственного вращения φ вокруг новой оси
. Положение ССК относительно ОСК задается тремя последовательными поворотами на угол
прецессии ψ вокруг оси Yo, угол атаки α вокруг новой оси ${{Z}_{{\text{o}}}}'$ и на угол собственного вращения φ вокруг новой оси 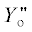 .
.
Вращательное движение КА описывается динамическими уравнениями Эйлера (2.1) и кинематическими уравнениями (2.2) [5]. В правых частях динамических уравнений Эйлера учитываются гравитационный и дипольный моменты. Уравнения движения имеют следующий вид:
(2.1)
${{\dot {\omega }}_{y}} = \frac{{1 - \lambda }}{{1 + \lambda \mu }}({{\omega }_{x}}{{\omega }_{z}} - v{{a}_{{31}}}{{a}_{{11}}}) + \frac{\lambda }{{1 + \lambda \mu }}({{p}_{3}}{{b}_{1}} - {{p}_{1}}{{b}_{3}}),$
(2.2)
$\frac{{d{{q}_{1}}}}{{dt}} = 0.5(({{\omega }_{x}} - {{\omega }_{{rx}}}){{q}_{0}} + ({{\omega }_{z}} - {{\omega }_{{rz}}}){{q}_{2}} - ({{\omega }_{y}} - {{\omega }_{{ry}}}){{q}_{3}}),$Матрицу A перехода из ОСК в ССК запишем следующим образом:
3. Процедура нахождения численного решения. Исходя из метода наименьших квадратов, аппроксимацией движения КА на отрезке времени будем считать совместное решение систем (2.1) и (2.2) из условия наилучшего сглаживания с их помощью телеметрических данных о токе, снимаемом с панелей СБ, т.е. доставляющее минимум функционалу:
(3.1)
$J(b) = \sum\limits_{i = 1}^6 {\sum\limits_{k = 1}^{{{N}_{t}}} {{{{({{I}_{{ik}}} - {{{\hat {I}}}_{{ik}}}(b))}}^{2}}} } ,$Величины Aср, λ, μ являются параметрами согласования. Следует заметить, что расчеты при аппроксимации углового движения производятся в кватернионах, однако для удобства интерпретации результатов на входе и выходе алгоритма используются углы Эйлера.
Поиск минимума функционала (3.1) осуществляется с помощью алгоритма дифференциальной эволюции [7], который заключается в выполнении следующих этапов:
1) задание исходного массива X, состоящего из N векторов b (N на каждой итерации постоянно и является одним из параметров АДЭ), причем каждый элемент вектора b генерируется случайным образом в требуемых пределах;
2) генерация нового массива Xnew векторов b: для каждого вектора bi из массива X выбираются случайным образом три различных вектора b1, b2, b3 индексы которых не совпадают с индексом вектора bi, и вычисляется так называемый модифицированный вектор (mutant vector) по формуле bm = b1 + F(b2 – b3), где F – константа в интервале [0, 1], являющаяся параметром алгоритма АДЭ;
3) над модифицированным вектором bm выполняется операция “скрещивания” (crossover), состоящая в том, что некоторые его элементы замещаются соответствующими элементами из исходного вектора bi (каждый элемент замещается с вероятностью P, которая также является еще одним параметром алгоритма АДЭ);
4) если полученный вектор оказывается лучше вектора bi, т.е. значение целевой функции уменьшается J(bt) < J(bi), то в новом массиве Xnew вектор bi заменяется на новый вектор bt (называется пробным вектором, trial vector), в противном случае сохраняется bi;
5) пункты 1–4 повторяются, пока не будет выполнен критерий остановки.
Критерий остановки зависит от решаемой задачи. В данной статье алгоритм прекращает работу, как только разность между значениями функции на следующей и предыдущей итерациях становится меньше 0.001 А2.
4. Оценка эффективности использования алгоритма АДЭ на реальных измерениях, полученных с МКА Аист. Разработан ФГУП ГНПРКЦ “ЦСКБ – Прогресс” совместно с Самарским университетом и предназначен для научных исследований. Запуск спутника осуществлен 21 апреля 2013 г. попутным образом посредством отделения от КА Бион M1, находящегося на почти круговой орбите с высотой 570 км и наклонением 54.9°. Режим орбитального полета спутника – неориентированный, время активного существования составляет до 3 лет [5]. При такой высоте орбиты аэродинамический момент оказывает значительно меньшее влияние на вращательное движение КА по сравнению с гравитационным моментом, поэтому в уравнениях (2.1) не учитывается влияние атмосферы на движение КА.
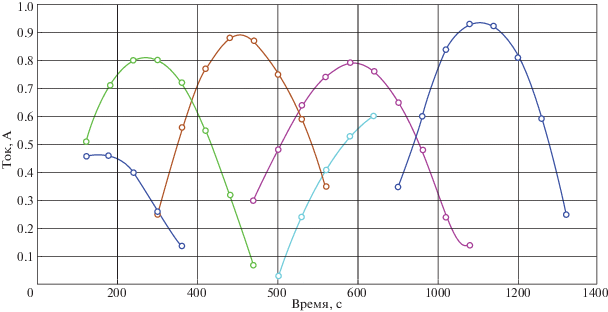
Предварительная обработка информации о токосъеме с панелей СБ МКА Аист заключается в аппроксимации измерений, полученных с каждой из шести панелей, кубическими сплайнами. Аппроксимация необходима для пересчета измерений на моменты времени вычисления углового движения. Измерения тока проводились с периодом в 60–61 с, поэтому аппроксимации изменения токосъема проводятся с шагом в 10 с. Выбранный временной шаг аппроксимации позволяет производить интегрирование уравнений (2.1) и (2.2) с требуемой точностью. Результаты сглаживания представлены на рис. 4. Измерения получены на интервале времени 16.03.2013 21:13–16.03.2013 22:21 ДМВ.
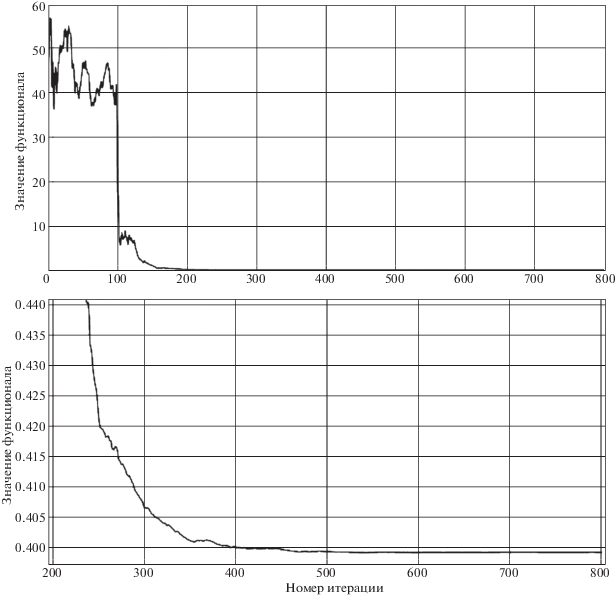
Для решения задачи восстановления углового движения МКА Аист применялись следующие параметры АДЭ (такие параметры традиционно рекомендуются для данного алгоритма): N = 140; F = 0.5; P = 0.9. Результаты работы алгоритма приведены на рис. 5. Поиск оцениваемых параметров производился в следующих областях: начальные углы ориентации (ψ(t0), α(t0), φ(t0)) определялись в области от 0 до 2π радиан, начальные угловые скорости (x(t0), y(t0), z(t0)) – в области ±2 град/с, безразмерные коэффициенты λ и μ – в областях от 0.7 до 1.5 и от –0.5 до 0.5 соответственно, среднее альбедо Земли – в диапазоне от 0 до 1, на коэффициент дипольного момента p ограничения не накладывались. В результате работы алгоритма были получены следующие оценки искомых параметров (таблица), на рис. 5 приведена аппроксимация измерений тока математической моделью, на рис. 6 – зависимость значения функционала (3.1) от номера итерации.
Рис. 5.
Аппроксимация измерений, (“○” – сглаженные значения тока, линии – аппроксимация математической моделью (1.2))
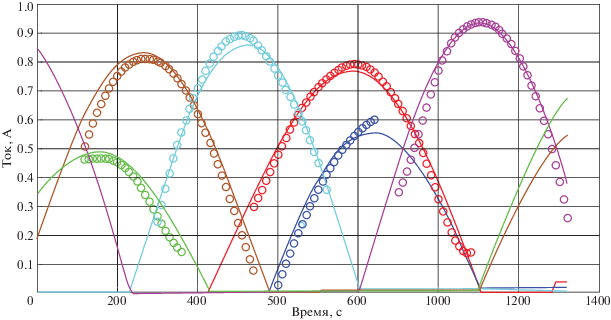
Таблица.
Результаты работы алгоритма
| Величина | Значение |
|---|---|
| ωx(t0), рад/с | 0.0041 |
| ωy(t0), рад/с | 0.002 |
| ωz(t0), рад/с | –0.0026 |
| ψ(t0), рад | 5.448 |
| α(t0), рад | 1.3 |
| φ(t0), рад | 3.93 |
| Aср | 0.102 |
| λ | 0.832 |
| μ | 0.214 |
| p, Ас/кг | –18 × 109 |
Для оценки точности аппроксимации применялась следующая формула стандартного отклонения [6]:
где J(bk) – значение функционала на последней итерации, в данной задаче J(bk) = 0.2515 А2, N = 234, σ = 0.04 А.Относительную погрешность аппроксимации значений тока определим как σотн = (σ/Imax) ⋅ 100%. Для полученного в данной работе решения σотн = 4%, а результат в аналогичной задаче, решенной в [6], близок по точности – σотн = 3.8%, что свидетельствует о достоверности приведенного решения.
Согласно рис. 2 [21], величина отраженного Землей солнечного излучения на высоте полета МКА Аист составляет порядка 180 Вт/м2. Учитывая, что величина прямого солнечного излучения равно 1400 Вт/м2, значение среднего альбедо составит Аср = 180/1400 = 0.128, что близко к полученной в данной работе оценке Аср = 0.102.
Заметим, что определенные в данной работе коэффициенты инерции λ = 0.832 и μ = 0.214 значительно отличаются от соответствующих коэффициентов (обозначим их как λ5, μ5), приведенных в [5]. Это объясняется тем, что связанная система координат в работе [5], в которой определяются моменты инерции МКА Аист, отличается от связанной системы координат, из данной статьи. Установим соответствие между моментами инерции в настоящей работе и [5]. Для этого расположим моменты инерции в порядке их возрастания. Из анализа величин λ и μ публикации [5] следует соотношение I2 > I1 > I3, а в данной работе Iy > Iz > Ix. Так как объектом исследования в обеих работах является один и тот же КА, то можно построить следующие соответствия между моментами инерции Iy ↔ I2, Iz ↔ I1, Ix ↔ I3. Пересчитаем полученные λ и μ с учетом соотношений λ1 = 1/λ = 1.202, μ1 = (1 – λ + λμ) = 0.346. Пересчитанные значения коэффициентов соответствуют данным, приведенным в [5].
Таким образом, можно сделать вывод о пригодности использования алгоритма АДЭ и предложенной математической модели измерений токосъема для определения параметров вращательного движения КА. Найденная оценка модуля угловой скорости вращения МКА Аист на время 21:13 16.05.2013 ДМВ |ω| = 0.346 град/с близка к значению |ω| = 0.338 град/с, из работы [5] на тот же момент времени, что также подтверждает правильность полученного результата и возможность применения алгоритма АДЭ для решения задач восстановления углового движения.
5. Оценка влияния учета альбедо Земли в задаче восстановления углового движения. Для оценки влияния учета альбедо Земли было проведено статистическое моделирование решения задачи. Моделирование происходило следующим образом:
1. Было сгенерировано случайным образом 400 вариантов начальных условий углового движения ωx(t0), ωy(t0), ωz(t0), ψ(t0), α(t0), φ(t0), в предположении равновероятного закона их распределения. Полагалось, что |ω| ≤ 1 град/с, ψ(t0) и φ(t0) лежат в диапазоне от 0 до 360°, а α(t0) – от 0 до 180°.
2. Для каждого варианта начальных условий были смоделированы измерения тока, учитывающие влияние альбедо Земли, согласно формуле (1.2), в предположении отсутствия шума в измерениях.
3. Каждый набор измерений использовался для восстановления начальных условий углового движения дважды: в первом случае алгоритм восстановления учитывал влияние альбедо Земли, а во втором – нет.
4. Результаты решения задачи в обоих случаях сравнивались с начальными условиями, которые применялись для моделирования измерений. В результате были получены методические ошибки алгоритма восстановления углового движения и определено влияние учета альбедо Земли на результаты восстановления углового движения.
Результаты моделирования приведены на рис. 7, 8, где использованы следующие обозначения: М – математическое ожидание, σ – среднеквадратическое отклонение. Согласно полученным результатам, неучет отраженного от Земли излучения приводит к ошибкам в определении ориентации порядка 12° (3σ) и угловой скорости порядка 0.075 град/с (3σ).
Рис. 7.
Распределение вероятности ошибок восстановления параметров углового движения с учетом альбедо Земли
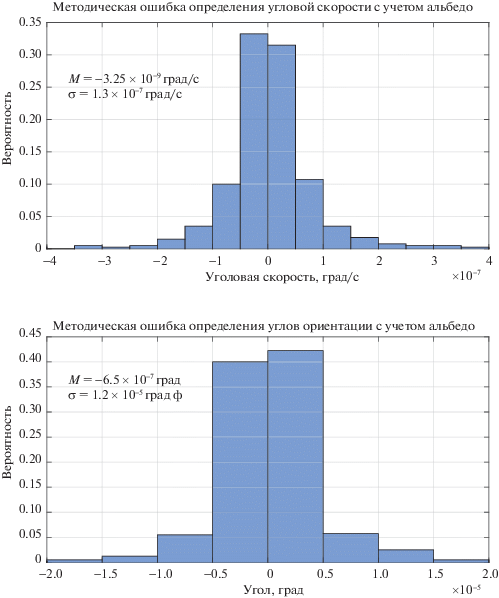
Рис. 8.
Распределение вероятности ошибок восстановления параметров углового движения без учета альбедо Земли
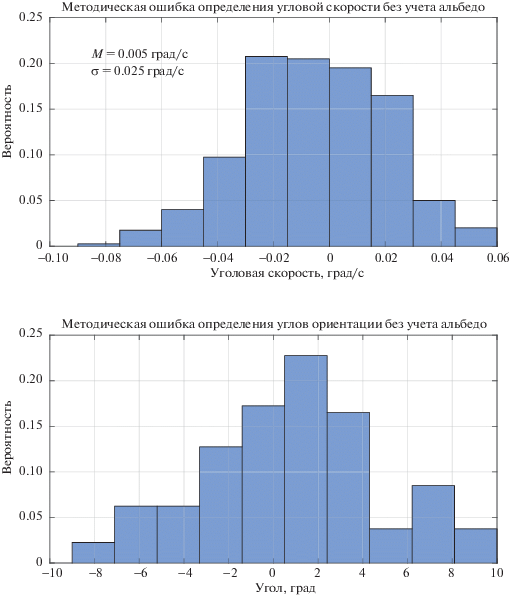
Заключение. Предложенный в работе алгоритм позволяет не только восстановить угловое движение КА по измерениям токосъема, но и оценить с достаточной точностью моменты инерции, что подтверждено на примере МКА Аист.
Полученные результаты согласуются с данными технической документации на КА и не противоречат работе [5]. Найденная оценка среднего альбедо Земли по результатам обработки показаний токосъема согласуется с работой [21]. Обоснована целесообразность использования модели отраженного солнечного излучения в задаче определения вращательного движения КА. Оценен вклад ошибок в восстановлении углового движения, возникающих, вследствие неучета отраженного солнечного излучения. Используемый алгоритм АДЭ, благодаря отсутствию необходимости задания “хорошего” начального приближения, имеет большую область сходимости и может быть применен для идентификации объектов, параметры которых заранее неизвестны.
Список литературы
Абрашкин В.И., Балакин В.Л., Белоконов И.В., Воронов К.Е., Зайцев А.С., Иванов В.В., Казакова А.Е., Сазонов В.В., Семкин Н.Д. Определение вращательного движения спутника “Фотон-12” по данным бортовых измерений магнитного поля Земли // Препринт ИПМ им. М.В. Келдыша. 2000. № 60.
Беляев М.Ю., Волков О.Н., Монахов М.И., Сазонов В.В. Оценка точности методики реконструкции вращательного движения спутника по измерениям его угловой скорости и магнитного поля Земли // Препринт ИПМ им. М.В. Келдыша. 2016. № 4.
Аванесов Г.А., Бессонов Р.В., Куркина А.Н., Никитин А.В., Сазонов В.В. Определение движения космического аппарата по измерениям четырех звездных датчиков // Препринт ИПМ им. М.В. Келдыша. 2016. № 57.
Беляев М.Ю., Матвеева Т.В., Монахов М.И., Сазонов В.В., Цветков В.В. Определение вращательного движения кораблей Прогресс по данным измерений угловой скорости и токосъема с солнечных батарей // Препринт ИПМ им. М.В. Келдыша. 2012. № 39.
Абрашкин В.И., Воронов К.Е., Пияков А.В., Пузин Ю.Я., Сазонов В.В., Семкин Н.Д., Филиппов А.С., Чебуков С.Ю. Определение вращательного движения спутника Аист по данным бортовых измерений магнитного поля Земли // Препринт ИПМ им. М.В. Келдыша. 2014. № 17.
Давыдов А.А., Сазонов В.В. Определение параметров вращательного движения малого спутника связи по данным измерений тока солнечных батарей // Препринт ИПМ им. М.В. Келдыша. 2009. № 32.
Storn R., Price K. Differential Evolution – A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces // International Computer Science Institute. Berkeley, 1995.
Chakraborti N. Genetic Algorithms and Related Techniques for Optimizing Si-H Clusters: A Merit Analysis for Differential Evolution // Natural Computing Series. Berlin: Springer, 2005. P. 313–326.
Růžek B., Kvasnička M. Determination of the Earthquake Hypocenter: A Challenge for the Differential Evolution Algorithm. In: Differential Evolution // Natural Computing Series. Berlin: Springer, 2005. P. 379–391.
Wormington M., Matney K.M., Bowen D.K. Application of Differential Evolution to the Analysis of X-Ray Reflectivity Data. In: Differential Evolution // Natural Computing Series. Berlin: Springer, 2005. P. 463–478.
Joshi R., Sanderson A.C. Minimal Representation Multi-Sensor Fusion Using Differential Evolution // Natural Computing Series. Berlin: Springer, 2005. P. 353–377.
Changqing W., Rui X., Shengying Z., Pingyuan C. Time-optimal Spacecraft Attitude Maneuver Path Planning Under Boundary // Acta Astronautica. 2017. April. P. 128–137.
Mingming W., Jianjun L., Jing F., Jianping Y. Optimal Trajectory Planning of Free-Floating Space Manipulator Using Differential Evolution Algorithm // Advances in Space Research. 2018. March. P. 1525–1536.
Mingliang S., Xinlong C., Shunli L. Identification of Mass Characteristic Parameters for Spacecraft Based on Differential Evolution Algorithm // Instrumentation and Measurement, Computer, Communication and Control (IMCCC), 2015 Fifth International Conf. Qinhuangdao, 2015.
Kirilin A.N., Akhmetov R.N., Abrashkin V.I., Shakhmatov E.V., Soifer V.A., Tkachenko S.I., Prokofiev A.B., Stratilatov N.R., Salmin V.V., Semkin N.D., Tkachenko I.S. Design, Testing and Operation of Aist Small Satellites // Pro. 7th Intern. Conf. on Recent Advances in Space Technologies. Istanbul, 2015. P. 819–823.
Hoots F.R., Roehrich R.L. Models for Propagation of NORAD Element Sets, Spacetrack report 3. USA, 1988.
Мантуров А.И. Механика управления движением космических аппаратов. Самара, СГАУ, 2003. С. 38, 39.
Прогноз орбитального движения космического аппарата. Численная модель 2007. URL: http://vadimchazov.narod.ru/text_pdf/comalg.pdf
Srivastava V.K., Pitchaimani A.M., Chandrasekhar B.S. Eclipse Prediction Methods for LEO Satellites With Cylindrical and Cone Geometries: A Comparative Study of ECSM and ESCM to IRS satellites // Astronomy and Computing. 2013. V. 2. P. 88–96.
Козлов Л.В., Нусинов М.Д., Акишин А.И. Моделирование тепловых режимов космического аппарата и окружающей его среды. М.: Машиностроение, 1971.
Bhanderi D., Bak T. Modeling Earth Albedo for Satellites in Earth Orbit // Pro. AIAA Conf. on Guidance, Navigation and Control. San Francisco, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления