Известия РАН. Теория и системы управления, 2019, № 2, стр. 117-132

Введение. Рассматривается задача использования электродинамической тросовой системы (ЭДТС) на низкой околоземной орбите для компенсации атмосферных возмущений, действующих на систему. Система состоит из двух наноспутников (НС), связанных проводящим ток тросом. Тросовая система работает в режиме генерации тяги, что обеспечивает при определенном направлении тока подъем высоты орбиты.

До настоящего времени известно большое количество работ, посвященных использованию ЭДТС для различных целей [1], в частности, для изменения параметров орбит космических аппаратов (КА) [2]. Теоретические исследования в этом направлении сопровождаются проведением реальных экспериментов в космосе в различных странах, которых насчитывается более десятка [3]. Режим генерации тяги при использовании ЭДТС обеспечивается разностью потенциалов [1], которая возникает за счет бортовых источников энергии КА. При этом можно изменять величину тока в тросе, а значит, и величину силы Ампера, которая действует на проводник (трос) в магнитном поле Земли.

При использовании ЭДТС для изменения параметров орбиты трос должен находиться вблизи вертикали, так как в этом случае вектор силы Ампера почти параллелен вектору скорости центра масс системы, и использование ЭДТС наиболее эффективно. Поэтому положения равновесия системы вблизи вертикали называются “рабочими” положениями равновесия системы [1]. В многих статьях [2, 4, 5] показано, что “рабочие” положения равновесия ЭДТС при постоянном токе в тросе динамически неустойчивы, что проявляется в возрастании амплитуд колебаний переменных системы относительно этих положений равновесия. Ниже в статье показано, что при учете аэродинамических сил, действующих на все части ЭДТС, включая трос, динамическая неустойчивость “рабочих” состояний равновесия системы сохраняется. Однако, с другой стороны, также показано, что выбором параметров ЭДТС можно уменьшить скорость изменения амплитуд колебаний в системе и приблизить “рабочие” равновесные положения троса к вертикали.

Для компенсации неустойчивости в движении ЭДТС применяются как пассивные [6], так и активные методы стабилизации [7–9]. В данной статье описан активный алгоритм стабилизации, основанный на определении поправок к номинальной величине тока, т.е. величина тока определяется как сумма $I = {{I}_{n}} + \Delta I$, где ${{I}_{n}}$ – номинальная величина тока, $\Delta I$ – управляющие стабилизирующие воздействия, определяемые на основании принципа обратной связи. В известных алгоритмах поправки $\Delta I$ определяются в соответствии с моделями, в которых трос приближается прямой линией [7–9]. Однако известно, что если масса троса много меньше массы концевых тел (т.е. трос можно считать невесомым), то форма троса в каждый момент времени приближается частью окружности определенного радиуса [1, 10]. Изменение радиуса дуги окружности можно рассматривать как изгибные колебания троса под действием распределенных нагрузок от сил Ампера и аэродинамических сил. Изгиб троса возрастает, если концевые тела системы имеют сравнительно малую массу, например, если в состав ЭДТС входят НС. При определeнных условиях (они будут описаны ниже) именно возрастание амплитуд изгибных колебаний троса приводит к динамической неустойчивости в рассматриваемой системе. Поэтому в настоящей работе предлагается алгоритм стабилизации, в котором производится контроль над расстоянием между концевыми телами системы (хордой части окружности) и его производной.

1. Постановка задачи. Для синтеза алгоритма стабилизации и оценки его эффективности производится построение двух математических моделей, учитывающих изгибные колебания троса. Первая модель, полученная методом Лагранжа для невесомого троса в [10] с помощью методики, изложенной в [1], дополняется обобщенными аэродинамическими силами. В этой модели в отличие от [1] рассматривается случай произвольного соотношения масс концевых тел и наклонные эллиптические орбиты. Вторая модель движения ЭДТС используется для оценки эффективности применения разработанного алгоритма стабилизации, так как в ней нет многих допущений первой модели: трос считается весомым, распределенные нагрузки не являются постоянными вдоль троса, форма троса может быть произвольной и т.д. Эту модель можно рассматривать как некоторое приближение к модели с распределенными параметрами в частных производных [1], так как в ней трос представляется как совокупность материальных точек, связанных между собой односторонними упругими механическими связями. Модель с распределенными параметрами записывается в геоцентрической прямоугольной системе координат. Аналогичные модели использовались во многих работах [11–14] при описании движения космических тросовых систем при другой совокупности действующих на систему сил.

Для приближенного синтеза алгоритма регулирования (или регулятора) проводится линеаризация модели движения, полученной методом Лагранжа, относительно “рабочих” положений равновесия, и применяется принцип динамического программирования Беллмана [15, 16]. Синтез регулятора осуществляется с помощью квадратичного критерия оптимальности, зависящего от отклонений переменных системы относительно рассматриваемых положений равновесия и величины управляющих воздействий. Эффективность предложенного подхода подтверждается результатами численного моделирования.

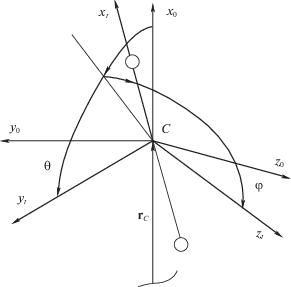
2. Уравнения движения ЭДТС для невесомого троса. Известно, что форма невесомого троса при действии постоянной распределенной нагрузки является дугой окружности некоторого радиуса [1]. Введем систему координат (рис. 1), связанную с хордой этой дуги $C{{x}_{t}}{{y}_{t}}{{z}_{t}}$, где $C$ – центр масс системы, а ось $C{{x}_{t}}$ направлена для определенности от нижней концевой точки троса к верхней точке. Положение системы координат $C{{x}_{t}}{{y}_{t}}{{z}_{t}}$ определим относительно правой орбитальной прямоугольной системы $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ углами ${\theta ,}\,{\varphi }$, как это показано на рис. 1, где ось $C{{x}_{o}}$ направлена по радиус-вектору центра масс системы вверх, ось $C{{y}_{o}}$ – в плоскости орбиты по направлению движения центра масс. Здесь кручением троса пренебрегается, т.е. предполагается, что трос располагается в одной плоскости $C{{x}_{t}}{{y}_{t}}$. Углы ${\theta ,}\,{\varphi }$ определяются следующим образом: первый поворот против часовой стрелки осуществляется относительно оси $C{{z}_{o}}$ на угол ${\theta }$; второй поворот по часовой стрелке – относительно оси $C{{y}_{t}}$ на угол ${\varphi }$.

В качестве обобщенных координат при применении метода Лагранжа используются переменные $r,{\theta ,}\,{\varphi }$, где $r$ – расстояние между концевыми точками (длина хорды). В [1] для случая, когда масса одной концевой точки много больше другой для круговой экваториальной орбиты в координатах $r,{\theta ,}\,{\varphi }$, получены уравнения, описывающие угловые движения ЭДТС относительно верхней концевой точки. С применением методики [1] в статье [10] проведено обобщение этих уравнений на случай произвольных масс концевых точек и на наклонные эллиптические орбиты. С точностью до обобщенных сил, которые определяют действие сил Ампера и аэродинамических сил, эти уравнения имеют вид [10]

где ${{Q}_{{{\theta ,}r{,\varphi }}}}$ – обобщенные силы, ${{m}_{e}} = {{m}_{a}}{{m}_{b}}{\text{/}}m$, $m = {{m}_{a}} + {{m}_{b}}$, ${{m}_{{a,b}}}$ – массы концевых точек (${{m}_{b}}$ – верхняя точка), $m = {{m}_{a}} + {{m}_{b}}$, ${\omega } = \dot {\vartheta } = {{({\mu /}{{p}^{{\text{3}}}})}^{{0.5}}}{{{\nu }}^{2}}$, ${\dot {\omega }} = \ddot {\vartheta } = - 2{\mu }{{{\nu }}^{3}}e\sin \vartheta {\text{/}}{{p}^{3}}$, ${\nu } = 1 + e\cos \vartheta $, ${\mu }$ – гравитационный параметр Земли, $e$ – эксцентриситет орбиты, $\vartheta $ – истинная аномалия, $p$ – параметр орбиты.

При выводе уравнений (2.1)–(2.3) предполагается: 1) движение центра масс системы происходит по невозмущенной орбите; 2) трос невесом; 3) длина хорды $r$ много меньше, чем расстояние центра масс системы до притягивающего центра; 4) концевые тела – материальные точки; 5) гравитационное поле ньютоновское.

Сила Ампера, действующая на элементарный участок троса, определяется известной формулой [1]

где $I$ – величина тока, $B$ – вектор магнитной индукции, $\tau $ – единичный вектор касательной к тросу, $ \times $ – знак векторного произведения.

При определении сил Ампера модель магнитного поля Земли представляет собой прямой диполь [1], поэтому

где ${{B}_{0}} = {{{\mu }}_{m}}{\text{/}}r_{c}^{3}$, ${{{\mu }}_{m}} = 8 \times {{10}^{6}}\,\,{\text{Т л }}\,{\text{к }}{{{\text{м }}}^{{\text{3}}}}$ – магнитный момент земного диполя, ${{e}_{r}} = {{r}_{c}}{\text{/}}{{r}_{c}}$, ${{e}_{z}}$ – единичный вектор оси вращения Земли; $\left( {{{e}_{z}}{{e}_{R}}} \right)$ – скалярное произведение.

Обобщенные силы определяются как суммы

где $Q_{{{\theta ,}r{,\varphi }}}^{{(1)}}$ и $Q_{{{\theta ,}r{,\varphi }}}^{{(2)}}$ – составляющие обобщенных сил, соответствующие силам Ампера и аэродинамическим силам.

Составляющие $Q_{{{\theta ,}r{,\varphi }}}^{{(1)}}$ определены в [10] и имеют вид

где $i$ – наклонение орбиты, $u$ – аргумент широты, $\Delta = 0.5r({{m}_{b}} - {{m}_{a}}){\text{/}}m$, ${\psi }$ – угол между касательной к окружности, проведенной через концевые точки, и хордой, соединяющей их (рис. 2); $Q_{{\psi }}^{{(1)}} = 0.5{{B}_{0}}\cos i{\text{|}}I{\text{|}}{{r}^{2}}\sin {\varphi }\cos {\varphi (ctg\psi } - {{{\psi }}^{{ - 1}}}{\text{)}}$, $\Delta Q_{{\theta }}^{{(1)}} = 3{{B}_{0}}Ir\Delta \sin i\cos {\theta }\sin {\varphi }\sin u$, $I$ – величина тока. Для определенности величина тока $I$ считается положительной, если он направлен от точки ${{m}_{a}}$ к точке ${{m}_{b}}$.

Составляющие (2.7) в отличие от [10], где использовалась более простая модель для магнитного поля $B = {{B}_{o}}{{e}_{z}}$, определяются в соответствии с моделью (2.5).

Угол ${\psi }$ находится из геометрического соотношения [1]

где $L$ – недеформированная длина троса, ${{{\gamma }}_{t}} = 2{{E}_{t}}{\psi /(}2{{E}_{t}}{\psi } - B{\text{|}}I{\text{|}}L{\text{)}}$ – относительное удлинение троса, ${{E}_{t}}$ – жесткость троса. Здесь предполагается, что при растяжении трос подчиняется закону Гука. Выражение (2.8) представляет собой нелинейное алгебраическое уравнение, которое решается численно при известных значениях $r,{\varphi }$, определенных из системы (2.1)–(2.3). При этом радиус ${{r}_{t}} = r{\text{/(}}2\sin {\psi )}$ характеризует часть окружности, которая описывает форму троса.

При определении обобщенных аэродинамических сил $Q_{{{\theta ,}r{,\varphi }}}^{{(2)}}$ примем следующие допущения: 1) вращением атмосферы Земли пренебрегается; 2) плотность атмосферы в пределах ЭДТС считается постоянной и равной плотности атмосферы на высоте центра масс системы; 3) скорости любого элемента ЭДТС за счет ее вращения относительно центра масс и изменения расстояния $r$ между концевыми точками много меньше, чем соответствующие переносные скорости за счет вращения орбитальной системы координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$. В частности, из приведенных допущений следует, что векторы скоростей всех элементов системы приблизительно одинаковы и равны вектору скорости центра масс ЭДТС, т.е. параллельны оси $C{{y}_{o}}$.

При определении аэродинамических сил ${{R}_{{a,b}}}$ для концевых тел учитываются только силы лобового сопротивления, поэтому

где ${{c}_{v}}$ – коэффициент силы лобового сопротивления, ${{S}_{{a,b}}}$ – характерные площади, ${{{\rho }}_{c}}$ – плотность атмосферы на высоте центра масс, ${{{\mathbf{V}}}_{c}}$ – вектор скорости центра масс, ${{V}_{c}} = {\text{|}}{{{\mathbf{V}}}_{c}}{\text{|}}$.

Аэродинамическая сила, действующая на единицу длины троса, вычисляется следующим образом [1]:

где ${{c}_{t}}$ – коэффициент аэродинамической силы, ${{D}_{t}}$ – диаметр троса, ${\alpha }$ – угол атаки в данной точке троса (острый угол между вектором ${{V}_{c}}$ и касательной к тросу). Формула (2.10) соответствует диффузному варианту отражения частиц от поверхности троса в свободномолекулярном потоке газа, который является доминирующим на околоземных орбитах [1]. При достаточно малых изгибах троса (малых углах ${\psi }$) имеем ${\alpha } \approx {\pi /}2 - {\theta } = {\text{const}}$ по длине троса, поэтому равнодействующая аэродинамическая сила для троса равна ${{R}_{t}} = \Delta {{R}_{t}}L$, параллельна векторам ${{R}_{{a,b}}}$(в данной модели) и приложена в средней точке троса.

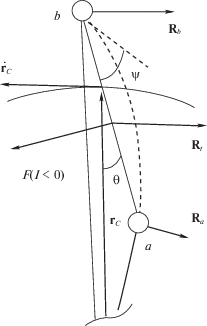
Для определения дополнительных слагаемых в обобщенных силах от действия аэродинамических сил вектора ${{R}_{{a,b}}}$, ${{R}_{t}}$ надо разложить на две проекции: на линию $ab$ ($R_{{a,b}}^{{(r)}}$, $R_{t}^{{(r)}}$) и на нормаль к этой линии ($R_{{a,b}}^{{(n)}}$, $R_{t}^{{(n)}}$). Составляющая $R_{t}^{{(n)}}$ (проекция на ось $C{{y}_{t}}$) характеризует распределенную нагрузку от аэродинамических сил, действующих на трос. Действие этой составляющей аналогично действию распределенной нагрузки от сил Ампера на трос. Поэтому эта составляющая алгебраически складывается с распределенной нагрузкой от сил Ампера и в зависимости от направления тока или увеличивает деформацию (изгиб) троса, или уменьшает ее. Кроме того, составляющие $R_{{a,b}}^{{(n)}}$, $R_{t}^{{(n)}}$, $R_{t}^{{(n)}}$ характеризуют моменты аэродинамических сил относительно центра масс системы, которые входят дополнительными слагаемыми в обобщенные силы $Q_{{{\theta ,\varphi }}}^{{(2)}}$. При этом составляющие $R_{{a,b}}^{{(r)}}$, $R_{t}^{{(r)}}$ совершают работу на возможном перемещении ${\delta }r$, что приводит к дополнительному слагаемому:

С учетом вышесказанного составляющие обобщенных сил $Q_{{{\theta ,}r,{\varphi }}}^{{(2)}}$ будут иметь вид

где $Q_{{\psi }}^{{(2)}} = 0.5{\text{sign(}}I{\text{)}}{{R}_{t}}r\sin {\varphi }\cos {\varphi (ctg\psi } - {{{\psi }}^{{ - 1}}}{\text{)}}\cos {\theta }$, ${{\Delta }_{a}} = r{{m}_{b}}{\text{/}}m$, ${{\Delta }_{b}} = r{{m}_{a}}{\text{/}}m$.

Таким образом, уравнения (2.1)–(2.3) совместно с выражениями для обобщенных сил (2.7), (2.12) и геометрическим соотношением (2.8) описывают движение ЭДТС относительно ее центра масс, который перемещается по заданной невозмущенной орбите. Для приближенного учета изменения параметров орбиты можно использовать уравнения движения центра масс системы, записанные в той или иной форме, например в геоцентрической прямоугольной системе координат [10] или в оскулирующих элементах орбиты [17]. В этом случае орбитальные параметры можно рассматривать как медленно изменяющиеся переменные в системе (2.1)–(2.3).

Ниже для проведения сравнительных расчетов будет использована более полная математическая модель движения ЭДТС в геоцентрической системе координат для весомого троса, при использовании которой проверяются многие допущения, принятые в модели (2.1)–(2.3).

3. Квазиравновесные положения ЭДТС на экваториальной круговой орбите. При определении положений равновесия ЭДТС предполагается, что плоскость магнитного экватора совпадает с плоскостью экватора Земли. Для представления результатов в более общей форме запишем уравнения (2.1)–(2.3), используя безразмерное время ${\tau } = {\omega }t$, где ${\omega }$ – угловая скорость движения центра масс по круговой орбите, тогда

Здесь ${\theta '} = d{\theta /}d{\tau }$, ${\theta ''} = {{d}^{2}}{\theta /}d{{{\tau }}^{2}},...$ и далее знаком ${\text{(}}\,{\text{'}}\,{\text{)}}$ обозначается операция дифференцирования по безразмерному времени ${\tau }$.

Если рассматривать недеформированный трос ($r = L$,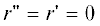), то представление о “рабочих” положениях равновесия системы в плоскости орбиты (${\varphi } = {\varphi '} = 0$) можно получить из уравнения (3.1), которое примет вид

где ${{a}_{1}} = {{B}_{o}}I({{m}_{b}} - {{m}_{a}}){\text{/}}2{{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}$, ${{a}_{2}} = {{c}_{v}}{{{\rho }}_{c}}V_{c}^{2}{\text{(}}{{S}_{a}}{{m}_{b}} - {{S}_{b}}{{m}_{a}}{\text{)/}}2{{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}$, ${{a}_{3}} = {{c}_{t}}{{{\rho }}_{c}}V_{c}^{2}{{D}_{t}}{\text{(}}{{m}_{b}} - {{m}_{a}}{\text{)/}}4{{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}$.

При постоянных безразмерных коэффициентах ${{a}_{1}},{{a}_{2}}{\text{/}}L,{{a}_{3}}$ уравнение (3.4) исследуется методом фазовой плоскости, имея в виду, что для нее существует аналог потенциальной энергии:

В частности, можно определить верхнюю оценку предельной величины тока. Если

то положений равновесия в системе не существует.

Если рассматривается деформированный трос, то положения равновесия в системе (3.1)–(3.3) в плоскости орбиты ${\varphi } = {\varphi '} = 0$ определяются, когда 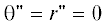, ${\theta '} = r{\text{'}} = 0$, из нелинейных уравнений

где ${{a}_{4}} = {{B}_{o}}I{\text{/}}2{{m}_{e}}{{{\omega }}^{2}}$, ${{a}_{5}} = {{c}_{t}}{{{\rho }}_{c}}V_{c}^{2}{{D}_{t}}{\text{/}}4{{m}_{e}}{{{\omega }}^{2}}$. Причем уравнения (3.6)–(3.7) рассматриваются совместно с геометрическим соотношением (2.8), которое в этом случае принимает вид $r = L{{{\gamma }}_{t}}{sin\psi /\psi }$.

Уравнения (3.6)–(3.7) в общем случае могут быть решены только численно. Однако можно рассмотреть частный случай этих уравнений, характерный для данной задачи. При использовании ЭДТС для подъема орбиты равнодействующая сила Ампера естественно должна превышать по величине равнодействующую аэродинамических сил, действующих на систему. Поэтому рассмотрим приближенное решение уравнений (3.6)–(3.7), когда коэффициенты ${{a}_{{2,3,5}}}$, зависящие от аэродинамических сил, принимаются за возмущения. Тогда, вводя вектор-функцию $F({\theta },r) = {{({{F}_{1}}({\theta },r),{{F}_{2}}({\theta },r))}^{{\text{T}}}}$, представим систему (3.6)–(3.7) как

приписав формально слагаемым, зависящим от коэффициентов ${{a}_{{2,3,5}}}$, малый параметр ${\varepsilon }$ (масштабный коэффициент). После построения приближенного решения можно положить ${\varepsilon } = 1$, вернувшись к исходным функциям.

В этом случае положения равновесия, расположенные вблизи вертикали, для невозмущенной системы ${{F}^{{(0)}}}({{{\theta }}^{{(0)}}},{{r}^{{(0)}}}) = 0$ (без аэродинамических сил) определяются в аналитическом виде [10]:

Поправки к невозмущенным решениям (3.9)–(3.10) запишем стандартным образом:

где $F{\text{'}}({\theta }_{{1,2}}^{{(0)}},r_{{1,2}}^{{(0)}})$ – матрица частных производных (Якобиан) вектор функции ${{F}^{{(0)}}}({\theta },r)$.

Для поправок ${\theta }_{{1,2}}^{{(1)}},r_{{1,2}}^{{(1)}},{\psi }_{{1,2}}^{{(1)}}$ нетрудно получить аналитические решения:

где а функции $F_{1}^{{(1)}}({\theta }_{{1,2}}^{{(0)}},r_{{1,2}}^{{(0)}})$ и $F_{2}^{{(1)}}({\theta }_{{1,2}}^{{(0)}},r_{{1,2}}^{{(0)}})$ – слагаемые в уравнениях (3.6)–(3.7), зависящие от коэффициентов ${{a}_{{2,3,5}}}$.

Анализ погрешности приближенного аналитического решения (3.9)–(3.10), (3.12) показывает, что если, например, безразмерные коэффициенты ${{a}_{2}}{\text{/}}r,{{a}_{3}},{{a}_{5}}$ по модулю не превышаю $1{\text{/}}3$, то относительная погрешность определения положений равновесия по всем переменным не превышает $2\% $.

4. Анализ устойчивости “рабочих” положений равновесия ЭДТС. Известно, что положения равновесия ЭДТС, расположенные вблизи вертикали, при постоянном токе неустойчивы [1, 2, 4, 5]. Оценим влияние аэродинамических сил на устойчивость (или неустойчивость) положений равновесия, определенных выше. Для этого составим систему, линеаризованную относительно положений равновесия. При линеаризации система разделяется на две подсистемы:

где $x = {{(\Delta {\theta ,}\Delta r)}^{{\text{T}}}}$ – вектор отклонений от положения равновесия, Здесь малый параметр ${\varepsilon }$, как и выше, приписан к слагаемым, которые определяют действие аэродинамических сил в системе. Из вида системы (4.1)–(4.2) следует, что наличие аэродинамических сил приводит к поправкам в матрице жесткости (к частотам) системы и никак не изменяет ее структуру. Причем уравнение (4.2) описывает колебания ЭДТС вне плоскости орбиты по переменной ${\varphi }$ с постоянной амплитудой. Характеристическое уравнение остальной части (4.1) системы имеет вид где ${{p}_{0}} = ({{c}_{{11}}} + {\varepsilon }{{{\eta }}_{{11}}})({{c}_{{22}}} + {\varepsilon }{{{\eta }}_{{22}}}) - {\varepsilon }{{{\eta }}_{{12}}}({{c}_{{21}}} + {\varepsilon }{{{\eta }}_{{21}}}),\,\,\quad {{p}_{1}} = {{b}_{{12}}}{{c}_{{21}}} + {\varepsilon (}{{{\eta }}_{{21}}}{{b}_{{12}}} + {{{\eta }}_{{12}}}{{b}_{{21}}}{\text{)}}$, ${{p}_{2}} = {{c}_{{11}}} + {{c}_{{22}}}$ + + ${\varepsilon }{{{\eta }}_{{11}}} + {\varepsilon }{{{\eta }}_{{22}}} + 4$.

Если аэродинамические силы не учитываются (${\varepsilon } = 0$), то коэффициенты ${{c}_{{11}}},{{c}_{{22}}}$ дают оценку частот системы ${{c}_{{11}}} = {\omega }_{1}^{2}$, ${{c}_{{22}}} = {\omega }_{2}^{2}$, причем при малой деформации троса ${\omega }_{2}^{2} \gg {\omega }_{1}^{2}$, так как ${{c}_{{22}}} \to \infty $ при ${{{\psi }}_{{1,2}}} \to 0$. Если ${{p}_{1}} = 0$, то характеристическое уравнение (4.3) имеет только мнимые корни. Причем ${{p}_{1}} \approx 0$, если ${{c}_{{21}}} = 3{{r}_{{1,2}}}\sin 2{{{\theta }}_{{1,2}}} \approx 0$, т.е. положение равновесия системы приближается к вертикали, в частности, этот случай реализуется, когда массы концевых точек близки ${{m}_{a}} \approx {{m}_{b}}$ и сумма моментов всех внешних сил относительно центра масс системы приблизительно равна нулю. Если ${{p}_{1}} \ne 0$, то положения равновесия вблизи вертикали системы (3.7)–(3.8) всегда неустойчивы, в частности, это следует из критерия Рауса–Гурвица, так как определитель Гурвица ${{\Delta }_{h}} = - p_{1}^{2}{{p}_{0}} < 0$ (${{p}_{0}} > 0$ для малых ${{{\psi }}_{{1,2}}} > 0$). При малых коэффициентах ${{p}_{1}}$ имеем асимптотическую оценку для вещественных частей корней уравнения (4.5) ${\text{Re(}}{{{\lambda }}_{{1,2}}}{\text{)}} = - {{p}_{1}}{\text{/}}2\sqrt {(p_{2}^{2} - 4{{p}_{0}})} ,$ ${\text{Re(}}{{{\lambda }}_{{3,4}}}{\text{)}} = {{p}_{1}}{\text{/}}2\sqrt {(p_{2}^{2} - 4{{p}_{0}})} $, причем корни ${{{\lambda }}_{{1,2}}}$ соответствуют частоте поперечных маятниковых колебаний, а корни ${{{\lambda }}_{{3,4}}}$ – продольным изгибным колебаниям троса. Поэтому когда ${{p}_{1}} = - 6\sin {{{\theta }}_{{1,2}}} + {\varepsilon }...{\text{ < 0}}$, т.е. нижняя концевая точка смещается противоположно направлению орбитального движения центра масс, неустойчивость проявляется в возрастании амплитуды маятниковых колебаний системы. А если ${{p}_{1}} = - 6\sin {{{\theta }}_{{1,2}}} + {\varepsilon }...{\text{ > 0}}$, то происходит возрастание амплитуды изгибных колебаний троса.

Проведенный анализ показывает, что аэродинамические силы, действующие на ЭДТС, качественно не изменяют свойств устойчивости “рабочих” положений равновесия системы. Причем причиной неустойчивости “рабочих” положений равновесия всегда является наличие отличного от нуля момента внешних сил, представляющего собой (для экваториальной орбиты) алгебраическую сумму моментов от сил Ампера и аэродинамических сил. Чем меньше ${\text{|}}\sin {{{\theta }}_{{1,2}}}{\text{|}}$ (меньше ${\text{|}}{{p}_{1}}{\text{|}}$), тем меньше скорость возрастания соответствующих амплитуд колебаний в системе без управления. Поэтому при проектировании низкоорбитальных ЭДТС необходимо стремиться к тому, чтобы направление момента от сил Ампера было противоположно направлению аэродинамического момента. В этом случае величина ${\text{|}}{{p}_{1}}{\text{|}}$ будет меньше и потеря устойчивости системы относительно вертикали будет затягиваться. С другой стороны, если назначением ЭДТС является подъем орбиты, то ток должен быть направлен от верхней концевой точки ${{m}_{b}}$ к нижней точке ${{m}_{a}}$. Тогда сила Ампера будет направлена в сторону орбитального движения, что обеспечит подъем высоты орбиты.

5. Стабилизация движения низкоорбитальной ЭДТС. Так как в общем случае движение низкоорбитальной ЭДТС относительно вертикали неустойчиво, то для обеспечения ее функционирования на орбите необходимо использовать методы стабилизации движения. В данной работе стабилизация движения ЭДТС осуществляется с помощью изменений величины тока в проводящем тросе: $I = {{I}_{n}} + \Delta I$, где ${{I}_{n}}$ – номинальная величина тока, $\Delta I$ – управление. Причем управления $\Delta I$ определяются с учетом изгибных колебаний троса, что является особенностью рассматриваемого способа управления.

Синтез регулятора осуществляется с помощью полученной линеаризованной модели (4.1)–(4.2) при постоянных параметрах орбиты. Линеаризованная модель представляется как совокупность уравнений первого порядка с введенным управлением

где $y = (\Delta {\theta ,\theta '},\Delta r,r{\text{'}},{\varphi ,\varphi '})$ – вектор отклонений обобщенных координат и скоростей от положений равновесия, $A$ – матрица частных производных, записанная в соответствии с системой (4.1)–(4.2), $U = \Delta I{\text{/}}{{I}_{n}}$, $M = {{(\begin{array}{*{20}{c}} 0&{{{M}_{2}}}&0&{{{M}_{4}}}&0&0 \end{array})}^{{\text{T}}}}$ – вектор коэффициентов при управлении, ${{M}_{2}} = {{B}_{o}}{{I}_{n}}{\text{(}}{{m}_{b}} - {{m}_{a}}{\text{)/(}}2{{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}{\text{)}}$, ${{M}_{4}} = - {{B}_{o}}{{I}_{n}}{{r}_{{1,2}}}{\text{ctg}}{{{\psi }}_{{1,2}}}{\text{/(}}2{{m}_{e}}{{\omega }^{2}}{\text{)}}$.

Из вида вектора $M$ следует, что при данном способе управления в линейном приближении система неуправляема по переменной ${\varphi }$, которая определяет колебания ЭДТС вне плоскости орбиты. Кроме того, если ${{m}_{b}} = {{m}_{a}}$, то система становится неуправляемой также по переменной ${\theta }$, определяющей колебания ЭДТС относительно центра масс в плоскости орбиты. Поэтому далее рассматривается случай ${{m}_{b}} \ne {{m}_{a}}$, а поведение переменной ${\varphi }$ оценивается по нелинейным моделям движения ЭДТС. При этом вид системы (5.1) остается таким же, однако размерности матрицы $A$ и вектора $M$ уменьшаются вычеркиванием двух последних строк и столбцов.

Для синтеза управления воспользуемся стандартной процедурой метода динамического программирования Беллмана с квадратичным критерием оптимальности [16]

где $D$ – диагональная положительно определенная матрица весовых коэффициентов, $h > 0$. Причем весовые коэффициенты удовлетворяют соотношению ${{D}_{1}} + {{D}_{2}} + {{D}_{3}} + {{D}_{4}} + h = 1$.

Тогда выражение для линейного регулятора записывается в виде

где $q = - BM{\text{/}}h$ – вектор коэффициентов регулятора. При этом матрица $B$ удовлетворяет уравнению Здесь решение для $B$ ищется в классе положительно определенных матриц и представляет собой установившееся решение дифференциального уравнения Риккати [18].

6. Математическая модель движения низкоорбитальной ЭДТС с весомым тросом. При выводе уравнений движения ЭДТС в подвижной орбитальной системе координат (2.1)–(2.3) и при построении управления был принят ряд допущений: трос невесом, форма троса – часть окружности и др. Для проверки правомерности принятых допущений обычно применяются более полные модели движения орбитальных тросовых систем, которые описывают их движение как системы с распределенными параметрами. Например, можно представить трос как совокупности материальных точек, соединенных между собой упругими односторонними механическими связями [11–14].

В этом случае запишем уравнения движения распределенной низкоорбитальной ЭДТС в виде

где ${{r}_{k}}$, ${{V}_{k}}$ и ${{m}_{k}}$ – радиус-вектор, скорость и масса $k$-й материальной точки; ${{F}_{k}}$ и ${{R}_{k}}$– сила Ампера и аэродинамическая сила, действующие на $k$-ю материальную точку; ${{G}_{k}}$ – гравитационные силы, ${{T}_{k}} = {{T}_{k}}{{\tau }_{k}}$ – силы натяжения троса, действующие между $k$-й и $k + 1$-й точками, ${{\tau }_{k}} = ({{r}_{{k + 1}}} - {{r}_{k}}){\text{/|}}{{r}_{{k + 1}}} - {{r}_{k}}{\text{|}}$. На крайние точки действует только одна сила натяжения, поэтому ${{T}_{0}} = {{T}_{n}} = 0$. При записи системы (6.1) полагается, что ${{m}_{1}} = {{m}_{a}}$, ${{m}_{n}} = {{m}_{b}}$ (верхняя точка).

Для определения ${{F}_{k}}$ сначала вычисляются силы Ампера, действующие на $k$-й участок троса:

где $I$ – величина тока, ${{B}_{k}}$ – вектор магнитной индукции, определенный в середине отрезка троса.

Распределение сил $\Delta {{F}_{k}}$ по материальным точкам ЭДТС осуществляется следующим образом:

Аэродинамические силы определяются по аналогичному алгоритму:

где $\Delta {{R}_{k}}$ – аэродинамическая сила, действующая на $k$-й участок троса (цилиндр); $\Delta {{L}_{k}}$ – длина участка троса; ${{V}_{{c,k}}}$ – векторы относительной скорости, определенные в средней точке участков троса; ${{V}_{{r,k}}}$ – векторы относительных скоростей материальных точек, ${{{\rho }}_{a}},{{{\rho }}_{b}}$ и ${{{\rho }}_{k}}$ – плотности атмосферы, вычисленные в крайних точках и в средних точках участков троса, ${{\alpha }_{k}}$ – угол атаки $k$-го участка троса.

Векторы абсолютных скоростей и скоростей относительно атмосферы материальных точек связаны известным соотношением

где ${{{\mathbf{\Omega }}}_{e}}$ – вектор угловой скорости вращения Земли, ${{{\mathbf{V}}}_{k}} = {{{\mathbf{\dot {r}}}}_{k}}$.

При определении аэродинамических сил учитываются только силы лобового сопротивления для концевых точек и предположение о диффузном отражении молекул в свободномолекулярном потоке [19] для троса. Причем участки, на которые разбивается трос, рассматриваются как цилиндры. Поэтому аэродинамические силы (6.4) направлены противоположно соответствующим относительным скоростям ${{V}_{{r,1}}},{{V}_{{r,n}}}$ и ${{V}_{{c,k}}}$ [1, 19].

При использовании системы (6.1) гравитационные силы ${{G}_{k}}$ (центральное ньютоновское поле) и силы натяжения троса ${{T}_{k}}$ определяются так же, как в статье [14], где при растяжении применялся закон Гука и рассматривалась односторонняя механическая связь между точками.

Система (6.1) интегрируется в геоцентрической неподвижной системе координат при заданных начальных условиях.

7. Численные результаты. При проведении численного моделирования рассматривается ЭДТС, состоящая из двух наноспутников, соединенных проводящим тросом. В начальном состоянии после этапа развертывания (в момент, когда по тросу начинают пропускать ток) система находится на местной вертикали в режиме гравитационной стабилизации. Исходные данные для моделирования представлены в таблице. Плотность атмосферы (в номинальном случае) соответствует ГОСТу 25645.101-83.

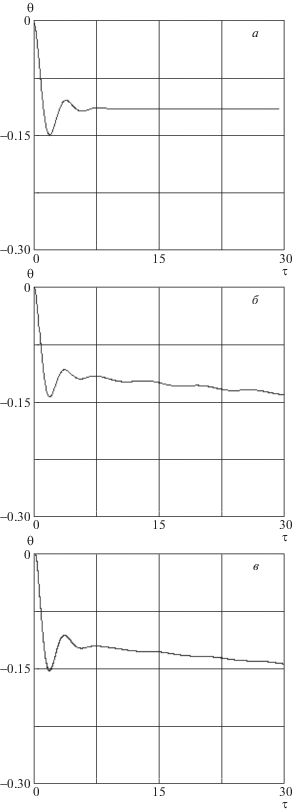
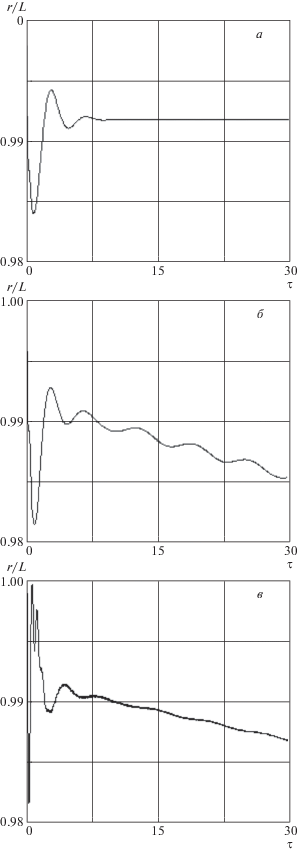
На экваториальной орбите, как известно [1], эффективность использования ЭДТС наиболее высокая, так как вектор магнитной индукции $B$ ортогонален тросу (в номинальном случае, расположенном в плоскости орбиты) и модуль силы Ампера (2.4) максимален. На рис. 3, 4 представлены переходные процессы в системе управления при движении ЭДТС по экваториальной круговой орбите (высота 270 км), определенные по трем моделям: линеаризованной системе (a), уравнениям в подвижной системе координат (2.1)–(2.3) (б) и по модели с распределенными параметрами (6.1) (в). В этом идеальном случае экваториальной орбиты переходные процессы, которые соответствуют представленным моделям, очень близки. Разница заключается лишь в том, что после окончания переходного процесса модели (2.1)–(2.3) и (6.1) описывают эволюцию квазиравновесных положений системы из-за изменения параметров орбиты центра масс системы. В конечном итоге при подъеме орбиты (увеличении высоты полета) квазиравновесные положения ЭДТС стремятся к положениям, которые соответствуют случаю, когда атмосфера практически не влияет на движение системы (${\varepsilon } = 0$). Для данного примера это имеет место, когда высота почти круговой орбиты достигает приблизительно 520 км. Для этого требуется 71 ч. При этом квазиравновесные положения ЭДТС изменяются следующим образом:

При решении задачи синтеза регулятора выбирался достаточно низкий уровень управляющих воздействий, что обеспечивалось соотношением весовых коэффициентов в критерии оптимальности (5.2): ${{D}_{{1,2,3,4}}}{\text{/}}h = 0.1$. При этом ${{\max }_{\tau }}(\Delta I{\text{/}}{{I}_{n}}) \approx 0.2$. Здесь необходимо отметить, что, не снижая качества управления (переходные процессы практически не изменяются), в данной задаче можно применять дифференциальный регулятор, т.е. использовать $q = {{(\begin{array}{*{20}{c}} 0&{{{q}_{2}}}&0&{{{q}_{4}}} \end{array})}^{{\text{T}}}}$. В приведенном примере ${{q}_{2}} = - 0.359$, ${{q}_{4}} = 0.320$. При наличии ограниченных начальных возмущений по углу ${\varphi } < 1$ поведение системы соответствует прогнозу, сделанному по линеаризованной системе, т.е. амплитуда колебания переменной ${\varphi }$ слабо изменяется (почти постоянна).

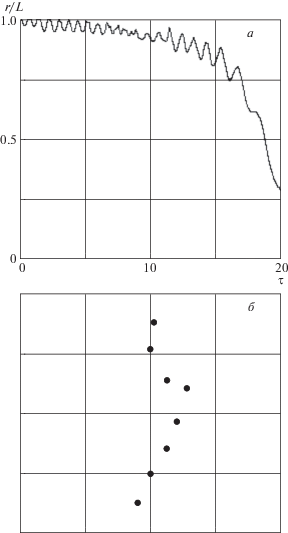
Если исключить в данной задаче контроль над изгибными колебаниями троса, т.е. положить ${{q}_{4}} = 0$, то движение системы становится неустойчивым, что иллюстрируется рис. 5. Неустойчивость, прежде всего, проявляется в уменьшении расстояния между крайними точками $r$ (рис. 5а), т.е. в увеличении изгиба троса, что соответствует проведенному выше анализу неуправляемого движения системы для ${{{\theta }}_{1}} < 0$. При достижении относительной величины $r{\text{/}}L \approx 0.75$ имеет место большая деформация троса и происходит его ослабление (трос сминается) (рис. 5б, время ${\tau } \approx 17$, деление сетки составляет 0.25 км). Естественно подобные эволюции в движении ЭДТС могут быть определены только при использовании модели с распределенными параметрами, для которой не делалось предположений о форме троса. Здесь следует отметить, что в данном примере использовалось восемь материальных точек для моделирования движения ЭДТС. Дальнейшее увеличение количества точек (даже в 2 раза) практически не влияло на полученные результаты, однако существенно увеличивало затраты на вычисления (в несколько раз).

Для наклонных и эллиптических орбит на систему, как следует из вида уравнений (2.1)–(2.3), начинают действовать периодические возмущения, связанные с изменением аргумента широты $u$ и угла ${\varphi }$. Причем пространственный случай движения системы ${\varphi } \ne {\text{0}}$ реализуется всегда, даже когда в начальный момент ${\varphi } = 0$. Кроме того, как было указано выше, на наклонных орбитах эффективность применения ЭДТС падает, что приводит к необходимости увеличения номинального тока в ${\text{1/}}\cos i$ раз по сравнению с аналогичным вариантом при движении по экваториальной орбите.

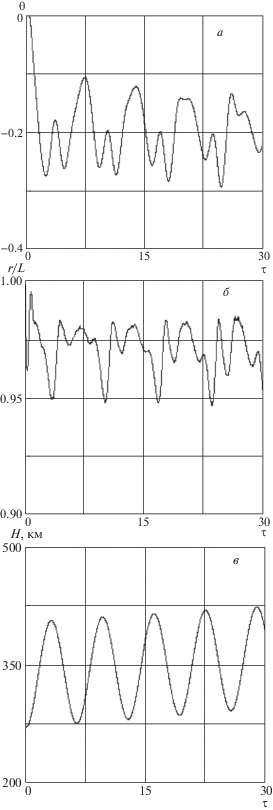
С увеличением наклона орбиты, как показал анализ численных результатов, движение ЭДТС усложняется из-за увеличения уровня возмущающих воздействий. Это в свою очередь приводит к необходимости увеличения уровня управления (уменьшения весового коэффициента $h$). В конечном итоге отношение $\Delta I{\text{/}}{{I}_{n}}$ приближается к 1, и направление тока может измениться на противоположное, что не желательно, так как во многих случаях является техническим ограничением. Для исходных данных (см. таблицу) с учетом рассматриваемого ограничения для высоты начальной орбиты 270 км удается обеспечить стабилизацию движения ЭДТС до наклонений орбиты $\pi {\text{/}}4$. На рис. 6 показаны зависимости, которые характеризуют процесс стабилизации движения ЭДТС для орбиты с начальным наклонением $\pi {\text{/}}6$ и с эксцентриситетом 0.01. В этом случае процесс стабилизации движения сопровождается незатухающими вынужденными колебаниями переменных системы относительно квазиравновесных положений ЭДТС (рис. 6a, б). Рисунок 6в характеризует процесс подъема высоты орбиты ($H$) в этом случае. Особенностью изменения параметров орбиты при использовании ЭДТС является почти линейное изменение высот апогея и перигея (рис. 6в), большой полуоси орбиты. При этом наклонение и эксцентриситет орбиты при ее подъеме почти постоянны (немного уменьшаются).

Здесь следует отметить, что изменение эксцентриситета орбиты (порядка 0.01) слабо влияют на численные результаты, приведенные на рис. 3–6. Вариации плотности атмосферы (в пределах $ \pm 30\% $) качественно не изменяют графиков, представленных на рис. 3–6.

Аналогичные особенности при управлении движением ЭДТС возникают при уменьшении высоты начальной орбиты. Для экваториальной орбиты удается стабилизировать движение системы до высоты 200 км, для орбиты с наклонением $\pi {\text{/}}6$ – до высоты около 250 км. Однако низкие орбиты естественно приводят к необходимости увеличивать величину номинального тока. С другой стороны, с течением времени имеет место подъем орбиты, и увеличенная величина тока уже не требуется. Тем более, при подъеме орбиты начинает увеличиваться равновесный угол отклонения троса от вертикали и эффективность применения ЭДТС падает. Поэтому хорошим решением представляется применение переменного номинального тока, что делает процесс подъема орбиты адаптивным.

Был проведен анализ влияния дискретности управления (обновление управляющих воздействий) на переходные процессы в системе стабилизации. Увеличение дискретности управления до 100 с практически не сказывалось на качестве управления. Другие особенности реальных систем регулирования в данной работе не учитывались.

8. О выборе параметров ЭДТС. При проектировании низкоорбитальных ЭДТС необходимо учитывать ряд особенностей их движения относительно центра масс.

1. При выборе параметров ЭДТС желательно, чтобы моменты от равнодействующих сил Ампера и аэродинамических сил имели разные знаки, в противном случае увеличиваются равновесные значения угла ${\theta }$ по отношению к вертикали и уменьшаются равновесные значения для переменной $r$ (увеличивается изгиб троса), что ограничивает по величине номинальный ток. Если ЭДТС используется для подъема орбиты, то $I < 0$ и равнодействующие от сил Ампера и аэродинамических сил троса противоположно направлены, и точки их приложения почти совпадают (расположены вблизи средней точки троса). Поэтому знак момента равнодействующей от аэродинамических сил определяется моментами от аэродинамических сил концевых тел. Точнее, величиной и знаком параметра ${{a}_{2}} = {{c}_{v}}{{{\rho }}_{c}}V_{c}^{2}{\text{(}}{{S}_{a}}{{m}_{b}} - {{S}_{b}}{{m}_{a}}{\text{)/(}}2{{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}{\text{)}}$, который зависит от соотношения масс и характерных размеров концевых тел.

2. Управление движением ЭДТС относительно центра масс связано с наличием не нулевого момента, который создают распределенные по тросу силы Ампера. Этот момент будет близок к нулю, если массы концевых точек будут близки ${{m}_{a}} \approx {{m}_{b}}$, и система станет слабо управляемой по переменной ${\theta }$, так как ${{M}_{2}} \approx 0$. Это приведет к необходимости использования больших по модулю токов при управлении и, следовательно, к большим затратам энергии.

3. Если ЭДТС предназначена для удаления КА с орбиты $I > 0$, т.е. для ускоренного их торможения, то точки приложения и направления равнодействующих сил Ампера и аэродинамических сил троса почти совпадают, а значит, совпадают знаки моментов. В этом случае управление движением ЭДТС усложняется, так как создаются благоприятные условия для потери устойчивости системы относительно вертикали.

4. При проектировании низкоорбитальных ЭДТС необходимо учитывать возможные вариации параметров атмосферы, в частности, неопределенность в знании ее плотности.

Заключение. Рассмотрена задача стабилизации движения низкоорбитальной ЭДТС, состоящей из двух соединенных проводящим тросом НС, на околоземной орбите. На основе простой модели, в которой трос приближается дугой окружности, проведен синтез линейного регулятора в соответствии с квадратичным критерием оптимальности. Показано, что при стабилизации движения ЭДТС необходимо осуществлять контроль над расстоянием между НС, а значит, за линией изгиба троса. Приводится пример потери устойчивости движения ЭДТС при отсутствии контроля над изгибными колебаниями троса.

Как следует из выражения (3.10), величина прогиба троса зависит (при прочих равных условиях) от параметра ${{a}_{4}} = {{B}_{o}}I{\text{/}}2{{m}_{e}}{{{\omega }}^{2}}$, а значит, от приведенной массы ${{m}_{e}}$. При увеличении величины ${{m}_{e}} = {{m}_{a}}{{m}_{b}}{\text{/}}m$ форма троса приближается к прямой линии. В статье описывается пример управляемого движения ЭДТС с НС, для которых приведенная масса (см. таблицу) достаточно мала: ${{m}_{e}} = 1.5\,{\text{к г }}$.

Даются рекомендации по выбору параметров ЭДТС, направленные на уменьшение влияния аэродинамических сил на движение системы относительно центра масс. Результаты анализа подтверждаются численным моделированием по более сложным уравнениям управляемого движения ЭДТС, в которых система рассматривается как система с распределенными параметрами.