Известия РАН. Теория и системы управления, 2019, № 3, стр. 55-65

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ ТВЕРДОГО ТЕЛА С КОМБИНИРОВАННЫМ КРИТЕРИЕМ КАЧЕСТВА

А. В. Молоденков^a, *, Я. Г. Сапунков^a

^a Институт проблем точной механики и управления РАН
Саратов, Россия

Поступила в редакцию 30.07.2018
После доработки 21.12.2018
Принята к публикации 28.01.2019

DOI: 10.1134/S0002338819030120

Аннотация

Представлены результаты численного и аналитического решения задачи оптимального управления вращательным движением твердого тела с комбинированным критерием качества процесса управления и использованием кватернионов. Критерий оптимизации учитывает продолжительность процесса управления, суммарные импульсы квадрата угловой скорости твердого тела и величины управляющего момента, приложенного к телу. Управляемое движение твердого тела может содержать особые участки управления.

Введение. В статье представлены результаты численного и аналитического решения задачи об оптимальном управлении угловым движением твердого тела с одной неподвижной точкой с комбинированным функционалом, определяющим качество процесса управления. Функционал учитывает с помощью весовых множителей продолжительность процесса управления, суммарные импульсы квадрата угловой скорости тела и величину управляющего момента. В разд. 1 дается постановка задачи оптимального управления для произвольного тела и произвольных граничных условий. В разд. 2 производится переход к безразмерным переменным. В разд. 3 с помощью принципа максимума Л.С. Понтрягина решение задачи оптимального управления сводится к решению краевой задачи для системы дифференциальных уравнений по определению фазовых и сопряженных переменных. Оптимальное управление состоит из активных этапов, на которых величина управляющего момента принимает максимальное значение, и пассивных этапов, на которых тело вращается вокруг неподвижной точки по инерции. В разд. 4 приводятся результаты численного решения задачи для различных тел и различных граничных условий и различных весовых множителей, входящих в функционал. Дается анализ результатов. В разд. 5 для тела со сферической симметрией получено аналитическое решение задачи оптимального управления для частных случаев, когда тело из одного состояния покоя переводится в другое состояние покоя или когда тело из состояния покоя переводится в новое положение, но угловая скорость в конце движения не задается. В разд. 6 при тех же условиях строится аналитическое решение задачи для случая, когда в функционале качества процесса не учитывается суммарный импульс величины управляющего момента. В этом случае оптимальное управление может содержать особый этап управления, на котором оптимальное управление не определяется непосредственно из условия максимума функции Гамильтона–Понтрягина. Для определения оптимального управления проводится дополнительное исследование.

Следует отметить, что ранее были рассмотрены задачи оптимальных разворотов твердого тела различных динамических конфигураций с классическими критериями качества переходных процессов (быстродействие, минимум энергетических затрат и их комбинация, суммарный импульс) [1–10], где не учитывалась угловая скорость движения твердого тела.

1. Постановка задачи. Движение твердого тела с одной неподвижной точкой О в связанной с твердым телом системе координат $O{{Х }_{1}}{{Х }_{2}}{{Х }_{3}}$, оси которой направлены по главным осям инерции тела, под действием управляющего момента M описывается системой уравнений [1]:

(1.1)

$\frac{{d{\mathbf{\Lambda }}}}{{dt}} = \frac{1}{2}L\left( {\mathbf{\Lambda }} \right){\mathbf{\omega }}\,,\,\,\,\,\frac{{d{\mathbf{\omega }}}}{{dt}} = {{R}^{{ - 1}}}{\mathbf{M}} - {{R}^{{ - 1}}}\left[ {{\mathbf{\omega }},R{\mathbf{\omega }}} \right]\,,$

где ${\mathbf{\Lambda }} = ({{\Lambda }_{0}},\,{{\Lambda }_{1}},\,{{\Lambda }_{2}},\,{{\Lambda }_{3}})$ – нормированный кватернион, определяющий положение твердого тела, ${\mathbf{\omega }}$ – вектор угловой скорости тела, L(Λ) – матрица, R – тензор инерции тела, в котором ${{I}_{1}},\,{{I}_{2}},\,{{I}_{3}}$ – главные моменты инерции,

(1.2)

$L\left( {\mathbf{\Lambda }} \right) = \left\| {\begin{array}{*{20}{c}} {{{\Lambda }_{1}}}&{ - {{\Lambda }_{2}}}&{ - {{\Lambda }_{3}}} \\ {{{\Lambda }_{0}}}&{ - {{\Lambda }_{3}}}&{{{\Lambda }_{2}}} \\ {{{\Lambda }_{3}}}&{{{\Lambda }_{0}}}&{ - {{\Lambda }_{1}}} \\ { - \Lambda {}_{2}}&{{{\Lambda }_{1}}}&{{{\Lambda }_{0}}} \end{array}} \right\|,\quad R = \left\| {\begin{array}{*{20}{c}} {{{I}_{1}}}&0&0 \\ 0&{{{I}_{2}}}&0 \\ 0&0&{{{I}_{3}}} \end{array}} \right\|.$

В начальный момент $t = 0$ положение и угловая скорость тела определяются соотношениями:

(1.3)

${\mathbf{\Lambda }}\left( 0 \right) = {{{\mathbf{\Lambda }}}_{n}},\quad {\mathbf{\omega }}\left( 0 \right) = {{{\mathbf{\omega }}}_{n}}.$

В конечный момент t = t_k, который заранее не задается, положение тела и его угловая скорость должны определяться соотношениями:

(1.4)

${\mathbf{\Lambda }}\left( {{{t}_{k}}} \right) = {{{\mathbf{\Lambda }}}_{k}},\quad {\mathbf{\omega }}\left( {{{t}_{k}}} \right) = {{{\mathbf{\omega }}}_{k}}.$

На управляющий момент наложено ограничение

(1.5)

$\left| {\mathbf{M}} \right| \leqslant {{M}_{*}}.$

Качество процесса перевода тела из состояния (1.3) в состояние (1.4) определяется комбинированным функционалом с неотрицательными весовыми множителями ${{\alpha }_{1}},\,{{\alpha }_{2}},\,{{\alpha }_{3}}$:

(1.6)

$J = \int\limits_0^{{{t}_{k}}} {({{\alpha }_{1}} + {{\alpha }_{2}}{{{\mathbf{\omega }}}^{2}} + {{\alpha }_{3}}\left| {\mathbf{M}} \right|)} {\kern 1pt} {\kern 1pt} dt.$

Функционал (1.6) представляет собой линейную свертку трех критериев: промежутка времени, суммарного импульса квадрата угловой скорости и импульса величины управляющего момента, затраченных на процесс управления. С увеличением или уменьшением величины весового множителя будет увеличиваться или уменьшаться влияние соответствующего критерия на процесс управления. В частности, с увеличением ${{\alpha }_{1}}$ будет уменьшаться длительность процесса управления, с увеличением ${{\alpha }_{2}}$ будет уменьшаться средняя величина угловой скорости тела, с увеличением ${{\alpha }_{3}}$ будет уменьшаться суммарный расход топлива на создание управляющего момента. Предполагается, что можно пренебречь влиянием расхода топлива на моменты инерции тела.

Требуется найти оптимальный управляющий момент, удовлетворяющий ограничению (1.5), который переводит управляемую систему (1.1) из начального состояния (1.3) в конечное состояние (1.4) и сообщает минимальное значение функционалу (1.6).

2. Переход к безразмерным переменным. Безразмерные переменные $t*,{\mathbf{\omega }}*,{\mathbf{M}}*,I_{i}^{*},J*,\alpha _{2}^{*},\alpha _{3}^{*}$ связаны с соответствующими размерными переменными по формулам, в которых $T,{{M}_{*}},{{I}_{*}}$ – масштабы времени, управляющего момента и моментов инерции:

(2.1)

$\begin{gathered} t* = t{\text{/}}T,\quad {\mathbf{\omega }}* = {\mathbf{\omega }}T,\quad {\mathbf{M}}* = {\mathbf{M}}{\text{/}}{{M}_{*}},\quad I_{i}^{*} = {{I}_{i}}{\text{/}}{{I}_{*}},\quad i = 1,2,3,\quad J* = J{\text{/}}T, \\ \alpha _{2}^{*} = {{\alpha }_{2}}{\text{/}}{{T}^{2}},\quad \alpha _{3}^{*} = {{\alpha }_{3}}{{M}_{*}},\quad {{I}_{*}} = \sqrt {{\text{(}}I_{1}^{2} + I_{2}^{2} + I_{3}^{2}{\text{)/}}3} ,\quad T = \sqrt {{{I}_{*}}{\text{/}}{{M}_{*}}} . \\ \end{gathered} $

Далее используются только безразмерные переменные и верхний индекс “*” у безразмерных величин будет опущен. Тогда в безразмерных переменных уравнения (1.1), соотношения (1.2)–(1.4), (1.6) сохранят свой вид, а ограничение на управляющий момент (1.5) запишем как

(2.2)

$\left| {\mathbf{M}} \right| \leqslant 1.$

Далее будем иметь в виду постановку задачи в безразмерных переменных и верхние индексы у них будут опущены.

3. Решение задачи с помощью принципа максимума. При решении задачи применяется принцип максимума Л.С. Понтрягина [11]. Функция Гамильтона–Понтрягина $H$ для рассматриваемой задачи имеет вид

(3.1)

$H = - ({{\alpha }_{1}} + {{\alpha }_{2}}{{{\mathbf{\omega }}}^{2}} + {{\alpha }_{3}}\left| {\mathbf{M}} \right|) + \frac{1}{2}\left( {{\mathbf{\psi }},L({\mathbf{\Lambda }}){\mathbf{\omega }}} \right) + ({\mathbf{\nu }},{{R}^{{ - 1}}}{\mathbf{M}} - {{R}^{{ - 1}}}\left[ {{\mathbf{\omega }},R{\mathbf{\omega }}} \right]),$

где ${\mathbf{\psi }} = {{({{\psi }_{0}},\,{{\psi }_{1}},\,{{\psi }_{2}},\,{{\psi }_{3}}\,)}^{{\text{Т }}}},\,\,{\mathbf{\nu }}\, = {{({{\nu }_{1}},\,{{\nu }_{2}},\,{{\nu }_{3}})}^{{\text{Т }}}}$ – векторы сопряженных переменных. Матрицу $L({\mathbf{\Lambda }})$ в скалярном произведении в формуле (3.1) можно передать кватерниону ${\mathbf{\psi }}$. Если ввести новую векторную сопряженную переменную p по формуле с участием транспонированной матрицы ${{L}^{T}}({\mathbf{\Lambda }})$:

(3.2)

${\mathbf{p}} = {{L}^{{\text{T}}}}({\mathbf{\Lambda }}){\mathbf{\psi }},$

то функция $H$ примет вид:

(3.3)

$H = - ({{\alpha }_{1}} + {{\alpha }_{2}}{{{\mathbf{\omega }}}^{2}} + {{\alpha }_{3}}\left| {\mathbf{M}} \right|) + \frac{1}{2}\left( {{\mathbf{p}},{\mathbf{\omega }}} \right) + ({\mathbf{\nu }},{{R}^{{ - 1}}}{\mathbf{M}} - {{R}^{{ - 1}}}\left[ {{\mathbf{\omega }},R{\mathbf{\omega }}} \right]),$

а сопряженная система уравнений для ${\mathbf{p}}$ и ${\mathbf{\nu }}$ запишется как

(3.4)

$\frac{{d{\mathbf{p}}}}{{dt}} = \left[ {{\mathbf{p}},{\mathbf{\omega }}} \right],\quad \frac{{d{\mathbf{\nu }}}}{{dt}} = 2{{\alpha }_{2}}{\mathbf{\omega }} - \frac{1}{2}{\mathbf{p}} - [{{R}^{{ - 1}}}{\mathbf{\nu }},R{\mathbf{\omega }}] + R[{{R}^{{ - 1}}}{\mathbf{\nu }},{\mathbf{\omega }}].$

Из условия максимума для функции H при учете ограничения на управление (2.2) следует, что оптимальное управление определяется через функцию ${\mathbf{\nu }}$ по формуле:

(3.5)

${{{\mathbf{M}}}_{{opt}}} = \frac{{{{R}^{{ - 1}}}{\mathbf{\nu }}}}{{\left| {{{R}^{{ - 1}}}{\mathbf{\nu }}} \right|}},\quad {\text{е с л и }}\quad \left| {{{R}^{{ - 1}}}{\mathbf{\nu }}} \right| \geqslant {{\alpha }_{3}},\quad и \quad {{{\mathbf{M}}}_{{opt}}} = 0,\quad {\text{е с л и }}\quad \left| {{{R}^{{ - 1}}}{\mathbf{\nu }}} \right| < {{\alpha }_{3}}.$

Соотношение (3.5) показывает, что оптимальное управление может состоять из этапов двух видов. На одних этапах (активных) управляющий момент по величине принимает максимальное значение, на других (пассивных) управляющий момент равен нулю и тело совершает вращение по инерции.

Таким образом, принцип максимума Понтрягина сводит решение задачи оптимального управления к решению краевой задачи для системы дифференциальных уравнений (1.1), (3.4) по определению фазовых и сопряженных переменных ${\mathbf{\Lambda }},\,{\mathbf{\omega }},\,{\mathbf{p}},\,{\mathbf{\nu }}$, в которых в каждый момент времени управление M определяется по формуле (3.5) с граничными условиями (1.3) при t = 0, условиями (1.4) при $t = {{t}_{k}}$ и условием

(3.6)

$H({{t}_{k}}) = 0.$

Так как ${\mathbf{\Lambda }}$ – нормированный кватернион, то граничное условие (1.4) в конце процесса управления при $t = {{t}_{k}}$ для численного решения краевой задачи оптимального управления удобно заменить условием

(3.7)

${\text{vect}}({{{\mathbf{\tilde {\Lambda }}}}_{k}} \circ {\mathbf{\Lambda }}({{t}_{k}})) = 0\,,\quad {\mathbf{\omega }}({{t}_{k}}) = 0,$

где “${\text{vect}}$” обозначает векторную часть кватерниона, а “$ \circ $” – кватернионное произведение.

Если рассматривать задачу оптимального управления с подвижным правым концом траектории, когда задается значение кватерниона положения тела

(3.8)

${\mathbf{\Lambda }}({{t}_{k}}) = {{{\mathbf{\Lambda }}}_{k}},$

а угловая скорость тела подлежит определению, то при постановке краевой задачи оптимального управления на правом подвижном конце траектории с учетом условия трансверсальности условие (3.7) заменяется условием

(3.9)

${\text{vect}}({{{\mathbf{\tilde {\Lambda }}}}_{k}} \circ {\mathbf{\Lambda }}({{t}_{k}})) = 0,\quad {\mathbf{\nu }}({{t}_{k}}) = 0.$

Для численного решения краевой задачи оптимального управления использован известный алгоритм Левенберга–Марквардта, представляющий собой комбинацию модифицированного метода Ньютона и метода градиентного спуска. Так как управляющий момент содержит разрывы, то для улучшения сходимости итерационного процесса производилось уточнение положения точек разрыва управляющего момента.

4. Примеры решения задачи оптимального управления. В настоящем разделе приводятся решения задачи для трех различных тел.

Тело 1 – тело со сферической симметрией, его безразмерные моменты инерции

(4.1)

${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 1.$

Тело 2 – произвольное тело с безразмерными моментами инерции

(4.2)

${{I}_{1}} = 0.91161,\quad {{I}_{2}} = 1.36741,\quad {{I}_{3}} = 0.54696.$

Тело 3 – международная космическая станция (МКС), рассматриваемая как твердое тело [12], с размерными моментами инерции

${{I}_{1}} = 4853000\,\,{\text{к г }} \cdot {{{\text{м }}}^{2}},\,\,{{I}_{2}} = 23601000\,\,{\text{к г }} \cdot {{{\text{м }}}^{2}},\quad {{I}_{3}} = 26278000\,\,{\text{к г }} \cdot {{{\text{м }}}^{2}}$

или с безразмерными моментами инерции

(4.3)

${{I}_{1}} = 0.23577,\quad {{I}_{2}} = 1.14658,\quad {{I}_{3}} = 1.27663.$

Начальное состояние тела в безразмерных переменных определяется соотношениями:

(4.4)

$\begin{gathered} {{\Lambda }_{0}} = 0.79505,\quad {{\Lambda }_{1}} = 0.29814,\quad {{\Lambda }_{2}} = - 0.39752,\quad {{\Lambda }_{3}} = 0.34783, \\ {{\omega }_{1}} = {{\omega }_{2}} = {{\omega }_{3}} = 0. \\ \end{gathered} $

Конечное состояние тела, в которое его необходимо было перевести, в безразмерных переменных задается соотношениями:

(4.5)

$\begin{gathered} {{\Lambda }_{0}} = 0.66009,\quad {{\Lambda }_{1}} = 0.54564,\quad {{\Lambda }_{2}} = 0.02023,\quad {{\Lambda }_{3}} = - 0.51589, \\ {{\omega }_{1}} = {{\omega }_{2}} = {{\omega }_{3}} = 0. \\ \end{gathered} $

Угол поворота между начальной (4.4) и конечной (4.5) ориентацией тела составляет 120°. Для безразмерных весовых множителей в функционале качества процесса управления (1.6) выбраны значения ${{\alpha }_{1}} = 1.0,{{\alpha }_{2}} = 0.5,{{\alpha }_{3}} = 2.0$.

Для всех трех тел оптимальное управление каждый раз состоит из трех этапов. На первом этапе $0 \leqslant t < {{t}_{{p1}}}$ угловая скорость тела увеличивалась под действием разгоняющего управляющего момента, который по величине принимал максимальное значение. На втором этапе ${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$ управляющий момент равен нулю и тело вращается по инерции. На третьем этапе ${{t}_{{p2}}} \leqslant t \leqslant {{t}_{k}}$ угловая скорость тела уменьшается до нуля под действием тормозящего управляющего момента, который по величине принимает максимальное значение.

В табл. 1 для трех тел приводятся значения моментов времени окончания первого, второго и третьего этапов. В последней колонке рассматриваются значения функционалов качества управления процессом.

Таблица 1

Тело	t_p1	t_p2	t_k	J
1	0.59739	3.50593	4.10331	7.08291
2	0.41858	2.76637	3.18494	5.61282
3 (МКС)	0.68527	3.89169	4.57694	7.84945

В табл. 2 для трех тел представлены результаты расчетов для другого набора весовых множителей в функционале (1.6): ${{\alpha }_{1}} = 1.0,\,$ ${{\alpha }_{2}} = 0.5,{{\alpha }_{3}} = 1.0$.

Таблица 2

Тело	t_p1	t_p2	t_k	J
1	0.74541	2.80973	3.55514	5.75752
2	0.50890	2.27550	2.78437	4.69509
3 (МКС)	0.86141	3.09692	3.95756	6.32456

Из сравнения табл. 1, 2 видно, что уменьшение весового множителя ${{\alpha }_{3}}$ приводит к увеличению длительности активных этапов управления, на которых величина управляющего момента максимальная, и, следовательно, приводит к увеличению суммарного расхода топлива, уменьшению длительности этапа движения по инерции и уменьшению общей длительности переходного процесса.

При решении задачи с подвижным концом траектории, когда на правом конце вместо условия (4.5) ставится условие

(4.6)

${{\Lambda }_{0}} = 0.66009,\quad {{\Lambda }_{1}} = 0.54564,\quad {{\Lambda }_{2}} = 0.02023,\quad {{\Lambda }_{3}} = - 0.51589,$

а условие (4.4) на левом конце траектории сохраняется, оптимальное управление для тех же трех тел состоит из двух этапов. На первом этапе $0 \leqslant t < {{t}_{p}}$ угловая скорость тела увеличивается под действием разгоняющего управляющего момента, который по величине принимает максимальное значение. На втором этапе ${{t}_{p}} \leqslant t \leqslant {{t}_{k}}$ управляющий момент равен нулю и тело вращается по инерции до заданного конечного положения (4.6).

В табл. 3 для весовых множителей ${{\alpha }_{1}} = 1.0,{{\alpha }_{2}} = 0.5,{{\alpha }_{3}} = 2.0$ рассмотрены моменты окончания первого и второго этапов, координаты угловой скорости в конечный момент времени, а в последней колонке – значение функционала.

Таблица 3

Тело	t_p	t_k	ω₁	ω₂	ω₃	J
1	0.78568	3.05856	0.03536	–0.05907	–0.78265	5.41226
2	0.52708	2.46050	0.08460	–0.03699	–0.94874	4.47407
3(МКС)	0.91366	3.37526	–0.00051	–0.10226	–0.70974	5.91681

В табл. 4 приводятся результаты расчета задачи с подвижным правым концом траектории при граничных условиях (4.4), (4.6) для других значений весовых множителей в функционале (1.6): ${{\alpha }_{1}} = 1.0,{{\alpha }_{2}} = 1.0,{{\alpha }_{3}} = 2.0$.

Таблица 4

Тело	t_p	t_k	ω₁	ω₂	ω₃	J
1	0.69357	3.36651	0.03121	–0.05215	–0.69090	6.15066
2	0.44064	2.85032	0.07065	–0.03096	–0.79247	5.35382
3(МКС)	0.82294	3.65231	0.00062	–0.09156	–0.63932	6.59746

Из сравнения табл. 3 и 4 видно, что увеличение весового множителя ${{\alpha }_{2}}$ приводит к уменьшению длительности активного этапа управления, увеличению длительности этапа движения по инерции и длительности всего процесса управления, а также к уменьшению величины угловой скорости тела в конечный момент времени.

Согласно табл. 1–4 , распределение массы в твердом теле, которое характеризуется значениями моментов инерции тела, существенно влияет на длительности этапов управления и на значение функционала.

Надо отметить, что при решении задачи оптимального управления с закрепленными концами и задачи с подвижным правым концом траектории для тела 1 (тело со сферической симметрией) с выбранными граничными условиями (4.4)–(4.6) на втором этапе, когда тело вращается по инерции, угловая скорость тела сохраняется постоянной.

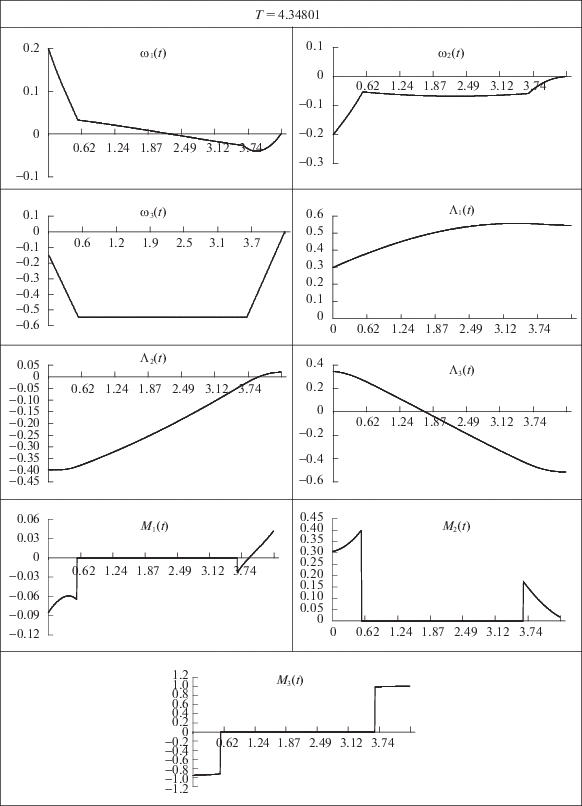
На рисунке приводятся результаты решения задачи оптимального управления для перевода МКС (тело 3) из начального состояния

(4.7)

$\begin{gathered} {{\Lambda }_{0}} = 0.79505,\quad {{\Lambda }_{1}} = 0.29814,\quad {{\Lambda }_{2}} = - 0.39752,\quad {{\Lambda }_{3}} = 0.34783, \\ {{\omega }_{1}} = 0.2,\quad {{\omega }_{2}} = - 0.2,\quad {{\omega }_{3}} = - 0.15 \\ \end{gathered} $

в конечное состояние (4.5), при этом весовые множители в функционале (1.6) принимают значения ${{\alpha }_{1}} = 1.0,{{\alpha }_{2}} = 0.5,{{\alpha }_{3}} = 2.0$. Управление состоит из трех этапов: первый этап $0 \leqslant t < {{t}_{{p1}}}$ = = 0.55015 – активный, с управлением максимальным по величине, второй этап ${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$ = = 3.64588 – этап вращения по инерции, на третьем этапе ${{t}_{{p2}}} \leqslant t < {{t}_{k}} = 4.34801$ угловая скорость уменьшается под действием тормозящего момента и тело приходит в конечное состояние (4.5). Значение функционала (1.6) $J = 7.40341$.

Отметим, что на рисунке представлены графики изменения во времени компонент угловой скорости ${{\omega }_{i}}(t),i = \overline {1,3} ,$ векторной части кватерниона ориентации ${{\Lambda }_{i}}(t),i = \overline {1,3} ,$ и компонент вектора управляющего момента $М _{i}^{{}}(t),i = \overline {1,3} $, МКС.

5. Аналитическое решение задачи оптимального управления разворотом твердого тела со сферической симметрией. Ниже рассматриваются случаи, когда твердое тело со сферической симметрией (${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 1$) из состояния покоя

(5.1)

${\mathbf{\Lambda }}\left( 0 \right) = {{{\mathbf{\Lambda }}}_{n}},\quad {\mathbf{\omega }}\left( 0 \right) = 0$

переводится в состояние покоя

(5.2)

${\mathbf{\Lambda }}\left( {{{t}_{k}}} \right) = {{{\mathbf{\Lambda }}}_{k}},\quad {\mathbf{\omega }}\left( {{{t}_{k}}} \right) = 0.$

Качество процесса управления определяется функционалом (1.6).

В случае граничных условий (5.1) и (5.2) во время оптимального процесса управления сферически-симметричное тело будет вращаться вокруг неподвижной оси, направление которой будет определяться единичным вектором ${\mathbf{e}}$ через кватернион ${\mathbf{N}}$:

(5.3)

${\mathbf{e}} = \frac{{{\text{vect}}{\mathbf{N}}}}{{\left| {{\text{vect}}{\mathbf{N}}} \right|}},\quad {\mathbf{N}} = {{{\mathbf{\tilde {\Lambda }}}}_{n}} \circ {{{\mathbf{\Lambda }}}_{k}}.$

Угол поворота тела ${{\varphi }_{k}}$ в процессе управления находится по формуле

(5.4)

${{\varphi }_{k}} = 2{\text{arctg}}\frac{{\left| {{\text{vect}}{\mathbf{N}}} \right|}}{{\left| {{\text{scal}}{\mathbf{N}}} \right|}},$

где ${\text{scal}}\,{\mathbf{N}}$ задает скалярную часть кватерниона ${\mathbf{N}}$. В случае сферически-симметричного тела формула (3.5), определяющая оптимальное управление, упрощается и принимает вид

(5.5)

${{{\mathbf{M}}}_{{opt}}} = \frac{{\mathbf{\nu }}}{{\left| {\mathbf{\nu }} \right|}},\quad {\text{е с л и }}\quad \left| {\mathbf{\nu }} \right| \geqslant {{\alpha }_{3}},\quad {{{\mathbf{M}}}_{{opt}}} = 0,\quad {\text{е с л и }}\quad \left| {\mathbf{\nu }} \right| < {{\alpha }_{3}}.$

Так как вектор угловой скорости ${\mathbf{\omega }}$ параллелен вектору e, то из второго уравнения системы (1.1), соотношения (5.5), системы уравнений (3.4) следует, что в случае сферически-симметричного тела и граничных условий (3.7), (5.1), (5.2) вектор управляющего момента M, сопряженные векторные переменные ${\mathbf{p}},\,{\mathbf{\nu }}$ также параллельны вектору e и, более того, во все время процесса ${\mathbf{p}} = {\mathbf{const}}$.

Оптимальное управление, как отмечено в разд. 4, состоит из трех этапов. Для тела со сферической симметрией тензор инерции R единичный. Это существенно упрощает интегрирование системы уравнений (1.1), (3.4). На первом этапе $0 \leqslant t < {{t}_{{p1}}}$ фазовые и сопряженные переменные и управляющий момент определяются по формулам:

(5.6)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ (\cos (0.25{{t}^{2}}) + {\mathbf{e}}\sin (0.25{{t}^{2}})),\quad {\mathbf{\omega }} = {\mathbf{e}}t, \\ {\mathbf{M}} = {\mathbf{e}},\quad {\mathbf{\nu }} = {\mathbf{e}}(\beta + {{\alpha }_{2}}{{t}^{2}} - ct),\quad {\mathbf{p}} = 2c{\mathbf{e}}. \\ \end{gathered} $

На втором этапе ${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$:

(5.7)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ \left( {\cos {{\varphi }_{2}}(t) + {\mathbf{e}}\sin {{\varphi }_{2}}(t)} \right),\quad {{\varphi }_{2}}(t) = 0.5{{t}_{{p1}}}(t - 0.5{{t}_{{p1}}}),\quad {\mathbf{\omega }} = {\mathbf{e}}{{t}_{{p1}}}, \\ {\mathbf{M}} = 0,\quad {\mathbf{\nu }} = {\mathbf{e}}(\beta - {{\alpha }_{2}}t_{{p1}}^{2} + (2{{\alpha }_{2}}{{t}_{{p1}}} - c)t),\quad {\mathbf{p}} = 2c{\mathbf{e}}. \\ \end{gathered} $

На третьем этапе ${{t}_{{p2}}} \leqslant t \leqslant {{t}_{k}}$:

(5.8)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ \left( {\cos {{\varphi }_{3}}(t) + {\mathbf{e}}\sin {{\varphi }_{3}}(t)} \right),\quad {{\varphi }_{3}}(t) = 0.25(2({{t}_{{p1}}} + {{t}_{{p2}}})t - {{t}^{2}} - t_{{p1}}^{2} - t_{{p2}}^{2}), \\ {\mathbf{\omega }} = {\mathbf{e}}({{t}_{k}} - t),\quad {\mathbf{M}} = - {\mathbf{e}},\quad {\mathbf{p}} = 2c{\mathbf{e}}, \\ {\mathbf{\nu }} = - {\mathbf{e}}({{\alpha }_{3}} + 2{{\alpha }_{2}}(0.5({{t}^{2}} + t_{{p2}}^{2}) - ({{t}_{{p1}}} + {{t}_{{p2}}})t + {{t}_{{p1}}}{{t}_{{p2}}}) - c(t - {{t}_{{p2}}})). \\ \end{gathered} $

Постоянные величины $\beta ,\,\,c,\,\,{{t}_{{p1}}},\,\,{{t}_{{p2}}},\,\,{{t}_{k}}$, которые входят в решения (5.6)–(5.8), задаются граничными условиями краевой задачи оптимального управления:

(5.9)

$\beta = {{\alpha }_{1}} + {{\alpha }_{3}},\quad {{t}_{k}} = {{t}_{{p1}}} + {{t}_{{p2}}},\quad c = \frac{{{{\alpha }_{1}}}}{{{{t}_{{p1}}}}} + {{\alpha }_{2}}{{t}_{{p1}}},\quad {{t}_{{p2}}} = \frac{{{{\varphi }_{k}}}}{{{{t}_{{p1}}}}},$

где ${{t}_{{p1}}}$ определяется из уравнения

(5.10)

${{\alpha }_{2}}t_{{p1}}^{4} - \left( {{{\alpha }_{1}} + {{\alpha }_{2}}{{\varphi }_{k}} + 2{{\alpha }_{3}}} \right)t_{{p1}}^{2} + {{\alpha }_{1}}\varphi _{k}^{{}} = 0$

по формуле

(5.11)

${{t}_{{p1}}} = \sqrt {\frac{1}{{2{{\alpha }_{2}}}}({{\alpha }_{1}} + {{\alpha }_{2}}{{\varphi }_{k}} + 2{{\alpha }_{3}} - \sqrt {{{{({{\alpha }_{1}} + {{\alpha }_{2}}{{\varphi }_{k}} + 2{{\alpha }_{3}})}}^{2}} - 4{{\alpha }_{1}}{{\alpha }_{2}}{{\varphi }_{k}}} )} .$

Из выражения для ${{t}_{k}}$ в формуле (5.9) видно, что длительности первого и третьего этапов управления совпадают.

В частном случае, когда ${{\alpha }_{2}} = 0$, уравнение (5.10) упрощается и ${{t}_{{p1}}}$ находится из выражения

(5.12)

${{t}_{{p1}}} = \sqrt {\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{1}} + 2{{\alpha }_{3}}}}{{\varphi }_{k}}} .$

Значение функционала качества управления выражается через весовые множители функционала и моменты окончания этапов процесса:

(5.13)

$J = {{\alpha }_{1}}{{t}_{k}} + {{\alpha }_{2}}\left( {{{t}_{{p2}}} - \frac{1}{3}{{t}_{{p1}}}} \right)t_{{p1}}^{2} + 2{{\alpha }_{3}}{{t}_{{p1}}}.$

В случае, когда правый конец траектории подвижный (не задается угловая скорость) и на этом конце ставится условие (3.9), оптимальное управление, как отмечалось в разд. 4, состоит из двух этапов. На первом этапе $0 \leqslant t < {{t}_{p}}$ решение для фазовых и сопряженных переменных описывается соотношениями (5.6). На втором этапе ${{t}_{p}} \leqslant t \leqslant {{t}_{k}}$ решение для фазовых и сопряженных переменных определяется соотношениями (5.7), в которых ${{t}_{{p1}}}$ надо заменить на ${{t}_{p}}$. Постоянные величины $\beta ,\,\,c,\,\,{{t}_{p}}\,,\,\,{{t}_{k}}$ в этих решениях вычисляются из условий (3.9):

(5.14)

$\beta = {{\alpha }_{1}} + {{\alpha }_{3}},\quad c = \frac{{{{\alpha }_{1}}}}{{{{t}_{p}}}} + {{\alpha }_{2}}{{t}_{p}},\quad {{t}_{k}} = \frac{{{{\varphi }_{k}}}}{{{{t}_{p}}}} + \frac{{{{t}_{p}}}}{2},$

где ${{t}_{p}}$ удовлетворяет уравнению

(5.15)

${{\alpha }_{2}}t_{p}^{4} - ({{\alpha }_{1}} + 2{{\alpha }_{2}}{{\varphi }_{k}} + 2{{\alpha }_{3}})t_{p}^{2} + 2{{\alpha }_{1}}{{\varphi }_{k}} = 0$

и определяется как

(5.16)

${{t}_{p}} = \sqrt {\frac{1}{{{{\alpha }_{2}}}}\left( {\frac{{{{\alpha }_{1}}}}{2} + {{\alpha }_{2}}{{\varphi }_{k}} + {{\alpha }_{3}} - \sqrt {{{{\left( {\frac{{{{\alpha }_{1}}}}{2} + {{\alpha }_{2}}{{\varphi }_{k}} + {{\alpha }_{3}}} \right)}}^{2}} - 2{{\alpha }_{1}}{{\alpha }_{2}}{{\varphi }_{k}}} } \right)} {\kern 1pt} {\kern 1pt} .$

В частном случае, когда ${{\alpha }_{2}} = 0$, уравнение для t_p упрощается и его решение имеет вид

(5.17)

${{t}_{p}} = \sqrt {\frac{{{{\alpha }_{1}}{{\varphi }_{k}}}}{{0.5{{\alpha }_{1}} + {{\alpha }_{3}}}}} .$

(5.18)

$J = {{\alpha }_{1}}{{t}_{k}} + {{\alpha }_{2}}\left( {{{t}_{k}} - \frac{2}{3}{{t}_{p}}} \right)t_{p}^{2} + {{\alpha }_{3}}{{t}_{p}}.$

По формулам разд. 5 проводились расчеты для задач об оптимальном управлении движением сферически-симметричного тела для граничных условий и весовых множителей в функционале (1.6), которые использовались в разд. 4. Результаты расчетов по формулам разд. 5 полностью совпали с данными табл. 1–4 для сферически-симметричного тела, т.е. тела 1.

6. Оптимальное управление сферически-симметричным телом в случае укороченного функционала (${{\alpha }_{3}} = 0$). В этом разделе рассматривается оптимальное управление движением сферически-симметричного твердого тела при условии, что в функционале (1.6) весовой множитель ${{\alpha }_{3}} = 0$. В этом случае системы дифференциальных уравнений (1.1), (3.4) упрощаются, а из условия максимума для функции Гамильтона–Понтрягина следует, что оптимальное управление определяется через сопряженную переменную ${\mathbf{\nu }}$:

(6.1)

${{{\mathbf{M}}}_{{opt}}} = \frac{{\mathbf{\nu }}}{{\left| {\mathbf{\nu }} \right|}},\quad {\text{е с л и }}\quad {\mathbf{\nu }} \ne 0\quad {{{\mathbf{M}}}_{{opt}}} = {{{\mathbf{M}}}_{{{\text{о с о б о е }}}}},\quad {\text{е с л и }}\quad {\mathbf{\nu }} \equiv 0,\quad t \in [{{t}_{*}},{{t}_{{{\text{**}}}}}].$

Если на некотором промежутке времени ${\mathbf{\nu }} \equiv 0$, то из условия максимума функции Гамильтона–Понтрягина управляющий момент непосредственно не определяется. Управление на таком промежутке называется особым и для его определения необходимо проводить дополнительное исследование.

Второе уравнение системы (3.4) в случае сферически-симметричного твердого тела упрощается и принимает вид

(6.2)

$\frac{{d{\mathbf{\nu }}}}{{dt}} = 2{{\alpha }_{2}}{\mathbf{\omega }} - \frac{{\mathbf{p}}}{2}.$

Из (6.2) следует, что на этапе особого управления, когда ${\mathbf{\nu }} \equiv 0$,

(6.3)

${\mathbf{p}} = 4{{\alpha }_{2}}{\mathbf{\omega }}.$

Из первого уравнения системы (3.4) и соотношения (6.3) следует, что на этапе особого управления

(6.4)

${\mathbf{p}} = {\mathbf{const}},\quad {\mathbf{\omega }} = {\mathbf{const}}.$

Тогда из второго уравнения системы (1.1) следует, что для сферически-симметричного твердого тела на особом этапе управляющий момент обращается в нуль и тело на этом этапе вращается по инерции:

(6.5)

${{{\mathbf{M}}}_{{{\text{о с о б о е }}}}} = {\mathbf{0}}.$

Как указано в разд. 5, при заданных граничных условиях в начальный и конечный моменты времени (5.1) и (5.2) во время оптимального процесса тело вращается вокруг неподвижной оси, направление которой определяется единичным вектором ${\mathbf{e}}$ по формуле (5.3), а угол поворота тела ${{\varphi }_{k}}$ – по формуле (5.4).

Исследования показали, что если угол поворота ${{\phi }_{k}}$ удовлетворяет условию

(6.6)

${{\varphi }_{k}} \leqslant {{\alpha }_{1}}{\text{/}}{{\alpha }_{2}},$

то оптимальное управление состоит из двух этапов. На первом этапе $0 \leqslant t < {{t}_{p}}$ угловая скорость тела увеличивается под действием максимального по величине ускоряющего момента, а на втором этапе ${{t}_{p}} \leqslant t \leqslant {{t}_{k}}$ угловая скорость тела уменьшается до нуля под действием максимального по величине тормозящего момента, и оно останавливается в заданном положении. В случае, когда угол поворота ${{\varphi }_{k}}$ удовлетворяет условию

(6.7)

${{\varphi }_{k}} > {{\alpha }_{1}}{\text{/}}{{\alpha }_{2}},$

оптимальное управление состоит из трех этапов. На первом этапе $0 \leqslant t < {{t}_{{p1}}}$, под действием ускоряющего момента, происходит разгон вращательного движения тела, на втором особом этапе ${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$ тело вращается по инерции, на третьем этапе ${{t}_{{p2}}} \leqslant t \leqslant {{t}_{k}}$ под действием тормозящего момента вращение тела замедляется, и оно останавливается в заданном конечном положении.

В случае ${{\varphi }_{k}} \leqslant {{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}$ общее время процесса управления определяется по формуле

(6.8)

${{t}_{k}} = 2\sqrt {{{\varphi }_{k}}} .$

Решение для фазовых и сопряженных переменных и управляющего момента на первом этапе $0 \leqslant t < {{t}_{p}} = 0.5{{t}_{k}}$ задается как

(6.9)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ (\cos (0.25{{t}^{2}}) + {\mathbf{e}}\sin (0.25{{t}^{2}})),\quad {\mathbf{\omega }} = {\mathbf{e}}t, \\ {\mathbf{M}} = {\mathbf{e}},\quad {\mathbf{\nu }} = {\mathbf{e}}({{\alpha }_{1}} + {{\alpha }_{2}}{{t}^{2}} - ct),\quad {\mathbf{p}} = 2c{\mathbf{e}},\quad c = \frac{{{{\alpha }_{1}}}}{{\sqrt {{{\varphi }_{k}}} }} + {{\alpha }_{2}}\sqrt {{{\varphi }_{k}}} . \\ \end{gathered} $

На втором этапе ${{t}_{p}} \leqslant t \leqslant {{t}_{k}}$:

(6.10)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ \left( {\cos {{\varphi }_{2}}(t) + {\mathbf{e}}\sin {{\varphi }_{2}}(t)} \right),\quad {{\varphi }_{2}}(t) = 0.5{{t}_{k}}t - 0.25{{t}^{2}} - 0.125t_{k}^{2}, \\ {\mathbf{\omega }} = {\mathbf{e}}({{t}_{k}} - t),\quad {\mathbf{M}} = - {\mathbf{e}}, \\ {\mathbf{\nu }} = {\mathbf{e}}(2{{\alpha }_{2}}({{t}_{k}}t - 0.5{{t}^{2}} - 0.375t_{k}^{2}) - c(t - 0.5{{t}_{k}}),\quad {\mathbf{p}} = 2c{\mathbf{e}}. \\ \end{gathered} $

Значение функционала (1.6) для оптимального процесса вычисляется по формуле:

(6.11)

$J = 2\left( {{{\alpha }_{1}} + \frac{1}{3}{{\alpha }_{2}}{{\varphi }_{k}}} \right)\sqrt {{{\varphi }_{k}}} .$

В случае ${{\varphi }_{k}} > {{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}$ моменты окончания первого и второго этапов ${{t}_{{p1}}}\,,\,{{t}_{{p2}}}$ и общее время процесса ${{t}_{k}}$ рассчитывается как

(6.12)

${{t}_{{p1}}} = \sqrt {{{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}} ,\quad {{t}_{{p2}}} = {{\varphi }_{k}}\sqrt {{{\alpha }_{2}}{\text{/}}{{\alpha }_{1}}} ,\quad {{t}_{k}} = {{t}_{{p1}}} + {{t}_{{p2}}}.$

Из последней формулы в (6.9) следует, что длительности первого и третьего этапов совпадают. Решение для фазовых и сопряженных переменных и управляющего момента на первом этапе $0 \leqslant t < {{t}_{{p1}}}$ определяется следующим образом:

(6.13)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ (\cos (0.25{{t}^{2}}) + {\mathbf{e}}\sin (0.25{{t}^{2}})),\quad {\mathbf{\omega }} = {\mathbf{e}}t, \\ {\mathbf{M}} = {\mathbf{e}},\quad {\mathbf{\nu }} = {\mathbf{e}}{{\alpha }_{2}}({{t}^{2}} - 2{{t}_{{p1}}}t + t_{{p1}}^{2}),\quad {\mathbf{p}} = 4\sqrt {{{\alpha }_{1}}{{\alpha }_{2}}} {\mathbf{e}}. \\ \end{gathered} $

На втором этапе ${{t}_{{p1}}} \leqslant t < {{t}_{{p2}}}$:

(6.14)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ \left( {\cos {{\varphi }_{2}}(t) + {\mathbf{e}}\sin {{\varphi }_{2}}(t)} \right),\quad {{\varphi }_{2}}(t) = 0.5{{t}_{{p1}}}(t - 0.5{{t}_{{p1}}}), \\ {\mathbf{\omega }} = {\mathbf{e}}{{t}_{{p1}}},\quad {\mathbf{M}} = 0,\quad {\mathbf{\nu }} = 0,\quad {\mathbf{p}} = 4\sqrt {{{\alpha }_{1}}{{\alpha }_{2}}} {\mathbf{e}}. \\ \end{gathered} $

На третьем этапе ${{t}_{{p2}}} \leqslant t \leqslant {{t}_{k}}$:

(6.15)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ \left( {\cos {{\varphi }_{3}}(t) + {\mathbf{e}}\sin {{\varphi }_{3}}(t)} \right),\quad {{\varphi }_{3}}(t) = 0.25(2{{t}_{k}}t - {{t}^{2}} - t_{{p1}}^{2} - t_{{p2}}^{2}), \\ {\mathbf{\omega }} = {\mathbf{e}}({{t}_{k}} - t),\quad {\mathbf{M}} = - {\mathbf{e}},\quad {\mathbf{\nu }} = - {\mathbf{e}}{{\alpha }_{2}}({{t}^{2}} - 2{{t}_{{p2}}}t + t_{{p2}}^{2}),\quad {\mathbf{p}} = 4\sqrt {{{\alpha }_{1}}{{\alpha }_{2}}} {\mathbf{e}}. \\ \end{gathered} $

Значение функционала для оптимального процесса вычисляется как

(6.16)

$J = 2({{\alpha }_{1}}{\text{/}}3 + {{\alpha }_{2}}{{\varphi }_{k}})\sqrt {{{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}} .$

Если правый конец траектории является подвижным, т.е. ставится условие (3.7), то в случае, когда выполняется условие

(6.17)

${{\varphi }_{k}} \leqslant {{\alpha }_{1}}{\text{/}}(2{{\alpha }_{2}}),$

оптимальное управление состоит из одного этапа, на котором угловая скорость увеличивается и тело приходит в заданное конечное положение. Если верно условие

(6.18)

${{\varphi }_{k}} > {{\alpha }_{1}}{\text{/}}(2{{\alpha }_{2}}),$

то оптимальное управление состоит из двух этапов. На первом этапе угловая скорость тела возрастает под действием ускоряющего момента, максимального по величине, а на втором этапе, который является этапом особого управления, тело с постоянной скоростью вращается по инерции и приходит в заданное конечное положение.

В случае выполнения условия (6.17) длительность процесса ${{t}_{k}}$ определяется по формуле

(6.19)

${{t}_{k}} = \sqrt {2{{\varphi }_{k}}} ,$

а фазовые и сопряженные переменные и управляющий момент имеют вид

(6.20)

$\begin{gathered} {\mathbf{\Lambda }} = {{{\mathbf{\Lambda }}}_{n}} \circ (\cos (0.25{{t}^{2}}) + {\mathbf{e}}\sin (0.25{{t}^{2}})),\quad {\mathbf{\omega }} = {\mathbf{e}}t, \\ {\mathbf{M}} = {\mathbf{e}},\quad {\mathbf{\nu }} = {\mathbf{e}}({{\alpha }_{1}} + {{\alpha }_{2}}{{t}^{2}} - ct),\quad {\mathbf{p}} = 2c{\mathbf{e}},\quad c = \frac{{{{\alpha }_{1}}}}{{\sqrt {2{{\varphi }_{k}}} }} + {{\alpha }_{2}}\sqrt {2{{\varphi }_{k}}} . \\ \end{gathered} $

Значение функционала(1.6) вычисляется как

(6.21)

$J = \left( {{{\alpha }_{1}} + \frac{2}{3}{{\alpha }_{2}}{{\varphi }_{k}}} \right)\sqrt {2{{\varphi }_{k}}} .$

Если верно условие (6.18), то длительность процесса, состоящего из двух этапов, определяется по формуле

(6.22)

${{t}_{k}} = {{\varphi }_{k}}\sqrt {{{\alpha }_{2}}{\text{/}}{{\alpha }_{1}}} + \frac{1}{2}\sqrt {{{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}} .$

На первом этапе $0 \leqslant t < {{t}_{p}} = \sqrt {{{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}} $ решение описывается формулами (6.13), только ${{t}_{{p1}}}$ надо заменить на t_p, а на втором этапе ${{t}_{p}} \leqslant t \leqslant {{t}_{k}}$ решение описывается формулами (6.14) с той же заменой. Значение функционала (1.6) в этом случае вычисляется как

(6.23)

$J = {{\alpha }_{1}}\left( {2{{\varphi }_{k}}\sqrt {{{\alpha }_{2}}{\text{/}}{{\alpha }_{1}}} + \frac{1}{3}\sqrt {{{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}} } \right).$

Заключение. Представленные в статье результаты численного и аналитического решения задачи оптимального управления вращательным движением твердого тела с комбинированным критерием качества процесса управления и использованием кватернионов могут найти свое применение при построении систем управления космических аппаратов, как и известные аналитические решения задачи оптимального разворота твердого тела, полученные в классах плоских эйлеровых разворотов и конических движений [1, 4]. Учет угловой скорости твердого тела в функционале качества процесса управления позволяет построить более плавные (комфортные) оптимальные законы движения.

Рисунок.

Пример решения задачи оптимального разворота

Список литературы

Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973.
Scrivener S.L., Thompson R.C. Survey of Time-Optimal Attitude Maneuvers // J. Guidance, Control, and Dynamics. 1994. V. 17. № 2.
Петров Б.Н., Боднер В.А., Алексеев К.Б. Аналитическое решение задачи управления пространственным поворотным маневром // ДАН СССР. 1970. Т. 192. № 6.
Бранец В.Н., Черток М.Б., Казначеев Ю.В. Оптимальный разворот твердого тела с одной осью симметрии // Космич. исслед. 1984. Т. 22. Вып. 3.
Левский М.В. Применение принципа максимума Л.С. Понтрягина к задачам оптимального управления ориентацией космического аппарата // Изв. РАН. ТиСУ. 2008. № 6.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального разворота сферически-симметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2013. № 3.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота сферически-симметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2014. № 2.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2016. № 6.
Молоденков А.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2018. № 2.
Молоденков А.В., Сапунков Я.Г. Аналитическое приближенное решение задачи оптимального разворота космического аппарата при произвольных граничных условиях // Изв. РАН. ТиСУ. 2015. № 3.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1961.
Банит Ю.Р., Беляев М.Ю., Добринская Т.А., Ефимов Н.И., Сазонов В.В., Стажков В.М. Определение тензора инерции международной космической станции по телеметрической информации. Препринт ИПМ им. М.В. Келдыша РАН. 2002. № 57.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал