Известия РАН. Теория и системы управления, 2019, № 3, стр. 48-54

Об управлении движением механических систем с избыточным числом управляющих воздействий

Е. С. Брискин^a, *, Н. Г. Шаронов^a

^a Волгоградский государственный технический ун-т
Волгоград, Россия

Поступила в редакцию 21.08.2018
После доработки 24.12.2018
Принята к публикации 28.01.2019

DOI: 10.1134/S0002338819030053

Аннотация

Рассматриваются особенности управления механическими системами в случае превышения количества приводов над числом степеней свободы. Сформулированы задачи управления силами для реализации режима движения, обеспечивающего оптимальность по заданному критерию, и управления силами при заданных режиме движения и функциональной зависимости между ними. Приводятся методики решения и результаты моделирования поставленных задач.

Введение. Одна из задач механики состоит в определении действующих на механическую систему сил, если известны уравнения ее движения [1]. Необходимым условием однозначного ее решения является равенство количества описывающих движение уравнений количеству степеней свободы рассматриваемой механической системы. Однако известны такие машины и механизмы, у которых число учитываемых степеней свободы не совпадает с числом управляемых приводов, в частности, последних может быть больше. Введение избыточного числа приводов обусловлено или необходимостью расширения рабочей зоны выходного звена [2, 3], или снижения нагрузки на каждый из приводов с улучшением энергоэффективности их работы [4–6], или точности позиционирования выходного звена, например для механизмов с параллельной структурой. Могут быть и другие причины [7].

Примером превышения количества приводов над числом степеней свободы механической системы является перемещение одного твердого тела группой транспортных средств из одного произвольного положения в другое. В этом случае рабочим органом служит переносимое тело, а приводами – транспортные средства, взаимодействующие своими движителями с опорной поверхностью, с одной стороны, и корпусом перемещаемого твердого тела в каких-либо его точках – с другой [7]. Другим случаем может являться плоское движение (три степени свободы) корпуса шагающей машины “Ортоног” (рис. 1), осуществляемое четырьмя ортогональными движителями, приводимых в движение приводами: четырьмя поворотными и четырьмя линейными [8, 9].

Рис. 1.

Шагающая машина “Ортоног”

1. Постановка задачи. Рассматривается голономная механическая система с S степенями свободы, которая приводится в движение N приводами (N > S). Движение такой системы можно описать уравнениями Лагранжа

(1.1)

$\frac{d}{{dt}}\left( {\frac{{\partial {\rm T}}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial {\rm T}}}{{\partial {{q}_{j}}}} = {{P}_{j}} + \sum\limits_{n = 1}^N {{{Q}_{n}}{{B}_{{nj}}}} ,\quad j = \overline {1,S} ,$

где ${{q}_{j}}$, ${{\dot {q}}_{j}}$ – обобщенные координаты и скорости, T – кинетическая энергия, P_j – обобщенная сила, соответствующая j обобщенной координате и обусловленная известными силами (кроме развиваемых приводами управляющих воздействий, по величине равных Q_n), B_nj – скалярный сомножитель, с помощью которого управляющее воздействие Q_n преобразуется в обобщенную силу.

Если привод обеспечивает поступательное движение выходного звена, например поршня гидроцилиндра, то

(1.2)

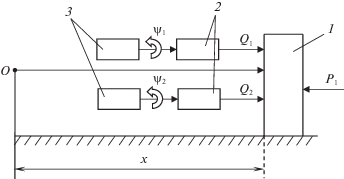
${{B}_{{nj}}} = \left| {\frac{{\partial {{{\mathbf{r}}}_{n}}}}{{\partial {{q}_{j}}}}} \right|\cos \left( {{{{\mathbf{Q}}}_{n}},\frac{{\partial {{{\mathbf{r}}}_{n}}}}{{\partial {{q}_{j}}}}} \right),$

где ${{{\mathbf{r}}}_{n}}$ – радиус–вектор точки приложения вектора ${{{\mathbf{Q}}}_{n}}$, соответствующего силе, развиваемой n-м приводом.

Так, например, если механизм с одной степенью свободы, расчетная схема которого представлена на рис. 2, состоит из поступательно перемещающегося в горизонтальной плоскости тела под воздействием двух генерируемых приводами сил Q₁ и Q₂ и силы сопротивления P₁, то

${{{\mathbf{r}}}_{1}} = {{{\mathbf{r}}}_{2}},\quad {{q}_{1}} = x,\quad \left| {\frac{{\partial {{{\mathbf{r}}}_{n}}}}{{\partial {{q}_{j}}}}} \right| = 1,\quad {{B}_{{11}}} = {{B}_{{21}}} = 1.$

Рис. 2.

Расчетная схема механизма с одним избыточным приводом

Предложенная на рис. 2 расчетная схема может соответствовать, например, работе движителя (рис. 3) шагающей машины “Ортоног” при одновременной работе приводов курсового движения двух механизмов шагания одного движителя.

Рис. 3.

Движитель шагающей машины “Ортоног”

Если привод обеспечивает вращательное движение выходного звена, например ротора электродвигателя, то

(1.3)

${{B}_{{nj}}} = \left| {\frac{{\partial {{\varphi }_{n}}}}{{\partial {{q}_{j}}}}} \right|\cos \left( {{{{\mathbf{Q}}}_{n}},{{e}_{n}}} \right),$

где e_n – вектор, задающий направление оси поворота на угол ${{\varphi }_{n}}$ выходного звена n-го привода, развивающего управляющее воздействие в виде вектора момента Q_n.

Так, например, в случае вращательного движения кривошипа циклового механизма шагания [10] машины “Восьминог” (рис. 4) развиваемый электродвигателем момент идет на преодоление силы, приложенной в шарнире соединения кривошипа с криволинейным шатуном, обеспечивающим тяговое усилие или перенос опоры на соответствующих этапах цикла.

Рис. 4.

Шагающая машина “Восьминог”

В общем случае S уравнений (1.1) содержат N + S неизвестных функций. Поэтому для однозначного решения (1.1) требуется или задание дополнительных N функций или составление N дополнительных уравнений. Причем дополнительные уравнения могут быть получены различными способами исходя из различных требований, предъявляемых к исследуемой механической системе, или гипотез, выдвигаемых о действующих на тело силах, например гипотезе о совместности деформаций [11].

Рассматриваются два варианта постановки задачи:

1) определение таких уравнений движения механической системы, удовлетворяющего начальным (граничным) и возможным изопериметрическим условиям (например, прохождения определенного расстояния за определенное время), которые обеспечивают минимум задаваемого функционала качества, как правило, состоящего из нескольких показателей;

2) при заранее заданных уравнениях движения ставится задача определения усилий в приводах при дополнительно целенаправленно введенных условиях

(1.4)

${{f}_{i}}({{Q}_{1}},\; \ldots ,\;{{Q}_{N}}) = 0,\quad i = \overline {1,N - S} .$

2. Метод решения на основе введенного функционала качества. В общем случае функционал качества состоит из суммы взвешенных показателей, в частности определяемых функционалами [12]. Поэтому составляются уравнения Эйлера–Пуассона, обеспечивающие минимум введенного функционала. Среди показателей могут быть следующие.

Показатель H₁ необратимых потерь мощности W (тепловые потери), который для различных типов двигателей различным образом зависит от развиваемого приводом момента M или силы F (в общем случае обобщенной силы Q). Так, например, для электрических двигателей [13]

(2.1)

$W = \beta {{Q}^{2}} + \gamma Q + \delta .$

Для двигателей внутреннего сгорания зависимость тепловых потерь с достаточной степенью точности можно представить в виде [14]

(2.2)

$W = \alpha {{Q}^{3}} + \beta {{Q}^{2}} + \gamma Q + \delta .$

В (2.1), (2.2) коэффициенты α, β, γ, δ – постоянные, характерные для конкретного типа двигателя. В общем случае, тепловые потери для n-го привода можно представить в форме

(2.3)

${{W}_{n}} = \sum\limits_{l = 0}^L {{{\alpha }_{{ln}}}Q_{n}^{l}} ,$

где L – количество учитываемых членов ряда. Тогда энергоэффективность будет определяться тепловыми потерями A за характерное время τ (для цикловых механизмов за один период):

(2.4)

$A = {{H}_{1}} = \int\limits_0^\tau {\sum\limits_{n = 1}^N {\sum\limits_{l = 0}^L {{{\alpha }_{{ln}}}Q_{n}^{l}dt} } } .$

Показатели H_2j, H_3j, характеризующие среднеквадратичное обобщенное ускорение и обобщенную скорость, которые соответствуют j-й обобщенной координате, равны:

(2.5)

${{H}_{{2j}}} = \int\limits_0^\tau {\ddot {q}_{j}^{2}dt,} \quad {{H}_{{3j}}} = \int\limits_0^\tau {\dot {q}_{j}^{2}dt} .$

Могут быть и другие показатели H₁… H_r, $r = \overline {4,R} $, из которых строится критерий оптимальности I:

(2.6)

$I = {{k}_{1}}{{H}_{1}} + \sum\limits_{j = 1}^S {{{k}_{{2j}}}{{H}_{{2j}}}} + \sum\limits_{j = 1}^S {{{k}_{{3j}}}{{H}_{{3j}}}} + \sum\limits_{r = 4}^R {{{k}_{r}}{{H}_{r}}.} $

Метод определения режима движения q_j(t) механической системы основан на решении вариационной задачи по минимизации функционала (2.4) с учетом начальных и (или) граничных, а также изопериметрических условий.

Для этого из уравнений (1.1) выражаются S неизвестных развиваемых приводами сил Q_n, $n = \overline {1,S} $, через S обобщенных координат q_j и N–S сил Q_k, $k = \overline {S + 1,N} $:

(2.7)

${{Q}_{n}} = \sum\limits_{j = 1}^S {{{C}_{{nj}}}\left\{ {\frac{d}{{dt}}\left( {\frac{{\partial {\rm T}}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial {\rm T}}}{{\partial {{q}_{j}}}} - {{P}_{j}} - \sum\limits_{k = S + 1}^N {{{Q}_{k}}{{B}_{{kj}}}} } \right\}} ,$

где C_nj – матрица, обратная квадратной усеченной матрице ${{B}_{{kj}}}$, $k,j = \overline {1,S} $:

(2.8)

$\sum\limits_{j = 1}^S {{{C}_{{nj}}}{{B}_{{kj}}}} = {{\delta }_{{nk}}},\quad n,k = \overline {1,S} ,$

где δ_nk – символы Кронекера.

В развернутом виде (2.7) имеет вид

(2.9)

${{Q}_{n}} = \sum\limits_{j = 1}^S {{{C}_{{nj}}}\left\{ {\sum\limits_{i = 1}^S {{{a}_{{ij}}}{{{\ddot {q}}}_{i}}} + \frac{1}{2}\sum\limits_{\mu = 1}^S {\sum\limits_{i = 1}^S {\left( {\frac{{\partial {{a}_{{ij}}}}}{{\partial {{q}_{\mu }}}} - \frac{1}{2}\frac{{\partial {{a}_{{i\mu }}}}}{{\partial {{q}_{j}}}}} \right){{{\dot {q}}}_{i}}{{{\dot {q}}}_{\mu }} - {{P}_{j}} - \sum\limits_{k = S + 1}^N {{{Q}_{k}}{{B}_{{kj}}}} } } } \right\},} \quad (n = \overline {1,S} ),$

где a_ij – компоненты матрицы инерционных коэффициентов механической системы.

Уравнения (2.9) позволяют сформировать показатель тепловых потерь H₁, а общий вид функционала (2.6) имеет вид

(2.10)

$\begin{gathered} I = \int\limits_0^\tau {\left\{ {{{k}_{1}}\sum\limits_{n = 1}^S {\sum\limits_{l = 0}^L {{{\alpha }_{{ln}}}} } } \right.{{{\left\{ {\sum\limits_{j = 1}^S {{{C}_{{nj}}}} \left[ {\sum\limits_{i = 1}^S {{{a}_{{ij}}}{{{\ddot {q}}}_{i}}} + \frac{1}{2}\sum\limits_{\mu = 1}^S {\sum\limits_{i = 1}^S {\left( {\frac{{\partial {{a}_{{ij}}}}}{{\partial {{q}_{{^{\mu }}}}}} - \frac{1}{2}\frac{{\partial {{a}_{{i\mu }}}}}{{\partial {{q}_{{^{j}}}}}}} \right){{{\dot {q}}}_{i}}{{{\dot {q}}}_{\mu }}} } - {{P}_{j}} - \sum\limits_{k = S + 1}^N {{{Q}_{k}}{{B}_{{kj}}}} } \right]} \right\}}}^{l}} + } \\ + \left. {\left. {\sum\limits_{k = S + 1}^N {\sum\limits_{l = 0}^L {{{\alpha }_{{lk}}}Q_{k}^{l}} } } \right\} + \sum\limits_{j = 1}^S {{{k}_{{2j}}}\ddot {q}_{j}^{2}} + \sum\limits_{j = 1}^S {{{k}_{{3j}}}\dot {q}_{j}^{2}} + \sum\limits_{r = 4}^R {{{k}_{r}}{{H}_{r}}} } \right\}dt = \int\limits_0^\tau {\Phi dt} . \\ \end{gathered} $

Особенность функционала (2.10) состоит в зависимости подынтегральной функции Φ от ${{q}_{i}}$, ${{\dot {q}}_{i}}$, ${{\ddot {q}}_{i}}$, $i = \overline {1,S} $, и Q_k, $k = \overline {S + 1,N} $. Поэтому Q_k рассматриваются как дополнительные независимые переменные, а уравнения Эйлера–Пуассона сводятся к двум группам уравнений:

(2.11)

$\begin{gathered} \frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {\frac{{\partial \Phi }}{{\partial {{{\ddot {q}}}_{i}}}}} \right) - \frac{d}{{dt}}\left( {\frac{{\partial \Phi }}{{\partial {{{\dot {q}}}_{i}}}}} \right) + \frac{{\partial \Phi }}{{\partial {{q}_{i}}}} = 0,\quad i = \overline {1,S} , \\ \frac{{\partial \Phi }}{{\partial {{Q}_{k}}}} = 0,\quad k = \overline {S + 1,N} . \\ \end{gathered} $

В развернутой форме уравнения (2.9) достаточно громоздки и поэтому их целесообразно составлять при решении конкретных задач.

3. Пример реализации метода. Рассматривается (рис. 2) поступательное перемещение твердого тела 1 массы m вдоль горизонтальной оси под действием двух приводов с редукторами 2 и двигателями 3, роторы которых поворачиваются на углы ψ₁ и ψ₂ (механизм “параллельной” структуры [15]).

В соответствии с (1.1) дифференциальное уравнение движения имеет вид

(3.1)

$m\ddot {x} = {{Q}_{1}} + {{Q}_{2}} - P,$

где P – преодолеваемая постоянная сила сопротивления движению. Если в (2.2) α = γ = δ = 0, что характерно, например, для двигателей постоянного тока, то тепловые потери определяются интегралом

(3.2)

$A = {{A}_{1}} + {{A}_{2}} = \int\limits_0^\tau {{{\beta }_{1}}Q_{1}^{2}dt} + \int\limits_0^\tau {{{\beta }_{2}}Q_{2}^{2}dt} ,$

где τ – время движения, А₁, А₂ – соответственно тепловые потери в каждом из приводов.

Тогда если принять во внимание изопериметрическое условие

(3.3)

$\int\limits_0^\tau {\dot {x}dt} = l,$

что соответствует прохождению тела B расстояния l за время τ и (3.2) считать единственным показателем, то подынтегральная функция качества Φ имеет вид

(3.4)

$\Phi = {{\beta }_{2}}Q_{2}^{2} + {{\beta }_{1}}{{(m\ddot {x} - {{Q}_{2}} + P)}^{2}} + \mu \dot {x},$

где µ – неопределенный множитель Лагранжа, а независимыми переменными являются q(t) и Q₂(t). Уравнения Эйлера–Пуассона имеют вид

(3.5)

$\left\{ \begin{gathered} 2{{\beta }_{1}}{{m}^{2}}\dddot x - 2{{\beta }_{1}}m{{{\dot {Q}}}_{2}} - \mu = C, \hfill \\ 2({{\beta }_{1}} + {{\beta }_{2}}){{Q}_{2}} - 2{{\beta }_{1}}m\ddot {x} - 2{{\beta }_{1}}P = 0, \hfill \\ \end{gathered} \right.$

где С – произвольная постоянная, которую можно определить из граничных условий

(3.6)

$\begin{gathered} x(0) = 0\quad \dot {x}(0) = 0, \hfill \\ x(\tau ) = l\quad \dot {x}(\tau ) = 0. \hfill \\ \end{gathered} $

Условие x(τ) = l является излишним, так как тождественно изопериметрическому (3.3). Однако, учитывая его, можно определить сумму

(3.7)

$C + \mu = - \frac{{24l{{m}^{2}}{{\beta }_{1}}{{\beta }_{2}}}}{{({{\beta }_{1}} + {{\beta }_{2}}){{\tau }^{3}}}}.$

Тогда решением уравнений (3.5) являются функции

(3.8)

$\left\{ \begin{gathered} x = \frac{{3l}}{{{{\tau }^{2}}}}{{t}^{2}}\left( {1 - \frac{2}{3}\frac{t}{\tau }} \right), \hfill \\ {{Q}_{1}} = \frac{{{{\beta }_{2}}}}{{{{\beta }_{1}} + {{\beta }_{2}}}}m\frac{{6l}}{{{{\tau }^{2}}}}\left( {1 - 2\frac{t}{\tau } + \frac{{P{{\tau }^{2}}}}{{6lm}}} \right), \hfill \\ {{Q}_{2}} = \frac{{{{\beta }_{1}}}}{{{{\beta }_{1}} + {{\beta }_{2}}}}m\frac{{6l}}{{{{\tau }^{2}}}}\left( {1 - 2\frac{t}{\tau } + \frac{{P{{\tau }^{2}}}}{{6lm}}} \right). \hfill \\ \end{gathered} \right.$

Для того, чтобы обеспечить усилия, развиваемые приводами в соответствии с (3.8) необходимо привлечь уравнения вращения роторов двигателей (в рассматриваемом случае постоянного тока) [13]

(3.9)

${{J}_{j}}{{\ddot {\varphi }}_{j}} = {{k}_{j}}{{u}_{j}} - {{\mu }_{j}}{{\dot {\varphi }}_{j}} - {{\psi }_{j}}({{Q}_{j}}),$

где J_j, φ_j – соответственно момент инерции ротора j-го двигателя и угол его поворота, k_j, µ_j – характеристики j-го двигателя, ψ_j(Q_j) – приведенный к валу двигателя момент сил полезного сопротивления, обусловленный усилиями, которые действуют со стороны перемещаемого тела на двигатель, u_j – напряжение, подаваемое на обмотки двигателя.

Если ψ_j(Q_j) – линейная функция, то

(3.10)

${{\psi }_{j}}({{Q}_{j}}) = {{\lambda }_{j}}{{Q}_{j}},$

а между φ_j и x существует голономная связь, обусловленная кинематической схемой привода:

(3.11)

${{\varphi }_{j}} = {{\varphi }_{j}}(x),\quad {{\dot {\varphi }}_{j}} = \frac{{\partial {{\varphi }_{j}}}}{{\partial x}}\dot {x},\quad {{\ddot {\varphi }}_{j}} = \frac{{{{\partial }^{2}}{{\varphi }_{j}}}}{{\partial {{x}^{2}}}}{{\dot {x}}^{2}} + \frac{{\partial {{\varphi }_{j}}}}{{\partial x}}\ddot {x},$

то из (3.9) можно найти напряжение u_j, обеспечивающее программное движение и программные усилия (3.8):

(3.12)

${{u}_{j}} = \frac{1}{{{{k}_{j}}}}\left[ {{{J}_{j}}\frac{{\partial {{\varphi }_{j}}}}{{\partial x}}\ddot {x} + {{J}_{i}}\frac{{{{\partial }^{2}}{{\varphi }_{j}}}}{{\partial {{x}^{2}}}}{{{\dot {x}}}^{2}} + {{\mu }_{j}}\frac{{\partial {{\varphi }_{j}}}}{{\partial x}}\dot {x} + {{\lambda }_{j}}{{Q}_{j}}} \right].$

4. Метод решения на основе задания режима движения и дополнительно введенных линейных условий на развиваемые приводами усилия. При заданном режиме движения q_j = q_j(t) уравнения (1.1) удобно представить в форме

(4.1)

$\sum\limits_{n = 1}^N {{{Q}_{n}}{{B}_{{nj}}} = } \frac{d}{{dt}}\left( {\frac{{\partial {\rm T}}}{{\partial {{{\dot {q}}}_{j}}}}} \right) - \frac{{\partial {\rm T}}}{{\partial {{q}_{j}}}} - {{P}_{j}},\quad j = \overline {1,S} ,$

в которых правые части являются известными функциями времени. Уравнения (4.1) – это S линейных уравнений относительно N (N > S) неизвестных усилий Q_n.

Для определения неизвестных усилий Q_n необходимо ввести дополнительные условия, записываемые в форме уравнений. Наиболее простой вид имеют линейные уравнения

(4.2)

$\sum\limits_{n = 1}^N {{{Q}_{n}}{{D}_{{nj}}} = } {{E}_{j}},\quad j = \overline {1,N - S} .$

Матрицу D_nj и, следовательно, уравнения (4.2) можно задавать произвольно таким образом, чтобы ранг квадратной матрицы, состоящей из двух прямоугольных B_nj и D_nj, равнялся N. За условием (4.2) могут стоять и определенные требования, накладываемые на приводы. Например, если одно из уравнений (4.2) имеет вид

(4.3)

${{Q}_{k}} - \rho {{Q}_{p}} = 0,$

то это означает, что усилие, развиваемое p-м приводом, должно быть в ρ раз меньше усилия, развиваемого k-м приводом.

Таким образом, решив совместно уравнения (4.1), (4.2), можно из уравнений типа (3.12) определить управляющее напряжение u_j, обеспечивающее задаваемое программное движение.

5. Пример реализации метода. Рассматривается, как и в первом случае, та же механическая система (рис. 2), но с заданным режимом движения

(5.1)

$x(t) = {{V}_{0}}t.$

На силы, развиваемые приводами, накладывается условие типа (4.3)

(5.2)

${{Q}_{1}} - \rho {{Q}_{2}} = 0.$

Тогда решением системы уравнений (4.1) совместно с уравнением (5.2) являются

(5.3)

${{Q}_{1}} = \frac{{\rho {{P}_{1}}}}{{1 + \rho }};\quad {{Q}_{2}} = \frac{{{{P}_{1}}}}{{1 + \rho }}.$

Для обеспечения таких управляющих сил двигателями постоянного тока следует решать уравнения типа (3.12) относительно подаваемых на обмотки напряжений u_j.

Заключение. Обоснована актуальность задачи управления механических систем с избыточным числом управляющих воздействий. Сформулированы две задачи управления:

управление силами для реализации режима движения, обеспечивающего оптимальность по заданному критерию;

управление силами при заданном режиме движения и заданной функциональной зависимости между ними.

Разработаны методики решения поставленных задач, состоящие в решении:

вариационной задачи, приводящей к двум группам уравнений Эйлера–Пуассона;

в решении объединенной системы алгебраических уравнений относительно неизвестных сил.

На примере одной и той же простейшей механической системы проиллюстрированы реализации двух поставленных задач. Полученные или задаваемые (программные) режимы движения требуют исследования на устойчивость.

Список литературы

Бухгольц Н.Н. Основной курс теоретической механики. Т. 2. Динамика системы материальных точек. М.: Наука, 1966.
Жога В.В., Несмиянов И.А., Дяшкин-Титов В.В. и др. Система управления манипулятора-трипода // Робототехника и техническая кибернетика. 2014. Т. 1. № 1. С. 399–408.
Пащенко В.Н. Определение конфигурации рабочего пространства двухсекционного механизма параллельной структуры // Тр. конф. МИКМУС-2016, ИМАШ РАН. М., 2017. С. 256–259.
Вульфсон И.И. Динамика цикловых машин. СПб.: Политехника, 2013. 425 с.
Коловский М.З., Петров Г.Н., Слоущ А.В. Об управлении движением замкнутых рычажных механизмов с несколькими степенями свободы // Проблемы машиностроения и надежности машин. 2000. № 4. С. 18–25.
Евграфов А.Н., Петров Г.Н. Расчет геометрических и кинематических параметров пространственного рычажного механизма с избыточной связью // Проблемы машиностроения и надежности машин. 2013. № 3. С. 3–8.
Брискин Е.С., Шаронов Н.Г. Управление движением группы шагающих машин при перемещении моногруза // Искусственный интеллект. 2007. № 4. С. 408–415.
Брискин Е.С., Вершинина И.П., Малолетов А.В. и др. Об управлении движением шагающей машины со сдвоенными ортогонально-поворотными движителями // Изв. РАН. ТиСУ. 2014. № 3. С. 168–176.
Briskin E.S., Shurygin V.A., Chernyshev V.V. et al. Problems of Increasing Efficiency and Experience of Walking Machines Elaborating // Advances on Theory and Practice of Robots and Manipulators: Proc. ROMANSY 2014. Springer, 2014. P. 383–390.
Briskin E.S., Zhoga V.V., Chernishev V.V. et al. Walking Machines (Elements of Theory, Experience of Elaboration, Application) // Emerging Trends in Mobile Robotics: Proc. 13th CLAWAR. World Scientific, 2010. P. 769–776.
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М.: Наука, 1986. 560 с.
Брискин Е.С., Калинин Я.В., Малолетов А.В. Об оценке эффективности цикловых механизмов // Изв. РАН. МTТ. 2017. № 2. С. 13–19.
Костенко М.П., Пиотровский Л.М. Электрические машины. В 2-х ч. Ч. 1. Машины постоянного тока. Л.: Энергия, 1972. 543 с.
Брискин Е.С., Калинин Я.В., Малолетов А.В. и др. Об энергетической эффективности цикловых механизмов // Изв. РАН. МTТ. 2014. № 1. С. 18–25.
Глазунов В.А., Колискор А.Ш., Крайнев А.Ф. и др. Принципы классификации и методы анализа пространственных механизмов с параллельной структурой // Проблемы машиностроения и надежности машин. 1990. № 1. С. 41–49.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал