Известия РАН. Теория и системы управления, 2019, № 5, стр. 10-19

Введение. Проблемы оценивания неизвестных параметров возникают при решении задач обработки статистической информации в самых различных отраслях науки и техники. Надежность оценок параметров движения является фундаментальным фактором при реализации алгоритмов навигации и управления объектами авиационной и космической техники [1]. Нарушение стандартного предположения о нормальности распределения измерительных ошибок ведет к неоправданно оптимистическим выводам о качестве используемых оценок [2]. Поэтому весьма актуальной является постановка задачи оценивания, в которой ошибки наблюдения имеют априори неизвестное распределение, но удовлетворяют естественному предположению унимодальности (одновершинности). Теория унимодальных распределений изложена в [3].

В статистике предположение об унимодальности играет важную роль для повышения надежности точечных и интервальных оценок [4]. В сравнении с чебышевской границей неравенство Гаусса [5] позволяет снизить наихудшее значение вероятности ошибки более чем в 2 раза. Нахождение верхней границы вероятности на классе унимодальных распределений составляет проблему моментов Маркова [5], которая в многомерном случае сводится к задаче выпуклого программирования [6, 7].

В данной работе рассматривается задача оценивания линейной комбинации неизвестных неограниченных параметров по наблюдениям, имеющим центрированные случайные помехи с неопределенным симметричным унимодальным распределением и заданной ковариационной матрицей. Оценка считается надежной, если ее ошибка оказалась по модулю не выше заданного порога. Поэтому критерием качества оценки является максимум надежности или, что то же самое, минимум вероятности выхода ошибки оценивания из заданного диапазона [8]. Поскольку указанная вероятность является неопределенной, для математически корректной формулировки используется минимаксный подход [9]. Цель решения соответствующей минимаксной задачи – определение линейной оценки, минимизирующей наихудшее значение указанной выше вероятности. Вместе с тем важным представляется решение двойственной задачи – задачи определения наихудшего представителя из класса унимодальных распределений вектора помех.

Основной результат работы состоит в том, что для рассматриваемой линейной регрессионной модели наблюдения известная граница, описываемая неравенством Гаусса, оказывается неулучшаемой с точки зрения надежности произвольной линейной несмещенной оценки. Необходимость рассмотрения только несмещенных оценок вытекает из предположения о неограниченности вектора неизвестных параметров. Полученная граница надежности занимает промежуточное положение между двумя крайними случаями: случай, соответствующий оптимистичному предположению о нормальном распределении, и пессимистичный случай, описываемый чебышевской границей. Наихудшее распределение унимодального вектора помех найдено в форме линейного преобразования гауссовского вектора и равномерной случайной величины. Доказано, что оценка, минимаксная по вероятностному критерию, совпадает с оценкой метода наименьших квадратов (МНК). Надежность полученной оценки проанализирована в задаче оценивания параметров движения для нескольких гипотез о виде распределения ошибок наблюдений.

1. Постановка задачи. Рассмотрим модель линейной регрессии

в которой скалярная величина X подлежит оцениванию по результатам наблюдений {Y₁, …, Y_n}, составляющим вектор Y ∈ Rⁿ. При этом θ ∈ R^p – вектор неизвестных параметров, относительно которых отсутствует какая-либо априорная информация; η ∈ Rⁿ – вектор случайных ошибок наблюдений (вектор помех); a ∈ R^p – известный вектор коэффициентов; 〈a, θ〉 – скалярное произведение векторов a, θ; B ∈ R^{n ×p} – заданная матрица регрессии, где n > p и det[B^TB] ≠ 0.

Кроме того, предположим, что наблюдения не содержат систематической погрешности и образуют случайный вектор с известной положительно определенной ковариационной матрицей K. Эти условия можно кратко записать в виде

Специфика исследуемой модели наблюдений состоит в том, что распределение ошибок наблюдений предполагается симметричным относительно нуля, унимодальным и имеющим заданные моментные характеристики (1.2), но в остальном – полностью неопределенным.

Для скалярной случайной величины ξ условие симметричности и унимодальности означает, что либо она имеет четную плотность, монотонно невозрастающую на положительной полуоси, либо ее распределение есть смесь распределения с указанной плотностью и δ₀, где δ₀ – распределение константы, равной нулю. Таким образом, ноль – это и точка симметрии, и наиболее вероятное значение (мода), и математическое ожидание. Если дополнительно известна дисперсия Dξ = s², то указанные предположения будем кратко записывать в виде ξ ~ $\mathcal{U}$(s²).

Распределение случайного вектора называется унимодальным (точнее, линейно унимодальным [3]), если любая линейная комбинация его координат подчиняется одномерному унимодальному распределению. Предположение о том, что случайный вектор η имеет симметричное относительно нуля унимодальное распределение с моментными характеристиками (1.2), будем кратко записывать в виде

Рассмотрим произвольную линейную оценку величины X:

Допустим, что задан порог h > 0 величин ошибки оценивания $\tilde {X}$ – X. Надежность оценки $\tilde {X}$ будет определяться вероятностью превышения ее ошибкой указанного порога:

Для краткости будем называть (1.5) вероятностью ошибки. Чем меньше вероятность ошибки, тем более надежной следует признать оценку. Поэтому построение наиболее надежной оценки равносильно минимизации вероятности ошибки. Однако эта вероятность не определена однозначно, поскольку распределение ошибки $\tilde {X}$ – X априори неизвестно. Для того чтобы корректно сформулировать оптимизационную постановку задачи оценивания, воспользуемся минимаксным подходом.

Рассмотрим задачу нахождения минимаксной оценки $\hat {X}$ = 〈$\hat {f}$, Y〉 + $\hat {c}$. Вектор коэффициентов $\hat {f}$ ∈ R ⁿ и величина сдвига $\hat {c}$ ∈ R минимаксной оценки выбираются из условия минимума наихудшего значения вероятности ошибки:

где argmin обозначает точку минимума, $\tilde {X}$– оценка вида (1.4), а величина X и вектор Y удовлетворяют уравнениям (1.1).

Важно отметить, что при определении минимаксной оценки вместо исходного показателя надежности (1.5) рассматривается его наихудшее значение, т.е. берется супремум вероятности ошибки с учетом того, что вектор неизвестных параметров θ пробегает все евклидово пространство R ^p, а распределение вектора помех η может быть любым из класса всех допустимых унимодальных распределений (1.3).

Помимо минимаксной оценки $\hat {X}$ важно знать, какое наихудшее распределение ${{\hat {P}}_{\eta }}$ может иметь вектор помех. По определению на наихудшем распределении достигается наибольшее значение вероятности ошибки:

где символ $\hat {P}$ указывает на то, что вероятность вычислена с учетом η ~ ${{\hat {P}}_{\eta }}$.

2. Минимаксная оценка и наихудшее распределение. Вывод минимаксной оценки и синтез наихудшего распределения основаны на неравенстве Гаусса для случайных величин с унимодальным распределением [5]:

где ξ – произвольная случайная величина из класса $\mathcal{U}$(s²), s > 0.

Таким образом, в сравнении с неравенством Чебышева

которое справедливо для любой случайной величины ξ с нулевым средним и дисперсией s², неравенство Гаусса определяет более точную границу, учитывающую унимодальность распределения. Эта граница u_h(s) никогда не обращается в единицу и, как минимум, в 9/4 раз меньше чебышевской границы p_h(s) в случае p_h(s) < 1. Например, если порог h составляет две “сигмы”, т.е. h = 2s, то вероятность превышения этого порога для унимодальной величины в наихудшем случае будет составлять 1/9, что при использовании неравенства Чебышева достижимо только начиная со значения h, равного трем “сигмам”. Если h = 3s, то u_h(s) = 4/81 ≈ 0.0494. Несмотря на то, что эта вероятность на порядок больше, чем для нормальной случайной величины ξ ~ $\mathcal{N}$(0, s²): этот факт позволяет строить стандартные 95%-ные доверительные интервалы, лишь в 1.5 раза более широкие, чем при соблюдении гипотезы о нормальном распределении. Если же h = s, то чебышевская граница p_h(s) становится бессмысленной, так как p_h(s) = 1, в то время как u_h(s) = 1 – – 1/$\sqrt 3 $ ≈ 0.4226, что не намного хуже, чем для нормальной случайной величины: v_h(s) ≈ 0.3173.

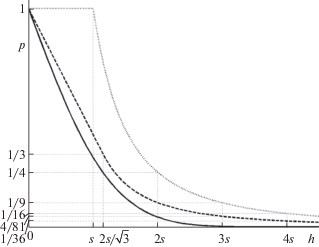
На рис. 1 представлены графики зависимости вероятности p = P(|ξ| ≥ h) от величины порога h для трех случаев: p = v_h(s) при ξ ~ $\mathcal{N}$(0, s²); p = u_h(s) при наихудшем выборе унимодальной величины ξ ~ $\mathcal{U}$(s²); p = p_h(s) при наихудшем выборе произвольной величины ξ, такой, что Mξ = 0, Dξ = s².

Наконец, граница, описываемая неравенством Гаусса, является неулучшаемой, т.е. существует унимодальное распределение ${{\mathcal{W}}_{h}}$(s²), на котором неравенство (2.1) обращается в равенство. Определим это распределение [5]:

а) если s ≤ h$\sqrt 3 $/2, то ${{\mathcal{W}}_{h}}$(s²) представляет собой смесь равномерного распределения $\mathcal{R}$(–3h/2, 3h/2) с весом q = 4s²/(3h²) и распределения δ₀ с весом 1 – q;

б) если $s \geqslant h\sqrt 3 {\text{/}}2$, то ${{\mathcal{W}}_{h}}({{s}^{2}}) = \mathcal{R}( - s\sqrt 3 ,~s\sqrt 3 )$.

Для нахождения минимаксной оценки необходимо выполнить несколько этапов исследования. Первый этап состоит в том, чтобы установить равенство (см. теорему 1 из [8])

для любой оценки $\tilde {X}$ вида (1.4), у которой вектор коэффициентов  f не является решением уравнения

На втором этапе необходимо убедиться, что нулевое значение аддитивного коэффициента с соответствует минимуму наихудшего значения вероятности ошибки при условии (2.4). Этот факт доказан в [10]. Тем самым можно ограничиться только несмещенными оценками, т.е. оценками вида $\tilde {X}$ = 〈f, Y〉, где вектор коэффициентов удовлетворяет уравнению (2.4).

На третьем этапе исходная минимаксная задача (1.6) сводится к следующей:

где ε пробегает класс случайных величин, допускающих представление в виде линейной формы ε = 〈f, η〉 от вектора η с произвольным распределением из класса $\mathcal{U}$(K). Этот факт – прямое следствие соотношений

На последнем этапе решается основная проблема – проверка того, что указанный супремум совпадает с границей из неравенства Гаусса:

Левая часть (2.5), очевидно, не превосходит правую, так как любая величина ε указанного вида центрирована, имеет дисперсию 〈Kf, f〉 и подчиняется симметричному унимодальному распределению.

Чтобы проверить обратное неравенство, достаточно для величины ξ ~ ${{\mathcal{W}}_{h}}$(〈Kf, f〉) подобрать случайный вектор η так, чтобы его распределение принадлежало классу $\mathcal{U}$(K) и с вероятностью 1 было выполнено равенство ξ = 〈f, η〉. Согласно методу, изложенному в [8], искомый вектор η определим по правилу

где T – квадратная матрица, участвующая в представлении K = TT^T, g = T^Tf, I_n – единичная матрица размера n × n, а ζ – стандартный n-мерный гауссовский вектор, не зависящий от случайной величины ξ.

Проверим сначала равенство ξ = 〈f, η〉:

Вычислим ковариационную матрицу

где учтено, что D{ξ} = 〈Kf, f〉 = |g|².

Для проверки η ~ $\mathcal{U}$(K) остается установить, что каким бы ни был детерминированный вектор b ∈ R ⁿ, распределение величины 〈b, η〉 будет унимодальным. Этот факт следует из унимодальности свертки двух симметричных унимодальных одномерных распределений, каковыми являются нормальное и равномерное [3].

Теперь можно сформулировать основной результат. Поскольку вероятностная граница (2.5) монотонно зависит от дисперсии 〈Kf, f〉, ее минимизация на подпространстве (2.4) приводит к оценке МНК [11]:

Тем самым (2.7) – искомая минимаксная оценка, а наихудшее значение вероятности ошибки для нее совпадает с границей из неравенства Гаусса (2.1):

где ${{s}^{2}} = \langle {{({{B}^{{\text{T}}}}{{K}^{{ - 1}}}B)}^{{ - 1}}}~a,a~\rangle $ – дисперсия оценки МНК.

Наихудшее распределение вектора помех можно определить как закон распределения случайного вектора (2.6) c учетом того, что f = $\hat {f}$, $\xi \sim {{\mathcal{W}}_{h}}({{s}^{2}})$ и $\zeta \sim \mathcal{N}(0,{{I}_{n}})$, причем ξ и ζ независимы.

3. Оценивание параметров движения. Рассмотрим задачу оценивания движения материальной точки при наличии измерительных ошибок с унимодальным распределением.

Предположим, что положение материальной точки описывается функцией x(t) = x₀ + ${v}$t, где начальное положение x₀ и постоянная скорость движения ${v}$ неизвестны. Наблюдения положения

проводятся в моменты t_k, k = 1, …, n, через равные промежутки времени и содержат помехи η_k, которые имеют нулевое среднее и одинаковую дисперсию σ², являются некоррелированными и образуют случайный вектор с унимодальным распределением. Располагая небольшим количеством наблюдений n, требуется наиболее надежным способом восстановить будущее положение объекта X = x(t'), где t' > max{t₁, …, t_n}.

Описанная модель может быть задана в виде уравнений (1.1) с учетом условий (1.2), (1.3), если положить

Согласно результату предыдущего раздела, при любом выборе порога ошибки h > 0 для наиболее надежного оценивания величины X = x(t') с учетом имеющейся априорной информации достаточно вычислить оценку МНК (2.7):

и ее дисперсию ${{s}^{2}} = {{\sigma }^{2}}\langle {{({{B}^{{\text{T}}}}B)}^{{ - 1}}}~a,a\rangle $.

Отметим, что $\hat {X}$ естественным образом выражается через оценку МНК вектора параметров $\hat {\theta }$ [11]:

Проанализируем надежность данной оценки в зависимости от уровня информированности о совместном распределении помех. Рассмотрим следующие четыре гипотезы:

1) вектор помех представляет собой гауссовский вектор $\eta \sim \mathcal{N}(0,{{\sigma }^{2}}{{I}_{n}})$, что равносильно тому, что помехи η₁, …, η_n независимы и распределены по нормальному закону $\mathcal{N}$(0, σ²);

2) вектор η составлен из независимых величин η₁, …, η_n, каждая из которых подчиняется распределению Тьюки, т.е. смеси двух нормальных распределений $(1 - p)\mathcal{N}(0,\sigma _{0}^{2}) + p\mathcal{N}(0,\sigma _{1}^{2})$, где σ₀ и σ₁ – средние квадратичные отклонения (с.к.о.) помех в номинальном случае и в случае выброса соответственно, а p – вероятность выброса, причем $(1 - p)\sigma _{0}^{2} + p\sigma _{1}^{2} = {{\sigma }^{2}}$, σ₁/σ₀ = 5 и p = 0.1;

3) вектор помех может иметь произвольное симметричное унимодальное распределение, т.е. $\eta \sim \mathcal{U}({{\sigma }^{2}}{{I}_{n}})$;

4) вектор η подчиняется неизвестному распределению, но удовлетворяет

Важно отметить, что во всех четырех случаях помехи имеют одни и те же моментные характеристики (3.1). При этом гипотезы 1) и 2) описывают вполне определенный совместный закон распределения величин η₁, …, η_n, а при использовании гипотез 3) и 4) распределение является неопределенным и выбирается из расчета на наихудший случай. Кроме того, в случае 1) и 2) помехи предполагаются независимыми, в то время как гипотезы 3) и 4) накладывают только требование некоррелированности в силу (3.1).

Для гипотезы 3) конструкция унимодального вектора помех η с наихудшим распределением была описана в предыдущем разделе, а именно

где случайная величина $\xi \sim {{\mathcal{W}}_{h}}({{s}^{2}})$ и случайный вектор ζ ~ $\mathcal{N}$(0, I_n) независимы, $\hat {f}$ – вектор коэффициентов оценки МНК, а s² – ее дисперсия.

В случае гипотезы 4) при h > s для построения наихудшего вектора помех η заменим в (3.2) распределение величины ξ трехточечным [8]:

Если h ≤ s, то достаточно взять двухточечное распределение:

Теперь для каждой из четырех гипотез укажем выражения для вероятности ошибки и частной плотности помех.

В рамках гипотезы 1) имеем $\eta \sim \mathcal{N}(0,{{\sigma }^{2}}{{I}_{n}})$, откуда $\hat {X}~--~X\sim \mathcal{N}(0,{{s}^{2}})$, поэтому с использованием обозначения (2.3) искомая вероятность ошибки равна $P\{ {\text{|}}\hat {X}~ - ~X{\text{|}} \geqslant h\} = {{{\mathbf{v}}}_{h}}(s)$. Укажем также явный вид плотности f(x) частного распределения помех η_k:

В случае гипотезы 2) вероятность ошибки можно найти по формуле полной вероятности. Предположим, что известны номера наблюдений $1 \leqslant {{k}_{1}} < \ldots < {{k}_{m}} \leqslant n$, в которых произошли выбросы, и определим матрицу E размера n × n, у которой на главной диагонали в позициях с указанными номерами стоят единицы, а остальные элементы равны нулю. Тогда ошибку оценивания можно представить в виде где векторы $\left( {{{I}_{n}} - E} \right)\eta $, Eη независимы и подчиняются распределениям $\mathcal{N}(0,\sigma _{0}^{2}({{I}_{n}} - E))$ и $\mathcal{N}(0,\sigma _{1}^{2}E)$ соответственно. Теперь вероятность ошибки в модели Тьюки можно записать как где сумма берется по всем матрицам E указанного вида, m обозначает число единиц в матрице E, p – вероятность выброса, а функция Ψ(x) определена в (2.3). Укажем также выражение для плотности помех

Рассмотрим гипотезу 3), согласно которой $\eta \sim \mathcal{U}({{\sigma }^{2}}{{I}_{n}})$. Поскольку распределение вектора помех выбирается наихудшим образом, вероятность ошибки определяется правой частью неравенства Гаусса:

Для того чтобы определить частную плотность  f_k(x) компонент η_k вектора (3.2), воспользуемся следующим фактом. Если условное распределение величины V при условии U = u является нормальным $\mathcal{N}$(u, b²), а величина U распределена по закону $\mathcal{R}$(–d, d), то плотность величины V имеет вид

Из (3.2) следует, что условное распределение величины η_k при условии c_kξ = u является нормальным $\mathcal{N}$$(u,b_{k}^{2})$, где $b_{k}^{2} = {{\sigma }^{2}}(1 - \,{\text{|}}\hat {f}{{{\text{|}}}^{{ - 2}}}\hat {f}_{k}^{2})$ и ${{c}_{k}} = {\text{|}}\hat {f}{{{\text{|}}}^{{ - 2}}}{\text{|}}{{\hat {f}}_{k}}{\text{|}}$. Поэтому в силу $\xi \sim {{\mathcal{W}}_{h}}({{s}^{2}})$ и ${{\hat {f}}_{k}}$ ≠ 0 получаем:

а) если $s \leqslant h\sqrt 3 {\text{/}}2$, то с учетом $q = 4{{s}^{2}}{\text{/}}(3{{h}^{2}})$

б) если $s \geqslant h\sqrt 3 {\text{/}}2$, то Наконец, рассмотрим гипотезу 4). Случай произвольного распределения, связанного только моментными ограничениями (3.1), приведен в [8]. Там доказано, что наихудшее значение вероятности ошибки определяется чебышевской границей (2.2), т.е. $P\{ {\text{|}}\hat {X}~ - ~X{\text{|}} \geqslant h\} = {{{\mathbf{p}}}_{h}}(s)$.

Воспользуемся указанным выше условным распределением помехи η_k при ${{c}_{k}}\xi = u$ тем фактом, что наихудшее распределение величины ξ имеет вид (3.3)–(3.4). В результате получаем искомую плотность помехи

если s < h, а в противном случае имеем

Перейдем к описанию результатов численного эксперимента, который проводился со следующими параметрами:

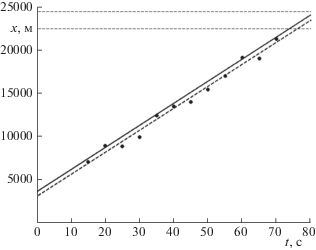
На рис. 2 изображена истинная траектория движения x = x(t) и ее оценка x = $\hat {x}$(t), имеющая вид $\hat {x}$(t) = ${{\hat {x}}_{0}}$ + ${\hat {v}}$t, где ${{\hat {x}}_{0}}$, ${\hat {v}}$ образуют оценку МНК вектора параметров $\hat {\theta }$ при наличии нормальных помех. Кроме того, для случая h = 1000 м изображены границы интервала ($\hat {X}$ – h, $\hat {X}$ + h), который представляет собой интервальную оценку терминального положения X = x(t'). Надежность этого доверительного интервала равна

где учтено, что с.к.о. оценки $\hat {X}$ = $\hat {x}$(t') равно s ≈ 690 м.

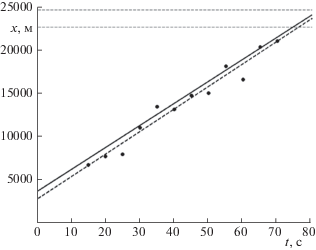
На рис. 3 представлены результаты оценивания для случая, когда помехи соответствовали наихудшему унимодальному распределению. В сравнении со случаем нормальных помех заметен больший разброс наблюдений относительно истинной траектории. При этом надежность той же интервальной оценки оказывается несколько меньше

Данные о вероятности ошибки для всех четырех гипотез и нескольких значений порога h сведены в таблицу. Результаты, полученные на основе гипотезы 3) об унимодальности помех, занимают промежуточное положение между двумя крайними случаями: гипотеза 1) о нормальном распределении соответствует слишком оптимистичным выводам о надежности оценивания, а гипотеза 4), основанная на знании только моментных характеристик, приводит к неоправданно пессимистичному заключению о качестве оценки.

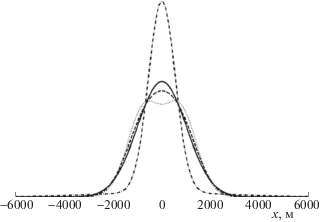
Для исходного набора параметров частные плотности помех в случае гипотез 1), 3) и 4) визуально совпадают. Это связано с тем, что плотности наихудшего распределения получаются из плотности нормального распределения с помощью свертки с величиной, принимающей относительно малые значения при небольшом с.к.о. s = $\sqrt {D\{ \hat {X}\} } $. Поэтому для демонстрации различия плотностей, соответствующих разным гипотезам, взята модель с другим набором параметров:

при которых с.к.о. оценки оказалась значительно больше: s ≈ 1342 м.

На рис. 4 представлен вид частной плотности помех для всех четырех гипотез и указанного набора параметров в случае h = 1000 м.

Заключение. В работе сформулирована задача минимаксного оценивания по вероятностному критерию для линейной регрессионной модели наблюдения с помехами, имеющими неопределенное унимодальное распределение и фиксированные моментные характеристики. Вектор параметров предполагался полностью неизвестным, оцениванию подлежала линейная комбинация его координат, а качество линейных оценок определялось вероятностью превышения ошибкой заданного порога.

Изложены схема нахождения минимаксной оценки и метод построения наихудшего распределения вектора помех. Используемая методология исследования основана на минимаксном подходе в сочетании с методами регрессионного анализа и теории унимодальных распределений (неравенство Гаусса). Установлено, что если вектор помех имеет известную ковариационную матрицу и произвольное унимодальное распределение, то оценка, минимаксная по вероятностному критерию, совпадает с оценкой МНК. Описана конструкция случайного вектора, соответствующего случаю наихудшего распределения. Проведен сравнительный анализ качества оценок МНК для нескольких вариантов совместного распределения помех.

Полученные теоретические результаты могут быть использованы для повышения надежности параметрических оценок в различных прикладных областях, где необходимо обрабатывать статистические данные, содержащие случайные ошибки и возмущения с унимодальным распределением.