Известия РАН. Теория и системы управления, 2019, № 5, стр. 3-9

КВАЗИОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ ТОРМОЖЕНИЕ ВРАЩЕНИЙ ГИРОСТАТА С ПОДВИЖНОЙ МАССОЙ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ

Л. Д. Акуленко^a, *, Т. А. Козаченко^b, **, Д. Д. Лещенко^b, ***

^a ИПМех РАН
Москва, Россия

^b Одесская государственная академия строительства и архитектуры
Одесса, Украина

^* E-mail: gavrikov@ipmnet.ru
^** E-mail: kushpil.t.a@gmail.com
^*** E-mail: leshchenko_d@ukr.net

Поступила в редакцию 28.01.2019
После доработки 19.04.2019
Принята к публикации 20.05.2019

DOI: 10.1134/S0002338819050020

Полный текст (PDF)

Аннотация

Исследуется задача о квазиоптимальном (близком к оптимальному) по быстродействию торможении вращений твердого тела, несущего элементы с распределенными и сосредоточенными параметрами. Предполагается, что тело содержит сферическую полость, заполненную жидкостью большой вязкости (при малых числах Рейнольдса), и вязкоупругий элемент, моделируемый подвижной массой, соединенной сильным демпфером с корпусом. Наличие подвижной массы моделирует присутствие нежестко закрепленных элементов на космическом аппарате, что при длительном воздействии оказывает существенное влияние на его движение относительно центра масс. Кроме того, на тело действует малый момент сил сопротивления среды, а также малый управляющий момент, ограниченный эллипсоидальной областью. Проведено асимптотическое решение на основе процедуры усреднения по фазе невозмущенного прецессионного движения и численное интегрирование.

Введение. Анализ объектов, содержащих элементы с распределенными и сосредоточенными параметрами, представляет интерес в теоретическом и прикладном аспектах. Получены конструктивные результаты для систем, содержащих квазитвердые тела. Эти модели предполагают, что их движение близко движению абсолютно твердых тел. Влияние неидеальностей может быть определено на основе асимптотических методов нелинейной механики. Оно сводится к наличию дополнительных возмущающих моментов в уравнениях углового движения Эйлера некоторого фиктивного твердого тела. Исследованию динамики твердых тел с внутренними степенями свободы посвящен ряд работ, например [1–5] и др.

Анализу пассивных движений твердого тела с полостью, заполненной жидкостью большой вязкости, уделялось значительное внимание [2, 3, 6]. Исследование неуправляемых движений твердого тела в сопротивляющейся среде было проведено в [3, 4, 7, 8]. Проблеме управления вращательными движениями квазитвердых тел с помощью сосредоточенных (приложенных к корпусу) моментов сил, важной для приложений, уделялось меньше внимания [4, 9–12].

Рассматривается задача квазиоптимального (близкого к оптимальному) по быстродействию торможения вращений динамически симметричного твердого тела с полостью, заполненной жидкостью большой вязкости. К точке на оси симметрии тела прикреплена вязкоупругим демпфером подвижная масса. Кроме того, на тело извне действует момент сил сопротивления вязкой среды.

1. Постановка задачи. Рассматриваются управляемые вращательные движения динамически симметричного твердого тела со сферической полостью, заполненной жидкостью большой вязкости [2, 3]. Кроме того, к телу, находящемуся в среде с сопротивлением, прикреплена вязкоупругим демпфером подвижная масса [1, 3].

На основании подхода [9] приближенные уравнения Эйлера управляемых вращений в связанной с телом системе координат записываются следующим образом:

(1.1)

${\mathbf{\dot {G}}} + {\mathbf{\omega }} \times {\mathbf{G}} = {{{\mathbf{M}}}^{u}}{\mathbf{ + }}{{{\mathbf{M}}}^{p}} + {{{\mathbf{M}}}^{\nu }}{\mathbf{ + }}{{{\mathbf{M}}}^{r}}.$

Здесь ${{{\mathbf{M}}}^{u}}$ – вектор управляющего внешнего реактивного момента, ${{{\mathbf{M}}}^{p}}$ – вектор внутреннего возмущающего момента сил, обусловленный наличием вязкой жидкости в сферической полости, ${{{\mathbf{M}}}^{\nu }}$ – вектор внутреннего возмущающего момента сил, обусловленный вязкоупругим элементом, ${{{\mathbf{M}}}^{r}}$ – момент сил сопротивления среды [3, 4, 7, 8]. Вектор ${\mathbf{G}} = {\mathbf{J\omega }}$ – кинетический момент тела, где ${\mathbf{J}} = \operatorname{diag} ({{A}_{1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{A}_{1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {{A}_{3}})$ – симметричный тензор инерции невозмущенного твердого тела, ${\mathbf{\omega }} = {{(p,{\kern 1pt} {\kern 1pt} {\kern 1pt} q,{\kern 1pt} {\kern 1pt} {\kern 1pt} r)}^{{\text{T}}}}$ – вектор угловой скорости, определяемый проекциями на связанные оси. Модуль кинетического момента тела равен

$G = \left| {\mathbf{G}} \right| = {{[A_{1}^{2}({{p}^{2}} + {{q}^{2}}) + A_{3}^{2}{{r}^{2}}]}^{{1/2}}},\quad {{A}_{1}} \ne {{A}_{3}}.$

Величина управляющего момента сил ${{{\mathbf{M}}}^{u}}$ предполагается малой порядка $\varepsilon $. Компоненты управляющих моментов представлены в виде произведений постоянных ${{b}_{i}}$, имеющих размерность момента сил, на малый числовой (безразмерный) параметр $\varepsilon $ и безразмерные управляющие функции, подлежащие определению [9, 13]:

(1.2)

$M_{i}^{u} = \varepsilon {{b}_{i}}{{u}_{i}},{\kern 1pt} \quad {{u}_{i}} = - {{G}_{i}}{{G}^{{ - 1}}},\quad i = 1,2,3,\quad \left| {\mathbf{u}} \right| \leqslant 1.$

Произведения $\varepsilon {{b}_{i}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1\,,2\,,3$, характеризуют эффективность системы управления по соответствующей оси связанной системы координат.

В работе предполагается, что момент сил сопротивления среды пропорционален кинетическому моменту тела [3, 7, 8]

(1.3)

${{{\mathbf{M}}}^{r}} = - \varepsilon \,\lambda {\mathbf{J\omega }},$

где $\lambda $ – постоянный коэффициент пропорциональности, зависящий в основном от свойств среды и формы тела.

С учетом (1.2), (1.3) уравнения управляемого движения (1.1) в проекциях на главные оси инерции тела имеют вид [3, 4, 7–9]

(1.4)

$\begin{gathered} {{A}_{1}}\dot {p} + \left( {{{A}_{3}} - {{A}_{1}}} \right)qr = - \varepsilon {{b}_{1}}{{A}_{1}}p{{G}^{{ - 1}}} + Lp{{r}^{2}} + F{{G}^{2}}qr + D{{r}^{4}}p - \varepsilon \lambda {{A}_{1}}p, \\ {{A}_{1}}\dot {q} + \left( {{{A}_{1}} - {{A}_{3}}} \right)pr = - \varepsilon {{b}_{2}}{{A}_{1}}q{{G}^{{ - 1}}} + Lq{{r}^{2}} - F{{G}^{2}}pr + D{{r}^{4}}q - \varepsilon \lambda {{A}_{1}}q, \\ {{A}_{3}}\dot {r} = - \varepsilon {{b}_{3}}{{A}_{3}}r{{G}^{{ - 1}}} + H({{p}^{2}} + {{q}^{2}})r - {{A}_{1}}A_{3}^{{ - 1}}D{{r}^{3}}({{p}^{2}} + {{q}^{2}}) - \varepsilon \lambda {{A}_{3}}r, \\ 0 < {{A}_{3}} \leqslant 2{{A}_{1}},\quad {{A}_{3}} \ne {{A}_{1}}. \\ \end{gathered} $

В случае ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = b\,\,\,(b > 0)$, где параметр $b$ может быть функцией времени, управление (1.2) является оптимальным для любых значений $\varepsilon $. Если величины ${{b}_{i}}$ близки, то указанное управление можно считать квазиоптимальным [9, 13].

Введенные в (1.4) коэффициенты $F,\,\,D,\,\,H,\,\,L$ выражаются через параметры системы следующим образом [1, 3, 9]:

(1.5)

$\begin{gathered} F = m{{\rho }^{2}}{{\Omega }^{{ - 2}}}A_{1}^{{ - 3}}{{A}_{3}},\quad D = m{{\rho }^{2}}\Lambda {{\Omega }^{{ - 4}}}A_{3}^{3}\left( {{{A}_{1}} - {{A}_{3}}} \right)A_{1}^{{ - 4}}, \\ H = \beta P{{\nu }^{{ - 1}}}A_{1}^{{ - 1}}\left( {{{A}_{3}} - {{A}_{1}}} \right),\quad L = \beta P{{\nu }^{{ - 1}}}A_{1}^{{ - 2}}{{A}_{3}}\left( {{{A}_{1}} - {{A}_{3}}} \right). \\ \end{gathered} $

Здесь первая пара коэффициентов $F,D$ характеризует моменты сил, вызываемые вязкоупругим элементом, $m$ – масса точки, $\rho $ – расстояние от центра масс недеформированной системы до точки крепления на теле. Частота колебаний и скорость их затухания имеют вид ${{\Omega }^{2}} = c{\text{/}}m,$ $\Lambda = {\delta \mathord{\left/ {\vphantom {\delta m}} \right. \kern-0em} m}$, здесь c – жесткость, $\delta $ – коэффициент вязкости. Рассматривается случай, когда выполняются сильные неравенства [1, 3]

(1.6)

${{\Omega }^{2}} \gg \Lambda {{\omega }_{0}} \gg \omega _{0}^{2},$

где ${{\omega }_{0}}$ – величина начального значения вектора угловой скорости. Неравенство (1.6) позволяет ввести малый параметр в (1.5) и считать возмущающие моменты малыми для применения метода усреднения вне возможного начального переходного процесса.

Вторая пара коэффициентов H, L в (1.5) характеризует момент сил, обусловленный сильно вязкой жидкостью в полости тела, $\beta $ – объемная плотность, $\nu $ – кинематический коэффициент вязкости, P – коэффициент, определяемый формой полости; для сферической полости радиуса $d$ он равен $P = 8\pi {{d}^{7}}{\text{/}}525$; основное допущение заключается в малости числа $\operatorname{Re} \sim \varepsilon \ll 1$.

2. Решение задачи квазиоптимального торможения. Для решения задачи квазиоптимального управления обезразмерим задачу. В качестве характерных параметров рассматриваемой задачи возьмем момент инерции твердого тела относительно оси ${{x}_{1}}$ – ${{A}_{1}} = {{A}_{2}}$ и величину ${{\omega }_{0}}$ порядка начальной скорости. Вводятся безразмерные коэффициенты инерции ${{\tilde {A}}_{i}} = {{{{A}_{i}}} \mathord{\left/ {\vphantom {{{{A}_{i}}} {{{A}_{1}}}}} \right. \kern-0em} {{{A}_{1}}}}$ и $\tau = {{\omega }_{0}}t$ – безразмерное время.

Тогда система (1.4) примет вид

(2.1)

$\begin{gathered} \frac{{d\tilde {p}}}{{d\tau }} = - ({{{\tilde {A}}}_{3}} - 1)\tilde {q}\tilde {r} - \varepsilon {{{\tilde {b}}}_{1}}\tilde {p}{{{\tilde {G}}}^{{ - 1}}} + \varepsilon \tilde {L}\tilde {p}{{{\tilde {r}}}^{2}} + \varepsilon \tilde {F}{{{\tilde {G}}}^{2}}\tilde {q}\tilde {r} + \varepsilon \tilde {D}\tilde {p}{{{\tilde {r}}}^{4}} - \varepsilon \tilde {\lambda }\tilde {p}, \\ \frac{{d\tilde {q}}}{{d\tau }} = - (1 - {{{\tilde {A}}}_{3}})\tilde {p}\tilde {r} - \varepsilon {{{\tilde {b}}}_{2}}\tilde {q}{{{\tilde {G}}}^{{ - 1}}} + \varepsilon \tilde {L}\tilde {q}{{{\tilde {r}}}^{2}} - \varepsilon \tilde {F}{{{\tilde {G}}}^{2}}\tilde {p}\tilde {r} + \varepsilon \tilde {D}\tilde {q}{{{\tilde {r}}}^{4}} - \varepsilon \tilde {\lambda }\tilde {q}, \\ \frac{{d\tilde {r}}}{{d\tau }} = - \varepsilon {{{\tilde {b}}}_{3}}\tilde {r}{{{\tilde {G}}}^{{ - 1}}} + \varepsilon \tilde {H}({{{\tilde {p}}}^{2}} + {{{\tilde {q}}}^{2}})\tilde {r} - \varepsilon \tilde {A}_{3}^{{ - 2}}\tilde {D}{{{\tilde {r}}}^{3}}({{{\tilde {p}}}^{2}} + {{{\tilde {q}}}^{2}}) - \varepsilon \tilde {\lambda }\tilde {r}. \\ \end{gathered} $

Здесь на основе принятых допущений введены следующие новые обозначения:

(2.2)

$\begin{gathered} \varepsilon \tilde {F} = m{{\rho }^{2}}{{\Omega }^{{ - 2}}}A_{1}^{{ - 1}}{{{\tilde {A}}}_{3}}\omega _{0}^{2},\quad \varepsilon \tilde {D} = m{{\rho }^{2}}\Lambda {{\Omega }^{{ - 4}}}(1 - {{{\tilde {A}}}_{3}})A_{1}^{{ - 1}}\tilde {A}_{3}^{3}\omega _{0}^{3}, \\ \varepsilon \tilde {L} = \beta P{{\nu }^{{ - 1}}}A_{1}^{{ - 1}}{{{\tilde {A}}}_{3}}(1 - {{{\tilde {A}}}_{3}}){{\omega }_{0}},\quad \varepsilon \tilde {H} = \beta P{{\nu }^{{ - 1}}}\tilde {A}_{3}^{{ - 1}}({{{\tilde {A}}}_{3}} - 1)A_{1}^{{ - 1}}{{\omega }_{0}}, \\ {{{\tilde {b}}}_{i}} = {{{{b}_{i}}} \mathord{\left/ {\vphantom {{{{b}_{i}}} {{{A}_{1}}\omega _{0}^{2}}}} \right. \kern-0em} {{{A}_{1}}\omega _{0}^{2}}},\quad \tilde {\lambda } = {\lambda \mathord{\left/ {\vphantom {\lambda {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}},\quad \tilde {G} = {G \mathord{\left/ {\vphantom {G {{{A}_{1}}{{\omega }_{0}}}}} \right. \kern-0em} {{{A}_{1}}{{\omega }_{0}}}},\quad {{{\tilde {A}}}_{1}} = {{{\tilde {A}}}_{2}} = 1. \\ \end{gathered} $

Далее будем использовать безразмерные переменные, опуская знак ~.

Общее порождающее решение системы (2.1) при $\varepsilon = 0$ имеет вид

(2.3)

$p = a\cos \psi ,\quad q = a\sin \psi ,\quad a > 0,\quad r = \operatorname{const} \ne 0.$

Здесь $\psi = \left( {{{A}_{3}} - 1} \right)r\tau + {{\psi }_{0}}$ – фаза колебаний экваториальной составляющей вектора угловой скорости.

Подставим (2.3) в третье уравнение системы (2.1). Учитываем, что ${{a}^{2}}\, = \,{{p}^{2}}\, + \,{{q}^{2}}$ и $\dot {a}\, = \,\dot {p}{\text{cos}}\psi \, + \,\dot {q}{\text{sin}}\psi $ для первых двух уравнений (2.1). Полученную систему уравнений для $a$ и $r$ усредним по фазе $\psi $. После усреднения, введя медленный аргумент $\theta = \varepsilon \tau $ и обозначение производной по нему $' = {d \mathord{\left/ {\vphantom {d {d\theta }}} \right. \kern-0em} {d\theta }}$, получим

(2.4)

$\begin{gathered} a' = - \frac{a}{2}[{{G}^{{ - 1}}}\left( {{{b}_{1}} + {{b}_{2}}} \right) - 2L{{r}^{2}} - 2D{{r}^{4}} + 2\lambda ], \\ r' = - r({{b}_{3}}{{G}^{{ - 1}}} - H{{a}^{2}} + A_{3}^{{ - 2}}D{{r}^{2}}{{a}^{2}} + \lambda ). \\ \end{gathered} $

Среднее выражений, содержащих множитель $F$, равно нулю. При ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = b$ уравнения для $a$ и $r$ интегрируются полностью и данная задача оптимального управления решена аналитически в [4].

3. Приближенный анализ. Рассмотрим частный случай

(3.1)

$0.5({{b}_{1}} + {{b}_{2}}) = {{b}_{3}} = b.$

Домножим первое уравнение (2.1) на p, второе – на q, а третье – на $A_{3}^{2}r$ и сложим. После усреднения получим следующее уравнение:

(3.2)

$G' = - b - \lambda G.$

Учитывая начальное и конечные условия

(3.3)

$G({{\theta }_{0}}) = {{G}^{0}},\quad G(T,{{\theta }_{0}},{{G}^{0}}) = 0,\quad T = T({{\theta }_{0}},{{G}^{0}}),$

решение уравнения (3.2) с условиями (3.3) записывается в виде

(3.4)

$G\left( \theta \right) = - \frac{b}{\lambda } + \left( {{{G}^{0}} + \frac{b}{\lambda }} \right)\exp \left( { - \lambda \theta } \right),\quad \Theta = \frac{1}{\lambda }\ln \left( {{{G}^{0}}\frac{\lambda }{b} + 1} \right).$

Отметим, что величина $\Theta \to \infty $ при ${{{{G}^{0}}} \mathord{\left/ {\vphantom {{{{G}^{0}}} b}} \right. \kern-0em} b} \to \infty $ для различных $\lambda $; наоборот, $\Theta \to 0$ при ${{{{G}^{0}}\lambda } \mathord{\left/ {\vphantom {{{{G}^{0}}\lambda } b}} \right. \kern-0em} b} \to 0$ ($\lambda $– любое) или при $\lambda \to \infty $.

Для системы (2.4) при условии (3.1) рассмотрим замену переменных: $r = \eta G,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a = \alpha G$. Уравнения системы (2.4) записываются следующим образом:

(3.5)

$\frac{{d\alpha }}{{d\theta }} = \alpha {{\eta }^{2}}{{G}^{2}}(L + D{{G}^{2}}{{\eta }^{2}}),\quad \frac{{d\eta }}{{d\theta }} = \eta {{G}^{2}}{{\alpha }^{2}}(H - A_{3}^{{ - 2}}D{{G}^{2}}{{\eta }^{2}}).$

Разделим первое уравнение на второе, получим

$\frac{{d\alpha }}{{d\eta }} = \frac{{\eta (L + D{{G}^{2}}{{\eta }^{2}})}}{{\alpha (H - A_{3}^{{ - 2}}D{{G}^{2}}{{\eta }^{2}})}}.$

После ряда преобразований находим искомый первый интеграл системы (3.5)

(3.6)

${{\alpha }^{2}} = \alpha _{0}^{2} + A_{3}^{2}(\eta _{0}^{2} - {{\eta }^{2}}) + \frac{{HA_{3}^{2} + L}}{k}\ln \left| {\frac{{H + k{{\eta }^{2}}}}{{H + k\eta _{0}^{2}}}} \right|.$

Здесь $k = - A_{3}^{{ - 2}}D{{G}^{2}}.$ Тогда с помощью выражения (3.6) уравнение (3.5) для $\eta $ примет вид

(3.7)

$\frac{{d\eta }}{{d\theta }} = \eta {{G}^{2}}(H + k{{\eta }^{2}})\left[ {\alpha _{0}^{2} + A_{3}^{2}(\eta _{0}^{2} - {{\eta }^{2}}) + \frac{{HA_{3}^{2} + L}}{k}\ln \left| {\frac{{H + k{{\eta }^{2}}}}{{H + k\eta _{0}^{2}}}} \right|} \right].$

Это уравнение (3.7) может быть решено численно.

4. Численный расчет. Для решения системы (2.4) были проведены численные исследования при разных начальных условиях и параметрах задачи. В начальный момент перенормированные величины имеют значение ${{\omega }_{0}} = 1$, ${{A}_{3}} = 1.2$, а также коэффициенты управляющего момента ${{b}_{1}} = 1.625$, b₂ = 1, ${{b}_{3}} = 1.25$, причем $0.5{\kern 1pt} {\kern 1pt} ({{b}_{1}} + {{b}_{2}}) \ne {{b}_{3}}$. Рассмотрим два случая, соответствующие начальным данным

(4.1)

${{a}_{0}} = 0.35,$

(4.2)

${{a}_{0}} = 0.626.$

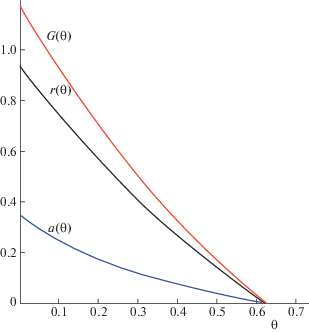
Угловую скорость вращения относительно оси динамической симметрии находим по формуле ${{r}_{0}} = {{(1 - a_{0}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Исследования, проведены при значениях перенормированного, коэффициента сопротивления $\lambda = 1.2$, 1.8 и коэффициентов $D = - 0.05, - 0.5,$ $H = 1.0,3.0$. Параметры выбраны так, чтобы выполнялись следующие условия: ${{A}_{3}} \leqslant 2$, ${\kern 1pt} {{a}_{0}} < {{r}_{0}}$. Для построения графика величины кинетического момента использовалось выражение $G = \left| {\mathbf{G}} \right| = {{({{a}^{2}} + A_{3}^{2}{{r}^{2}})}^{{1/2}}}$. На рис. 1–4 изображены однотипные графики функций a, r, G для указанных случаев, полученные в результате численного расчета.

Рис. 1.

$\lambda = 1.2$; $D = - 0.05$; $H = 1.0$

Рис. 2.

$\lambda = 1.2$; $D = - 0.5$; $H = 3.0$

Рис. 3.

$\lambda = 1.8$; $D = - 0.05$; $H = 1.0$

Рис. 4.

$\lambda = 1.8$; $D = - 0.5$; $H = 3.0$

На рис. 1, 2 представлены графики изменения функций a, r, G при значениях $\lambda = 1.2$ и начальных условиях (4.1). При различных значениях коэффициентов $D$ и $H$ время торможения равно $T \simeq 0.63$, однако при увеличении коэффициента $H$ график функции $a(\theta )$ более выгнут (рис. 2).

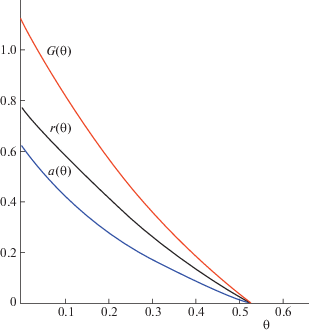
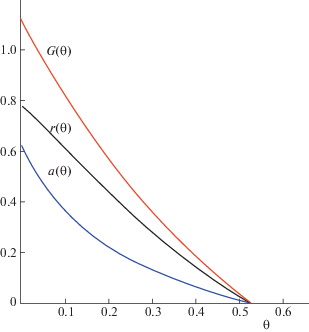
При начальных значениях (4.2) результат численного интегрирования системы, когда $\lambda = 1.8$, изображен на рис. 3, 4 . Время торможения равно $T \simeq 0.53$. Как видно из рисунка, увеличение коэффициента момента сил вязкой жидкости в полости приводит к изменению характера убывания $a(\theta )$.

Из графиков видно, что при увеличении коэффициента сопротивления $\lambda $ торможение твердого тела происходит быстрее. Также время торможения зависит от начальных значений $a$ и $r$. Отметим, что изменение переменных $a$, $r$, $G$ носит монотонный характер. Таким образом, задача квазиоптимального быстродействия решена.

Заключение. Аналитически и численно исследована задача квазиоптимального по быстродействию торможения вращений динамически симметричного твердого тела с полостью, заполненной вязкой жидкостью, и с вязкоупругим элементом в среде с сопротивлением. Получена усредненная система уравнений, определены время быстродействия $T \simeq 0.63$ и $T \simeq 0.53$, а также построены графики изменения кинетического момента и величин a, r экваториальной и осевой компонент вектора угловой скорости квазитвердого тела.

Список литературы

Черноусько Ф.Л. О движении твердого тела с подвижными внутренними массами // Изв. АН СССР. МТТ. 1973. № 4. С. 33–44.

Черноусько Ф.Л. Движение твердого тела с полостями, содержащими вязкую жидкость. М.: Изд-во ВЦ АН СССР, 1968. 230 с.

Chernousko F.L., Akulenko L.D., Leshchenko D.D. Evolution of Motions of a Rigid Body About its Center of Mass. Cham: Springer, 2017. 241 p.

Акуленко Л.Д., Лещенко Д.Д., Рачинская А.Л., Зинкевич Я.С. Возмущенные и управляемые вращения твердого тела. Одесса: Одесский национальный ун-т им. И.И. Мечникова, 2013. 288 с.

Thomson W.T. Introduction to Space Dymamics. N.Y.: Dover, 1986. 317 p.

Disser K., Galdi G.R., Mazzone G., Zunino P. Inertial motions of a rigid body with a cavity filled with a viscous fluid // Arch. Rational Mech. 2016. V. 221. № 1. P. 487–526.

Кошляков В.Н. Задачи динамики твердого тела и прикладной теории гироскопов: Аналитические методы. М.: Наука, 1985. 288 с.

Раус Э.Дж. Динамика системы твердых тел. Т. II. М.: Наука, 1983. 544 с.

Акуленко Л.Д. Асимптотические методы оптимального управления. М.: Наука, 1987. 368 с.

Акуленко Л.Д., Лещенко Д.Д., Щетинина Ю.С. Квазиоптимальное торможение вращений твердого тела с подвижной массой в среде с сопротивлением // Изв. РАН. ТиСУ. 2017. № 2. С. 16–21.

Akulenko L.D., Kozachenko T.A., Leshchenko D.D. Quasi-Optimal Braking of Rotations of a Body with a Moving Mass Coupled to It through a Quadratic Friction Damper in a Resisting Medium // J. Computer and Systems Sciences International. 2018. V. 57. № 5. P. 689–694.

Зинкевич Я.С. Квазиоптимальное торможение вращательного движения динамически симметричного твердого тела с полостью, заполненной вязкой жидкостью, в сопротивляющейся среде // Вісник Од. нац. ун-ту. Мат. і мех. 2014. Т. 19. Вип. 2 (22). С. 100–105.

Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал