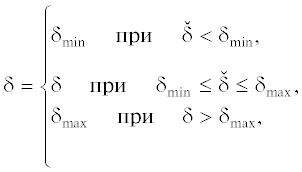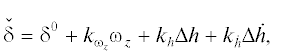Известия РАН. Теория и системы управления, 2019, № 5, стр. 130-144

Введение. Алгоритмы автоматического управления полетом беспилотных летательных аппаратов (БЛА) самолетного типа в большинстве случаев основаны на использовании пропорционально-интегрально-дифференцирующих (ПИД) регуляторов и их различных модификаций. Подобные законы управления доказали свою надежность и универсальность, однако они имеют ряд недостатков. Системы управления, базирующиеся на таких регуляторах, оказываются чувствительными к параметрам управляемого объекта. Кроме того, настройка ПИД-регуляторов при помощи логарифмической фазово-частотной характеристики (ЛФХЧ) или анализа переходных процессов в каждом контуре управления [1] – непростая инженерная процедура, результат которой зависит от опыта и интуиции исследователя.

Существуют и более современные методы управления полетом БЛА, обзор которых приведен в монографии [2]. К ним относятся классические методы теории оптимального управления, а также некоторые другие, например методы “синергетической теории управления”. Однако проблемы оптимального управления сводятся к краевым нелинейным задачам, порядок которых вдвое больше, чем порядок исходных систем (за счет добавления уравнений сопряженной системы) [3, 4]. Применение же других методов затруднено сложностью алгоритмов, особенно в условиях сильно зашумленных измерений.

На фоне перечисленных способов управления выделяется алгоритмически простой дискретный метод управления БЛА, базирующийся на методологии “дельта-преобразований второго порядка” [5]. Термин “дельта-преобразование” является синонимом понятия “дельта-модуляция”, использующегося в теории сигналов с конца 1940-х гг. Дельта-модуляцией называется преобразование аналогового сигнала в дискретную форму [6, 7]. Суть дельта-преобразования второго порядка (далее уточнение “второго порядка” будет опускаться) для данной непрерывной функции заключается в построении некоторой приближенной функции, вторая производная которой на каждом малом шаге дискретизации принимает постоянное значение [6]. Известно, что стандартные алгоритмы дельта-преобразований имеют такие недостатки, как затяжной переходный процесс и сильные колебания ошибки установившегося процесса [7, 8]. Заслугой П.П. Кравченко является создание в 1980-е гг. оптимизированного алгоритма дельта-преобразований, лишенного упомянутых недостатков. Этот метод привел к решению целого ряда актуальных на ту пору задач, относящихся к различным областям науки и техники [8–10]. Этот же алгоритм лег в основу синтеза и в задаче управления полетом БЛА на этапе посадки (далее везде имеется в виду оптимизированный вариант алгоритма, поэтому слово “оптимизированный” также опускается).

В рассматриваемой задаче синтез управления устроен следующим образом. Четыре уравнения движения БЛА в вертикальной плоскости, представленные в форме Коши, приводятся к двум, в левых частях которых стоят вторые производные (высоты и угла атаки). Предлагаемый алгоритм дельта-преобразований заключается в замене этих вторых производных программными параметрами управления, принимающими постоянные значения, которые вычисляются специальным алгоритмом на каждом дискрете времени. Затем на основании правых частей полученных уравнений выполняется расчет управляющих воздействий, задающих отклонение руля высоты, необходимого для достижения требуемого угла атаки. Такой подход известен в литературе как метод обратных задач динамики [11].

Для формируемых параметров управления отдельно выбираются абсолютное значение и знак: абсолютное значение – в зависимости от текущего положения относительно программной траектории; алгоритм выбора знака базируется на использовании переключающих функций, полученных ранее П.П. Кравченко на основе решения известной задачи синтеза оптимального по быстродействию управления [3, 12] для разностных уравнений. Авторская методика предполагает наличие “нулевого режима управления” в дополнение к релейному управлению, поэтому представленный алгоритм дельта-преобразований в источниках [9, 13] носит название “троичного”. Выбор программных параметров управления при помощи переключающих функций позволяет минимизировать как длительность переходного процесса, возникающего при начальном отклонении от программной траектории, так и отклонение от нее в установившемся режиме [9].

В настоящей статье для малого БЛА самолетного типа строится упомянутый алгоритм управления движением в вертикальной плоскости, позволяющий совершить посадку на взлетно-посадочную полосу (ВПП) в автоматическом режиме. Наряду с этим методом управления, для сравнения, рассматривается и другой, основанный на применении пропорционально-дифференцирующего (ПД) регулятора, который описан, например, в работах [14, 15].

Ранее по теме применения метода дельта-преобразований к задаче управления полетом БЛА самолетного типа были опубликованы статьи [13, 16]. Однако в них не показано, какие преимущества имеет этот способ управления по сравнению с другими. В настоящей работе проводится сравнение результатов численного моделирования, полученных при использовании одного и другого методов управления. Кроме того, впервые публикуются результаты исследований с учетом ошибок измерений датчиков.

1. Математическая модель. В качестве объекта управления рассматривается легкий БЛА самолетного типа массой m = 2 кг с высоким аэродинамическим качеством, управляемый рулем высоты, рулем направления и элеронами.

Для описания полета “беспилотника” вводится земная система координат $O\xi \eta \zeta $ (ЗСК), связанная с ВПП ($O$ – точка на торце ВПП, ось $O\xi $ направлена вдоль ВПП, ось $O\eta $ является местной вертикалью, а ось $O\zeta $ дополняет тройку до правой). Также рассматривается связанная (с аппаратом) система координат $Cxyz$ (ССК), где $C$ – центр масс БЛА. В случае плоской задачи ориентация ССК относительно ЗСК задается углом тангажа $\vartheta $.

Пространственное движение БЛА описывается системой обыкновенных дифференциальных уравнений 12-го порядка, в которую входят уравнения движения центра масс, уравнения движения вокруг центра масс, уравнения Крылова и уравнения кинематической связи земных координат и скоростей в ССК [14, 15, 17]. Для синтеза закона управления рулем высоты будем использовать следующие четыре дифференциальных уравнения, описывающие полет БЛА в вертикальной плоскости:

Здесь ${{{v}}_{x}}$, ${{{v}}_{y}}$ – проекции вектора скорости центра масс БЛА на оси $Ox$, $~Oy$, $~{{\omega }_{z}}$ – угловая скорость тангажа БЛА; $h$ – высота центра масс беспилотника; $Y$ – подъемная сила, действующая на БЛА; $g$ – ускорение свободного падения в районе ВПП; ${{I}_{z}}$ – главный момент инерции БЛА относительно поперечной оси Cz; $q$ – скоростной напор набегающего потока; $S$ – площадь крыльев; ${{b}_{A}}$ – средняя аэродинамическая хорда (САХ); ${{M}_{z}}$ – безразмерный коэффициент момента тангажа.

К дифференциальным уравнениям (1.1)–(1.4) добавляется ряд алгебраических соотношений [14, 15]. Среди них в дальнейшем используются следующие выражения для описания аэродинамических величин:

где $\alpha $ – угол атаки, $\rho $ – плотность воздуха, ${v}$ – скорость центра масс БЛА, ${{С}_{y}}$ – безразмерный коэффициент подъемной силы, $\delta $ – отклонение руля высоты, $C_{y}^{\alpha }$, $~C_{y}^{{{{\omega }_{z}}}}$, $~C_{y}^{\delta }$ – заданные постоянные коэффициенты аэродинамических сил, $M_{z}^{\alpha }$, $~M_{z}^{{{{\omega }_{z}}}}$, $~M_{z}^{\delta }~$ – заданные постоянные производные момента тангажа, $C_{y}^{0}$, $~M_{z}^{0}$ – коэффициенты подъемной силы и продольного момента при α = 0 [17].

2. Синтез закона управления на основе дельта-преобразований. Синтезируемый закон управления отклонением руля высоты $\delta $ является дискретным. Зададим моменты времени ${{t}_{i}}$: ${{t}_{i}} = i~\Delta t$, здесь i – номер временного шага, $\Delta t$ – дискрет времени. Тогда отклонение руля высоты в момент времени ${{t}_{{i + 1}}}$ обозначим как ${{\delta }_{{i + 1}}} = \delta \left( {{{t}_{{i + 1}}}} \right)$. Закон управления представляет собой функцию следующих измеряемых величин:

где ${{q}_{i}} = q\left( {{{t}_{i}}} \right)$, ${{\alpha }_{i}} = \alpha \left( {{{t}_{i}}} \right)$, ${{\omega }_{{z,i}}} = {{\omega }_{z}}\left( {{{t}_{i}}} \right)$, ${{h}_{i}} = h\left( {{{t}_{i}}} \right)$, ${{\dot {h}}_{i}} = \dot {h}\left( {{{t}_{i}}} \right)$, ${{\xi }_{i}} = \xi \left( {{{t}_{i}}} \right)$.

Для синтеза закона управления на каждом i-м шаге необходимо выполнить два этапа расчета параметров. На первом этапе по отклонению $\Delta {{h}_{i}} = {{h}_{i}} - {{h}_{{d,~i}}}$ текущей высоты ${{h}_{i}}$ от программной ${{h}_{{d,~~i}}} = {{h}_{{d,~i}}}\left( {{{\xi }_{i}}} \right)$ и производной этого отклонения $\Delta {{\dot {h}}_{i}}$ на каждом шаге вычисляется программное (желаемое) приращение вертикальной перегрузки аппарата $\Delta {{\eta }_{{d,i}}} = \Delta {{\eta }_{{d,i}}}(\Delta {{h}_{i}},~\Delta {{\dot {h}}_{i}},{{q}_{i}})$, с учетом которой формируется программное значение угла атаки ${{\alpha }_{{d,i}}} = {{\alpha }_{{d,i}}}\left( {\Delta {{\eta }_{{d,i}}},~{{q}_{i}}} \right)$. На втором этапе вычисляется разность $\Delta {{\alpha }_{i}} = {{\alpha }_{i}} - {{\alpha }_{{d,~i}}}$, на основе которой определяется программное значение второй производной угла атаки, обозначаемое символом ${{\ddot {\alpha }}_{{d,i}}}$, где ${{\ddot {\alpha }}_{{d,i}}} = {{\ddot {\alpha }}_{{d,i}}}\left( {\Delta {{\alpha }_{i}},~{{\omega }_{{z,i}}}} \right)$. Далее задается закон управления рулем высоты ${{\delta }_{{i + 1}}} = {{\delta }_{{i + 1}}}\left( {{{{\ddot {\alpha }}}_{{d,i}}},~{{\alpha }_{i}},~{{\omega }_{{z,i}}},~{{q}_{i}}} \right)$, что является уточнением формулы (2.1).

Таким образом, первый этап заключается в настройке контура управления поступательным движением БЛА, а второй – контура управления угловым движением БЛА. Такой принцип синтеза алгоритма управления следует из того, что при управлении полетом БЛА первичным является вращательное движение вокруг центра масс, вызываемое отклонением органа управления, следствием которого будет изменение аэродинамических сил и соответственно требуемое изменение траектории движения центра масс БЛА [1].

В синтезируемом законе управления следует учесть ограничения на допустимые значения углов атаки, тангажа и отклонения руля высоты: $\left| \alpha \right| \leqslant {{\alpha }_{{{\text{max}}}}}$, $\left| \vartheta \right| \leqslant {{\vartheta }_{{{\text{max}}}}}$ и $\left| \delta \right| \leqslant {{\delta }_{{{\text{max}}}}}$ соответственно.

Первый этап. Для формирования сигнала ${{\alpha }_{{d,i}}}$ используем уравнения (1.1), (1.2), (1.8). Дифференцируем соотношение (1.1) по времени:

В правой части формулы (2.2) первое и четвертое слагаемые малы по сравнению с другими двумя: продольная скорость ${{{v}}_{x}}$ меняется медленно, скорость ${{{v}}_{y}}$ мала и угол $\vartheta $ мал, поэтому ${{{\dot {v}}}_{x}}\sin \vartheta \ll 1$ и $\dot {\vartheta }{{{v}}_{y}}\sin \vartheta \ll 1$, и ими можно пренебречь. Кроме того, с учетом уравнения (1.3) имеем

В правой части соотношения (2.3) для рассматриваемой динамической модели оба слагаемых соизмеримы, однако результаты проведенных численных исследований показывают, что из двух слагаемых допустимо оставить только первое, при этом точность стабилизации программного режима и время переходного процесса не ухудшаются. Учитывая малость угла ϑ, можно принять $\cos \vartheta \approx 1$. Подставим соотношение (1.2) в полученное из (2.3), с учетом сделанных допущений, выражение $\ddot {h} = {{{\dot {v}}}_{y}}$ имеем

Заметим, что из соотношения (2.3) вытекает определение понятия приращения вертикальной перегрузки $\Delta \eta $ [1]:

Тогда, пренебрегая последними двумя членами в соотношении (1.8), подставим (1.8) в уравнение (2.5) и выразим из него угол атаки. Получаем формулу для определения угла атаки:

На основе формулы (2.6) определим соотношение, задающее программное значение угла атаки ${{\alpha }_{{d,i}}}$ на каждом шаге:

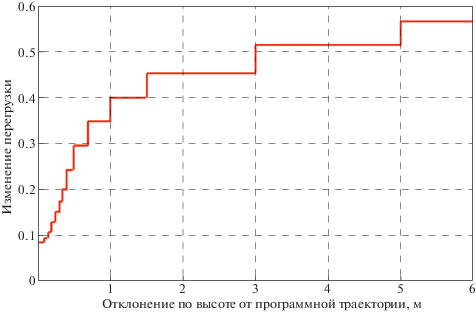
$\Delta {{\eta }_{{d,i}}}$ – постоянный на каждом шаге параметр управления приращением перегрузки. Он определяется формулой где $\Delta {{\eta }_{i}}$ – это модуль программного приращения перегрузки, которое должно быть отработано БЛА для обеспечения его движения вдоль программной траектории ($\Delta {{\eta }_{i}} = {\text{const}}$, $t \in \left[ {{{t}_{i}};~{{t}_{{i + 1}}}} \right]$), а величина ${{\Delta }_{i}}$ определяет знак такого параметра, ${{\Delta }_{i}}$ может принимать одно значение из набора {–1, 0, 1} на каждом шаге преобразования. Поэтому, как уже упоминалось выше, такой тип дельта-преобразований в литературе называется троичным [9]. Ниже приводится алгоритм получения $\Delta {{\eta }_{i}}$ и ${{\Delta }_{i}}$.

Величину $\Delta {{\eta }_{i}}$ определим как значение кусочно-постоянной монотонно возрастающей функции $\Delta \eta \left( {\Delta h} \right)$ отклонения $\Delta h$ по высоте от программной траектории: $\Delta {{\eta }_{i}} = \Delta \eta \left( {\Delta {{h}_{i}}} \right)$ (рис. 1). Конечный набор значений, которые может принимать функция $\Delta \eta \left( {\Delta h} \right)$, определяется путем численного моделирования переходных процессов для каждого конкретного БЛА. Тот же набор значений $\Delta \eta \left( {\Delta h} \right)$ (как на рис. 1) был успешно аппробирован при моделировании полета другого БЛА массой m = 14 кг, аэродинамические характеристики которого существенно отличались от характеристик БЛА, рассматриваемого в текущей работе. Такой результат позволяет сделать предположение о применимости рассматриваемой конкретной функции изменения перегрузки (рис. 1) для достаточно широкого класса БЛА.

Если окажется, что при каком-то задаваемом значении изменения перегрузки $\Delta {{\eta }_{i}}$ программный угол атаки $\left| {{{\alpha }_{{d,i}}}} \right| > {{\alpha }_{{{\text{max}}}}}$, то константа $\Delta {{\eta }_{i}}$  устанавливается соответствующей углу атаки ${{\alpha }_{{{\text{max}}}}}$ (2.6):

Значение ${{\Delta }_{i}}$ на каждом шаге определяется посредством троичного алгоритма дельта-преобразований [5, 8, 9]:

Здесь ${{\dot {h}}_{i}}$ и ${{\dot {h}}_{{d,i}}} = {{\dot {h}}_{{d,i}}}\left( \xi \right) = \dot {\xi }d{{h}_{{d,i}}}{\text{/}}d\xi $ – текущее и программное значения вертикальной скорости. Величина ${{C}_{i}} = 0.75~\Delta {{\eta }_{i}}g\Delta {{t}^{2}}$ имеет размерность длины и характеризует точность стабилизации программной траектории. Характерной особенностью алгоритма дельта-преобразований является наличие переключающих функций $F_{i}^{1}$, $~F_{i}^{2}$. Они были получены в [9] на основе известного решения задачи Фельдбаума [12], записанного в дискретной форме. Как и в классической задаче быстродействия, переключающие функции $F_{i}^{1}$, $~F_{i}^{2}$ в зависимости от начальных условий определяют знак управляющего параметра – программной перегрузки $\Delta {{\eta }_{{d,i}}}$ (2.8), обеспечивающей оптимальное по времени движение к точке $\Delta {{h}_{i}} = 0$, $\Delta {{\dot {\tilde {h}}}_{i}} = 0$, т.е. в сторону программной траектории. Разница с задачей Фельдбаума состоит в том, что предлагаемое управление имеет три варианта, а не два, поэтому возникает две линии переключения, задаваемые условиями $F_{i}^{1} = 0$ и $F_{i}^{2} = 0$. Здесь ${{b}_{h}} \geqslant 1$ – постоянный коэффициент усиления, стоящий при отклонении текущего значения вертикальной скорости от программного. Он задается априорно для того, чтобы демпфировать протекающие переходные процессы.

При получении значения ${{\Delta }_{i}}$ ограничение на угол тангажа учитывается следующим образом: в случае если угол тангажа $\left| {{{\vartheta }_{i}}} \right| > {{\vartheta }_{{{\text{max}}}}}$, то

иначе вычисляется из соотношений (2.9).

Таким образом, соотношения (2.7)–(2.11) полностью определяют программное значение угла атаки ${{\alpha }_{{d,i}}}$. Использование переключающих функций позволяет называть применяемый в данной задаче метод дельта-преобразований оптимизированным.

Второй этап. Для того чтобы получить выражение для ${{\delta }_{{i + 1}}}$, используем соотношения (1.3), (1.4), (1.9), описывающие движение БЛА вокруг центра масс. Продифференцируем по времени уравнение (1.3), а затем подставим в него соотношения (1.4) и (1.9):

Будем считать, что первая и вторая производные траекторного угла $\dot {\theta } \approx \ddot {\theta } \approx 0$, тогда, используя известное соотношение $\alpha = \vartheta - \theta $, примем, что $\ddot {\vartheta } \approx \ddot {\vartheta } - \ddot {\theta } = \ddot {\alpha }$. Выразим угол отклонения руля высоты $\delta $ из уравнения (2.12) и запишем полученное соотношение в дискретной форме, предварительно заменив $\ddot {\vartheta }$ на ${{\ddot {\alpha }}_{{d,i}}}$:

С учетом ограничений, наложенных на отклонение руля высоты, закон управления (2.13) уточняется следующим образом:

Для определения постоянного на каждом i-м шаге параметра управления ${{\ddot {\alpha }}_{{d,i}}}$ используется соотношение:

${{L}_{\alpha }} = {{L}_{\alpha }}\left( {\Delta h} \right)$ – программное значение модуля второй производной угла атаки, а величина ${{\nabla }_{i}}$ аналогично ${{\Delta }_{i}}$ определяет знак параметра ${{\ddot {\alpha }}_{{d,i}}}$ и может принимать три значения: 0, 1, –1. Для рассматриваемой модели БЛА величина ${{L}_{\alpha }}$ принимает значения, согласно формуле (2.15). Однако те же значения ${{L}_{\alpha }}$ успешно применялись в уже упоминавшемся исследовании полета более крупного БЛА, из чего можно сделать предположение о том, что эти значения пригодны для целого класса БЛА.

Далее аналогично алгоритму (2.10) определяется значение ${{\nabla }_{i}}$ параметра ${{\ddot {\alpha }}_{{d,i}}}$:

Здесь $G_{i}^{1}$, $G_{i}^{2}$ – переключающие функции, идентичные по своей структуре функциям $F_{i}^{1}$, $F_{i}^{2}$; $D = 0.75~{{L}_{\alpha }}\Delta {{t}^{2}}$; ${{b}_{\alpha }} \geqslant 1$ – коэффициент усиления при продольной угловой скорости ${{\omega }_{{z,i}}}$. Как и в соотношениях (2.10), с его помощью можно регулировать возникающие в системе переходные процессы.

Стоит отметить, что в ходе синтеза настоящего алгоритма были выбраны такие параметры, как набор значений, принимаемых функцией $\Delta \eta \left( {\Delta h} \right)$, а также величины констант ${{b}_{h}}$, ${{C}_{i}}$, ${{b}_{\alpha }}$, D. Процедура настройки их значений представляет собой задачу, которая выходит за рамки данной статьи и подробна изложена в работе [9].

Таким образом, алгоритм управления рулем высоты (2.13)–(2.16), в основе которого лежит троичный алгоритм дельта-преобразований второго порядка, полностью построен. Такой подход к синтезу управления соответствует принципу обратной задачи динамики: по заданному программному закону движения БЛА ${{h}_{{d,~i}}} = {{h}_{{d,~i}}}\left( {{{\xi }_{i}}} \right)$ (конкретный вид программной траектории представлен в разд. 6) определяются силы, под действием которых это движение происходит [11]. После вычисления необходимого ускорения по формуле (2.8) происходит расчет управляющего воздействия (2.14), обеспечивающего появление такой силы, а значит, обеспечивающего компенсацию отклонения центра масс БЛА от програмной траектории.

3. Управление на основе ПД-регулятора. В данном разделе приводится алгоритм управления рулем высоты, который был построен в работах [14, 15]:

Здесь ${{k}_{{{{\omega }_{z}}}}}$, ${{k}_{h}}$, ${{k}_{{\dot {h}}}}$ – коэффициенты обратной связи; ${{\delta }^{0}}$ – балансировочное значение отклонения руля высоты; $\Delta {{h}_{{{\text{min}}}}}$, $\Delta {{h}_{{{\text{max}}}}}$ – устанавливаемые ограничения на приращение сигнала по высоте. Остальные обозначения такие же, как и в разд. 3.

4. Управление тягой. В обоих случаях управление тягой $P$ осуществляется при помощи автомата тяги [15]:

где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{P} = {{P}_{0}} + {{k}_{{v}}}({{{v}}_{{air}}} - {{{v}}_{d}})$, ${{P}_{0}}$ – балансировочное значение тяги; ${{{v}}_{d}}$ – программная скорость; ${{P}_{{{\text{min}}}}}$, ${{P}_{{{\text{max}}}}}$ – нижнее и верхнее ограничения на тягу двигателя. Здесь для простоты будем считать, что ${{P}_{{{\text{max}}}}}$ – постоянное значение, не зависящее от воздушной скорости ${{{v}}_{{air}}}$. Хотя, в действительности, это не так [18].

5. Ошибки навигационного блока. Группой инженеров АО “ЦНИИАГ” разработана автоматическая система посадки (АСП), состоящая из блока навигации (БН) и блока управления [19]. В основе АСП лежит радиотехническая система локальной навигации (РТСЛН), в состав которой входят запросчик с антенной, установленный на борту БЛА, вычислитель и радиомаяки, располагаемые в районе ВПП [20, 21]. Кроме того, в состав БН входят бесплатформенная инерциальная навигационная система (БИНС) на базе микромеханических датчиков первичной информации (ДПИ), система воздушных сигналов (СВС), лазерный дальномер, используемый на высотах менее 5 м, и баровысотомер – для высот более 5 м; блок комплексной обработки навигационной информации (БО), который выдает навигационное решение.

Из-за присутствия в первичной информации сильных шумов различной природы (для разных датчиков), несмотря на комплексирование информации, получаемое из БО навигационное решение характеризуется большой шумовой составляющей и пропаданием решения. Для объективного сравнения работы двух алгоритмов управления предлагается тестировать их на предлагаемом навигационном решении БН.

6. Результаты моделирования. В текущем разделе представлено сравнение основных результатов численного моделирования полета БЛА в вертикальной плоскости при использовании представленных выше алгоритмов управления: основанного на использовании оптимизированных дельта-преобразований (2.7)–(2.16) и ПД-регулятора (3.1). И в том и в другом случае алгоритм управления тягой задается соотношениями (4.1). Настоящий раздел включает в себя две части: в первой сравнение проводится при идеальных измерениях, во второй – на прошедших через БО смоделированных зашумленных измерениях ДПИ.

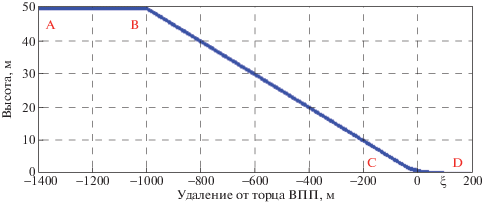
Для корректности сравнения все условия моделирования берутся идентичными. Выбирается дискрет времени $\Delta t = 0.02~$ с. В качестве программной посадочной траектории рассматривается классическая глиссада, состоящая из горизонтального участка $AB$ (высота ${{h}_{{progr}}} = 50$ м), наклонного прямолинейного участка $BC$ и экспоненты $CD$, уходящей “под ВПП” (рис. 2). В начальный момент времени центр масс БЛА находится на высоте ${{h}_{0}} - {{h}_{{progr}}} = 20$ м в плоскости ВПП на расстоянии ${{D}_{0}} = 1200$ м от торца ВПП. Целью обоих алгоритмов управления является как можно более быстрый выход на программную траекторию и ее удержание. Кроме того, на заключительном этапе полета (выравнивании) отклонение высоты БЛА от программной должно быть минимально возможным, иначе в результате жесткой посадки беспилотник может быть поврежден.

Необходимо отметить, что при моделировании учитывается динамика сервоприводов. Предполагается, что присутствует запаздывание, моделируемое апериодическим звеном первого порядка с постоянной времени ${{T}_{{rm}}} = 0.05~$ с, а также конструкционное ограничение на скорость перемещения поверхности рулей в 50 град/с.

На рис. 3–8 представлена динамика основных параметров, описывающих полет БЛА в вертикальной плоскости при идеальных измерениях. Все рисунки слева соответствуют использованию алгоритма на основе дельта-преобразований, справа – ПД-регулятора.

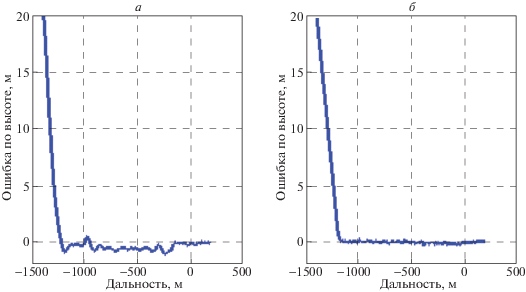
На рис. 3 представлена динамика изменения ошибки по высоте. На рис. 4 эта ошибка показана в увеличенном виде. Легко заметить, что время переходного процесса слева немного меньше, чем справа. После завершения переходного процесса система переходит в установившийся режим. Слева он характеризуется установившимися колебаниями с амплитудой до 5 см, справа – асимптотическим процессом со статической ошибкой 1 см.

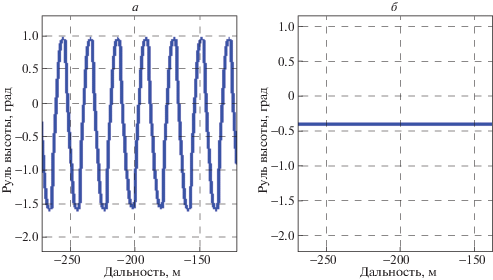
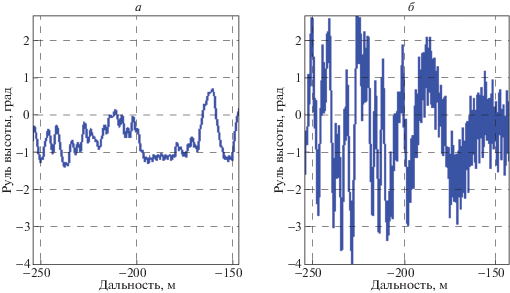
На рис. 5, 6 представлены графики отклонения руля высоты. На крупном плане (рис. 6) особенно заметно, что слева руль высоты работает в скользящем режиме, совершая высокочастотные колебания с амплитудой примерно A = 1.2° и частотой около $\nu = 1~$ Гц. Процесс справа асимптотически стабилизуется около постоянного балансировочного значения.

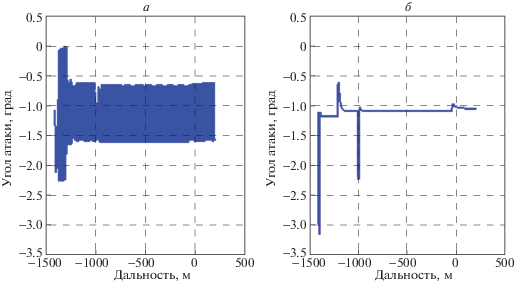
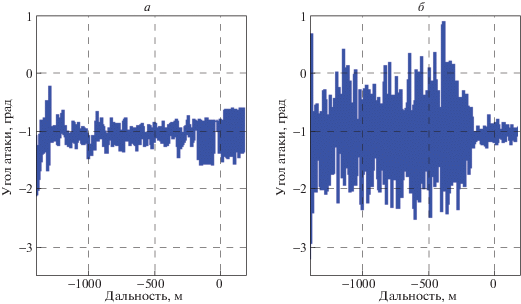
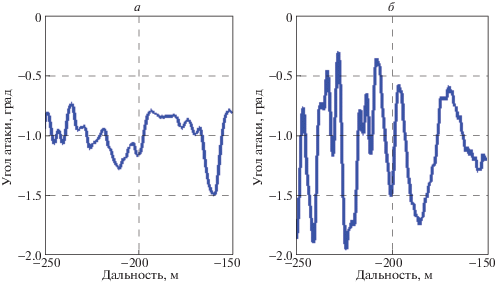
На рис. 7, 8 изображено изменение угла атаки. Видно, что и в том и другом случае угол атаки не превышает допустимых значений.

Анализируя приведенные графики на рис. 3–8, можно сделать вывод о том, что оба алгоритма приводят систему к желаемому установившемуся режиму. Однако управление на основе двойных дельта-преобразований в установившемся режиме характеризуется постоянными переключениями управления, вследствие чего в системе возникают колебания параметров движения с малой амплитудой и высокой частотой. Синтезированный алгоритм предусматривает настройку частоты таких колебаний и их амплитуду путем варьирования параметров алгоритма, но полностью избавиться от колебаний не представляется возможным в силу его дискретности.

На рис. 9–15 показаны аналогичные графики при наличии шумов в измерениях. Легко видеть, что с появлением шумов характеристики установившегося процесса ухудшились. Выбросы по высоте слева и справа достигают величины 1 м при снижении вдоль наклонного участка траектории, а за несколько метров до касания резко уменьшаются (рис. 10, 11). Это связано с выбором датчиков для измерения высоты. На высотах более 10 м используется баровысотомер, а непосредственно у Земли – лазерный дальномер, который выдает более точные измерения.

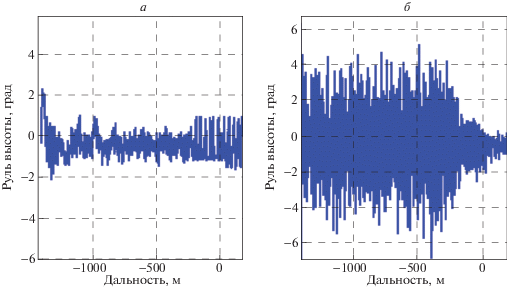
Работа руля высоты не претерпевает особых изменений при появлении шумов в случае использования алгоритма дельта-преобразований: амплитуда колебаний увеличивается всего в 1.5–2 раза (рис. 12, 13). Классический же алгоритм заставляет руль высоты совершать интенсивные колебания амплитудой до A = 12°. Такой эффект можно устранить проведением более качественной фильтрации измерений в БО.

Значения угла атаки (рис. 14, 15) лежит в допустимых пределах, однако для классического алгоритма управления колебание угла атаки оказывается в несколько раз больше.

Добавление шумов к измерениям существенно ухудшило установившиеся процессы на рисунках справа и почти не изменило их на рисунках слева. Этот факт приводит к выводу о том, что алгоритм дельта-преобразований оказывается менее чувствительным к качеству измерений ДПИ, в то время как для классического алгоритма управления требуется более качественное навигационное решение.

Заключение. Данная статья является результатом большого сравнительного исследования применения двух различных подходов к задаче управления полетом БЛА. Основными параметрами сравнения могут считаться длительность переходного процесса, возникшего в результате возмущения начальных условий, и величина ошибки по высоте после его завершения, особенно на этапе выравнивания. Что касается переходного процесса, по результатам моделирования время переходного процесса в обоих случаях примерно одинаковое.

При идеальных измерениях установившийся режим работы синтезированного алгоритма характеризуется постоянными переключениями с частотой 1 Гц в окрестности программного режима (рис. 3–8, слева), в то время как классический алгоритм характеризуется асимптотическими процессами (рис. 3–8, справа). Однако при наличии сильных шумов в измерениях асимптотическая картина нарушается (рис. 9–15, справа). При одних и тех же случайных характеристиках шумов амплитуда колебаний углов атаки, отклонения руля высоты до начала выравнивания при использовании ПД-регулятора существенно больше. Особенно это заметно на графиках при увеличенном масштабе (рис. 13, 15). Такой “фильтрующий” эффект алгоритма управления на основе дельта-преобразований в условиях действия помех полностью согласуется с выводами, сделанными в работах [8, 16]. На выравнивании (участок CD, рис. 2) оба метода управления демонстрируют близкие результаты.

Анализ графиков на рис. 3–15 показал, что предлагаемый новый метод управления по некоторым количественным показателям превосходит классический метод, основанный на использовании ПД-регулятора. Одним из преимуществ синтезированного алгоритма управления является его робастность (слабая чувствительность к характеристикам БЛА). Кроме того, построенный алгоритм, в отличие от стандартных ПИД-регуляторов, предусматривает непосредственный контроль за величиной угла атаки (2.9). Это ограничение играет важную роль, так как при выходе БЛА на критические углы атаки возможно его сваливание.

Синтезированный алгоритм не требует увеличения количества измерений по сравнению с классическим. Это свойство тоже имеет большое значение, так как каждое новое измерение содержит шумы, которые ухудшают точность стабилизации БЛА на программной траектории.

Полученные результаты являются основой для формирования программного обеспечения автопилота для данного БЛА и экспериментальной проверки полученных выводов, что будет осуществлено на следующем этапе работы.