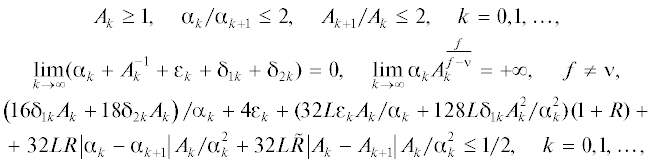Известия РАН. Теория и системы управления, 2019, № 5, стр. 75-86
АНАЛИЗ ВЗАИМНЫХ ВОЗДЕЙСТВИЙ ИННОВАЦИОННЫХ ПРОЕКТОВ ВНУТРИ ПОРТФЕЛЯ
В. В. Топка *
* E-mail: Topka3@mail.ru
Поступила в редакцию 24.08.2018
После доработки 20.11.2018
Принята к публикации 20.05.2019
Аннотация
Рассмотрены некоторые виды взаимодействия пар проектов внутри формируемого портфеля. Эта перекрестная взаимосвязь может быть технологическая, ресурсная, вероятностная, бюджетная и т.п. Бинарное взаимное воздействие проектов по вероятности в рамках портфеля приводит к синергетическому эффекту: совместное осуществление двух и более проектов может усилить (или ослабить) их результирующий эффект. Приведен подход к анализу таких взаимных воздействий – cross-impact (анализ взаимовлияний) в виде логистической модели. В этих условиях сформулирована задача отыскания совместных значений вероятностей технического успеха реализации инновационных проектов внутри портфеля, которая является неустойчивой к возмущениям исходных данных, известных с некоторой погрешностью. Для ее решения используется соответствующий специфике регуляризованный метод Ньютона.
Введение. Часто при формировании портфеля проектов происходит такое явление, что различные пары проектов взаимозависимы. Включение в портфель таких пар приводит к дополнительному синергетическому (или напротив) эффекту, который, вообще говоря, следует учитывать. Для определения параметров влияния в [1] применяется метод коэффициентов чувствительности. В этом случае для каждого результирующего фактора i строится непрерывная многопараметрическая шкала ${{f}_{i}}\left( {{{x}_{1}},\; \ldots ,\;{\text{ }}{{x}_{n}}} \right)$, отражающая зависимость значения этого фактора от факторов влияния xj, $j = \overline {1,n} $, после чего рассчитывается матрица оценок чувствительности в виде ${{m}_{{ij}}} = \partial {{f}_{i}}{\text{(}}x{\text{)/}}\partial {{x}_{j}}$.
Еще одним видом взаимодействия является конкуренция. Конкурирующие проекты возникают, и не только, в портфелях исследований и разработок, информационных технологиях или бюджетировании капитала. Для задачи выбора проектов с частичным финансированием проектов, множественными (стохастическими) целевыми функциями, взаимозависимостями проектов в целевых функциях и линейной структуре ресурсных ограничений в [2] предложен эволюционный метод поиска генетического алгоритма, чтобы получить недоминируемое множество портфелей при неопределенности в показателях.
В рамках работ по планированию НИОКР выделяется направление исследований, рассматривающих взаимодействие проектов одной и той же программы. В [3] рассмотрена модель выбора проектов, когда они внутри программы взаимодействуют между собой в следующих формах: 1) по совместному использованию ресурсов; 2) имеет место техническое вероятностное взаимодействие; 3) взаимодействие результатов программы. Первый относится к тому случаю, когда проекты используют общие ресурсы – оборудование, персонал. Второй осуществляется, когда успех или неудача одного раздела проекта значительно усиливает или задерживает выполнение других разделов проекта операций. При этом вероятность технического успеха некоторой операции является функцией вероятности технического успеха других операций. В третьем случае успех обоих проектов приводит к снижению цены выпускаемых товаров. В условиях взаимодействия разделов проекта ставится задача выбора такого множества проектов, которое доставляет максимум функции текущего значения дохода Present Value (PV) при ограничениях на ассигнования. Эта задача решается методами целочисленного линейного программирования. Далее в [4] рассмотрено множество проектов, которые характеризуются детерминированным текущим значением PV, и предложена линейная модель взаимодействий между PV. Соответствующая оптимизационная задача отбора проектов также решена методами линейного целочисленного программирования.
В [5] рассматривается экономико-математическая модель, описывающая риски, возникающие при реализации портфеля проектов с учетом их взаимного влияния. В наиболее распространенной трактовке риска он определяется при помощи трех элементов: рискового события, вероятности, с которой это событие может наступить, и величины влияния (чаще всего – ущерба), которое рисковое событие может нанести предполагаемым результатам проекта. Следуя подходу Г. Марковица, величина σ2 = Var[NPV] трактуется как риск портфеля проектов. Постановка и решение задачи излагается в простейшем варианте. А именно предполагается, что цель (критерий качества) формирования портфеля состоит в максимизации чистого дисконтированного дохода (NPV) при выполнении ограничений по ресурсам и риску.
В [6] представлена модель, развитая для Boeing Co., чтобы оптимизировать портфель проектов усовершенствования разработки изделия. Используя матрицу зависимости, которая определяет количество взаимозависимостей между проектами, чтобы оптимизировать проектный выбор, была разработана модель нелинейного целочисленного программирования. Модель также находит баланс между риском, общими целями, стоимостью и выгодой всего портфеля. В этой модели матрица взаимозависимостей проектов представляет собой квадратную $n \times n$-матрицу $D = \left( {{{d}_{{ij}}}} \right)$, ${{d}_{{ij}}} \in \left[ {0,{\text{ }}1} \right]$, где n – количество проектов. Если ${{d}_{{ij}}}$ = 0, то реализация проекта i не зависит от выполнения проекта j. Если ${{d}_{{ij}}}$ = 1, то это означает, что проекты i и j зависимы и успешность реализации одного проекта напрямую зависит от реализации другого проекта, и поэтому оба проекта включаются в портфель. Значения коэффициентов ${{d}_{{ij}}}$ матрицы взаимозависимостей D определяются экспертным путем. В сегодняшней интенсивной конкуренции на рынках высоких технологий фирмы сталкиваются с задачей управления одновременно несколькими проектами исследований и разработок (R&D) при наличии ограниченных ресурсов. Поскольку успех в бизнесе зависит от умения делать больше с меньшими затратами, важно понять в этих фирмах высоких технологий, почему некоторые проекты потребляют меньше денежных средств, но по-прежнему все-таки добиваются улучшенного продукта и результатов развития. Для ответа на этот вопрос была разработана теоретическая методика [7] в качестве основы для понимания взаимозависимости между проектами и их отношения к деятельности проекта в нескольких параллельных проектах высокотехнологичной среды R&D. Структура развита посредством нескольких тематических исследований, проектов, осуществляемых в Fortune 500, производственных фирмах высоких технологий. Семь проектов, которые составляют выборку для нескольких случаев исследования, были выбраны из большого портфеля проектов, принадлежащих к группе технологий в компании в области корпоративного центра R&D. Выбор из семи проектов руководствовался data envelopment analysis (DEA) (анализ путем огибания данных – англ.). DEA-проект отбирался на основе метрики производительности, также предложенной в данной статье. В ней рассматриваются ресурсные и технологические взаимозависимости. Чтобы поддерживать конкурентоспособность, компании должны непрерывно вкладывать капитал в проекты технологии. Однако ограничения ресурса требуют, чтобы организация стратегически ассигновала ресурсы только подмножеству возможных (приоритетных) проектов. Могут быть использованы различные инструменты и методы, чтобы выбрать оптимальный набор проектов технологии. Но эти методы применимы только тогда, когда проекты независимы и оценены в общем цикле финансирования.
1. Сложность решения задачи о рюкзаке при применении метода получения оценок. В [8] рассматривается задача формирования портфеля проектов, ряд из которых взаимозависим в том смысле, что включение обоих проектов дает дополнительный эффект (положительный или отрицательный). На включение в состав портфеля имеется n проектов-претендентов. Обозначим через ai эффект от проекта ί, aij – дополнительный эффект, если в портфель включены оба проекта ί, и j, ci – затраты на проект ί. Введем переменные хi = {0; 1}. Если проект ί включен в проект, то хi = 1, в противном случае хi = 0. Задача заключается в формировании портфеля проектов, имеющего максимальный эффект при ограниченных средствах R на реализацию проектов. В задаче имеется довольно обременительное предположение, что ai, aij, ci – целые числа для всех i, j; R – целое положительное число. Частный случай изложенной задачи приведен в последующей статье [9]. Другой частный случай описан в [10], где взаимозависимость интерпретируется как способность бизнес-проекта развивать целый ряд сопутствующих бизнесов, поэтому такие проекты авторы назвали “бизнесобразующими”. Верхняя оценка решения задач максимизации из [8–10] может быть найдена методом получения оценок [11], что позволяет в дальнейшем применять метод ветвей и границ.
В [12] дано описание подхода для получения оценок в задачах дискретной оптимизации, названного методом сетевого программирования [11], в основу которого положена возможность представления функции многих переменных в виде суперпозиции более простых функций. Структура такой суперпозиции представляется в виде сети, входы которой соответствуют переменным, а выходы – функции. Показано, что если сеть является деревом, то решение задачи сводится к последовательному решению более простых задач. В общем случае предложено преобразовать сеть в дерево путем разделения вершин сети. Доказано, что решение задачи для преобразованной структуры дает верхнюю оценку для целевой функции исходной задачи целочисленного линейного программирования (если решается задача максимизации).
Метод ветвей и границ является вариацией метода полного перебора с той разницей, что мы исключаем заведомо неоптимальные ветви дерева полного перебора. Как и метод полного перебора, он позволяет найти оптимальное решение и поэтому относится к точным алгоритмам. В [13, с. 29, 50] говорится, что в алгоритмах типа ветвей и границ сортируются проекты по их удельной полезности (отношению полезности к стоимости) и строится дерево полного перебора. Улучшение заключается в том, что в процессе построения дерева для каждого узла оценивается верхняя граница полезности решения и продолжается построение дерева только для узла с максимальной оценкой. Когда максимальная верхняя граница оказывается в листе дерева, алгоритм заканчивает свою работу. Способность метода ветвей и границ уменьшать количество вариантов перебора сильно основана на структуре входных данных. Его целесообразно применять только в том случае, когда удельные полезности проектов отличаются значительно.
Известно [14, c. 54], что для задачи об одномерном рюкзаке (портфель проектов) алгоритмы ветвей и границ с полиномиальными алгоритмами расчета верхних и нижних оценок для числа вершин в дереве ветвления, т.е. числа решаемых оценочных линейных задач, которое считается оценкой эффективности метода, имеют асимптотику, близкую к ${{2}^{{n + 1.5}}}{\text{/}}\sqrt {{\pi }(n + 1)} $, т.е. ${{2}^{{О{\text{(n)}}}}}$ – операций, где n – количество элементов. В многомерной задаче о рюкзаке (МЗР) для поиска ${\varepsilon }$-оптимального решения оценка числа ветвлений, полученная в [14, с. 156], имеет вид ${{2}^{{m/({\gamma \varepsilon })}}}$, где m – число ограничений, ${\varepsilon }$ – заданная точность, $\gamma = f\left( {x{\text{'}}} \right){\text{/}}c(n)$, здесь
а $x{\text{'}}$ – вектор (1, 0, …, 0) или любое допустимое решение, такое, что $f\left( {x{\text{'}}} \right) \geqslant {{c}_{1}}$. Для решения МЗР применяется дихотомическое ветвление, при котором на каждом шаге решается не более двух оценочных задач. Общее число решенных оценочных задач для ${\varepsilon }$-оптимального алгоритма не превосходит ${{2}^{{1 + m/({\gamma \varepsilon })}}}$.2. Портфель с рекомендательными, временн ми и другими зависимостями. В [15] рассматриваются задачи формирования и планирования процесса реализации портфеля
взаимосвязанных проектов с одним типом ограничений. Пусть имеется портфель из N проектов, рекомендательные зависимости между которыми описаны сетевым графиком. Вершины
сетевого графика соответствуют проектам портфеля. Для каждого проекта задана его базовая
продолжительность ti. Дуги соответствуют рекомендательным зависимостям между проектами. Для каждой дуги
задан параметр aij > 0, который определяет увеличение продолжительности проекта j, если зависимость (i, j) нарушается, т.е. если проект j начат до окончания проекта i.
ми и другими зависимостями. В [15] рассматриваются задачи формирования и планирования процесса реализации портфеля
взаимосвязанных проектов с одним типом ограничений. Пусть имеется портфель из N проектов, рекомендательные зависимости между которыми описаны сетевым графиком. Вершины
сетевого графика соответствуют проектам портфеля. Для каждого проекта задана его базовая
продолжительность ti. Дуги соответствуют рекомендательным зависимостям между проектами. Для каждой дуги
задан параметр aij > 0, который определяет увеличение продолжительности проекта j, если зависимость (i, j) нарушается, т.е. если проект j начат до окончания проекта i.
1. Требуется определить календарный план с минимальной общей продолжительностью, который находится методами минимизации продолжительности сетевых графиков без контуров.
2. Требуется определить набор проектов с максимальной суммой эффектов, при условии, что общее время их выполнения не превышает T.
Если связи между проектами заданы сетевым графиком без контуров, то предложенный эвристический алгоритм решения представляет собой последовательное исключение из исходного сетевого графика вершин, не входящих в оптимальное решение задачи.
В [16] рассматриваются задачи формирования и планирования процесса реализации портфеля
взаимосвязанных проектов с одним типом ограничений – по времени. При решении практических
задач приходится иметь дело с различными проектными ограничениями. В современной литературе
часто выделяют четыре их типа (так называемое пирамидальное ограничение) – качество,
время, стоимость, стратегия. Задачи, учитывающие несколько типов ограничений, являются
более сложными и требуют других методов решения. В данном случае в портфеле взаимозависимых
строительных проектов между проектами имеются жесткие, в общем случае – рекомендательные
связи по последовательности их реализации. Это, по сути, делает неразличимым рассматриваемый
в статье портфель проектов от одного укрупненного комплексного проекта. Здесь возникают
задачи формирования и планирования процесса реализации портфеля взаимосвязанных проектов
с одним типом – временн х – ограничений, когда требуется определить календарный план с минимальной общей продолжительностью,
которые можно решить, на самом деле, методами календарного планирования сетевых графиков
без учета ресурсных и стоимостных ограничений.
х – ограничений, когда требуется определить календарный план с минимальной общей продолжительностью,
которые можно решить, на самом деле, методами календарного планирования сетевых графиков
без учета ресурсных и стоимостных ограничений.
В [17] предложен метод оценки взаимосвязанности проектов, входящих в портфель компании, основанный на степени использования общих ресурсов. Сформирован прототип системы поддержки принятия решения (СППР), наглядно демонстрирующий, как зависимость от общих ресурсов и их потенциальный дефицит или профицит сказываются на рискованности портфеля проектов. СППР позволяет распределять ресурсы между проектами, максимизируя прибыль при заданном уровне риска либо минимизируя риск при заданном уровне дохода. Однако следует отметить, что подобным образом могут взаимодействовать и технологически независимые проекты, использующие общий бюджет или общий пул ресурсов.
В [18] предложена модель эффективного распределения ресурсов по проектам портфеля в условиях неопределенности, учитывающая влияние комплектности выделяемых ресурсов на продолжительность операций. Целевая функция модели – минимизация взвешенного срока завершения всех проектов портфеля. При практическом применении модели возможно отсутствие допустимых вариантов решений (например, при явной недостаточности имеющихся в распоряжении ресурсов). Поэтому разработчиками модели предлагается также дополнить целевую функцию штрафными санкциями за перерасход ресурсов каждого вида. В этом случае представляется возможным получить оценки дефицитности ресурсов. А в [19–21] целевая функция модели – минимаксное распределение ресурса, которое имеет довольно широкое применение на практике.
3. Анализ взаимовлияний. При изучении взаимосвязи социально-экономических явлений ряд авторов (см. [22] и имеющуюся там библиографию) предполагает наличие вектора наблюдений рассматриваемых показателей, что позволяет им широко использовать методы корреляционного и регрессионного анализа. При анализе неповторяющихся событий в практике научно-технического прогнозирования применяется подход, именуемый cross-impact (анализ взаимовлияний – англ.), который основан на обработке экспертных данных о степени их взаимосвязи. Пусть дана система $j,k = \overline {1,n} $, событий, каждому из которых поставлена в соответствие переменная ${{p}_{j}} \in \left[ {0,1} \right]$. Если рассматривается система событий, наступление которых в будущем вероятно, то будем говорить о величине ${{p}_{j}}$ как о вероятности того, что j-е событие произойдет. Предполагается, что рассматриваемые события влияют друг на друга и существует некоторая мера оценки влияния вероятности реализации события k на вероятность реализации события j – число ${{c}_{{jk}}}$, которые заданы в виде матрицы C = $\left( {{{c}_{{jk}}}} \right)$. Задача состоит в том, чтобы на основании оценки текущего состояния системы при принятых гипотезах относительно ее поведения дать оценку возможного будущего состояния системы. Согласно [23], ${{p}_{к}}$ есть функциональная причина ${{p}_{j}}$, если существует такая функция Р, что ${{p}_{j}} = Р({{р}_{к}})$. В литературе описаны различные виды функций Р, которые имеют эвристическую ценность, однако широко применяются в практике научно-технического прогнозирования.
В [24] рассмотрен подход к анализу взаимовлияний, который приводит к отказу от использования аппарата чистых условных вероятностей в качестве коэффициентов взаимовлияния ${{c}_{{jk}}}$, а вместо него предложен другой способ – априорное построение причинных функций. В качестве одной из них была приведена функция, удовлетворяющая уравнению
(3.1)
$d{{p}_{j}} = {{p}_{j}}(1 - {{p}_{j}})\sum\limits_{k \ne j}^n {{{c}_{{jk}}}d{{p}_{k}}} ;\quad j,k = \overline {1,n} .$Вид функции в правой части (3.1) выбирается из тех соображений, что никакие изменения в вероятностях взаимовлияющих событий не могут изменить вероятность события, которое достоверно происходит или достоверно не происходит. Поэтому функция в правой части (3.1) должна иметь корни ${{p}_{j}}$ и $1 - {{p}_{j}}$. Эмпиризм предлагаемого подхода состоит в том, что остальная часть функции (учитывающая члены высших степеней) принимается равной константе ${{c}_{{jk}}}$, величина которой определяется путем экспертного опроса.
Решением (3.1), как нетрудно показать, является логистическая функция
Действительно, представив (3.1) в виде
Граничными условиями для (3.1) являются следующие: ${{\left. {{{p}_{j}}} \right|}_{{({{c}_{{jk}}}) = (0)}}} = p_{j}^{0}$, поэтому логистическая функция без константы интегрирования приобретает вид
(3.2)
${{p}_{j}} = \frac{1}{{1 + \frac{{1 - p_{j}^{0}}}{{p_{j}^{0}}}\exp \left( { - \sum\limits_{k \ne j}^n {{{c}_{{jk}}}{{p}_{k}}} } \right)}}.$В отсутствие взаимовлияния матрица C = $\left( {{{c}_{{jk}}}} \right) = \left( 0 \right)$, a индивидуальные вероятности $p_{j}^{0}$ независимых проектов в этом случае определяются из решения задачи максимизации совместной вероятности выполнения независимых проектов с неточными исходными данными (2.1) из [25] – $p_{j}^{0}: = {{P}_{j}}(u_{j}^{*})$, где
(3.3)
$u_{j}^{*} = \arg \mathop {\max }\limits_{u \in U} {{P}_{{\left\{ R \right\}}}}\left( u \right),\quad {\text{ }}j = \overline {1,R} ;\quad j \in \left\{ R \right\}.$Как было показано в [26], функция распределения вероятности $p_{j}^{0}\left( {{{u}_{j}}} \right) = {{P}_{j}}\left( {{{u}_{j}}} \right)$ подчиняется 2-параметрическому распределению Вейбулла: ${{{\text{P}}}_{j}}({{u}_{j}};{{{\alpha }}_{j}},{{b}_{j}})$ = $1 - \exp ( - {{b}_{j}}u_{j}^{{{{{\alpha }}_{j}}}})$, где αj > 0, ${{{\alpha }}_{j}} \ne 1$ – параметр формы, ${{b}_{j}} > 0$ – параметр масштаба, ${{u}_{j}} > 0$ – однородный невозобновимый (складируемый) ресурс, $j = \overline {1,n} $.
Поскольку для ${{p}_{k}}$ можно выписать такое же соотношение, как и (3.2) то, объединяя их, получим
(3.4)
${{p}_{j}} = {{\left[ {1 + \exp \left( { - \sum\limits_{k \ne j}^n {{{c}_{{jk}}}{{{\left[ {{{1 + \exp \left( { - \sum\limits_{j \ne k}^n {{{c}_{{kj}}}{{p}_{j}}} } \right)(1 - p_{k}^{0})} \mathord{\left/ {\vphantom {{1 + \exp \left( { - \sum\limits_{j \ne k}^n {{{c}_{{kj}}}{{p}_{j}}} } \right)(1 - p_{k}^{0})} {p_{k}^{0}}}} \right. \kern-0em} {p_{k}^{0}}}} \right]}}^{{ - 1}}}} } \right){{(1 - p_{j}^{0})} \mathord{\left/ {\vphantom {{(1 - p_{j}^{0})} {p_{j}^{0}}}} \right. \kern-0em} {p_{j}^{0}}}} \right]}^{{ - 1}}}.$Итак, в модели (3.2), (3.4) рассматривается n событий, разработок, между которыми существует взаимное воздействие, такое, что осуществление или принципиальная невозможность события k влияет на вероятность pj реализации события j и эта связь описывается матрицей взаимовлияний С = (сjk.). При этом обоснованность выбора логистической модели подтверждается широтой применения такого рода зависимостей в научно-техническом прогнозировании [27–30], когда показатели, характеризующие рассматриваемую систему, являются монотонно возрастающими с насыщением. В отсутствие взаимовлияния вероятность pj осуществления события j совпадает с индивидуальной вероятностью $p_{j}^{0}$ осуществления независимого события j и монотонно стремится к 1 по мере роста коэффициентов взаимовлияния ${{c}_{{jk}}}$. Данная модель используется для повышения обоснованности получаемых традиционными методами прогнозных оценок развития образцов новой техники путем учета перекрестного влияния между некоторыми разработками.
Чтобы избежать неточной процедуры шкалирования, возникающей при оценке cjk, воспользуемся граничными условиями в точках pk = 1 и pk = 0 для соотношения (3.2):
Тогда
(3.5)
${{c}_{{jk}}} = \ln \left[ {{{R}_{{jk}}}{\text{/}}\left( {1 - {{R}_{{jk}}}} \right)} \right] - \ln \left[ {{{Q}_{{jk}}}{\text{/}}\left( {1 - {{Q}_{{jk}}}} \right)} \right],$Таким образом, для получения коэффициентов взаимовлияния ${{с}_{{jk}}}$ необходимо задать значения условных вероятностей $p(j\left| {{{p}_{k}}} \right. = 1)$ и $p(j\left| {{{p}_{k}}} \right. = 0)$, которые определяются методами обработки экспертных оценок [31]. При ${{c}_{{jk}}} = 0$ модель pj (3.2) редуцируется к модели ${{p}_{j}}\left( {{{u}_{j}}} \right): = p_{j}^{0}$ – независимых проектов, которые были исследованы в [25].
В двумерном случае имеем систему из двух уравнений. Координаты $p_{j}^{*}$ и $p_{k}^{*}$ совместных (непротиворечивых) оценок вероятностей технического успеха pj при известных ${{c}_{{jk}}}$, $j,k = \overline {1,n} $, отыскиваются из одного из уравнений, например, относительно pj (3.6):
(3.6)
${{F}_{{jk}}}({{p}_{j}}) = {{p}_{j}} - {{[1 + \exp ( - {{c}_{{jk}}}{{[1 + \exp \left( { - {{c}_{{kj}}}{{p}_{j}}} \right)(1 - p_{k}^{0}){\text{/}}p_{k}^{0}]}^{{ - 1}}})(1 - p_{j}^{0}){\text{/}}p_{j}^{0}]}^{{ - 1}}} = 0$global cij cji pi pj
rji = 0.8;
qji = 0.2;
cji = log(rji/(1 – rji)) – log(qji/(1 – qji))
rij = 0.8;
qij = 0.2;
cij = log(rij/(1 – rij)) – log(qij/(1 – qij))
pj = 0.5;
pi = 0.5;
function y = logist(x)
global cij cji pi pj
y = 1 + ((1 – pi)/pi)*exp(–cij*x);
y = –cji./y;
y = 1 + ((1 – pj)/pj)*exp(y);
y = 1./y;
y = x – y;
x1 = fzero(‘logist’, [0 1])
x1 = 0.9293
Результаты пяти тестовых просчетов с различными исходными данными приведены в таблице.
Таблица.
Учет взаимовлияний при начальных значениях ${{P}_{i}} = {{P}_{j}} = 0.5$
| Пример | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| Rji = 0.9 | Rji = 0.8 | Rji = 0.5 | Rji = 0.2 | Rji = 0.1 |
| Qji = 0.1 | Qji = 0.2 | Qji = 0.5 | Qji = 0.8 | Qji = 0.9 |
| Cji = 4.3944 | Cji = 2.7726 | Cji = 0 | Cji = –2.7726 | Cji = –4.3944 |
| Rij = 0.9 | Rij = 0.8 | Rij = 0.5 | Rij = 0.2 | Rij = 0.1 |
| Qij = 0.1 | Qij = 0.2 | Qij = 0.5 | Qij = 0.8 | Qij = 0.9 |
| Cij = 4.3944 | Cij = 2.7726 | Cij = 0 | Cij = –2.7726 | Cij = –4.3944 |
| X1 = 0.9871 | X1 = 0.9293 | X1 = 0.5 | X1 = 0.3021 | X1 = 0.2500 |
Проведенные расчеты наглядно показывают наличие эффекта “взаимовлияния”.
4. Нахождение совместных значений вероятностей технического успеха реализации проектов. Одной из основных задач анализа взаимовлияний является отыскание совместных (непротиворечивых) оценок вероятностей технического успеха pj при известных cjk; $j,k = \overline {1,n} $. Предлагается оптимизационная задача с неточными исходными данными нахождения совместных оценок в логистической модели анализа взаимовлияний в виде (4.1), где коэффициенты взаимовлияния cji определены выше (3.5); условные вероятности $p(j\left| {{{p}_{k}}} \right. = 1)$ и $p(j\left| {{{p}_{k}}} \right. = 0)$ определяются при помощи методов обработки экспертных оценок [31]; $p_{j}^{0}: = {{P}_{j}}(u_{j}^{*})$, где (3.3) – решение задачи максимизации совместной вероятности выполнения независимых проектов с неточными исходными данными (2.1) из [25]; $j,i = \overline {1,R} < n$:
(4.1)
$\begin{gathered} J(p)\,{\text{ = }}\,F_{1}^{2}({{p}_{1}}) + \; \ldots \; + F_{j}^{2}({{p}_{j}}) + \; \ldots \; + F_{R}^{2}({{p}_{R}}) = \sum\limits_{j = 1}^R {F_{j}^{2}({{p}_{j}})} \to \mathop {\inf }\limits_{0 \leqslant {{p}_{j}} \leqslant 1} , \\ {{F}_{j}}({{p}_{j}}) = {{p}_{j}} - {{\left[ {1 + \exp \left( { - \sum\limits_{i \ne j}^R {{{c}_{{ji}}}{{{[1 + \exp \left( { - {{c}_{{ij}}}{{p}_{j}}} \right)(1 - p_{i}^{0}){\text{/}}p_{i}^{0}]}}^{{ - 1}}}} } \right)(1 - p_{j}^{0}){\text{/}}p_{j}^{0}} \right]}^{{ - 1}}}. \\ \end{gathered} $5. Метод решения. Параметры cji задачи (4.1) получены в результате экспертного оценивания, обладающего определенной погрешностью, так же как и решение $p_{j}^{0}: = {{P}_{j}}(u_{j}^{*})$ $\left( {{\text{см}}{\text{. (3}}{\text{.3)}}} \right)$ задачи (2.1) из [25] с неточными исходными данными. Рассматриваемая задача (4.1) неустойчива к возмущениям исходных данных и является, вообще говоря, некорректной не только по аргументу, но и по функции [32]. Значит, для ее решения следует применять методы регуляризации [33, 34]. А поскольку целевая функция и ограничения задачи являются выпуклыми, то к ним как раз и можно, в силу принципа итеративной регуляризации [33], применять регуляризованные методы решения задач при неточных исходных данных. В качестве такого метода оптимизации выберем регуляризованный метод Ньютона [35, c. 880].
Для решения задачи
согласно общей схеме метода Ньютона [36, c. 348], по известному приближению ${{p}_{k}} \in U$ следующее приближение ${{p}_{{k + 1}}} \in U$ определяется как решение задачи(5.2)
$z \in U:\langle J_{k}^{'}(z),{\text{ }}p - z\rangle \equiv \left\langle {J{\text{'}}({{p}_{k}}) + J{\text{''}}({{p}_{k}})(z - {{p}_{k}}),{\text{ }}p - z} \right\rangle \geqslant 0,\quad \forall p \in U.$Исходя из этого, для решения исходной задачи (4.1) используется [35, с. 880] регуляризованный метод Ньютона, где
(5.3)
$U = \left\{ {p \in {{U}_{0}}:{\text{ }}{{g}_{i}}(p) \leqslant 0,\;i = \overline {1,m} } \right\},$(5.5)
$\begin{gathered} {{T}_{k}}(p) = J(p) + {{A}_{k}}\Phi (p) + 0.5{{\alpha }_{k}}{{\left\| p \right\|}^{2}}, \\ p \in {{U}_{0}},\quad {{A}_{k}} \geqslant 1,\quad {{\alpha }_{k}} > 0,\quad k = 0,1, \ldots \\ \end{gathered} $Если в (5.4) параметр f достаточно велик, то при сделанных предположениях функция (5.4) дважды непрерывно дифференцируема на ${{U}_{0}}$, причем
(5.6)
$T_{k}^{'}(p) = J{\text{'}}(p) + {{A}_{k}}\Phi {\text{'}}(p) + {{\alpha }_{k}}p,\quad T_{k}^{{''}}(p) = J{\text{''}}(p) + {{A}_{k}}\Phi {\text{''}}(p) + {{\alpha }_{k}}I,$(5.7)
$\langle T_{k}^{'}({{p}_{k}}) + T_{k}^{{''}}({{p}_{k}})(z - {{p}_{k}}),{\text{ }}p - z\rangle \geqslant 0,\quad \forall p \in {{U}_{0}}.$Предположим, что вместо точных значений производных $J{\text{'}}(p)$, $\Phi {\text{'}}(p)$, $J{\text{''}}(p)$, $\Phi {\text{''}}(p)$ известны их приближения $J_{\delta }^{'}(p)$, $J_{\delta }^{{''}}(p)$, $\Phi _{\delta }^{'}(p)$, $\Phi _{\delta }^{{''}}(p)$, такие, что
(5.8)
$\max \{ {\text{||}}J_{\delta }^{'}(p) - J{\text{'}}(p){\text{||}};\;{\text{||}}\Phi _{\delta }^{'}(p) - \Phi {\text{'}}(p){\text{||}}\} \leqslant {{\delta }_{1}}(1 + \left\| p \right\|),\quad p \in {{U}_{0}},$(5.9)
$\max \{ {\text{||}}J_{\delta }^{{''}}(p) - J{\text{''}}(p){\text{||}};\;{\text{||}}\Phi _{\delta }^{{''}}(p) - \Phi {\text{''}}(p){\text{||}}\} \leqslant {{\delta }_{{2k}}},\quad p \in {{U}_{0}},$Согласно формальному описанию [35, с. 881] регуляризованного метода Ньютона для поиска решения задачи (4.1), представленной в общем виде в (5.1)–(5.3) с неточными исходными данными, если задано начальное приближение ${{p}_{0}} \in {{U}_{0}}$ и если приближение pk, $k \geqslant 0$, известно, то следующее приближение ${{p}_{{k + 1}}} \in {{U}_{0}}$ определяется из условий
(5.10)
$\left\| {{{p}_{{k + 1}}} - {{{\tilde {p}}}_{{k + 1}}}} \right\| \leqslant {{\varepsilon }_{k}}\left( {1 + \left\| {{{p}_{k}}} \right\|} \right),$(5.11)
$\langle t_{k}^{'}({{p}_{k}}) + t_{k}^{{''}}({{p}_{k}})(z - {{p}_{k}}),p - z\rangle \geqslant 0,\quad \forall p \in {{U}_{0}},$(5.12)
${\text{||}}t_{k}^{'}(p) - T_{k}^{'}(p){\text{||}} \leqslant 2{{\delta }_{{1k}}}{{A}_{k}}\left( {1 + \left\| p \right\|} \right),\quad {\text{||}}t_{k}^{{''}}(p) - T_{k}^{{''}}(p){\text{||}} \leqslant 2{{\delta }_{{2k}}}{{A}_{k}},\quad p \in {{U}_{0}},\quad k = 0,1,\; \ldots ,$(5.13)
$t_{k}^{'}({{p}_{k}}) = J_{\delta }^{'}({{p}_{k}}) + {{A}_{k}}\Phi _{\delta }^{'}({{p}_{k}}) + {{\alpha }_{k}}{{p}_{k}},\quad t_{k}^{{''}}({{p}_{k}}) = J_{\delta }^{{''}}({{p}_{k}}) + {{A}_{k}}\Phi _{\delta }^{{''}}({{p}_{k}}) + {{\alpha }_{k}}I.$Условие (5.10) означает, что вариационное неравенство (5.11) мы решаем приближенно и вместо его точного решения $z = {{\tilde {p}}_{{k + 1}}}$ берем какую-либо точку ${{p}_{{k + 1}}} \in {{U}_{0}}$, удовлетворяющую неравенству (5.10) где ${{\varepsilon }_{k}} \geqslant 0$ – xарактеристика возникающей при этом погрешности.
Но в рассматриваемой нами задаче (4.1), как видно из (5.2) , ${{U}_{0}} \equiv H$, поэтому вариационное неравенство (5.11) равносильно операторному уравнению
относительно неизвестной точки $z$. Отсюда в случае существования обратного оператора ${{(t_{k}^{{''}}({{p}_{k}}))}^{{ - 1}}}$ получаем известное явное выражение для $(k + 1)$-го приближения метода Ньютона:(5.14)
$\begin{gathered} R = \mathop {\sup }\limits_{k \geqslant 0} {{R}_{k}},\quad {{R}_{k}} = {{\left( {{{{\left\| {{{p}_{*}}} \right\|}}^{2}} + B{\text{/}}{{{\alpha }}_{k}}A_{k}^{{\frac{f}{{f - \nu }}}}} \right)}^{{1/2}}},\quad f > \nu , \\ {\text{ }}{{R}_{k}} = \left\| {{{p}_{*}}} \right\|,\quad {\text{ }}f = \nu , \\ B = \left( {f - \nu } \right){{f}^{{\frac{{ - f}}{{f - \nu }}}}}{{\nu }^{{\frac{\nu }{{f - \nu }}}}}\left( {\sum\limits_{i = 1}^m {{{{\left| {{{c}_{i}}} \right|}}^{{\frac{f}{{f - \nu }}}}}} } \right),\quad \tilde {R} = \mathop {\sup }\limits_{\left\| \nu \right\| \leqslant R} \left\| {\Phi {\text{'}}(\nu )} \right\|, \\ \end{gathered} $При каждом ${\delta } = \left( {{{{\delta }}_{1}},{\text{ }}{{{\delta }}_{2}}} \right) > 0$ итерации (5.10), (5.11), (5.13) будем продолжать до такого наибольшего номера $k = k({\delta })$, при котором одновременно выполняются неравенства
(5.15)
${{{\delta }}_{{1k}}} \geqslant {{{\delta }}_{1}},\quad {{{\delta }}_{{2k}}} \geqslant {{{\delta }}_{2}},\quad k = 0,1,\; \ldots ,\;k({\delta }).$Поскольку $\left\{ {{{{\delta }}_{{1k}}}} \right\},\;\left\{ {{{{\delta }}_{{2k}}}} \right\} \to 0$, то при каждом ${\delta } = \left( {{{{\delta }}_{1}},{\text{ }}{{{\delta }}_{2}}} \right) > 0$ такой номер $k\left( {\delta } \right) \geqslant 0$ непременно существует. Если при k = 0 окажется, что либо ${{{\delta }}_{{10}}} < {{{\delta }}_{1}}$, либо ${{{\delta }}_{{20}}} < {{{\delta }}_{2}}$, то по определению в (5.15) примем $k({\delta }) = 0$. Обоснованием правила останова (5.15) процесса (5.10), (5.11), (5.13) служит следующая теорема.
Теорема 1 [35, с. 882]. Условия. 1. Пусть ${{U}_{0}}$ – выпуклое замкнутое множество из гильбертова пространства с непустой внутренностью $\operatorname{int} {{U}_{0}}$, функции $J(p)$, ${{g}_{i}}(p)$, $i = \overline {1,m} $, дважды непрерывно дифференцируемы по Фреше на U0, функции $J(p)$, ${{g}_{i}}(p)$, $i = \overline {1,m} $, выпуклы на ${{U}_{0}}$; ${{J}_{*}} > - \infty $, ${{U}_{*}} \ne \emptyset $, ${{p}_{*}}$ – нормальное решение задачи (5.1), (5.3); выполнено условие Липшица
(5.16)
$\max \left\{ {\left\| {J{\text{''}}(p) - J{\text{''}}(\nu )} \right\|;\;\left\| {\Phi {\text{''}}(p) - \Phi {\text{''}}(\nu )} \right\|} \right\} \leqslant L\left\| {p - \nu } \right\|,\quad \forall p,\nu \in {{U}_{0}}.$Задача (5.1), (5.3) имеет сильно согласованную постановку, т.е. существуют числа ${{c}_{i}} \geqslant 0$, $i = 1,\; \ldots ,\;m$, $\nu > 0$, такие, что
(5.17)
$ - \infty < {{J}_{*}} \leqslant J(p) + \sum\limits_{i = 1}^m {{{c}_{i}}{{{(g_{i}^{ + }(p))}}^{f}}} ,\quad p \in {{U}_{0}};\quad f \geqslant \nu ,\quad f > 2,$2. Числовые последовательности $\left\{ {{{{\alpha }}_{k}}} \right\}$, $\left\{ {{{A}_{k}}} \right\}$, $\left\{ {{{{\varepsilon }}_{k}}} \right\} = 0$, $\left\{ {{{{\delta }}_{{1k}}}} \right\}$, $\left\{ {{{{\delta }}_{{2k}}}} \right\}$, положительны и удовлетворяют условиям (5.14).
3. Начальное приближение ${{p}_{0}} \in {{U}_{0}} \equiv H$ таково, что $\left\| {{{p}_{0}} - {{\nu }_{0}}} \right\| \leqslant {{{\alpha }}_{0}}{\text{/}}8L{{A}_{0}}$, где ${{\nu }_{0}} \in {{U}_{0}} \equiv H$, ${{T}_{0}}({{\nu }_{0}}) = \mathop {\min }\limits_{p \in {{U}_{0}}} {{T}_{0}}(p)$.
4. Пусть приближения $J_{\delta }^{'}(p)$, $J_{\delta }^{{''}}(p)$, $\Phi _{\delta }^{'}(p)$, $\Phi _{\delta }^{{''}}(p)$ удовлетворяют условиям (5.8), (5.9).
В рассматриваемом нами случае функция $J({\text{p)}} = F_{1}^{2}({{p}_{1}}) + \; \ldots \; + F_{R}^{2}({{p}_{R}})$ из (4.1) определена и непрерывна на отрезке [0, 1]. В нее входят функции вида
Таким образом, для $J{\text{''}}({\text{p)}}$ и $\Phi {\text{''}}({\text{p)}}$ выполняются условия (5.16). И для некоторых ${{c}_{1}},\;{{c}_{2}} > 0$; $\nu > 0$ будет справедливо (5.17).
Теорема 2 [35, с. 891]. Пусть выполнены условия 1–4 теоремы 1. Тогда точка $p({\delta }) = {{p}_{k}}({\delta })$, полученная методом (5.10), (5.11), (5.13), (5.15), обладает свойством
Заключение. В практике выполнения инновационных проектов не исключено, что часть из проектов портфеля будет оказывать некоторое влияние (положительное или отрицательное) на результат выполнения других как-то связанных с ними инновационных проектов. Эта перекрестная взаимосвязь может быть технологическая, ресурсная, вероятностная, бюджетная и т.п. Поэтому такое перекрестное бинарное взаимовлияние проектов внутри сформированного портфеля следует, вообще говоря, учитывать. Бинарное взаимное воздействие проектов в рамках портфеля НИОКР приводит к синергетическому эффекту: совместное осуществление двух и более проектов может усилить (или ослабить) их результирующий эффект. Для этих целей предложено использовать известный из научно-технического прогнозирования подход анализа взаимовлияний (cross-impact). Для сформированного портфеля независимых инновационных проектов [25] построена логистическая модель учета перекрестных бинарных взаимных воздействий, рассмотрена и решена задача нахождения совместных значений вероятностей технического успеха реализации проектов, в которой ее параметры – коэффициенты взаимовлияния, полученные в результате экспертного оценивания и значения индивидуальной кумулятивной вероятности технического успеха каждого проекта, полученные из решения оптимизационной задачи для независимых проектов, без взаимовлияния [25], известны неточно. Сформулированная задача является выпуклой. В этом случае регуляризованный метод Ньютона оказывается соответствующим специфике задачи определения совместных значений кумулятивной вероятности технического успеха реализации проектов портфеля с учетом их перекрестного взаимовлияния. Поэтому отбор приоритетных направлений исследований и разработок [25] будет более обоснованным при использовании подхода и результатов данной работы.
Список литературы
Гусев В.Б., Павельев В.В. Использование непрерывных шкал и принятие решений в сложных проблемных ситуациях. М.: ИПУ РАН, 2013. 118 с.
Medaglia A A., Graves S., Ringquest J. A Multiobjective Evolutionary Approach for Linearly Constrained Project Selection under Uncertainty // European J. Operational Res. 2007. V. 179. № 3. P. 869–894.
Aaker D.A., Tyebjee T.T. A Model for the Selection of Interdependent R&D Projects // IEEE Transactions on Engineering Management. 1978. V. EM-25. № 2.
Fox G.E., Baker N.R., Bryant J.L. Economic Model for R and D Project Selection in the Presence of Project Interactions // Management Sci. 1984. V. 30. № 7.
Ходоровский М.Я., Никонов В.О. Управление рисками портфеля проектов // Вестн. УрФУ. Сер.: Экономика и управление. 2006. № 7. С. 116–122.
Dickinson M.W., Thornton A.C., Graves S. Technology Portfolio Management: Optimizing Interdependent Projects over Multiple Time Periods // IEEE Transactions on Engineering Management. 2001. № 11. P. 518–527.
Verma D., Sinha K.K. Toward a Theory of Project Interdependencies in High tech R&D Environments // J. Op. Man. 2002. № 7. P. 451–468.
Дранко О.И. Формирование портфеля взаимозависимых проектов // Вестн. Воронежского гос. техн. ун-та. 2011. Т. 7. № 5. С. 209–212.
Дранко О.И., Андрианова И.И., Зенищева Г.В. Задача формирования портфеля проектов, ряд из которых взаимозависимы // Системы управления и информационные технологии. 2012. Т. 50. № 4.1. С. 138–141.
Буркова И.В., Моисеева Ю.В., Цветков А.В., Андрианова И.И. Задача формирования портфеля бизнес-образующих проектов // Экономика и менеджмент систем управления. 2012. № 4.3(6). С. 349–355.
Бурков В.Н., Буркова И.В., Попок М.В., Овчинникова Т.И. Метод сетевого программирования // Проблемы управления. 2005. № 3. С. 23–29.
Буркова И.В., Пужанова Е.О., Марин О.Л. Задача о ранце и ее модификации // Научный вестн. Воронежского гос. архитектурно-строительного ун-та. Сер.: Управление строительством. 2014. Вып. № 1(6). С. 103–112.
Martello S., Toth P. Knapsack Problems: Algorithms and Computer Implementations // Series in Discrete Mathematics and Optimization. N.Y.: Wiley Inter Sciences, 1990. 296 p.
Финкельштейн Ю.Ю. Приближенные методы и прикладные задачи дискретного программирования. М.: Наука, 1976. 264 с.
Зубарев В.В. Задача выбора оптимального портфеля взаимозависимых проектов с ограничением по времени // Вестн. Воронежского гос. техн. ун-та. 2011. Т. 7. № 5. С. 201–203.
Бабкин В.Ф., Колпачев В.Н., Баринов В.Н., Недовесов М.В. Модель формирования оптимального портфеля взаимозависимых строительных проектов с ограничением по времени // Научн. вестн. Воронежского гос. архитектурно-строительного ун-та. Сер.: Строительство и архитектура . 2012. № 2. С. 85–89.
Шомова Е.Н. Модель формирования оптимального портфеля взаимозависимых инновационных проектов // Управление проектами и программами. 2011. № 4. С. 262–269.
Аньшин В.М., Демкин И.В., Царьков И.Н., Никонов И.М. Анализ подходов к распределению ресурсов по проектам портфеля в условиях неопределенности // Проблемы анализа риска. 2007. Т. 4. № 3. С. 207–221.
Цвиркун А.Д., Топка В.В. Минимаксная задача равномерного распределения ресурсов // Тр. 8-й Московской междунар. конф. по исследованию операций. (ORM-2016, Москва). М.: Изд-во ФИЦ ИУ РАН, 2016. Т. II. С. 103–104.
Миронов А.А., Цурков В.И. Минимакс в моделях транспортного типа с интегральными ограничениями. I // Изв. РАН. ТиСУ. 2003. № 4. С. 69–81.
Миронов А.А., Федорчук В.В., Цурков В.И. Минимакс в моделях транспортного типа с интегральными ограничениями. II // Изв. РАН. ТиСУ. 2005. № 5. С. 66–86.
Бородкин Ф.М. Статистическая оценка связей экономических показателей. М.: Статистика, 1968. 204 с.
Suppes P. Probabilistic Theory of Causality // Acta Philosophycal Fennicay Fasc. XXIV. Amsterdam: North-Holland Publishing Company, 1970.
Turoff M. An Alternative Approach to a Cross-Impact Analysis // Technological Forecasting and Social Change. 1972. № 3. P. 309–339.
Топка В.В. Отбор приоритетных направлений исследований и разработок // Изв. РАН. ТиСУ. 2019. № 4. С. 97–107.
Топка В.В. Лексикографическое решение двухкритериальной задачи планирования проекта при ограничении на показатель его надежности // Изв. РАН. ТиСУ. 2014. № 6. С. 105–123.
Бешелев С.Д. Интенсификация научных исследований. М.: Машиностроение, 1983.
Рабочая книга по прогнозированию / Отв. ред. И.В. Бестужев-Лада. М.: Мысль, 1982.
Янч Э. Прогнозирование научно-технического прогресса. М.: Прогресс, 1970.
Bright I.R. A Guide to Practical Technological Forecasting. N.Y.: Prentice-Hall, 1972.
Литвак Б.Г. Экспертная информация. Методы получения и анализа. М.: Радио и связь, 1982.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.
Бакушинский А.Б., Гончарский А.В. Итеративные методы решения некорректных задач. М.: Наука, 1989.
Бакушинский А.Б., Гончарский А.В. Некорректные задачи. Численные методы и приложения. М.: Изд-во МГУ, 1989.
Васильев Ф.П. Методы оптимизации: В 2-х кн. Новое изд., перераб. и доп. Кн. 2. М.: МЦНМО, 2011.
Васильев Ф.П. Методы оптимизации: В 2-х кн. Новое изд., перераб. и доп. Кн. 1. М.: МЦНМО, 2011.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления