Известия РАН. Теория и системы управления, 2019, № 5, стр. 56-74
АНАЛИЗ И ОПТИМИЗАЦИЯ СИСТЕМ С ГЕТЕРОГЕННЫМИ СЕРВЕРАМИ И СКАЧКООБРАЗНЫМИ ПРИОРИТЕТАМИ
А. З. Меликов a, *, Э. В. Мехбалыева a
a Институт систем управления, Национальная академия наук Азербайджана
Баку, Азербайджан
* E-mail: agassi.melikov@gmail.com
Поступила в редакцию 07.11.2018
После доработки 18.04.2019
Принята к публикации 20.05.2019
Аннотация
Предлагаются марковские модели систем с гетерогенными серверами, разнотипными запросами и скачкообразными приоритетами. Считаются, что поступают запросы высокого и низкого приоритетов, при этом запросы высокого приоритета обслуживаются в сервере с высокой скоростью обслуживания, в то время как запросы низкого приоритета обслуживаются в сервере с низкой скоростью обслуживания. Изучаются модели двух типов: с раздельными очередями и общей очередью для разнотипных запросов. Скачкообразные приоритеты определяют правила изменения типа низкоприоритетных запросов в зависимости от состояния очереди. Разработаны методы расчета распределения вероятностей состояний системы, найдены формулы для вычисления ее характеристик и решена задача их оптимизации. Даны результаты численных экспериментов.
Введение. При разработке математических моделей процессов обработки запросов в компьютерных и коммуникационных системах, как правило, предполагается, что серверы являются идентичными по всем показателям (по скорости обработки запросов, надежности, стоимости эксплуатации и т.д.). Однако допущение о том, что сервера идентичны зачастую является грубым приближением к реальной ситуации, так как в процессе расширения существующих систем приходится использовать гетерогенные сервера (heterogeneous servers (HS)). Сервера с различными скоростями особенно часто встречаются в системах, где в процессе обработки запросов участвуют не машины (аппараты, компьютеры и т.д.), а люди.
Вкратце рассмотрим публикации, посвященные математическому анализу систем с гетерогенными серверами.
Прежде всего отметим, что в отличие от систем с гомогеными серверами, в системах с гетерогенными серверами важное значение имеют правила доступа запросов к серверам. Наиболее часто используемыми правилами являются рандомизированный доступ (randomized access), упорядоченный доступ (ordered entry), а также доступ, основанный на схеме “первым используется быстрый сервер” (fast server first (FSF)). При рандомизированном доступе с равными вероятностями назначается один из свободных серверов; при упорядоченном доступе заранее все сервера нумеруются и назначается свободный сервер, который имеет минимальный номер; при FSF-схеме доступа всегда назначается сервер, который имеет максимальную скорость среди всех свободных серверов.
Первая публикация, посвященная изучению систем с HS, была [1]. В ней рассматривалась марковская система с бесконечной очередью и рандомизированным доступом. Предложены формулы для нахождения вероятностей состояний и среднее число запросов в системе и в очереди. Указывается, что в частном случае, когда все серверы являются гомогенными (идентичными), получаются известные классические результаты. Кроме того, показано, что если скорости HS сильно отличаются друг от друга, то замена исходной системы на систему с аналогичным числом гомогенных серверов, где скорость каждого сервера равна среднеарифметическому значению гетереогенных серверов, ведет к тому, что характеристики этих систем будут сильно отличаться друг от друга; иначе если скорости HS мало отличаются друг от друга, то “ощибка” будет незначительной.
После данной работы модели систем с HS долгое время не подвергались исследованиям, и лишь с 70-х годов прошлого века начались интенсивные исследования таких систем. В [2, 3] вычислены характеристики систем с двумя и тремя серверами и рандомизированным доступом. Полученные результаты сравниваются с аналогичными результатами систем с гомогенными серверами.
Одним из ведущих направлений было обобщение классических результатов, полученных ранее для систем с гомогенными серверами. Так, в [4] предложено обобщение известной В-формулы Эрланга для системы с гетерогенными серверами без буфера для ожидания заявок и произвольной функцией распределения (ф.р.) времени их обслуживания с рандомизированным доступом. В [5 ] рассмотрено обобщение последней модели, т.е. в ней считается, что поступающие запросы могут терятся с определенными вероятностями, если даже в моменты их поступления имеются свободные сервера, при этом эти вероятности зависят от числа свободных серверов. Получен аналог В-формулы Эрланга для такой модели и показано, что в стациоанарном режиме выходящий поток также является Пуассоновским. Согласно [6], вероятность потери в марковской системе с гетерогенными серверами и без буфера для ожидания заявок имеет минимальное значение при использовании FSF-схемы доступа.
Среднее время ожидания в марковской системе с гетерогенными серверами и бесконечной очередью при использовании рандомизированного доступа будет минимальным, если суммарную интенсивность обслуживания серверов равномерно распределить между ними, т.е. для гомогенной системы [7].
Подробно изучены модели, в которых принято правило упорядоченного доступа [8–16]. Детальный анализ этих работ можно найти в [16], где предложен метод нахождения вероятности потери в системе с гетерогенными серверами без буфера для ожидания заявок и произвольной ф.р. интервалов между поступлениями запросов.
Практический интерес представляют работы, в которых учитывается эффект катастрофы [17–21] (это такое случайное явление, при возникновании которого система полностью прекращает работу и все запросы теряются) и прогулки серверов [22–25]. В [26] изучается модель системы, в которой HS расположены не параллельно, а последовательно. Определенный научный интерес представляют работы, в которых изучаются асимптотические свойства систем при наличии огромного количества HS [27–30]. Здесь же отметим, что из-за сложности математического анализа в них в основном рассматриваются модели систем с двумя или тремя серверами [31–34].
Задачи оптимизации систем обслуживания с HS имеют важное практическое значение. Они подробно рассмотрены в монографии [35]. Следует отметить, что методы многокритеральной оптимизации являются эффективным аппаратом для решения задач оптимального распределения ресурсов гетерогенных вычислительных систем [36, 37] (в них можно найти подробный список работ в этом направлении).
Анализ доступной литературы показал, что до сих пор изучались модели систем обслуживания с HS при наличии лишь идентичных (по важности) запросов. Авторам неизвестны работы, посвященные изучению моделей систем обслуживания с HS и разнотипными запросами, хотя наличие HS подсказывает о необходимости определенной классификации обрабатываемых в них запросов. Иными словами, для повышения экономической эффективности (относительно выбранного критерия качества) работы системы с HS следует выделить высокоприоритетные (H-запросы) и низкоприоритетные запросы (L-запросы) и организовать обработки H-запросов в высокоскоростных серверах (F-серверы), а медленные сервера (S-сервера) будут обрабатывать L-запросы.
Если принимается конкретная классификация запросов, то в системах с HS естественным образом возникает проблема введения надлежащих приоритетов для организации обслуживания разнотипных запросов. Хорошо известно, что независящие от состояния системы приоритеты (внесистемные приоритеты) являются малоэффективными, и потому для повышения экономической эффективности системы следует использовать зависящие от состояния системы приоритеты (внутрисистемные приоритеты).
Среди разнообразных приоритетов особое место занимают скачкообразные приоритеты (jump priorities (JP)), которые легко реализуются на практике. Эти приоритеты в дискретных (по времени) системах с одним сервером и бесконечными буферами для ожидания разнотипных запросов впервые были определены в [38–40]. В них предполагалось, что скачки L-запросов в очередь H-запросов происходят, согласно схеме Бернулли, с постоянными параметрами. В дальнейшем зависящие от состояния JP в непрерывных (по времени) системах с одним сервером и конечными буферами (раздельными или общий) для ожидания разнотипных запросов определены в [41, 42], в которых также решены задачи их оптимизации.
Следует отметить, что использование JP в системах с гетерогенными серверами напрашивается само по себе, так как в таких системах именно за счет введения зависящих от состояния системы JP можно организовать переход L-запроса в очередь H-запросов и таким образом избежать нежелательной ситуации долгого ожидания в очереди L-запросов. При этом также следует учитывать и ограничения, предъявляемые к качеству обслуживания H-запросами.
В настоящей работе разработаны модели систем с гетерегенными серверами и скачкообразными приоритетами, при этом рассматриваются модели с раздельными и общей очередью. Предложены методы расчета и оптимизации их характеристик.
1. Описание моделей и постановка задачи. Сначала рассмотрим системы с раздельными очередями разнотипных запросов. Ее структурная схема показана на рис. 1. Система содержит два гетерогенных сервера: быстрый (F-сервер) и медленный серверы (S-сервер). Эти серверы предназначены для обслуживания потоков запросов двух типов – высокоприоритетных (H-запросы) и низкоприоритетных (L-запросы), при этом H-запросы обслуживаются в F-сервере, а L-запросы – в S-сервере.
Рис. 1.
Структурная схема изучаемой системы при наличии раздельных очередей для разнотипных запросов

Считается, что оба потока запросов являются пуассоновскими с интенсивностями ${{\lambda }_{H}}$ и ${{\lambda }_{L}}$ для H-запросов и L-запросов соответственно. Время обслуживания запросов в обоих серверах являются случайными величинами с показательной ф.р.; среднее время обслуживания в F-сервере и S-сервере равны $\mu _{F}^{{ - 1}}$ и $\mu _{S}^{{ - 1}}$ соответственно, при этом скорость обслуживания F-сервера больше, чем скорость обслуживания S-сервера, т.е. ${{\mu }_{F}} > {{\mu }_{S}}$.
Для ожидания запросов в очереди имеются раздельные буфера конечных размеров, при этом максимальное число H-запросов и L-запросов в системе равны ${{K}_{H}}$ и ${{K}_{L}}$. Иными словами, размер буфера для H-запросов (H-буфер) равен ${{K}_{H}} - 1$, а соответствующий буфер для L-запросов (L-буфер) имеет размерность ${{K}_{L}} - 1$.
Для предотвращения “старения” L-запросов в очереди рандомизированные JP определяются следующим образом. Поступающие H-запросы всегда присоединяются к H-буферу, если там имеется свободное место. Вместе с тем L-запросы в зависимости от состояния системы могут переходить в H-буфер, при этом состояния системы в каждый момент времени задаются двумерным вектором (${{n}_{H}},{{n}_{L}}$), где компоненты ${{n}_{H}}$ и ${{n}_{L}}$ указывают на число H-запросов и L-запросов в системе соответственно. Иными словами, в момент поступления L-запроса один из них с вероятностью $J\left( {{{n}_{H}},{{n}_{L}}} \right)$, $0 < J\left( {{{n}_{H}},{{n}_{L}}} \right) \leqslant 1$, переходит в H-буфер (если там имеется свободное место) или с дополнительной вероятностью $1 - J\left( {{{n}_{H}},{{n}_{L}}} \right)$ либо присоединяется в L-буфер (если тут имеется свободное место), либо покидает систему необслуженным (если тут не имеется свободное место). Если L-запрос переходит в H-буфер, то в дальнейшем он обслуживается как H-запрос.
На практике зависящие от состояния рандомизированные JP $J\left( {{{n}_{H}},{{n}_{L}}} \right)$ могут быть определены различными способами. Так, интуитивно эффективным и легко реализумым способом задания этих приоритетов является следующая схема их определения. Вводится некоторый пороговый параметр r, $1 \leqslant r \leqslant {{K}_{L}}$, и если в момент поступления L-запроса разница между числом L-запросов и H-запросов меньше, чем $r,$ то поступивший L-запрос присоединяется к L-буферу; иначе один из L-запросов (для определенности считается, что L-запрос, стоящий в начале очереди) либо с вероятностью $\alpha $ переходит в конец очереди H-буфера (если там имеется свободное место), либо с вероятностью $1 - \alpha $ поступивший L-запрос принимается в L-буфер при наличии тут свободных мест; иначе он с такой же вероятностью теряется. Если в момент поступления L-запроса H-буфер переполнен, то $J\left( {{{K}_{H}},{{n}_{L}}} \right) = 0$ для любого ${{n}_{L}}$. Иными словами, в этой схеме рандомизированные JP $J\left( {{{n}_{H}},{{n}_{L}}} \right)$ определяются так:
(1.1)
$J\left( {{{n}_{H}},{{n}_{L}}} \right) = \left\{ \begin{gathered} \alpha ,\quad {\text{если }}{{n}_{L}} - {{n}_{H}} \geqslant r,\quad {{n}_{H}} < {{K}_{H}}, \hfill \\ 0\quad {\text{в других случаях}}. \hfill \\ \end{gathered} \right.$Ниже для определенности изложения используются JP, которые определяются соотношением (1.1). Если в соотношение (1.1) считать, что α = 1, то получаются детерминированные JP, т.е. каждый раз, когда разница между числом L-запросов и H-запросов не меньше, чем r, то L-запрос, стоящий в начале очереди, присоединяется к очереди H-запросов.
В случае системы с общей очередью для разнотипных запросов считается, что размер буфера равен K, $K < \infty $ , при этом после изменения типа L-запрос остается в том же буфере, но он рассматривается уже как H-запрос. Здесь допустимыми значениями порогового параметра r являются $1 \leqslant r \leqslant K$. В этой модели возможны ситуации, когда общий буфер полностью занят запросами одного типа, но сервер, который обслуживает запросы другого типа, свободен, а поступающий запрос соответствующего типа не может занимать свободный сервер. Для устранения подобных нежелательных ситуаций в этой модели принимается следующая схема доступа: если буфер полностью оккупирован H-запросами (L-запросами), а S-сервер (F-сервер) является свободным, то при поступлении L-запроса (H-запроса) допускается доступ данного запроса прямо к S-серверу (F-сервер), минуя процесс буферизации.
Задача состоит в нахождении совместного распределения числа разнотипных запросов в описанных выше системах с гетерогенными серверами и разработке методов вычисления их характеристик.
2. Точный метод расчета вероятностей состояний и характеристик изучаемых систем. Сначала рассмотрим системы с раздельными очередями. Математической моделью системы является двумерная цепь Маркова (ЦМ) с состояниями вида $\left( {{{n}_{H}},{{n}_{L}}} \right)$, при этом ее пространство состояний определяется как $E = \{ \left( {{{n}_{H}},{{n}_{L}}} \right){\text{:}}\;{{n}_{H}} = \overline {0,{{K}_{H}}} ,\;{{n}_{L}} = \overline {0,{{K}_{L}}} \} $.
Рассмотрим задачи определения элементов производящей матрицы (ПМ) данной ЦМ, которые определяют интенсивности переходов между ее состояниями (см. рис. 2, a).
Рис. 2.
Граф переходов между состояниями системы с раздельными очередями (а) и общей очередью (б); а – ${{K}_{H}} = 6$, ${{K}_{L}} = 7$, $r = 2$; б – $K = 7$, $r = 2$

Замечание 1. Во избежание загромождений на рис. 2, а, б на дугах графов указаны интенсивности переходов лишь для тех состояний, начиная с которого эти интенсивности в соответствующих строках и столбцах не меняются. В графах жирными кружками обозначены состояния, в которых возможны скачки L-запросов. В них также приняты следующие обозначения: $x = \left( {1 - \alpha } \right){{\lambda }_{L}}$, $y = {{\lambda }_{H}} + \left( {1 - \alpha } \right){{\lambda }_{L}}$.
Пусть $q(({{n}_{H}},{{n}_{L}}),(n_{H}^{'},n_{L}^{'}))$ – интенсивность перехода из состояния $({{n}_{H}},{{n}_{L}}) \in E$ в состояние $(n_{H}^{'},n_{L}^{'}) \in E$. Учитывая соотношение (1.1) эти величины определяются следующим образом (для простоты изложения ниже указываются лишь положительные элементы ПМ):
случаи ${{n}_{L}} - {{n}_{H}} < r$:
(2.1)
$q(({{n}_{H}},{{n}_{L}}),(n_{H}^{'},n_{L}^{'})) = \left\{ {\begin{array}{*{20}{l}} {{{\lambda }_{H}},}&{{\text{если }}{{n}_{H}} < {{K}_{H}},\quad n_{H}^{'} = {{n}_{H}} + 1,\quad n_{L}^{'} = {{n}_{L}},} \\ {{{\lambda }_{L}},}&{{\text{если }}{{n}_{L}} < {{K}_{L}},\quad n_{H}^{'} = {{n}_{H}},\quad n_{L}^{'} = {{n}_{L}} + 1,} \\ {{{\mu }_{F}},}&{{\text{если }}{{n}_{H}} > 0,\quad n_{H}^{'} = {{n}_{H}} - 1,\quad n_{L}^{'} = {{n}_{L}},} \\ {{{\mu }_{S}},}&{{\text{если }}{{n}_{L}} > {\text{0,}}\quad n_{H}^{'} = {{n}_{H}}{\text{,}}\quad n_{L}^{'} = {{n}_{L}};{\text{ }}} \end{array}} \right.$(2.2)
$q(({{n}_{H}},{{n}_{L}}),(n_{H}^{'},n_{L}^{'})) = \left\{ {\begin{array}{*{20}{l}} {{{\lambda }_{H}} + \alpha {{\lambda }_{L}},}&{{\text{если}}\quad n_{H}^{'} = {{n}_{H}} + 1,\quad n_{L}^{'} = {{n}_{L}},} \\ {\left( {1 - \alpha } \right){{\lambda }_{L}},}&{{\text{если}}\quad n_{H}^{'} = {{n}_{H}},\quad n_{L}^{'} = {{n}_{L}} + 1,} \\ {{{\mu }_{F}},}&{{\text{если}}\quad {{n}_{H}} > 0,\quad n_{H}^{'} = {{n}_{H}} - 1,\quad n_{L}^{'} = {{n}_{L}},} \\ {{{\mu }_{S}},}&{{\text{если}}\quad {{n}_{L}} > {\text{0,}}\quad n_{H}^{'} = {{n}_{H}}{\text{,}}\quad n_{L}^{'} = {{n}_{L}}{\text{. }}} \end{array}} \right.$Из формул (2.1) и (2.2) заключаем, что все состояния изучаемой ЦМ сообщаются друг с другом (см. рис. 2, а), т.е. существуют стационарные вероятности состояний. Пусть p(nH, nL), $({{n}_{H}},{{n}_{L}}) \in E,$ обозначают вероятности состояний этой ЦМ. Известно, что эти вероятности находятся в результате решения соответствующей системы уравнений равновесия (СУР), которая составляется на основе соотношений (2.1), (2.2) (из-за очевидности ее составления явный вид этой СУР здесь не приводится).
После нахождения вероятностей состояний системы удается определить характеристики исследуемой системы, которые представляют собой маргинальные распределения данной цепи: вероятности потери разнотипных запросов; средняя интенсивность скачков L-запросов в H-буфер; среднее число разнотипных запросов в системе.
Поскольку H-запросы теряются лишь тогда, когда в моменты их поступления в системе уже имеются KH запросов данного типа, то вероятность потери H-запросов $\left( {P{{B}_{H}}} \right)$ определяется как
(2.3)
$P{{B}_{H}} = \sum\limits_{{{n}_{L}} = 0}^{{{K}_{L}}} {p\left( {{{K}_{H}},{{n}_{L}}} \right)} .$Для нахождения вероятности потери L-запросов следует рассматривать состояния типа $\left( {{{n}_{H}},\,{{K}_{L}}} \right)$, при этом необходимо различать два случая: 1) $0 \leqslant {{n}_{H}} \leqslant {{K}_{L}} - r$; 2) ${{K}_{L}} - r < {{n}_{H}} \leqslant {{K}_{L}}$. Если в момент поступления L-запроса имеет место случай 1), то он теряется с вероятностью 1 – α, а в случаях 2) этот запрос теряется с вероятностью единица. Следовательно, используя формулы полной вероятности, заключаем, что вероятность потери L-запросов $\left( {P{{B}_{L}}} \right)$ определяется следующим образом:
(2.4)
$P{{B}_{L}} = \left( {1 - \alpha } \right)\sum\limits_{{{n}_{H}} = 0}^{\min \left( {{{K}_{L}} - r,{{K}_{H}} - 1} \right)} {p\left( {{{n}_{H}},{{K}_{L}}} \right)} + \sum\limits_{{{n}_{H}} = {{K}_{L}} - r + 1}^{{{K}_{H}}} {p\left( {{{n}_{H}},{{K}_{L}}} \right)} .$Скачки L-запросов в H-буфер происходят в моменты поступления L-запросов с вероятностью α, если в эти моменты система находится в состоянии $\left( {{{n}_{H}},\,{{n}_{L}}} \right)$, в котором выполняется условие ${{n}_{L}} - {{n}_{H}} \geqslant r$. Отсюда заключаем, что средняя интенсивность скачков L-запросов в H-буфер $\left( {R{{J}_{{LH}}}} \right)$ вычисляется как
(2.5)
$R{{J}_{{LH}}} = {{\lambda }_{L}}\alpha \sum\limits_{{{n}_{L}} = r}^{{{K}_{L}}} {\sum\limits_{{{n}_{H}} = 0}^{{{n}_{L}} - r} {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } .$Среднее число H-запросов $\left( {{{N}_{H}}} \right)$ и L-запросов $\left( {{{N}_{L}}} \right)$ в системе определяются как математические ожидания соответствующих случайных величин, т.е.
(2.6)
${{N}_{H}} = \sum\limits_{{{n}_{{_{H}}}} = 1}^{{{K}_{H}}} {{{n}_{H}}\sum\limits_{{{n}_{L}} = 0}^{{{K}_{L}}} {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } ;$(2.7)
${{N}_{L}} = \sum\limits_{{{n}_{L}} = 1}^{{{K}_{L}}} {{{n}_{L}}\sum\limits_{{{n}_{H}} = 0}^{{{K}_{H}}} {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } .$Таким образом, приведенные выше формулы (2.1)–(2.7) позволяют вычислить стационарные вероятности состояний и характеристик системы с раздельными очередями.
Теперь рассмотрим системы с общей очередью. Как и выше, математической моделью данной системы является двумерная ЦМ с состояниями вида $\left( {{{n}_{H}},{{n}_{L}}} \right),$ но здесь ее пространство состояний определяется как
Элементы ПМ данной ЦМ определяются аналогично (2.1), (2.2), но при этом в правой части формулы (2.1) в первой и во второй строке оба условия ${{n}_{H}} < {{K}_{H}}$ и ${{n}_{L}} < {{K}_{L}}$ заменяются условием ${{\left( {{{n}_{H}} - 1} \right)}^{ + }} + {{\left( {{{n}_{L}} - 1} \right)}^{ + }} < K$.
Далее составляется соответствующая СУР для стационарных вероятностей состояний данной модели и определяются характеристики изучаемой системы. В результате анализа работы системы, заключаем, что искомые характеристики (2.3)–(2.7) для данной модели определяются из следующих формул:
(2.8)
$P{{B}_{H}} = p\left( {K + 1,0} \right) + \sum\limits_{{{n}_{H}} = 1}^{K + 1} {p\left( {{{n}_{H}},K + 2 - {{n}_{H}}} \right)} ;$(2.9)
$P{{B}_{L}} = p\left( {0,K + 1} \right) + \sum\limits_{{{n}_{H}} = 1}^{K + 1} {p\left( {{{n}_{H}},K + 2 - {{n}_{H}}} \right)} ;$(2.10)
$R{{J}_{{LH}}} = {{\lambda }_{L}}\alpha \sum\limits_{{{n}_{L}} = r}^{K + 1} {\sum\limits_{{{n}_{H}} = 0}^{\min \{ {{n}_{L}} - r,K + 1 - {{{\left( {{{n}_{L}} - 1} \right)}}^{ + }}\} } {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } ;$(2.11)
${{N}_{H}} = \sum\limits_{{{n}_{{_{H}}}} = 1}^{K + 1} {{{n}_{H}}\sum\limits_{{{n}_{L}} = 0}^{K + 1 - {{{\left( {{{n}_{H}} - 1} \right)}}^{ + }}} {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } ;$(2.12)
${{N}_{L}} = \sum\limits_{{{n}_{{_{L}}}} = 1}^{K + 1} {{{n}_{L}}\sum\limits_{{{n}_{H}} = 0}^{K + 1 - {{{\left( {{{n}_{L}} - 1} \right)}}^{ + }}} {p\left( {{{n}_{H}},{{n}_{L}}} \right)} } .$Разработанный выше подход для нахождения стационарных вероятностей состояний и с их помощью характеристик изучаемых моделей систем с гетерогоенными серверами является точным и легко реализуется для моделей умеренной размерности. Вместе с тем, с ростом размерности моделей применение разработанного подхода требует неоправданно больших затрат машинного времени. Более того, в случаях плохой обусловленности ПМ изучаемой модели возникают проблемы вычислительной неустойчивости. Известные матрично-геометрические методы [43–45] частично решают эти проблемы (о недостатках этих методов см. [46]).
Ниже предлагается альтернативный и унифицированный приближенный метод, который позволяет решить рассматриваемые задачи для обеих моделей с помощью явных формул.
3. Приближенный метод расчета вероятностей состояний и характеристик системы. Сначала рассмотрим системы с раздельными очередями. Предложенный метод основан на принципах фазового укрупенения состояний двумерных ЦМ. Его применение требует расщепления ПС модели на такие классы, чтобы интенсивности переходов между состояниями внутри классов намного превосходили интенсивности между состояниями из разных классов.
В данной модели такое расщепление легко осуществляется. Действительно, поскольку F-сервер имеет более высокую скорость обслуживания, чем S-сервер, и принимая допущение о том, что интенсивность H-запросов намного больше, чем интенсивность L-запросов, то разбиение графа состояний по строкам (см. рис. 2а) удовлетворяет указанному выше требованию. Иными словами, рассматривается следующее расщепление ПС модели:
(3.1)
$E = \bigcup\limits_{l = 0}^{{{K}_{L}}} {{{E}_{l}}} ,\quad {{E}_{{{{l}_{1}}}}} \cap {{E}_{{{{l}_{2}}}}} = \emptyset ,\quad {{l}_{1}} \ne {{l}_{2}},$Замечание 2. Здесь и далее во избежание многоярусных индексов и для упрощения обозначений в некоторых формулах вектор состояния $\left( {{{n}_{H}},{{n}_{L}}} \right)$ заменяется на вектор (h, l).
На основе расщепления (3.1) ПС исходной модели все микросостояния внутри каждого класса ${{E}_{l}}$ объединяются в одно укрупненное состояние $\left\langle l \right\rangle $, и таким образом, определяется множество укрупненных состояний $\Omega = \{ \left\langle l \right\rangle {\text{:}}\;l = \overline {0,{{K}_{L}}} \} $.
Приближенные значения вероятностей состояний $\tilde {p}\left( {h,l} \right)$, $\left( {h,l} \right) \in E$ исходной модели определяются как [46]
где ${{\rho }_{l}}(h)$ – вероятность состояния $\left( {h,l} \right)$ внутри расщепленной модели с пространством состояний ${{E}_{l}}$, а $\pi \left( {\left\langle l \right\rangle } \right)$ – вероятность укрупненного состояния $\left\langle l \right\rangle \in \Omega $.Для вычисления ${{\rho }_{l}}(h)$ необходимо раздельно рассматривать два случая: 1) $0 \leqslant l \leqslant r - 1$; 2) $r \leqslant l \leqslant {{K}_{L}}$.
Для первого случая из соотношений (2.1) получаем, что искомые вероятности состояний внутри всех расщепленных моделей с пространством состояний ${{E}_{l}}$, $0 \leqslant l \leqslant r - 1$, совпадают с вероятностями состояний одномерного процесса размножения-гибели с постоянными интенсивностями (см. рис. 2, а), т.е.
(3.3)
${{\rho }_{l}}\left( h \right) = {{\nu _{H}^{h}\left( {1 - {{\nu }_{H}}} \right)} \mathord{\left/ {\vphantom {{\nu _{H}^{h}\left( {1 - {{\nu }_{H}}} \right)} {(1 - \nu _{H}^{{{{K}_{H}} + 1}}),\quad h = \overline {0,{{K}_{H}}} }}} \right. \kern-0em} {(1 - \nu _{H}^{{{{K}_{H}} + 1}}),\quad h = \overline {0,{{K}_{H}}} }},$Для второго случая из соотношений (2.2) получаем, что вероятности состояний внутри расщепленной модели с пространством состояний El, $r \leqslant l \leqslant {{K}_{L}}$, совпадают с вероятностями состояний одномерного процесса размножения-гибели с переменными интенсивностями (см. рис. 2, а), т.е.
(3.4)
${{\rho }_{l}}\left( h \right) = \left\{ {\begin{array}{*{20}{l}} {{{{\left( {{{\nu }_{H}} + \alpha b} \right)}}^{h}}{{\rho }_{l}}\left( 0 \right),}&{{\text{если }}0 \leqslant h \leqslant l - r + 1,} \\ {\nu _{H}^{h}{{{\left( {1 + \alpha c} \right)}}^{{l - r + 1}}}{{\rho }_{l}}\left( 0 \right),}&{{\text{если }}l - r + 1 \leqslant h \leqslant {{K}_{H}},} \end{array}} \right.$Пусть $q\left( {\left\langle {{{l}_{1}}} \right\rangle ,\left\langle {{{l}_{2}}} \right\rangle } \right)$, $\left\langle {{{l}_{1}}} \right\rangle ,\left\langle {{{l}_{2}}} \right\rangle \in \Omega $ обозначает интенсивность перехода из укрупненного состояния $\left\langle {{{l}_{1}}} \right\rangle $ в укрупненное состояние $\left\langle {{{l}_{2}}} \right\rangle $. Тогда с учетом результатов [46] после определенных математических выкладок находим, что указанные интенсивности переходов вычисляются следующим образом:
(3.5)
$q\left( {\left\langle {{{l}_{1}}} \right\rangle ,\left\langle {{{l}_{2}}} \right\rangle } \right) = \left\{ {\begin{array}{*{20}{l}} {{{\lambda }_{L}},}&{{\text{если}}\quad 0 \leqslant {{l}_{1}} < r,\quad {{l}_{2}} = {{l}_{1}} + 1,} \\ {{{{\tilde {\lambda }}}_{L}},}&{{\text{если}}\quad r \leqslant {{l}_{1}} < {{K}_{L}},\quad {{l}_{2}} = {{l}_{1}} + 1,} \\ {{{\mu }_{L}}}&{{\text{если}}\quad {{l}_{2}} = {{l}_{1}} - 1,} \end{array}} \right.$Следовательно, из (3.5) имеем
(3.6)
$\pi ( < l > ) = \left\{ {\begin{array}{*{20}{l}} {\nu _{L}^{l}\pi \left( {\left\langle 0 \right\rangle } \right),}&{{\text{если}}\quad 0 \leqslant l \leqslant r,} \\ {{{{\left( {\frac{{{{\nu }_{L}}}}{{{{{\tilde {\nu }}}_{L}}}}} \right)}}^{r}}\tilde {\nu }_{L}^{l}\pi \left( {\left\langle 0 \right\rangle } \right),}&{{\text{если}}\quad r + 1 \leqslant l \leqslant {{K}_{L}},} \end{array}} \right.$С учетом соотношений (3.3)–(3.6) из (3.2) вычисляются приближенные значения вероятностей состояний. После нахождения этих вероятностей легко определяются приближенные значения характеристик (2.3)–(2.7) системы с раздельными очередями:
(3.7)
$P{{B}_{H}} \approx \sum\limits_{l = 0}^{{{K}_{L}}} {{{\rho }_{l}}\left( {{{K}_{H}}} \right)\pi \left( {\left\langle l \right\rangle } \right)} ;$(3.8)
$P{{B}_{L}} \approx \pi \left( {\left\langle {{{K}_{L}}} \right\rangle } \right)\left( {\left( {1 - \alpha } \right)\sum\limits_{h = 0}^{{{K}_{L}} - r} {{{\rho }_{{{{K}_{L}}}}}\left( h \right)} + \sum\limits_{h = {{K}_{L}} - r + 1}^{{{K}_{H}}} {{{\rho }_{{{{K}_{L}}}}}\left( h \right)} } \right);$(3.9)
$R{{J}_{{LH}}} \approx {{\lambda }_{L}}\alpha \sum\limits_{l = r}^{{{K}_{L}}} {\pi \left( {\left\langle l \right\rangle } \right)\sum\limits_{h = 0}^{l - r} {{{\rho }_{l}}\left( h \right)} } ;$(3.10)
${{N}_{H}} \approx \sum\limits_{h = 1}^{{{K}_{H}}} {h\sum\limits_{l = 0}^{{{K}_{L}}} {{{\rho }_{l}}\left( h \right)\pi \left( {\left\langle l \right\rangle } \right)} } ;$(3.11)
${{N}_{L}} \approx \sum\limits_{l = 1}^{{{K}_{L}}} {l\pi \left( {\left\langle l \right\rangle } \right)} .$Далее вкратце рассмотрим применение разработанного приближенного подхода для изучения системы с общей очередью. В данном случае вероятности состояний внутри расщепленных моделей с пространством состояний El при $0 \leqslant l \leqslant r - 1$ и при $r \leqslant l \leqslant K + 1$ также вычисляются по формулам (3.3) и (3.4) соответственно, но при этом в этих формулах параметр KH заменяется параметром $K + 1 - {{\left( {h - 1} \right)}^{ + }}$. Интенсивности переходов между состояниями укрупненной модели определяются аналогично (3.5), где в правой части этой формулы во второй строке параметр KL заменяется на K + 1, а параметр ${{K}_{H}}$ (см. выражение для параметра $\tilde {\lambda }$), как и выше, заменяется параметром $K + 1 - {{\left( {h - 1} \right)}^{ + }}$. Следовательно, вероятности укрупненных состояний вычисляются по формуле (3.6), где параметр KL опять заменяется на K + 1.
После определенных математических выкладок для вычисления характеристик системы с общей очередью получаем следующие приближенные формулы:
(3.12)
$P{{B}_{H}} \approx {{\rho }_{0}}\left( {K + 1} \right)\pi \left( {\left\langle 0 \right\rangle } \right) + \sum\limits_{l = 1}^{K + 1} {{{\rho }_{{K + 2 - l}}}\left( l \right)\pi \left( {\left\langle {K + 2 - l} \right\rangle } \right)} ;$(3.13)
$P{{B}_{L}} \approx {{\rho }_{{K + 1}}}\left( 0 \right)\pi \left( {\left\langle {K + 1} \right\rangle } \right) + \sum\limits_{l = 1}^{K + 1} {{{\rho }_{{K + 2 - l}}}\left( l \right)\pi \left( {\left\langle {K + 2 - l} \right\rangle } \right)} ;$(3.14)
$R{{J}_{{LH}}} \approx {{\lambda }_{L}}\alpha \sum\limits_{l = r}^{K + 1} {\pi \left( {\left\langle l \right\rangle } \right)\sum\limits_{h = 0}^{\min \left\{ {l - r,K + 1 - {{{\left( {l - 1} \right)}}^{ + }}} \right\}} {{{\rho }_{l}}\left( h \right)} } ;$(3.15)
${{N}_{H}} \approx \sum\limits_{h = 1}^{K + 1} {h\sum\limits_{l = 0}^{K + 1 - {{{\left( {h - 1} \right)}}^{ + }}} {{{\rho }_{l}}\left( h \right)\pi \left( {\left\langle l \right\rangle } \right)} } ;$(3.16)
${{N}_{L}} \approx \sum\limits_{l = 1}^{K + 1} {l\pi \left( {\left\langle l \right\rangle } \right)} .$4. Численные результаты. Проводимые здесь численные эксперименты имеют три цели: 1) оценить точность разработанных приближенных формул для расчета стационарных вероятностей состояний и характеристик изучаемых систем; 2) изучить зависимость этих характеристик от значений порогового параметра $r$ скачкообразных приоритетов; 3) решить задачи оптимизации этих характеристик.
Сначала рассмотрим результаты для модели с раздельными очередями. Относительно первой цели отметим, что точность приближенных значений вероятностей состояний оценивается с помощью следующих мер близости [46]:
подобия косинуса:
(4.1)
${{\left\| {\rm N} \right\|}_{1}} = {{{{\sum\limits_{n \in E} {p(n)\tilde {p}(n)} } \mathord{\left/ {\vphantom {{\sum\limits_{n \in E} {p(n)\tilde {p}(n)} } {{{{\left( {\sum\limits_{n \in E} {{{{(p(n))}}^{2}}} } \right)}}^{{1/2}}}\left( {\sum\limits_{n \in E} {{{{(\tilde {p}(n))}}^{2}}} } \right)}}} \right. \kern-0em} {{{{\left( {\sum\limits_{n \in E} {{{{(p(n))}}^{2}}} } \right)}}^{{1/2}}}\left( {\sum\limits_{n \in E} {{{{(\tilde {p}(n))}}^{2}}} } \right)}}}^{{1/2}}};$(4.2)
${{\left\| {\rm N} \right\|}_{2}} = \mathop {\max }\limits_{n \in E} \left| {p(n) - \tilde {p}(n)} \right|.$Результаты сравнительного анализа значений вероятностей состояний при точном и приближенном подходах показаны в табл. 1. Здесь исходные данные модели выбраны так: ${{\mu }_{F}} = 50$, ${{\mu }_{S}}$ = 30, $\alpha = 0.2$. Кроме того, для двух пар размеров буферов $\left( {{{K}_{H}},{{K}_{L}}} \right) = \left( {5,5} \right)$ и $\left( {{{K}_{H}},{{K}_{L}}} \right) = \left( {10,5} \right)$ значения порогового параметра $r = 3$, а для пары $({{K}_{H}},{{K}_{L}})$ = (10, 10) выбран $r = 8$.
Таблица 1.
Оценка точности вычисления вероятностей состояний относительно различных норм близости для модели с раздельными очередями
| (λH, λL) | (KH, KL) | Значения нормы | |
|---|---|---|---|
| (4.1) | (4.2) | ||
| (45, 30) | (5, 5) | 0.981 | 0.016 |
| (10, 5) | 0.977 | 0.009 | |
| (10, 10) | 0.973 | 0.008 | |
| (45, 35) | (5, 5) | 0.993 | 0.007 |
| (10, 5) | 0.984 | 0.006 | |
| (10, 10) | 0.971 | 0.006 | |
| (50, 30) | (5, 5) | 0.984 | 0.012 |
| (10, 5) | 0.975 | 0.007 | |
| (10, 10) | 0.976 | 0.005 | |
| (50, 35) | (5, 5) | 0.993 | 0.006 |
| (10, 5) | 0.976 | 0.009 | |
| (10, 10) | 0.968 | 0.004 | |
| (55, 30) | (5, 5) | 0.987 | 0.009 |
| (10, 5) | 0.977 | 0.009 | |
| (10, 10) | 0.977 | 0.004 | |
| (55, 35) | (5, 5) | 0.993 | 0.007 |
| (10, 5) | 0.973 | 0.012 | |
| (10, 10) | 0.967 | 0.005 | |
Из табл. 1 видно, что мера близости (4.1) равна почти 1, а также в подавляющем большинстве экспериментов точные и приближенные значения вероятностей состояний в наихудших случаях отличаются в третьем знаке после десятичной точки, иными словами, на высокую степень точности разработанных приближенных формул указывает и мера близости (4.2). Заметим, что проведенные численные эксперименты показали и высокую степень точности разработанных приближенных формул для характеристик (2.3)–(2.7), при этом в них исходные данные остались прежними (см. табл. 2 и 3).
Таблица 2.
Оценка точности вычисления характеристик (2.3)–(2.5) модели с раздельными очередями
| (λH, λL) | (KH, KL) | PBH | PBL | RJLH | |||
|---|---|---|---|---|---|---|---|
| точный | прибли-женный | точный | прибли-женный | точный | прибли-женный | ||
| (45, 30) | (5, 5) | 0.119 | 0.117 | 0.147 | 0.105 | 1.884 | 1.382 |
| (10, 5) | 0.063 | 0.041 | 0.154 | 0.115 | 1.253 | 1.009 | |
| (10, 10) | 0.041 | 0.040 | 0.083 | 0.052 | 0.756 | 0.453 | |
| (45, 35) | (5, 5) | 0.119 | 0.119 | 0.148 | 0.157 | 1.892 | 1.799 |
| (10, 5) | 0.068 | 0.041 | 0.156 | 0.171 | 1.238 | 1.302 | |
| (10, 10) | 0.041 | 0.041 | 0.083 | 0.112 | 0.758 | 0.851 | |
| (50, 30) | (5, 5) | 0.158 | 0.155 | 0.149 | 0.109 | 1.763 | 1.304 |
| (10, 5) | 0.108 | 0.075 | 0.158 | 0.122 | 0.929 | 0.785 | |
| (10, 10) | 0.076 | 0.075 | 0.085 | 0.055 | 0.581 | 0.355 | |
| (50, 35) | (5, 5) | 0.159 | 0.157 | 0.151 | 0.163 | 1.769 | 1.704 |
| (10, 5) | 0.114 | 0.076 | 0.160 | 0.181 | 0.912 | 1.015 | |
| (10, 10) | 0.077 | 0.075 | 0.086 | 0.119 | 0.582 | 0.667 | |
| (55, 30) | (5, 5) | 0.198 | 0.195 | 0.152 | 0.113 | 1.623 | 1.213 |
| (10, 5) | 0.159 | 0.120 | 0.161 | 0.128 | 0.650 | 0.575 | |
| (10, 10) | 0.121 | 0.119 | 0.087 | 0.058 | 0.419 | 0.261 | |
| (55, 35) | (5, 5) | 0.199 | 0.197 | 0.154 | 0.168 | 1.628 | 1.589 |
| (10, 5) | 0.166 | 0.120 | 0.163 | 0.189 | 0.634 | 0.745 | |
| (10, 10) | 0.122 | 0.120 | 0.088 | 0.124 | 0.420 | 0.491 | |
Таблица 3.
Оценка точности вычисления характеристик (2.6) и (2.7) модели с раздельными очередями
| (λH, λL) | (KH, KL) | NH | NL | ||
|---|---|---|---|---|---|
| точный | приближенный | точный | приближенный | ||
| (45, 30) | (5, 5) | 2.110 | 2.141 | 2.503 | 2.202 |
| (10, 5) | 4.061 | 3.693 | 2.507 | 2.235 | |
| (10, 10) | 3.624 | 3.649 | 5.001 | 4.282 | |
| (45, 35) | (5, 5) | 2.114 | 2.173 | 2.514 | 2.634 |
| (10, 5) | 4.139 | 3.738 | 2.517 | 2.673 | |
| (10, 10) | 3.626 | 3.694 | 5.007 | 5.769 | |
| (50, 30) | (5, 5) | 2.414 | 2.436 | 2.504 | 2.216 |
| (10, 5) | 5.113 | 4.674 | 2.506 | 2.257 | |
| (10, 10) | 4.625 | 4.639 | 5.003 | 4.304 | |
| (50, 35) | (5, 5) | 2.418 | 2.463 | 2.514 | 2.651 |
| (10, 5) | 5.197 | 4.710 | 2.515 | 2.699 | |
| (10, 10) | 4.628 | 4.675 | 5.009 | 5.802 | |
| (55, 30) | (5, 5) | 2.691 | 2.706 | 2.5041 | 2.229 |
| (10, 5) | 6.051 | 5.605 | 2.504 | 2.275 | |
| (10, 10) | 5.576 | 5.579 | 5.005 | 4.322 | |
| (55, 35) | (5, 5) | 2.695 | 2.729 | 2.514 | 2.666 |
| (10, 5) | 6.129 | 5.631 | 2.512 | 2.719 | |
| (10, 10) | 5.579 | 5.606 | 5.011 | 5.828 | |
Относительно второй цели численных экспериментов отметим, что здесь изучается поведение характеристик моделей при изменении значений порогового параметра r; при этом сравниваются характеристики системы при использовании детерминированных ($\alpha = 1$) и рандомизированных JP ($\alpha < 1$).
На рис. 3 показаны зависимости характеристик системы от параметра $r$ в модели с раздельными очередями, при этом исходные параметры системы выбираются так: ${{\lambda }_{H}} = 50$, ${{\lambda }_{L}} = 30$, ${{\mu }_{F}} = 40$, ${{\mu }_{S}} = 20$, ${{K}_{H}} = {{K}_{L}} = 10$.
Рис. 3.
Зависимости характеристик системы от параметра $r$ в модели с раздельными очередями: $P{{B}_{H}}$ (а), $P{{B}_{L}}$ (б), $R{{J}_{{LH}}}$ (в), ${{N}_{H}}$ (г), ${{N}_{L}}$ (д)
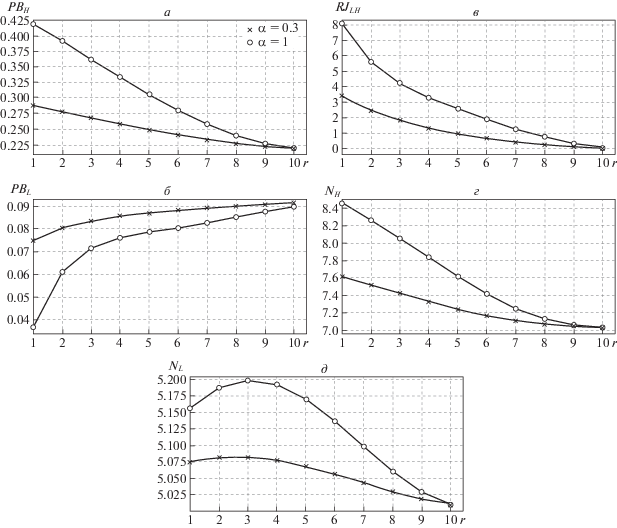
Из рис. 3, а видно, при использовании обоих типов JP функция $P{{B}_{H}}$ – убывающая функция. Этого следовало ожидать, так как с ростом параметра r L-запросы реже переходят в H-буфер, и тем самым увеличиваются шансы H-запросов для доступа в свой буфер; также ожидаемым является тот факт, что при использовании детерминированных JP, вероятность потери H-запросов больше, чем при использовании рандомизированных JP. Действительно, при использовании детерминированных JP L-запросы с большей интенсивностью переходят в H-буфер, чем при использовании рандомизированных JP, иными словами, при использовании рандомизированных JP H-запросы имеют больше шансов для доступа в буфер.
Обратная картина наблюдается для функции $P{{B}_{L}}$, т.е. она является возрастающей функцией и при использовании детерминированных JP, вероятность потери L-запросов меньше, чем при использовании рандомизированных JP (см. рис. 3, б). Возрастание этой функции объясняется тем, что, как это было отмечено выше, с ростом параметра r L-запросы реже переходят в H-буфер, и тем самым они больше загружают свой буфер, т.е. уменьшаются шансы L-запросов для доступа в свой буфер. С другой стороны, при использовании детерминированных JP L-запросы с большей интенсивностью переходят в H-буфер, чем при использовании рандомизированных JP, и тем самым при использовании детерминированных JP L-запросы имеют больше шансов для доступа в свой буфер.
Как и следовало ожидать, функция $R{{J}_{{LH}}}$ является убывающей относительно параметра $r$, так как с ростом этого параметра уменьшается интенсивность перехода L-запросов в H-буфер, при этом эта величина при использовании детерминированных JP больше, чем при использовании рандомизированных JP (см. рис. 3, в).
Функция NH является убывающей (см. рис. 3, г), так как с ростом параметра r уменьшается интенсивность перехода L-запросов в H-буфер, и тем самым уменьшается среднее число H-запросов в системе; здесь значения этой функции больше при использовании детерминированных JP, так как при этом интенсивность переходов из L-буфера в H-буфер больше, чем при использовании рандомизированных JP.
Поведение функции NL отличается от поведения функции NH (см. рис. 3, д). Несколько неожиданным, на первый взгляд, кажется факт о том, что при использовании детерминированных JP среднее число L-запросов в системе чуть больше, чем при использовании рандомизированных JP (вообще значения этой функции при использовании обоих типов JP почти совпадают). Однако этот факт имеет следующее объяснение: при использовании детерминированных JP и при малых значениях параметра $r$ интенсивность перехода L-запросов в H-буфер больше, чем при рандомизированных JP, и тем самым при использовании детерминированных JP все больше шансов появляются для доступа L-запросов в свой буфер.
Теперь рассмотрим результаты для модели с общей очередью. Для данной модели результаты сравнительного анализа значений вероятностей состояний при точном и приближенном подходах показаны в табл. 4. Здесь исходные данные модели выбраны так: ${{\mu }_{F}} = 50$, ${{\mu }_{S}} = 35$, $\alpha = 0.2$. Из табл. 5 и 6 видно, что и для такой модели предложенные алгоритмы имеют высокую точность.
Таблица 4.
Оценка точности вычисления вероятностей состояний относительно различных норм близости для модели с общей очередью
| (λH, λL) | (K, r) | Значения нормы | |
|---|---|---|---|
| (4.1) | (4.2) | ||
| (35, 30) | (5, 2) | 0.929 | 0.029 |
| (10, 5) | 0.838 | 0.027 | |
| (15, 7) | 0.841 | 0.033 | |
| (40, 30) | (5, 2) | 0.930 | 0.030 |
| (10, 5) | 0.873 | 0.017 | |
| (15, 7) | 0.873 | 0.019 | |
| (40, 35) | (5, 2) | 0.977 | 0.018 |
| (10, 5) | 0.976 | 0.009 | |
| (15, 7) | 0.933 | 0.009 | |
| (45, 30) | (5, 2) | 0.909 | 0.047 |
| (10, 5) | 0.863 | 0.027 | |
| (15, 7) | 0.807 | 0.017 | |
| (45, 35) | (5, 2) | 0.955 | 0.027 |
| (10, 5) | 0.958 | 0.012 | |
| (15, 7) | 0.952 | 0.007 | |
| (45, 40) | (5, 2) | 0.931 | 0.029 |
| (10, 5) | 0.900 | 0.019 | |
| (15, 7) | 0.906 | 0.012 | |
Таблица 5.
Оценка точности вычисления характеристик (2.8)–(2.10) модели с общей очередью
| (λH, λL) | (K, r) | PBH | PBL | RJLH | |||
|---|---|---|---|---|---|---|---|
| точный | прибли-женный | точный | прибли-женный | точный | прибли-женный | ||
| (35, 30) | (5, 2) | 0.117 | 0.102 | 0.111 | 0.099 | 2.282 | 1.898 |
| (10, 5) | 0.067 | 0.034 | 0.095 | 0.066 | 2.091 | 1.963 | |
| (15, 7) | 0.046 | 0.009 | 0.065 | 0.031 | 2.407 | 1.901 | |
| (40, 30) | (5, 2) | 0.140 | 0.142 | 0.166 | 0.146 | 2.026 | 1.851 |
| (10, 5) | 0.084 | 0.065 | 0.102 | 0.076 | 1.784 | 0.964 | |
| (15, 7) | 0.058 | 0.026 | 0.071 | 0.042 | 2.052 | 1.909 | |
| (40, 35) | (5, 2) | 0.142 | 0.166 | 0.168 | 0.171 | 2.356 | 2.123 |
| (10, 5) | 0.085 | 0.092 | 0.103 | 0.099 | 2.077 | 1.911 | |
| (15, 7) | 0.059 | 0.047 | 0.072 | 0.051 | 2.189 | 1.999 | |
| (45, 30) | (5, 2) | 0.163 | 0.187 | 0.171 | 0.154 | 1.769 | 1.521 |
| (10, 5) | 0.106 | 0.121 | 0.113 | 0.090 | 1.041 | 0.976 | |
| (15, 7) | 0.077 | 0.072 | 0.083 | 0.052 | 1.115 | 0.996 | |
| (45, 35) | (5, 2) | 0.175 | 0.207 | 0.173 | 0.192 | 2.056 | 1.989 |
| (10, 5) | 0.107 | 0.122 | 0.114 | 0.136 | 1.674 | 1.463 | |
| (15, 7) | 0.078 | 0.089 | 0.084 | 0.085 | 1.851 | 1.972 | |
| (45, 40) | (5, 2) | 0.187 | 0.204 | 0.185 | 0.204 | 2.339 | 2.636 |
| (10, 5) | 0.109 | 0.137 | 0.116 | 0.149 | 1.905 | 2.116 | |
| (15, 7) | 0.080 | 0.109 | 0.085 | 0.114 | 2.103 | 2.399 | |
Таблица 6.
Оценка точности вычисления характеристик (2.11) и (2.12) модели с общей очередью
| (λH, λL) | (K, r) | NH | NL | ||
|---|---|---|---|---|---|
| точный | прибли- женный | точный | прибли- женный | ||
| (35, 30) | (5, 2) | 1.367 | 1.749 | 2.623 | 1.921 |
| (10, 5) | 1.729 | 2.060 | 4.958 | 3.014 | |
| (15, 7) | 1.914 | 2.102 | 7.375 | 3.615 | |
| (40, 30) | (5, 2) | 1.994 | 2.128 | 2.295 | 1.921 |
| (10, 5) | 2.990 | 3.231 | 4.671 | 4.014 | |
| (15, 7) | 2.845 | 3.028 | 6.955 | 5.615 | |
| (40, 35) | (5, 2) | 1.899 | 2.022 | 2.499 | 2.421 |
| (10, 5) | 2.407 | 2.846 | 4.670 | 4.270 | |
| (15, 7) | 2.867 | 3.066 | 6.950 | 5.846 | |
| (45, 30) | (5, 2) | 2.037 | 2.189 | 2.354 | 1.921 |
| (10, 5) | 3.925 | 4.011 | 4.291 | 4.014 | |
| (15, 7) | 4.254 | 5.005 | 6.294 | 5.915 | |
| (45, 35) | (5, 2) | 2.055 | 2.310 | 2.356 | 2.421 |
| (10, 5) | 3.254 | 3.709 | 4.284 | 4.270 | |
| (15, 7) | 4.807 | 5.020 | 6.274 | 5.946 | |
| (45, 40) | (5, 2) | 2.072 | 2.149 | 2.358 | 2.899 |
| (10, 5) | 3.283 | 3.221 | 4.277 | 5.071 | |
| (15, 7) | 4.362 | 4.150 | 6.952 | 8.010 | |
На рис. 4 приводятся графики, которые показывают поведение характеристик этой модели при изменении значений порогового параметра r; при этом сравниваются характеристики системы при использовании детерминированных и рандомизированных скачкообразных приоритетов. Нагрузочные параметры системы выбираются, как и для модели с раздельными очередями, а размер общего буфера K = 10.
Рис. 4.
Зависимости характеристик системы от параметра $r$ в модели с общей очередью: $P{{B}_{H}}$ (а), $P{{B}_{L}}$ (б), $R{{J}_{{LH}}}$ (в), ${{N}_{H}}$ (г), ${{N}_{L}}$ (д)
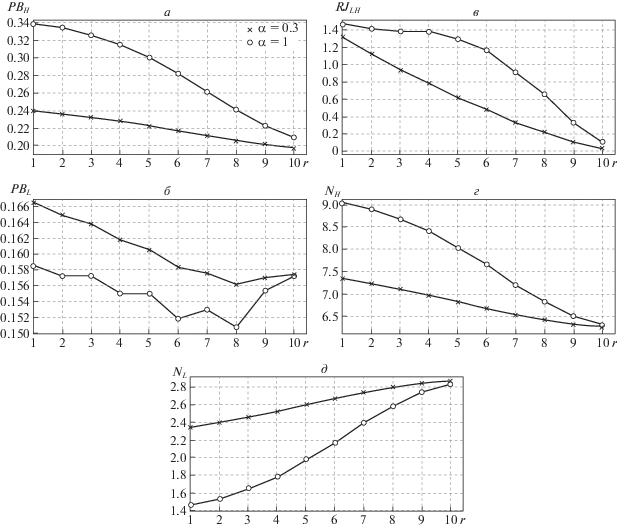
Прежде всего, отметим, что в отличие от модели с раздельными буферами здесь заранее невозможно гарантировать вид поведения некоторых характеристик системы, так как они существенным образом зависят от конкретных значений нагрузочных парметров системы. Потому приведенный далее анализ базируется исключительно на выбранных исходных данных.
Из рис. 4, а видно, как и в случае модели с раздельными очередями (см. рис. 3, а), что при использовании обоих типов JP функция $P{{B}_{H}}$ является убывающей функцией. При использовании детерминированных JP вероятность потери H-запросов больше, чем при использовании рандомизированных JP. Несмотря на то, что в данной модели размер общего буфера (K = 10) в 2 раза меньше, чем суммарный размер общего буфера в модели с раздельными буферами (${{K}_{H}} = {{K}_{L}}$ = 10), здесь при использовании обоих типов JP вероятности потери H-запросов оказываются меньше, чем в модели с раздельными буферами (см. также рис. 3, а). Вместе с тем здесь, как и в случае модели с раздельными буферами, при использовании детерминированных JP вероятность потери H-запросов больше, чем при использовании рандомизированных JP.
В отличие от модели с раздельными буферами (см. рис. 3, б) функция $P{{B}_{L}}$ здесь не является возрастающей функцией, одновременно она и не является убывающей (см. рис. 4, б). Это объясняется тем, что с ростом параметра r L-запросы реже меняют свой тип, и тем самым загрузка F-сервера уменьшается, следовательно, уменьшается и тотальная загрузка общего буфера, т.е. уменьшается и вероятность потери L-запросов. Вместе с тем с ростом параметра $r$ эти запросы больше загружают свой медленный S-сервер, т.е. следует ожидать, что при определенных значениях нагрузочных параметров разнотипных запросов загрузка общего буфера будет возрастать, что является причиной увеличения вероятности потери L-запросов. Здесь, как и в случае модели с раздельными буферами, при использовании рандомизированных JP вероятность потери L-запросов больше, чем при использовании детерминированных JP. Однако абсолютные значения вероятности потери L-запросов при использовании JP различного типа отличаются друг от друга лишь в третьем знаке после десятичной точки.
Функция $R{{J}_{{LH}}}$ в этой модели также является убывающей (см. рис. 4, в), при этом, как и следовало ожидать, значения этой функции при использовании детерминированных JP больше, чем при использовании рандомизированных JP. Следует также отметить, что абсолютные значения этой функции в несколько раз меньше, чем в модели с раздельными очередями (см. также рис. 3, в).
Функция NH, как и в модели с раздельными очередями, является убывающей (см. рис. 4, г), при этом, как и при использовании детерминированных JP, значения этой функции больше, чем при использовании рандомизированных JP. Интересным является факт о том, что в обеих моделях абсолютные значения этой функции при использовании JP обоих типов близки друг другу (см. рис. 3, г).
Неожиданным оказывается поведение функции NL, так как вопреки ожиданиям с ростом параметра r она хоть с очень малой скоростью, но растет (рис. 4, д), т.е. разница между максимальным и минимальным значениями этой функции составляет меньше 0.5. Это объясняется тем, что с ростом параметра r эти запросы больше загружают свой медленный S-сервер, и именно за счет этого имеется такая малая разница. Вместе с тем, как и следовало ожидать, значения этой функции при использовании детерминированных JP меньше, чем при использовании рандомизированных JP. Следует также отметить, что абсолютные значения этой функции почти 2 раза меньше, чем в модели с раздельными очередями.
Интересно отметить, что в моделях обеих типов с ростом параметра r значения всех функций при использовании JP обоих типов очень близки и при $r = {{K}_{L}}$ их разница имеет минимальное значение (см. рис. 3 и 4). Это объясняется тем, что с ростом параметра r число состояний, при котором происходят переходы из L-буфера в H-буфер, уменьшается, и поэтому выбор схемы определения JP мало влияет на характеристики системы.
В конце данного раздела рассмотрим третью цель проводимых численных экспериментов, а именно рассмотрим задачи минимизации суммарных штрафов (Total Cost, TC), связанных с функционированием системы для обеих моделей; при этом для краткости изложения, а также с учетом возможности их практической реализации здесь рассматриваются лишь системы с рандомизированными скачкообразными приоритетами.
Предположим, что размер буфера (а для модели с раздельными очередями – размеры буферов), а также нагрузочные параметры системы являются фиксированными величинами и единственный параметр оптимизации – пороговый параметр $r$.
В стационарном режиме суммарные штрафы определяются как
(4.3)
$TC\left( r \right) = {{c}_{{JP}}}RJ\left( r \right) + {{\lambda }_{H}}{{c}_{{LH}}}P{{B}_{H}}\left( r \right) + {{\lambda }_{L}}{{c}_{{LL}}}P{{B}_{L}}\left( r \right) + {{c}_{{WH}}}{{N}_{H}}\left( r \right) + {{c}_{{WL}}}{{N}_{L}}\left( r \right),$Тогда задача оптимизации формально записывается в виде
При любых значениях входных параметров задача (4.4) имеет решение, так как множество возможных (допустимых) решений является дискретным и конечным.
В табл. 7 приводятся результаты решения задачи (4.4) для моделей обеих типов со следующими исходными данными: ${{\lambda }_{H}} = 25$, ${{\lambda }_{L}} = 35$, ${{\mu }_{H}} = 30$, ${{\mu }_{L}} = 20$, $\alpha = 0.7.$
Таблица 7.
Результаты решения задачи (4.4); TC* – минимальное значение целевой функции (4.3)
| Система с раздельными очередями | Система с общей очередью | ||||
|---|---|---|---|---|---|
| (KH, KL) | r* | TC* | K | r* | TC* |
| (10, 10) | 9 | 11.172 | 5 | 4 | 27.791 |
| (10, 15) | 12 | 9.631 | 10 | 9 | 18.030 |
| (10, 20) | 17 | 9.288 | 15 | 14 | 13.941 |
| (15, 10) | 9 | 12.947 | 20 | 19 | 11.999 |
| (15, 15) | 13 | 8.948 | 25 | 24 | 11.032 |
| (15, 20) | 17 | 8.432 | 30 | 29 | 10.571 |
| (20, 10) | 9 | 25.987 | 35 | 34 | 10.399 |
| (20, 15) | 14 | 9.439 | 40 | 39 | 10.404 |
| (20, 20) | 18 | 8.297 | 45 | 44 | 10.525 |
Коэффициенты в выражении функционала (4.3) выбирались как
Результаты решения задачи (4.4) показаны в табл. 3. Их анализ позволяет сделать следующие выводы:
в модели системы с раздельными очередями при фиксированных значениях размера буфера для H-запросов рост размера буфера для L-запросов ведет к увеличению оптимального решения задачи (4.4), при этом уменьшается минимальное значение целевой функции (4.3);
в модели системы с общей очередью рост размера буфера ведет к увеличению оптимального решения задачи (4.4), при этом минимальное значение целевой функции (4.3) также уменьшается;
для обоих типов моделей оптимальное значение параметра $r{\text{*}}$ близко к его максимально возможному значению.
Заключение. Предложены марковские модели систем с гетерогенными серверами и разнотипными запросами, при этом рассмотрены случаи раздельной и общей очередей. Вводятся новые схемы определения рандомизированных и детерминированных скачкообразных приоритетов, которые зависят от разности количества разнотипных запросов в системе.
Разработаны методы определения стационарных вероятностей состояний моделей обоих типов и предложены формулы расчета их характеристик. Сравнение характеристик системы при различных схемах организации очереди и определения скачкообразных приоритетов выполняется с помощью численных экспериментов. Согласно результатам, поведение характеристик системы с раздельными очередями при использовании JP обоих типов в основном являются предсказуемым. Однако в модели с общей очередью поведение характеристик системы существенным образом зависит от значений нагрузочных параметров системы. Показано, что с помощью введения скачкообразных приоритетов удается оптимизировать работы систем обоих типов, при этом в качестве целевой функции выбираются суммарные штрафы.
В данной работе для простоты изложения рассмотрено наличие лишь одного сервера каждого типа. Вместе с тем предложенный подход позволяет исследовать системы с произвольным числом серверов каждого типа. Кроме того, здесь также для простоты изложения при определении рандомизированных скачкообразных приоритетов считается, что вероятность скачка из L-буфера в H-буфер является постоянной величиной. С использованием предложенного подхода можно рассматривать случаи, когда эта вероятность зависит от разности количества разнотипных запросов, т.е. можно исследовать случаи, когда с ростом разницы количества разнотипных запросов указанная вероятность также увеличивается, например $\alpha \left( {{{n}_{L}} - {{n}_{H}}} \right) = {{\left( {{{n}_{L}} - {{n}_{H}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{n}_{L}} - {{n}_{H}}} \right)} {\left( {{{n}_{L}} - {{n}_{H}} + 1} \right)}}} \right. \kern-0em} {\left( {{{n}_{L}} - {{n}_{H}} + 1} \right)}}$. Эти задачи могут быть предметами специальных исследований.
Список литературы
Gumbel H. Waiting Lines with Heterogeneous Servers // Operations Research. 1960. V. 8. Iss. 4. P. 504–511.
Singh V.S. Two-Server Markovian Queues with Balking: Heterogeneous vs Homogeneous Servers // Operations Research. 1970. V. 18. P. 145–159.
Singh V.S. Markovian Queues with Three Servers // IIE Transactions. 1971. V. 3. P. 45–48.
Fakinos D. The M/G/k Blocking System with Heterogeneous Servers // J. Operations Research Society. 1980. V. 31. P. 919–927.
Fakinos D. The Generalized M/G/k Blocking System with Heterogeneous Servers // J. Operations Research Society. 1982. V. 33. P. 801–809.
Nath G., Enns E. Optimal Service Rates in the Multiserver Loss System with Heterogeneous Servers // J. Applied Probability. 1981. V. 18. P. 776–781.
Alpaslan F., Shahbazov A. An Analysis and Optimization of Stochastic Service with Heterogeneous Channels and Poisson Arrivals // Pure and Apllied Mathematika Science. 1996. V. 43. P. 15–20.
Lin B.W., Elsayed E.A. A General Solution for Multichannel Queuing Systems with Ordered Entry // Computers & Operations Research. 1978. V. 5. P. 219–225.
Elsayed E.A. Multichannel Queuing Systems with Ordered Entry and Finite Source // Computers & Operations Research. 1983. V. 10. P. 213–222.
Yao D.D. The Arrangement of Servers in an Ordered Entry System // Operations Research. 1987. V. 35. P. 759–763.
Pourbabai B., Sonderman D. Server Utilization Factors in Queuing Loss Systems with Ordered Entry and Heterogeneous Servers // J. Applied Probability. 1986. V. 23. P. 236–242.
Pourbabai B. Markovian Queuing Systems with Retrials and Heterogeneous Servers // Computational Mathematics Applications. 1987. V. 13. Iss. 12. P. 917–923.
Nawijn W.M. On a Two-Server Finite Queuing System with Ordered Entry and Deterministic Arrivals // Europ. J. Operations Research. 1984. V. 18. P. 388–395.
Nawijn W.M. A Note on Many-Server Queuing Systems with Ordered Entry with an Application to Conveyor Theory // J. Applied Probability. 1983. V. 20. P. 144–152.
Yao D.D. Convexity Properties of the Overflow in an Ordered Entry System with Heterogeneous Servers // Operations Research Letters. 1986. V. 5. P. 145–147.
Isguder H.O., Kocer U.U. Analysis of GI/M/n/n Queuing System with Ordered Entry and no waiting line // Applied Mathematical Modelling. 2014. V. 38. P. 1024–1032.
Kumar B.K., Madheswari S.P., Venkatakrishnan K.S. Transient Solution of an M/M/2 Queue with Heterogeneous Servers Subject to Catastrophes // Intern. J. Information Management Science. 2007. V. 18. P. 63–80.
Dharmaraja S., Kumar R. Transient Solution of a Markovian Queuing Models with Heterogeneous Servers and Catastrophes // OPSEARCH. 2015. V. 52. Iss. 4. P. 810–8217.
Ammar S.I. Transient Behavior of a Two-Processor Heterogeneous Systems with Catastrophes, Server Failures and Repairs // Applied Mathematical Modelling. 2014. V. 38. P. 2224–2234.
Kumar B.K., Arivudainambi D. Transient Solution of an M/M/c Queue with Heterogeneous Servers and Balking // Information and Management Science. 2001. V. 12. Iss. 3. P. 15–27.
Selvamuthu D. Transient Solution of a Two-Processor Heterogeneous Systems // Mathematical and Computer Modeling. 2000. V. 32. Iss. 10. P. 1117–1123.
Krishnamoorthy A., Sreenivasan C. An M/M/2 Queuing Systems with Heterogeneous Servers Including One with Working Vacation // Intern. J. Stochastic Analysis. V. 2012. Article ID 145867.
Sridhar A., Pitchai R.A. Analysis of a Markovian Queue with Two Heterogeneous Servers and Working Vacation // Intern. J. Applied Operational Research. 2015. V. 5. Iss. 4. P. 1–15.
Xu J., Liu L., Zhu T. Transient Analysis of Two-Heterogeneous Server Queue with Impatient Behavior and Multiple Vacations // J. Systems Science and Information. 2018. V. 6. Iss. 1. P. 69–84.
Yue D., Yu J., Yue W. A Markovian Queue with Two-Heterogeneous Servers and Multiple Vacations // J. Industrial and Management Optimization. 2009. V. 5. Iss. 3. P. 453–465.
Bakmaz B., Bojkovic Z., Bakmaz M. Queuing Loss Models with More Alternative Heterogeneous Groups // Intern. J. of Communication Systems. 2018. V. 31. Iss. 6. P. 1724–1735.
Chow Y.C., Kohler W.H. Models for Dynamic Load Balancing in a Heterogeneous Multiple Processor System // IEEE Transactions on Computers. 1979. V. 28. Iss. 5. P. 354–361.
Armony M. Dynamic Routing in Large-Scale Service Systems with Heterogeneous Servers // Queuing Systems. 2005. V. 51. P. 287–329.
Armony M., Ward A.R. Fair Dynamic Routing in Large-Scale Heterogeneous Servers Systems // Operations Research. 2010. V. 58. Iss. 3. P. 624–637.
Neuts M.F., Takahashi Y. Asymptotic Behavior of the Stationary Distributions in the GI/PH/c Queues with Heterogeneous Servers // Applied Mathematics Institute Technical Report. University of Delaware. Neware. 1980. 57B. 30 p.
Legros B., Jouini O. Routing in a Queuing System with Two Heterogeneous Servers in Speed and in Quality of Resolution // Stochastic Models. 2017. V. 33. Iss. 3. P. 392–410.
Isguder H.O., Kocer U.U. Analysis of K-Capacity Queuing System with Two Heterogeneous Server // Lecture Notes in Computer Science. 2017. V. 10684. P. 23–30.
Saglam V., Shahbazov A. Minimizing of Loss Probabilty in Queuing Systems with Heterogeneous Servers // Iranian J. Science and Technology Transactions. Seria A. 2007. V. 31. P. 199–206.
Bouchentouf A.A., Messabihi A. A Heterogeneous Two-Server Queuing System with Reneging and No Waiting Line // ProbStat Forum. 2018. V. 11. P. 67–76.
Efrosinin D. Controlled Queuing Systems with Heterogeneous Servers. Saarbrucken: VDM Verlag, 2008. 236 p.
Малашенко Ю.Е., Назарова И.А. Нормативный динамический анализ предельных режимов функционирования гетерогенной вычислительной системы // Изв. РАН. ТиСУ. 2015. № 5. С. 73–89.
Малашенко Ю.Е., Назарова И.А. Модель управления поэтапной модернизацией гетерогенной вычислительной системы // Изв. РАН. ТиСУ. 2016. № 6. С. 50–60.
Maertens T., Walraevens J., Bruneel H. On Priority Queues with Priority Jumps // Performance Evaluation. 2006. V. 63. Iss. 12. P. 1235–1252.
Maertens T., Walraevens J., Bruneel H. A Modified HOL Priority Scheduling Discipline: Performance Analysis // Europ. J. Operations Research. 2007. V. 180. Iss. 3. P. 1168–1185.
Maertens T., Walraevens J., Bruneel H. Performance Comparison of Several Priority Schemes with Priority Jumps // Annals of Operations Research. 2008. V. 162. P. 109–125.
Меликов А.З., Пономаренко Л.А., Ким Ч.С. Приближенный метод анализа моделей систем массового обслуживания со скачкообразными приоритетами // АиТ. 2013. Т. 74. № 1. С. 79–97.
Melikov A.Z., Rustamov A.M., Sztrik J., Jafarzade T.I. Methods to Analysis of Queueing Models with State-Dependent Jump Priorities // Annales Mathematicae et Informaticae. 2016. V. 46. P. 143–163.
Neuts M.F. Matrix-geometric Solutions in Stochastic Models: An Algorithmic Approach. Baltimore: John Hopkins University Press, 1981. 332 p.
Mitrani I., Chakka R. Spectral Expansion Solution for a Class of Markov Models: Application and Comparison with the Matrix-geometric Method // Performance Evaluation. 1995. V. 23. P. 241–260.
Chakka R. Spectral Expansion Solution for Some Finite Capacity Queues // Annals of Operations Research. 1998. V. 79. P. 27–44.
Меликов А.З., Шахмалыев М.О. Марковские модели систем управления запасами с положительным временем обслуживания заявок // Изв. РАН. ТиСУ. 2018. № 5. С. 107–127.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


