Известия РАН. Теория и системы управления, 2019, № 6, стр. 26-42

Введение. Известно, что среди методов пассивной локации [1–33 ] наиболее популярным считается триангуляционный метод, поскольку является достаточно простым в плане практической реализации и эффективным с технико-экономической точки зрения. Основу процедур оптимального и квазиоптимального оценивания параметров движения цели применительно к триангуляционной измерительной системе (ТИС) составляют классические статистические методы [1–5, 12–27]: метод максимального правдоподобия (ММП – простой, РММП – расширенный), метод наименьших квадратов (МНК), а также методы, базирующиеся на теории фильтрации Калмана. Известно [24], что при выполнении ряда ограничений на условия пеленгования цели данные методы реализуют свои потенциальные возможности и вполне приемлемы для решения целевых задач, возлагаемых на ТИС. Такие условия функционирования ТИС, при которых целесообразно применять классические статистические методы, можно назвать нормальными.

Ситуация кардинально меняется для некорректных условий наблюдения, при которых результаты измерений отдельных пеленгаторов могут допускать наличие не только ожидаемых случайных погрешностей, но и неопределенных аномальных ошибок измерений (АОИ), т.е. речь идет о появлении недостоверных измерительных каналов как по азимуту, так и по углу места. Для борьбы с такими ошибками могут эффективно использоваться известные аналитические методы (оптимальные, квазиоптимальные и эмпирические) и математический инструментарий, которые оперируют с такими понятиями, как плотность вероятности, функция и отношение правдоподобия, функции принадлежности и влияния, нечеткое множество, расширенное пространство состояний, гипотеза, риск, множество допустимости, доверительное, гарантированное, квазиправдоподобное и робастное оценивание, факторный анализ, линейное, нелинейное и стохастическое программирование, невязка, порог, расстояние, инвариант, центр и линия “тяжести” и др. (см., например, [34–42]). Многообразие аналитических методов соответствует такой неопределенности, которую можно описать для всех измерительных каналов ТИС (с помощью тех или иных моделей – от простых до сложных) и в итоге получить единственное решение задачи оценивания параметров местоположения и движения цели без участия оператора. Данную неопределенность назовем корректной, для ее описания можно воспользоваться известными подходами задания компактных множеств допустимости (например, эллипсоидального [38]).

Однако ТИС зачастую функционируют при некорректных условиях наблюдения, когда отсутствие необходимых исходных данных не позволяет аналитически описать возможную неопределенность, либо сформированное множество допустимости имеет настолько сложный вид и большие размеры, что у него нет никакой практической ценности [17, 18, 21]. Данную неопределенность будем называть некорректной. Для ТИС факторами такой неопределенности выступают: отсутствие прямой видимости цели; явления рефракции, интерференции и многолучевости; эффект Доплера; влияние естественных и искусственных помех; инструментальные и методические ошибки; сбои и отказ аппаратуры; деградация структуры ТИС и др. [17, 18, 21]. Попытка обнаружения недостоверных каналов (с последующей компенсацией АОИ) в рамках ряда аналитических методов оценивания (например, на основе РММП и метода инвариантов) приводит на практике к хорошо известному эффекту “размазывания” точности, неустойчивости применяемых вычислительных процедур, необходимости указания номеров недостоверных каналов и выбора достаточно хорошего начального условия для “запуска” соответствующего итерационного алгоритма. Указанный эффект наиболее выражен для задачи триангуляции, характеризующейся в ряде случаев плохой наблюдаемостью (например, при попадании излучающей цели в триангуляционно-некорректную область [18]).

Все многообразие эмпирических методов борьбы с АОИ основано на построении нескольких вариантов объединения линий визирования от различных пеленгаторов, выявлении и отбраковке недостоверных вариантов (с использованием некоторого заранее назначаемого порога) и построении результирующей оценки местоположения цели в соответствии с одним из критериев (например, минимума расстояния между этими линиями и минимума дисперсии их разброса [12], минимума объема параллелепипеда [13], минимума невязки между значениями инвариантов [17–19]). К недостаткам этих методов можно отнести то, что они не позволяют в полном объеме реализовать идею максимально возможного “размножения” единичных отметок (с учетом всех возможных вариантов разбиения линий и поверхностей положения, отвечающих измеренным углам места и азимута), не учитывают топологических особенностей расположения этих отметок в пространстве при различных ракурсах и дальностях наблюдения цели, а также не используют навыки опытного оператора. Кроме того, проблемным является выбор оптимального порога в эмпирических методах.

В работах [21, 25–27] впервые предложен альтернативный интеллектуально-аналитический метод триангуляционного оценивания параметров движения цели, ориентированный на идею максимально возможного “размножения” первичных отметок (оценок местоположения цели в пространстве) и возможное участие опытного оператора, который базируется на принципах мультиструктурности и кластеризации для учета указанных топологических особенностей. Метод учитывает такую некорректную неопределенность, когда нельзя дать адекватное количественное описание условий функционирования измерительных каналов ТИС, поскольку априорно не известны ни номера недостоверных каналов, ни их общее количество. С помощью опытного оператора, исходя из реальной радиоэлектронной обстановки, можно лишь указать максимально возможное число недостоверных каналов и количество приоритетных кластеров, отметки которых могут быть связаны с истинной отметкой цели. При этом для учета топологических особенностей распределения отметок в пространстве привлекается математический аппарат кластерного анализа [43–45].

В настоящей работе для случая некорректной неопределенности развивается интеллектуально-аналитический мультиструктурный метод триангуляционного оценивания (ММТО) параметров движения излучающей цели, основанный на теории фильтрации Калмана, а также указанных выше принципах мультиструктурности и кластеризации, который позволяет обнаруживать недостоверные измерительные каналы (как по азимуту, так и по углу места). В отличие от указанных выше работ [21, 25–27], в которых рассматривались либо стационарные цели, либо цели с невозмущенным полиномиальным движением, ниже описывается общий стохастический случай. Принципиально новым является возможность участия опытного оператора в схеме оценивания на основе ММТО. В качестве исходных данных фигурируют лишь допуски на погрешности пеленгования в нормальных условиях и ограничение на максимально возможное число недостоверных каналов в некорректных условиях наблюдения.

1. Модели, ограничения, постановка задачи. Для описания движения цели будем использовать общую правую декартовую прямоугольную систему координат $Oxyz$ и дискретное время t_k (где $k = 0,1,2,\; \ldots $), а также вектор состояния ${{{\mathbf{X}}}_{k}} = {{\left[ {{\mathbf{\Lambda }}_{k}^{{\text{T}}},{\mathbf{V}}_{k}^{{\text{T}}},{\mathbf{W}}_{k}^{{\text{T}}},{\mathbf{P}}_{k}^{{\text{T}}}} \right]}^{{\text{T}}}}$, где ${{{\mathbf{\Lambda }}}_{k}} = {{\left[ {{{x}_{k}},{{y}_{k}},{{z}_{k}}} \right]}^{{\text{T}}}}$ – вектор местоположения цели, ${{{\mathbf{V}}}_{k}} = {{\left[ {{v}_{k}^{x},{v}_{k}^{y},{v}_{k}^{z}} \right]}^{{\text{T}}}}$ – вектор ее скорости, ${{{\mathbf{W}}}_{k}} = {{\left[ {w_{k}^{x},w_{k}^{y},w_{k}^{z}} \right]}^{{\text{T}}}}$ – вектор ее ускорения, ${\mathbf{P}}_{k}^{{\text{T}}}$ – вектор вспомогательных параметров, используемых для расширения пространства состояний. Как правило, начало системы координат $Oxyz$ связано с геометрическим центром одного из пеленгаторов, входящих в состав ТИС, а ее оси направлены так: ось Ox – на север, ось Oy – на восток, ось Oz – дополняет оси Ox и Oy до правой системы координат.

Полагаем, что изменение во времени вектора состояния описывается заданным векторным нелинейным уравнением

где ${\mathbf{F}}\left( {{{{\mathbf{X}}}_{k}},k} \right)$ – функция, дифференцируемая по аргументу ${{{\mathbf{X}}}_{k}}$, ${{{\mathbf{\Xi }}}_{k}}$ – дискретный формирующий белый шум с заданными статистическими характеристиками: ${\text{M}}\left\{ {{{{\mathbf{\Xi }}}_{k}}} \right\} = {\mathbf{0}},$ ${\text{M}}\left\{ {{{{\mathbf{\Xi }}}_{k}}{\mathbf{\Xi }}_{i}^{{\text{T}}}} \right\} = {\mathbf{K}}_{k}^{{\mathbf{\Xi }}}{{\delta }_{{ki}}}$ (здесь ${\text{M}}\left\{ \cdot \right\}$ – символ математического ожидания, ${{\delta }_{{ki}}}$ – символ Кронекера, ${\mathbf{K}}_{k}^{{\mathbf{\Xi }}}$ – корреляционная матрица шума ${{{\mathbf{\Xi }}}_{k}}$ для момента времени t_k).

Рассмотрим ТИС, состоящую из M пеленгаторов $\left\{ {{{{\text{П}}}_{m}}} \right\}_{{m = 1}}^{M}$. Для каждого из них используется местная радиотехническая система координат $({{\alpha }_{m}},{{\beta }_{m}},R{}_{m})$, где ${{\alpha }_{m}}$ – азимут, ${{\beta }_{m}}$ – угол места, R_m – наклонная дальность до цели. Начало этой системы координат связано с геометрическим центром Π_m, азимут ${{\alpha }_{m}} \in \left[ {0,2\pi } \right]$ отсчитывается в плоскости xOy от положительного направления оси Ox против часовой стрелки, а угол места ${{\beta }_{m}} \in \left[ { - \pi ,\pi } \right]$ – отсчитывается от плоскости xOy, при этом ${{\beta }_{m}} \geqslant 0$ для любой цели, находящейся не ниже плоскости xOy, в противном случае ${{\beta }_{m}} < 0$.

Вектор измерений ТИС для дискретного времени t_k, $k \in \left\{ {0,1,2,\; \ldots } \right\}$, будем представлять в виде ${{{\mathbf{H}}}_{k}} = {{[(h_{{mk}}^{\alpha },h_{{mk}}^{\beta }),m = \overline {1,M} ]}^{{\text{T}}}}$, где $h_{{mk}}^{\alpha }$ и $h_{{mk}}^{\beta }$ – соответственно измерения азимута ${{\alpha }_{{mk}}} = {{\alpha }_{m}}\left( {{{{\mathbf{X}}}_{k}},{{t}_{k}}} \right)$ и угла места ${{\beta }_{{mk}}} = {{\beta }_{m}}\left( {{{{\mathbf{X}}}_{k}},{{t}_{k}}} \right)$ цели, относящиеся к Π_m (стационарному или мобильному) и моменту времени t_k.

Для нормальных условий функционирования ТИС вектор измерений (будем называть их “незасоренными”) зададим в виде

где ${{{\mathbf{Y}}}_{k}} = {\mathbf{Y}}\left( {{{{\mathbf{X}}}_{k}},k} \right) = {{[({{\alpha }_{{mk}}},{{\beta }_{{mk}}}),m = \overline {1,M} ]}^{{\text{T}}}}$ – вектор измеряемых параметров ${{\alpha }_{{mk}}} = \alpha {}_{m}\left( {{{{\mathbf{X}}}_{k}},{{t}_{k}}} \right)$ и ${{\beta }_{{mk}}} = \beta {}_{m}\left( {{{{\mathbf{X}}}_{k}},{{t}_{k}}} \right)$, дифференцируемых по ${{{\mathbf{X}}}_{k}}$, ${{{\mathbf{\Psi }}}_{k}} = {{[(\psi _{{mk}}^{\alpha },\psi _{{mk}}^{\beta }),m = \overline {1,M} ]}^{{\text{T}}}}$ – вектор дискретных белых шумов измерений, для которого: ${\text{M}}\left\{ {{{{\mathbf{\Psi }}}_{k}}} \right\} = {\mathbf{0}}$, ${\text{M}}\left\{ {{{{\mathbf{\Psi }}}_{k}}{\mathbf{\Psi }}_{i}^{{\text{T}}}} \right\} = {\mathbf{K}}_{k}^{{\mathbf{\Psi }}}{{\delta }_{{ki}}}$ (здесь ${\mathbf{K}}_{k}^{{\mathbf{\Psi }}}$ – корреляционная матрица шума измерений для момента времени t_k).

Далее будем полагать, что процессы ${{{\mathbf{\Xi }}}_{k}}$ и ${{{\mathbf{\Psi }}}_{k}}$ независимы, а для связи двух систем координат использовать известные формулы:

где ${{r}_{{mk}}}$ и ${{R}_{{mk}}}$ – соответственно горизонтальная и наклонная дальности до цели относительно Π_m, а $\rho _{{mk}}^{x} = \rho _{m}^{x}\left( {{{t}_{k}}} \right)$, $\rho _{{mk}}^{y} = \rho _{m}^{y}\left( {{{t}_{k}}} \right)$, $\rho _{{mk}}^{z} = \rho _{m}^{z}\left( {{{t}_{k}}} \right)$ – компоненты вектора ${{{\mathbf{\rho }}}_{{mk}}} = {{{\mathbf{\rho }}}_{m}}\left( {t{}_{k}} \right)$, характеризующего местоположение Π_m в момент t_k относительно начала общей системы координат $Oxyz$.

На возможные положения цели накладываются ограничения типа

где ${{\mathfrak{M}}_{R}} = \left[ {{{R}_{{\min }}},{{R}_{{\max }}}} \right]$,${{\mathfrak{M}}_{\alpha }} = \left[ {{{\alpha }_{{\min }}},{{\alpha }_{{\max }}}} \right]$ и ${{\mathfrak{M}}_{\beta }} = \left[ {{{\beta }_{{\min }}},{{\beta }_{{\max }}}} \right]$ – диапазоны возможного изменения величин R, $\alpha $ и $\beta $ (для единой системы координат, в которой рассматривается ТИС и цель).

Используя информацию о матрице ${\mathbf{K}}_{k}^{{\mathbf{\Xi }}}$, для нормальных условий функционирования ТИС (когда в каналах азимута и угла места всех пеленгаторов допускаются лишь флуктуационные ошибки) с заданной вероятностью можно обеспечить выполнение неравенств:

где $\varepsilon _{k}^{\alpha }$ и $\varepsilon _{k}^{\beta }$ – рассчитываемые по известным правилам пороговые значения. В частных случаях можно принять $\varepsilon _{k}^{\alpha } = {{\varepsilon }^{\alpha }}$ и $\varepsilon _{k}^{\beta } = {{\varepsilon }^{\beta }}$ или $\varepsilon _{k}^{\alpha } = \varepsilon _{k}^{\beta } = \varepsilon $. Для некорректных условий наблюдения, о которых говорилось во Введении, указанные неравенства по некоторым координатам вектора ${{{\mathbf{\Psi }}}_{k}}$ не выполняются, т.е. речь идет о неопределенных АОИ. Полагается, что нам неизвестны номера этих координат и величины соответствующих им АОИ. Все АОИ можно разделить на классы: постоянные (например, систематические), медленно- и быстроменяющиеся, а также произвольные. Данные ошибки мы не относим к случайным, и, следовательно, для их описания не применимы традиционные характеристики, используемые в теории вероятностей и случайных процессов. Полагаем, что строгие математические модели для АОИ нам не известны.

Каждому ${{{\text{П}}}_{m}}$ ставится в соответствие два измерительных канала: ${\text{K}}_{m}^{\alpha }$ – азимутальный и ${\text{K}}_{m}^{\beta }$ – угломестный. Если в момент t_k канал не содержит АОИ, то такой канал будем называть достоверным для данного момента времени и данного пеленгатора, в противном случае – недостоверным. Применительно к ТИС рассматривается множество каналов ${\mathbf{K}} = {{{\mathbf{K}}}^{\alpha }} \cup {{{\mathbf{K}}}^{\beta }},$ где K^α = = $\{ {\text{K}}_{m}^{\alpha }{\text{,}}m = \overline {1,M} \} $ и ${{{\mathbf{K}}}^{\beta }} = \left\{ {{\text{K}}_{m}^{\beta },\;m = \overline {1,M} } \right\}$. С каждым Π_m для фиксированного k можно связать две “возмущенные” поверхности положения цели, описываемые уравнениями

В (1.4) первое уравнение, соответствующее измерению $h_{{mk}}^{\alpha }$, описывает “возмущенную” плоскость, а второе уравнение, соответствующее $h_{{mk}}^{\beta }$, – “возмущенный” круговой конус. Очевидно, что “невозмущенные” поверхности положения цели получаем, когда $\psi _{{mk}}^{\alpha } = 0$ и $\psi _{{mk}}^{\beta } = 0$ соответственно. Для ТИС с числом пеленгаторов три и более проявляется так называемый геометрический фактор – образуется избыточное число поверхностей положения, на базе которых можно строить альтернативные измерительные структуры (ИС) и применять принцип “размножения” первичных отметок, соответствующих этим ИС [21, 25, 26].

С учетом (1.1) и (1.2) для нормальных условий функционирования ТИС решение задачи оценивания параметров движения излучающей цели можно осуществить на базе обобщенного фильтра Калмана (ОФК) [46, 47]:

где ${{{\mathbf{A}}}_{{k + 1}}} = {\mathbf{A}}({\mathbf{X}}_{{_{{k + 1/k}}}}^{ * }) = {{\left. {\partial {\mathbf{Y}}\left( {{\mathbf{x}},k} \right){\text{/}}\partial {\mathbf{x}}} \right|}_{{{\mathbf{x}} = {\mathbf{X}}_{{_{{k + 1/k}}}}^{ * }}}}$ – матрица частных производных от ${\mathbf{Y}}\left( {{\mathbf{x}},k} \right)$ по ${\mathbf{x}}$, вычисленных в точке ${\mathbf{x}} = {\mathbf{X}}_{{_{{k + 1/k}}}}^{ * }$, ${{{\mathbf{G}}}_{{k + 1}}} = {\mathbf{G}}({\mathbf{X}}_{{_{{k/k + 1}}}}^{ * })$ – коэффициент усиления фильтра.

Предположим теперь, что наблюдения ТИС являются “засоренным”, т.е. вектор H_k = ${{{\mathbf{Y}}}_{k}} + {{{\mathbf{\Psi }}}_{k}}$ может содержать координаты с АОИ, относительно которых отсутствует какая-либо априорная информация. Будем полагать, что число измерительных каналов, не содержащих АОИ, должно быть не менее D^αβ, при этом

Такое ограничение является вполне естественным, поскольку только в этом случае можно говорить о нахождении недостоверных каналов и построении надежной оценки параметров движения цели (по аналогии с помехоустойчивым кодированием, когда речь идет об обнаружении и исправлении искаженных символов принятой кодограммы).

Ранее было показано [24–27], что попытка реализации известных алгоритмов триангуляционного оценивания на “засоренных” данных приводит, как правило, к отрицательному результату. Если известны номера недостоверных каналов из множества ${\mathbf{K}} = {{{\mathbf{K}}}^{\alpha }} \cup {{{\mathbf{K}}}^{\beta }}$ для каждого фиксированного момента времени t_k, $k \in \left\{ {0,1,2,\; \ldots } \right\}$, то для решения задачи оценивания параметров движения цели в аномальных условиях можно воспользоваться известным принципом расширения пространства состояний. Для этого в вектор ${{{\mathbf{P}}}_{k}}$ вводятся координаты, соответствующие неизвестным АОИ этих каналов. Очевидно, что для большинства ТИС, фигурирующих в условиях некорректной неопределенности, такой подход, как правило, не применим, поскольку априорно информацией о недостоверных каналах мы зачастую не располагаем. Кроме того, расширение пространства состояний приводит к известному эффекту “размазывания точности” и росту вычислительных затрат.

Требуется с учетом (1.1)–(1.6) разработать ММТО, который в некорректных условиях функционирования ТИС (с учетом принятых моделей и ограничений) обеспечивал бы построение удовлетворительной по точности оценки параметров движения излучающей цели без традиционного расширения пространства состояний, а в нормальных условиях приближался бы по своим характеристикам к классическим аналитическим методам. Необходимо на модельных примерах показать возможности ММТО в задаче оценивания местоположения цели для фиксированного момента времени (статический случай) и в задаче фильтрации параметров движения цели по выборке измерений нарастающего объема (динамической случай). В основу метода необходимо положить указанные выше принципы мультиструктурности и кластеризации первичных отметок, формируемых на основе ИС.

2. Формирование рабочих измерительных структур и соответствующих им отметок. Поскольку в разд. 2–5 все рассуждения относятся к фиксированному моменту времени ${{t}_{k}}$, $k \in \{ 0,1,2, \ldots \} $, то в этих разделах (с целью сокращения записей) индекс $k$ будет опущен.

По аналогии с [27] сформируем семейство измерительных структур $\{ {{\overline {{\text{ИС}}} }_{1}},{{\overline {{\text{ИС}}} }_{2}},\; \ldots ,\;{{\overline {{\text{ИС}}} }_{{\overline N }}}\} $ как наблюдаемых, так и ненаблюдаемых. Под ${{\overline {{\text{ИС}}} }_{n}}$ (где $n \in \{ \overline {1,\bar {N}} \} $) понимается произвольный набор измерительных каналов из ${\mathbf{K}} = {{{\mathbf{K}}}^{\alpha }} \cup {{{\mathbf{K}}}^{\beta }}$, при этом ${{\overline {{\text{ИС}}} }_{n}}$ и ${{\overline {{\text{ИС}}} }_{m}}$ не совпадают для всех $n,m \in \{ \overline {1,\bar {N}} \} $, $n \ne m$. Для выделения из множества $\{ {{\overline {{\text{ИС}}} }_{1}},{{\overline {{\text{ИС}}} }_{2}},\; \ldots ,\;{{\overline {{\text{ИС}}} }_{{\overline N }}}\} $ только наблюдаемых измерительных структур зададимся парой чисел $({{\gamma }_{\alpha }},{{\gamma }_{\beta }})$, где γ_α и γ_β соответствуют минимально необходимому числу ${{\gamma }_{{\alpha \beta }}} = {{\gamma }_{\alpha }} + {{\gamma }_{\beta }}$ азимутальных и угломестных каналов, достаточных для наблюдаемости задачи оценивания. Будем также полагать, что число измерительных каналов, не содержащих АОИ, должно быть не менее ${{D}^{{\alpha \beta }}} = D_{s}^{\alpha } + D_{s}^{\beta }$, $s = \overline {1,S} $, $D_{s}^{\alpha },D_{s}^{\beta } \in \{ \overline {1,M} \} $, где $D_{s}^{\alpha }$, $D_{s}^{\beta }$ – составляющие числа ${{D}^{{\alpha \beta }}}$ для s-го варианта представления, обеспечивающего наблюдаемость задачи (S – общее число таких вариантов). Понятно, что для наблюдаемости задачи необходимо, чтобы $D_{s}^{\alpha } \geqslant {{\gamma }_{\alpha }}$ и $D_{s}^{\beta } \geqslant {{\gamma }_{\beta }}$.

Замечание. Общее количество наблюдаемых ИС для пары $({{\gamma }_{\alpha }},{{\gamma }_{\beta }})$ равно

Соответственно количество наблюдаемых ИС, образованных каналами без АОИ,

а минимальное их количество

Например, пусть $2M = 10$, ${{\gamma }_{\alpha }} = 2$, ${{\gamma }_{\beta }} = 1$ и ${{D}^{{\alpha \beta }}} = 6$ (т.е. шесть каналов из 10 не содержат АОИ). Тогда, с учетом (2.1)–(2.3) возможны следующие варианты $(D_{s}^{\alpha },D_{s}^{\beta })$: (2, 4), (3, 3), (4, 2) и (5, 1). При этом $N = 806$, ${{N}^{{\left( {2,4} \right)}}} = 15$, ${{N}^{{\left( {3,3} \right)}}} = 28$, ${{N}^{{\left( {4,2} \right)}}} = 33$, ${{N}^{{\left( {5,1} \right)}}} = 26$, а ${{N}^{{\left( 6 \right)}}} = {{N}^{{\left( {2,4} \right)}}}$ = 15.

Выделим из $\{ {{\overline {{\text{ИС}}} }_{1}},{{\overline {{\text{ИС}}} }_{2}},\; \ldots ,\;{{\overline {{\text{ИС}}} }_{{\overline N }}}\} $ множество наблюдаемых структур $\{ {\text{И}}{{{\text{С}}}_{1}},{\text{И}}{{{\text{С}}}_{2}},\; \ldots ,\;{\text{И}}{{{\text{С}}}_{N}}\} $, где $N < \bar {N}$. Для всех этих структур задача определения местоположения цели (без учета ошибок измерений) имеет единственное решение. Полагается, что ${\text{И}}{{{\text{С}}}_{k}}$ и ${\text{И}}{{{\text{С}}}_{l}}$ (где $k,l \in \{ \overline {1,N} \} $, $k \ne l$) не должны совпадать. Каждой сформированной ${\text{И}}{{{\text{С}}}_{n}}$ (где $n \in \{ \overline {1,N} \} $) соответствует вектор первичных измерений ${{{\mathbf{H}}}_{n}} = {{[h_{{np}}^{\alpha }{\text{,}}\;p = \overline {1,M_{n}^{\alpha }} {\text{;}}\;h_{{np}}^{\beta },\;p = \overline {1,M_{n}^{\beta }} ]}^{{\text{T}}}}$, при этом ${{L}_{n}} = M_{n}^{\alpha } + M_{n}^{\beta }$ – общее число измерений, $h_{{np}}^{\alpha } \in \left\{ {h_{1}^{\alpha },h_{2}^{\alpha },\; \ldots ,\;h_{M}^{\alpha }} \right\}$ и $h_{{np}}^{\beta } \in \left\{ {h_{1}^{\beta },h_{2}^{\beta },\; \ldots ,\;h_{M}^{\beta }} \right\}$. Для каждой ${\text{И}}{{{\text{С}}}_{n}}$ сформируем первичную отметку местоположения цели ${\mathbf{\Lambda }}_{n}^{*} = {{[x_{n}^{*},~y_{n}^{*},~z_{n}^{*}]}^{{\text{T}}}}$, например, на базе одного из квазиоптимальных методов, рассмотренных в работе [24], при этом с учетом (1.3) полагаем, что ${\mathbf{\Lambda }}_{n}^{*}$ = = ${{[R_{n}^{*},\alpha _{n}^{*},\beta _{n}^{*}]}^{{\text{T}}}} \in \mathfrak{M}$ = ${{\mathfrak{M}}_{R}} \times {{\mathfrak{M}}_{\alpha }} \times {{\mathfrak{M}}_{\beta }}$. Для фиксированной ${\text{И}}{{{\text{С}}}_{n}}$ и соответствующей ей отметки ${\mathbf{\Lambda }}_{n}^{*}$ по отношению ко всем Π_m, $m = \overline {1,M} $, строим так называемые “вторичные” пеленги $\alpha _{{mn}}^{*}$ и $\beta _{{mn}}^{*}$, для которых проверяем выполнение условий (отдельно по азимуту и углу места):

Если для всех сформированных “вторичных” пеленгов $\alpha _{{mn}}^{*}$ и $\beta _{{mn}}^{*}$ (их суммарное количество по азимуту и углу места равно 2M) выполняется менее M условий (2.4) (суммарное по азимуту и углу места), то рассматриваемая ${\text{И}}{{{\text{С}}}_{n}}$ отсеивается. Оставшиеся после отсеивания (селекции) ИС назовем рабочими измерительными структурами (РИС) , т.е. ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$, где $i = \overline {1,{{N}_{1}}} $, ${{N}_{1}} \leqslant N$, ${{n}_{i}} \in \left\{ {\overline {1,N} } \right\}$. Таким ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$ соответствуют первичные отметки ${\mathbf{\Lambda }}_{{{{n}_{i}}}}^{{ * * }} = {{[x_{{{{n}_{i}}}}^{{ * * }},~y_{{{{n}_{i}}}}^{{ * * }},~z_{{{{n}_{i}}}}^{{ * * }}]}^{{\text{T}}}}$. Следует помнить, что при формировании таких отметок наряду с нормальными могут участвовать и аномальные измерительные каналы, поскольку еще не решена задача их обнаружения. На этом заканчивается этап предварительной обработки измеренных пеленгов на базе ММТО, в результате которого отсеиваются “грубые” ИС и соответствующие им отметки. Далее рассматриваются только первичные отметки, прошедшие этап селекции и соответствующие ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$.

3. Кластеризация и вычисление параметров кластеров. Для анализа топологических особенностей полученного множества первичных отметок ${\mathbf{\Lambda }}_{{{{n}_{i}}}}^{{ * * }} = {{[x_{{{{n}_{i}}}}^{{ * * }},~y_{{{{n}_{i}}}}^{{ * * }},~z_{{{{n}_{i}}}}^{{ * * }}]}^{{\text{T}}}}$ и построения результирующей отметки воспользуемся иерархическим агломеративным алгоритмом кластеризации с евклидовой нормой (${{\left\| {\, \cdot \,} \right\|}_{2}}$) [43–45]. Суть этой кластеризации проста и состоит в поглощении меньших кластеров большими кластерами путем последовательного объединения (с использованием заданной метрики) исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все отметки рассматриваются как отдельные кластеры. Поскольку кластеры (применительно к ТИС) имеют так называемую “цепочечную” структуру, то была выбрана метрика “ближайшего соседа”, согласно которой расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими отметками (“ближайшими соседями”) из этих кластеров.

Итак, на множестве сформированных отметок ${\mathbf{\Lambda }}_{{{{n}_{i}}}}^{{ * * }}$, $i = \overline {1,{{N}_{1}}} $, осуществляется последовательная операция кластеризации, обеспечивающая, в конечном итоге, разбиение всех отметок на $Q$ кластеров (в развиваемом методе выбор значения Q зависит от геометрии ТИС, условий наблюдения цели с учетом имеющейся статистики эксплуатации данной ТИС и опыта оператора). Алгоритм кластеризации устанавливает отображение $f:\{ {{n}_{1}},{{n}_{2}},\; \ldots ,\;{{n}_{{{{N}_{1}}}}}\} \to \{ \overline {1,Q} \} $, которое номерам ${{n}_{i}}$, сформированным ранее ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$, ставит в соответствие метку (номер кластера) $q \in \{ \overline {1,Q} \} $. В результате этого семейство номеров $\{ {{n}_{1}},{{n}_{2}},\; \ldots ,\;{{n}_{{{{N}_{1}}}}}\} $ разбивается на $Q$ непересекающихся множеств–кластеров $\{ {{\mathbb{K}}_{1}},{{\mathbb{K}}_{2}},\; \ldots ,\;{{\mathbb{K}}_{Q}}\} $, где ${{\mathbb{K}}_{q}} = \left\{ {{{n}_{{1q}}},{{n}_{{2q}}},\; \ldots ,\;{{n}_{{{{L}_{q}}q}}}} \right\}$, ${{n}_{{dq}}} \in \{ {{n}_{1}},{{n}_{2}},\; \ldots ,\;{{n}_{{{{N}_{1}}}}}\} $, $d = \overline {1,{{L}_{q}}} $. Здесь ${{L}_{q}}$ – количество элементов в кластере ${{\mathbb{K}}_{q}},$ ${{\mathbb{K}}_{q}} \ne \emptyset ~$ $\forall q = \overline {1,Q} $, при этом $\{ {{n}_{1}},{{n}_{2}},\; \ldots ,\;{{n}_{{{{N}_{1}}}}}\} = {{\mathbb{K}}_{1}} \cup {{\mathbb{K}}_{2}} \cup \ldots \cup {{\mathbb{K}}_{Q}}$, где ${{\mathbb{K}}_{l}} \cap {{\mathbb{K}}_{r}} = \emptyset $ $\forall ~l,r \in \{ \overline {1,Q} \} $, $~l \ne r$. Результатом такой кластеризации является дендрограмма [43–45], которая характеризует близость отдельных отметок и кластеров друг к другу. Она описывает в графическом виде последовательность объединения кластеров для различных уровней иерархии. Каждый уровень дендрограммы соответствует одному из шагов процесса последовательного укрупнения кластеров.

Для первичных отметок ${\mathbf{\Lambda }}_{{{{n}_{i}}}}^{{ * * }}$ и ${\mathbf{\Lambda }}_{{{{n}_{j}}}}^{{ * * }}$ используется евклидово расстояние

а для двух кластеров ${{\mathbb{K}}_{l}}$ и ${{\mathbb{K}}_{r}}$ – расстояние “ближнего соседа”

Первичные отметки ${\mathbf{\Lambda }}_{{{{n}_{1}}}}^{{ * * }},{\mathbf{\Lambda }}_{{{{n}_{2}}}}^{{ * * }},\; \ldots ,\;{\mathbf{\Lambda }}_{{{{n}_{{{{N}_{1}}}}}}}^{{ * * }}$ последовательно (по шагам) объединяются в группы: сначала самые близкие, а затем все более отдаленные друг от друга (в смысле метрик (3.1) и (3.2)). На каждом шаге алгоритма происходит объединение двух самых близких кластеров ${{\mathbb{K}}_{l}}$ и ${{\mathbb{K}}_{r}}$, образуя новый кластер ${{\mathbb{K}}_{p}} = {{\mathbb{K}}_{l}} \cup {{\mathbb{K}}_{r}}$, при этом общее количество кластеров уменьшается на единицу. Процесс кластеризации завершится, когда количество кластеров станет равным Q.

Каждый кластер ${{\mathbb{K}}_{q}}$, $q \in \{ \overline {1,Q} \} $, характеризуется параметрами: L_q – мощность кластера, g_q = = ${{D}_{q}}{\text{/}}{{L}_{q}}$ – “разряженность” кластера,

– центр кластера. Здесь ${{n}_{{dq}}} \in {{\mathbb{K}}_{q}}$, ${{D}_{q}} = \mathop {\max }\limits_{i,j} {\text{||}}{\mathbf{\Lambda }}_{{{{n}_{{iq}}}}}^{{ * * }} - {\mathbf{\Lambda }}_{{{{n}_{{jq}}}}}^{{ * * }}{\text{||}}$ – диаметр кластера ${{\mathbb{K}}_{q}}$ (где $i,j = \overline {1,{{L}_{q}}} $, ${{n}_{{iq}}},{{n}_{{jq}}} \in {{\mathbb{K}}_{q}}$). Кластер ${{\mathbb{K}}_{q}}$ по своей топологической структуре может быть сосредоточенным или распределенным, однородным или неоднородным, иметь или не иметь “близких соседей-кластеров”. Для учета этих особенностей для каждого кластера ${{\mathbb{K}}_{q}}$ сформируем множество Ω_q = = $\{ {{n}_{{{\mathbf{\Omega }},q,i}}},i = \overline {1,{{L}_{{{\mathbf{\Omega }},q}}}} \} $ (где ${{n}_{{{\mathbf{\Omega }},q,i}}} \in \{ {{n}_{1}},{{n}_{2}},\; \ldots ,\;{{n}_{{{{N}_{1}}}}}\} $), которое объединяет в себе все метки, соответствующие тем элементам из множества $\{ {\mathbf{\Lambda }}_{{{{n}_{1}}}}^{{ * * }},{\mathbf{\Lambda }}_{{{{n}_{2}}}}^{{ * * }},\; \ldots ,\;{\mathbf{\Lambda }}_{{{{n}_{{{{N}_{1}}}}}}}^{{ * * }}\} $, которые наиболее близки к центру ${{\Upsilon }_{q}}$ кластера ${{\mathbb{K}}_{q}}$. При этом используется следующий критерий близости: где $\alpha _{m}^{{{{\Upsilon }_{q}}}}$ и $\beta _{m}^{{{{\Upsilon }_{q}}}}$ – “вторичные” пеленги оценки ${{\Upsilon }_{q}}$ по отношению к Π_m, $\alpha _{{m{{n}_{{{\mathbf{\Omega }},q,i}}}}}^{{ * * }}$ и $\beta _{{m{{n}_{{{\mathbf{\Omega }},q,i}}}}}^{{ * * }}$ – “вторичные” пеленги оценки ${\mathbf{\Lambda }}_{{{{n}_{{{\mathbf{\Omega }},q,i}}}}}^{{ * * }}$, соответствующие ${\text{РИ}}{{{\text{С}}}_{{{{n}_{{{\mathbf{\Omega }},q,i}}}}}}$, по отношению к Π_m.

Множество ${{{\mathbf{\Omega }}}_{q}}$ назовем ядром кластера ${{\mathbb{K}}_{q}}$. Его основные характеристики: мощность ${{L}_{{{\mathbf{\Omega }},q}}} \geqslant 1$, разреженность ${{g}_{{{\mathbf{\Omega }},q}}}$ и центр

Таким образом, с учетом (3.3) и (3.4) в пространстве ${{\mathbb{R}}^{3}}$ сформирована некоторая окрестность ${{O}_{{{{{\mathbf{\Omega }}}_{q}}}}}$ (с центром в точке ${{{\mathbf{I}}}_{{{\mathbf{\Omega }},q}}}$), которую назовем доверительной областью ядра ${{{\mathbf{\Omega }}}_{q}}$, отвечающего кластеру ${{\mathbb{K}}_{q}}$. Каждому ядру ${{{\mathbf{\Omega }}}_{q}}$ можно поставить в соответствие множество измерительных каналов ${{{\mathbf{K}}}_{{{\mathbf{\Omega }},q}}} = \left\{ {{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{\alpha },{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{\beta }} \right\} \subseteq {\mathbf{K}} = {{{\mathbf{K}}}^{\alpha }} \cup {{{\mathbf{K}}}^{\beta }}$, где ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{\alpha }$ = $\{ {\text{K}}_{{{\mathbf{\Omega }},q,i}}^{\alpha },\;i = \overline {1,M_{{{\mathbf{\Omega }},q}}^{\alpha }} \} $ и ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{\beta } = \{ {\text{K}}_{{{\mathbf{\Omega }},q,i}}^{\beta },\;i = \overline {1,M_{{{\mathbf{\Omega }},q}}^{\beta }} \} $ – множества азимутальных и угломестных каналов, использованных при построении ядра ${{{\mathbf{\Omega }}}_{q}}$, при этом $M_{{{\mathbf{\Omega }},q}}^{\alpha } + M_{{{\mathbf{\Omega }},q}}^{\beta } \leqslant 2M$.

4. Обнаружение недостоверных каналов, формирование результирующей оценки. Далее для каждого множества ${{{\mathbf{K}}}_{{{\mathbf{\Omega }},q}}}$ определяем множества условно достоверных ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{0} = \{ {\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{0\alpha }},{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{0\beta }}\} \subseteq {\mathbf{K}}$ и недостоверных ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{1} = \{ {\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{1\alpha }},{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{1\beta }}\} \subseteq {\mathbf{K}}$ измерительных каналов, где ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{r\alpha }} = \{ {\text{K}}_{{{\mathbf{\Omega }},q,i}}^{{r\alpha }},\;i = \overline {1,M_{{{\mathbf{\Omega }},q}}^{{r\alpha }}} \} $, ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{r\beta }} = \{ {\text{K}}_{{{\mathbf{\Omega }},q,i}}^{{r\beta }},\;i = \overline {1,M_{{{\mathbf{\Omega }},q}}^{{r\beta }}} \} $, $r \in \left\{ {0,1} \right\}$, ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{0} \cap {\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{1} = \emptyset $, ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{0} \cup {\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{1} = {\mathbf{K}}$, ${\text{||}}{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{0}{\text{||}} + \,{\text{||}}{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{1}{\text{||}} = \left\| {\mathbf{K}} \right\| = 2M$, $\left\| {\; \cdot \;} \right\|$ – оператор вычисления мощности множества. При этом для элементов множеств ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{0\alpha }}$ и ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{0\beta }}$ справедливы неравенства:

где $\alpha _{m}^{{{{{\mathbf{I}}}_{{{\mathbf{\Omega }},q}}}}}$ и $\beta _{m}^{{{{{\mathbf{I}}}_{{{\mathbf{\Omega }},q}}}}}$ – “вторичные” пеленги центра ${{{\mathbf{I}}}_{{{\mathbf{\Omega }},q}}}$ ядра ${{{\mathbf{\Omega }}}_{q}}$. Соответственно для элементов множеств ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{1\alpha }}$ и ${\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{{1\beta }}$ неравенства (4.1) не выполняются.

Вариант 1: ${\text{||}}{\mathbf{K}}_{{{\mathbf{\Omega }},q}}^{1}{\text{||}} \ne 0$ $\forall q = \overline {1,Q} $, т.е. у каждого ядра ${{{\mathbf{\Omega }}}_{q}}$ есть условно недостоверные измерительные каналы.

Вариант 2: существует семейство ядер $\{ {\mathbf{\Omega }}_{i}^{ * },i = \overline {1,Q{\text{*}}} \} $ (где ${\mathbf{\Omega }}_{i}^{ * } \in \left\{ {{{{\mathbf{\Omega }}}_{1}},{{{\mathbf{\Omega }}}_{2}},\; \ldots ,\;{{{\mathbf{\Omega }}}_{Q}}} \right\}$, $Q* \leqslant Q$), у которых отсутствуют недостоверные измерительные каналы.

В случае варианта 1 выбираем приоритетное ядро ${\mathbf{\Omega }}* \in \left\{ {{{{\mathbf{\Omega }}}_{1}},{{{\mathbf{\Omega }}}_{2}},\; \ldots ,\;{{{\mathbf{\Omega }}}_{Q}}} \right\}$, для которого

Таким образом, данному ядру, согласно (4.2), соответствует максимальное число достоверных каналов. Решение, формируемое на базе критерия (4.2), может быть не единственным, в этом случае предпочтение отдается наиболее плотному ядру (по принципу ранжирования).

В случае варианта 2 приоритетное ядро ${\mathbf{\Omega }}{\text{*}}$ теперь выбирается из множества $\{ {\mathbf{\Omega }}_{i}^{ * },i = \overline {1,Q{\text{*}}} \} $ с учетом указанного выше принципа ранжирования.

Таким образом, результатом реализации ММТО является формирование вектора скорректированных измерений ${{{\mathbf{H}}}_{{{\mathbf{\Omega }}*}}}$ (в него включаются только первичные пеленги достоверных каналов) и соответствующей ему результирующей оценки ${\mathbf{\Lambda }}_{{\mathbf{\Omega }}}^{ * }$ местоположения цели.

5. Пример оценивания местоположения излучающей цели. Для фиксированного момента времени (стационарный случай) воспользуемся следующими исходными данными:

Здесь и далее положение пеленгаторов и цели указаны в метрах, угловые величины – в градусах.

Используя датчик случайных чисел с параметрами ${{\sigma }_{\alpha }} = 0.25$ и ${{\sigma }_{\beta }} = 0.5$ (для гауссовского закона распределения и нулевого математического ожидания), была сформирована флуктуационная ошибка измерений для пяти пеленгаторов ТИС. К ней были добавлены АОИ, присутствующие в каналах ${\text{K}}_{5}^{\alpha }$ и ${\text{K}}_{3}^{\beta }$ (для ${\text{K}}_{5}^{\alpha }$ значение АОИ равно минус 11, а для ${\text{K}}_{3}^{\beta }$ – плюс 9). С учетом этого был сформирован вектор ошибок измерений

и вектор наблюдений пятипозиционной ТИС. Видим, что условия нормального функционирования ТИС $\left| {\psi _{m}^{\alpha }} \right| < {{\varepsilon }^{\alpha }}$ = 0.75 и $\left| {\psi _{m}^{\beta }} \right| < {{\varepsilon }^{\beta }} = 1.5$ не выполнены для каналов ${\text{K}}_{5}^{\alpha }$ и ${\text{K}}_{3}^{\beta }$, следовательно, данные каналы являются недостоверными. Требуется на базе ММТО и вектора измерений ${\mathbf{H}}$ определить номера недостоверных каналов и оценить местоположение цели при наличии АОИ, а также дать сравнительный анализ ММТО с указанными ранее традиционными методами триангуляционного оценивания.

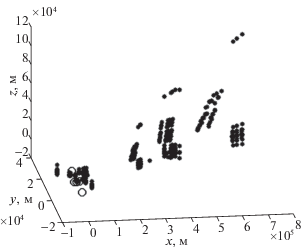
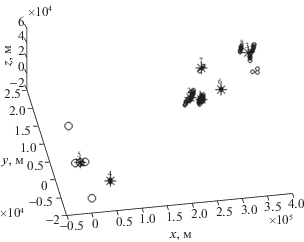
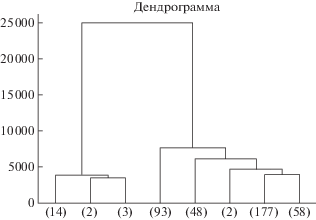
Основные этапы ММТО на исходных измерениях (${\mathbf{H}}$) отражены на рис. 1–4 и в таблице. Отметки ${\mathbf{\Lambda }}_{n}^{*}$ потенциально наблюдаемых ИС изображены на рис. 1, где звездочкой показано положение отметки ${\mathbf{\Lambda }}_{n}^{*}$ (символ *), а большими кружками (символом $\bigcirc $) – положения пеленгаторов ${{{\text{П}}}_{m}}$. На рис. 2 представлены результаты кластеризации отметок ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$, где звездочкой с верхним индексом (символом $_{*}q$) обозначен центр ${{\Upsilon }_{q}}$ соответствующего кластера, маленькими кружками (символом ○) характеризуются положения отметок ${\text{PИ}}{{{\text{С}}}_{{{{n}_{i}}}}}$. На рис. 3 приведена дендрограмма предпоследнего шага агломеративного алгоритма кластеризации, которая показывает последовательность объединения кластеров. На дендрограмме на оси абсцисс (в круглых скобках) указано количество элементов в кластере (${{L}_{q}}$, $q \in \{ \overline {1,Q + 1} \} $), а на оси ординат – расстояние между кластерами. На последнем шаге алгоритма происходит объединение двух наиболее близких (в смысле метрики (3.2)) кластеров с количеством элементов 2 и 3, образуя кластер из пяти элементов. В результате объединения общее количество кластеров становится равным семи и процесс кластеризации прекращается. Полученному на последнем шаге новому кластеру соответствует номер 4 (см. таблицу), т.е. ${{L}_{4}} = 5$. Кластерам с количеством элементов 14, 93, 48, 2, 177, 58 (см. рис. 3) соответствуют номера 5, 7, 3, 6, 2, 1 (таблица), т.е. ${{L}_{5}} = 14$, ${{L}_{7}} = 93$, ${{L}_{3}} = 48$, ${{L}_{6}} = 2$, ${{L}_{2}} = 177$, ${{L}_{1}} = 58$.

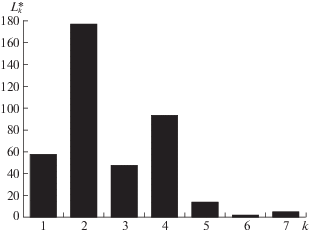
Количественное распределение отметок по кластерам показано рис. 4, где на оси абсцисс указывается номер соответствующего кластера, а на оси ординат – количество отметок, образующих данный кластер. Сводные результаты ММТО приведены в таблице. Из этой таблицы видно, что общее количество отметок, участвующих в кластеризации ${{N}_{1}} = 397$, т.е. это те отметки из $N~ = {\text{8}}0{\text{6}}$ потенциально возможных (соответствующих наблюдаемым ИС), которые прошли отсев (селекцию) с учетом условий (2.4). Согласно критерию (4.2), из семейства $\left\{ {{{{\mathbf{\Omega }}}_{1}},{{{\mathbf{\Omega }}}_{2}},\; \ldots ,\;{{{\mathbf{\Omega }}}_{7}}} \right\}$ были выбраны приоритетные ядра ${\mathbf{\Omega }}_{1}^{ * } = {{{\mathbf{\Omega }}}_{1}}$ и ${\mathbf{\Omega }}_{2}^{ * } = {{{\mathbf{\Omega }}}_{2}}$, а ранжированием (по параметру ${{L}_{k}}$) осуществлен отбор оптимального ядра ${\mathbf{\Omega }}* = {{{\mathbf{\Omega }}}_{2}}$ (см. таблицу, в которой строка, соответствующая оптимальному варианту, затемнена). Далее для ядра ${{{\mathbf{\Omega }}}_{2}}$ были правильно обнаружены недостоверные измерительные каналы ${\mathbf{K}}_{{{\mathbf{\Omega }},2}}^{{1\alpha }} = \left\{ 5 \right\}$ и ${\mathbf{K}}_{{{\mathbf{\Omega }},2}}^{{1\beta }} = \left\{ 3 \right\}$.

Для сравнения качества оценки, получаемой при помощи разработанного ММТО, местоположение цели оценивали еще двумя методами: ММП и РММП (неизвестные АОИ включаются в вектор оцениваемых параметров). При этом для РММП полагалось, что номера каналов с АОИ известны, а неизвестны лишь значения соответствующих АОИ, а для ММП были исключены из рассмотрения пеленгаторы, у которых хотя бы один измерительный канал (азимута или угла места) являлся аномальным (в нашем примере это ${{{\text{П}}}_{3}}$ и ${{{\text{П}}}_{5}}$). Сравнение производилось для различных положений цели (использовано круговое размещение цели) в полярных координатах: ${{\varphi }_{{\text{ц}}}} \in \{ 3 \times i,\;i = \overline {1,120} \} $, ${{\rho }_{{\text{ц}}}} \in \{ 50,100,150,200,250,300,350\} \times {{10}^{3}}$ и ${{z}_{{\text{ц}}}} = 3 \times {{10}^{3}}$. Усреднение оценок производилось по 100 измерениям текущего положения цели с независимой шумовой составляющей. При этом флуктуационные составляющие ошибок $\psi _{m}^{\alpha }$ и $\psi _{m}^{\beta }$ считались распределенными по нормальному закону со среднеквадратическим отклонением 0.5° и 1° соответственно.

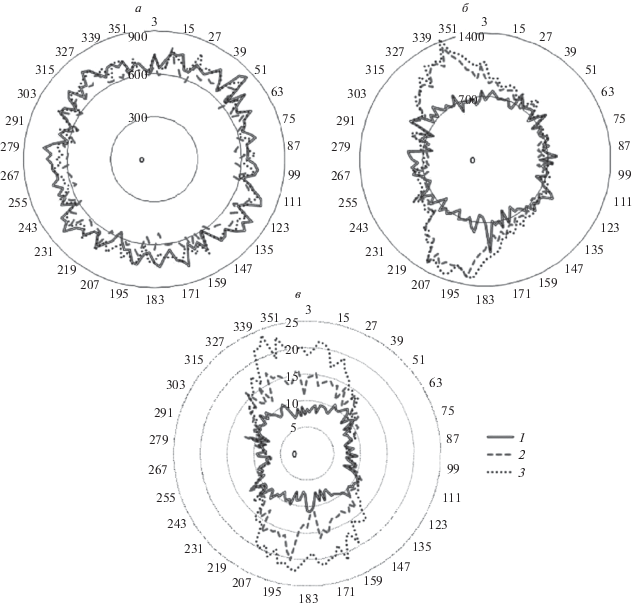
Зависимость усредненной ошибки оценивания (в м) местоположения цели от параметра ${{\varphi }_{{\text{ц}}}}$ для трех методов ММТО, ММП и РММП при ${{\rho }_{{\text{ц}}}} = 50 \times {{10}^{3}}$ и отсутствии АОИ приведена на рис. 5, а (1 – ММТО, 2 – ММП и 3 – РММП). Видим, что в нормальных условиях функционирования ТИС рассматриваемые методы сравнимы по точности. Ситуация кардинально меняется, если ТИС функционирует в некорректных условиях (см. рис. 5, б и 5, в: для ${{\rho }_{{\text{ц}}}} = 50 \times {{10}^{3}}$ и ${{\rho }_{{\text{ц}}}} = 200 \times {{10}^{3}}$ соответственно, где на рис. 5, б ошибка приведена в м, а на рис. 5, в – в км). Видим, что только ММТО обеспечивает построение надежной оценки для всех направлений визирования.

Выше мы использовали ограничения: при анализе РММП полагались известными номера недостоверных каналов и оценивались только значения АОИ, а для ММП показания пеленгаторов с АОИ (хотя бы в одном из каналов) вовсе исключались из рассмотрения. Теперь осуществим сравнение ММТО с одним из эмпирических методов для общего случая, не прибегая к этим ограничениям. Суть метода заключается в следующем. Строятся всевозможные комбинации пеленгов, так чтобы в каждой комбинации было более чем $M{\text{/}}2$ пеленгов. Каждой комбинации соответствует свой вектор первичных измерений, для которого строится первичная отметка цели. Далее по аналогии с ММТО находятся вторичные пеленги и формируется усредненная (по количеству пеленгов, входящих в комбинацию) суммарная (по азимутам и углам места) невязка. Результирующей комбинацией будет та, невязка которой минимальна. Пеленги, не входящие в эту комбинацию, считаем аномальными.

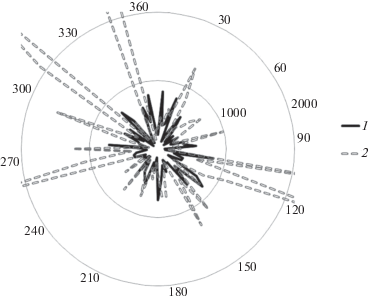
Для общего случая зависимость усредненной (по 30 измерениям) ошибки оценивания (в м) местоположения цели от параметра ${{\varphi }_{{\text{ц}}}} \in \{ 5 \times i,\;i = \overline {1,72} \} $ для двух методов (ММТО и эмпирического метода (ЭМ)) при ${{\rho }_{{\text{ц}}}} = 50 \times {{10}^{3}}$ приведена на рис. 6 (1 – ММТО, 2 – ЭМ). Если принять за 100% площадь диаграммы ошибок ЭМ, то площадь диаграммы ошибок ММТО снижается на 43% (см. рис. 6), что наглядно демонстрирует преимущества ММТО.

6. Оценивание параметров движения излучающей цели. Возвращаясь к задаче фильтрации (см. разд. 1), для каждого момента времени ${{t}_{k}}$ (где $k \in \{ 0,1,2, \ldots \} $) можно сформировать оптимальное ядро ${\mathbf{\Omega }}_{k}^{ * }$ с центром ${{{\mathbf{I}}}_{{{\mathbf{\Omega }}*,k}}} = {\mathbf{\Lambda }}_{{{\mathbf{\Omega }},k}}^{ * }$ и вектор скорректированных измерений

где ${{{\mathbf{\Psi }}}_{{{\mathbf{\Omega }}*,k}}}$ – вектор ошибок скорректированных измерений. Корреляционная матрица ошибок измерений ${\mathbf{K}}_{{{\mathbf{\Omega }}*,k}}^{{\mathbf{\Psi }}}$ получается из исходной матрицы ${\mathbf{K}}_{k}^{{\mathbf{\Psi }}}$ путем отбрасывания тех строк и столбцов, которые соответствуют недостоверным каналам.

В рамках ММТО получаем следующий алгоритм фильтрации:

Для его запуска необходимо использовать начальные условия, которые получаем на основе более ранних скорректированных оценок ММТО, формируемых с учетом разд. 2–5.

При нормальных условиях функционирования ТИС вектор ${\mathbf{P}}_{{{\mathbf{\Omega }},k}}^{ * }$ можно опустить, т.е. рассматривать усеченный вектор ${\mathbf{X}}_{{{\mathbf{\Omega }}*,k/k}}^{*} = {{[{\mathbf{\Lambda }}_{{{\mathbf{\Omega }},k}}^{ * },{\mathbf{V}}_{{{\mathbf{\Omega }},k}}^{ * }]}^{{\text{T}}}}$.

7. Пример оценивания параметров движения излучающей цели. Рассмотрим ТИС с пеленгаторами кругового обзора, обеспечивающими сопровождение излучающей цели. Для описания геометрии задачи воспользуемся данными из разд. 5, и, кроме того, для всех

${\mathbf{K}}_{k}^{{\mathbf{\Psi }}} = {{{\mathbf{K}}}^{{\mathbf{\Psi }}}} = {\text{diag}}[({{(\sigma _{m}^{\alpha })}^{2}},{{(\sigma _{m}^{\beta })}^{2}}),m = \overline {1,5} ]$, $\sigma _{m}^{\alpha } = {{\sigma }^{\alpha }} = 0.25$, $\sigma _{m}^{\beta } = {{\sigma }^{\beta }} = 0.5$. Для этих исходных данных с учетом (1.1) получаем простейшую модель невозмущенного прямолинейного равномерного движения ${{{\mathbf{X}}}_{{k + 1}}} = {\mathbf{F}}{{{\mathbf{X}}}_{k}}$. Как и в разд. 5 положения пеленгаторов и цели указаны в м, скорость цели – в м/с, угловые величины – в град. Для классического метода в качестве начального условия ${\mathbf{\Lambda }}_{0}^{ * }$ принимается оценка местоположения цели, вычисляемая на основе метода минимума суммы пространственных невязок [24] по измерениям пеленгов, выполненных в момент времени t₀ = 0. Для ММТО в качестве начального условия принимается ${\mathbf{\Lambda }}_{{{\mathbf{\Omega }},0}}^{ * }$. Соответственно для начального условия ${\mathbf{V}}_{0}^{ * }$ (в классическом методе) используется первая конечная разность и оценки ${\mathbf{\Lambda }}_{0}^{ * }$ и ${\mathbf{\Lambda }}_{{ - 1}}^{ * } = {\mathbf{\Lambda }}{\text{*}}\left( { - \tau } \right)$ для моментов времени t₀ = 0 и ${{t}_{{ - 1}}} = - \tau $ соответственно. Аналогично формируется оценка ${\mathbf{V}}_{{{\mathbf{\Omega }},0}}^{ * }$ для ММТО. Кроме того, примем что соответствует оценке (в момент t₀ = 0) местоположения цели с точностью 20% и скорости – 40%.

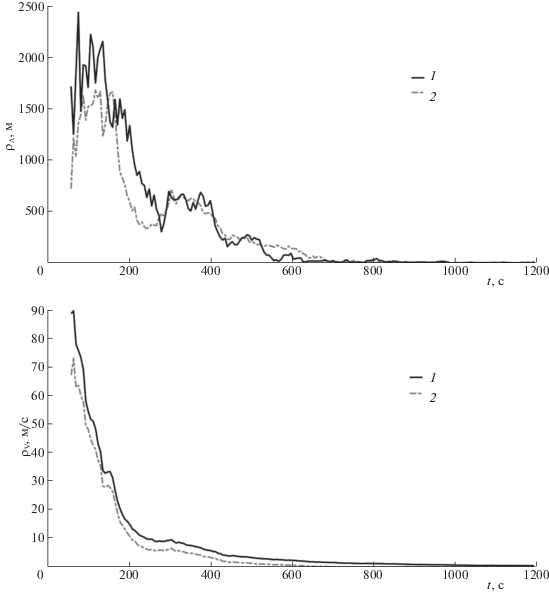
Предположим, что в каналах ${\text{K}}_{5}^{\alpha }$ и ${\text{K}}_{3}^{\beta }$ для всех t_k помимо допустимой флуктуационной ошибки присутствуют и постоянные АОИ (для ${\text{K}}_{5}^{\alpha }$ значение АОИ равно минус 11, а для ${\text{K}}_{3}^{\beta }$ – плюс 9). Для сравнения ММТО (6.2) и классического метода фильтрации (1.5) проводилось 100 независимых экспериментов с последующим усреднением результатов. На рис. 7, а и 7, б показаны результирующие погрешности ${{\rho }_{{\mathbf{\Lambda }}}}(k)$ и ${{\rho }_{{\mathbf{V}}}}(k)$ оценивания (в евклидовой метрике) местоположения и скорости цели (на рисунках цифра 1 соответствует ММТО при наличии АОИ, 2 – классическому методу (1.5) при отсутствии АОИ), попытка реализации (1.5) в аномальных условиях приводит к расходимости фильтра (поэтому результаты эксперимента не приводятся). Из рис. 7, а и 7 б следует, что ММТО дает несмещенные оценки (при вхождении фильтра в стационарный режим оценивания) и незначительно проигрывает в точности классическому методу даже в аномальных условиях функционирования ТИС.

Была также проверена возможность реализации классического метода (1.5) в аномальных условиях с использованием расширения пространства состояний (возможные АОИ всех 10 каналов включались в число фильтруемых координат вектора P_k). В качестве начальной оценки корреляционной матрицы ошибок оценивания принималась диагональная матрица

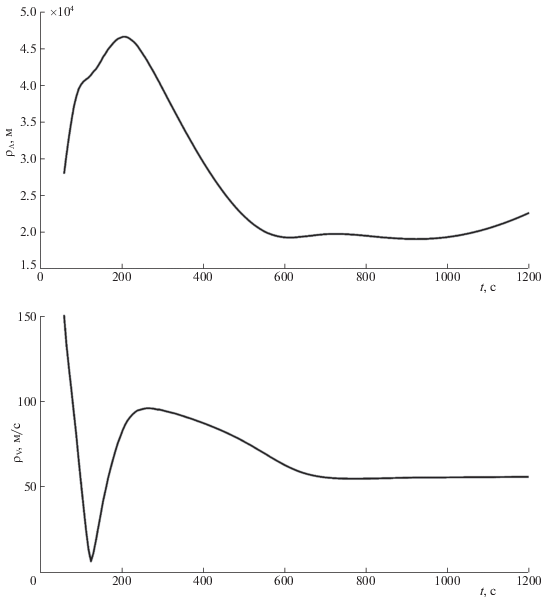
В эту матрицу добавлено 10 компонент (${{2}^{2}},\; \ldots ,\;{{2}^{2}}$), являющихся характеристиками точности оценивания АОИ в момент времени t₀ = 0. Матрица F дополнена теперь новыми строками и столбцами (состоящими из нулей и единиц), соответствующими принятой модели АОИ в виде постоянной ошибки. Начальные условия для АОИ принимались нулевыми. Результаты усредненной фильтрации (по 100 экспериментам) представлены на рис. 8, а и 8, б, где по аналогии с рис. 7, а и 7, б приводятся графики зависимости погрешности оценивания местоположения и скорости цели от времени. Сравнение рис. 7, а, 7, б и рис. 8, а, 8, б показывает, что процедура расширения не обеспечивает хорошей устойчивости вычислительного процесса, при этом точность оценивания на базе ММТО существенно выше.

Заключение. Развитый ММТО можно отнести к классу интеллектуально-аналитических методов, поскольку он предполагает выполнение традиционных аналитических операций, связанных с нахождением решений систем уравнений, поиском максимумов и минимумов, сравнением чисел и т.д., а также интеллектуальных операций, присущих ЭВМ-оператору и относящихся к перебору вариантов, распознаванию ситуаций, формированию кластеров и др. Анализ показал, что развитый метод обеспечивает: возможность эффективной обработки измерений при наличии неопределенности; обнаружение недостоверных каналов для всех пеленгаторов ТИС; существенный выигрыш в точности оценивания параметров движения цели на базе ТИС по сравнению с классическими подходами (типа МНК, ММП и РММП) при аномальных условиях наблюдения; асимптотическую сходимость оценок ММТО к оценкам МНК, ММП, РММП и линеаризованного метода фильтрации в нормальных условиях функционирования ТИС.

Поскольку ММТО сопряжен со значительными вычислительными затратами, то его целесообразно комплексировать с классическими аналитическими методами оценивания, указанными во Введении. Участие опытного оператора особенно эффективно на этапе, связанном с определением необходимого числа кластеров. В этом случае можно минимизировать вычислительные затраты на получение результирующей оценки параметров движения цели. Наибольший эффект от применения ММТО достигается в ТИС с большим числом измерительных каналов, поскольку именно в этом случае обеспечивается формирование необходимого количества ИС и соответствующих им первичных отметок. Подобные многоканальные ТИС широко используются на практике как в гражданских, так и военных областях, например в задачах радиотехнической разведки [10, 23].