Известия РАН. Теория и системы управления, 2019, № 6, стр. 43-56

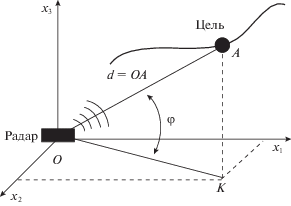
Введение. Теория оценивания – мощный подход для построения моделей сложных систем управления. Калмановская фильтрация и ее обобщения являются широко известными методами оценивания состояния динамических систем, используемыми в различных областях, таких, как навигация и слежение, коммуникация, биомедицина, химия и др. [1–6]. Однако во многих приложениях представляется интересным оценивать не только состояние системы ${{x}_{t}} \in {{\mathbb{R}}^{n}}$, но и нелинейную функцию вектора состояния (НФС), ${{z}_{t}} = f\left( {{{x}_{t}}} \right),$ которая дает практически полезную информацию для систем управления. Первым мотивационным примером такой функции служит местонахождение цели и радара. Угол (φ) и расстояние (d) от радара до цели показаны на рис. 1:

Вторым примером НФС может быть произвольная квадратичная форма, $f({{x}_{t}}) = x_{t}^{T}{\Omega }{{x}_{t}}$, представляющая собой энергию объекта [7] или Евклидово расстояние $f({{x}_{t}}) = {\text{||}}{{x}_{t}} - x_{t}^{n}{\text{||}}$, между текущим ${{x}_{t}}$ и номинальным $x_{t}^{n}$ состояниями соответственно. Таким образом, оценивание и прогнозирование НФС может быть полезным в различных приложениях, таких, как управление системой или отслеживание целей.

Проблема оценивания нелинейных функций с неизвестными параметрами или сигналами на базе минимаксной теории оценивания хорошо изучена многими авторами ([8–11] и ссылки в них). Оценивание параметров нелинейных функциональных соотношений с известными ковариациями представлено в [12]. Минимаксная квадратическая оценка интеграла от квадрата производной периодической функции получена в [13]. В [14, 15] оптимальная матрица квадратичного функционала ищется на базе кумулянтных критериев. Оценивание штрафа, рассматриваемого как квадратичная функция потерь для гармонического осцилятора, дается в [16]. Оценивание интегралов от нелинейных функций плотности вероятности разработано в [17, 18]. Также мы упомянем оценивание нелинейных функционалов от спектральной плотности и периодограммы линейных стационарных сигналов [19–21]. Некоторое обобщение этих результатов дается в [22]. В [23] неизвестное расстояние между целью и радаром аппроксимируется рядом Тейлора с последующим оцениванием его коэффициентов. Изучение теории и алгоритмов оценивания информационной меры, представляющей собой нелинейный функционал от сигнала, приведено в [24, 25]. Однако большинство авторов не фокусируются на оценивании НФС от векторных сигналов, определяемых динамическими моделями, такими, как стохастические дифференциальные системы.

Целью статьи является разработка оптимального двухшагового среднеквадратического оценивателя (estimator) для произвольной НФС в линейно-гауссовских стохастических дифференциальных системах и подробное изучение специальных полиномиальных оценивателей, для которых можно получить важные результаты по среднеквадратичному оцениванию. К основным достижениям статьи можно отнести следующие.

1. Изучение проблемы оценивания НФС в рамках модели калмановской фильтрации. Используя подход среднеквадратического оценивания, предложен оптимальный двухшаговый нелинейный оцениватель.

2. Выводится оптимальный среднеквадратический оцениватель для полиномиальных функций, таких, как квадратическая, кубическая и полиномиальная четвертой степени. Показано, что полиномиальный оцениватель представляется в замкнутой форме, зависящей только от калмановской оценки состояния и ее ковариации.

3. Важный класс квадратичных оценивателей всесторонне исследован, включая вывод матричного выражения для истинной среднеквадратической ошибки (СКО).

4. Реализация предложенных оценивателей для типовых НФС иллюстрирует их теоретическую и практическую полезность.

Статья организована следующим образом. В разд. 1 дается постановка проблемы среднеквадратического оценивания НФС в рамках калмановской фильтрации. В разд. 2 предложен оптимальный среднеквадратический оцениватель. Здесь же представлен сравнительный анализ оптимального и субоптимального оценивателей на нескольких теоретических примерах с практическими НФС. В разд. 3 изучается проблема получения оптимального оценивателя в замкнутой форме. Доказывается, что оптимальный полиномиальный оцениватель представляется в замкнутой форме через калмановскую оценку и ковариационную матрицу ошибки. Дается вывод матричных формул для СКО оптимального и субоптимального квадратичного оценивателей. Изучается эффективность квадратичных оценивателей для скалярного случайного сигнала и на реальной модели аэродинамической трубы.

1. Постановка проблемы. Рассмотрим калмановскую модель оценивания вектора состояния непрерывной линейно-гауссовской динамической системы с аддитивным шумом:

Здесь ${{x}_{t}} \in {{\mathbb{R}}^{n}}$ – вектор состояния, ${{y}_{t}} \in {{\mathbb{R}}^{m}}$ – вектор наблюдения, ${{v}_{t}} \in {{\mathbb{R}}^{r}}$ и ${{w}_{t}} \in {{\mathbb{R}}^{m}}$ – гауссовские белые шумы с нулевым средним и интенсивностями Q_t и R_t соответственно, т.е. ${\mathbf{E}}({{v}_{t}}v_{s}^{{\text{T}}})$ = ${{Q}_{t}}{{\delta }_{{t - s}}}$, ${\mathbf{E}}({{w}_{t}}w_{s}^{{\text{T}}}) = {{R}_{t}}{{\delta }_{{t - s}}}$, ${{\delta }_{t}}$ – дельта-функция, ${{F}_{t}} \in {{\mathbb{R}}^{{n \times n}}}$, ${{G}_{t}} \in {{\mathbb{R}}^{{n \times r}}}$, ${{Q}_{t}} \in {{\mathbb{R}}^{{r \times r}}}$, ${{R}_{t}} \in {{\mathbb{R}}^{{m \times m}}}$ и ${{H}_{t}} \in {{\mathbb{R}}^{{m \times n}}}$, ${\mathbf{E}}(X)$ – оператор математического ожидания случайного вектора X.

Предположим, что начальное состояние ${{x}_{0}}\sim \mathbb{N}\left( {{{{\bar {x}}}_{0}},{{P}_{0}}} \right),$ а также шумы системы и наблюдения ${{v}_{t}}$, ${{w}_{t}}$ взаимно некоррелированы.

Проблема, связанная с системой (1.1), состоит в оценивании нелинейной функции вектора состояния

по результатам зашумленных наблюдений $y_{0}^{t} = \left\{ {{{y}_{s}}:0 \leqslant s \leqslant t} \right\}.$

Существует множество статистических методов оценивания неизвестной функции $z = f(x)$ по реальным наблюдениям $y_{0}^{t}.$ Мы интересуемся выбором наилучшей оценки $\hat {z}$, минимизирующей СКО: $\mathop {\min }\limits_{\hat {z}} {\mathbf{E}}[{{\left\| {z - \hat {z}} \right\|}^{2}}].$

В общем случае оптимальное среднеквадратическое решение (далее “оценка” или “оцениватель”) представляет собой условное математическое ожидание, $\hat {z} = {\mathbf{E}}(z{\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t})$ [26, 27] и основная проблема состоит в том, как его вычислить. В статье дается решение этой проблемы для НФС (1.2) в рамках калмановской фильтрации.

В следующем разделе рассмотрим оптимальный и субоптимальный алгоритмы оценивания НФС и их реализацию.

2. Оптимальный двухшаговый оцениватель для произвольной НФС. Здесь выводится оптимальный двухшаговый оцениватель для произвольной НФС. Также предлагается простой субоптимальный оцениватель. Оба оценивателя состоят из двух шагов: оптимальная калмановская оценка вектора состояния ${{\hat {x}}_{t}}$, вычисленная на первом шаге, далее используется на втором шаге для оценивания НФС (1.2).

2.1. Оптимальный двухшаговый алгоритм.

Шаг 1 (вычисление калмановской оценки). Оценка ${{\hat {x}}_{t}} = {\mathbf{E}}({{x}_{t}}|y_{0}^{t})$ вектора состояния x_t по наблюдениям $y_{0}^{t}$, и ковариация ошибки ${{P}_{t}} = {\mathbf{E}}({{e}_{t}}e_{t}^{{\text{T}}}),~\;{{e}_{t}} = {{x}_{t}} - {{\hat {x}}_{t}},$ описываются непрерывным фильтром Калмана–Бьюси (ФКБ) [4–6]:

Шаг 2 (оптимальный оцениватель для НФС). Оптимальная оценка НФС, ${{z}_{t}} = f({{x}_{t}})$ на основе наблюдений $y_{0}^{t}$ также представляет собой условное среднее, т.е.,

где ${{p}_{t}}(x{\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t}) = \mathbb{N}\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$ – многомерная условно-гауссовская плотность распределения, определяемая условным средним ${{\hat {x}}_{t}} = {\mathbf{E}}({{x}_{t}}|y_{0}^{t})$ и ковариацией ${{P}_{t}} = {\text{cov}}({{x}_{t}},{{x}_{t}}{\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t}) = {\mathbf{E}}({{e}_{t}}e_{t}^{{\text{T}}})$.

Таким образом, оценка (2.2) представляет собой оптимальный оцениватель для произвольной НФС, зависящий от калмановской оценки ${{\hat {x}}_{t}}$ и ковариации ошибки ${{P}_{t}}.$

На практике нелинейная функция (1.2) может зависеть не только от вектора состояния, но и от его оценки. Тогда НФС принимает вид

Учитывая, что оценка состояния ${{\hat {x}}_{t}}$ представляет собой известную функцию наблюдений, ${{\hat {x}}_{t}} = {{\hat {x}}_{t}}(y_{0}^{t})$, оптимальная среднеквадратическая оценка неизвестной функции ${{z}_{t}} = f({{x}_{t}},{{\hat {x}}_{t}})$ задается формулой, аналогичной (2.2), а именно

Далее рассмотрим несколько теоретических примеров применения общего нелинейного оценивателя (2.2).

2.2. Примеры двухшагового оценивателя. Пусть ${{x}_{t}} = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{{1,t}}}}&{{{x}_{{2,t}}}} \end{array}} \right]}^{{\text{T}}}}$ – двумерный гауссовский вектор, а ${{\hat {x}}_{t}} \in {{\mathbb{R}}^{2}}$ и ${{P}_{t}} \in {{\mathbb{R}}^{{2 \times 2}}}$ – калмановская оценка и ковариция ошибки соответственно.

Пример 1 (ожидаемое значение Евклидовой нормы). Ошибка оценивания определяется как

Учитывая, что Евклидова норма ошибки зависит от разности между вектором состояния и его оценкой, $\left\| {{{e}_{t}}} \right\| = \sqrt {e_{t}^{{\text{T}}}{{e}_{t}}} = \sqrt {{{{({{x}_{t}} - {{{\hat {x}}}_{t}})}}^{{\text{T}}}}({{x}_{t}} - {{{\hat {x}}}_{t}})} ,$ мы преобразуем формулу (2.2) в виде

где ${{p}_{t}}(e{\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t}) = \mathbb{N}\left( {0,{{P}_{t}}} \right)$ – условная плотность распределения ошибки ${{e}_{t}} = {{x}_{t}} - {{\hat {x}}_{t}}.$

Далее, используя [28], получаем аналитическое выражение для оценки Евклидовой нормы ${{z}_{t}} = \left\| {{{e}_{t}}} \right\|$:

где ${}_{2}^{{}}{{F}_{1}}\left( {a,b;c;x} \right)~$ – гипергеометрическая функция, а ${{\lambda }_{{1,t}}}$ и ${{\lambda }_{{2,t}}}$ – собственные значения матрицы ${{P}_{t}}.$

Пример 2 (управление с обратной связью, зависящее от максимума переменных состояния). В механических системах кусочно-постоянное управление задается в виде

где D – пороговое расстояние. Тогда среднеквадратическая оценка максимума ${{z}_{t}} = {\text{max}}\left( {{{x}_{{1,t}}},{{x}_{{2,t}}}} \right)$ дается в виде [29] где $\phi \left( \cdot \right)$ и $\Phi \left( \cdot \right)$ – стандартная гауссовская плотность и соответствующая функция распределения.

Пример 3 (оценивание функции синуса). Пусть $\theta $ – неизвестный случайный угол, измеряемый в присутствии аддитивного белого шума. Тогда

где ${{x}_{t}} = \theta ,$ а w_t – гауссовский белый шум с нулевым средним и интенсивностью r.

Уравнения ФКБ (2.1) имеют вид

Решая уравнение Риккати для ${{P}_{t}} = {\mathbf{E}}[{{(\theta - {{\hat {x}}_{t}})}^{2}}]$, получаем ${{P}_{t}} = \sigma _{\theta }^{2}{\text{/}}(1 + t\sigma _{\theta }^{2}{\text{/}}r)$. Далее рассмотрим функцию синуса неизвестного угла θ. Тогда НФС имеет вид $z = f(\theta ) = \sin \theta $.

1. Оптимальная оценка. Используя (2.2), получаем оптимальную оценку синуса

где ${{\hat {\theta }}_{t}} = {{\hat {x}}_{t}}$ и ${{P}_{t}}$ определяются в (2.8).

2. Субоптимальная оценка. Параллельно с оптимальной оценкой (2.9) рассмотрим простую субоптимальную оценку ${{\tilde {z}}_{t}} = f({{\hat {\theta }}_{t}}) = {\text{sin}}{{\hat {\theta }}_{t}}$.

Для сравнения точности двух оценок выведем аналитические формулы для их СКО: $P_{{z,t}}^{{opt}}$ = = ${\mathbf{E}}[{{({\text{sin}}\theta - {{\hat {z}}_{t}})}^{2}}]$ и $P_{{z,t}}^{{sub}} = {\mathbf{E}}[{{\left( {\sin \theta - {{{\tilde {z}}}_{t}}} \right)}^{2}}],$ и приведем сравнительный анализ. Получаем

где

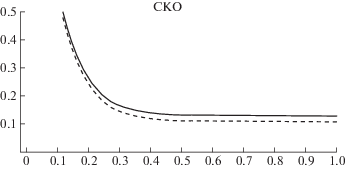
Рисунок 2 иллюстрирует точные значения $P_{{z,t}}^{{opt}}$ и $P_{{z,t}}^{{sub}}$ для параметров ${{m}_{\theta }} = 0$; $\sigma _{\theta }^{2} = 2$; $r = 1$, а рисунок 3 показывает относительную ошибку, ${{\Delta }_{t}} = {\text{|}}(P_{{z,t}}^{{opt}} - P_{{z,t}}^{{sub}}){\text{/}}P_{{z,t}}^{{opt}}{\text{|}} \cdot 100\% .$ Не является сюрпризом, что на рис. 2 и 3 оптимальная оценка лучше субоптимальной, т.е. $P_{{z,t}}^{{opt}} < P_{{z,t}}^{{sub}}.$ Мы также наблюдаем, что разница между этими оценками становится незначительной по мере увеличения времени наблюдения.

Пример 4 (оценивание расстояния между случайным положением θ и фиксированной точкой $a$). В этом случае НФС имеет вид $z = \left| {\theta - a} \right|$. Используя модель (2.7) для случайного положения ${{x}_{t}} = \theta $, мы получаем наилучшую оценку (2.2) для расстояния $\left| {\theta - a} \right|$. Имеем

где ${{\hat {\theta }}_{t}} = {{\hat {x}}_{t}}$ и ${{P}_{t}}$ определяются в (2.8).

В частном случае, когда a = 0 оптимальная оценка неизвестного модуля $z = f\left( \theta \right) = \left| \theta \right|$ принимает вид

В дополнение рассмотрим простую субоптимальную оценку модуля ${{\tilde {z}}_{t}} = f({{\hat {\theta }}_{t}}) = {\text{|}}{{\hat {\theta }}_{t}}{\text{|}}.$

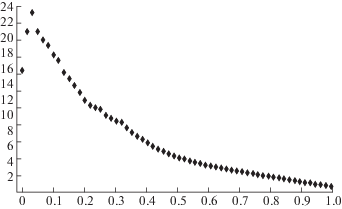
Для изучения поведения СКО $P_{t}^{{opt}} = {\mathbf{E}}[{{\left( {\left| \theta \right| - {{{\hat {z}}}_{t}}} \right)}^{2}}]$ и $P_{t}^{{sub}} = {\mathbf{E}}[{{\left( {\left| \theta \right| - {{{\tilde {z}}}_{t}}} \right)}^{2}}]$ положим ${{m}_{\theta }} = 1$; $~\sigma _{\theta }^{2} = 1$; $r = 0.2$. Метод Монте-Карло с 1000 реализаций был применен для их вычисления. Как показано на рис. 4, оптимальная оценка ${{\hat {z}}_{t}}$ имеет существенные преимущества над субоптимальной ${{\tilde {z}}_{t}}$.

2.3. Альтернативная идея субоптимального оценивания НФС. В отличие от предложенного оптимального СКО решения (2.1) и (2.2) имеется альтернативная идея для оценивания НФС. В этом случае НФС ${{z}_{t}} = f({{x}_{t}})$ рассматривается как дополнительная переменная состояния ${{z}_{t}},$ которая описывается нелинейным стохастическим уравнением ${{\dot {z}}_{t}} = a\left( {{{x}_{t}},{{z}_{t}}} \right) + b\left( {{{x}_{t}},{{z}_{t}}} \right){{v}_{t}},$ в котором коэффициент сноса $a\left( {{{x}_{t}},{{z}_{t}}} \right)$ и матрица диффузии $b\left( {{{x}_{t}},{{z}_{t}}} \right)$ определяются формулой Ито, примененной к сложной функции $f\left( {{{x}_{t}}} \right)$, в которой аргумент задается уравнением ${{\dot {x}}_{t}} = {{F}_{t}}{{x}_{t}} + {{G}_{t}}{{v}_{t}}$ [30]. Добавляя z_t в исходный вектор состояния ${{x}_{t}} \in {{\mathbb{R}}^{n}},$ получаем систему с расширенным вектором состояния ${{X}_{t}} = [\begin{array}{*{20}{c}} {x_{t}^{{\text{T}}}}&{{{z}_{t}}} \end{array}] \in {{\mathbb{R}}^{{n + 1}}}$. Таким образом, проблема оценивания НФС сводится к проблеме нелинейной фильтрации путем замены исходного состояния x_t на расширенное X_t. И далее приближенные методы нелинейной фильтрации могут быть использованы для одновременного оценивания x_t и z_t. Огромное количество нелинейных приближенных фильтров предложено в [5, 6, 30–35], среди которых выделим расширенный фильтр Калмана [5], условно оптимальный фильтр Пугачева с заданной и оптимальной структурой [30–32] и сигма-точечный фильтр [33]. Но их вычислительная сложность значительно превышает сложность линейного ФКБ. Предложенная двухшаговая процедура оценивания (2.1) и (2.2) более обещающая, чем нелинейное оценивание расширенного вектора состояния X_t.

2.4. Простая субоптимальная оценка НФС. Параллельно с оптимальной оценкой ${{\hat {z}}_{t}}$ = ${\mathbf{E}}({{z}_{t}}{\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t})$ мы предлагаем простую субоптимальную оценку для НФС, например ${{\tilde {z}}_{t}} = f({{\hat {x}}_{t}})$, которая зависит только от калмановской оценки вектора состояния ${{\hat {x}}_{t}}$ и не требует знания ковариации ошибки P_t в отличие от оптимальной оценки ${{\hat {z}}_{t}}$. Численные результаты показывают, что субоптимальная оценка ${{\tilde {z}}_{t}}$ может быть как близкой к оптимальной оценке (пример 3), так и сильно отличающейся от нее (пример 4 и далее пример 6).

2.5. О реализации оптимального оценивателя в реальном времени. Ковариация ошибки ${{P}_{t}}$ может быть предварительно вычислена (до проведения эксперимента), потому что она не зависит от сенсорных наблюдений $y_{0}^{t} = \left\{ {{{y}_{s}}:0 \leqslant s \leqslant t} \right\},$ а зависит только от статистики шумов ${{Q}_{t}}$, R_t, матриц системы ${{F}_{t}},\;{{G}_{t}},\;{{H}_{t}}$ и от начальной ковариации ${{P}_{0}},$ которые являются частью динамической модели (1.1). Таким образом, после того, как расписание наблюдений будет установлено, реализация оценивателя в реальном времени ${{\hat {z}}_{t}} = {{\hat {z}}_{t}}\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$ требует только вычисления калмановской оценки вектора состояния ${{\hat {x}}_{t}}$.

2.6. Замкнутая форма для СКО оценивателя. Для произвольной НФС ${{z}_{t}} = f\left( {{{x}_{t}}} \right)$ вычисление оптимальной оценки сводится к вычислению многомерного интеграла (2.2). Аналитическое вычисление этого интеграла (или замкнутая форма СКО оценивателя) возможно лишь в специальных случаях, таких, как в примерах 1–4.

Далее рассмотрим полиномиальную функцию от вектора состояния, для которой возможно получение простой среднеквадратической оценки в замкнутой форме, зависящей только от калмановской статистики $\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$.

3. Оптимальная замкнутая форма оценивателя для полиномиальной функции. Рассмотрим специальный класс НФС (1.2), представляющий собой многомерную полиномиальную функцию (полиномиальная форма), такую, как:

где $x \in {{\mathbb{R}}^{n}}$ и $A,B \in {{\mathbb{R}}^{{n \times n}}}$. Для простоты опустим в этом разделе индекс t.

3.1. Оптимальные полиномиальные оцениватели. В случае полиномиальных форм (3.1) оптимальный оцениватель $\hat {z} = {\mathbf{E}}[f\left( x \right){\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t}]$ имеет замкнутую форму, так как условное математическое ожидание зависит только от моментов высокого порядка условно-гауссовского распределения $\mathbb{N}({{\hat {x}}_{t}},{{P}_{t}})$, которые могут быть явно вычислены через моменты первого и второго порядков, а именно калмановскую оценку и ковариацию ошибки $(\hat {x},P)$. Следующая теорема описывает наилучшие полиномиальные оцениватели.

Теорема 1. Оптимальные среднеквадратические оцениватели $\hat {z} = {\mathbf{E}}[f\left( x \right){\kern 1pt} {\text{|}}{\kern 1pt} y_{0}^{t}]$ для полиномиальных форм (3.1) описываются следующими аналитическими формулами:

Вывод оценивателей (3.2) дается в Приложении.

Пример 5 (оптимальное и субоптимальное оценивание Евклидовой нормы). Для определения относительного местоположения в беспроводных сенсорных сетях нам нужно оценить функцию потерь, представляющую собой Евклидовую норму ошибки:

где $e \in {{\mathbb{R}}^{n}}$ – случайный вектор ошибки, $e\sim \mathbb{N}(0,P)$.

При $n = 2$ оптимальная оценка $\hat {z}$ определяется формулами (2.5) и (2.6):

При n > 2 трудно вывести аналитическую формулу для оптимальной оценки $\hat {z}$, аналогичную (3.3). В этом случае можно предложить простую субоптимальную оценку $\tilde {z}$ для Евклидовой нормы. Вначале, используя квадратичный оцениватель из (3.2), вычисляем оптимальную оценку квадрата нормы ${{\left\| {{\kern 1pt} e{\kern 1pt} } \right\|}^{2}} = {{e}^{{\text{T}}}}e,$ а далее извлекаем квадратный корень из полученной оценки. Имеем

где ${\text{tr(}}P{\text{)}}$ – след матрицы P.

Для изучения точности оптимальной и субоптимальной оценок (3.3) и (3.4) при $n = 2$ положим

Тогда $\hat {z} = 1.524$, $\tilde {z} = 1.732$. Относительная ошибка $\left| {\frac{{\tilde {z} - \tilde {z}}}{{\tilde {z}}}} \right| \cdot 100\% {\text{\;}} = 13.6\% $ показывает, что субоптимальная оценка $\tilde {z}$ значительно хуже оптимальной оценки $\hat {z}$.

3.2. Точные матричные формулы для квадратичных оценивателей. Рассмотрим произвольную квадратичную форму (КФ):

Применяя теорему 1, оптимальный квадратичный оцениватель в (3.2) явно выражается через оценку вектора состояния и ковариацию ошибки P_t, т.е.

Параллельно с оптимальной оценкой предложим субоптимальную оценку $\tilde {z}$ для КФ, которая зависит только от калмановской оценки ${{\hat {x}}_{t}}$ и не зависит от ковариации ошибки ${{P}_{t}}$ в отличие от (3.6). Предложенная субоптимальная оценка получается путем прямого вычисления КФ в точке ${{x}_{t}} = {{\hat {x}}_{t}}.$ Имеем

Далее сравним точность оптимальной (3.6) и субоптимальной (3.7) оценок. Следующая теорема определяет СКО этих оценок:

Теорема 2. СКО $P_{{z,t}}^{{opt}}$ и $~~P_{{z,t}}^{{sub}}$ находятся как

и соответственно. Здесь безусловные среднее ${{\mu }_{t}} = {\mathbf{E}}\left( {{{x}_{t}}} \right)$ и ковариация $~~{{C}_{t}} = {\text{cov}}\left( {{{x}_{t}},{{x}_{t}}} \right)$ вектора состояния x_t определяются уравнениями метода моментов [6]:

Вывод СКО (3.8) и (3.9) дается в Приложении.

Заметим, что разница между $P_{{z,t}}^{{opt}}$ и $P_{{z,t}}^{{sub}}$ равняется $P_{{z,t}}^{{sub}} - P_{{z,t}}^{{opt}} = {\text{t}}{{{\text{r}}}^{2}}(A{{P}_{t}}).$

Таким образом, уравнения (3.8)–(3.10) полностью определяют истинные СКО оптимального и субоптимального квадратичного оценивателей.

3.3. Теоретические и практические примеры применения квадратичных оценивателей.

Пример 6 (теоретический пример – оценивание мощности скалярного сигнала). Пусть ${{x}_{t}}$ – скалярный случайный сигнал, измеряемый с аддитивным белым шумом. Тогда модель системы имеет вид

где ${{v}_{t}}$ и ${{w}_{t}}$ – некоррелированные гауссовские белые шумы с интенсивностями $q$ и $r$, соответственно и ${{x}_{0}}\sim \mathbb{N}({{m}_{0}},\sigma _{0}^{2}).$

Уравнения ФКБ (2.1) запишем как

Рассмотрим мощность сигнала ${{x}_{t}}$, которая пропорциональна его квадрату. Тогда z_t = = $f({{x}_{t}}) = x_{t}^{2}$. Используя (3.6) и (3.7), получаем оптимальную и субоптимальную оценки мощности сигнала соответственно:

Сравним точность этих оценок. Используя теорему 2, получаем истинные СКО:

где среднее ${{\mu }_{t}}$ и ковариация ${{C}_{t}}$ сигнала ${{x}_{t}}$ определяются уравнениями (3.10):

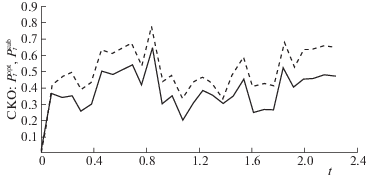
Рисунок 5 показывает относительную ошибку ${{\Delta }_{t}} = {\text{|}}(P_{{z,t}}^{{opt}} - P_{{z,t}}^{{sub}}){\text{/}}P_{{z,t}}^{{opt}}{\text{|}} \cdot 100\% $ для значений параметров $a = - 1$, $q = 0.5$, ${{m}_{\theta }} = 0$, $\sigma _{\theta }^{2} = 4$, r = 0.1. Из него видно, что относительная ошибка ${{\Delta }_{t}}$ изменяется от 3 до 6% в интервале $t \in \left[ {0.1;~~1.1} \right]$ и далее она возрастает. В установившемся режиме $t > 4$ эта ошибка достигает значения ${{\Delta }_{\infty }} = 20.4{\text{\% }}$, на этом интервале времени абсолютные значения СКО равны $P_{\infty }^{{opt}} = 0.1029{\text{\;}}$ и $P_{\infty }^{{sub}} = 0.1239$. Таким образом, численные расчеты показали, что субоптимальная оценка ${{\tilde {z}}_{t}} = \hat {x}_{t}^{2}$ может быть значительно хуже оптимальной оценки ${{\hat {z}}_{t}} = \hat {x}_{t}^{2} + {{P}_{t}}.$

Пример 7 (практический пример – модель аэродинамической трубы). Рассматривается экспериментальный анализ квадратичного оценивателя на примере расчета общей кинетической энергии высокоскоростной аэродинамической системы закрытого типа [36]. Вектор состояния ${{x}_{t}} \in {{\mathbb{R}}^{3}}$ включает три переменные ${{x}_{{1t}}},\;~{{x}_{{2t}}}$ и ${{x}_{{3t}}},$ представляющие собой отклонения от выбранного положения равновесия: x₁ – число Маха, ${{x}_{2}}$ – угол наклона направляющей лопатки привода при движении вентилятора, и ${{x}_{3}}$ – скорость привода. Тогда модель системы имеет вид

где начальные значения ${{\bar {x}}_{0}} = {{\left[ {3~\;28\;10} \right]}^{{\text{T}}}}$ и ${{P}_{0}} = {\text{diag}}\left[ {1\;~1\;~0} \right]$.

Двухсенсорная модель измерения имеет вид

Интенсивности белых шумов ${{v}_{t}} \in {{\mathbb{R}}^{3}}$ и ${{w}_{t}} \in {{\mathbb{R}}^{2}}$ равны $Q = {\text{diag}}\left[ {0.01\;0.01~\;0.01} \right]$ и R = ${\text{diag}}[\begin{array}{*{20}{c}} {0.05}&{0.05} \end{array}]$ соответственно.

Общая кинетическая энергия привода выражается в виде суммы поступательной энергии центра масс ${{E}^{{tr}}} = mv_{t}^{2}{\text{/}}2$ и вращательной энергии вокруг центра масс ${{E}^{r}} = {\mathbf{I}}\omega _{t}^{2}{\text{/}}2$, где I – инерция вращения, ${{\omega }_{t}} = {{\dot {x}}_{{2t}}}$ – угловая скорость, m – масса привода, и ${{v}_{t}} = {{x}_{{3t}}}$ – линейная скорость. Тогда общая кинетическая энергия может быть представлена как КФ:

где ${{X}_{t}} \in {{\mathbb{R}}^{4}}$ – расширенный вектор состояния I = 0.136 кгм², и m = 7.39 кг.

Используя теорему 1, оптимальный и субоптимальный квадратичные оцениватели принимают вид

где оценка вектора состояния ${{\hat {X}}_{t}} \in {{\mathbb{R}}^{4}}$ и ковариация ошибки ${{P}_{t}} \in {{\mathbb{R}}^{{4 \times 4}}}$ определяются в (2.1).

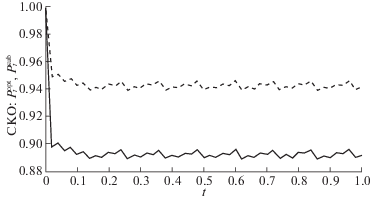
Мы интересуемся поведением СКО $P_{{z,t}}^{{opt}} = E\left[ {{{{({{z}_{t}} - {{{\hat {z}}}_{t}})}}^{2}}} \right]$ и $P_{{z,t}}^{{sub}} = E\left[ {{{{({{z}_{t}} - {{{\tilde {z}}}_{t}})}}^{2}}} \right]$, которые вычисляются с применением теоремы 2. Из рис. 6 видно, что оптимальный оцениватель более эффективный, чем субоптимальный: $P_{{z,t}}^{{opt}} < P_{{z,t}}^{{sub}}$. Относительная ошибка Δ_t изменяется от 6.2 до 10% в интервале работы системы $t \in \left[ {0.02;\;0.07} \right]$, и далее она уменьшается. В интервале t > 0.07 значения СКО и относительной ошибки равны $P_{{z,t}}^{{opt}} = 0.89$, $P_{{z,t}}^{{sub}} = 0.94$ и Δ_t = 5.6% соответственно.

В результате, можно констатировать, что предложенный оптимальный квадратичный оцениватель более подходит для обработки данных на практике.

Заключение. В некоторых прикладных задачах нелинейная функция переменных состояния содержит полезную информацию для целей систем управления. Для ее оценки предложен оптимальный двухшаговый СКО алгоритм оценивания. На первом шаге рассчитывается предварительная оценка вектора состояния путем применения стандартного ФКБ. Затем полученная оценка используется на втором шаге для оценивания исходной функции.

Особое внимание уделено полиномиальным функциям вектора состояния. В этом случае можно получить оптимальную полиномиальную оценку в замкнутой форме, которая зависит только от статистики ФКБ. Интерпретация квадратичной функции как мощность или энергия объекта рассматривается в примерах 6 и 7.

Ввиду важности нелинейной функции для практики предложенные алгоритмы оценивания иллюстрируются на теоретических и численных примерах для реальных нелинейных функций. Примеры показывают, что оптимальный оцениватель дает достаточно хорошую точность.

Используя среднеквадратический подход, предложен оптимальный двухшаговый нелинейный оцениватель. Установлено, что полиномиальный оцениватель (квадратичный, кубический, четвертой степени и т.д.) может быть представлен в компактной замкнутой форме, зависящей только от выходных характеристик ФКБ (теорема 1). Важный класс квадратичных функций подробно исследован, включая вывод матричных уравнений для истинной СКО (теорема 2). Эффективность предложенных оценивателей для реальных функций показывает их практическую и теоретическую полезность.