Известия РАН. Теория и системы управления, 2019, № 6, стр. 18-25

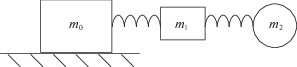
Введение. Изучается задача управления механической системой, представляющей собой платформу, которая несет упругое звено. Упругое звено моделируется присоединенным к платформе с помощью пружины твердым телом, к которому подвешен линейный диссипативный осциллятор (рис. 1). Платформа перемещается вдоль горизонтальной прямой под действием ограниченной управляющей силы и неконтролируемого непостоянного воздействия внешней среды, например силы сухого трения, параметры которого неизвестны и могут изменяться в процессе движения. Предполагается, что координата и скорость платформы, а также координата несущего тела в каждый момент времени известны, а фазовые переменные, описывающие динамику осциллятора, не доступны для измерений. Необходимо с помощью ограниченного по модулю управления остановить платформу в заданном терминальном положении за конечное (нефиксированное) время и полностью погасить колебания несущего тела и осциллятора. Искомое управление должно иметь форму обратной связи и зависеть лишь от известных фазовых переменных – координаты и скорости платформы и координаты несущего тела.

Рассматриваемая система служит упрощенной моделью сложного объекта, содержащего упругое звено или контейнер с жидкой средой, информация о текущем состоянии которого не доступна для измерений. Действие на платформу упругих сил со стороны промежуточного несущего тела и осциллятора (или контейнера с жидкостью) существенно затрудняет точное позиционирование платформы. Другим фактором, осложняющим решение задачи, служит наличие неконтролируемых внешних возмущений, что приводит к необходимости искать управление в форме обратной связи. Отметим также, что изучаемую систему отличает дефицит управлений, так как она состоит из трех связанных твердых тел, совершающих поступательные горизонтальные перемещения, и, следовательно, имеет три степени свободы, тогда как управляющее воздействие скалярно.

Одним из технических объектов, для которого применима данная модель, является прецизионная поворотная платформа, устанавливаемая на орбитальном космическом аппарате. С помощью платформы можно изменять ориентацию закрепленного на ней контейнера с полезной нагрузкой, что повышает эффективность проводимых на орбите технологических процессов [1]. Ранее задача о перемещении платформы в заданное положение, аналогичная рассматриваемой ниже, была решена для случая, когда осцилляторы, фазовые состояния которых не измеряются, располагались непосредственно на платформе без промежуточного несущего тела [2, 3].

Используемый ниже для управления такой системой подход основан на методике, развитой в [4].

1. Постановка задачи и уравнения движения. Динамика рассматриваемой системы описывается уравнениями

Здесь ${{x}_{0}}$ – координата платформы на прямой, m₀ – масса платформы, ${{x}_{1}}$ – координата несущего тела, m₁ – масса несущего тела, ${{x}_{2}}$ – координата массы m₂ осциллятора, ${{c}_{1}} > 0$ – жесткость пружины, соединяющей платформу и несущее тело, ${{c}_{2}} > 0$ – жесткость пружины осциллятора, $\gamma > 0$ – коэффициент диссипации.

На управляющую силу $u$ и возмущение $v$ накладываются ограничения

Предполагается, что в каждый момент времени известны текущие значения фазовых переменных ${{x}_{0}},{{\dot {x}}_{0}},{{x}_{1}}$, а переменные ${{\dot {x}}_{1}},{{x}_{2}},{{\dot {x}}_{2}}$ не доступны для измерений.

Задача. Построить управление как функцию известных фазовых переменных ${{x}_{0}},\;{{\dot {x}}_{0}},\;{{x}_{1}}$, удовлетворяющее ограничению (1.2) и приводящее систему (1.1) в начало координат за конечное (нефиксированное) время из любого начального состояния.

2. Наблюдаемость системы. Покажем сначала, что по результатам наблюдений переменных ${{x}_{0}},{{\dot {x}}_{0}},{{x}_{1}}$ недоступные для измерений переменные ${{\dot {x}}_{1}},\;{{x}_{2}},\;{{\dot {x}}_{2}}$ могут быть вычислены. Для этого наряду с системой (1.1) рассмотрим систему уравнений, описывающую лишь динамику несущего тела с осциллятором (исключая платформу):

Здесь $x = ({{x}_{1}},{{x}_{2}},{{\dot {x}}_{1}},{{\dot {x}}_{2}}{{)}^{{\rm T}}}$ и

По условию задачи координата несущего тела доступна измерению, т.е. наблюдается величина

Пара $({{A}_{0}},e)$ наблюдаема, так как

Для восстановления в момент времени t текущих значений всего фазового вектора x(t) системы (2.1) воспользуемся стандартной процедурой нахождения фазового состояния по результатам наблюдений [5–7].

Пусть величина y(s) наблюдается на отрезке $[{{t}_{0}},t]$. Решение системы (2.1) и измеренный выход могут быть записаны в виде

Введем обозначения $H({{t}_{0}},s) = {{e}^{{\rm T}}}X({{t}_{0}},s)$. Тогда

Домножим обе части равенства (2.4) на ${{H}^{{\rm T}}}({{t}_{0}},s)$ и проинтегрируем на $[{{t}_{0}},t]$. Получим уравнение для нахождения вектора $x({{t}_{0}})$:

где

Из условия (2.2) следует, что координаты вектор-функции $H({{t}_{0}},s)$ линейно независимы на $[{{t}_{0}},t]$ и матрица $\hat {H}({{t}_{0}},t)$ обратима [6]. Поскольку координата x₀ доступна для измерений, то вектор-функция $w(\tau )$ известна, поэтому известна и вся правая часть уравнения (2.5). Следовательно, это уравнение однозначно разрешимо относительно $x({{t}_{0}})$. Текущее значение фазового вектора x(t) системы (2.1) может быть найдено теперь путем интегрирования этой системы и определяется первым из соотношений (2.3) при s = t.

3. Алгоритм построения управления. Положим $\bar {x} = ({{x}_{0}},{{x}_{1}},{{x}_{2}},{{\dot {x}}_{0}},{{\dot {x}}_{1}},{{\dot {x}}_{2}}{{)}^{{\rm T}}}$ и запишем систему уравнений (1.1) в векторной форме

Здесь матрица A₁ и вектор b₁ имеют вид

Можно показать, что определитель матрицы управляемости

равен $c_{1}^{4}c_{2}^{2}{\text{/}}m_{1}^{4}m_{2}^{2} \ne 0$. Следовательно, пара $({{A}_{1}},{{b}_{1}})$ управляема.

Наблюдаемость системы (2.1) позволяет считать вектор $x$ известным, следовательно, известен и весь фазовый вектор $\bar {x}$ системы (3.1). Учитывая управляемость системы (3.1), для приведения ее в начало координат может быть использован подход, развитый в [4] и примененный ниже. Этот подход позволяет построить закон управления в форме обратной связи, т.е. как функцию вектора текущего фазового состояния $\bar {x}$, удовлетворяющий ограничению (1.2) и при некоторых предположениях относительно $\rho $ останавливающий систему (3.1) в начале координат за конечное время.

Приведем систему (3.1) к более удобной для построения управления форме [4, 8]. Обозначим через  f последнюю строку матрицы ${{F}^{{ - 1}}}$ и составим построчно матрицу

Невырожденное линейное преобразование координат

с диагональной матрицей приводит систему (3.1) к виду

Здесь

Составим вектор $a \in {{R}^{6}}$ из элементов верхней строки матрицы A₂ и введем новое управление

Система (3.2) примет вид

где

Построим управление u(z) как функцию фазового вектора z, которое приводит систему (3.4) в окрестность начала координат. С этой целью введем в рассмотрение скалярную функцию T(z), диагональные матрицы

положительно-определенные матрицы R, Q и вектор $q \in {{\mathbb{R}}^{6}}$:

Функцию T(z) зададим неявно уравнением

Уравнение (3.5) относительно T для любого $z \ne 0$ имеет единственное положительное решение [4]. Функция $T(z) > 0$ является аналитической, обладает свойствами

доопределяется в нуле T(0) = 0 с сохранением непрерывности и служит функцией Ляпунова для системы (3.4).

Зададим теперь управление следующим образом:

Из соотношений (3.5), (3.7) вытекает, что функция $u(z)$ подчиняется неравенству

поэтому выбором постоянной d в уравнении (3.5) можно обеспечить выполнение любого наперед заданного ограничения на модуль управляющей функции.

В обозначениях

производная функции T в силу системы (3.4), управляемой по закону (3.7), удовлетворяет равенству где отрицательно определенная матрица P задана выражением

Из равенства (3.8) вытекает, что если выполнено соотношение

то имеет место неравенство которое вместе со свойствами (3.6) гарантирует убывание функции T вдоль траекторий системы до нуля за конечное время и тем самым приведение системы (3.4) в начало координат. Для выполнения же соотношения (3.9) достаточно, чтобы константа $\rho $ из ограничения (1.2) подчинялась неравенству

Здесь ${{q}_{ - }}$ и ${{q}_{ + }}$ – наименьшее и наибольшее собственные числа матрицы Q, а ${{p}_{ - }}$ – наименьшее собственное число матрицы P.

Из приведенных рассуждений следует, что управление

полученное с учетом соотношения (3.3), приводит в начало координат систему (3.2), а неравенство (3.10) служит достаточным условием такого приведения.

Как уже отмечалось выше, с помощью выбора постоянной d в уравнении (3.5) можно обеспечить выполнение любого наперед заданного ограничения на модуль функции u(z) во всем фазовом пространстве $z \in {{R}^{6}}$. Однако управление ${{u}_{0}}(z)$, в силу наличия дополнительного слагаемого u(z) в выражении (3.11), будет удовлетворять условию (1.2) лишь в некоторой ограниченной области. Тем не менее, используя предложенный алгоритм построения управления и последовательно переводя систему на некоторое конечное расстояние из одного состояния покоя в другое, с помощью управления, удовлетворяющего условию (1.2), можно из любого начального состояния переместить платформу в заданное положение и остановить колебания несущего тела и осциллятора.

4. Численное моделирование. Ниже приведены результаты компьютерного моделирования динамики рассматриваемой системы при следующих значениях параметров:

В качестве возмущения $v$ выступала сила трения, которая задавалась соотношением

Начальные состояния были выбраны следующими:

Система переводилась в начало координат.

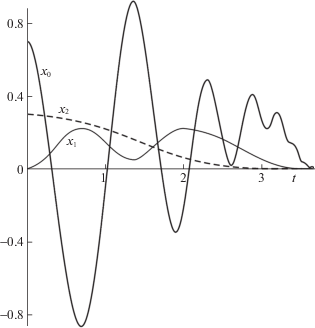
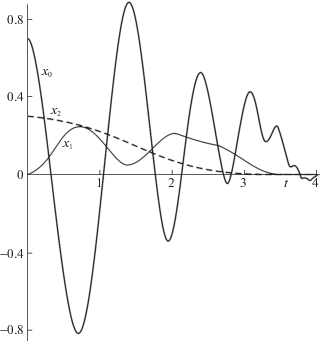
На рис. 2 изображены зависимости от времени координат всех трех масс системы, движущейся под действием предложенного управления в отсутствие возмущений. Жирная сплошная линия отвечает координате платформы, тонкая – координате контейнера, а штриховая – координате осциллятора. На рис. 3 представлены те же зависимости для системы с трением.

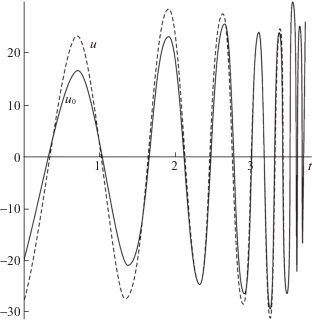
На рис. 4 приведены графики управляющих функций, реализовавшихся на полученной траектории системы. Сплошная линия здесь отвечает управлению ${{u}_{0}}(t)$, применяемому к исходной системе (1.1), а штриховая – управлению u(z), построенному для системы (3.4). Разность между значениями этих функций определяется слагаемым ${{a}^{{\rm T}}}z$ в выражении (3.3) и стремится к нулю по мере приближения системы к терминальному состоянию равновесия. При выбранном в уравнении (3.5) параметре $d = 100$, как видно из рисунка, максимальная абсолютная величина управления приблизительно равна 30 H.

Заключение. Развиваемый в работе подход позволяет управлять движением сложных механических систем, содержащих колебательные звенья, в условиях неполноты информации о фазовом состоянии системы. С помощью предлагаемых законов управления такие системы могут быть точно позиционированы в заданном положении за конечный промежуток времени даже при наличии неконтролируемых внешних возмущений. Приведенные результаты численного моделирования показывают, что при возмущениях, примерно на порядок меньших величины управления, динамика системы существенно не изменяется, а время движения увеличивается незначительно.