Известия РАН. Теория и системы управления, 2019, № 6, стр. 3-17
УПРАВЛЕНИЕ ОРИЕНТАЦИЕЙ ОБЪЕКТА НА ВРАЩАЮЩЕМСЯ ОСНОВАНИИ С ПОМОЩЬЮ ДВУХСТУПЕНЧАТОГО ЭЛЕКТРОПРИВОДА
Л. Д. Акуленко a, b, Н. Н. Болотник a, *, А. Е. Борисов a, А. А. Гавриков a, Г. А. Емельянов a
a ИПМех РАН
Москва, Россия
b ФГУП ЦНИИМаш
Королев, Россия
* E-mail: bolotnik@ipmnet.ru
Поступила в редакцию 21.06.2019
После доработки 02.07.2019
Принята к публикации 22.07.2019
Аннотация
Исследуется процесс управления поворотом объекта относительно вращающегося основания с помощью двухступенчатого электропривода, который представляет два последовательно соединенных безредукторных электропривода постоянного тока. Статор одного из электродвигателей жестко закреплен на основании, а на роторе другого двигателя закреплен объект. Между ротором и статором второго двигателя имеется крутильная пружина (торсион) с относительно малой жесткостью. Цель управления – отслеживание объектом заданной ориентации относительно основания. Строится алгоритм управления приводом с учетом неполноты информации о динамических параметрах механической системы, действующего в ней трения, законах движения основания и изменения отслеживаемой ориентации.
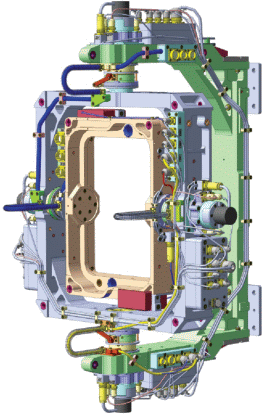
Введение. Проблема, рассматриваемая в данной статье, возникла в связи с разработкой системы управления поворотной платформой, которая устанавливается на орбитальном космическом аппарате и служит для прецизионного ориентирования закрепленного в ней объекта. Общий вид платформы показан на рис. 1 [1]. Основным компонентом конструкции платформы служит двухстепенной подвес, состоящий из двух жестких рамок (внешней и внутренней), вращающихся вокруг взаимно перпендикулярных осей. Внешняя рамка вращается вокруг оси, жестко связанной с космическим аппаратом, а внутренняя рамка – вокруг оси, жестко связанной с внешней рамкой. Во внутренней рамке закрепляется объект, ориентация которого контролируется с помощью поворотной платформы. Управление вращением рамок осуществляется посредством двух независимых электроприводов с двигателями постоянного тока. Платформа может использоваться для различных целей, в частности для управления уровнем микроускорений в заданных зонах объекта, что важно при проведении технологических экспериментов по выращиванию монокристаллов из расплавов в условиях, близких к невесомости [2–4]. В этом случае платформа служит активным виброзащитным устройством. Термин “микроускорение” используется в литературе по космонавтике. Под микроускорением материальной частицы понимается разность между ее ускорением относительно инерциальной системы отсчета и ускорением силы тяготения в точке нахождения частицы. По физическому содержанию термин “микроускорение” совпадает с термином “кажущееся ускорение”, использующимся в теории инерциальной навигации [5]. Процесс выращивания монокристаллов весьма чувствителен к так называемой боковой составляющей микроускорений, направленной перпендикулярно оси роста кристалла, и поэтому желательно поддерживать ориентацию технологического устройства, при которой ось роста кристалла будет направлена вдоль текущего направления вектора микроускорения. В [6] установлена принципиальная возможность устранения с помощью поворотной платформы боковой составляющей микроускорения взаданной точке чувствительной оси объекта и построен соответствующий “кинематический” закон управления рамками платформы, формируемый по принципу обратной связи. Для реализации этой возможности необходимо в каждый момент времени знать микроускорение в точке пересечения осей вращения рамок подвеса, угловое ускорение и угловую скорость основания, а также значения углов поворота рамок подвеса и их первых производных. Закон управления формирует значения текущих относительных угловых ускорений рамок подвеса, которые должны быть реализованы приводами.
Микроускорения, подлежащие снижению с помощью поворотной платформы, весьма малы и могут оказаться сравнимыми с ускорениями, создаваемыми трением в подшипниках осей вращения рамок подвеса платформы. Поэтому алгоритмы управления приводами рамок подвеса должны строиться на основе динамической модели с учетом трения, параметры которого (в частности, коэффициент сухого трения) заранее не известны и могут существенно (в несколько раз) изменяться в процессе движения. Такой алгоритм для упрощенной модели с одной степенью свободы предложен и исследован в [7]. Механическая система состоит из вращающегося основания и твердого тела, которое может поворачиваться относительно основания вокруг оси, совпадающей с осью вращения основания. Управление движением тела относительно основания осуществляется с помощью безредукторного электропривода. Управляющей переменной служит напряжение, подаваемое на клеммы якоря электродвигателя. Предложена динамическая модель системы, учитывающая момент сил трения в подшипниках качения относительно оси вращения. Момент сил трения качения представляется нечетной функцией угловой скорости вращения тела, имеющей разрыв первого рода в нуле, подобно характеристике сухого трения. Решается задача оптимального управления приведением тела в заданное угловое положение в отсутствие трения. Минимизируемым функционалом служит интеграл по времени от квадратичной функции управляющих и фазовых переменных. Для системы с трением построены квазиоптимальные законы управления в форме синтеза и оценены зоны застоя, обусловленные наличием сухого трения скольжения при качении. Предложены режимы управления с компенсацией неидеальностей и возмущающих факторов. Проведено математическое моделирование и определены динамические характеристики управляемого процесса.
Для повышения точности отработки требуемой ориентации рамок подвеса и изоляции рамок от непосредственного влияния трения в подшипниках предлагается двухступенчатая конструкция приводов. Двухступенчатый привод содержит два независимо управляемых электродвигателя. Статор электродвигателя первой ступени расположен на теле, относительно которого вращается соответствующая рамка (на основании, связанном с космическим аппаратом, для внешней рамки и на внешней рамке для внутренней рамки). Ротор двигателя первой ступени вращается в подшипниках, жестко закрепленных на статоре. На роторе двигателя первой ступени жестко закреплен статор двигателя второй ступени, а ротор двигателя второй ступени связан со статором посредством крутильной пружины (торсиона) относительно небольшой жесткости. Ротор двигателя второй ступени привода жестко связан с соответствующей рамкой платформы. В настоящей работе проводится исследование возможностей и качества управления ориентацией жесткого объекта относительно вращающегося основания с помощью двухступенчатого электропривода. Динамическая модель исследуемой системы отличается от модели, рассмотренной в [7], тем, что одноступенчатый электропривод заменен двухступенчатым, в результате чего система имеет две степени свободы. Предлагается закон управления, обеспечивающий желаемое качество переходных процессов в каждой ступени в отсутствие трения и других возмущений. В основе этого закона управления лежат линейные пропорционально-дифференциальные (ПД) регуляторы. Затем предложенный алгоритм управления применяется к системе, в которой имеется трение в подшипниках и, кроме того, в отличие от [7], некоторые переменные, входящие в закон управления, недоступны прямому измерению с достаточной точностью. Для этих переменных предлагается процедура оценивания на основе полиномиальной фильтрации. Проводятся численные эксперименты с целью оценки влияния трения и погрешностей измерений на качество переходных процессов в приводах и точность отслеживания объектом требуемой ориентации относительно основания, которая в общем случае изменяется со временем.
В [8, 9] построены альтернативные законы управления с обратной связью для модельных систем с одноступенчатым и двухступенчатым электроприводами соответственно. Эти законы обладают робастностью по отношению к малым возмущениям и ошибкам измерения и в случае отклонения объекта от желаемой ориентации обеспечивают возврат к этой ориентации за конечное время. Построенные законы управления позволяют учесть ограничения, налагаемые на управляющие переменные (входные напряжения электродвигателей), однако их алгоритмическая реализация значительно сложнее, чем реализация режимов управления, предложенных в [7] и в настоящей работе.
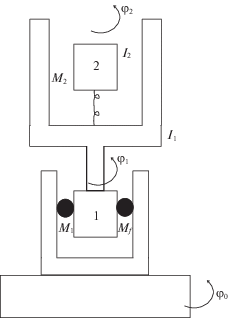
1. Модель электромеханической системы. Рассматривается система, состоящая из основания, которое может вращаться вокруг неподвижной оси, объекта, который может вращаться относительно основания вокруг той же оси, и двухступенчатого электропривода, управляющего движением объекта относительно основания (рис. 2). Двухступенчатый электропривод представляет собой два независимых электропривода постоянного тока, объединенных в каскад. Статор электродвигателя первой ступени привода жестко связан с основанием, а с валом ротора этого двигателя жестко связан статор двигателя второй ступени. Ротор двигателя первой ступени вращается в подшипниках, закрепленных на основании. Ротор и статор двигателя второй ступени связаны посредством торсиона (крутильной пружины). На валу ротора двигателя второй ступени жестко закреплен объект. Роторы обоих электродвигателей вращаются вокруг общей оси, совпадающей с осью вращения основания. Между статором и ротором двигателя первой ступени имеется трение, вызванное контактным взаимодействием ротора с подшипниками, в которых он вращается относительно статора.
Введем обозначения: φ0 – угол поворота основания относительно неподвижной (инерциальной) системы отсчета, φ1 – угол поворота ротора двигателя первой ступени относительно основания, φ2 – угол поворота объекта относительно статора двигателя второй ступени, ${{I}_{1}}$ – момент инерции ротора двигателя первой ступени вместе со статором двигателя второй ступени, ${{I}_{2}}$ – момент инерции объекта вместе с ротором двигателя второй ступени, c – коэффициент крутильной жесткости торсиона, M1 – управляющий момент, создаваемый двигателем первой ступени и приложенный к ротору этого двигателя, M2 – управляющий момент, создаваемый двигателем второй ступени и приложенный к ротору этого двигателя, ${{M}_{f}}$ – момент сил трения, действующих между статором и ротором двигателя первой ступени. Все моменты инерции и крутящие моменты вычисляются относительно общей оси вращения соответствующих тел.
Движение описанной механической системы относительно основания при заданном законе ${{\varphi }_{0}}(t)$ вращения последнего подчиняется уравнениям
(1.1)
${{I}_{1}}({{\ddot {\varphi }}_{0}} + {{\ddot {\varphi }}_{1}}) = c{{\varphi }_{2}} + {{M}_{1}} - {{M}_{2}} + {{M}_{f}}({{\dot {\varphi }}_{1}}),$(1.2)
${{I}_{2}}({{\ddot {\varphi }}_{0}} + {{\ddot {\varphi }}_{1}} + {{\ddot {\varphi }}_{2}}) = {{M}_{2}} - c{{\varphi }_{2}}.$Моменты ${{M}_{\alpha }},\alpha = 1,2$, связаны с управляющими электрическими напряжениями ${{U}_{\alpha }}$ известными соотношениями для двигателей постоянного тока [10]:
(1.3)
${{L}_{\alpha }}\frac{{d{{i}_{\alpha }}}}{{dt}} + {{R}_{\alpha }}{{i}_{\alpha }} + {{k}_{\alpha }}{{\dot {\varphi }}_{\alpha }} = {{U}_{\alpha }},\quad {{M}_{\alpha }} = {{k}_{\alpha }}{{i}_{\alpha }},\quad \alpha = 1,2,$Предположим, что электромагнитная постоянная времени электродвигателя $L{\text{/}}R$ много меньше времени T, на котором рассматривается движение системы и времени выхода электропривода на стационарный режим вращения при постоянном напряжении. В этом случае можно пренебречь электродвижущей силой самоиндукции и вместо уравнений (1.3) пользоваться приближенными уравнениями
(1.4)
${{R}_{\alpha }}{{i}_{\alpha }} + {{k}_{\alpha }}{{\dot {\varphi }}_{\alpha }} = {{U}_{\alpha }},\quad {{M}_{\alpha }} = {{k}_{\alpha }}{{i}_{\alpha }},\quad \alpha = 1,2.$Момент сил трения ${{M}_{f}}({{\dot {\varphi }}_{1}})$ будем характеризовать следующей модельной зависимостью:
(1.5)
${{M}_{f}} = \left\{ \begin{gathered} - \varkappa ({{{\dot {\varphi }}}_{1}}){\text{sign}}{{{\dot {\varphi }}}_{1}},\quad {{{\dot {\varphi }}}_{1}} \ne 0, \hfill \\ - {{M}_{e}},\quad {{{\dot {\varphi }}}_{1}} = 0,\quad \left| {{{M}_{e}}} \right| \leqslant \kappa (0), \hfill \\ - \varkappa (0){\text{sign}}{{M}_{e}},\quad {{{\dot {\varphi }}}_{1}} = 0,\quad \left| {{{M}_{e}}} \right| > \kappa (0), \hfill \\ \end{gathered} \right.$Функция $\kappa ({{\dot {\varphi }}_{1}})$ характеризует модуль момента сил трения в зависимости от угловой скорости ${{\dot {\varphi }}_{1}}$ и может сильно изменяться при изменении ${{\dot {\varphi }}_{1}}$. Величина $\kappa (0)$ есть максимальное значение момента сил трения покоя. Выражение (1.5) обобщает закон сухого трения Кулона, для которого $\kappa ({{\dot {\varphi }}_{1}})$ – постоянная величина. Выбором подходящей функции $\kappa ({{\dot {\varphi }}_{1}})$ в выражении (1.5) можно удовлетворительно смоделировать влияние на систему момента сил трения в подшипниках качения.
Подобная модель трения использовалась в [11] при моделировании процесса прецизионного управления электромеханической системой.
2. Основная задача и принцип формирования управления. Обозначим через Φ угол поворота объекта относительно основания: $\Phi = {{\varphi }_{1}} + {{\varphi }_{2}}$. Цель управления системой – обеспечить устойчивое отслеживание объектом ориентации относительно основания, определяемой заданной функцией ${{\Phi }_{0}}(t)$. Построим, исходя из уравнений (1.1) и (1.2), управляющие моменты M1 и ${{M}_{2}}$, при которых поведение переменных $\Psi = \Phi - {{\Phi }_{0}}$ и ${{\varphi }_{2}}$ подчиняется независимым уравнениям с постоянными коэффициентами:
(2.1)
$\ddot {\Psi } + {{a}_{1}}\dot {\Psi } + {{b}_{1}}\Psi = 0,\quad {{a}_{1}} > 0,\quad {{b}_{1}} > 0,\quad \Psi = {{\varphi }_{1}} + {{\varphi }_{2}} - {{\Phi }_{0}},$(2.2)
${{\ddot {\varphi }}_{2}} + {{a}_{2}}{{\dot {\varphi }}_{2}} + {{b}_{2}}{{\varphi }_{2}} = 0,\quad {{a}_{2}} > 0,\quad {{b}_{2}} > 0.$Уравнение (2.1) описывает переходный процесс отслеживания объектом заданной ориентации ${{\Phi }_{0}}(t)$ относительно основания, а уравнение (2.2) – динамику изменения угла ${{\varphi }_{2}}$ закрутки торсиона. На этом этапе будем предполагать, что все параметры механической системы и закона трения известны точно, а фазовые переменные измеряются в каждый момент времени без погрешностей. Будем также предполагать точно известными вместе с производными нужного порядка функции ${{\varphi }_{0}}(t)$ и ${{\Phi }_{0}}(t)$, характеризующие движение основания относительно неподвижной системы отсчета и отслеживаемый угол поворота объекта относительно основания соответственно.
Разрешив уравнения (2.1) и (2.2) относительно угловых ускорений ${{\ddot {\varphi }}_{1}}$ и ${{\ddot {\varphi }}_{2}}$, получим
(2.3)
${{\ddot {\varphi }}_{1}} = {{\ddot {\Phi }}_{0}} + {{a}_{1}}{{\dot {\Phi }}_{0}} + {{b}_{1}}{{\Phi }_{0}} - {{a}_{1}}{{\dot {\varphi }}_{1}} - {{b}_{1}}{{\varphi }_{1}} - ({{a}_{1}} - {{a}_{2}}){{\dot {\varphi }}_{2}} - ({{b}_{1}} - {{b}_{2}}){{\varphi }_{2}},$Подставив эти выражения в уравнения (1.1), (1.2), найдем управляющие моменты
(2.5)
$\begin{gathered} {{M}_{1}} = \left( {{{I}_{1}} + {{I}_{2}}} \right)\left( {{{{\ddot {\Phi }}}_{0}} + {{a}_{1}}{{{\dot {\Phi }}}_{0}} + {{b}_{1}}{{\Phi }_{0}} + {{{\ddot {\varphi }}}_{0}}} \right) - {{M}_{f}}({{{\dot {\varphi }}}_{1}}) - \\ \, - \left( {{{I}_{1}} + {{I}_{2}}} \right)\left[ {{{a}_{1}}({{{\dot {\varphi }}}_{1}} + {{{\dot {\varphi }}}_{2}}) + {{b}_{1}}({{\varphi }_{1}} + {{\varphi }_{2}})} \right] + {{I}_{1}}({{a}_{2}}{{{\dot {\varphi }}}_{2}} + {{b}_{2}}{{\varphi }_{2}}), \\ \end{gathered} $(2.6)
${{M}_{2}} = {{I}_{2}}({{\ddot {\Phi }}_{0}} + {{a}_{1}}{{\dot {\Phi }}_{0}} + {{b}_{1}}{{\Phi }_{0}}) + {{I}_{2}}\left[ {{{{\ddot {\varphi }}}_{0}} - {{a}_{1}}({{{\dot {\varphi }}}_{1}} + {{{\dot {\varphi }}}_{2}}) - {{b}_{1}}({{\varphi }_{1}} + {{\varphi }_{2}})} \right] + c{{\varphi }_{2}}.$Выражения (2.5) и (2.6) определяют управляющие моменты, формируемые по принципу обратной связи как функции текущих значений фазовых переменных ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\dot {\varphi }}_{1}}$, ${{\dot {\varphi }}_{2}}$ и времени t.
Для того, чтобы получить соответствующие законы формирования управляющих напряжений ${{U}_{1}}$ и ${{U}_{2}}$ для двигателей первой и второй ступеней, нужно в левой части первого уравнения (1.4) для соответствующего $\alpha $ сделать подстановку ${{i}_{\alpha }} = {{M}_{\alpha }}{\text{/}}{{k}_{\alpha }}$, где ${{M}_{\alpha }}$ определяется соотношениями (2.5) и (2.6). В итоге придем к выражениям, формирующим управляющие напряжения по принципу обратной связи по переменным ${{\varphi }_{\alpha }}$, ${{\dot {\varphi }}_{\alpha }}$ и t:
(2.7)
${{U}_{\alpha }} = \frac{{{{R}_{\alpha }}}}{{{{k}_{\alpha }}}}{{M}_{\alpha }}({{\varphi }_{1}},{{\varphi }_{2}},{{\dot {\varphi }}_{1}},{{\dot {\varphi }}_{2}},t) - {{k}_{\alpha }}{{\dot {\varphi }}_{\alpha }},\quad \alpha = 1,2.$Законы управления, выражаемые равенствами (2.5)–(2.7), обеспечивают динамику переходных процессов по переменным $\Psi $ и φ2, подчиняющуюся уравнениям (2.1) и (2.2). Переходные процессы можно регулировать подбором коэффициентов ai, bi, $i = 1,2$, входящих в законы управления, причем качество переходных процессов по переменным Ψ и φ2 можно регулировать независимо. Качество переходных процессов определяется корнями характеристического полинома уравнений (2.1) или (2.2), которые задаются выражениями
(2.8)
$\lambda _{i}^{ \pm } = \frac{{ - {{a}_{i}} \pm \sqrt {a_{i}^{2} - 4{{b}_{i}}} }}{2},\quad i = 1,2.$Если, например, выбрать параметры, удовлетворяющие неравенству $a_{i}^{2} - 4{{b}_{i}} \geqslant 0$, то оба корня будут действительными и соответствующий переходный процесс будет апериодическим (неколебательным), а выбор параметра ${{b}_{i}}$, согласованного с параметром ai равенством ${{b}_{i}} = a_{i}^{2}{\text{/}}4$, отвечает наискорейшему затуханию переходного процесса при заданном ai. Время затухания переходного процесса при произвольных положительных ai и ${{b}_{i}}$ характеризуется величиной τi = = $ - 1{\text{/min}}[{\text{Re}}\lambda _{i}^{ - },{\text{Re}}\lambda _{i}^{ + }]$; ${{\tau }_{i}} > 0$, если ${{a}_{i}} > 0$ и ${{b}_{i}} > 0$. Величина ${{\eta }_{i}} = - min[{\text{Re}}\lambda _{i}^{ - },{\text{Re}}\lambda _{i}^{ + }]$ называется степенью устойчивости линейной системы второго порядка (2.1) или (2.2). Понятие степени устойчивости для линейной системы дифференциальных уравнений произвольного порядка с постоянными коэффициентами введено в [12]. Геометрически степень устойчивости асимптотически устойчивой линейной системы с постоянными коэффициентами определяется расстоянием точки, представляющей на комплексной плоскости корень характеристического полинома с минимальным модулем вещественной части, от мнимой оси.
При настройке параметров устройства управления вращением объекта с целью поддержания требуемой его ориентации относительно вращающегося основания нужно учитывать много критериев, зачастую противоречащих друг другу: время переходного процесса по соответствующей переменной, максимальное отклонение регулируемой переменной от номинального программного значения, максимальный момент, создаваемый электродвигателем, максимально допустимое напряжение, которое можно подать на соответствующий электродвигатель, максимально допустимый ток в цепи якоря электродвигателя и другие характеристики. Кроме того, при проектировании и эксплуатации системы управления нужно учитывать неполноту информации о динамических параметрах механической системы, закона трения, а также законов движения основания ${{\varphi }_{0}}(t)$ и изменения номинальной ориентации ${{\Phi }_{0}}(t)$, которую необходимо отслеживать. Величины ${{\varphi }_{0}}(t)$ и ${{\Phi }_{0}}(t)$ или их производные могут быть не заданными заранее, а оцениваться в ходе процесса управления по данным текущих изменений. Сказанное обусловливает целесообразность выбирать коэффициенты ${{a}_{i}}$ и ${{b}_{i}}$ исходя из результатов теоретического анализа поведения системы на основе упрощенной идеализированной модели, математического моделирования с учетом неидеальностей и экспериментальной отработки системы.
3. Модификация основного алгоритма управления с учетом неполноты информации о параметрах системы и действующих возмущениях. Двухступенчатый электропривод, описанный в разд. 1, был предложен для управления поворотной платформой, расположенной на орбитальном космическом аппарате и служащей для поддержания ориентации оси закрепленного на ней объекта в направлении микроускорения контрольной точки, лежащей на оси объекта.
Мгновенное значение микроускорения с достаточной степенью точности можно измерить с помощью трехосного акселерометра, расположенного вблизи контрольной точки объекта. На основе этого измерения можно определить мгновенную ориентацию вектора микроускорения. В упрощенной модели, описанной в разд. 1 и 2, этой ориентации отвечает угол ${{\Phi }_{0}}(t)$. С помощью датчиков угловых скоростей можно измерить мгновенное значение угловой скорости вращения космического аппарата. Этой величине в модели отвечает угловая скорость ${{\dot {\varphi }}_{0}}(t)$.
В дальнейшем предполагается, что величины ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\dot {\varphi }}_{1}}$ и ${{\dot {\varphi }}_{2}}$ доступны точному измерению в каждый момент времени, причем эти измерения производятся без запаздывания. Входящие в закон управления (2.5), (2.6) величины ${{\Phi }_{0}},$ ${{\dot {\Phi }}_{0}}$, ${{\ddot {\Phi }}_{0}}$ и ${{\ddot {\varphi }}_{0}}$ непосредственному измерению недоступны, и вместо них в соответствующие формулы должны быть подставлены оценки ${{\hat {\Phi }}_{0}}(t),$ ${{\hat {\dot {\Phi }}}_{0}}(t)$, ${{\hat {\ddot {\Phi }}}_{0}}(t)$ и ${{\hat {\ddot {\varphi }}}_{0}}(t)$, формирующиеся для каждого момента времени $t$ на основе доступной к этому моменту измерительной информации о ${{\Phi }_{0}},$ ${{\ddot {\Phi }}_{0}}$ и ${{\ddot {\varphi }}_{0}}$.
Кроме того, затруднено точное измерение крутильной жесткости торсиона $c$, которая может изменяться в процессе эксплуатации системы, и недоступно точное знание о характеристиках трения, в частности о функции $\kappa ({{\dot {\varphi }}_{1}})$ в модели (1.5). Поэтому вместо $c$ и ${{M}_{f}}({{\dot {\varphi }}_{1}})$ будут использоваться оценки $\hat {c}$ и ${{\hat {M}}_{f}}({{\dot {\varphi }}_{1}})$ этих величин.
Таким образом, выражения (2.5) и (2.6) для управляющих моментов ${{M}_{1}}$ и ${{M}_{2}}$, примут вид
(3.1)
$\begin{gathered} {{M}_{1}} = \left( {{{I}_{1}} + {{I}_{2}}} \right)({{{\hat {\ddot {\Phi }}}}_{0}} + {{a}_{1}}{{{\hat {\dot {\Phi }}}}_{0}} + {{b}_{1}}{{{\hat {\Phi }}}_{0}} + {{{\hat {\ddot {\varphi }}}}_{0}}) - {{{\hat {M}}}_{f}}({{{\dot {\varphi }}}_{1}}) - \\ \, - \left( {{{I}_{1}} + {{I}_{2}}} \right)\left[ {{{a}_{1}}({{{\dot {\varphi }}}_{1}} + {{{\dot {\varphi }}}_{2}}) + {{b}_{1}}({{\varphi }_{1}} + {{\varphi }_{2}})} \right] + {{I}_{1}}({{a}_{2}}{{{\dot {\varphi }}}_{2}} + {{b}_{2}}{{\varphi }_{2}}), \\ \end{gathered} $(3.2)
${{M}_{2}} = {{I}_{2}}({{\hat {\ddot {\Phi }}}_{0}} + {{a}_{1}}{{\hat {\dot {\Phi }}}_{0}} + {{b}_{1}}{{\hat {\Phi }}_{0}}) + {{I}_{2}}[{{\hat {\ddot {\varphi }}}_{0}} - {{a}_{1}}({{\dot {\varphi }}_{1}} + {{\dot {\varphi }}_{2}}) - {{b}_{1}}({{\varphi }_{1}} + {{\varphi }_{2}})] + \hat {c}{{\varphi }_{2}}.$В результате переходные процессы по переменным $\Psi $ и ${{\varphi }_{2}}$ будут описываться уравнениями
(3.3)
$\begin{array}{*{20}{c}} {\ddot {\Psi } + {{a}_{1}}\dot {\Psi } + {{b}_{1}}\Psi = ({{{\hat {\ddot {\Phi }}}}_{0}} - {{{\ddot {\Phi }}}_{0}}) + ({{{\hat {\ddot {\varphi }}}}_{0}} - {{{\ddot {\varphi }}}_{0}}) + \frac{{\hat {c} - c}}{{{{I}_{2}}}}{{\varphi }_{2}} + } \\ {\, + {{a}_{1}}({{{\hat {\dot {\Phi }}}}_{0}} - {{{\dot {\Phi }}}_{0}}) + {{b}_{1}}({{{\hat {\Phi }}}_{0}} - {{\Phi }_{0}}),} \end{array}$(3.4)
${{\ddot {\varphi }}_{2}} + {{a}_{2}}{{\dot {\varphi }}_{2}} + \left[ {{{b}_{2}} + \frac{{{{I}_{1}} + {{I}_{2}}}}{{{{I}_{1}}{{I}_{2}}}}(c - \hat {c})} \right]{{\varphi }_{2}} = \frac{{{{{\hat {M}}}_{f}}({{{\dot {\varphi }}}_{1}}) - {{M}_{f}}({{{\dot {\varphi }}}_{1}})}}{{{{I}_{1}}}}.$Эти уравнения в сочетании с алгоритмами оценивания величин, недоступных непосредственному измерению, будут использоваться для моделирования и оценки качества процесса управления вращением объекта с помощью двухступенчатого электропривода.
4. Алгоритмы построения оценок неизвестных величин. Кратко опишем используемые рекуррентные алгоритмы эквидистантной (с равноотстоящими замерами) полиномиальной фильтрации [13, 14] динамических параметров. Для определенности и простоты описания рассматривается последовательность измерений $z(t) = {{z}_{i}}$ скалярной динамической величины $x(t)$ в эквидистантные моменты времени $t = {{t}_{i}} = {{t}_{0}} + ih,$ $i = 0,1,2, \ldots $, где h – постоянный промежуток времени между двумя последовательными измерениями, который предполагается достаточно малым. Считается, что величина x измеряется с погрешностью $\xi ,$ т.е. показание измерительного прибора zi при i-м измерении величины x задается выражением ${{z}_{i}} = {{x}_{i}} + {{\xi }_{i}},$ где $\xi $ – центрированная случайная погрешность измерений со стационарным (нормальным) распределением. Полагается, что значения ${{x}_{i}}$ функции $x(t)$ в моменты ${{t}_{i}}$ могут быть аппроксимированы некоторым простым семейством функций (полиномов типа отрезков ряда Тейлора) на достаточно большом множестве ${\text{\{ }}j{\text{\} }} \subset \mathbb{N}{\text{:}}$
Величина N может быть ограниченной некоторым значением $N = N{\text{*}}$ или неограниченно возрастающей, например $N = N(i) = i;$ количество замеров $N + 1$ должно быть достаточно большим для возможности приближенного определения искомых параметров ${{\alpha }_{0}},{{\alpha }_{1}},{{\alpha }_{2}}, \ldots ,{{\alpha }_{n}},$ имеющих смысл текущих значений величины x и ее производных до порядка $n$ включительно в момент измерения ti:
Ограничимся параболической оценкой [13] фазового вектора $\alpha = ({{\alpha }_{0}},{{\alpha }_{1}},{{\alpha }_{2}}),$ достаточной для построения режимов управления, на основе модифицированного стандартного метода наименьших квадратов Гаусса.
Проводится минимизация среднеквадратического критерия по вектору параметров $({{\alpha }_{0}},{{\alpha }_{1}},{{\alpha }_{2}}){\text{:}}$
При фиксированном значении величины N ≥ 2 искомые оптимальные параметры имеют вид оценок
Весовые функции Fn, $n = 0,1,2$, фильтра (4.1) определяются выражениями [13, 14]
Алгоритм требует хранения в памяти более $N \geqslant 2$ замеров, и их число возрастает со временем с ростом $N.$ Поэтому естественно стремление к построению рекуррентного алгоритма, позволяющего экономить оперативную память аналогично фильтрации Калмана. В случае, когда величина $N = N(i) = i$ неограниченно возрастает, рекуррентная процедура оценки фазового вектора при измерении ${{z}_{{i + 1}}}$ на $(i + 1)$-м шаге имеет вид формул уточнения предыдущей оценки, получаемых из сравнения формул (4.1) для $N = i$ и $N = i + 1$ с выражением соответствующей невязки:
(4.2)
$\begin{gathered} {{{\hat {\alpha }}}_{1}}(i + 1) = {{{\hat {\alpha }}}_{1}}(i) + {{{\hat {\alpha }}}_{2}}(i)h + \\ \, + \frac{{18(2i + 3)}}{{h(i + 2)(i + 3)(i + 4)}}\left[ {{{z}_{{i + 1}}} - \left( {{{{\hat {\alpha }}}_{0}}(i) + {{{\hat {\alpha }}}_{1}}(i)h + {{{\hat {\alpha }}}_{2}}(i)\frac{{{{h}^{2}}}}{2}} \right)} \right], \\ \end{gathered} $Последние слагаемые в этих выражениях имеют смысл коррекции прогноза, определяемого предшествующими слагаемыми. Для получения оценок ${{\hat {\alpha }}_{k}}(i + 1),$ $k = 0,1,2$, на $(i + 1)$-м шаге требуется знать оценки, определенные на предыдущем i-м шаге, и результаты измерения ${{z}_{{i + 1}}}$ на $(i + 1)$-м шаге. Для вычисления последующих оценок хранить в памяти компьютера величины ${{\hat {\alpha }}_{k}}(i),$ $k = 0,1,2$, и ${{z}_{{i + 1}}}$ не нужно.
Параболическая аппроксимация переменной $x({{t}_{i}})$ на большом (неограниченном) интервале может оказаться недостаточной, тогда потребуются более сложные выражения и увеличение числа коэффициентов аппроксимации $\alpha (i)$. Это может привести к резкому росту стохастических погрешностей. Для увеличения точности фильтрации понадобится согласование порядка степени полинома и числа измеряемых значений при фиксированных других конструктивных параметрах алгоритма.
Рекуррентные алгоритмы полиномиальной фильтрации на основе фиксированного (заданного) числа измерений $0 \leqslant j \leqslant N(i)$ посредством отрезков парабол по временным интервалам существенно сложнее и задаются более громоздкими выражениями:
(4.3)
$\begin{gathered} \, - \frac{{12}}{h}\frac{{{{N}^{2}} - 13N - 3}}{{(N - 1)N(N + 2)(N + 3)}}{{{\hat {\alpha }}}_{0}}(i) + h\frac{{13{{N}^{3}} + 55{{N}^{2}} + 19N + 3}}{{(N - 1)(N + 2)(N + 3)}}{{{\hat {\alpha }}}_{2}}(i) + \\ \, + \frac{{18}}{h}\frac{{2N + 1}}{{(N + 1)(N + 2)(N + 3)}}{{z}_{{i + 1}}} - \frac{6}{h}\frac{{4N + 1}}{{(N - 1)N(N + 1)}}{{z}_{{i - N}}}, \\ \end{gathered} $Начальные величины (при $i \leqslant N(i)$) ${{\hat {\alpha }}_{0}}(i),\;{{\hat {\alpha }}_{1}}(i),\;{{\hat {\alpha }}_{2}}(i)$ берутся из предыдущего алгоритма. Таким образом, для получения оценок ${{\hat {\alpha }}_{k}}(i + 1),$ $k = 0,1,2$, на $(i + 1)$-м шаге требуется знать оценки, полученные на предыдущем i-м шаге, результаты измерения ${{z}_{{i + 1}}}$ на $(i + 1)$-м шаге и результаты измерения ${{z}_{{i - N}}}$ на $(i - N)$-м шаге. Последнее свойство существенно изменяет характер рекуррентности, поскольку нужно хранить в памяти $N + 1$ последних замеров, а для оценки на текущем шаге i + 1 используется замер ${{z}_{{i - N}}}$. Аналогично рекуррентным выражениям (4.2) формулы (4.3) выводятся из формул (4.1) для оценок в моменты i + 1 и $i - N$ с коррекцией получаемых выражений на величину невязки.
5. Моделирование процесса управления с учетом неидеальностей. Будем считать доступными точному измерению текущие значения фазовых переменных ${{\varphi }_{i}}$, ${{\dot {\varphi }}_{i}}$, $i = 1,2.$ Будем также считать точно известными значения моментов инерции ${{I}_{1}}$ и ${{I}_{2}}$ соответствующих тел системы. Крутильная жесткость торсиона полагается заданной с помощью оценки $\hat {c},$ действительная жесткость имеет вид $c = c(t) = \hat {c}(1 + \xi ),$ где $\xi $ – равномерно распределенная на отрезке $[ - 0.05,0.05]$ случайная величина. Таким образом, в каждый момент времени крутильная жесткость известна с погрешностью, не превышающей 5%.
Истинные значения отслеживаемого угла ${{\Phi }_{0}}$ и угла поворота основания φ0 при моделировании задаются гармоническими функциями
Далее полагается ${{a}_{{\varphi ,\Phi }}} = 0.01$, ${{\omega }_{\varphi }} = 0.01$ Гц, ${{\omega }_{\Phi }} = 0.02$ Гц. Функции ${{\hat {\dot {\Phi }}}_{0}},$ ${{\hat {\ddot {\Phi }}}_{0}},$ ${{\hat {\ddot {\varphi }}}_{0}}$ строятся с помощью вышеописанных алгоритмов оценивания на основе замеров ${{\Phi }_{0}}({{t}_{i}}) + 2{{\eta }_{e}},$ ${{\ddot {\Phi }}_{0}}({{t}_{i}}) + 2\omega _{\Phi }^{2}{{\eta }_{e}}$ и ${{\ddot {\varphi }}_{0}}({{t}_{i}}) + \omega _{\varphi }^{2}{{\eta }_{e}}$ соответственно, где ${{\eta }_{e}} = {{10}^{{ - 4}}}\eta ,$ $\eta $ – случайная величина со стандартным нормальным распределением.
В приводимых ниже расчетах значения величин ${{I}_{1}},\;{{I}_{2}},\;\hat {c}$ соответствуют экспериментальной установке: ${{I}_{1}} = 3.2 \times {{10}^{{ - 4}}}$ кг ⋅ м2, ${{I}_{2}} = 3.5$ кг ⋅ м2, $\hat {c} = 3.6649 \times {{10}^{{ - 4}}}$ Н · м/рад. Функция, характеризующая момент сил трения $\kappa ({{\dot {\varphi }}_{1}}),$ задается зависимостью
На рис. 3–11 приведены результаты моделирования поведения исследуемой системы при различных значениях коэффициентов обратной связи. Интегрирование системы (3.3), (3.4) проводится по методу Эйлера первого порядка (выбор схемы низкого порядка обусловлен наличием разрывных членов в правой части). Шаг интегрирования (равный шагу замеров) в силу используемой схемы интегрирования выбирается достаточно малым: $h = T{\text{/}}{{10}^{5}},$ где (0, T) – интервал численного интегрирования системы (3.3). Для повышения качества работы фильтров (4.1)–(4.3) проводится их предварительная настройка: часть замеров, а именно на интервале $( - T{\text{/}}10,0),$ проводится до начала движения системы и включения алгоритма управления. Размер памяти фильтра (4.3) полагается равным 5 × 104 замеров. Поскольку при численном моделировании достоверно отразить режим движения с залипаниями, свойственный системам с сухим трением (т.е. отследить обращение в ноль величины ${{\dot {\varphi }}_{1}}(t)$), представляется затруднительным, то вместо закона (1.5) используется следующее его приближение:
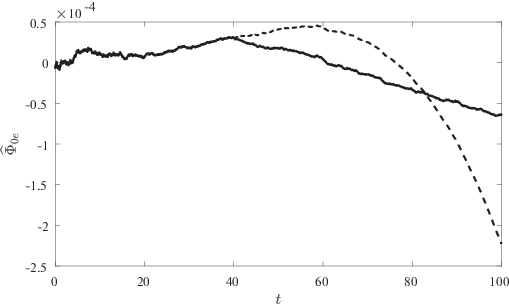
Рис. 10.
Разность между выходными сигналами фильтров с неограниченной памятью и с рекуррентным алгоритмом фильтрации по переменной ${{\Phi }_{0}}$
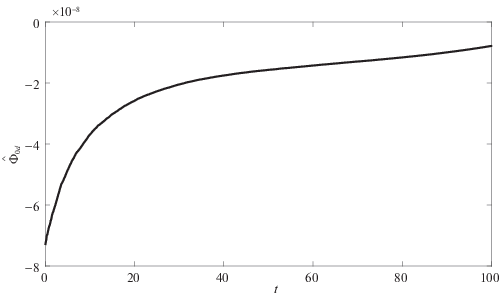
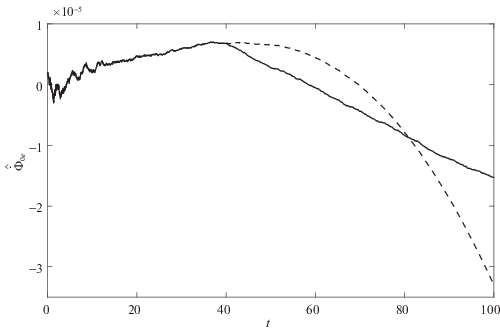
Рис. 11.
Погрешность восстановления величины ${{\dot {\Phi }}_{0}}$ по данным измерений ${{\Phi }_{0}}$
В расчетах полагалось $\varepsilon = {{h}^{3}},$ где $h$ – шаг интегрирования.
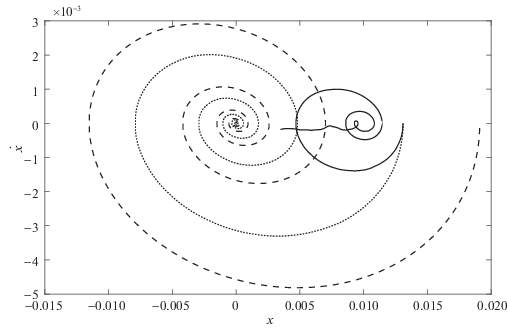
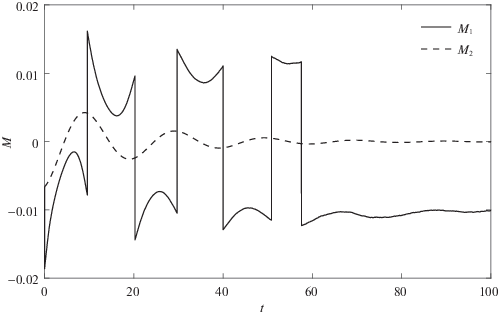
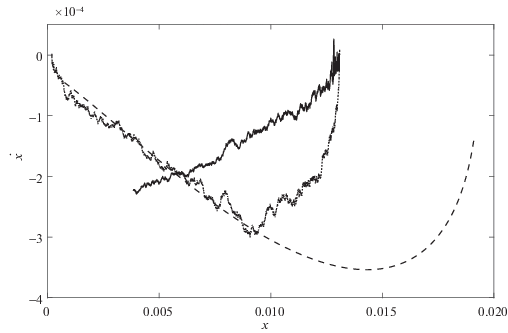
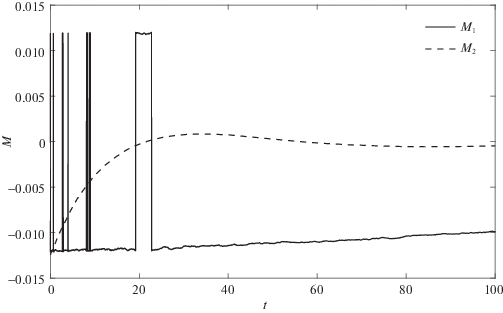
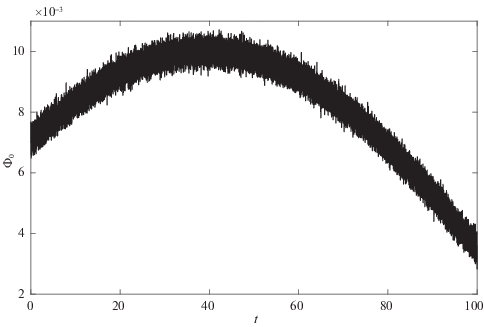
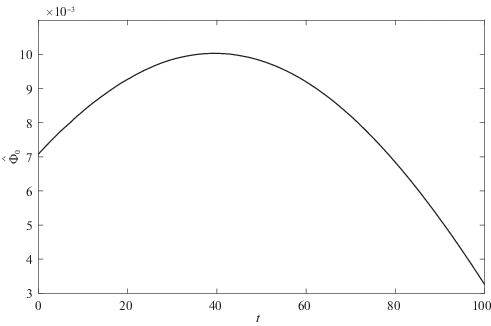
На рис. 3, 4 приведены результаты расчетов для колебательного переходного процесса (${{a}_{i}} = {{b}_{i}} = 0.1,$ $i = 1,2$), а на рис. 5, 6 – в режиме без колебаний (${{a}_{i}} = 0.1,$ ${{b}_{i}} = a_{i}^{2}{\text{/}}4,$ $i = 1,2$). На рис. 3 и 5 изображены кривые на фазовой плоскости $x,\;\dot {x},$ где x соответствует φ1 (сплошные кривые), φ2 (точечные кривые) и $\Psi $ (штриховые), при условии работы фильтра с ограниченной памятью (4.3). Как видно из этих рисунков, переменные φ2, $\Psi $ и их производные приходят в окрестность нуля в соответствии с целью управления. На рис. 4, 6 приведены соответствующие управляющие моменты ${{M}_{1}}$ и ${{M}_{2}}$, причем на рис. 6 момент M2 масштабирован – изображено ${{10}^{2}} \cdot {{M}_{2}}.$ Рисунки 7–11 демонстрируют результаты применения алгоритмов фильтрации к зашумленным сигналам. На рис. 7 и 8 показаны зашумленный сигнал и кривая, построенная с помощью фильтра с ограниченной памятью, на рис. 9 – ошибка (разность между построенным на основании замеров с погрешностями и истинным значением) работы фильтра с фиксированной памятью (сплошная кривая) и фильтра, задаваемого рекуррентно (штриховая линия), на рис. 10 – разность между сигналами, восстановленными с помощью фильтра с нарастающей памятью и его рекуррентной модификацией. На рис. 11 представлены кривые, демонстрирующие ошибку оценки производной ${{\hat {\dot {\Phi }}}_{0}}$, построенной на основании замеров $\Phi ({{t}_{i}})$ и используемой в алгоритме управления для рекуррентной модификации фильтра с неограниченной памятью (штриховая кривая) и фильтра с ограниченной памятью (сплошная линия).
Из проведенных расчетов следует, что при колебательном переходном процессе влияние различных типов алгоритмов фильтрации не сильно сказывается, хотя алгоритм фильтрации с фиксированной памятью показывает меньшие ошибки приближения как сигнала, так и его производной. Отметим также небольшое количество моментов переключения (разрывов) управляющего воздействия ${{M}_{1}}.$ При режиме без колебаний влияние выбора алгоритма фильтрации сказывается значительней, особенно при малых значениях величины ${{\dot {\varphi }}_{1}}$. В этом случае погрешности и незначительные ошибки фильтрации приводят к неточной оценке величины момента сил трения и, как следствие, к построению управляющего момента, не полностью компенсирующего возмущения. Этим же вызвано и большее число переключений момента M1 в алгоритме управления. В силу этого колебательный режим может оказаться предпочтительным.
Отметим, что на поведении управляющих моментов в режиме приведения величин $\Psi ,$ ${{\varphi }_{2}}$ к нулю существенным образом сказывается амплитуда функции ${{\Phi }_{0}}(t).$ Действительно, при малых $\Psi ,$ ${{\varphi }_{2}}$ имеем ${{\varphi }_{1}} \approx {{\Phi }_{0}},$ ${{\dot {\varphi }}_{1}} \approx {{\dot {\Phi }}_{0}},$ и, значит, малые значения ${{\dot {\Phi }}_{0}}$ приведут к движениям с залипаниями соответственно используемому закону трения, а следовательно, к переключениям управляющего момента ${{M}_{1}}$. Случайные возмущения при измерении ${{\Phi }_{0}}$ при этом ухудшают ситуацию, поскольку малые погрешности в оценке ${{\hat {\dot {\Phi }}}_{0}}$ приведут к дополнительным переключениям. Таким образом, на выбор предпочтительной стратегии управления (в колебательном режиме или в режиме без колебаний) при стремлении уменьшить воздействия на электродвигатель и полезную нагрузку, вызываемые резкими изменениями управляющего момента, значительным образом сказывается характер возмущения, моделируемого функцией ${{\Phi }_{0}}(t)$.
Заключение. Анализ и компьютерное моделирование динамического поведения объекта, связанного с вращающимся основанием двухступенчатым электроприводом с торсионом, свидетельствуют о возможности использования такого привода в системах прецизионной ориентации объектов. Предложенные алгоритм управления на основе пропорционально-дифференциальных регуляторов и методика оценивания переменных и параметров, недоступных непосредственному точному измерению, позволяют осуществлять отслеживание объектом желаемой переменной ориентации с высокой степенью точности. Целесообразно провести экспериментальную отработку предложенной методики управления на физическом образце поворотной платформы, предназначенной для прецизионной ориентации закрепленных в ней объектов на борту орбитальных космических аппаратов.
Список литературы
https://ru.wikipedia.org/wiki/Автоматическая поворотная виброзащитная платформа.
Борисов А.Е., Иванов А.И., Федосеев С.В. и др. Пат. 2369535 РФ, МПК Н 04 B64G1/22 (2006.01), B64G1/36 (2006.01). Способ оптимизации динамических условий функционирования гравитационно-чувствительных установок в условиях остаточных микроускорений на борту орбитальных космических аппаратов и устройство для его реализации. 2008107131/11, заяв. 28.02.2008, опуб. 10.10.2009, Бюл. 28.
Борисов А.Е., Иванов А.И., Емельянов Г.А. Поворотная платформа для стабилизации углового положения технологической установки по вектору микроускорения // Матер. XLVI научных чтений памяти К.Э. Циолковского. Калуга: Наша типография, 2011. С. 124–125.
Борисов А.Е., Левтов В.Л., Романов В.В., Тарасенко Н.В. Комплекс технических средств обеспечения контролируемых динамических условий при проведении исследований гравитационно-чувствительных систем // Космонавтика и ракетостроение. 2007. № 4 (49). С. 168–173.
Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 670 с.
Акуленко Л.Д., Болотник Н.Н., Борисов А.E., Гавриков А.А., Емельянов Г.А. Управление кажущимся ускорением твердого тела, закрепленного в двухстепенном подвесе на подвижном основании // Изв. РАН. ТиСУ. 2012. № 3. С. 3–12.
Акуленко Л.Д., Болотник Н.Н., Борисов А.E., Гавриков А.А., Емельянов Г.А. Квазиоптимальное управление поворотом твердого тела вокруг неподвижной оси с учетом трения // Изв. РАН. ТиСУ. 2015. № 3. С. 3–20.
Ананьевский И.М., Ишханян Т.А. Управление поворотной платформой на подвижном основании в присутствии возмущений // Изв. РАН. ТиСУ. 2016. № 3. С. 154–162.
Ананьевский И.М., Ишханян Т.А. Управление двухкаскадной электромеханической системой, подверженной возмущениям // ПММ. 2016. Т. 80. Вып. 5. С. 515–524.
Чиликин М.Г., Сандлер А.С. Общий курс электропривода. М.: Энергоиздат, 1981. 577 с.
Акуленко Л.Д., Каушинис С.К., Костин Г.В. Влияние сухого трения на управление движением электромеханических систем // Изв. РАН. Техн. кибернетика. 1994. № 1. С. 65–74.
Цыпкин Я.З., Бромберг П.В. О степени устойчивости линейных систем // Изв. АН СССР. Сер. ОТН. 1945. № 12. С. 1163–1168.
Чернявский Г.М., Чернов А.А. Лазерные системы в космосе. М.: Радио и связь, 1995. 224 с.
Акуленко Л.Д. Квазиоптимальный алгоритм обнаружения и определения параметров маневра динамического объекта // Изв. РАН. ТиСУ. 2002. № 2. С. 47–52.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления