Известия РАН. Теория и системы управления, 2020, № 1, стр. 109-118
ОБОБЩЕННЫЙ МЕТОД МНОЖЕСТВА ЭКВИВАЛЕНТНОСТИ ДЛЯ РЕШЕНИЯ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Р. В. Хачатуров *
* E-mail: rv_khach@yahoo.ie
Поступила в редакцию 18.06.2019
После доработки 28.06.2019
Принята к публикации 22.07.2019
Аннотация
Рассмотрены различные аспекты решения многокритериальных задач дискретной оптимизации. Показаны преимущества метода множества эквивалентности по сравнению с другими методами, часто использующимися при решении многокритериальных задач, такими, как метод последовательных уступок и метод поиска множества оптимальных по Парето решений. Сформулированы и доказаны теоремы, отражающие основные свойства метода множества эквивалентности и показывающие соотношение и взаимосвязь множества парето-оптимальных решений и множества эквивалентности.
Введение. В настоящее время в различных областях науки, экономики, при планировании развития стран, регионов, освоении месторождений полезных ископаемых, в космической отрасли и т.д. возникает необходимость решения многокритериальных задач, когда нужно найти оптимальное решение не по одному, а одновременно по нескольким критериям [1–9]. В этой работе описан обобщенный метод множества эквивалентности для решения многокритериальных задач дискретной оптимизации. Приведено сравнение предложенного метода с методом поиска множества парето-оптимальных решений и методом последовательных уступок. Показаны преимущества метода множества эквивалентности по сравнению с этими известными методами решения многокритериальных задач.
Как известно, задачи многокритериальной оптимизации возникают, когда необходимо оптимизировать векторную функцию $F\left( X \right) = F\left( {{{x}_{1}},\;{{x}_{2}}\;,\;...\;,\;{{x}_{n}}} \right)$ размерности $m > 1$:
1. Метод нахождения множества эквивалентных решений (метод множества эквивалентности) по нескольким критериям. Суть этого метода заключается в следующем.
1. По каждому критерию ${{y}_{l}}\left( X \right)$ решается задача однокритериальной оптимизации и находится оптимальное решение $X_{0}^{l}$, $l = \overline {1,m} $.
2. По каждому критерию ${{y}_{l}}\left( X \right)$ в многомерном псевдометрическом пространстве критериев [1, 2] находится множество решений, близких к оптимальному по этому критерию, т.е. отличающихся от оптимального значения не более чем на заданное число ${{R}_{l}} \geqslant 0$, $l = \overline {1,m} $, которое назовем допуском по соответствующему критерию. Само найденное множество обозначим через ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$. В случае максимизации оно будет определено следующим образом:
3. Затем находится множество решений, являющееся пересечением всех таких множеств по всем критериям ${{y}_{l}}\left( X \right)$. Обозначим это множество через ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$, формально определяемое следующим образом:
(1.1)
${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right) = \bigcap\limits_{l = 1}^m {{{\Omega }_{l}}\left( {{{R}_{l}}} \right)} .$Применение этого метода на примерах решения конкретных многокритериальных задач подробно описано в работах [1, 2].
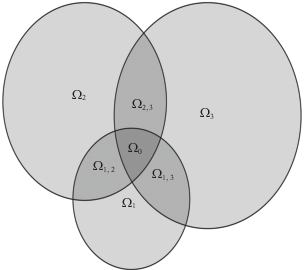
Полученное множество ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ (1.1) называется множеством эквивалентности (рис. 1). Любое решение из него удовлетворяет всем формализованным критериям и может быть принято экспертом в качестве окончательного решения. Описанный метод не имеет недостатка метода нахождения множества оптимальных по Парето решений, поскольку при добавлении дополнительного критерия множество эквивалентности никогда не растет, а наоборот, как правило, сужается [1], что будет формально доказано ниже в теореме 1.
Рис. 1.
Иллюстрация нахождения множества эквивалентных решений ${{\Omega }_{0}}({{R}_{1}},...,{{R}_{m}})$ многокритериальной задачи
Заметим, что методы, определяющие ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right) \ne \emptyset $, являются методами регуляризации [10] для некорректных задач в псевдометрическом пространстве [1, 2], а решение $X{\kern 1pt} '\, = \,(x_{1}^{'},x_{2}^{'},...,x_{n}^{'})\, \in \,{{\Omega }_{0}}$(R1, ..., Rm) – решением такой некорректной задачи. В самом деле, наличие нескольких формализованных критериев ${{y}_{l}}\left( X \right)$, $X \in D$, $l = \overline {1,m} $, позволяет на множестве D определить $m$ функций расстояния между двумя элементами $X{\kern 1pt} ' \in D$ и $X{\kern 1pt} '{\kern 1pt} ' \in D$:
Эти функции обладают следующими свойствами:
Введенные нами функции являются псевдометриками, а множество D с такой метрикой называется псевдометрическим пространством. В отличие от метрического пространства, условие ${{P}_{l}}\left( {X,Y} \right) = 0$ может выполняться также и для некоторых $X \ne Y$.
Поэтому в нашем случае для любых $X{\kern 1pt} ',X{\kern 1pt} '{\kern 1pt} ' \in {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ будет выполнено условие устойчивости типа Тихоновских условий для устойчивых задач [10]:
Таким образом, методы, определяющие множество ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$, можно считать методами регуляризации для некорректных задач в многомерном псевдометрическом пространстве D при наличии нескольких критериев.
Теорема 1. При увеличении числа критериев множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ не расширяется или сужается.
Доказательство. По определению (1.1) множество эквивалентности является пересечением всех множеств оптимальных и близких к оптимальным решений по каждому критерию yl, $l = \overline {1,m} $, поэтому при добавлении еще одного критерия ${{y}_{{m + 1}}}\left( X \right)$ с допуском ${{R}_{{m + 1}}}$ новое множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{m + 1}}}} \right)$ будет определяться следующим образом:
Отсюда следует, что ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{{m + 1}}}} \right) \subseteq {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$.
Теорема 1 доказана.
Отметим, что на практике при добавлении новых критериев множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$, как правило, быстро сужается (рис. 1). Следует отметить также, что геометрическая форма множеств оптимальных и близких к оптимальным решений ${{\Omega }_{1}}\left( {{{R}_{1}}} \right),...,{{\Omega }_{m}}\left( {{{R}_{m}}} \right)$ в пространстве искомых начальных (входных) параметров может быть самой разнообразной [1].
Вследствие вышесказанного при решении реальных задач из полученного описанным методом множества эквивалентности (1.1) эксперт может выбирать решения, удовлетворяющие не только формализованным критериям, но и неформализованным, основанным на его опыте и интуиции, при этом гарантированно не упуская наилучшее решение, которое при любом количестве дополнительных критериев никогда не окажется вне найденного множества ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ (в отличие от множества Парето, которое, как правило, растет при увеличении количества критериев [1]).
2. Обобщенный метод множества эквивалентности. В этом разделе будут описаны алгоритмы, обеспечивающие заведомую непустоту множества эквивалентности, сужение области его поиска и возможность решения многокритериальных задач без поиска оптимальных решений по каждому из критериев.
2.1. Обеспечение заведомой непустоты множества эквивалентности. Важным вопросом при нахождении множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ является способ определения значений допусков ${{R}_{l}} \geqslant 0$, $l = \overline {1,m} $, по каждому из критериев так, чтобы множество эквивалентности ${{\Omega }_{0}}$(R1, ..., Rm) было заведомо не пусто. Предлагаемый ниже метод позволяет решить эту задачу при любом количестве выходных параметров (критериев) ${{y}_{l}}\left( X \right)$.
После решения однокритериальных задач оптимизации по каждому из m критериев получим m решений $X_{0}^{l},\;l = \overline {1,m} $. Выберем некоторую точку $\bar {X} \in D$, исходя из условия наименьшего среднеквадратического отклонения значений критериев задачи ${{y}_{l}}\left( X \right),\;l = \overline {1,m} $, в этой точке $\bar {X}$ от значений критериев задачи ${{y}_{l}}\left( X \right),\;l = \overline {1,m} $, в найденных точках $X_{0}^{l},\;l = \overline {1,m} $. Для этого надо решить задачу минимизации следующей функции $g\left( X \right)$:
Заметим, что при таком способе определения начальной общей точки $\bar {X} \in D$ неявным образом подразумевается, что все критерии задачи равноправны. Вообще, метод множества эквивалентности не нуждается в каком-либо изначальном ранжировании критериев (как это необходимо, например, для метода последовательных уступок). Важность критерия естественным образом определяется величиной соответствующего допуска – чем меньше допуск, тем важнее критерий. Поэтому, если необходимо распределить критерии по степени важности, то можно просто ввести соответствующее масштабирование единиц измерения и использовать тот же способ определения начальной общей точки.
Можно также напрямую ввести соответствующие веса для каждого из критериев в функцию g(X) для определения $\bar {X} \in D$. Тогда задача минимизации будет выглядеть следующим образом:
В дальнейших рассуждениях без ограничения общности будем полагать, что решается задача максимизации по всем критериям. Тогда значения допусков ${{R}_{l}} \geqslant 0$, $l = \overline {1,m} $, по каждому из критериев ${{y}_{l}}\left( X \right)$ определяются исходя из условия, что получаемые множества решений ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, близких к оптимальному по каждому критерию, включают в себя найденную точку $\overline {{{X}_{{}}}} \in D$, т.е.
Все полученные с такими значениями допусков ${{R}_{l}}$ множества оптимальных и близких к оптимальным решений ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $,
(2.1)
${{\Omega }_{l}}\left( {{{R}_{l}}} \right) = \{ X \in D\left| {\,{{y}_{l}}\left( {\bar {X}} \right) \leqslant {{y}_{l}}\left( X \right) \leqslant {{y}_{l}}\left( {\bar {X}} \right) + {{R}_{l}} = {{y}_{l}}(X_{0}^{l}) = y_{l}^{{\max }}} \right.\} ,$В качестве такой “общей” точки $\bar {X} \in D$ на практике может быть выбрана любая точка в пространстве входных параметров
которая по тем или иным соображениям эксперта-проектировщика является приемлемой с точки зрения критериев задачиОднако описанный выше метод позволяет формализовать и полностью автоматизировать этот процесс принятия решения по определению начальной и общей для всех множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, l = $\overline {1,m} $, точки $\bar {X} \in D$.
2.2. Решение многокритериальных задач без поиска оптимальных решений по каждому из критериев. Важно отметить, что метод множества эквивалентности позволяет полностью отказаться от поиска оптимальных решений по каждому из критериев при решении многокритериальных задач оптимизации.
В самом деле, достаточно выбрать в пространстве входных параметров любую приемлемую точку $\bar {X} \in D$, вычислить значения критериев ${{y}_{l}}\left( {\bar {X}} \right)$, $l = \overline {1,m} $, в этой точке и задать любые желаемые допуски ${{R}_{l}},\;l = \overline {1,m} $, по каждому из критериев в сторону их улучшения.
Таким образом мы получаем интервалы допустимых значений каждого из критериев задачи. Затем для каждого из критериев находим соответствующее множество решений ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $:
(2.2)
${{\Omega }_{l}}\left( {{{R}_{l}}} \right) = \left\{ {X \in D\left| {{{y}_{l}}\left( {\bar {X}} \right) \leqslant {{y}_{l}}\left( X \right) \leqslant {{y}_{l}}\left( {\bar {X}} \right) + {{R}_{l}}} \right.} \right\}$Таким образом, в этом случае мы вообще не ищем оптимальные решения по каждому из критериев ${{y}_{1}},{{y}_{2}},...,{{y}_{m}}$, а только задаем приемлемые или желаемые интервалы значений для каждого из них. Полученное множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ будет содержать все решения поставленной многокритериальной задачи.
2.3. Быстрый алгоритм поиска множества эквивалентности. Когда заведомо известно, что искомое множество эквивалентности не пусто, так как выбрана общая для всех множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, точка $\bar {X} \in D$ и определены соответствующие допуски ${{R}_{l}},\;l = \overline {1,m} $ (см. разд. 2.1), его поиск можно существенно ускорить за счет сужения области поиска. Для этого разработан следующий алгоритм нахождения множества эквивалентности.
1. По первому критерию ${{y}_{1}}\left( X \right)\;\left( {X \in D} \right)$ находится соответствующее множество решений ${{\Omega }_{1}}({{R}_{1}})\;(\bar {X} \in {{\Omega }_{1}}({{R}_{1}}))$.
2. По второму критерию ${{y}_{2}}\left( X \right)\;\left( {X \in {{\Omega }_{1}}\left( {{{R}_{1}}} \right)} \right)$ находится соответствующее множество решений ${{\Omega }_{2}}\left( {{{R}_{2}}} \right) \subset {{\Omega }_{1}}\left( {{{R}_{1}}} \right)$ $\left( {\bar {X} \in {{\Omega }_{2}}\left( {{{R}_{2}}} \right)} \right)$.
3. По $l$-му критерию ${{y}_{l}}\left( X \right)\;\left( {X \in {{\Omega }_{{l - 1}}}\left( {{{R}_{{l - 1}}}} \right)} \right)$ находится соответствующее множество решений ${{\Omega }_{l}}\left( {{{R}_{l}}} \right) \subset {{\Omega }_{{l - 1}}}\left( {{{R}_{{l - 1}}}} \right)$ $\left( {\bar {X} \in {{\Omega }_{l}}\left( {{{R}_{l}}} \right)} \right)$.
4. Так повторяется до $l = m$.
Таким образом, все найденные в результате применения этого быстрого алгоритма множества ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, будут последовательно включены друг в друга:
Очевидно, что последнее найденное при помощи этого алгоритма множество будет являться искомым множеством эквивалентности:
Такой подход существенно сужает область поиска множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, и, как показали многочисленные вычислительные эксперименты, значительно ускоряет процесс решения многокритериальных задач дискретной оптимизации.
Важно заметить, что в качестве первого критерия может быть выбран любой из $m$ критериев задачи, а множества ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, можно всегда искать во всей области $X \in D$ и потом уже искать их общее пересечение, так как все допуски ${{R}_{l}},\;l = \overline {1,m} ~$, определены заранее и не зависят друг от друга (в отличие от метода последовательных уступок, например). Но если найдено одно из множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, то нет смысла искать ${{\Omega }_{{l + 1}}}\left( {{{R}_{{l + 1}}}} \right)$ вне ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, так как для нахождения множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ необходимо найти лишь пересечение всех множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $. Поэтому описанный в этом разделе быстрый алгоритм естественен и не приводит к потере каких-либо решений.
Отметим также, что этот ускоренный алгоритм можно применять как в случае, когда находятся оптимальные и близкие к оптимальным решения по всем критериям ${{R}_{l}}\;,\;l = \overline {1,m} ~$ (см. разд. 2.1), так и в случае, когда в качестве начальной общей точки выбирается произвольная точка $\bar {X} \in D$ (см. разд. 2.2).
Кроме того, можно скомбинировать алгоритмы, описанные в разд. 2.1 и 2.2, – найти лишь k $\left( {1 \leqslant k \leqslant m} \right)$ оптимальных решений $X_{0}^{l},\;l = \overline {1,k} $, определить по ним начальную общую точку $\bar {X} \in D$ и соответствующие допуски ${{R}_{l}},\;l = \overline {1,k} $, как это описано в разд. 2.1:
Допуски по оставшимся $m{\text{--}}k$ критериям определить, как это описано в разд. 2.2, и применить быстрый алгоритм поиска множества эквивалентности, предложенный в текущем разд. 2.3.
3. Преимущества метода множества эквивалентности по сравнению с методом последовательных уступок. Еще одним распространенным методом решения многокритериальных задач дискретной оптимизации является метод последовательных уступок. В этом разделе будут показаны преимущества и принципиальные отличия метода множества эквивалентности по сравнению с методом последовательных уступок. Сначала кратко опишем этот метод.
3.1. Метод последовательных уступок. Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности. Предположим, что все критерии ${{Z}_{1}}, \ldots ,{{Z}_{m}}$ рассматриваемой задачи максимизируются и пронумерованы в порядке убывания их важности. Вначале определяется максимальное значение $Z_{1}^{0}$ (первого по важности критерия в области $X \in D$), решив задачу
Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения ${{\delta }_{1}} > 0$ (экономически оправданной уступки) критерия Z1 и отыскивается максимальное значение второго критерия Z2 при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, т.е. решается задача
Снова назначается величина уступки ${{\delta }_{2}} > 0$ по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия, и т.д. Наконец, выявляется экстремальное значение последнего по важности критерия Zm при условии, что значение каждого из первых m – 1 частных критериев отличается от экстремального не более чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным. Для него также может быть задана соответствующая уступка ${{\delta }_{m}} > 0$, чтобы определить множество близких к этому “оптимальному” решений.
Существенным недостатком метода последовательных уступок является то, что решение, полученное этим методом, и все множество близких к нему решений могут оказаться неоптимальными по Парето [3, 6].
3.2. Основные отличия метода множества эквивалентности от метода последовательных уступок. Перечислим эти отличия.
1. Главным различием этих двух методов является то, что в методе множества эквивалентности все критерии абсолютно равноценны. Нет никакой необходимости упорядочивать их по значимости (что является отдельной и далеко не всегда выполнимой задачей), как это в обязательном порядке делается в методе последовательных уступок.
2. Множества оптимальных и близких к оптимальным решений ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, по всем критериям задачи в методе множества эквивалентности определяются независимо друг от друга во всей области $X \in D$ в соответствии с заранее заданными допусками ${{R}_{l}},\;l = \overline {1,m} $. В методе множества эквивалентности абсолютно не важен порядок нахождения множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, и последовательность их пересечения – результирующее множество эквивалентности от этого не зависит. При этом его заведомую непустоту обеспечивает алгоритм, описанный в разд. 2.1.
3. Существенное и принципиальное отличие метода множества эквивалентности от метода последовательных уступок заключается в том, что начальная точка $\bar {X}$ в методе множества эквивалентности всегда является общей для всех множеств ${{\Omega }_{l}}\left( {{{R}_{l}}} \right)$, $l = \overline {1,m} $, т.е. заведомо входит во все эти множества. А в методе последовательных уступок начальная точка (оптимум по первому, “самому важному” критерию) может быть утрачена уже на втором шаге алгоритма, как и вторая точка (максимум по второму критерию) на третьем шаге алгоритма, и т.д. вплоть до последнего шага. Это является существенным недостатком метода последовательных уступок, которого нет у метода множества эквивалентности.
4. Важнейший недостаток метода последовательных уступок состоит в том, что множество решений, полученных этим методом, может не содержать ни одного оптимального по Парето решения [3]. А множество эквивалентности всегда содержит хотя бы одно парето-оптимальное решение, что будет доказано в следующем разд. 4.
4. Соотношение и взаимосвязь множества эквивалентности и множества оптимальных по Парето решений. Сначала сформулируем и докажем теорему, описывающую важное свойство множества эквивалентности и его пространственную структуру.
Теорема 2 (о вложенности множеств эквивалентности). Если точка $X{\kern 1pt} '{\kern 1pt} ' \in D$ не хуже по всем критериям, чем точка $X{\kern 1pt} ' \in D$, т.е. выполнено
Доказательство. В $m$-мерном пространстве критериев множество эквивалентности ограничено снизу по каждому критерию ${{y}_{l}}$ $\left( {m - 1} \right)$-мерной гиперплоскостью (рис. 2):
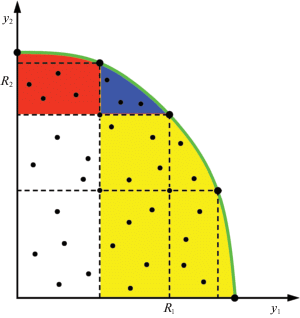
Рис. 2.
Характерное расположение множества Парето (зеленый цвет), множеств ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$ (желтый цвет), ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$ (красный цвет) и множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}}} \right)$ (синий цвет)
Поэтому если ${{y}_{l}}(X{\kern 1pt} ')\, \leqslant \,{{y}_{l}}(X{\kern 1pt} '{\kern 1pt} '),$ то соответствующие множества эквивалентности ${{\Omega }_{0}}({{R}_{1}}(X{\kern 1pt} ')$, ..., Rm(X ')) и ${{\Omega }_{0}}\left( {{{R}_{1}}\left( {X{\kern 1pt} '{\kern 1pt} '} \right),...,{{R}_{m}}\left( {X{\kern 1pt} '{\kern 1pt} '} \right)} \right)$ ограничены снизу $\left( {m - 1} \right)$-мерными гиперплоскостями (рис. 2) :
Теорема 2 доказана.
Пусть $P\left( {{{y}_{1}},...,{{y}_{m}}} \right)$ – множество оптимальных по Парето решений, определенное традиционным способом [3]:
Теорема 3. Множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ содержит хотя бы одно решение, оптимальное по Парето.
Доказательство. В соответствии с определением $P\left( {{{y}_{1}},...,{{y}_{m}}} \right)$ для любого $X{\kern 1pt} ' \in {{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right)$ найдется хотя бы одна точка $X{\kern 1pt} '{\kern 1pt} ' \in D$, оптимальная по Парето $X{\kern 1pt} '{\kern 1pt} ' \in P\left( {{{y}_{1}},...,{{y}_{m}}} \right)$, такая, что ${{y}_{l}}(X{\kern 1pt} '{\kern 1pt} ')\, \geqslant \,{{y}_{l}}(X{\kern 1pt} ')$, $l = \overline {1,m} $.
Но это означает, что $X{\kern 1pt} '{\kern 1pt} '$ соответствует меньшим либо равным значениям допусков ${{R}_{1}},...,{{R}_{m}}$ по всем критериям, чем $X{\kern 1pt} '$, и, следовательно, в соответствии с теоремой 2
Теорема 3 доказана.
Следствие из теоремы 3. Если множество эквивалентности содержит единственное решение, то это решение оптимально по Парето.
Теорема 4. Если в методе множества эквивалентности в качестве начальной общей точки $\bar {X} \in D$ взять единственное оптимальное решение по любому из критериев, то полученное множество эквивалентности всегда будет содержать хотя бы одно парето-оптимальное решение, даже если по остальным критериям оптимальные решения не ищутся, а соответствующие им множества ${{\Omega }_{l}}({{R}_{l}})$ задаются по формуле (2.2) из разд. 2.2.
Доказательство. По определению множеств ${{\Omega }_{l}}({{R}_{l}})$ начальная точка $\bar {X}$ всегда входит в результирующее множество эквивалентности
При этом единственная оптимальная по одному из критериев точка всегда является и парето-оптимальной.
Теорема 4 доказана.
Рисунок 2 на примере двухкритериальной задачи оптимизации иллюстрирует характерное пространственное расположение и соотношение множества Парето, множеств ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$, ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$ оптимальных и близких к оптимальным решений по критериям ${{y}_{1}}$, ${{y}_{2}}$ соответственно и множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}}} \right)$.
Эти множества изображены следующими цветами:
множество парето-оптимальных решений – зеленым (жирная кривая, ограничивающая область значений критериев справа);
множество оптимальных и близких к оптимальным решений по первому критерию ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$ – желтым (закрашенная область справа внизу);
множество оптимальных и близких к оптимальным решений по второму критерию ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$ – красным (закрашенная область слева вверху);
множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}}} \right)$ – синим (пересечение этих двух закрашенных областей).
Оценим скорость роста числа элементов множества Парето при увеличении числа критериев задачи. Прежде всего заметим, что множество парето-оптимальных решений всегда принадлежит $\left( {m - 1} \right)$-мерной гиперповерхности, проходящей через точки максимумов всех критериев $y_{1}^{{\max }}, \ldots ,\;y_{m}^{{\max }}$ в $m$-мерном пространстве критериев, как это видно на рис. 2, 3. В зависимости от конкретного вида оптимизируемых функций, парето-оптимальные решения могут быть распределены либо по всей этой гиперповерхности, либо по определенным ее частям (рис. 3). Поэтому число элементов множества Парето, как правило, растет пропорционально $\left( {m - 1} \right)$-мерному объему этой гиперповерхности
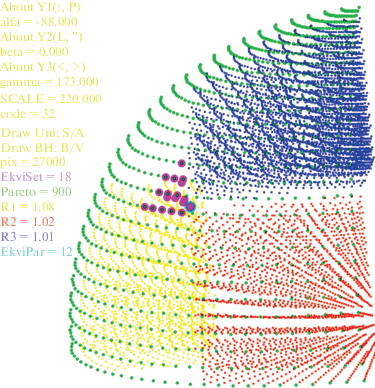
где a – характерный линейный размер множества всех возможных значений критериев ${{y}_{1}}, \ldots ,{{y}_{m}}$.Рис. 3.
3D-пример расположения множества Парето (зеленый цвет), множеств ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$ (желтый цвет), ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$ (красный цвет), ${{\Omega }_{3}}\left( {{{R}_{3}}} \right)$ (синий цвет) и множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}},{{R}_{3}}} \right)$ (фиолетовый цвет)
За a может быть принято, например, среднее геометрическое значение интервалов изменения всех критериев:
Это означает, что число элементов множества Парето в $m$-мерном пространстве критериев при увеличении числа этих критериев растет, как правило, со скоростью геометрической прогрессии (экспоненциально) и при $m > n$ может включить в себя все точки области определения задачи $X \in D$. При этом число элементов множества эквивалентности не растет никогда, а наоборот, в большинстве случаев быстро убывает при увеличении числа критериев (теорема 1), что иллюстрируют рисунки 2, 3.
На рис. 3, полученном в результате вычислений по специально разработанной компьютерной программе, видно взаимное расположение множества Парето, множеств оптимальных и близких к оптимальным решений ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$, ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$, ${{\Omega }_{3}}\left( {{{R}_{3}}} \right)$ и множества эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}},{{R}_{3}}} \right)$ при $m = 3$.
Элементы этих множеств изображены следующими цветами:
множество парето-оптимальных решений – зеленым (жирные точки, принадлежащие поверхности, ограничивающей область значений критериев);
множество оптимальных и близких к оптимальным решений по первому критерию ${{\Omega }_{1}}\left( {{{R}_{1}}} \right)$ – желтым (множество точек, заполняющих объем слева внизу);
множество оптимальных и близких к оптимальным решений по второму критерию ${{\Omega }_{2}}\left( {{{R}_{2}}} \right)$ – красным (множество точек, заполняющих объем справа внизу);
множество оптимальных и близких к оптимальным решений по второму критерию ${{\Omega }_{3}}\left( {{{R}_{3}}} \right)$ – синим (множество точек, заполняющих объем справа вверху);
множество эквивалентности ${{\Omega }_{0}}\left( {{{R}_{1}},{{R}_{2}},{{R}_{3}}} \right)$ – фиолетовым (пересечение этих трех множеств в середине рисунка).
Начальная общая точка для множества эквивалентности $\bar {X} \in D$, найденная при помощи алгоритма из разд. 2, изображена фиолетовым кружком с голубой границей. Общее число элементов множества всех возможных значений критериев в данном случае равно 27 000, число элементов множества Парето – 900, число элементов множества эквивалентности – 18. При этом 12 из них являются и парето-оптимальными (фиолетовые с зеленым центром).
Заключение. Получен обобщенный метод множества эквивалентности, обладающий следующими свойствами.
Искомое множество эквивалентности
Как было отмечено в разд. 1, методы, определяющие ${{\Omega }_{0}}\left( {{{R}_{1}},...,{{R}_{m}}} \right) \ne \emptyset $, являются методами регуляризации [10] для некорректных задач в псевдометрическом пространстве критериев ${{y}_{1}},...,{{y}_{m}}$ (даже при наличии неформализованных критериев), а каждое решение $X{\kern 1pt} '\, \in \,{{\Omega }_{0}}({{R}_{1}},...,{{R}_{m}})$ – решением такой некорректной задачи [1, 2]. Таким образом, метод множества эквивалентности можно считать обобщением метода регуляризации для некорректных задач в многомерном псевдометрическом пространстве D при наличии нескольких критериев в дискретном случае. Это позволяет применять метод множества эквивалентности как для решения многокритериальных задач дискретной оптимизации, так и для решения обратных задач математической физики.
Список литературы
Хачатуров Р.В. Многокритериальная оптимизация в псевдометрическом пространстве критериев на примере общей модели деятельности предприятия // ЖВМ и МФ. 2016. Т. 56. № 9. С. 1602–1613.
Khachaturov R.V. Single- and Multiobjective Optimization on the Lattice of Cubes // Computer and Systems Sciences International. 2018. V. 57. № 5. P. 750–758.
Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982.
Mas-Collel A., Whinston M.D., Green J.R. Microeconomic theory. N.Y.: Oxford University Press, 1995.
Мулен Э. Кооперативное принятие решений: аксиомы и модели. М.: Мир, 1991.
Штойер Р. Многокритериальная оптимизация (теория, вычисления и приложения). М.: Радио и связь, 1992.
Губко М.В., Новиков Д.А. Теория игр в управлении организационными системами. М.: Синтег, 2002.
Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. М.: Физматлит, 2002.
Лотов А.В., Поспелова И.И. Многокритериальные задачи принятия решений: Учебное пособие. М.: МАКС Пресс, 2008.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления


