Известия РАН. Теория и системы управления, 2020, № 1, стр. 96-108
РАСШИРЕННЫЙ МЕТОД “УВЕРЕННЫХ СУЖДЕНИЙ”
В. С. Брусов a, П. О. Корчагин a, В. В. Малышев b, *, С. А. Пиявский a
a Самарский филиал Московского городского педагогического ун-та
Самара, Россия
b МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: veniaminmalyshev@mail.ru
Поступила в редакцию 19.12.2018
После доработки 25.01.2019
Принята к публикации 30.09.2019
Аннотация
Рассматривается задача принятия многокритериальных решений, в которой лицо, принимающее решение, имеет возможность указывать диапазон политик выбора для определения наиболее эффективной сферы применения рассматриваемых альтернатив. Вводится понятие области Дирихле альтернативы в размытой области целевых установок лица, принимающего решение, и предлагаются четыре группы количественных характеристик для целостного описания этих областей. Разработан шестиэтапный алгоритм принятия решения. Предложены две математические модели многоцелевой оптимизации и систематизации политик выбора в области Дирихле. Предложенный метод проиллюстрирован решением задачи о выборе комплекса наиболее рациональных концепций высотного беспилотного летательного аппарата.
Введение. В работах [1–4] рассмотрена задача многокритериального принятия решений, в которой альтернативы характеризуются частными критериями и могут зависеть от ряда неопределенных факторов. В этих статьях предложен метод “Уверенных суждений”, позволяющий лицу, принимающему решение (ЛПР), легко и обоснованно решать такие задачи на основе естественных для него суждений.
Уверенное суждение первого типа. При своей уверенности ЛПР может отнести различные частные критерии к различным группам важности. Например, “критерии 1 и 4 наиболее важны, критерии 2 и 6 просто важны, а критерий 5 имеет наименьшую важность”. Подчеркнем, что не предполагается, что ЛПР дает количественную оценку степени сравнительной важности частных критериев, речь идет лишь об их качественном сравнении, притом необязательном.
Уверенное суждение второго типа. При желании ЛПР может сконструировать пары парето-несравнимых векторов частных критериев, в отношении которых он уверен, что один из векторов “лучше” другого.
Таким образом, метод не использует искусственных приемов, направленных на формализацию задачи за счет отыскания якобы адекватного ей единственного способа учета неопределенности, а учитывает все множество таких способов. От ЛПР-а лишь требуется отнести каждый частный критерий к той или иной группе важности, задав тем самым конкретную (хотя и размытую с позиций количественного сопоставления значимости различных групп важности) “политику выбора”. Это позволяет ЛПР не зависеть, по крайней мере на первоначальной стадии осмысления стоящей перед ним задачи принятия решения, от громоздких процедур привлечения экспертов. Задав политику выбора, он получает для каждого рассматриваемого варианта решений две комплексные числовые оценки: жесткий и мягкий рейтинг. Эти рейтинги рассчитываются на основе анализа всего множества допустимых в условиях решаемой задачи способов “свертывания” частных критериев в единую комплексную оценку. Например, это может быть множество всех весовых коэффициентов в линейной свертке частных критериев, при которых выполняются условия, сформулированные в уверенных суждениях ЛПР первого и второго типа. Если обозначит через Y совокупность вариантов решений $y \in Y$, через S – множество допустимых в условиях решаемой задачи способов “свертывания” частных критериев и считать, что оно содержит конечное число способов учета неопределенности $S = {{\left\{ {{{S}_{k}}} \right\}}_{{k = 1..K}}}$, а через Fs при способе учета неопределенности s, то жесткий рейтинг (ЖР) решения $y \in Y$ есть доля способов учета неопределенности, при которых это решение является наилучшим по сравнению с остальными решениями.
Мягкий рейтинг (МР) решения $y \in Y$ отражает среднюю сравнительную эффективность этого решения y по сравнению с решениями, оказавшимися наилучшими при различных способах учета неопределенности.
При принятии окончательного решения ЛПР может руководствоваться тем рейтингом, который он считает более адекватным решаемой задаче либо воспользоваться предложенными в [5, 6] простыми и наглядными методами двухкритериальной оптимизации.
1. Многоцелевой подход. Метод уверенных суждений с успехом использован в ряде прикладных задач из аэрокосмической отрасли [7–11]. Однако во многих масштабных задачах стратегического планирования и проектирования как в аэрокосмической, так и иных технических, социально-экономической и политической областях требуется принять наилучшее решение не при единственной политике выбора, а с учетом достаточно широкого их многообразия, отражающего разнообразие и неопределенность внешних ситуаций, множественность решаемых задач и возможное противодействие со стороны внешних игроков или природы. Назовем эту ситуацию размытостью целевой установки ЛПР. В этих случаях задача принятия решения попадает в рамки многоцелевого подхода, предложенного в [12–14] и затем нашедшего развитие и применение в [15–28].
Сущность многоцелевого подхода состоит в том, что он расширяет классическую постановку задачи оптимизации, предусматривая возможность формирования многоэлементного решения (так называемой многоэлементной стратегии), включающего несколько вариантов решения из множества допустимых решений, с тем, чтобы наиболее эффективно учесть многообразие внешних факторов. В рассматриваемой ситуации внешним множеством является множество политик выбора, отражающих совокупность целевых установок ЛПР.
Дадим формальное описание многоцелевого подхода. Обозначим через $X = {{\left\{ {{{x}_{i}}} \right\}}_{{i = 1,...,n}}}$ множество элементов, представляющих многообразие внешних факторов, через $Y = {{\left\{ {{{y}_{j}}} \right\}}_{{j = 1,...,m}}}$ – множество вариантов (элементов), из которых конструируется искомое, возможно многоэлементное, оптимальное решение, через $f(x,y)$, $x \in X$, y ∈ Y – функцию, определяющую эффективность использования элемента решения y ∈ Y при реализации внешних факторов $x \in X$. Будем называть X внешним множеством, Y – множеством элементов решений, f(x, y) – локальными потерями. Будем полагать, что допустимым решением (многоэлементной стратегией) A является любое непустое подмножество множества элементов решений $A \subseteq Y$.
Пусть $\bar {f}(x) = \mathop {\min }\limits_{y \in Y} f(x,y)$, $x \in X$ – оптимальное (минимальное) возможное значение локальных потерь в условиях реализации внешних факторов $x \in X$. Примем для определенности f(x, y) > 0, $x \in X$, y ∈ Y и перейдем от функции локальных потерь к функции относительных потерь:
Функция характеризует величину проигрыша из-за использования при внешних факторах $x \in X$ элемента решения y ∈ Y вместо элемента решения, оптимального для данных внешних факторов.
Примем, что при фиксированной многоэлементной стратегии $A \in Y$ каждому элементу внешнего множества сопоставляется тот из элементов стратегии $A \in Y$, которому отвечает наименьшее по сравнению с остальными элементами стратегии значение относительного проигрыша. При равенстве значений относительного проигрыша для нескольких элементов стратегии, ЛПР выбирает номер одного из них. Его номер задается целочисленной так называемой распределяющей функцией E(x), а совокупность определяемых этим элементов множества называется областью Дирихле этого элемента DE(x). Тогда значение относительных потерь при реализации внешних факторов x может быть записано как ρ(x, yE(x)), $x \in X$, ${{y}_{{E(x)}}} \in A$ или ${{\rho }_{{ij}}} \equiv \rho ({{x}_{{i,}}}{{y}_{j}})$, где ${{x}_{i}}$ = x, $j = E({{x}_{i}})$.
Эффективность F(X, A, E(x)) использования многоэлементной стратегии $A \in Y$ и распределяющей функции E(x) для “обслуживания” всего внешнего множества X будем характеризовать максимальным (гарантирующим) или средним проигрышем на всей совокупности элементов множества X.
В первом случае будем говорить о гарантирующей многоцелевой системе (ГМС), во втором – об интегральной многоцелевой системе (ИМС).
Оптимальной будем называть пару $(A,E(x))$, минимизирующую гарантирующий или средний проигрыш многоцелевой системы (МС) при заданном числе элементов стратегии p.
Многоцелевой подход позволяет ЛПР окончательно определить наиболее рациональное решение в том гипотетическом случае, если уверенно задано количество центров многоэлементной стратегии. Однако больший практический интерес представляет совокупность результатов оптимизации МС при различном количестве центров, поскольку она дает возможность в виде однопараметрической совокупности оценить возможности управляемой системы, гибко реагирующей на многообразие внешних факторов.
2. Расширенный метод уверенных суждений. Предлагаемый расширенный метод уверенных суждений (РМУС) объединяет метод уверенных суждений с многоцелевым подходом, что позволяет ЛПР достаточно глубоко и обоснованно принять решение в условиях множественности не только критериев, но и политик выбора, изначально представляющих собой интерес для ЛПР (и образующих внешнее множество X для многоцелевого подхода). При этом важное значение имеет формируемое у ЛПР представление об областях Дирихле как совокупности политик выбора, при которых эффективны соответствующие варианты решений.
Поясним РМУС поэтапно.
1. Формируется внешнее множество X, отображающее множество политик выбора, которое представляет интерес для ЛПР. Для этого формируется полный набор возможных сочетаний групп важности используемых частных критериев, и ЛПР, в случае надобности, удаляет из него политики выбора, заведомо не представляющие интереса.
2. Для каждой политики выбора x из внешнего множества Х методом уверенных суждений (УС) решается задача принятия решений и формируются жесткий и мягкий рейтинги, каждый из которых может рассматриваться ЛПР как комплексный рейтинг, характеризующий “успешность” каждого варианта решений из множества допустимых. В дальнейшем под термином рейтинга будем понимать любой из этих рейтингов, интересующих ЛПР.
3. Для каждой политики выбора х из Х из рассчитанных значений рейтинга для вариантов решения у из Y выбирается вариант с наименьшим значением и тем самым определяется оптимальный для данной политики выбора вариант решения $\bar {y}(x) \in Y$ и оптимальное значение рейтинга $\bar {f}(x)$.
4. Для каждой политики выбора, входящей во внешнее множество, рассчитывается значение локальных потерь $\rho (x,y)$.
5. Для ЛПР представляется общая характеристика решаемой проблемы в аспекте размытости целевой установки ЛПР. Для ее расчета решается задача оптимизации многоцелевой системы со сформированной функцией локальной эффективности при различном числе элементов многоэлементной стратегии. При этом определяются оптимальные варианты решений, входящие в оптимальные многоэлементные стратегии, и их области Дирихле, т.е. политики выбора (целевые установки), в рамках которых эти варианты решения оказываются оптимальными.
6. Рассчитываются сводные обобщенные характеристики областей Дирихле оптимальных вариантов решений, входящих в оптимальные многоцентровые стратегии, а также формируются графические представления этих областей в виде линейной последовательности входящих в них политик выбора [29–31]. На этой основе у ЛПР может сформироваться более глубокое представление о решаемой проблеме, которое, возможно, поможет ему сузить внешнее множество, т.е. уменьшить размытость своей целевой установки и повторить процесс или оптимальное количество элементов многоэлементной стратегии, тем самым окончательно определив количество элементов оптимальной стратегии и саму оптимальную стратегию.
3. Пример анализа концепций высотного беспилотного летательного аппарата. Рассмотрим пример, демонстрирующий сущность предлагаемого подхода. Используем приведенную в [6, 7] задачу анализа различных концепций высотного беспилотного летательного аппарата (БПЛА), представленных в табл. 1, в условиях многообразия критериев эффективности.
Таблица 1.
Варианты концепций БПЛА
| Варианты концепции БПЛА | Способ преобразования энергии | Аэродинамическая схема | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Номер | Код | С двигателем ВС (дизель) | С двигателем ВС (жидкий водород H2) | C топливными элементами и электрическим двигателем | С фотоэлектрическими преобразователями солнечной радиации, электрическим двигателем, химическими накопителями | С фотоэлектрическими преобразователями солнечной радиации, электролизером, топливными элементами, электрическим двигателем | Нормальная | Летающее крыло | Сочлененная |
| 1 | 1Н | + | + | ||||||
| 2 | 1Л | + | + | ||||||
| 3 | 1С | + | + | ||||||
| 4 | 2Н | + | + | ||||||
| 5 | 2Л | + | + | ||||||
| 6 | 2С | + | + | ||||||
| 7 | 3Н | + | + | ||||||
| 8 | 3Л | + | + | ||||||
| 9 | 3С | + | + | ||||||
| 10 | 4Н | + | + | ||||||
| 11 | 4Л | + | + | ||||||
| 12 | 4С | + | + | ||||||
| 13 | 5Н | + | + | ||||||
| 14 | 5Л | + | + | ||||||
| 15 | 5С | + | + | ||||||
Из 10 использованных в [6, 7] критериев в целях компактности изложения оставим четыре:
1) производительность;
2) относительная масса целевой аппаратуры;
3) степень покрытия пространственно-временной области заданий;
4) стоимость часа работы целевой аппаратуры.
Их значения для 15 рассматривавшихся вариантов концепции БПЛА приведены в табл. 2.
Таблица 2.
Значения вариантов концепций БПЛА
| Критерии | Производи- тельность | Относительная масса целевой аппаратуры | Степень покрытия | Стоимость | |
|---|---|---|---|---|---|
| Варианты концепций БПЛА | 1Н | 140 000 | 0.1 | 1 | 25 |
| 2Н | 140 000 | 0.1 | 1 | 20 | |
| 3Н | 80 000 | 0.15 | 1 | 18 | |
| 4Н | 80 000 | 0.24 | 0.5 | 5 | |
| 5Н | 80 000 | 0.2 | 0.45 | 6 | |
| 1Л | 140 000 | 0.15 | 1 | 30 | |
| 2Л | 140 000 | 0.15 | 1 | 28 | |
| 3Л | 80 000 | 0.18 | 1 | 27 | |
| 4Л | 80 000 | 0.26 | 0.48 | 6 | |
| 5Л | 80 000 | 0.22 | 0.42 | 7 | |
| 1С | 140 000 | 0.1 | 1 | 34 | |
| 2С | 140 000 | 0.1 | 1 | 32 | |
| 3С | 80 000 | 0.15 | 1 | 30 | |
| 4С | 80 000 | 0.25 | 0.45 | 7 | |
| 5С | 80 000 | 0.2 | 0.4 | 8 | |
Полагаем, что ЛПР интересует сравнительный анализ концепций БПЛА при многообразии политик выбора, в которых важность критерия производительности варьируется в вариантах “обычной важности”, “важный”, “наиболее важный”, а остальных трех критериев – в вариантах “обычной важности”, “важный”. Это определяет область целевой неопределенности ЛПР как совокупность 24 политик выбора, приведенных в табл. 3.
Таблица 3.
Область целевой неопределенности ЛПР в задаче анализа концепций БПЛА
| Варианты политик выбора концепции БПЛА | Группы важности критериев эффективности в политике выбора | |||
|---|---|---|---|---|
| Номер варианта политики выбора | Производи-тельность | Относительная масса целевой аппаратуры | Степень покрытия пространственно-временной области заданий | Стоимость часа работы целевой аппаратуры |
| 1 | Обычный | Обычный | Обычный | Обычный |
| 2 | >> | >> | >> | Важный |
| 3 | >> | >> | Важный | Обычный |
| 4 | >> | >> | >> | Важный |
| 5 | >> | Важный | Обычный | Обычный |
| 6 | >> | >> | >> | Важный |
| 7 | >> | >> | Важный | Обычный |
| 8 | >> | >> | >> | Важный |
| 9 | Важный | Обычный | Обычный | Обычный |
| 10 | >> | >> | >> | Важный |
| 11 | >> | >> | Важный | Обычный |
| 12 | >> | >> | >> | Важный |
| 13 | >> | Важный | Обычный | Обычный |
| 14 | >> | >> | >> | Важный |
| 15 | >> | >> | Важный | Обычный |
| 16 | >> | >> | >> | Важный |
| 17 | Наиболее важный | Обычный | Обычный | Обычный |
| 18 | >> | >> | >> | Важный |
| 19 | >> | >> | Важный | Обычный |
| 20 | >> | >> | >> | Важный |
| 21 | >> | Важный | Обычный | Обычный |
| 22 | >> | >> | >> | Важный |
| 23 | >> | >> | Важный | Обычный |
| 24 | >> | >> | >> | Важный |
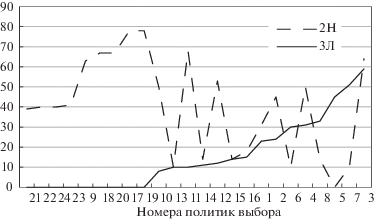
На рисунке 1 для примера показаны значения (МР) двух вариантов концепций БПЛА (2Н, 3Л) на области целевой неопределенности ЛПР. При этом для удобства зрительного восприятия последовательность политик выбора, расположенная по оси абсцисс, изменена таким образом, чтобы показать изменения мягкого рейтинга концепции 3Л наиболее закономерно. Видно, что при сопоставлении этих концепций 3Л отвечает наиболее широкая область Дирихле, а концепции 2Н – более узкая, включающая политики выбора 5–8.
Перейдем к рассмотрению оптимизации соответствующей многоцелевой системы, позволяющей построить оптимальные многоэлементные решения при заданном количестве входящих в них элементов. Предложим соответствующую математическую модель.
4. Математическая модель оптимизации МС для множества политик выбора. Введем следующие обозначения: i – номер политики выбора, i = 1, …, n; j – номер варианта решения, j = 1, …, m; fij – рейтинг i-го варианта решения при j-й политике выбора; xij = 0 или xij = 1 – распределяющая функция, равна 1, если i-я политика выбора принадлежит области Дирихле j-го варианта решения, i = 1, …, n, j = 1, …, m.
Очевидно, что
критерий оптимальности для ИМС(4.2)
${{F}_{{{\text{ИМС}}}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{f}_{{ij}}}{{x}_{{ij}}} \to \min } } ,$(4.3)
${{F}_{{{\text{ГМС}}}}} \geqslant \sum\limits_{j = 1}^m {{{f}_{{ij}}}{{x}_{{ij}}},\quad i = 1,...,n} ,$Введем теперь ограничение на количество вариантов решений в оптимальной многоэлементной стратегии. Обозначим через p заданное количество вариантов решений, входящих в стратегию A; uj = 0 или 1 – признак включения j-го варианта в стратегию A. Тогда
иУменьшим число ограничений в оптимизационной задаче, заменив (5) следующими соотношениями:
Действительно, в этом случае, если uj = 0, то и xij = 0, i = 1, …, n, а если uj = 1, то (4.7) не накладывает никаких ограничений на количество политик выбора, которые могут быть включены в область Дирихле варианта решения с номером j.
Несколько уменьшим размерность оптимизационной задачи аналитическими выкладками, исключив из нее переменную um, поскольку ее можно выразить из соотношения (4.6) как
а также исключив переменные xim, которые можно выразить из (4.1) какТогда переменные uj, j = 1,…, m – 1 будут связаны выражением
а переменные xij, i = 1, …, n, j = 1, …, m – 1 будут связаны соотношениямиКомплекс
примет вид(4.12)
${{F}_{{{\text{ИМС}}}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{m - 1} {({{f}_{{ij}}} - {{f}_{{im}}}){{x}_{{ij}}} \to \min } } .$Выражение в правой части (4.3) перейдет в
(4.13)
${{F}_{{{\text{ГМС}}}}} \geqslant \sum\limits_{j = 1}^{m - 1} {({{f}_{{ij}}} - {{f}_{{im}}}){{x}_{{ij}}},\quad i = 1,...,n} ,$Соотношения (4.7) переходят в (4.15) и (4.16)
и(4.16)
$\sum\limits_{i = 1}^n {{{x}_{{im}}} \leqslant mp - n\sum\limits_{j = 1}^{m - 1} {{{u}_{j}}} } .$Таким образом, в разработанную математическую модель входит (m – 1)n булевых переменных xij, i = 1, …, m, j = 1, …, (m – 1) и m – 1 переменная uj, i = 1, …, (m – 1), а также m + n + 1 ограничений для ИМС или m + 2n + 1 ограничений для ГМС.
5. Формирование оптимальных наборов концепций БПЛА. Используем описанный в предыдущем разделе многоцелевой подход в задаче анализа концепций БПЛА. Прежде всего, перейдем от мягкого рейтинга варианта концепции БПЛА при определенной политике выбора ЛПР к относительному проигрышу этого варианта по сравнению с вариантом концепцией, оптимальным при этой политике выбора.
После решения задачи видно, что если бы для каждой политики выбора проектировался БПЛА, концепция которого оптимальна при этой политике выбора, то вместо 15 было бы достаточно реализовать всего пять типов БПЛА, отвечающих концепциям 2Н, 3Н, 4Н, 2Л, 3Л. При этом проигрыш бы отсутствовал. Если же рассмотреть эффективность единственного варианта концепции по всей области целевой неопределенности ЛПР, то средний проигрыш, по сравнению с идеальным пятиэлементным комплексом типов БПЛА, составит 18 баллов по 100-балльной шкале. При этом наиболее эффективным вариантом концепций является вариант 2Л. Математическая модель, описанная в разд. 5, позволяет получить нетривиальные промежуточные решения при различном количестве реализуемых концепций БПЛА от двух до четырех. В табл. 4 приведены сводные результаты расчета оптимальных наборов концепций.
Таблица 4.
Концепции БПЛА, входящие в оптимальный набор концепций при различном заданном количестве элементов набора
| Заданное количество элементов в оптимальном наборе концепций | Средний проигрыш в эффективности (в баллах по 100-балльной шкале) | Концепции, входящие в оптимальный набор | ||||
|---|---|---|---|---|---|---|
| 1 | 18 | 2Л | ||||
| 2 | 11 | 2Л | 3Н | |||
| 3 | 3 | 2Л | 2Н | 4Н | ||
| 4 | 1 | 2Л | 2Н | 4Н | 3Л | |
| 5 | 0 | 2Л | 2Н | 4Н | 3Л | 3Н |
6. Количественные характеристики областей Дирихле политик выбора. При анализе полученных решений каждому элементу, входящему в многоэлементную оптимальную стратегию, отвечает своя область Дирихле, отражающая ту часть целевой неопределенности, которая “обслуживается” данным элементом.
Как указывалось, при сопоставлении областей Дирихле между собой, ЛПР полезно сформировать некоторое краткое обобщенное представление о каждой из них. Предлагаем ввести для этого следующие сравнительные количественные характеристики областей Дирихле многоэлементной стратегии А:
охват области целевой неопределенности данной областью Дирихле (в процентах) – относительная доля политик выбора, рассматриваемых ЛПР, входящих в данную область Дирихле;
средний уровень важности каждого критерия – среднее значение номеров групп важности каждого критерия, рассчитанное по политикам выбора, которые входят в данную область Дирихле;
средний уровень критериальной важности области Дирихле – среднее значение средних уровней важности критериев, входящих в политики выбора;
степень связности политик выбора, входящих в данную область Дирихле.
Поясним смысл последней характеристики. Она показывает, насколько близки между собой политики выбора в области Дирихле. При разработке метода количественной оценки этой характеристики следует учитывать, что если оценивать ее по попарной близости политик, которые для удобства восприятия располагаются в линейной последовательности, то существенное влияние на результат будет оказывать перестановка этих политик на различные места. Поэтому возникает присоединенная задача формирования последовательного расположения политик выбора, входящих в область Дирихле в таком порядке, в котором рядом стоящие политики выбора в минимальной степени отличаются по значимости входящих в них критериев. Далее опишем соответствующую математическую модель.
7. Математическая модель систематизации расположения политик выбора в области Дирихле. Введем понятие коэффициента градации, который показывает, насколько сильно отличаются соседние строки последовательности политик выбора.
Пусть n – количество политик выбора; i – номер политики выбора в исходном блоке; p – количество критериев; r – номер места, на которое ставится политика выбора в конструируемом блоке; aij – элементы политики выбора в исходном блоке, i = 1, …, n, j = 1, …, p; uri = 1, если i-я политика исходного блока ставится на j-е место в конструируемом блоке, а иначе равно нулю, r, i = 1, …, n; xrj – элементы политики выбора в конструируемом блоке, r, i = 1, …, n, j = 1, …, p:
(7.1)
$\mathop x\nolimits_{rj} = \sum\limits_{j = 1}^n {\mathop u\nolimits_{ri} } \mathop a\nolimits_{ij} .$Тогда xrj – xr + 1,j – разница значений критерия j в двух соседних политиках выбора в конструируемом блоке.
Обозначим через δrj оценку сверху для абсолютной величины этой разницы значений. Тогда
(7.2)
$ - {{\delta }_{{rj}}} \leqslant {{x}_{{rj}}} - {{x}_{{r + 1,j}}} \leqslant {{\delta }_{{rj}}}\quad r = 1,~...,~n,\quad j = 1,...,p$Назовем расстоянием dr между соседними политиками среднюю величину этих оценок:
(7.3)
${{d}_{r}} = \frac{1}{p}\mathop \sum \limits_{j = 1}^p {{\delta }_{{rj~}}},\quad r = 1,...,(n - 1),$Поставим задачу конструирования оптимальной последовательности политик выбора с минимальными расстояниями между соседними политиками. Для этого применим гарантирующий либо интегральный подход, т.е. потребуем, чтобы либо максимальное, либо среднее из этих расстояний было минимально. Это условие описывается следующими соотношениями:
Для гарантирующего подхода
Таким образом, сформулирована следующая задача смешанного линейного программирования:
критерий (7.5),
переменные uri, r, i = 1, …, n, δrj, dr, r = 1, …, (n – 1), j = 1, …, p.
Промежуточные переменные можно опустить, заменив их в (7.2) на (7.1), как и переменные dr , заменив их в (7.4) из (7.3)), а также
Теперь можно дать определение степени связности политик выбора в области Дирихле – это величина, дополняющая до единицы коэффициент градации.
Эти образы позволяют ЛПР содержательно сформулировать обобщенное представление оптимального целевого применения каждой концепции, входящей в оптимальную многоцентровую стратегии для конкретного количества центров. В табл. 5 и 6 представлены не оптимальная и оптимальная последовательности расположения политик выбора для трехцентровой стратегии концепции БПЛА 2Л.
Таблица 5.
Не оптимальная последовательность расположения политик выбора. Коэффициент градации 0.41
| 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 1 |
| 1 | 1 | 2 | 2 |
| 1 | 2 | 2 | 2 |
| 2 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 |
| 2 | 1 | 2 | 2 |
| 2 | 2 | 1 | 2 |
| 2 | 2 | 2 | 1 |
| 2 | 2 | 2 | 2 |
| 3 | 1 | 1 | 1 |
| 3 | 1 | 2 | 1 |
| 3 | 2 | 1 | 1 |
| 3 | 2 | 1 | 2 |
| 3 | 2 | 2 | 1 |
| 3 | 2 | 2 | 2 |
Таблица 6.
Оптимальная последовательность расположения политик выбора. Коэффициент градации 0.28
| 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 1 |
| 1 | 1 | 2 | 2 |
| 1 | 2 | 2 | 2 |
| 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 1 |
| 3 | 2 | 2 | 1 |
| 3 | 2 | 1 | 1 |
| 3 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 |
| 2 | 2 | 1 | 2 |
| 3 | 2 | 1 | 2 |
| 3 | 2 | 2 | 2 |
| 2 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 |
8. Обсуждение результатов анализа концепций БПЛА. Увеличение числа элементов в многоцелевом наборе повышает его эффективность, уменьшая проигрыш, по сравнению, с идеальной ситуацией, в которой каждой политике выбора отвечает оптимальный именно для нее вариант решения. Примечательно, что в исследуемой области целевых установок ЛПР содержится 24 политики выбора, однако из 15 вариантов решений в оптимальный набор концепций входит не более пяти из них. Таким образом, ЛПР может выбрать соответствующие наборы концепций БПЛА для выполнения поставленных задач с учетом материальных, ресурсных, производственных и других ограничений.
В табл. 7 представлено, для примера, описание областей Дирихле для оптимального трехэлементного набора концепций БПЛА.
Таблица 7.
Характеристики областей Дирихле для оптимального трехэлементного набора концепций БПЛА
| № п. п. | Описание элемента стратегии | Описание области Дирихле элемента стратегии | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Элемент оптимального решения | Охват политик выбора, % | Средний уровень важности критерия | Средний уровень критериальной важности | Степень связности политик выбора | |||||
| код концеп-ции | краткое описание | производи-тельность | относительная масса целевой аппаратуры | степень покрытия пространственно-временной области заданий | стоимость часа работы целевой аппаратуры | ||||
| 1 | 2Л | Двигатель ВС (жидкий водород H2); летающее крыло | 66.7 | 2.125 | 1.5 | 1.562 | 1.5 | 1.67 | 0.46 |
| 2 | 2Н | Двигатель ВС (жидкий водород H2); нормальная аэродинамическая схема | 20.8 | 1 | 1.6667 | 1.333 | 1.667 | 1.42 | 0.25 |
| 3 | 4Н | Фотоэлектрические преобразователи солнечной радиации, электрический двигатель, химические накопители; нормальная аэродинамическая схема | 12.5 | 2.2 | 1.4 | 1.4 | 1.4 | 1.6 | 0.15 |
Заключение. Предложенный в статье расширенный метод уверенных суждений даeт ЛПР инструмент для выбора многокритериальных альтернатив с дополнительным учетом широкого многообразия интересующего его целевых установок, условия функционирования и внешние факторы, влияющие на эффективность вырабатываемого решения. Предложены модели, позволяющие не только сформировать многоэлементные наборы решений оптимально взаимодействующих в условиях множественности целевых установок, но и предложить наиболее удобный для осмысления формы представления “зон влияния” отдельных элементов этих решений.
Список литературы
Малышев В.В., Пиявский С.А. Метод “Уверенных суждений” при выборе многокритериальных решений // Изв. РАН. ТИСУ. 2015. № 5. С. 90–101.
Malyshev V.V., Piyavsky S.A. The Confident Judgment Method in the Selection of Multiple Criteria Solutions // J. Computer and Systems Sciences International. 2015. V. 54. P. 754–764.
Пиявский С.А. Два новых понятия верхнего уровня в онтологии многокритериальной оптимизации // Онтология проектирования. 2013. № 1 (7). С. 65–85.
Пиявский С.А. Прогрессивность многокритериальных альтернатив // Онтология проектирования. 2013. № 4 (10). С. 60–71.
Komarov V.A., Piyavskiy S.A. Intellectual Data Analysis in Aircraft Design, Ceur Workshop Proceedings // International Conf. Information Technology and Nanotechnology. ITNT-2016. Samara. 2016. C. 873–881.
Брусов В.С., Пиявский С.А. Многокритериальный анализ концепций высотных беспилотных летательных аппаратов // Изв. вузов. Авиационная техника. 2016. № 4. С. 9–16.
Brusov V.S., Piyavskii S.A.Multi-criteria Analysis of High-altitude uav Concepts // Russian Aeronautics. 2016. V. 59. № 4. C. 447–451.
Малышев В.В., Пиявский С.А., Пиявский Б.С. Комплексная методика выбора варианта аэрокосмических целевых программ из множества заданных с избыточностью мероприятий // Космонавтика и ракетостроение. 2015. № 2 (81). С. 103–110.
Панов Д.В., Малышев В.В., Пиявский С.А., Ковков Д.В. Сравнительный многокритериальный анализ сложных технических и социальных систем в экономико-управленческом аспекте // МИР (модернизация, инновации, развитие). 2016. Т. 7. № 2 (26). С. 74–83.
Пиявский С.А., Галеев А.Х. Сравнение группы объектов с размытой характеристикой // Научное обозрение. 2014. № 4. С. 67–73.
Пиявский С.А. Простой и универсальный метод принятия решений в пространстве критериев “стоимость–эффективность”// Онтология проектирования. 2014. № 3 (10). С. 89–102.
Пиявский С.А. Об оптимизации сетей // Изв. АН СССР. Техн. кибернетика. 1968. № 1. С. 68–80.
Кротов В.Ф., Пиявский С.А. Достаточные условия оптимальности в задаче об оптимальных покрытиях // Изв. АН СССР. Техн. кибернетика. 1968. № 2. С. 10–17.
Пиявский С.А., Брусов В.С., Хвилон Е.А. Оптимизация параметров многоцелевых летательных аппаратов. М.: Машиностроение, 1974. 106 с.
Пиявский С.А., Бараховский Б.С. Блок обоснования решений в программном обеспечении МикроЭВМ // Центр программ и систем. Калинин, 1986. С. 7–10.
Смирнов О.Л., Падалко С.А., Пиявский С.А. САПР: формирование и функционирование проектных модулей. М.: Машиностроение, 1987. 272 с.
Пиявский С.А. Оптимизация обобщенных многоцелевых систем // Онтология проектирования. 2015. Т. 5. № 4 (18). С. 411–428.
Галиев Ш.И., Хорьков А.В. Некоторые экстремальные многократные покрытия квадрата кругами // Вестн. Казанск. гос. техн. ун-та. 2014. № 2. С. 154–159.
Galiev S.I., Karpova M.A. Optimization of Multiple Covering of bounded Setwith Circles // Computational Mathematics and Mathematical Physics. 2010. V. 50. № 4. P. 721–732.
Брусов B.C., Суздальцев А.Л. Применение теоретико-множественного подхода к учету неопределенностей при решении задач векторной оптимизации // АиТ. 2008. № 4. С. 94–100.
Brusov V.S., Suzdaltsev A.L. Application of the Set-theoretic Approach to Accounting of Uncertainties in the Solution of Vector Optimization Problems // Automation And Remote Control. 2008. T. 69. № 4. C. 630–636.
Брусов В.С., Тюменцев Ю.В. Синтез оптимального ансамбля нейроконтроллеров для многорежимного летательного аппарата // Вестн. МАИ. 2006. Т. 13. № 2. С. 67–78.
Брусов В.С., Салмин В.В. Комбинированная двигательная система, универсальная для диапазона маневров // Космич. исслед. 1974. Т. 12. № 3. С. 368.
Брусов В.С., Пиявский С.А. Вычислительный алгоритм оптимального покрытия областей плоскости // ЖВМиМФ. 1971. Т. 11. № 2. С. 304–312.
Brusov V.S., Piyavskii S.A. A Computational Algorithm for Optimally Covering a Plane Region // USSR Computational Mathematics and Mathematical Physics. 1971. T. 11. № 2. C. 17.
Брусов В.С., Пиявский С.А. Двигательная установка малой тяги, универсальная для двумерного диапазона маневров // Космич. исслед. 1970. Т. 8. № 4. С. 542.
Брусов В.С., Пиявский С.А. Применение теории оптимальных покрытий к задачам выбора мощности двигателя малой тяги // Изв. АН СССР. МТТ. 1969. № 2. С. 10.
Брусов В.С., Пиявский С.А. Применение теории оптимальных покрытий к выбору двигательной установки космического аппарата малой тяги // Изв. АН СССР. МТТ. 1968. № 5. С. 3.
Корчагин П.О., Пиявский С.А. Информационная система поддержки принятия многокритериальных решений // Информационные технологии в работе с одаренной молодежью / Под ред. М.И. Бальзанникова, С.А. Пиявского, В.В. Козлова. Самара: СГАСУ, 2015. С. 532–535.
Пиявский С.А., Корчагин П.О., Зыблев А.А. “Мозаичный” подход к представлению результатов многокритериальной сравнительной оценки объектов // Традиции и инновации в строительстве и архитектуре. Строительные технологии / Под ред. М.И. Бальзанникова, К.С. Галицкова, А.К. Стрелкова. Самара: АСИ СамГТУ, 2017. С. 547–551.
Корчагин П.О., Пиявский С.А. Квазигенетический алгоритм оптимизации “мозаики критериев”. Перспективные информационные технологии (ПИТ 2017) // Тр. Междунар. науч.-техн. конф. / Под ред. С.А. Прохорова. Самара: Изд. Самарск. научного центра РАН, 2017. С. 344–346.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления