Известия РАН. Теория и системы управления, 2020, № 2, стр. 128-142
Отказоустойчивая интегрированная навигационная система для беспилотного аппарата с использованием технического зрения
Д. А. Антонов a, *, К. К. Веремеенко a, М. В. Жарков a, Р. Ю. Зимин a, И. М. Кузнецов a, А. Н. Пронькин a
a МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: nio3@mai.ru
Поступила в редакцию 09.07.2019
После доработки 14.11.2019
Принята к публикации 25.11.2019
Аннотация
Представлены структура и математическое обеспечение комплексной навигационной системы для беспилотных аппаратов. В нее входят: бесплатформенная инерциальная навигационная система, приемники спутниковой навигационной системы и система технического зрения. Предложен подход к построению алгоритма исключения отказов. Даны результаты моделирования.
Введение. По мере роста числа задач, решаемых беспилотными аппаратами (БА), и в связи с необходимостью их интеграции в общее пространство с управляемыми человеком воздушными, водными и наземными транспортными средствами все острее становится задача повышения точности определения параметров движения БА и гарантирование требуемого уровня надежности навигационного обеспечения [1–5]. Решение этих задач путем использования более точных измерителей ведет к существенному повышению стоимости БА и снижению их конкурентоспособности, а иногда и просто невозможно из-за ограничений по массе, габаритам и энергопотреблению. Таким образом, перед разработчиками БА стоит задача построения навигационных комплексов (НК) повышенной точности и надежности навигационного обеспечения при условии сохранения требуемых массогабаритных, энергетических и стоимостных показателей.
Решение этой задачи возможно путем формирования универсального ядра НК, применимого для многих воздушных, водных и наземных беспилотных аппаратов (БА), которое будет строиться на минимальном наборе таких датчиков и систем, получивших широкое распространение в коммерческих приложениях и более доступных по стоимости и ограничениям на поставки. При этом должна быть разработана такая структура ядра и такой состав программно-алгоритмического обеспечения НК, которые гарантировали бы не только комплексную обработку информации (КОИ), позволяющую оценить погрешности подсистем, но и вести контроль первичной измерительной информации на предмет обнаружения и исключения возможных сбоев. Важной составляющей при этом является информация от системы технического зрения (СТЗ), обеспечивающей НК каналом оптических данных в дополнение к инерциальным и спутниковым измерениям [6–8].
Цель настоящей статьи – представление итогов работ по созданию структуры, математического обеспечения и результатов имитационного моделирования интегрированной навигационной системы для малогабаритных БА, обеспечивающей как комплексную обработку навигационных данных от различных источников, включая СТЗ, и в различных режимах работы, так и построение алгоритмов обнаружения и исключения сбоев в показаниях систем и датчиков.
1. Состав и структура системы. В качестве основы НК БА предлагается использовать инерциальную навигационную систему бесплатформенного типа (БИНС), а с целью ее коррекции – глобальную навигационную спутниковую систему (ГНСС), работающую по созвездиям ГЛОНАСС (Глобальная навигационная спутниковая система) и GPS (Global positioning system). Такая схема является уже устоявшейся и часто применяется в различных приложениях. Однако серьезный недостаток ГНСС – их низкая помехозащищeнность, что сказывается на надежности работы комплекса в целом. Предлагается повысить точность и надежность комплекса с помощью измерений оптических систем, организованных в СТЗ. В этой системе формируется навигационное поле реперных точек (РТ) на основе обнаружения, распознавания и привязки к некоторой системе координат хорошо опознаваемых точеных объектов с последующим отслеживанием движения БА относительно них.
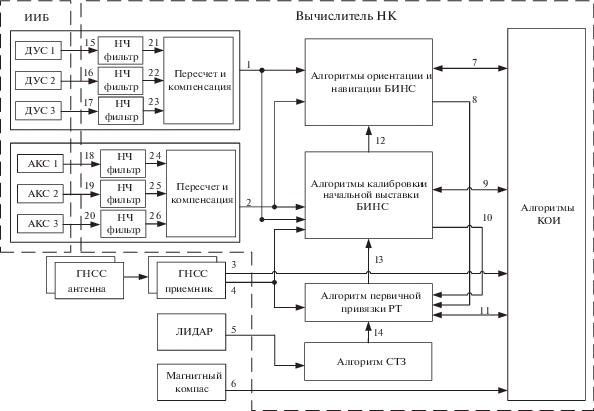
На рис. 1 представлена структура НК, представляющая состав измерительных средств и иллюстрирующая взаимосвязи между блоками основных алгоритмов. В состав измерительных средств входят:
инерциальный измерительный блок (ИИБ), объединяющий три датчика угловой скорости (ДУС) и три акселерометра (АКС);
два приемника ГНСС;
ЛИДАР (Light Identification Detection and Ranging, LIDAR);
магнитный компас (МК).
Информационные связи (ИС) 18–20 содержат измерения, пропорциональные проекциям кажущегося ускорения на соответствующие оси, а также текущее значение температуры акселерометров. ИС 15–17 содержат измерения, пропорциональные проекциям абсолютной угловой скорости на соответствующие оси, и текущее значение температуры гироскопов. Измерения ИИБ поступают на вход линейных цифровых фильтров (блоки “НЧ-фильтр”).
ИС 21–26 предназначены для передачи показаний ИИБ в блоки “Пересчет и компенсация”. Функции, реализуемые этими блоками: приведение измерений абсолютной угловой скорости, кажущегося ускорения и показания температурных датчиков к формату соответствующих вычислительных блоков; пересчет измерений инерциальных датчиков из приборной системы координат, образованной осями чувствительности ИИБ, в связанную с БА систему координат; компенсация погрешностей инерциальных датчиков с использованием коэффициентов математических моделей погрешностей, полученных на этапе калибровки ИИБ.
Таким образом, ИС 1 содержит проекции абсолютной угловой скорости, а ИС 2 – проекции кажущегося ускорения на оси связанной системы координат с учетом компенсации погрешностей инерциальных датчиков в блоке “Пересчет и компенсация”.
На вход блока “Алгоритмы ориентации и навигации БИНС” поступает следующая информация:
проекции кажущегося ускорения на оси связанной системы координат (ИС 2);
проекций абсолютной угловой скорости на оси связанной системы координат (ИС 1);
начальные значения географических широты, долготы и высоты, проекций путевой скорости, углов ориентации, дрейфов нулей ДУС, полученные на этапе начальной выставки в блоке “Алгоритм калибровки и начальной выставки БИНС” (ИС 12);
оценки погрешностей координат, скоростей, оценки погрешностей определения углов ориентации, сдвигов нулей и ошибок масштабных коэффициентов ДУС, постоянных ошибок и масштабных коэффициентов акселерометров, а также гиромагнитный курс, получаемые в блоке “Алгоритмы КОИ” (ИС 7).
При этом выходной информацией блока являются:
значения долготы, широты, северной и восточной проекций путевой скорости и углы ориентации, поступающие в блок “Алгоритмы КОИ” (ИС 7);
значения широты и долготы, а также горизонтальных проекций путевой скорости, необходимые для начальной привязки РТ СТЗ в блоке “Алгоритм первичной привязки РТ” (ИС 8).
В блоке “Алгоритмы калибровки и начальной выставки БИНС” реализованы алгоритмы:
ручного ввода начальных условий или использования показаний приемника ГНСС по координатам и скоростям (ИС 4);
начальной выставки (определение углов ориентации связанной системы координат);
оценка дрейфов нулей ДУС;
расчет магнитного склонения на основе вводимой вручную информации о координатах точки старта и текущей даты на этапе начальной выставки или на основе информации, поступающей с приемника ГНСС (ИС 4).
Наличие двух приемников при условии установки на БА двух разнесенных антенн ГНСС позволяет на основе спутниковых кодовых и фазовых измерений получать информацию о координатах, путевой скорости и двух углах ориентации БА (курс и тангаж или крен в зависимости от расположения антенн) [9]. По ИС 3 передаются в блок “Алгоритмы КОИ” измеренные приемниками ГНСС псевдодальности, псевдоскорости и углы ориентации БА.
С целью повышения надежности навигационного обеспечения предусматривается использование СТЗ. Основным измерительным средством СТЗ, согласно предлагаемой концепции, является ЛИДАР. Однако концепция системы позволяет применять различные измерения для построения системы технического зрения. В этой системе формируется навигационное поле на основе распознавания и привязки к некоторой системе координат реперных точек с последующим отслеживанием движения БА относительно них (блок “Алгоритм СТЗ”). Учитывая это, измерительной основой СТЗ может быть, например, комплекс из фото/видеокамеры и лазерного дальномера, аналогичный тому, который установлен, например, на шагающем роботе LS3, разработанном компанией Boston Dynamics (США) [10]. Другими вариантами измерителей СТЗ являются: две фото/видеокамеры, позволяющие оценивать дальности до реперных точек на основе стереоэффекта; акустический гидролокатор, устанавливаемый на подводных БА [11] и др. Основная функция блока “Алгоритм первичной привязки РТ” – выбор и получение начальных данных о РТ, определенных СТЗ в локальной или общеземной системах координат, с последующим использованием этой информации в алгоритмах КОИ.
Входной информацией блока “Алгоритмы КОИ” является:
время (внутренняя шкала НК, синхронизированная со шкалой всемирного координированного времени UTC (Universal time coordinated));
значения широты, долготы, проекций путевой скорости и углов ориентации от приемников ГНСС (ИС 4);
широта, долгота, горизонтальные проекции путевой скорости и углы ориентации, определяемые БИНС (ИС 7);
оценки погрешностей привязки РТ, определяемые алгоритмами КОИ (ИС 11).
Выходная информация алгоритма содержит данные о широте, долготе и высоте РТ (ИС 11).
Для повышения информационной избыточности и наблюдаемости в курсовом канале в состав комплекса включен магнитный компас. Выработка гиромагнитного курса осуществляется в блоке “Алгоритмы КОИ”.
Использование нескольких измерителей различной физической природы – ИИБ, ГНСС, СТЗ, МК – при глубокой интеграции в едином алгоритме КОИ создает предпосылки не только для повышения точности работы комплекса и уменьшения времени оценки параметров, но и для оценивания уровня возмущений и контроля как отдельных измерений подсистем, так и отказа подсистем в целом. При разработке алгоритмов обнаружения и исключения отказов был использован адаптивный подход к построению оценивателя.
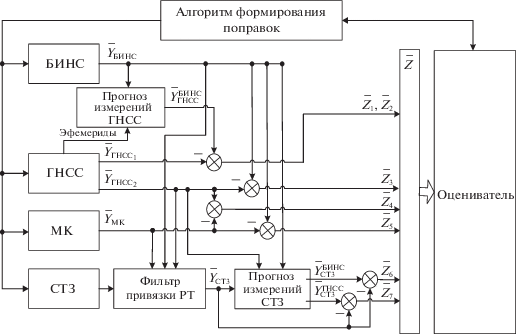
2. Алгоритм комплексной обработки навигационной информации. Для построения алгоритма комплексной обработки была применена жесткосвязанная схема комплексирования, функциональная схема алгоритма приведена на рис. 2. В соответствии с предложенным составом и структурой комплекса выходные векторы его подсистем содержат следующие компоненты:
В системе строятся и жесткосвязанное (tightly-coupled), и слабосвязанное решения. Второе, как видно из функциональной схемы алгоритма комплексной обработки, приведенной на рис. 2, используется для расчета дальностей до РТ – $\rho _{{{\text{СТЗ}}j}}^{{{\text{ГНСС}}}}$(где j – номер РТ). При неполном созвездии система находится в автономном инерциальном режиме и углы ориентации вычисляются в БИНС либо система работает в режиме коррекции от СТЗ, если имеется информация от достаточного количества РТ. При полном созвездии в системе функционируют как слабосвязанная, так и жесткосвязанная структура.
Учитывая использование жесткосвязанной схемы, вектор измерений $\bar {Z}$ (рис. 2) представляется разностью компонент выходных векторов подсистем комплекса:
Формируемые измерения могут быть представлены линейными моделями связи с вектором состояния комплексной системы (связи с ошибками подсистем), при этом на данном этапе исследований шумы измерений, обусловленные ошибками подсистем корректоров, принимались белыми с соответствующими интенсивностями.
Для формирования векторов измерений ${{\bar {Z}}_{1}}$ и ${{\bar {Z}}_{2}}$ с использованием координат и скорости БА от БИНС, а также координат и скорости навигационных космических аппаратов (НКА) вычисляются прогнозируемые дальности $\rho _{{{\text{ГНС}}{{{\text{С}}}_{i}}}}^{{{\text{БИНС}}}}$ и скорости $\dot {\rho }_{{{\text{ГНС}}{{{\text{С}}}_{i}}}}^{{{\text{БИНС}}}}$относительно всех НКА рабочего созвездия (где i – номер спутника):
Для формирования векторов измерений ${{\overline Z }_{6}}$ и ${{\overline Z }_{7}}$ на основе показаний БИНС и ГНСС по аналогии с дальностями до НКА вычисляются прогнозируемые дальности до РТ $\rho _{{{\text{СТ}}{{{\text{З}}}_{i}}}}^{{{\text{БИНС}}}}$ и $\rho _{{{\text{СТ}}{{{\text{З}}}_{i}}}}^{{{\text{ГНСС}}}}$, где i – номер РТ:
Размерность вектора измерений определяется соотношением dim$\overline Z $ = 2m + 2k + 4.
Для организации процедуры оценивания получаемые измерения необходимо связать с вектором состояния системы, в качестве которого принимается вектор ошибок системы, представляемый в виде
Для вектора состояния предложенного вида получены линейные уравнения динамики на основе линейных уравнений ошибок рассматриваемых систем, а также линейные уравнения связи между вектором измерений $\bar {Z}$ и вектором состояния $\overline {\Delta X} $, которые, например, можно найти в работах [12, 13]. При этом шумы измерений, обусловленные ошибками ГНСС, СТЗ и МК, а также шумы системы, обусловленные прежде всего случайными погрешностями гироскопов и акселерометров, принимаются белыми с нормальным распределением, интенсивности которых определяются их техническими характеристиками [14].
На основе сформированных измерений и принятой линейной модели состояния при условии неподвижности РТ строится оптимальный фильтр Калмана, производящий оценку вектора состояния $\overline {\Delta X} $. Размерность такого фильтра определяется размерностью векторов ${{\overline {\Delta {\text{X}}} }_{{{\text{БИНС}}}}}$, ${{\overline {\Delta {\text{X}}} }_{{{\text{ГНСС}}}}}$, ${{\overline {\Delta {\text{X}}} }_{{{\text{СТЗ}}}}}$, приведенных выше. Для рассматриваемого в статье случая она равна (21 + 3k), где k – число РТ, используемых в СТЗ. Оценка вектора состояния производится на основе следующих уравнений оптимального фильтра Калмана–Бьюси [14, 15]:
При переходе к дискретному виду на k-м шаге работы линейный оптимальный фильтр представляется в виде [14, 15]
Переход к дискретному виду осуществляется при использовании следующих соотношений для основных матриц фильтра [15]
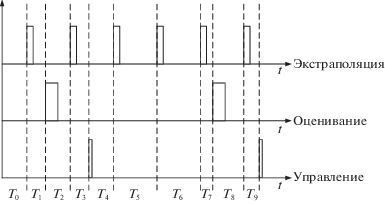
Фильтр Калмана реализует функции оценивания, экстраполяции (прогноза) и управления с одинаковой частотой в одни и те же моменты времени. Для повышения устойчивости алгоритмов оптимального фильтра Калмана (ОФК) в случае использования на динамичном объекте необходимо увеличение частоты решения задачи экстраполяции поведения оценки вектора состояния. Также следует учитывать то, что частота решения задачи управления по выработанным оценкам может не совпадать с частотой решения задачи оценивания. Временная диаграмма дискретного алгоритма ОФК в общем виде приведена на рис. 3.
Реализация ОФК в таком виде обеспечивает гибкость построения и вычислительную устойчивость. При этом на каждом такте работы вне зависимости от выполняемой функции необходимо переопределять шаг дискретизации T. На рис. 3 приведены шаги дискретизации ${{T}_{{\text{0}}}} \ldots {{T}_{{\text{9}}}}$. Шаги дискретизации обычно привязываются к шагу дискретизации навигационного алгоритма, который определяется на этапе разработки навигационной системы.
Для задачи экстраполяции [15, 16]
Для задачи оценивания [15, 16]
Для задачи управления
В зависимости от наличия или отсутствия обратной связи по элементам оценки вектора состояния ${{\hat {X}}_{{k - 1}}}$, а также от текущего режима работы фильтра (экстраполяция, оценка или управление) будет определяться матрица управления ${\mathbf{B}}_{{k/k - 1}}^{{{\text{EXTR}}}}$, ${\mathbf{B}}_{{k/k - 1}}^{{{\text{EST}}}}$, ${\mathbf{B}}_{{k/k - 1}}^{{{\text{CONTR}}}}$ и вектор управления $\bar {U}_{{k - 1}}^{{{\text{EXTR}}}}$, ${{\bar {U}}^{{{\text{EST}}}}}_{{k - 1}}$ $\bar {U}_{{k - 1}}^{{{\text{CONTR}}}}$ дискретного ОФК.
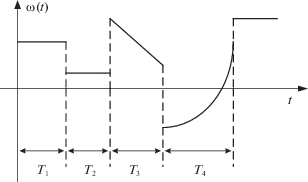
3. Исключение отказов. Одной из основных задач при построении комплексов является своевременное обнаружение и исключение первичных датчиков с высоким уровнем возмущений. Предлагается алгоритм, позволяющий в рассматриваемом комплексе выявлять аномальные измерения, исключать их из состава системы и организовывать перестройку структуры алгоритмов КОИ. Одна из особенностей этого алгоритма – использование волнового подхода к описанию возмущений [17] в спутниковых навигационных системах. Исследование реальных записей погрешностей определения местоположения по сигналам ГНСС показало наличие волновой составляющей погрешностей местоположения, в том числе их скачкообразного изменения при смене рабочего созвездия НКА. Применение как волнового подхода при формировании математической модели ошибок ГНСС, так и стохастического дает более достоверное описание погрешностей спутникового навигационного приeмника. У возмущений, обладающих волновой структурой (рис. 4), изменения связаны не только со стохастическими процессами, но и с детерминированными функциями, некоторые параметры которых изменяются случайным образом на неопределенных интервалах времени. Возмущения волновой структуры ω(t) могут быть математически представлены с помощью аналитических выражений:
Так, например, для волновых процессов, представленных на рис. 4, математическое описание можно представить в виде
Для повышения отказоустойчивости НК предлагается использовать алгоритм КОИ с переменной структурой ОФК, учитывающей возмущения волновой структуры в измерениях [14, 18]. Так, например, волновая составляющая погрешности определения псевдодальности $\delta \rho _{i}^{w}$ и псевдоскорости $\delta \dot {\rho }_{i}^{w}$ для i-го НКА рабочего созвездия ГНСС может быть представлена как
Расширенный (перестроенный) вектор состояния в этом случае примет вид
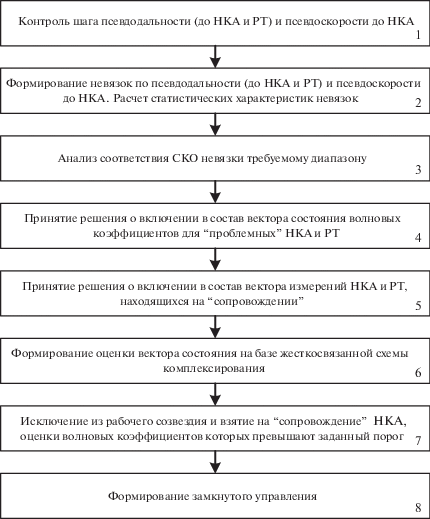
Обобщенная блок-схема алгоритма оценивания с переменной структурой приведена на рис. 5. Под переменностью структуры алгоритма оценивания понимается изменение составов измеряемых псевдодальностей и вектора состояния, что приводит к соответствующему изменению размерности матриц измерений и динамики системы. При этом из измерений исключаются те, которые не прошли допусковый контроль, а в векторе состояния изменяются компоненты волнового представления ошибок измерений. Алгоритм оптимального оценивания остается таким же, как и приведенный выше. В нем изменяется набор псевдодальностей и как следствие – размерность соответствующих матриц. Пример структурной перестройки алгоритма можно найти в монографии [14].
При построении предлагаемого алгоритма используется предположение, что наличие среднего в невязках вызвано наличием смещения в гауссовском законе распределения погрешностей ГНСС в определении псевдодальностей и псевдоскоростей. В блоке 1 осуществляется допусковый контроль шага псевдодальностей и псевдоскоростей. В блоке 2 на основе полученных невязок на текущем шаге измерений и массива предыдущих значений невязок рассчитываются статистические характеристики – скользящие среднее и среднеквадратическое отклонение (СКО).
Скользящее среднее для невязок спутниковых измерений для НКАi:
В блоке 3 осуществляется контроль СКО невязок с целью обнаружения и исключения измерений от НКА и РТ, СКО невязок псевдодальности или псевдоскорости которых превышает заданный порог. В блоке 4 на основе полученных значений статистических характеристик невязок и установленного порога принятия решения формируется набор “проблемных” НКА и РТ, измерения от которых предположительно содержат погрешности волновой структуры, превышающие заданный порог. В случае отсутствия в текущем векторе состояния параметров волновой модели погрешностей “проблемных” НКА и РТ осуществляется включение этих параметров в вектор состояния (перестройка оценивателя). В блоке 5 на основе невязок происходит анализ возможности использования измерений от ранее исключенных НКА и РТ. В блоке 6 реализуется алгоритм КОИ на базе жесткосвязанной схемы комплексирования с использованием уравнений ОФК, приведенных выше, с учетом расширенного вектора состояния. В блоке 7 на базе установленных порогов принимается решение о возможности исключения измерений от НКА и РТ на следующем шаге работы рекуррентного оценивателя. В блоке 8 вычисляются управляющие сигналы для замыкания обратной связи в алгоритмы БИНС и алгоритм привязки РТ. При замыкании обратной связи в алгоритм БИНС, приемника ГНСС и СТЗ по оценкам вектора состояния необходимо расширить вектор управления $\bar {U}\left( t \right)$. Вектор управления для дискретного ОФК $\bar {U}\left( t \right)$ и матрица управления $\left[ {B\left( t \right)} \right]~$ в зависимости от режима работы принимают следующий вид:
1) для задачи экстраполяции и оценивания:
2) для задачи управления:
Предлагаемую схему построения алгоритма с перестраиваемой структурой измерений при соответствующих изменениях можно применять и для контроля показаний (работоспособности) БИНС и МК.
4. Результаты имитационного моделирования. Для подтверждения работоспособности комплексной навигационной системы, построенной с использованием предложенного подхода, а также для оценки ее основных характеристик была разработана методика имитационного моделирования и создан программный комплекс. При проведении численных исследований осуществлялось моделирование движения БА, движения НКА ГНСС, а также измерений датчиков первичной навигационной информации с учетом созданных моделей погрешностей. Принятые характеристики гироскопов, входящих в состав ИИБ, соответствовали волоконно-оптическим гироскопам Оптолинк ОИУС-1000, акселерометров – АК-15. На рис. 6–11 приводятся результаты имитационного моделирования. При этом цифрами обозначены следующие события: 1 – инициализация СТЗ (30 с), 2 – нарастание погрешности определения псевдодальности до НКА 9 GPS со скоростью 2 м/с (с 60-й с), 3 – расширение вектора состояния параметрами волновой структуры для “проблемного” НКА 9 GPS (76 с), 4 – исключение НКА 9 GPS (84 с), 5 – нарастание погрешности определения псевдодальности до НКА 11 ГЛОНАСС со скоростью 1.3 м/с (с 70-й с), 6 – расширение вектора состояния параметрами волновой структуры для “проблемного” НКА 11 ГЛОНАСС (87 с), 7 – исключение НКА 11 ГЛОНАСС (94 с), 8 – движение РТ 15 со скоростью 1.1 м/с (с 200-й с), 9 – расширение вектора состояния параметрами волновой структуры для “проблемной” РТ 15 (216 с), 10 – исключение РТ 15 (219 с).
Рис. 6.
Количество НК и РТ: ___ количество НКА рабочего созвездия; ___ количество исключенных НКА; ___ количество РТ; ___ количество исключенных РТ
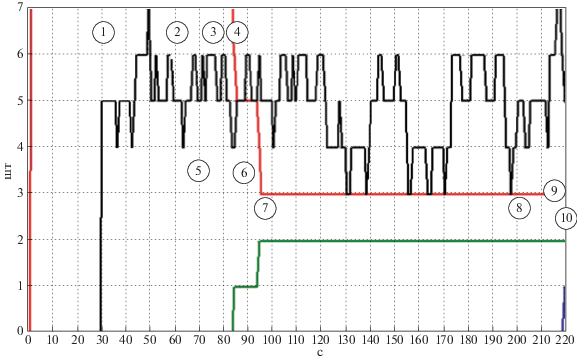
Рис. 7.
СКО ошибок оценок определения местоположения по долготе и широте и ошибок оценок для ОФК (полная модель): а – ошибка оценки по широте; б – СКО ошибки по широте; в – СКО ошибки по долготе; г – ошибка оценки по долготе
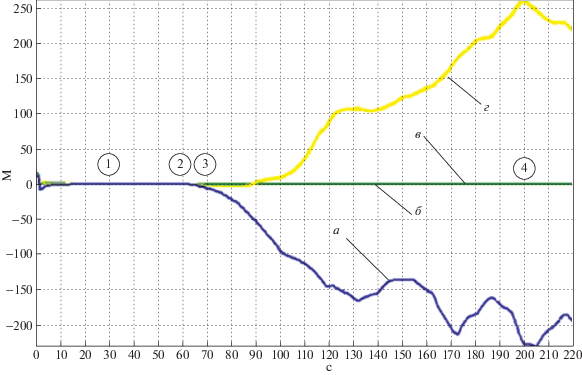
Рис. 8.
СКО ошибок оценок определения местоположения по долготе и широте и ошибок оценок ОФК (полная модель): а – ошибка оценки по широте; б – СКО ошибки по широте; в – СКО ошибки по долготе; г – ошибка оценки по долготе
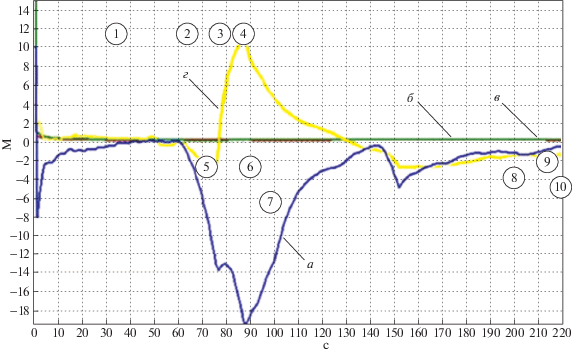
Рис. 9.
СКО ошибок оценок для составляющих путевой скорости и ошибок оценок для ОФК: а – ошибка оценки по Wn; б – СКО ошибки по Wn; в – СКО ошибки по We; г – ошибка оценки по We
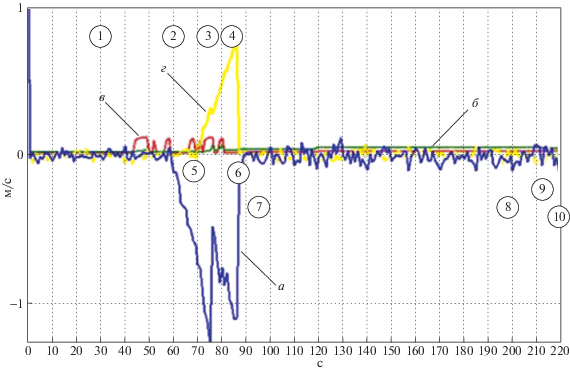
Рис. 10.
СКО ошибок оценок по углам Alfa, Betta и ошибки оценок данных углов для ОФК: а – ошибка оценки по Betta; б – СКО ошибки по Alfa; в – СКО ошибки по Betta; г – ошибка оценки по Alfa
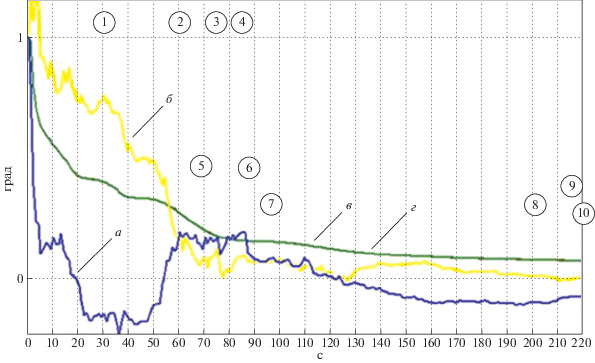
Рис. 11.
СКО ошибок оценок сдвига нуля акселерометров для ОФК (полная модель): а – СКО ошибки оценивания измерений акселерометров по оси 1; б – СКО ошибки оценивания измерений акселерометров по оси 2; в – СКО ошибки оценивания измерений акселерометров по оси 3; г – ошибка оценивания измерений акселерометров по оси 1; д – ошибка оценивания измерений акселерометров по оси 2; е – ошибка оценивания измерений акселерометров по оси 3
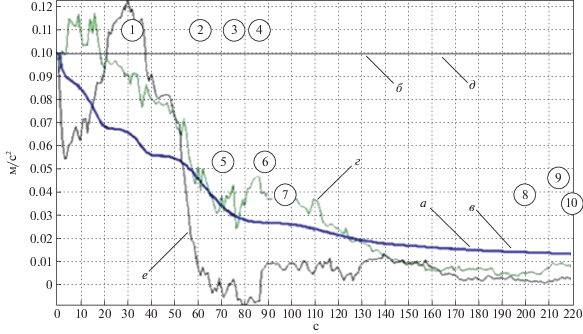
На рис. 6 представлены графики изменения числа НКА в рабочем созвездии (кривая а), число РТ (б), число исключенных НКА (в), число исключенных РТ (г), при этом видно, что при принятых скоростях нарастания погрешностей соответствующие сигналы от НКА и РТ исключаются из структуры измерений через 7–9 с после взятия сигнала на сопровождение.
Рис. 7 показывает, как растет ошибка оценивания при наличии возмущений, отличных от случайных, в традиционном фильтре Калмана (а, г – ошибка оценки СКО, б, в – СКО). Преимущества использования волнового подхода и построенного на его основе фильтра с перестраиваемой структурой показывают графики на рис. 8–11, на которых для того же случая, что и для графиков на рис. 7, отображены ошибки оценок координат, скорости, углов ориентации и сдвига нуля акселерометра (а, г – ошибка оценки СКО, б, в – СКО).
Сопоставление результатов имитационного моделирования работы линейного дискретного ОФК и разработанного описанного выше оптимального фильтра с переменной структурой измерений и вектора состояния, использующего сигналы СТЗ, показывает преимущества предлагаемого подхода к построению алгоритма оценивания с помощью процедуры обнаружения отказов.
Заключение. Предложенный подход к организации контроля показаний датчиков с использованием СТЗ продемонстрировал свою эффективность, позволяя за короткое время обнаруживать аномальные измерения и исключать их источники из вектора измерений, перестраивая структуру оценивателя. Полученные результаты имитационного моделирования, показавшие эффективность предлагаемого подхода, дают возможность перейти к этапу изготовления экспериментальных образцов и натурных испытаний.
Список литературы
Витковский А. Беспилотник будущего – машина, которая сможет все, 2010. http://www.uav.ru.
Волков М. Новые возможности беспилотной разведки, 2010. http://www.uav.ru.
Агеев М.Д., Киселев Л.В., Матвиенко Ю.В. и др. Автономные подводные роботы: системы и технологии / Под общ. ред. Агеева М.Д. М.: Наука, 2005. 398 с.
Каляев И.А., Лохин В.М., Макаров И.М. Интеллектуальные роботы: учеб. пособие по направлению 220400.65–“Мехатроника и робототехника”. М.: Машиностроение, 2007. 360 с.
Грумондз В.Т., Половинкин В.В., Яковлев Г.А. Теория движения двусредных аппаратов. Математические модели и методы исследования. М.: Вузовская книга, 2012. 643 с.
Veremeenko K.K., Antonov D.A., Zharkov V.M., Zimin R.Yu., Tchernodoubov A.Yu. Small-sized Integrated Navigation System // IEEE Aerospace and Electronic Systems Magazine. 2011. № 26 (3). P. 39–41.
Амирагов А.С., Антонов Д.А., Веременко К.К., Жарков М.В., Пронькин А.Н., Чехов Е.Л. Отказоустойчивый навигационный комплекс автоматического необитаемого аппарата // Новости навигации. 2017. № 2. С. 24–30.
Антонов Д.А., Жарков М.В., Кузнецов И.М., Лунёв Е.М., Пронькин А.Н. Определение навигационных параметров беспилотного летательного аппарата на базе фотоизображения и инерциальных измерений // Тр. МАИ. 2016. № 91. http://trudymai.ru/published.php.
Степанов О.А., Кошаев Д.А. Исследование методов решения задачи ориентации с использованием спутниковых систем // Гироскопия и навигация. 1999. № 2 (25). С. 30–55.
Интернет сайт компании Boston Dynamics – http://www.bostondynamics.com/ robot_ls3.html.
Веремеенко К.К., Антонов Д.А., Жарков М.В., Амирагов А.С. О концепции построения навигационного комплекса автоматического необитаемого подводного аппарата // Новости навигации. 2014. № 1. С. 28–33.
Степанов О.А. Основы теории оценивания с приложениями к задачам обработки навигационной информации. Ч. 2. Введение в теорию фильтрации. СПб.: 2012.
Степанов О.А. Основы теории оценивания с приложениями к задачам обработки навигационной информации. Ч. 1. Введение в теорию оценивания. СПб.: 2010.
Алёшин Б.С., Афонин А.А., Веремеенко К.К., Кошелев Б.В., Плеханов В.Е., Тихонов В.А., Тювин А.В., Черноморский А.И. Ориентация и навигация подвижных объектов. Современные информационные технологии / Под ред. Алешина Б.С., Веремеенко К.К., Черноморского А.И. М.: Физматлит, 2006. 422 с.
Ривкин С.С., Ивановский Р.И., Костров А.В. Статистическая оптимизация навигационных систем. Л.: Судостроение, 1976. 280 с.
Фильтрация и стохастическое управление в динамических системах / Под ред. Леондеса К.Т. М.: Мир, 1980. 408 с.
Салычев О.С. Волновое описание возмущений в задачах оценки ошибок инерциальных систем навигации. М.: Машиностроение, 1992. 216 с.
Алешин Б.С., Антонов Д.А., Веремеенко К.К., Зимин Р.Ю., Жарков М.В., Кузнецов И.М., Пронькин А.Н. Малогабаритный интегрированный навигационно-посадочный комплекс // Тр. МАИ. 2016. № 54. http://trudymai.ru/published.php?ID=29692.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления