Известия РАН. Теория и системы управления, 2020, № 2, стр. 83-88

Имитация углового положения объекта для двухпозиционных систем

А. В. Киселев^a, Т. И. Сабитов^a, М. А. Степанов^a, *

^a Новосибирский государственный технический ун-т
Новосибирск, Россия

Поступила в редакцию 27.08.19
После доработки 25.10.19
Принята к публикации 25.11.19

DOI: 10.31857/S0002338820020079

Аннотация

Рассмотрена задача моделирования эхосигналов двухпозиционных радиолокационных систем. Для ее решения предложено использовать четырехточечную конфигурацию двумерной геометрической модели. Получены соотношения для расстановки излучателей модели при условии синфазности сигналов в обеих точках приема. На основе этих соотношений разработан итерационный алгоритм формирования матрицы излучателей для расширения диапазона возможных положений имитируемого объекта. Полученные теоретические результаты подтверждены с помощью методов численного моделирования.

Введение. Одной из основных проблем при моделировании отражений от радиолокационных объектов является имитация их углового положения. Для ее решения в настоящее время применяются в основном следующие технические решения.

Имитаторы с механическим перемещением излучающей части [1–3]. В этом случае излучающая антенна имитатора является подвижной. Ее перемещение по угловым координатам моделирует пространственные перемещения объекта. Подобным устройствам присущи ограничения по возможностям имитации объектов, распределенных по угловым координатам (поверхность земли, метеорологические образования, распределенные пассивные помехи, распределенные цели и др.), по скорости перемещения, по возможностям моделирования пересекающихся траекторий.

Имитаторы с электронной перестройкой углового положения [4–6]. В основе их работы лежит двухточечная геометрическая модель. Она представляет собой две излучающие точки, не разрешаемые антенной радиолокационной станции (РЛС) по угловым координатам. В этом случае нормаль к фазовому фронту электромагнитной волны в точке приема указывает на некоторый кажущийся центр излучения (КЦИ), положение которого L зависит от амплитуд и фаз излучаемых сигналов [7]:

$L = \frac{B}{2}\frac{{E_{{m1}}^{2} - E_{{m2}}^{2}}}{{E_{{m2}}^{2} + 2{{E}_{{m1}}}{{E}_{{m2}}}\cos \psi + E_{{m1}}^{2}}},$

где B – база двухточечной модели (расстояние между излучающими точками); ${{E}_{{m1}}}$, ${{E}_{{m2}}}$ – амплитуды электромагнитных волн, излучаемых из первой и второй точек модели, приведенные в точку приема; $\psi = {{\phi }_{2}} - {{\phi }_{1}}$ – разность фаз электромагнитных волн, излучаемых моделью, которые приведены в точку приема; L – величина смещения КЦИ от центра базы.

Требуемое угловое положение объекта устанавливается за счет соответствующих ${{E}_{{m1}}}$ и ${{E}_{{m2}}}$. При этом наибольшая достоверность моделирования достигается при ψ = 0, т.е. при синфазном задании излучаемых сигналов [8].

Угловые диапазоны, в пределах которых осуществляется имитация, расширяются путем наращивания количества идентичных двухточечных моделей. Для моделирования двумерных перемещений от двух точек переходят к четырем (образующим прямоугольник) или трем (размещаемых в углах треугольника).

Такие имитаторы свободны от недостатков механических устройств и являются наиболее перспективными.

Однако кроме однопозиционных существуют многопозиционные системы (например, бортовые корреляционные измерители скорости и сноса) [9–12]. Их работа связана с использованием, по меньшей мере, двух разнесенных в пространстве приемных антенн. Очевидно, что разработанные для однопозиционных систем конфигурации геометрических моделей неприменимы для имитации эхосигналов многопозиционных систем. Точки модели и соответственно излучатели матрицы должны быть расположены таким образом, чтобы сигналы приходили в одной фазе ко всем антеннам исследуемой системы, а не одной, как для однопозиционных систем.

Цель работы – развить известные результаты для однопозиционных систем применительно к двуантенным системам, а именно обосновать размещение излучателей двумерной геометрической когерентной модели, при котором обеспечивается синфазность сигналов от точек модели в обеих точках приема.

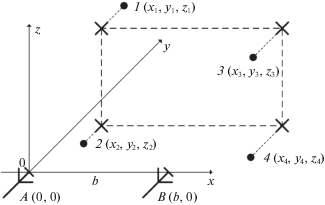
1. Условие синфазности сигналов в двух точках приема. Рассмотрим классическую четырехточечную конфигурацию, представленную на рис. 1, где введены обозначения: 1–4 – номера излучателей; A, B – приемные антенны; b – расстояние между ними; x_i, y_i, z_i, – координаты i-го излучателя модели.

Рис. 1.

Конфигурация двумерной модели

Излучатели модели располагаем так, чтобы их проекции на плоскость y = 0 лежали в углах прямоугольника (на рис. 1 они обозначены крестиками). Для введенной декартовой системы координат, связанной с антенной A, имеем: x₁ = x₂, x₃ = x₄, z₁ = z₃, z₂ = z₄ и, в общем случае, y_i ≠ y_j при i ≠ j.

Сигналы излучателей будут синфазны в обеих точках приема, если разность хода лучей составляет целое число длин волн:

(1.1)

$\left\{ \begin{gathered} {{R}_{{1A}}} - {{R}_{{2A}}} = {{n}_{2}}\lambda , \hfill \\ {{R}_{{1A}}} - {{R}_{{3A}}} = {{n}_{3}}\lambda , \hfill \\ {{R}_{{1A}}} - {{R}_{{4A}}} = {{n}_{4}}\lambda , \hfill \\ {{R}_{{1B}}} - {{R}_{{2B}}} = {{k}_{2}}\lambda , \hfill \\ {{R}_{{1B}}} - {{R}_{{3B}}} = {{k}_{3}}\lambda , \hfill \\ {{R}_{{1B}}} - {{R}_{{4B}}} = {{k}_{4}}\lambda , \hfill \\ \end{gathered} \right.$

где R_it – расстояние между i-м излучателем и t-й точкой приема, λ – рабочая длина волны, n_m и k_m – целые числа.

Для используемой системы координат условие (1.1) преобразуется к виду

(1.2)

$\left\{ \begin{gathered} \sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - \sqrt {x_{1}^{2} + y_{2}^{2} + z_{2}^{2}} = {{n}_{2}}\lambda , \hfill \\ \sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{x}_{3}}^{2} + y_{3}^{2} + z_{1}^{2}} = {{n}_{3}}\lambda , \hfill \\ \sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{x}_{3}}^{2} + y_{4}^{2} + z_{2}^{2}} = {{n}_{4}}\lambda , \hfill \\ \sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{2}^{2} + z_{2}^{2}} = {{k}_{2}}\lambda , \hfill \\ \sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{{\left( {{{x}_{3}} - b} \right)}}^{2}} + y_{3}^{2} + z_{1}^{2}} = {{k}_{3}}\lambda , \hfill \\ \sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{{\left( {{{x}_{3}} - b} \right)}}^{2}} + y_{4}^{2} + z_{2}^{2}} = {{k}_{4}}\lambda . \hfill \\ \end{gathered} \right.$

Решим полученную систему, считая координаты 1-го излучателя известными.

Выразив $z_{2}^{2}$ и $x_{3}^{2}$ из первых двух уравнений системы (1.2) и подставив в третье, получим

$y_{1}^{2} - y_{2}^{2} - y_{3}^{2} + y_{4}^{2} + (n_{2}^{2} + n_{3}^{2} - n_{4}^{2}){{\lambda }^{2}} - 2\lambda \left( {{{n}_{2}} + {{n}_{3}} - {{n}_{4}}} \right)\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} = 0.$

Аналогично для последних трех уравнений системы (1.2):

$y_{1}^{2} - y_{2}^{2} - y_{3}^{2} + y_{4}^{2} + (k_{2}^{2} + k_{3}^{2} - k_{4}^{2}){{\lambda }^{2}} - 2\lambda \left( {{{k}_{2}} + {{k}_{3}} - {{k}_{4}}} \right)\sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} = 0.$

Разность полученных соотношений:

$(n_{2}^{2} + n_{3}^{2} - n_{4}^{2} - k_{2}^{2} - k_{3}^{2} + k_{4}^{2}){{\lambda }^{2}} = 2\lambda \left( {{{n}_{2}} + {{n}_{3}} - {{n}_{4}}} \right)\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - $

$ - \;2\lambda \left( {{{k}_{2}} + {{k}_{3}} - {{k}_{4}}} \right)\sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + {{y}_{1}}^{2} + {{z}_{1}}^{2}} .$

Это уравнение имеет очевидное решение:

(1.3)

$\left\{ \begin{gathered} {{n}_{4}} = {{n}_{2}} + {{n}_{3}}, \hfill \\ {{k}_{4}} = {{k}_{2}} + {{k}_{3}}, \hfill \\ {{k}_{2}}{{k}_{3}} = {{n}_{2}}{{n}_{3}}. \hfill \\ \end{gathered} \right.$

Рассмотрим частный случай решения (1.3): n₂ = 0 или n₃ = 0. Тогда обязательно k₂ = 0 или k₃ = 0. При этом из (1.2) с учетом (1.3) имеем:

${{n}_{2}} = 0 \Leftrightarrow \left\{ \begin{gathered} y_{1}^{2} + z_{1}^{2} = y_{2}^{2} + z_{2}^{2}, \hfill \\ y_{3}^{2} + z_{1}^{2} = y_{4}^{2} + z_{2}^{2}, \hfill \\ \end{gathered} \right.\quad {{k}_{2}} = 0 \Leftrightarrow \left\{ \begin{gathered} y_{1}^{2} + z_{1}^{2} = y_{2}^{2} + z_{2}^{2}, \hfill \\ y_{3}^{2} + z_{1}^{2} = y_{4}^{2} + z_{2}^{2}, \hfill \\ \end{gathered} \right.$

${{n}_{3}} = 0 \Leftrightarrow \left\{ \begin{gathered} x_{1}^{2} + y_{1}^{2} = x_{3}^{2} + y_{3}^{2}, \hfill \\ x_{1}^{2} + y_{2}^{2} = x_{3}^{2} + y_{4}^{2}, \hfill \\ \end{gathered} \right.\quad {{k}_{3}} = 0 \Leftrightarrow \left\{ \begin{gathered} {{\left( {{{x}_{1}} - b} \right)}^{2}} + y_{1}^{2} = {{\left( {{{x}_{3}} - b} \right)}^{2}} + y_{3}^{2}, \hfill \\ {{\left( {{{x}_{1}} - b} \right)}^{2}} + y_{2}^{2} = {{\left( {{{x}_{3}} - b} \right)}^{2}} + y_{4}^{2}. \hfill \\ \end{gathered} \right.$

Очевидно, что n₂ и k₂ равны нулю совместно, а n₃ и k₃ одновременно равняться нулю не могут. Полагая n₂ = k₂ = 0, получим n₃ = n₄ = n, k₃ = k₄ = k. Тогда система (1.2) преобразуется к виду

(1.4)

$\left\{ \begin{gathered} \sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - \sqrt {x_{3}^{2} + y_{3}^{2} + z_{1}^{2}} = n\lambda , \hfill \\ \sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - \sqrt {{{{\left( {{{x}_{3}} - b} \right)}}^{2}} + y_{3}^{2} + z_{1}^{2}} = k\lambda , \hfill \\ y_{1}^{2} + z_{1}^{2} = y_{2}^{2} + z_{2}^{2}, \hfill \\ y_{3}^{2} + z_{1}^{2} = y_{4}^{2} + z_{2}^{2}. \hfill \\ \end{gathered} \right.$

Первые два уравнения (1.4) преобразуются как

$\left\{ \begin{gathered} x_{3}^{2} + y_{3}^{2} + z_{1}^{2} = {{(\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - n\lambda )}^{2}}, \hfill \\ x_{3}^{2} - 2b{{x}_{3}} + {{b}^{2}} + y_{3}^{2} + z_{1}^{2} = {{(\sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - k\lambda )}^{2}}. \hfill \\ \end{gathered} \right.$

Вычитая из первого уравнения второе, получим решение для x₃:

${{x}_{3}} = \frac{b}{2} + \frac{1}{{2b}}{{(\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - n\lambda )}^{2}} - \frac{1}{{2b}}{{(\sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - k\lambda )}^{2}}.$

Из первого уравнения системы (1.4) выражаем y₃:

${{y}_{3}} = \sqrt {{{{(\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - n\lambda )}}^{2}} - x_{3}^{2} - z_{1}^{2}} .$

Последние два уравнения (1.4) достаточно легко могут быть решены относительно y₂ и y₄. Таким образом, соотношения для расчета координат излучателей имеют вид

(1.5)

$\left\{ \begin{gathered} {{x}_{3}} = \frac{b}{2} + \frac{1}{{2b}}{{(\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - n\lambda )}^{2}} - \frac{1}{{2b}}{{(\sqrt {{{{\left( {{{x}_{1}} - b} \right)}}^{2}} + y_{1}^{2} + z_{1}^{2}} - k\lambda )}^{2}}, \hfill \\ {{y}_{3}} = \sqrt {{{{(\sqrt {x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} - n\lambda )}}^{2}} - x_{3}^{2} - z_{1}^{2}} , \hfill \\ {{y}_{2}} = \sqrt {y_{1}^{2} + z_{1}^{2} - z_{2}^{2}} , \hfill \\ {{y}_{4}} = \sqrt {y_{3}^{2} + z_{1}^{2} - z_{2}^{2}} . \hfill \\ \end{gathered} \right.$

Очевидно, что значение z₂ ограничено пределами:

$ - \sqrt {\min ((y_{1}^{2} + z_{1}^{2}),(y_{3}^{2} + z_{1}^{2}))} < {{z}_{2}} < \sqrt {\min ((y_{1}^{2} + z_{1}^{2}),(y_{3}^{2} + z_{1}^{2}))} .$

Наибольший интерес представляет случай z₂ = –z₁, тогда y₂ = y₁, y₄ = y₃ и получаем конфигурацию, симметричную относительно плоскости X0Y. Все излучатели лежат в одной плоскости, в углах прямоугольника.

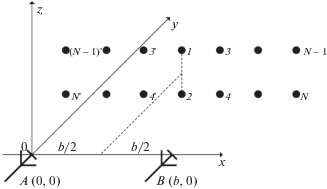
2. Алгоритм формирования матрицы излучателей. Если требуемый диапазон задания положений КЦИ превышает разнос излучателей, образующих рассмотренную выше четверку, то логично увеличивать их количество (рис. 2). На рис. 2 введены обозначения: 1–N – номера излучателей; A, B – приемные антенны РЛС; b – расстояние между антеннами.

Рис. 2.

Размещение излучателей двумерной модели

Принцип работы такой матрицы заключается в следующем: работает только та четверка излучателей (i, i + 1, i + 2, i + 3, где i – нечетное число), в пределах которой должен находиться КЦИ, остальные излучатели выключены.

Это позволяет сформулировать алгоритм поиска положений излучателей в следующем виде.

1. Задаются значения базы b и длины волны λ. Эти параметры определяются исследуемой двухантенной системой.

2. Вполне логично ограничиваемся случаем симметричности расположения точек относительно вертикальной и горизонтальной плоскостей x = b/2 и z = 0.

3. Задается положение исходного излучателя на вертикальной оси симметрии: x₁ = b/2, y₁, ${{z}_{1}} \leqslant {{y}_{1}}{\text{tg0}}{\text{.5}}\theta $, где $\theta $ – ширина диаграммы направленности по уровню половинной мощности в плоскости угла места.

4. Задаются желаемые (ориентировочные) координаты излучателя 3: ${{x}_{3}} \leqslant {{x}_{1}} + {{y}_{1}}{\text{tg0}}{\text{.5}}\alpha $, y₃ = y₁, z₃ = z₁, где $\alpha $ – ширина диаграммы направленности по уровню половинной мощности в плоскости азимута. С помощью (1.4) находятся ориентировочные значения n и k.

5. Рассчитанные n и k округляются до целочисленных значений. По соотношениям (1.5) уточняются координаты излучателя 3 x₃ и y₃.

6. Найденные координаты излучателя 3 становятся исходными для расчета координат следующего излучателя в соответствии с п. 4 и 5.

7. Пункты с 4 по 6 циклично повторяются, пока не будут получены координаты крайнего правого излучателя. Таким образом будут получены координаты рядя точек с номерами 1, 3, 5, …, N – 1 (рис. 2).

8. Найденные координаты излучателей отображаются относительно горизонтальной (точки 2, 4, 6, …, N на рис. 2) и вертикальной (точки 2', 3', …, N' на рис. 2) плоскостей симметрии.

Рассмотрим пример. Зададим начальные условия: b = 1; λ = 0.03; x₁ = 0.5; y₁ = 4; z₁ = 0.5. Диапазон перемещения КЦИ по координате x от –1 до 2. Шаг излучателей Δ_x = 0.5 (все координаты нормированы к базе).

Воспользовавшись полученным алгоритмом, получим координаты точек правой верхней части матрицы (таблица). Оставшаяся часть матрицы формируется, согласно п. 8 алгоритма.

Координаты остальных точек и соответственно излучателей матрицы получаются путем зеркального отображения найденных положений точек 1, 3, 5 и 7 относительно плоскостей симметрии.

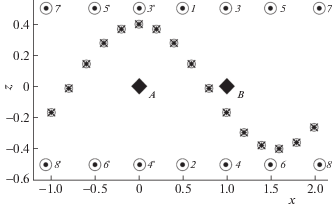
3. Апробация результатов. Осуществлялась методами численного моделирования. Для найденного выше положения излучателей (она представлена на рис. 3) задавалась траектория перемещения КЦИ: ${{x}_{{{\text{КЦИ}}}}} \in \left[ { - 1;{\text{ 2}}} \right]$, ${{z}_{{{\text{КЦИ}}}}} = 0.4\cos 2{{x}_{{{\text{КЦИ}}}}}$. Для четверки излучателей (i … i + 4, i = {1, 3, 5, 7, 9, 11, 13}), в область моделирования которых попадал КЦИ, рассчитывались его обобщенные координаты:

${{\xi }_{x}} = \frac{{2{{x}_{{{\text{КЦИ}}}}} - \left( {{{x}_{{i + 2}}} + {{x}_{i}}} \right)}}{{{{x}_{{i + 2}}} - {{x}_{i}}}},\quad {{\xi }_{z}} = \frac{{2{{z}_{{{\text{КЦИ}}}}} - \left( {{{z}_{i}} + {{z}_{{i + 1}}}} \right)}}{{{{z}_{i}} - {{z}_{{i + 1}}}}}.$

Рис. 3.

Результаты численного моделирования

По ним определялись амплитуды сигналов, излучаемых точками [13]:

${{E}_{i}} = \frac{{{{\gamma }_{z}}{{E}_{\Sigma }}}}{{\left( {1 + {{\gamma }_{x}}} \right)\left( {1 + {{\gamma }_{z}}} \right)}},\quad {{E}_{{i + 1}}} = \frac{{{{E}_{\Sigma }}}}{{\left( {1 + {{\gamma }_{x}}} \right)\left( {1 + {{\gamma }_{z}}} \right)}},$

${{E}_{{i + 2}}} = \frac{{{{\gamma }_{x}}{{\gamma }_{z}}{{E}_{\Sigma }}}}{{\left( {1 + {{\gamma }_{x}}} \right)\left( {1 + {{\gamma }_{z}}} \right)}},\quad {{E}_{{i + 3}}} = \frac{{{{\gamma }_{x}}{{E}_{\Sigma }}}}{{\left( {1 + {{\gamma }_{x}}} \right)\left( {1 + {{\gamma }_{z}}} \right)}},$

где ${{\gamma }_{x}}$ – отношение амплитуд сигналов для точек, расположенных вдоль оси x, ${{\gamma }_{z}}$ – отношение амплитуд сигналов для точек, расположенных вдоль оси z, ${{E}_{\Sigma }}$ – амплитуда суммарного сигнала в точке наблюдения. Их величины определяются выражениями:

${{\gamma }_{x}} = \frac{{{{E}_{{i + 2}}}}}{{{{E}_{i}}}} = \frac{{{{E}_{{i + 3}}}}}{{{{E}_{{i + 1}}}}} = \frac{{1 + {{\xi }_{x}}}}{{1 - {{\xi }_{x}}}};\quad {{\gamma }_{z}} = \frac{{{{E}_{i}}}}{{{{E}_{{i + 1}}}}} = \frac{{{{E}_{{i + 2}}}}}{{{{E}_{{i + 3}}}}} = \frac{{1 + {{\xi }_{z}}}}{{1 - {{\xi }_{z}}}};\quad {{E}_{\Sigma }} = \sum\limits_{s = i}^{i + 4} {{{E}_{s}}} .$

Предполагалось, что разность расстояний до точек влияет только на фазовый набег сигналов. Различия в изменениях амплитуд предполагались несущественными. Положение КЦИ определялось с помощью известного пеленгационного соотношения [14, 15].

Результаты моделирования представлены на рис. 3, где символами обозначено: х – теоретическое положение КЦИ; + – положение КЦИ для точки наблюдения А; Ο – положение КЦИ для точки наблюдения В. Видно, что координаты КЦИ, определенные обеими антеннами-пеленгаторами, совпадают. Это подтверждает справедливость полученных соотношений.

Заключение. Предложенное размещение точек модели и соответственно излучателей матричного имитатора позволяют обеспечить моделирование эхосигналов двухпозиционных радиотехнических систем. Они могут найти применение при разработке матричных имитаторов отражений от точечных и распределенных объектов.

Таблица 1.

Полученные координаты излучателей двумерной матрицы

Номер излучателя	Координаты (x_i; y_i; z_i)	Значения n и k
1	(0.5; 4; 0.5)	–3, 1
3	(0.991; 4.001; 0.5)	–5, –1
5	(1.504; 4; 0.5)	–7, –3
7	(2.06; 3.983; 0.5)	–

Список литературы

Урсатьев А.А., Погребная Н.П. Полунатурная модель сигнально-помеховой радиолокационной обстановки // Управляемые системы и машины. 1991. № 4. С. 102–111.
Устройство для имитации целей: пат. RU2125275, 1999.
Radar target simulator: пaт. 2934759 USA, 1960.
Sisle M.E., McCarthy E.D. Hardware-in-the-Loop Simulation for an Active Missile // Simulation. 1982. T. 39. № 5. C. 159–167.
Maples V.H., Eastman G.A. Radar Scene Simulator: пaт. 4660041 USA. 1987.
Имитатор источников радиосигналов: пат. RU2094915, 1997.
Островитянов Р.В., Басалов Ф.А. Статистическая теория радиолокации протяженных целей. М.: Радио и связь, 1982. 232 с.
Степанов М.А. Точность позиционирования кажущегося центра излучения в когерентном трехточечном матричном имитаторе // Вопросы радиоэлектроники. Сер. Общетехническая. 2015. № 5. С. 57–67.
Белоглазов И.Н., Джанджгава Г.И., Чигин Г.П. Основы навигации по геофизическим полям. М.: Наука, Физматлит, 1985. 328 с.
Антюфеев В.И., Быков В.Н. Сравнительный анализ алгоритмов совмещения изображений в корреляционно-экстремальных системах навигации летательных аппаратов // Авиационно-космическая техника и технология. 2008. Т. 48. № 1. С. 70–74.
Васильева А.В., Калмыков Н.Н., Мельников С.А., Соловьев В.В. Модель коррелированных сигналов для имитатора скорости корреляционного радиолокационного измерителя // Вестник концерна ПВО “Алмаз-Антей”. 2016. № 4. С. 18–23.
Richards M.A., Scheer J.A., Holm W.A. Principles of Modern Radar: Basic Principles. Edison, N.J.: Scitech Publishing, 2010. 960 c.
Тырыкин С.В., Киселев А.В. Экономичный алгоритм имитации сложных радиолокационных целей // Изв. вузов. Радиоэлектроника. 2003. Т. 4. С. 76–80.
Канащенков А.И., Меркулов В.И. Радиолокационные системы многофункциональных самолетов. Т. 1. РЛС – информационная основа боевых действий многофункциональных самолетов. Системы и алгоритмы первичной обработки радиолокационных сигналов. М.: Радиотехника, 2006. 656 с.
Леонов А.И., Фомичев К.И. Моноимпульсная радиолокация. М.: Радио и связь, 1984. 312 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал