Известия РАН. Теория и системы управления, 2020, № 3, стр. 30-38

Введение. Работа посвящена построению простого метода управления противоударным изолятором с наихудшими возмущениями. Рассматривается система с одной степенью свободы, состоящая из основания и расположенного на ней защищаемого объекта. Воздействие на основание характеризуется заданием ее ускорения и описывается функцией времени. Основание и защищаемый объект движутся вдоль одной прямой линии, и управляющая сила, создаваемая изолирующим устройством между основанием и объектом, ограничена по величине. В работах [1–3] ставилась задача о минимизации максимума модуля смещения объекта относительно основания при заданном возмущении. Основы теории оптимальной противоударной изоляции развивались в [4–7]. Возможности изоляции объекта, расположенного на подвижном основании, от кратковременных ударных воздействий с помощью активного изолятора с управлением без упреждения изучались в [8]. Для некоторых конкретных возмущений оптимальные упреждающие управления были построены численно или аналитически в [9]. Для задач с заданной длительностью возмущений и фиксированным управлением в [9] было также доказано, что наихудшие возмущения представляют собой дельта-функции, действующие либо в начальный момент возмущения либо в конечный. Поэтому представлялось разумным строить упреждающее управление с оптимизацией момента упреждения для наихудших возмущений на основе управления, полученного для дельта возмущений (мгновенных ударов). В [10, 11] такая оптимизация была проведена и построено соответствующее значение функционала. В этих работах было также построено гарантирующее упреждающее управление с одним переключением и время упреждения, позволяющие вычислять минимальную оценку максимальной величины смещения объекта относительно основания для целого класса возмущений. Сравнение этих двух решений по критерию качества показало, что для относительно больших длительностей возмущений оптимизация только по моменту упреждения при выбранном способе управления не является удачной. Обнаружилось, что если профиль управляющей функции (т.е. зависимость управляющей переменной от времени после включения управления) задан и выбирается только момент включения, то в ряде случаев лучший результат дает включение управления не с опережением, а с запаздыванием по отношению к моменту начала действия возмущения. Это наблюдение мотивировало написание данной статьи, где обнаруженный эффект исследуется для управления, профиль которого совпадает с профилем построенного ранее оптимального управления для мгновенного удара. Показано, что для возмущений достаточно большой длительности при таком профиле управления оптимизация по времени включения управления приводит к запаздыванию, а не к упреждению. Оптимизация с допущением только упреждения приводит к значительно большему значению критерия качества. Управление с запаздыванием приводит к значению функционала, совпадающему с оптимальным значением для управлений с одним варьируемым переключением. В [12] дан обзор современного состояния проблемы противоударной изоляции, в котором, в частности, есть ссылки на публикации по оптимальному управлению противоударными изоляторами. Судя по этому обзору, исследования по оптимальному управлению активными противоударными изоляторами в настоящее время практически не ведутся. Однако актуальность этой проблематики не представляется исчерпанной, и возможны новые постановки задач, решение которых позволит найти пути к существенному улучшению качества изоляции.

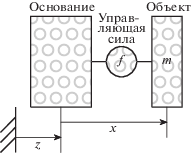
1. Механическая система. Пусть механическая система (рис. 1) состоит из основания и объекта, соединенного с основанием посредством противоударного изолятора – устройства, генерирующего управляющую силу f между основанием и объектом и предназначенного для защиты объекта при ударном воздействии на основание. Движения основания и объекта предполагаются поступательными вдоль одной прямой. Обозначим: $z$ – смещение основания относительно неподвижной (инерциальной) системы отсчета, $x$ – смещение объекта относительно основания, m – масса объекта. Ударное воздействие на основание моделируется его ускорением $\ddot {z}$, функцией времени, некоторые характеристики которой предполагаются известными.

Движение объекта относительно основания описывается уравнением

Далее полагаем, что сила  f  удовлетворяет ограничению $\left| f \right| \leqslant {{F}_{0}}$, где ${{F}_{0}}$ – заданная величина, тогда величина $u$ удовлетворяет неравенству

Предполагается, что в начальный момент времени t = 0 основание и объект покоятся в положениях, отвечающих нулевым значениям координат $x$ и $z$:

В качестве допустимых управлений будем рассматривать кусочно-непрерывные функции $u(t),$ удовлетворяющие ограничению $\left| {u(t)} \right| \leqslant {{u}_{0}}$.

2. Внешние возмущения. Предполагается, что возмущение ${v}(t)$ имеет вид

где кусочно-непрерывная функция $V(\xi )$ определена для всех вещественных $\xi $, причем $V(\xi ) \equiv 0$ для $\xi < 0$, а ${{t}_{0}} \geqslant 0$ – некоторый момент времени, который может быть задан или подлежать определению. Таким образом, возмущение $V$ начинает действовать на основание спустя время t₀ после включения системы противоударной изоляции (упреждающее управление).

Будем предполагать, что возбуждение 1) действует только в одном направлении и не меняет знака ($V(t) \geqslant 0$), 2) имеет конечную длительность $T$ ($V(t) \equiv 0$, если $t > T$) и 3) только на одном интервале, ${{t}_{1}} < t < {{t}_{2}}$, величина абсолютного ускорения $V(t)$ основания превышает верхнюю границу ${{u}_{0}}$ абсолютного ускорения защищаемого объекта:

Один или оба из интервалов $0 \leqslant t < {{t}_{1}}$ и ${{t}_{2}} < t \leqslant T$ могут быть пустыми, если $V(0) > {{u}_{0}}$ или $V(T) > {{u}_{0}}$. В случае, когда $V(t) \leqslant {{u}_{0}}$ для $0 \leqslant t \leqslant T$ оптимальное управление определяется тождеством $u(t) \equiv V(t)$ и обеспечивает тождественно равное нулю смещение объекта по отношению к основанию. Базовыми характеристиками ударного воздействия являются его длительность $T$ и интеграл

характеризующий величину скорости, приобретенной (или потерянной) основанием в результате удара. В дальнейшем параметры T и ${{{v}}_{0}}$ считаются известными. Класс описанных возмущений обозначим ${{V}_{*}}$.

3. Критерий качества. Будем считать, что возмущение $V(\xi )$ неизвестно, но известно множество $\Omega \subset {{V}_{*}}$, которому могут принадлежать возможные возмущения. Качество изоляции при заданных управлении $u(t)$ и времени упреждения ${{t}_{0}}$ будем оценивать функционалом J, характеризующим максимальную величину смещения объекта относительно основания при наихудшем возмущении:

где $x(t;u,V,{{t}_{0}})$ – решение уравнения (1.1) с начальными условиями (1.2) для заданных $u(t)$, $V(\xi )$ и ${{t}_{0}}$. Величину J желательно минимизировать выбором оптимального закона управления и времени упреждения.

4. Лемма о наихудшем возмущении. Вычисление функционала (3.1) предполагает определение наихудшего возмущения $V \in \Omega \subset {{V}_{*}}$, которое максимизирует максимум модуля отклонения защищаемого объекта относительно основания ($ma{{x}_{t}}\left| {x(t;u,V,{{t}_{0}})} \right|$) при заданных $u(t)$ и ${{t}_{0}}$.

Лемма [9]. Среди возмущений $V \in {{V}_{*}}$ наихудшее возмущение есть либо $V(\xi ) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (\xi )$, либо $V(\xi ) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (\xi - T)$. Иными словами, наихудшее возмущение есть мгновенный удар интенсивности ${{{v}}_{0}}$, подаваемый в начальный или в конечный момент допустимого интервала возмущения.

Согласно этой лемме, для нахождения наихудшего возмущения при заданных $u(t)$ и ${{t}_{0}}$ надо решить дифференциальное уравнение (1.1) с начальными условиями (1.2) при ${v}(t) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (t - {{t}_{0}})$ и ${v}(t) = {{{v}}_{0}}\delta {\kern 1pt} {\kern 1pt} (t - {{t}_{0}} - T)$, для каждого из решений вычислить соответственно $ma{{x}_{t}}\left| {x(t;u,V,{{t}_{0}})} \right|$, $ma{{x}_{t}}\left| {x(t;u,V,T)} \right|$, сравнить получившиеся величины и выбрать возмущение, отвечающее большему значению.

Введем безразмерные переменные

Далее будем использовать безразмерные переменные, опуская штрихи. В безразмерных единицах параметры ${{u}_{0}}$ и ${{{v}}_{0}}$ равны единице.

5. Задачи оптимизации. Поскольку условия информированности управляющей стороны о внешнем возмущении и множества допустимых законов управления U могут быть различными, то и задачи оптимального управления должны быть сформулированы по-разному.

Задача 1. Для системы (1.1) с начальными условиями (1.2) найти допустимое управление ${{u}_{*}}$ и время упреждения $t_{0}^{*}$, которые минимизируют величину (3.1):

где U – множество законов управления $u(t)$, среди которых ищется оптимум.

Это задача о гарантирующем оптимальном упреждающем управлении противоударным изолятором, защищающим объект от ударных воздействий из множества Ω. Она обобщает задачу, рассмотренную в [1–3] для заданного возмущения в отсутствие упреждения управления.

Задача 2. Для системы (1.1) при начальных условиях (1.2) и возмущении (2.1) найти кусочно-непрерывное управление $u(t)$, удовлетворяющее ограничению

и время упреждения ${{t}_{0}}$, которые минимизируют максимальную величину смещения объекта относительно основания (функционал $J$):

Эту задачу можно трактовать как задачу 1, в которой множество допустимых возмущений $\Omega $ состоит из одного элемента.

Множество допустимых законов управления может представлять собой параметрическое семейство управлений ${{u}_{s}}(t) \in {{U}_{s}}$, зависящих от параметра $s$, $s \in S$.

Задача 3. Для заданного класса допустимых управлений ${{u}_{s}}(t) \in {{U}_{s}}$ найти время упреждения $t_{0}^{*}$ и значение параметра s*, минимизирующие величину (3.1):

Решение задачи 3 дает возможность улучшать качество противоударной защиты путем изменения времени упреждения и параметра при заданном семействе законов управления ${{u}_{s}}(t)$, которое, например, может быть построено на основе оптимального управления для некоторого возмущения $V \in \Omega $ и представлено аналитическими выражениями.

6. Параметрическая оптимизация. В работе рассматриваются два основных параметрических множества допустимых законов управления: ${{U}_{\tau }}$ – класс управлений с одним переключением, ${{U}_{c}}$ – класс управлений с запаздыванием, основанный на оптимальном управлении для мгновенного удара.

Класс управлений ${{U}_{\tau }}$ описывается в размерных переменных параметрическим семейством допустимых релейных управлений ${{u}_{\tau }}(t)$ с переключением c $ - {{u}_{0}}$ на ${{u}_{0}}$ в момент времени $\tau $ и с ${{u}_{0}}$ на 0 в момент времени ${{{v}}_{0}}{\text{/}}{{u}_{0}} + 2\tau $, т.е. примем ${{U}_{\tau }} = \{ {{u}_{\tau }}\} $, где

Для управлений вида (6.1) имеем

Длина отрезков управления в (6.1) выбрана из условия $\dot {x} \to 0$ при $t \to + \infty ,$ что приводит к конечному смещению объекта относительно основания.

В безразмерных переменных соотношения (6.1), (6.2) приобретают вид

Для класса управлений ${{U}_{\tau }} = \{ {{u}_{\tau }}\} $ решение задачи 3 получено в [10, 11]. Оптимальное управление определяется формулой (6.3) со значением параметра τ:

Значение функционала и момент упреждения находят как

Заметим, что приведенное решение задачи 1 при $T > 1{\text{/}}2$ неединственно. Значение функционала $J = T{\text{/}}2$ для этого случая обеспечивается моментом переключения $\tau $ и моментом упреждения ${{t}_{0}}$, удовлетворяющим соотношениям

Класс управлений ${{U}_{c}} = \{ {{u}_{c}}\} $ описывается параметрическим семейством допустимых управлений ${{u}_{c}}(t)$, где

Управление ${{u}_{c}}(t)$ при c = 0 обозначим ${{u}_{\delta }}(t)$ и будем называть дельта-управлением, поскольку управление ${{u}_{\delta }}(t)$ с моментом упреждения t₀ = 1 представляет собой оптимальное управление с оптимальным упреждением для задачи 2 при возмущении $V(\xi ) = \delta (\xi )$. Очевидное равенство ${{u}_{c}}(t) = {{u}_{\delta }}(t - c)$ означает, что управление ${{u}_{c}}(t)$ представляет собой дельта-управление с запаздыванием $c.$

Введем функцию ${{J}_{{cd}}}(t*)$, определяемую как значение функционала J, отвечающее управлению ${{u}_{c}}(t)$ и возмущению ${v}(t) = \delta (t - t{\text{*}})$, т.е. мгновенному удару, действующему на основание в момент времени $t{\text{*}}$. Эта функция задается выражением

Формула (6.5) позволяет оценить влияние ошибки в определении момента удара при расчете упреждающего оптимального управления на величину критерия качества противоударной изоляции. Функция из (6.5) непрерывна, монотонно убывает от значения $17{\text{/}}16 + c$ до 1/16 при $t* \in [0,1 + c)$ и монотонно возрастает от 1/16 до бесконечности при $t* > 1 + c$. Формула (6.5) является обобщением формулы для величины ${{J}_{{dd}}}(t*)$, определяемой как максимум модуля отклонения объекта относительно основания для мгновенного удара ${v}(t) = \delta {\kern 1pt} {\kern 1pt} (t - t*)$ при управлении ${{u}_{\delta }}(t)$, $t* \geqslant 0$:

Очевидное равенство ${{J}_{{cd}}}(t*) = {{J}_{{dd}}}(t{\text{*}} - c)$ при $t* \geqslant c$ означает, что график функции ${{J}_{{cd}}}(t*)$ получается смещением графика ${{J}_{{dd}}}(t*)$ на величину c вдоль оси абсцисс с доопределением на интервале $[0,c)$, согласно формуле (6.5).

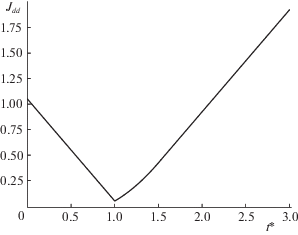
График функции ${{J}_{{dd}}}(t*)$ изображен на рис. 2. Для решения задачи 3 надо, с учетом леммы о наихудшем возмущении, для заданного T найти минимум по переменным t₀, c величины

Минимум величины из (6.7) достигается при выполнении условий

которые приводят к решению задачи 3 для класса управлений ${{U}_{c}}$:

Заметим, что значение функционала ${{J}_{c}}(T)$ из (6.10) обеспечивается не единственным образом. Оптимальные минимально возможные момент упреждения $t_{c}^{*}$ и величина запаздывания $c{\text{*}}$ определяются соотношениями

В [10, 11] была рассмотрена задача 3 для случая, когда множество допустимых управлений U₀ состоит из одного элемента ${{u}_{\delta }}(t),t \geqslant 0$ (случай c = 0, ${{J}_{{cd}}}(t*) \equiv {{J}_{{dd}}}(t*)$.) Для момента упреждения $t_{0}^{*}$ и значения функционала $J({{u}_{\delta }},t_{0}^{*})$ были получены следующие выражения:

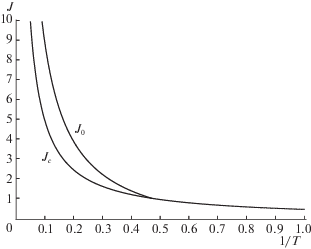
Значения функционалов из (6.10) и (6.13) при $T \leqslant 17{\text{/}}8$ совпадают, а при $T > 17{\text{/}}8$ имеем ${{J}_{c}}(T) < {{J}_{0}}(T)$, т.е. использование управления ${{u}_{\delta }}(t)$, $t \geqslant 0$ приводит к худшему результату, чем использование управления ${{u}_{c}}(t)$, $t \geqslant 0$. Эту разницу в значениях функционала демонстрирует рис. 3. Относительная разность значений функционалов ${{J}_{0}}(T)$ и ${{J}_{c}}(T)$ при T > 17/8 имеет следующий вид

т.е. при больших T значение ${{J}_{0}}(T)$ превышает значение ${{J}_{c}}(T)$ почти в 2 раза.

7. Сравнение качества изоляции для различных способов управления. Нетрудно убедиться в справедливости следующих соотношений:

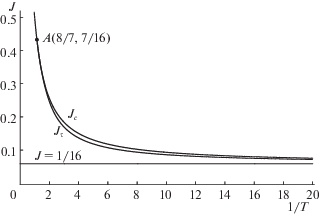
Заметим, что интерес представляют функции ${{J}_{\tau }}(T)$, ${{J}_{c}}(T)$, поскольку функция ${{J}_{c}}(T)$ является уточнением функции ${{J}_{0}}(T)$ и хорошим приближением функции ${{J}_{\tau }}(T)$, полученным на основе простого дельта-управления с запаздыванием и упреждением. Зависимости величин ${{J}_{\tau }}$ и ${{J}_{c}}$ от $1{\text{/}}T$ изображены на рис. 4. Левее точки A графики совпадают.

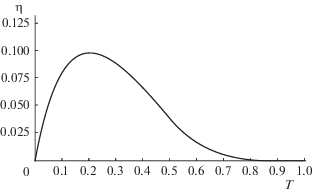
На рис. 5 представлена зависимость величины $\eta = ({{J}_{c}} - {{J}_{\tau }}){\text{/}}{{J}_{\tau }}$ от длительности возмущения T. Величина $\eta $ характеризует относительное отличие гарантированных значений критерия качества, обеспечиваемых управлением ${{u}_{c}}(t)$ при оптимальном выборе моментов времени упреждения и запаздывания, и оптимальным управлением ${{u}_{\tau }}(t)$ с оптимальным временем упреждения ${{t}_{{0\tau }}}$. Установлено, что $\eta \equiv 0$ при $T \geqslant 7{\text{/}}8$ и $\eta < 0.1$ для $T \in [0,7{\text{/}}8]$. Таким образом, управление ${{u}_{c}}(t)$ с моментами времени упреждения и запаздывания, определяемым согласно (6.9), (6.11), обеспечивает качество противоударной защиты, не более чем на 10% отличающееся от оптимального управления на всем диапазоне длительностей ударного воздействия, и совпадает с оптимальным для $T \in [7{\text{/}}8, + \infty )$.

Заключение. Рассматривалась задача изоляции объекта на подвижном основании от ударов, которым может подвергаться основание. Изучалась возможность применения управления, предназначенного для мгновенного удара, к задаче с возмущением с заданными длительностью и интегралом от возмущения. Предполагалось, что можно варьировать момент начала управления. Показано, что для возмущений безразмерной длительности, меньшей 17/8, нужно использовать упреждение, а при безразмерной длительности, большей 17/8, нужно применять запаздывание. При этом без запаздывания относительное смещение возрастает почти в 2 раза при больших длительностях возмущений, тогда как при использовании запаздывания и упреждения относительная ошибка по критерию качества относительного смещения не превышает 0.1 от оптимального значения для задачи с одним варьируемым переключением.