Известия РАН. Теория и системы управления, 2020, № 4, стр. 58-82
НЕУСТОЙЧИВЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ С ГИСТЕРЕЗИСОМ: ЗАДАЧИ СТАБИЛИЗАЦИИ И УПРАВЛЕНИЯ
А. Л. Медведский a, *, П. А. Мелешенко b, c, В. А. Нестеров d, О. О. Решетова b, М. Е. Семенов b, e, f, А. М. Соловьев g
a Федеральное государственное унитарное предприятие “Центральный аэрогидродинамический институт
им. проф. Н.Е. Жуковского”
Жуковский, Россия
b Воронежский государственный университет
Воронеж, Россия
c Целевая поисковая лаборатория прорывных технологий радиосвязи Фонда перспективных исследований
Воронеж, Россия
d Московский авиационный институт (национальный исследовательский ун-т)
Москва, Россия
e ФГБУН Федеральный исследовательский центр “Единая геофизическая служба Российской академии наук”
Москва, Россия
f Воронежский государственный технический ун-т
Воронеж, Россия
g АО “Концерн “Созвездие”, ГК “Ростех”
Воронеж, Россия
* E-mail: mkl150@mail.ru
Поступила в редакцию 11.01.2019
После доработки 20.12.2019
Принята к публикации 27.01.2020
Аннотация
Работа посвящена изучению динамики неустойчивых колебательных систем (в форме перевернутого маятника), управляемых посредством воздействия гистерезисной природы. Представлены результаты для различных типов движения точки подвеса, а именно для вертикального и горизонтального движения. Рассмотрена математическая модель обратного маятника с вертикально осциллирующим подвесом, для которого получены явные критерии устойчивости для линеаризованных уравнений движения. Описаны зависимости между начальными условиями и значением управляющих параметров, которые обеспечивают периодические колебания маятника.
Приведена математическая модель обратного маятника, управление которым строится по принципу обратной связи в условиях горизонтальных движений точки крепления. Получены условия, гарантирующие стабилизацию рассматриваемой системы, формулируемые в терминах ограничений на начальные условия. Представлено решение задачи об оптимальном управлении колебательной системой в смысле минимизации квадратичного целевого функционала.
В работе также рассмотрена задача стабилизации неустойчивой системы с распределенными параметрами – гибкого обратного маятника, для которой сформулированы условия. Их выполнение обеспечивает ограниченность фазовых координат на бесконечном промежутке времени. Идентифицированы оптимальные (в смысле минимизации квадратичного целевого функционала) параметры, отвечающие стабилизации распределенной системы.
Введение. Изучение динамики неустойчивых колебательных систем, на примере обратного или перевернутого маятника, имеет весьма длинную историю [1–3], однако практическая значимость этой задачи наиболее ярко проявилась лишь в последнее время [4–10]. Как известно, модель перевернутого маятника является классической задачей в теории управления [11–18]. В работах [19–21] приводятся различные варианты решения задачи оптимального по быстродействию управления для однозвенных и многозвенных маятников, а также рассмотрены вопросы, связанные со стабилизацией в верхнем неустойчивом положении равновесия таких систем [22]. Также указанная модель имеет широкое применение при тестировании алгоритмов управления (пропорционально-интегрально-дифференцирующих регуляторов, нейронных сетей, нечёткого управления и т.д.). Развитие идей и подходов, связанных с управлением и стабилизацией обратного маятника, имеет место в различных областях технических наук, начиная от робототехники (в этой связи отметим работу, в которой рассматривается задача о стабилизации обратного маятника, являющегося модельным приближением перемещения центра масс при ходьбе двуногих шагающих роботов [23]), до космических технологий [24], где возникает задача о стабилизации и управлении гибким манипулятором посредством вращательных движений. Также отметим, что стабилизация ракеты в вертикальном положении на начальном участке полета идейно близка к задаче стабилизации обратного маятника, поскольку двигатель ракеты размещен ниже центра масс.
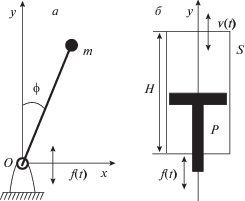
Модель обратного маятника с осциллирующей точкой подвеса (рис. 1,а) подробно исследована Капицей. Известно, что если движение точки подвеса имеет гармонический характер, то динамика маятника описывается уравнением Матье, подробно изученным в [25]. Однако для адекватного описания динамики реальных физических и механических систем необходимо учитывать эффекты гистерезисной природы, такие, как “люфты”, “упоры” и т.д. [26], возникающие в процессе длительного функционирования в силу естественного старения и износа механических составляющих.
Рис. 1.
Модель обратного маятника с осциллирующей точкой подвеса (а), цилиндр в основании маятника (б)
Математические модели таких нелинейностей, согласно классическим схемам Красносельского и Покровского [27], сводятся к операторным соотношениям, в которых соответствующие операторы трактуются как преобразователи, как правило, определенные на пространствах непрерывных функций, зависящие от своего начального состояния, как от параметра, динамика которых описывается следующими соотношениями: вход-состояние и состояние-выход.
В частности, люфт в точке подвеса представляет собой одну из типичных гистерезисных нелинейностей, при этом большинство реальных физических и технических систем содержат различные части, которые могут быть представлены в виде цилиндра с поршнем. Возникновение люфта в таких системах соответствует явлениям “износа” или “старения” материала.
В настоящей работе подробно исследованы различные варианты стабилизации обратного маятника посредством гистерезисного управления, т.е. рассматривается ситуация, когда маятник шарнирно закреплен на цилиндре, движение которого определяется находящимся внутри него поршнем в условиях горизонтального и вертикального его расположения. В свою очередь изучаются случаи с сосредоточенной и распределенной массой (гибкий маятник), а также различные алгоритмы стабилизации: на основе принципа обратной связи и управление, определяемое заданным законом движения поршня.
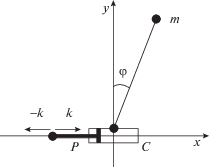
1. Обратный маятник с гистерезисным управлением: вертикальная осцилляция точки подвеса. 1.1. Математическая модель. Рассмотрим систему, в которой основание маятника является физической системой (P, S), образованной цилиндром длиной H и поршнем P. Цилиндр и поршень могут перемещаться в направлении вертикальной оси, как показано на рис. 1, б. Положение поршня определяется координатой $f (t)$, а положение цилиндра – координатой $v(t)$. Зададим, что “ведущий” элемент в системе (P, S) – цилиндр P. В этом предположении систему (P, S) можно рассматривать как преобразователь $\Gamma $ с входным сигналом $f(t)$ (положение поршня) и выходным сигналом $v(t)$ (положение цилиндра). Такой преобразователь называется люфтом, набор возможных состояний которого представляется полосой $f (t) \leqslant v(t) \leqslant f (t) + H\left( { - \infty < f(t) < \infty } \right)$, (H > 0). Положение цилиндра $v(t)$ при $t > {{t}_{0}}$ определяется как $v (t) = \Gamma {\text{[}}{{t}_{0}}, v ({{t}_{0}}){\text{]}} f (t)$, где $\Gamma {\text{[}}{{t}_{0}}, v ({{t}_{0}}){\text{]}}$ – оператор, найденный для каждого ${{v}_{0}} = v ({{t}_{0}})$ на множестве непрерывных входов $f(t) (t > {{t}_{0}})$ соотношением:
На всех непрерывных входах этот оператор доопределяется с помощью специальной предельной конструкции, детально описанной в [27], в этой же монографии приведены основные свойства указанного оператора.
Предположим, что ускорение поршня периодически изменяется от $ - a\omega _{0}^{2}$ до $a\omega _{0}^{2}$ с частотой ω0. Это предположение соответствует тому, что линеаризованное уравнение движения такого маятника можно записать в виде [28]
(1.1)
$\begin{gathered} \ddot {\phi } - \frac{1}{l}[g + a\omega _{0}^{2}G(t,H)w(t)]\phi = 0, \\ w(t) = - {\kern 1pt} \operatorname{sgn} [\sin ({{\omega }_{0}}t)], \\ \phi (0) = {{\phi }_{{10}}},\quad \dot {\phi }(0) = {{\phi }_{{20}}}, \\ \end{gathered} $Здесь t* – моменты, после которых происходит изменение знака ускорения, $\Delta t = \sqrt {2H{\text{/}}a\omega _{0}^{2}} $ – время, за которое поршень проходит через цилиндр.
1.2. Устойчивость линеаризованного уравнения. Введем следующие безразмерные параметры:
В результате из (1.1) получим уравнение, аналогичное уравнению Мейснера и совпадающее с ним, если цилиндр имеет нулевую длину:
(1.2)
$\begin{gathered} \ddot {x} - [k - sG(\tau ,H){\text{sgn}}({\text{sin}}\tau )]x = 0, \\ x(0) = {{x}_{{10}}},\quad \dot {x}(0) = {{x}_{{20}}}. \\ \end{gathered} $Уравнение (1.2) запишем в виде эквивалентной системы с соответствующими начальными условиями:
(1.3)
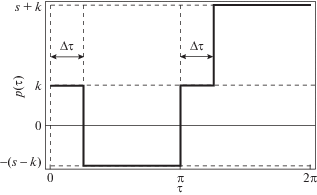
$\begin{gathered} \left\{ \begin{gathered} {{{\dot {x}}}_{1}} = {{x}_{2}}, \hfill \\ {{{\dot {x}}}_{2}} = p(\tau ){{x}_{1}}, \hfill \\ \end{gathered} \right. \\ x(0) = {{x}_{{10}}},\quad x(0) = {{x}_{{20}}}. \\ \end{gathered} $Поведение кусочно-постоянной функции $p(\tau ) = k - sG(\tau ,H){\text{sgn}}({\text{sin}}\tau )$ представлено на рис. 2. В рамках сделанных предположений матрица ${\mathbf{P}}(\tau )$ системы (1.3) является периодической с периодом 2π:
В дальнейшем будем исследовать систему (1.3) на устойчивость по Лагранжу, которая означает, что все решения x(τ) уравнения (1.3) ограничены на положительной временной полуоси.
Следуя результатам теории Флоке [29], устойчивость такой системы определяется спектром матрицы монодромии, т.е. оценкой ее собственных значений ρ или мультипликаторов. Для асимптотической устойчивости системы с периодической матрицей необходимо и достаточно, чтобы выполнялось следующее условие: $\left| \rho \right| < 1$ – все мультипликаторы расположены внутри единичного круга комплексной плоскости. При выполнении противоположного неравенства система неустойчива. Случай $\left| \rho \right| = 1$ будет рассмотрен ниже применительно к вопросу об устойчивости периодических решений.
Так как матрица системы (1.3) является кусочно-постоянной, матрица монодромии может быть представлена в явной форме. Для этого необходимо последовательно решить четыре системы линейных уравнений (соответствующие количеству участков постоянства матрицы системы (1.3), учитывая непрерывность данного решения).
В рассматриваемом случае матрица монодромии (являющаяся произведением матриц фундаментальных решений соответствующих систем на участках постоянства) имеет вид
(1.4)
$\begin{gathered} {\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{\text{ch}}(\sqrt k \Delta \tau )}&{\frac{1}{{\sqrt k }}{\text{sh}}(\sqrt k \Delta \tau )} \\ {\sqrt k {\text{sh}}(\sqrt k \Delta \tau )}&{{\text{ch}}(\sqrt k \Delta \tau )} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {\cos ({{k}_{2}}\gamma )}&{\frac{1}{{{{k}_{2}}}}\sin ({{k}_{2}}\gamma )} \\ {{{k}_{2}}\sin ({{k}_{2}}\gamma )}&{\cos ({{k}_{2}}\gamma )} \end{array}} \right) \times \\ \, \times \left( {\begin{array}{*{20}{c}} {{\text{ch}}(\sqrt k \Delta \tau )}&{\frac{1}{{\sqrt k }}{\text{sh}}(\sqrt k \Delta \tau )} \\ {\sqrt k {\text{sh}}(\sqrt k \Delta \tau )}&{{\text{ch}}(\sqrt k \Delta \tau )} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {{\text{ch}}({{k}_{1}}\gamma )}&{\frac{1}{{{{k}_{1}}}}{\text{sh}}({{k}_{1}}\gamma )} \\ {{{k}_{1}}{\text{sh}}({{k}_{1}}\gamma )}&{{\text{ch}}({{k}_{1}}\gamma )} \end{array}} \right), \\ \end{gathered} $Запишем характеристическое уравнение для матрицы A:
(1.5)
$\begin{gathered} \left\| {{\mathbf{A}} - \rho {\mathbf{E}}} \right\| = \left| {\begin{array}{*{20}{c}} {{{a}_{{11}}} - \rho }&{{{a}_{{12}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}} - \rho } \end{array}} \right| = {{\rho }^{2}} + \alpha \rho + \beta = 0, \\ \beta = {{( - 1)}^{2}}\exp \left( {\int\limits_0^T {{\text{Sp}}[{\mathbf{P}}(\tau )]d\tau } } \right) = 1,\quad \alpha = - ({{a}_{{11}}} + {{a}_{{22}}}). \\ \end{gathered} $Здесь ${\text{Sp}}[{\mathbf{P}}(\tau )]$ – операция взятия следа матрицы ${\mathbf{P}}(\tau )$. Произведение корней ρ1 и ρ2 (1.5) равно единице, поэтому движение будет устойчиво только при ${\text{|}}\alpha {\text{|}} < 2$, т.е. когда модули обоих мультипликаторов равны единице. Таким образом, условие, обеспечивающее устойчивость, имеет вид
Используя явное представление матрицы монодромии (1.4), условие (1.6) можно записать как:
(1.7)
$\left| \begin{gathered} \cos ({{k}_{2}}\gamma )\left[ {{\text{2ch}}(2\sqrt k \Delta \tau ){\text{ch}}({{k}_{1}}\gamma ) + {\text{sh}}(2\sqrt k \Delta \tau ){\text{sh}}({{k}_{1}}\gamma )\left( {\frac{{\sqrt k }}{{{{k}_{1}}}} + \frac{{{{k}_{1}}}}{{\sqrt k }}} \right)} \right] + \\ \, + \sin ({{k}_{2}}\gamma )\left[ \begin{gathered} 2{\text{sh}}(2\sqrt k \Delta \tau ){\text{ch}}({{k}_{1}}\gamma )\left( {\frac{{\sqrt k }}{{{{k}_{2}}}} - \frac{{{{k}_{2}}}}{{\sqrt k }}} \right) + {\text{c}}{{{\text{h}}}^{2}}(\sqrt k \Delta \tau ){\text{sh}}({{k}_{1}}\gamma )\left( {\frac{{{{k}_{1}}}}{{{{k}_{2}}}} - \frac{{{{k}_{2}}}}{{{{k}_{1}}}}} \right) + \hfill \\ {\text{s}}{{{\text{h}}}^{2}}(\sqrt k \Delta \tau ){\text{sh}}({{k}_{1}}\gamma )\left( {\frac{k}{{{{k}_{1}}{{k}_{2}}}} - \frac{{{{k}_{1}}{{k}_{2}}}}{k}} \right) \hfill \\ \end{gathered} \right] \\ \end{gathered} \right| < 2.$Таким образом, зоны устойчивости системы (1.3) в пространстве параметров определяются соотношением (1.7).
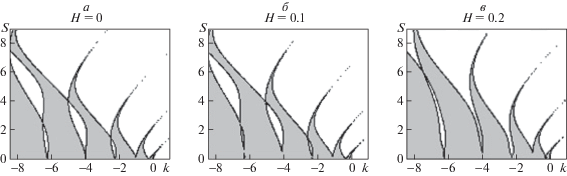
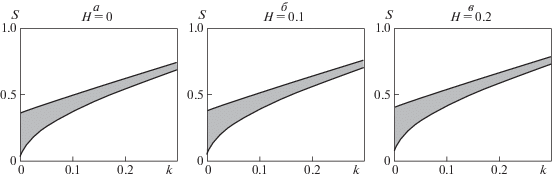
На рис. 3 построены зоны устойчивости в плоскости параметров k, s для системы (1.3) при различных значениях длины поршня H для маятника длиной l = 1 м. Из рис. 3 следует, что зоны устойчивости при варьировании параметра H качественно не изменяются, при этом незначительно меняется форма границ диаграммы с ростом H. Изменение зоны устойчивости в положительной полуплоскости показано на рис. 4. Также на этом рисунке видно, что рост параметра H приводит к увеличению нижней границы зоны устойчивости.
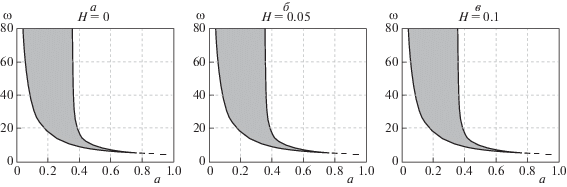
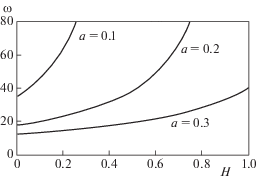
Зоны устойчивости в пространстве параметров системы ${{\omega }_{0}}$ и $а$ изображены на рис. 5. Как следует из графика, площадь зоны устойчивости практически не изменяется с увеличением длины поршня H. Это означает, что для любого H из представленного интервала существует пара значений ${{\omega }_{0}}$ и a, которые обеспечивают устойчивость вертикального положения обратного маятника с осциллирующим подвесом и гистерезисной нелинейностью. Однако при H = 1 существуют две области значений ${{\omega }_{0}}$ и a, которые обеспечивают устойчивость вертикального положения. Отметим также, что аналогично с рис. 4 границы зон устойчивости (функция${{\omega }_{0}}(a)$) становятся многозначными функциями при увеличении длины поршня H.
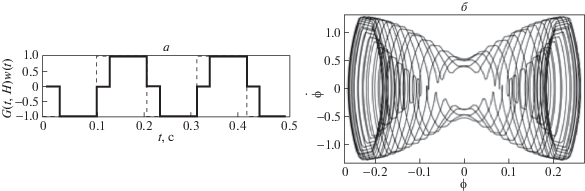
На рис. 6 изображена зависимость частоты колебаний ${{\omega }_{0}}$ (частота, которая лежит на границе зоны устойчивости) от длины поршня H при различных значениях амплитуды колебаний поршня. Параметры, удовлетворяющие неравенству (1.7), соответствуют почти периодическим колебаниям [30] относительно подвеса маятника. Для иллюстрации результатов на рис. 7, б представлен фазовый портрет системы (линеаризованная модель системы (1.3) при следующих значениях параметров: l = 1 m, $H = 0.05$ м, a = 0.15 м, ${{\omega }_{0}} = 30$ с–1, $\phi (0)$ = 0.2 и $\dot {\phi }(0)$ = 1 с–1).
Рис. 7.
График управляющего воздействия (сплошной – с гистерезисом, прерывыстый – без гистерезиса) (а), фазовая плоскость (б)
1.3. Периодические решения. Рассмотрим поведение маятника на границах зоны устойчивости. В характеристическом уравнении для матрицы монодромии (1.5) такая ситуация соответствует двум случаям: α = –2 (левый край) и α = 2 (правый край). Мультипликаторы в этом случае принимают значения ${{\rho }_{1}} = {{\rho }_{2}} = 1$ и ${{\rho }_{1}} = {{\rho }_{2}} = - 1$ соответственно.
Если ${{\rho }_{1}} = {{\rho }_{2}} = 1$, то решение ${\mathbf{X}}(t) = {{\left( {{{x}_{1}}(t){\text{ }}{{x}_{2}}(t)} \right)}^{{\text{T}}}}$ будет удовлетворять равенству ${\mathbf{X}}(t + 2\pi ) = {\mathbf{X}}(t)$ (при соответствующем выборе начальных условий). Поэтому (1.3) имеет периодическое решение с периодом колебаний ${{T}_{1}} = 2\pi {\text{/}}{{\omega }_{0}}$. Во втором случае (${{\rho }_{1}} = {{\rho }_{2}} = - 1$) решение будет удовлетворять равенству ${\mathbf{X}}(t + 2\pi ) = - {\mathbf{X}}(t)$ (через еще один период ${\mathbf{X}}(t + 4\pi ) = - {\mathbf{X}}(t + 2\pi ) = {\mathbf{X}}(t)$). Это означает, что в случае, когда мультипликаторы равны –1, система (1.3) имеет периодическое решение с периодом ${{T}_{2}} = 4\pi {\text{/}}{{\omega }_{0}}$.
Решения системы (1.3) являются периодическими и, следовательно, ограниченными в обоих случаях. Следовательно, параметры маятника (в периодическом режиме колебаний) должны удовлетворять следующим условиям:
Условия (1.8)–(1.9) являются необходимыми, но недостаточными для реализации периодических решений. Необходимо отметить, что для рассматриваемого управления, описываемого функцией $v(t)$ = $ - a\omega _{0}^{2}G(t,H)\operatorname{sgn} [\sin ({{\omega }_{0}}t)]$, начальные условия, отвечающие периодическим решениям, лежат в первой и третьих четвертях фазовой плоскости.
Рассмотрим случай периодических колебаний с периодом ${{T}_{1}}$. В этом случае имеет место равенство ${\mathbf{X}}(0 + {{T}_{1}}) = {\mathbf{AX}}(0) = {\mathbf{X}}(0)$, а также соотношение
(1.10)
$\left( {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\phi }_{{10}}}} \\ {{{\phi }_{{20}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\phi }_{{10}}}} \\ {{{\phi }_{{20}}}} \end{array}} \right).$Последнее в свою очередь означает, что начальные условия удовлетворяют следующим равенствам:
(1.11)
${{\phi }_{{10}}} = \frac{{{{a}_{{12}}}}}{{{{a}_{{11}}} - 1}}{{\phi }_{{20}}},\quad {{\phi }_{{20}}} = \frac{{{{a}_{{21}}}}}{{{{a}_{{22}}} - 1}}{{\phi }_{{10}}},$(1.12)
${{K}_{1}} = \frac{{{{a}_{{11}}} - 1}}{{{{a}_{{12}}}}} = \frac{{{{a}_{{21}}}}}{{{{a}_{{22}}} - 1}}.$Последнее равенство гарантирует выполнение условия (1.8). Если для начальных условий $({{\phi }_{{10}}},{{\phi }_{{20}}})$ можно найти пару параметров a и ${{\omega }_{0}}$, лежащих на границе зоны устойчивости (при фиксированном H) и удовлетворяющих соотношению (1.11), то эта пара единственна. Противоположное утверждение также верно. Аналогичным образом находим, что периодические решения с периодом T2 существуют для начальных условий, удовлетворяющих уравнениям:
(1.13)
${{\phi }_{{10}}} = \frac{{{{a}_{{12}}}}}{{1 + {{a}_{{11}}}}}{{\phi }_{{20}}},\quad {{\phi }_{{20}}} = \frac{{{{a}_{{21}}}}}{{1 + {{a}_{{22}}}}}{{\phi }_{{10}}}.$Аналогично эти начальные условия лежат на прямой z2: $\dot {\phi } = {{K}_{2}}\phi $ с коэффициентом
(1.14)
${{K}_{2}} = \frac{{{{a}_{{11}}} + 1}}{{{{a}_{{12}}}}} = \frac{{{{a}_{{21}}}}}{{{{a}_{{22}}} + 1}}.$Параметры a и ${{\omega }_{0}}$, соответствующие границам устойчивости, могут быть получены из численного решения неравенства (1.6), преобразованного в равенство. Для решений, отвечающих начальным условиям (1.13), критические значения параметров, соответствующие границам зон устойчивости, имеют вид a = 0.2 м и ${{\omega }_{0}} = 18.73$ с–1 (длина цилиндра $H = 0.05$ м). Для решений системы с начальными условиями (1.11) соответствующие параметры равны a = 0.43 м и ${{\omega }_{0}}$ = = 15.02 с–1 (при одном и том же значении длины цилиндра). Однако полученные периодические решения (с использованием параметров a и ${{\omega }_{0}}$) неустойчивы, так как матрица монодромии имеет вид
Следовательно, малым отклонениям начальных значений, отвечающих периодическим решениям, соответствуют линейно-возрастающие отклонения при возрастающем времени. Таким образом, численное построение этих решений не может быть выполнено без специальной стабилизирующей процедуры.
Множество начальных значений в пространстве параметров ${{\omega }_{0}}$, a и H, отвечающих существованию периодических решений, имеет достаточно сложную структуру (см. рис. 8). Отметим, что сложная форма полученных поверхностей связана с тем, что уравнения, определяющие зону устойчивости, существенно нелинейны – содержат преобразователи гистерезисной природы.
Рис. 8.
Поверхности в пространстве параметров $\omega $, $a$ и H, удовлетворяющие соотношениям (1.12) и (1.14)
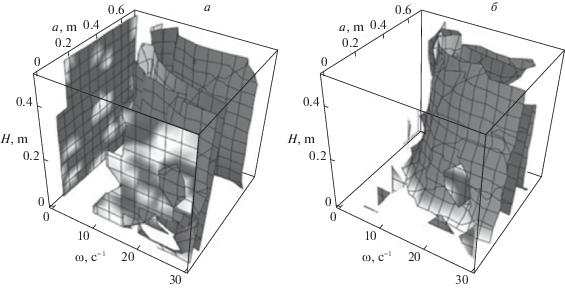
В заключение этого раздела, отметим, что решение исходной задачи стабилизации в нелинейной постановке требует иного подхода, поскольку оператор сдвига по траекториям системы за время, соответствующее периоду правой части (аналог матрицы монодромии), невозможно получить в явной форме. Области устойчивости в пространстве параметров можно идентифицировать по свойствам оператора сдвига, а именно значения параметров, при которых этот оператор является сжимающим, соответствуют устойчивым решениям. В рассматриваемом случае эти области могут быть получены путем “сканирования” пространства параметров и многочисленных вычислительных экспериментов.
2. Перевернутый маятник: стабилизация гистерезисным управлением на основе принципа обратной связи. Рассмотрим задачу стабилизации верхнего положения обратного маятника посредством горизонтальных движений нижней точки крепления в условиях “гистерезисных” связей между управлением и непосредственным воздействием на систему.
2.1. Математическая модель. Уравнения движения системы (рис. 9), представляется в следующем виде:
(2.2)
$\begin{gathered} \varphi (0) = {{\varphi }_{0}},\quad \dot {\varphi }(0) = \omega (0) = {{\omega }_{0}}, \\ u(t) = \Gamma [{{u}_{0}},h]x(t), \\ \end{gathered} $Далее будем рассматривать линеаризованную модель (отклонения маятника малы):
(2.3)
$\begin{gathered} A\ddot {\varphi } = mgl\varphi - m\ddot {u}l, \\ \varphi (0) = {{\varphi }_{0}},\quad \dot {\varphi }(0) = \omega (0) = {{\omega }_{0}}. \\ \end{gathered} $Опишем управление по принципу обратной связи, т.е. предположим, что ускорение поршня подчиняется следующему соотношению:
где α > 0.Уравнение (2.3) представим в эквивалентной матричной форме:
(2.5)
$\left( {\begin{array}{*{20}{c}} {\dot {\varphi }} \\ {\dot {\omega }} \end{array}} \right) = {\mathbf{V}}\left( {\begin{array}{*{20}{c}} \varphi \\ \omega \end{array}} \right) + {\mathbf{W}},$Собственными значениями матрицы V являются числа B и –B с соответствующими собственными векторами ${{(1{\text{ }}B)}^{{\text{T}}}}$ и ${{( - 1{\text{ }}B)}^{{\text{T}}}}$. Отметим, что прямая $B\varphi + \omega = 0$ является собственным подпространством, отвечающим отрицательному собственному числу. Следовательно, управление должно быть организовано (на концептуальном уровне) таким образом, чтобы “удержать” фазовые координаты в окрестности этой линии. На каждом из интервалов, где функция $\ddot {u}$ постоянна, система (2.5) может быть проинтегрирована:
(2.6)
$\left( {\begin{array}{*{20}{c}} {\varphi (t)} \\ {\omega (t)} \end{array}} \right) = {\mathbf{\Lambda }}(t)\left( {\begin{array}{*{20}{c}} {{{\varphi }_{0}}} \\ {{{\omega }_{0}}} \end{array}} \right) + {{\ddot {u}}_{0}}{\mathbf{v}}(t),$(2.7)
${\mathbf{\Lambda }}(t) = \left( {\begin{array}{*{20}{c}} {{\text{ch}}Bt}&{\frac{1}{B}{\text{sh}}Bt} \\ {B{\text{sh}}Bt}&{{\text{ch}}Bt} \end{array}} \right),\quad {\mathbf{v}}(t) = \left( {\begin{array}{*{20}{c}} { - \frac{1}{g}({\text{ch}}Bt - 1)} \\ { - \frac{B}{g}{\text{sh}}Bt} \end{array}} \right).$Здесь ${{\varphi }_{0}}$ и ${{\omega }_{0}}$ – начальное отклонение и угловая скорость маятника соответственно, ${{\ddot {u}}_{0}}$– ускорение цилиндра на интервале.
Поведение системы (2.6) на всем временном интервале может быть представлено следующим рекуррентным соотношением:
(2.8)
$\left( {\begin{array}{*{20}{c}} {{{\varphi }_{k}}(t)} \\ {{{\omega }_{k}}(t)} \end{array}} \right) = {\mathbf{\Lambda }}(t - {{t}_{{k - 1}}})\left( {\begin{array}{*{20}{c}} {{{\varphi }_{{{{t}_{{k - 1}}}}}}} \\ {{{\omega }_{{{{t}_{{k - 1}}}}}}} \end{array}} \right) + {{\ddot {u}}_{{{{t}_{{k - 1}}}}}}{\mathbf{v}}(t - {{t}_{{k - 1}}})$,Уравнение (2.3) называется диссипативным, если существует ограниченная область Ω в прямом произведении фазового пространства системы (2.6) и пространства состояний гистерезисного преобразователя, такая, что для любых начальных значений $({{\varphi }_{0}},{{\omega }_{0}},u) \in \Omega $ решения уравнения (2.3) остаются равномерно ограниченными. Другими словами, система называется диссипативной, если существует область в фазовом пространстве и согласованная с ней область в пространстве состояний гистерезисного преобразователя, такая, что решение, начавшееся в этой области, не уходит в бесконечность. Тогда справедлива следующая теорема.
Теорема 1. Область диссипативности системы (2.5) определяется неравенством:
(2.9)
${{e}^{{B\tau }}}\left| {B{{\varphi }_{0}} + {{\omega }_{0}}} \right| \leqslant \left| {\frac{{kB}}{g}} \right|,\quad \tau = \sqrt {\frac{{2h}}{k}} ,$Доказательство. Воспользовавшись (2.6), с учетом (2.7) легко получить соотношение, определяющее динамику изменения линейной комбинации начальных условий $B{{\varphi }_{0}} + {{\omega }_{0}}$:
(2.10)
$\begin{gathered} B{{\varphi }_{t}} + {{\omega }_{t}} = \left( {сhBt + shBt} \right)\left( {B{{\varphi }_{0}} + {{\omega }_{0}} - \frac{{Bk}}{g}} \right) + \frac{{Bk}}{g},\quad {\text{если}}\quad B{{\varphi }_{0}} + {{\omega }_{0}} > 0, \\ B{{\varphi }_{t}} + {{\omega }_{t}} = \left( {сhBt + shBt} \right)\left( {B{{\varphi }_{0}} + {{\omega }_{0}} + \frac{{Bk}}{g}} \right) - \frac{{Bk}}{g},\quad {\text{если}}\quad B{{\varphi }_{0}} + {{\omega }_{0}} < 0. \\ \end{gathered} $Очевидно, что для ограниченности этой линейной комбинации необходимо, чтобы выполнялось неравенство:
В условиях отсутствия управления поршень движется от одной стенки цилиндра к другой и соответственно k = 0:
Следовательно, стабилизация будет иметь место, если за время, отвечающее движению поршня от одной стенки до другой, линейная комбинация не покидает область, определяемую неравенством (2.11), т.е. выполняется неравенство
Теорема доказана.
2.2. Неидеальное реле в контуре обратной связи. Как известно, измерительные приборы любых механических систем не всегда работают корректно, а именно разнообразные эффекты, связанные с проявлением задержек измерительных сигналов, их отклонением от истинных значений можно моделировать посредством гистерезисных преобразователей, аналогичных неидеальному реле. Рассмотрим проблему стабилизации перевернутого маятника в случае, когда имеет место неопределенность в управлении. Предположим, что эта неопределенность фиксирована, т.е. ускорение точки подвеса (параметр управления) соответствует выходному состоянию преобразователя неидеального реле:
(2.13)
$\begin{gathered} y(t) = B\varphi (t) + \omega (t), \\ \ddot {u} = kR\left[ { - \varepsilon ,\varepsilon ,\operatorname{sgn} (\ddot {u}({{t}_{0}})),{{y}_{0}}} \right]y(t),\quad \varepsilon > 0. \\ \end{gathered} $Подробное описание этого преобразователя приведено в [26].
Параметр ε можно рассматривать как неопределенность в измерении значения $B\varphi + \omega $. Предположим также, что имеет место следующее неравенство:
в противном случае стабилизации маятника не происходит.Динамика системы с неидеальным реле в контуре обратной связи описывается уравнением:
(2.14)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} {\dot {\varphi }} \\ {\dot {\omega }} \end{array}} \right) = {\mathbf{V}}\left( {\begin{array}{*{20}{c}} \varphi \\ \omega \end{array}} \right) + {\mathbf{W}}, \\ \ddot {u} = kR\left[ { - \varepsilon ,\varepsilon ,\operatorname{sgn} (\ddot {u}({{t}_{0}})),{{y}_{0}}} \right]y(t), \\ \varphi (0) = {{\varphi }_{0}},\quad \omega (0) = {{\omega }_{0}}. \\ \end{gathered} $Здесь матрицы V и вектор W определяются так же, как и в уравнениях (2.5). Предположим, что в начальный момент времени выполняется равенство $y({{t}_{0}}) = \varepsilon .$ Время, в течение которого первая фазовая координата системы (2.7) под воздействием управления принимает значение $y({{t}_{c}}) = - \varepsilon $, находится посредством следующих соотношений:
(2.15)
$\begin{gathered} - \varepsilon = y({{t}_{c}}); \\ - \varepsilon = \left( {\begin{array}{*{20}{c}} B&1 \end{array}} \right){\mathbf{\Lambda }}({{t}_{c}})\left( {\begin{array}{*{20}{c}} {{{\varphi }_{0}}} \\ {{{\omega }_{0}}} \end{array}} \right) + k\left( {\begin{array}{*{20}{c}} B&1 \end{array}} \right){\mathbf{v}}({{t}_{c}}); \\ - \varepsilon = {{e}^{{B{{t}_{c}}}}}\varepsilon - \frac{{kB}}{g}({{e}^{{B{{t}_{c}}}}} - 1); \\ \end{gathered} $(2.16)
${{t}_{c}} = \frac{1}{B}\ln \left( {\frac{{\frac{{kB}}{g} + \varepsilon }}{{\frac{{kB}}{g} - \varepsilon }}} \right).$Аналогичный результат имеет место в случае, если $y({{t}_{0}}) = - \varepsilon $. Таким образом, общий период $T = 2{{t}_{c}}$ и $y(2{{t}_{c}}) = y({{t}_{0}}) = \varepsilon .$ Если $y({{t}_{0}}) \ne \varepsilon $и $y({{t}_{0}}) \ne - \varepsilon ,$ то за конечное время фазовые координаты системы перейдут в положение $y(t) = \varepsilon $ или $y(t) = - \varepsilon $. Оказывается, что среди решений с указанной выше динамикой существуют асимптотически устойчивые решения. Справедлива следующая теорема.
Теорема 2. Пусть параметр $\varepsilon $ удовлетворяет неравенству $kB{\text{/}}g - 1 > \varepsilon $, тогда система (2.1) с неидеальным реле в контуре обратной связи имеет асимптотически устойчивое по Ляпунову решение в форме замкнутого цикла:
(2.17)
$\left( {\begin{array}{*{20}{c}} {\varphi (\theta )} \\ {\omega (\theta )} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\text{ch}}B\theta }&{\frac{1}{B}{\text{sh}}B\theta } \\ {B{\text{sh}}B\theta }&{{\text{ch}}B\theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ \varepsilon \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - \frac{k}{g}({\text{ch}}B\theta - 1)} \\ { - \frac{{Bk}}{g}{\text{sh}}B\theta } \end{array}} \right),$(2.18)
$\left( {\begin{array}{*{20}{c}} {\varphi (\theta )} \\ {\omega (\theta )} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\text{ch}}B\theta }&{\frac{1}{B}{\text{sh}}B\theta } \\ {B{\text{sh}}B\theta }&{{\text{ch}}B\theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ { - \varepsilon } \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\frac{k}{g}({\text{ch}}B\theta - 1)} \\ {\frac{{Bk}}{g}{\text{sh}}B\theta } \end{array}} \right),$Доказательство. В силу непрерывной зависимости решения от начальных условий, достаточно доказать, что матрица, фигурирующая в правой части соотношения (2.18) при $\theta = {{t}_{c}}$, будет иметь спектральный радиус меньше 1. Как известно [31], для этого достаточно, чтобы собственные числа этой матрицы по модулю не превосходили 1.
Выпишем характеристическое уравнение матрицы из (2.17), введя обозначение $a = kB{\text{/}}g$:
(2.19)
${{\lambda }_{1}} = \frac{1}{{a - \varepsilon }},\quad {{\lambda }_{2}} = \frac{1}{{a + \varepsilon }}.$Выполнение неравенства в условиях теоремы гарантирует условия ${{\lambda }_{1}} < 1,$ ${{\lambda }_{2}} < 1$, которые в свою очередь означают, что спектральный радиус матрицы меньше 1. Теорема доказана.
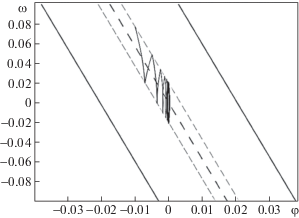
В качестве иллюстрации полученного результата на рис. 10 представлен фазовый портрет системы (2.14). Параметры моделирования: m = 1 кг, k = 0.2 м ⋅ с–2, $g = 9.8$ м ⋅ с–2, $l = {\text{0}}{\text{.3}}$ м, $\varepsilon = 0.02$ с–1, ${{\varphi }_{0}} = - 0.01{\text{ }}$, ${{\omega }_{0}} = 0.0771$ с–1. Случай, когда измерительные устройства имеют случайную неопределенность (десинхронизация в управлении), представляет особый интерес. Численные эксперименты показывают, что увеличение времени моделирования приводит к тому, что вероятность стабилизации системы уменьшается и стремится к нулю. Это означает, что маятник не может сохранить вертикальное положение при рассинхронизации управления.
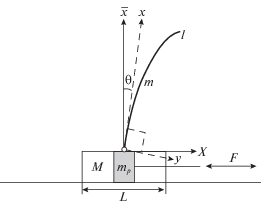
3. Гибкий перевернутый маятник под воздействием гистерезисной нелинейности: стабилизация и оптимальное управление. 3.1. Постановка задачи. Ниже рассматривается обратный маятник в виде упругого стержня, который шарнирно закреплен на цилиндре, а движение цилиндра в свою очередь определяется горизонтальным движением поршня (см. рис. 11). Система, близкая к изучаемой, исследовалась в [32], также отметим, что различные аспекты динамики гибкого обратного маятника изучались в работах [33–36]. Введем инерциальную систему координат $(x,y)$ (см. рис. 11), в которой рассматриваются движения гибкого стержня с массой m и плотностью $\rho $. При этом ось $Ox$ совпадает с касательной к профилю стержня в точке крепления; $\theta $ – угол наклона касательной к профилю стержня, I – осевой момент инерции сечения стержня; $(X,\bar {x})$ – система координат, связанная с маятником, $M$ – масса цилиндра с длиной L, F – сила, соединенная с поршнем с массой mp (трактуемая далее как управление). В настоящем разделе исследуется задача стабилизации описанной системы, т.е. идентификация условий на управляющее воздействие (ускорение поршня), а также параметры системы, обеспечивающие ограниченность отклонения маятника от положения равновесия на бесконечной временной полуоси.
Далее воспользуемся более удобной для дальнейших построений операторной трактовкой люфта [27]:
Здесь $X(t),\;Y(t)$ – выход и вход соответственно преобразователя люфта.
Предположим, что отклонение y и угол θ малы, т.е. $x \approx \bar {x},$ и граничные условия, определяющие кривизну стержня, однородны:
(3.1)
$\left\{ \begin{gathered} y(0,t) = {{y}_{{xx}}}(0,t) = 0, \hfill \\ {{y}_{{xx}}}(l,t) = {{y}_{{xxx}}}(l,t) = 0. \hfill \\ \end{gathered} \right.$Точка с координатами $(X,\bar {x})$ описывает поведение профиля маятника во времени и показывает отклонение точек маятника от вертикальной оси, при этом $X(0,t) = s(t)$ – смещение точки крепления в горизонтальной плоскости.
Системы координат $(X,\bar {x})$ и $(x,y)$ связаны следующим образом:
(3.2)
$\left( {\begin{array}{*{20}{c}} X \\ {\bar {x}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} y \\ x \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {X(0,t)} \\ 0 \end{array}} \right).$Рассмотрим математическую модель указанной механической системы. Для этого используем формализм Лагранжа. В предположении малости y и $\theta $ функция Лагранжа может быть записана в виде
(3.3)
$L(t) = \frac{{M\dot {s}_{{}}^{2}}}{2} + \frac{1}{2}\int\limits_0^l {[\rho \dot {s}_{{}}^{2} + \rho \dot {y}_{{}}^{2} + \rho {{{(x\dot {\theta })}}^{2}} + \rho (2\dot {s}x\dot {\theta } + 2x\dot {\theta }\dot {y} + 2\dot {s}\dot {y}) + 2\rho gy\theta - EIy_{{xx}}^{2}]} dx.$Проинтегрировав (3.3) на интервале $({{t}_{0}},{{t}_{f}})$, получим функцию действия:
(3.4)
$W = \frac{1}{2}\int\limits_{{{t}_{0}}}^{{{t}_{f}}} {M\dot {s}_{{}}^{2}} dt + \frac{1}{2}\int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\int\limits_0^l {\left[ {\rho (\dot {s}_{{}}^{2} + \dot {y}_{{}}^{2} + {{{(x\dot {\theta })}}^{2}} + 2\dot {s}x\dot {\theta } + 2x\dot {\theta }\dot {y} + 2\dot {s}\dot {y} + 2gy\theta ) - \frac{{EIy_{{xx}}^{2}}}{\rho }} \right]} \,dxdt.} $Используя классический вариационный принцип наименьшего действия и разложение подынтегральных функций в ряд Тейлора, ограничиваясь линейными слагаемыми, получим следующее уравнение:
Ниже θ будем трактовать как обобщенную координату в соответствии с уравнением Лагранжа и (3.3):
С учетом (3.5) последнее соотношение примет вид
(3.7)
$\int\limits_0^l {x\left( {g\theta - \frac{{El}}{g}{{y}_{{xxxx}}}} \right)dx = g} \int\limits_0^l {ydx} $(3.8)
$\frac{{g{{l}^{2}}\theta }}{2} - \frac{{El}}{g}\int\limits_0^l {x{{y}_{{xxxx}}}dx = g} \int\limits_0^l {ydx} .$Используя начальные условия (3.1), можно показать, что интеграл в левой части выражения (3.8) равен нулю, а правую часть запишем как
Проинтегрировав (3.5) по длине стержня, получим
(3.10)
$\begin{gathered} \rho \int\limits_0^l {\left( {\ddot {y} + \frac{{El}}{\rho }{{y}_{{xxxx}}}} \right)dx = \rho \int\limits_0^l {( - \ddot {s} - x\ddot {\theta } + g\theta )dx} .} \\ El\left[ {{{y}_{{xxx}}}(l,t) - {{y}_{{xxx}}}(0,t)} \right] + \rho \int\limits_0^l {\ddot {y}dx = } - {\kern 1pt} \ddot {s}\rho l - \frac{{\rho {{l}^{2}}\ddot {\theta }}}{2} + \rho gl\theta . \\ \end{gathered} $Принимая во внимание соотношения ρl = m и граничное условие ${{y}_{{xxx}}}(l,t) = 0$, а также следствие из (3.9)
имеем следующее уравнение:На следующем шаге, используя s как обобщенную координату в функции Лагранжа, получим
(3.12)
$\frac{d}{{dt}}\frac{{\partial L}}{{\partial{ \dot {s}}}} - \frac{{\partial L}}{{\partial s}} = f(t).$Здесь $f(t)$ – сила, приложенная к опоре стержня.
С учетом сделанных предположений воздействие, приложенное к опоре стержня, определится следующим образом:
(3.13)
$f(t) = \Gamma [X(0,t),Y(t),L,{{F}_{0}}]F = \left\{ \begin{gathered} 0,\quad \left| {X(0,t) - Y(t)} \right| \leqslant L; \hfill \\ F,\quad \left| {X(0,t) - Y(t)} \right| > L. \hfill \\ \end{gathered} \right.$Учтем уравнение движения поршня:
где Y – смещение поршня в горизонтальной плоскости.Подстановка (3.3) в (3.2) дает следующее соотношение:
Используя уравнение (3.5), найдем
(3.16)
$M\ddot {s} + \rho \int\limits_0^l {\left( {g\theta - \frac{{El}}{\rho }{{y}_{{xxxx}}}} \right)dx = f(t)} .$Сделав преобразования, аналогичные (3.10), получим следующее равенство:
Таким образом, система уравнений, описывающая динамику маятника, совместно с системой цилиндр-поршень будет иметь вид
(3.18)
$\left\{ \begin{gathered} ml\ddot {\theta } + m\ddot {s} = mg\theta + EI{{y}_{{xxxx}}}(0,t), \hfill \\ M\ddot {s} = f(t) - mg\theta - EI{{y}_{{xxxx}}}(0,t). \hfill \\ \end{gathered} \right.$В системе координат $(X,\bar {x})$ эти уравнения преобразуются к следующей форме:
(3.19)
$\left\{ \begin{gathered} \ddot {X} + \frac{{EI}}{\rho }{{X}_{{xxxx}}} = g{{X}_{x}}(0,t), \hfill \\ M\ddot {X}(0,t) = f(t) - mg{{X}_{x}}(0,t) - EI{{X}_{{xxx}}}(0,t), \hfill \\ ml{{(\ddot {X})}_{x}}(0,t) + m\ddot {X}(0,t) = mg{{X}_{x}}(0,t) + EI{{X}_{{xxx}}}(0,t) \hfill \\ f(t) = \Gamma [X(0,t),Y(t),L,{{F}_{0}}]F, \hfill \\ {{m}_{p}}\ddot {Y}(t) = F \hfill \\ \end{gathered} \right.,$Здесь учтено, что $X = X(x,t),$ в силу $\bar {x} \approx x.$
Система (3.19) путем последовательных изменений приводится к виду:
(3.20)
$\left\{ \begin{gathered} \ddot {X} + \frac{{EI}}{\rho }{{X}_{{xxxx}}} = g{{X}_{x}}(0,t), \hfill \\ M\ddot {X}(0,t) + mg{{X}_{x}}(0,t) + EI{{X}_{{xxx}}}(0,t) = f(t), \hfill \\ (M + m)\ddot {X}(0,t) + ml{{(\ddot {X})}_{x}}(0,t) = f(t), \hfill \\ g(M + m)X(0,t) - \frac{{MEI}}{\rho }{{X}_{{xxx}}} = lf(t). \hfill \\ f(t) = \Gamma [X(0,t),Y(t),L,{{F}_{0}}]F, \hfill \\ {{m}_{p}}\ddot {Y}(t) = F. \hfill \\ \end{gathered} \right.$Далее для решения задачи управления маятником будем использовать принцип обратной связи. Для этого силу, определяющую движение поршня, подчиним следующему соотношению:
(3.21)
$F = k\operatorname{sgn} (\alpha {{e}_{1}} + {{e}_{2}}),\quad {{e}_{1}} = \int\limits_0^l {{{X}_{x}}dl,} \quad {{e}_{2}} = \int\limits_0^l {{{{(\dot {X})}}_{x}}dl} ,\quad \alpha > 0,\quad k > 0.$Здесь e1 – средний угол отклонения стержня, e2 – средняя угловая скорость стержня.
С учетом сделанных предположений решение задачи стабилизации упругого перевернутого маятника сводится к системе:
(3.22)
$\left\{ \begin{gathered} \ddot {X} + \frac{{EI}}{\rho }{{X}_{{xxxx}}} = g{{X}_{x}}(0,t), \hfill \\ M\ddot {X}(0,t) + mg{{X}_{x}}(0,t) + EI{{X}_{{xxx}}}(0,t) = f(t), \hfill \\ (M + m)\ddot {X}(0,t) + ml{{(\ddot {X})}_{x}}(0,t) = f(t), \hfill \\ g(M + m)X(0,t) - \frac{{MEI}}{\rho }{{X}_{{xxx}}} = lf(t), \hfill \\ f(t) = \Gamma [X(0,t),Y(t),L,{{F}_{0}}]F, \hfill \\ {{m}_{p}}\ddot {Y}(t) = F, \hfill \\ F = k\operatorname{sgn} (\alpha {{e}_{1}} + {{e}_{2}}), \hfill \\ {{e}_{1}} = \int\limits_0^l {{{X}_{x}}dl,} \hfill \\ {{e}_{2}} = \int\limits_0^l {{{{({{X}_{t}})}}_{x}}dl.} \hfill \\ \end{gathered} \right.$3.2. Численная реализация решения. Для численной реализации решения системы (3.22) введем прямоугольную сетку (рис. 12). Для проекции функции $X(x,t)$ на узлы сетки примем следующие обозначения:
(3.23)
${{X}_{{i,j}}} = X(i{{h}_{x}},j{{h}_{t}}),\quad i = \overline {0,n} ,\quad j = \overline {0,m} ,\quad {{h}_{x}} = \frac{l}{n},\quad {{h}_{t}} = \frac{T}{m},$Для аппроксимации производных используем правые конечные разности:
(3.24)
${{X}_{x}}(x,t) = \frac{{{{X}_{{i + 1,j}}} - {{X}_{{i,j}}}}}{{{{h}_{x}}}} + o({{h}_{x}}),\quad {{X}_{t}}(x,t) = \frac{{{{X}_{{i,j + 1}}} - {{X}_{{i,j}}}}}{{{{h}_{t}}}} + o({{h}_{t}}).$Дискретный аналог системы (3.22) запишем следующим образом:
(3.25)
$\left\{ \begin{gathered} \frac{{{{X}_{{i,j + 2}}} - 2{{X}_{{i,j + 1}}} + {{X}_{{i,j}}}}}{{h_{t}^{2}}} + \hfill \\ + \frac{{EI}}{\rho }\frac{{6{{X}_{{i + 2,j}}} - 4{{X}_{{i + 1,j}}} - 4{{X}_{{i + 3,j}}} + {{X}_{{i + 4,j}}} + {{X}_{{i,j}}}}}{{h_{x}^{4}}} = g\frac{{{{X}_{{1,j}}} - {{X}_{{0,j}}}}}{{{{h}_{x}}}}, \hfill \\ M\frac{{{{X}_{{0,j + 2}}} - 2{{X}_{{0,j + 1}}} + {{X}_{{0,j}}}}}{{h_{t}^{2}}} + mg\frac{{{{X}_{{1,j}}} - {{X}_{{0,j}}}}}{{{{h}_{x}}}} + \hfill \\ + EI\frac{{3{{X}_{{1,j}}} - 3{{X}_{{2,j}}} + {{X}_{{3,j}}} - {{X}_{{0,j}}}}}{{h_{x}^{3}}} = {{f}_{j}}, \hfill \\ (M + m)\frac{{{{X}_{{0,j + 2}}} - 2{{X}_{{0,j + 1}}} + {{X}_{{0,j}}}}}{{h_{t}^{2}}} + \hfill \\ \, + ml\frac{{2{{X}_{{0,j + 1}}} - {{X}_{{0,j + 2}}} - 2{{X}_{{1,j + 1}}} + {{X}_{{1,j + 2}}} - {{X}_{{0,j}}} + {{X}_{{1,j}}}}}{{h_{t}^{2}{{h}_{x}}}} = {{f}_{j}}, \hfill \\ g(M + m){{X}_{{0,j}}} - \frac{{MEI}}{\rho }\frac{{3{{X}_{{1,j}}} - 3{{X}_{{2,j}}} + {{X}_{{3,j}}} - {{X}_{{0,j}}}}}{{h_{x}^{3}}} = {{f}_{j}}{{h}_{x}}, \hfill \\ {{f}_{j}} = \Gamma [{{X}_{{0,j}}},{{Y}_{j}},L,{{F}_{0}}]{{F}_{j}}, \hfill \\ {{m}_{p}}\frac{{{{Y}_{{j + 2}}} - 2{{Y}_{{j + 1}}} + {{Y}_{j}}}}{{h_{t}^{2}}} = {{F}_{j}}, \hfill \\ {{F}_{j}} = k\operatorname{sgn} (\alpha {{e}_{{1j}}} + {{e}_{{2j}}}), \hfill \\ {{e}_{1}} = \sum\limits_{i = 0}^n {({{X}_{{i + 1,j}}} - {{X}_{{i,j}}}),} \hfill \\ {{e}_{2}} = \sum\limits_{i = 0}^n {\frac{{{{X}_{{i,j}}} - {{X}_{{i,j + 1}}} - {{X}_{{i + 1,j}}} + {{X}_{{i + 1,j + 1}}}}}{{{{h}_{t}}}}.} \hfill \\ \end{gathered} \right.$Соответствующие начальные условия могут быть представлены в виде:
(3.26)
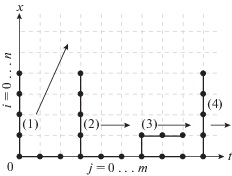
$\left\{ \begin{gathered} \frac{{{{X}_{{1,0}}} - {{X}_{{0,0}}}}}{{{{h}_{x}}}} = \varphi , \hfill \\ \frac{{{{X}_{{0,1}}} - {{X}_{{0,0}}}}}{{{{h}_{t}}}} = V, \hfill \\ \frac{{{{X}_{{0,0}}} - {{X}_{{0,1}}} - {{X}_{{1,0}}} + {{X}_{{1,1}}}}}{{{{h}_{t}}{{h}_{x}}}} = {{V}_{\varphi }}, \hfill \\ \frac{{{{X}_{{2,j}}} - 2{{X}_{{1,j}}} + {{X}_{{0,j}}}}}{{h_{x}^{2}}} = 0. \hfill \\ \end{gathered} \right.$Алгоритм решения состоит из двух этапов расчета: прямого и обратного (рис. 13).
Прямой расчет: из начальных условий (3.26) и четвертого уравнения системы (3.25) находим, что
(3.27)
$\begin{gathered} {{X}_{{3,j}}} = \left[ {(M + m)g{{X}_{{0,j}}} - {{f}_{j}}{{h}_{x}}} \right]\frac{{\rho h_{x}^{3}}}{{MEI}} + 3{{X}_{{2,j}}} + {{X}_{{0,j}}} - 3{{X}_{{1,j}}},\quad j = 1, \\ {{X}_{{0,1}}} = V{{h}_{t}} + {{X}_{{0,0}}}, \\ \end{gathered} $Далее вычисляются оставшиеся значения при $i = \overline {0,3} ,j = \overline {0,m{\kern 1pt} } {\text{:}}$
(3.28)
$\begin{gathered} {{f}_{j}} = \Gamma [{{X}_{{0,j}}},{{Y}_{j}},L,{{F}_{0}}]F, \\ {{X}_{{0,j + 2}}} = \frac{{{{h}_{t}}^{2}}}{M}\left[ {{{f}_{j}} - mg\frac{{{{X}_{{1,j}}} - {{X}_{{0,j}}}}}{{{{h}_{x}}}} - El\frac{{3{{X}_{{1,j}}} - 3{{X}_{{2,j}}} + {{X}_{{3,j}}} - {{X}_{{0,j}}}}}{{{{h}_{t}}^{2}}}} \right] + 2{{X}_{{0,j + 1}}} - {{X}_{{0,j}}}, \\ {{X}_{{1,j + 2}}} = \frac{{{{h}_{t}}^{2}{{h}_{x}}}}{{ml}}\left[ {{{f}_{j}} - (M + m)\frac{{{{X}_{{0,j + 2}}} - 2{{X}_{{0,j + 1}}} + {{X}_{{0,j}}}}}{{{{h}_{t}}^{2}}}} \right] + 2{{X}_{{0,j + 1}}} + {{X}_{{0,j + 2}}} + 2{{X}_{{1,j + 1}}} + {{X}_{{0,j}}} - {{X}_{{1,j}}}, \\ \end{gathered} $Обратный расчет: определяются Xi,j при $i = \overline {4,n} ,$ $j = \overline {0,m} $:
(3.29)
${{X}_{{i + 4,j}}} = \left( {g\frac{{{{X}_{{1,j}}} - {{X}_{{0,j}}}}}{{{{h}_{x}}}} - (M + m)\frac{{{{X}_{{i,j + 2}}} - 2{{X}_{{i,j + 1}}} + {{X}_{{i,j}}}}}{{{{h}_{t}}^{2}}}} \right)\frac{{\rho h_{x}^{4}}}{{EI}} - 6{{X}_{{i + 2,j}}} + 4{{X}_{{x + 1,j}}} + 4{{X}_{{i + 3,j}}} - {{X}_{{i,j}}}.$Далее переопределяются начальные параметры ${{X}_{{0,0}}},\varphi ,V,{{V}_{\varphi }}$ и контрольные параметры:
(3.30)
$\begin{gathered} {{e}_{1}} = \sum\limits_{i = 0}^n {({{X}_{{i + 1,0}}} - {{X}_{{i,0}}})} , \\ {{e}_{2}} = \sum\limits_{i = 0}^n {\frac{{{{X}_{{i,0}}} - {{X}_{{i,1}}} - {{X}_{{i + 1,0}}} + {{X}_{{i + 1,1}}}}}{{{{h}_{t}}}}} , \\ F = k\operatorname{sgn} (\alpha {{e}_{1}} + {{e}_{2}}). \\ \end{gathered} $Из приведенного алгоритма следует, что численное значение силы F должно пересчитываться на каждом новом временном интервале.
Предложенное управление по принципу обратной связи, формализованное в (3.21), включает в себя коэффициенты α и k, значения которых непосредственно влияют на возможность стабилизации системы (3.22) в окрестности вертикального положения равновесия. Очевидно, что существует область значений коэффициентов управления (включая их оптимальные значения), приводящих к стабилизации системы (3.22).
Проведем вычислительный эксперимент и, используя разностную схему, приведенную выше, найдем значения α и k, стабилизирующие систему (3.22). Рассмотрим систему со следующими параметрами:
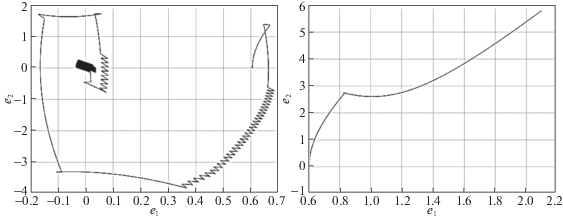
Экспериментальным путем были найдены значения коэффициентов α = 10 и k = 1, стабилизирующие систему (рис. 14, слева). Изменение значений коэффициентов (α = 12, k = 0.3) приводит к ситуации, когда величины управления F становится недостаточно для стабилизации системы (рис. 14, справа).
Рис. 14.
Фазовый портрет динамики системы с люфтом при коэффициентах управления α = 10 и k = 1 (слева) и α = 12, k = 0.3 (справа)
3.3. Оптимизация. Как было показано выше, параметры обратной связи существенным образом влияют на переходный процесс и возможность стабилизации. В связи с этим возникает вопрос об идентификации оптимальных в некотором смысле параметров. В настоящем разделе рассматривается задача оптимизации, соответствующая идентификации параметров $\alpha $ и k, которые минимизируют среднеквадратичное отклонение маятника от положения равновесия за конечное время.
Для оценки качества оптимизации введем функцию, характеризующую среднеквадратические отклонение и скорость элементов гибкого маятника:
(3.31)
$\begin{gathered} V = {{{\tilde {e}}}_{1}} + {{{\tilde {e}}}_{2}}, \\ {{{\tilde {e}}}_{1}} = \int\limits_0^L {{{{\left( {{{X}_{x}}} \right)}}^{2}}dl} , \\ {{{\tilde {e}}}_{2}} = \int\limits_0^L {{{{\left[ {{{{\left( {{{X}_{x}}} \right)}}_{t}}} \right]}}^{2}}dl} . \\ \end{gathered} $Тогда задача оптимизации управления будет соответствовать минимизации функционала следующего вида:
Для решения этой задачи воспользуемся бионическим алгоритмом [37], так как при применении классических методов возникают трудности, связанные с недифференцируемостью гистерезисных преобразователей.
Ниже используется модель адаптивного поискового поведения на примере личинок Chaetopteryx villosa [37]. Основная схема поведенческого поиска может быть охарактеризована двумя этапами: движение в выбранном направлении (консервативная тактика); случайное изменение направления движения (тактика стохастического поиска). Проиллюстрируем модель для случая поиска экстремума функционала двух переменных.
1. Рассмотрим анимата, который перемещается в двумерном пространстве $\alpha ,k$. Главная цель анимата – поиск минимума функционала $\Im (\alpha ,k)$.
2. Анимат функционирует в дискретном времени $t = 0,1,2, \ldots $, оценивая изменение текущего значения $\Im (\alpha ,k)$ по сравнению с предыдущим временем: $\Delta \Im (t) = \Im (t) - \Im (t - 1).$
3. Каждый раз, когда анимат перемещается, его координаты α и k изменяются на $\Delta \alpha (t)$ и $\Delta k(t)$ соответственно.
4. Анимат имеет в своем распоряжении две возможные тактики поведения: (А) консервативная; (Б) стохастическая.
Тактика (А). Анимат движется в выбранном направлении:
где угол ${{\varphi }_{0}}$ определяет постоянное направление движения анимата:(3.35)
$\cos {{\varphi }_{0}} = \frac{{\Delta \alpha (t) }}{{\sqrt {\Delta {{\alpha }^{2}} + \Delta {{k}^{2}}} }}$,(3.36)
$\sin {{\varphi }_{0}} = \frac{{\Delta k(t) }}{{\sqrt {\Delta {{\alpha }^{2}} + \Delta {{k}^{2}}} }}.$Тактика (Б). Анимат делает случайный ход:
где $\varphi = {{\varphi }_{0}} + w{\text{,}}$ ${{\varphi }_{0}}$ – угол, характеризующий направление движения за текущее время t, w – равномерно распределенная на отрезке [0, 2π] случайная величина.Переключение между указанными тактиками описывается знаком индикативной функции M(t):
где k1 – параметр, который определяет инерционность поведения анимата $(0 < {{k}_{1}} < 1),$ $\xi (t)$ – нормально распределенная случайная величина со средним значением, равным нулю, и среднеквадратическим отклонением σ, $I(t)$ – интенсивность раздражителя. В свою очередь, I(t) определяется одним из следующих соотношений:или где ${{k}_{2}} > 0$. Как следует из (3.40)–(3.41), интенсивность положительна, когда на очередном шаге происходит увеличение функции, в противном случае интенсивность отрицательна.
Будем считать, что при M(t) > 0 анимат следует тактике (А) и при M(t) < 0 следует за тактикой (Б). Таким образом, значение M(t) можно рассматривать как мотивацию к выбору тактики (А). Изложенный алгоритм использовался для минимизации функционала (3.32).
3.4. Численные результаты. Рассмотрим поведение гибкого обратного маятника, используя соответствующую разностную схему при отсутствии люфта (L = 0). Характеристики и начальные условия для рассматриваемой механической системы определяются следующим образом:
Бионический алгоритм позволяет найти оптимальные значения коэффициентов $\alpha $ и k. В процессе оптимизации с применением бионического алгоритма были получены следующие значения коэффициентов: α = 22 и k = 0.5. Для оценки качества оптимизации используем функции ${{\tilde {e}}_{1}}$, ${{\tilde {e}}_{2}}$ и V из (3.31).
Параметрическая зависимость величин ${{\tilde {e}}_{1}}$, ${{\tilde {e}}_{2}}$, функция, определяемая соотношением (3.31), а также ее производная в силу системы в зависимости от времени показаны на рис. 15 и 16. Как видно из рисунков, функция V асимптотически стремится к нулю, что в свою очередь означает стремление системы к вертикальному неустойчивому положению равновесия.
Рис. 15.
Фазовая траектория (слева), функция V (в центре) и производная функции V в силу системы (справа) $L = 0$ (α = 22 и k = 0.5)
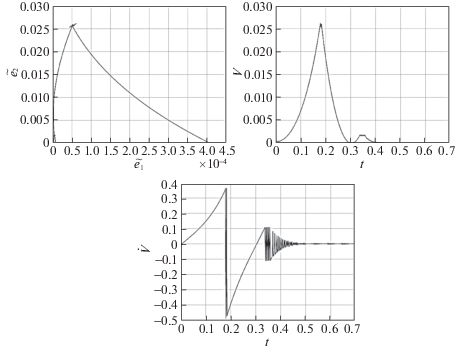
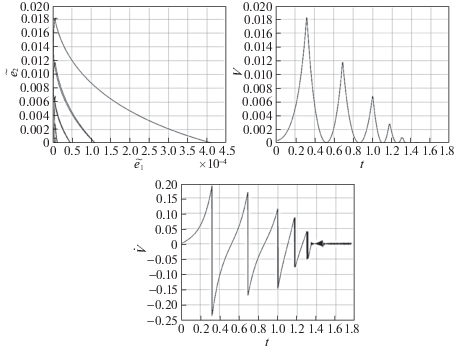
Рис. 16.
Фазовая траектория (слева), функция V (в центре) и производная функции V в силу системы (справа) $L = 0$ (α = 50 и k = 0.3)
При наличии люфта (L = 0.01 м) в точке подвеса рассматриваемой системы с использованием бионического алгоритма получены следующие оптимальные значения коэффициентов: α = 6 и k = 1.5 (при условии, что масса поршня равна 1 кг).
Динамические характеристики исследуемой системы при указанных значениях параметров в терминах обозначений (3.31) представлены на рис. 17–19. Согласно этим рисункам, рассматриваемая система за конечное время оказывается в сколь угодно малой окрестности неустойчивого положения равновесия.
Рис. 17.
Фазовая траектория (слева), функция V (в центре) и производная функции V в силу системы (справа) $L = 0.01$ м (α = 6 и k = 1.5)
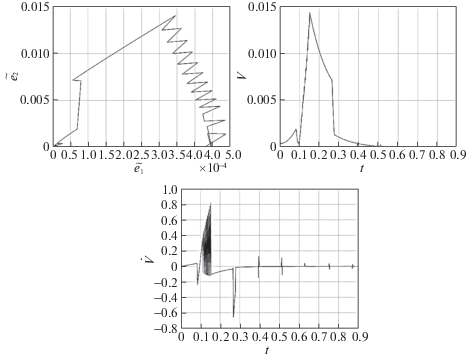
Рис. 18.
Фазовая траектория (слева), функция V (в центре) и производная функции V в силу системы (справа) $L = 0.01$ м (α = 10 и k = 1)
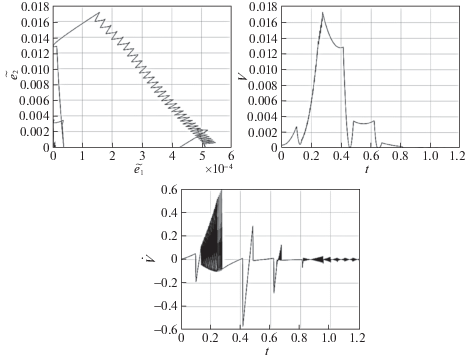
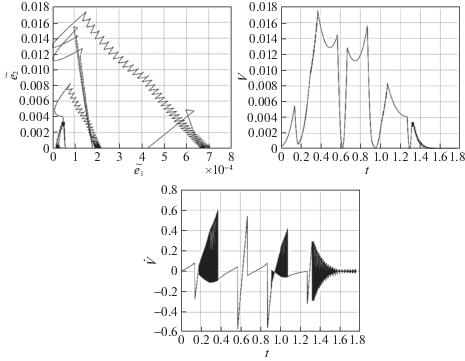
Рис. 19.
Фазовая траектория (слева), функция V (в центре) и производная функции V в силу системы (справа) $L = 0.02$ м (α = 10 и k = 1)
Заключение. Рассмотрена задача стабилизации перевернутого маятника в окрестности неустойчивого положения равновесия с учетом гистерезисных свойств управляющего воздействия. В частности, получено условие устойчивости обратного маятника посредством вертикальных движений нижней точки крепления в условиях гистерезисной связи между управляющим воздействием и стабилизируемой системой. Основные результаты основывались на анализе матрицы монодромии. Построены зоны устойчивости, исследована их эволюция в зависимости от параметров гистерезисной связи, также доказано существование континуума неустойчивых периодических решений в условиях, когда параметры рассматриваемой системы соответствуют граничным точкам зоны устойчивости.
Рассмотрена математическая модель обратного маятника с гистерезисным управлением на основе принципа обратной связи. Полученные результаты позволяют идентифицировать области в фазовом пространстве, начальным значениям из которой соответствуют ограниченные решения. Введение неидеального реле (как модели неопределенности в определении фазовых координат стабилизируемой системы) в управление на основе принципа обратной связи позволило идентифицировать устойчивые периодические режимы в соответствующей системе.
Исследована проблема стабилизации гибкого перевернутого маятника с люфтом в точке крепления, а также решена задача оптимизации в смысле минимизации квадратичного функционала (на конечном временном промежутке) по параметрам управляющего воздействия. Параметры, обеспечивающие решение задачи оптимизации, идентифицированы с использованием бионического алгоритма. Динамические особенности рассматриваемой системы проиллюстрированы результатами компьютерного моделирования.
Список литературы
Капица П.Л. Маятник с вибрирующим подвесом // УФН. 1951. № 44. С. 7–20.
Капица П.Л. Динамическая устойчивость маятника при колеблющейся точке подвеса // ЖЭТФ. 1951. № 21. С. 588–597.
Stephenson A. On an Induced Stability // Phylosophical Magazine. 1908. V. 15. 233 p.
Butikov E.I. An Improved Criterion for Kapitza’s Pendulum Stability // J. Phys. A: Math. Theor. 2011. V. 44. P. 295202.
Butikov E.I. Oscillations of a Simple Pendulum with Extremely Large Amplitudes // Europ. J. Phys. 2012. V. 33. P. 1555–1563.
Mikheev Y.V., Sobolev V.A., Fridman E.M. Asymptotic Analysis of Digital Control Systems // Autom. Remote Control. 1988. V. 49. P. 1175–1180.
Semenov M.E., Reshetova O.O., Tolkachev A.V., Solovyov A.M., Meleshenko P.A. Oscillations Under Hysteretic Conditions: From Simple Oscillator to Discrete Sine-Gordon Model // Topics in Nonlinear Mechanics and Physics : Selected Papers from CSNDD 2018 . Singapore, 2019. P. 229–253.
Семенов М.Е., Матвеев М.Г., Мелешенко П.А., Соловьев А.М. Динамика демпфирующего устройства на основе материала Ишлинского // Мехатроника, автоматизация, управление. 2019. № 20. С. 106–113.
Семенов М.Е., Матвеев М.Г., Лебедев Г.Н., Соловьёв А.М. Стабилизация обратного гибкого маятника с гистерезисными свойствами // Мехатроника, автоматизация, управление. 2017. № 8. С. 516–525.
Zhang Z.Y., Miao X.J. Global Existence and Uniform Decay Forwave Equation with Dissipative Term and Boundary Damping // Comput. Math. Appl. 2010. V. 59. P. 1003–1018.
Butikov E.I. Subharmonic Resonances of the Parametrically Driven Pendulum // J. Phys. A: Math. Theor. 2002. V. 35. P. 6209–6231.
Sun J.Y., Huang X.C., Liu X.T. Study on the Force Transmissibility of Vibration Isolators with Geometric Nonlinear // Nonlinear Dyn. 2013. V. 74. № 4. P. 1103–1112.
Ряжских В.И., Семенов М.Е., Рукавицын А.Г., Канищева О.И., Демчук А.А., Мелешенко П.А. Стабилизация обратного маятника на двухколесном транспортном средстве // Вестн. ЮУГУ. Сер. Математика, физика, механика. 2017. Т. 9. № 3. С. 27–33.
Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 383 с.
Wang Lipo, Ross J. Synchronous Neural Networks of Nonlinear Threshold Elements with Hysteresis // Neurobiology. 1990. V. 87. P. 988–992.
Zhang Z.Y., Liu Z.H., Miao X.J., Chen Y.Z. Global Existence and Uniform Stabilization of a Generalized Dissipative Klein–Gordon Equation Type with Boundary Damping // Math. Phys. 2011. V. 52. P. 023502.
Solovyov A.M., Semenov M.E., Meleshenko P.A., Reshetova O.O., Popov M.A., Kabulova E.G. Hysteretic Nonlinearity and Unbounded Solutions in Oscillating Systems // Procedia Engineering. 2017. V. 201. P. 578–583.
Semenov M.E., Solovyov A.M., Balthazar J.M., Meleshenko P. A. Nonlinear Damping: From Viscous to Hysteretic // Recent Trends in Applied Nonlinear Mechanics and Physics / ed. M. Belhaq. Springer Proceedings in Physics. 2018. V. 199. P. 259–275.
Решмин С.А. Поиск главного бифуркационного значения максимального управляющего момента в задаче синтеза оптимального управления маятником // Изв. РАН. ТиСУ. 2008. № 2. С. 5–20.
Решмин С.А., Черноусько Ф.Л. Оптимальное по быстродействию управление перевернутым маятником в форме синтеза // Изв. РАН. ТиСУ. 2006. № 3. С. 51–62.
Анохин Н.В. Приведение многозвенного маятника в положение равновесия с помощью одного управляющего момента // Изв. РАН. ТиСУ. 2012. № 5. С. 44–53.
Формальский А.М. О стабилизации двойного перевернутого маятника при помощи одного управляющего момента // Изв. РАН. ТиСУ. 2006. № 3. С. 5–12.
Арановский С.В., Бирюк А.Э., Никульчев Е.В., Рядчиков И.В., Соколов Д.В. Синтез наблюдателя в задаче стабилизации обратного маятника с учетом ошибки в датчиках положения// Изв. РАН. ТиСУ. 2019. № 2. С. 145–153.
Осинцев М.С., Соболев В.А. Понижение размерности задач оптимального оценивания для динамических систем с сингулярными возмущениями // ЖВМиМФ. 2014. № 54 (1). С. 50–64.
Магнус К. Колебания: Введение в исследование колебательных систем / Пер. с нем. В.И. Сидорова, В.В. Филатова. М.: Мир, 1982. 304 с.
Нелепин Р.А. Методы исследования нелинейных систем автоматического управления / Под ред. Р.А. Нелепина. М.: Наука, 1979. 447 с.
Красносельский М.А., Покровский А.В. Системы с гистерезисом. М.: Наука, 1983. 272 с.
Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.Л. Введение в теорию нелинейных колебаний. М.: Наука, 1987. 382 с.
Плисс В.А. Нелокальные проблемы теории колебаний. М.: Наука, 1964. 367 с.
Красносельский М.А., Покровский А.В. Периодические колебания в системах с релейными нелинейностями // ДАН СССР. 1974. Т. 216. № 4. С. 733–736.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966. 576 с.
Xu Chao, Yu Xin. Mathematical Model of Elastic Inverted Pendulum Control System // J. Control Theory and Applications. 2004. V. 3. P. 281–282.
Dadfarnia M., Jalili N., Xian B., Dawson D.M. A Lyapunov-Based Piezoelectric Controller for Flexible Cartesian Robot Manipulators // J. Dynamic Systems, Measurement and Control. 2004. V. 126/347.
Dadios E.P., Fernandez P.S., Williams D.J. Genetic Algorithm On Line Controller For the Flexible Inverted Pendulum // J. Advanced Computational Intelligence and Intelligent Informatics. 2006. V. 10. № 2.
Luo Zheng-Hua, Guo Bao-Zhu. Shear Force Feedback Control of a Single-link Flexible Robot with a Revolute Joint // IEEE Transaction On Automatic Control. 1997. V. 42. № 1.
Xia Guangpu, Tang Zheng, Li Yong. Hopfield Neural Network with Hysteresis for Maximum Cut Problem // Neural Information Processing – Letters and Reviews. 2004. V. 4. № 5.
Pierce-Shimomura J.T., Morse T.M., Lockery S.R. The Fundamental Role of Pirouettes in Caenorhabditis Elegance Chemotaxis // Neuroscience. 1999. V. 19. № 21. P. 9557–9569.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления