Известия РАН. Теория и системы управления, 2020, № 4, стр. 28-41
МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ ПОВОРОТА НАГРУЖЕННОГО УПРУГОГО СТЕРЖНЯ, УПРАВЛЯЕМОГО ЭЛЕКТРОПРИВОДОМ
Г. В. Костин *
* E-mail: kostin@ipmnet.ru
Поступила в редакцию 07.02.2020
После доработки 28.02.2020
Принята к публикации 30.03.2020
Аннотация
Рассматривается плоский поворот управляемого электроприводом упругого прямолинейного стержня, нагруженного на свободном конце точечной массой. Ставится задача оптимального управления напряжением в обмотке двигателя, переводящего систему в конечное состояние с гашением упругих колебаний. Предлагается обобщенная формулировка уравнений состояния стержня и способ аппроксимации неизвестных перемещений, плотности импульса и изгибающего момента. Описывается процедура минимизации целевого функционала и регуляризации численной ошибки.
Введение. Актуальным направлением теории управления является развитие методов оптимизации движения систем с распределенными параметрами. Математическая основа для решения задач оптимального управления динамическими системами, которые описываются линейными дифференциальными уравнениями в частных производных (УЧП), в случае выпуклых целевых функционалов была заложена в работах научной школы Лионса [1]. Управляемость систем с УЧП гиперболического типа, в частности, рассматривались и другими авторами [2, 3]. Введение в теорию управления распределенными колебаниями с подробным обзором литературы можно найти в [4]. Колебания в сетевых моделях исследуются, например, в [5–7]. Практическая необходимость достоверного моделирования подобных систем обусловила развитие особых подходов к решению прямых и обратных задач динамики.
Можно обозначить два важных направления исследования управляемости для пространственно-распределенных процессов. В первом подходе используется так называемая поздняя дискретизация, при которой закон оптимального управления напрямую выводится для исходной модели с УЧП. Лишь при необходимости на последнем этапе входное воздействие как функция времени и, возможно, как функция пространственных координат аппроксимируется элементом из конечномерного подпространства исходного бесконечномерного функционального пространства. Оптимизация в этом случае может опираться на спектральную теорию линейных операторов [8, 9]. Используется [10] метод разделения переменных и декомпозиция на основе метода Фурье, что для некоторых простейших систем математической физики позволяет построить квазиоптимальное ограниченное воздействие, приводящее систему в заданное состояние за конечное время. Еще один подход к задачам оптимального управления с ограничениями в виде УЧП гиперболического типа связан с методом выбора [11]. Даже для простейшей системы, описывающей движения замкнутой струны, получение явного вида управления и доказательство его оптимальности требует привлечения тонкого математического аппарата [12]. Важную роль в задачах управления динамическими системами, описываемыми УЧП или интегродифференциальными уравнениями, играет анализ управляемости и, в частности, доказательство возможности или невозможности точного приведения системы в заданное состояние за конечное время с помощью ограниченных воздействий [13, 14].
Второй подход, назовем его ранней дискретизацией, часто используется для построения управления численными (приближенными) методами. Согласно этой методологии, начально-краевая задача сперва дискретизируется и сводится к системе алгебраических или обыкновенных дифференциальных уравнений (ОДУ). Как показано в [15], для этой цели применим метод конечных элементов (МКЭ), а также методы конечного объема и конечных разностей [16, 17]. В случае, когда используется МКЭ, его реализация может основываться на методе коллокации, модификации метода Бубнова–Галеркина [18], его версии Петрова–Галеркина [19], методе наименьших квадратов [20] и т.п. Если собственные функции линейной динамической системы выражаются в явном виде, спектральный анализ может обеспечить существенные преимущества [9].
Для моделирования колебаний в упругих и вязкоупругих телах и конструкциях предложены вариационные формулировки задач оптимального управления на основе метода интегродифференциальных соотношений (далее МИДС) [21]. Вводя интегральные законы состояния, с помощью этого подхода можно явно оценить достоверность конечномерной модели для уточнения или огрубления полученных приближений и скорректировать закон управления для улучшения точности вычислений. Эффективный алгоритм решения задач оптимального управления в линейной упругости на основе метода Ритца и МКЭ был предложен в [22] для однородных упругих стержней.
Как показано, точность приближенного решения может резко понизиться в результате оптимизации управления. Чтобы ограничить ошибку, вводится изопериметрическое условие и в результате целевой функционал изменяется путем добавления интегрального значения квадрата невязки уравнений состояния системы. С помощью такого приема можно явно оценить достоверность конечномерной модели для любого допустимого закона управления. Эта информация в зависимости от вычислительных ресурсов и требуемой точности используется либо для уточнения, либо для огрубления применяемых приближений, а также, возможно, для дальнейшей корректировки управляющего воздействия.
В этой работе, по сравнению с [22], обобщенная формулировка начально-краевой задачи линейной упругости, которая основана на интегральном представлении закона состояния, распространена на случай пространственной неоднородности системы. Различные граничные условия рассматриваются в новой вариационной постановке в виде как естественных, так и существенных ограничений. В качестве приложения исследуется плоский поворот управляемого приводом манипуляционного звена с неоднородным упругим стержнем, шарнирно закрепленным с одного конца и нагруженным на свободном конце точечной массой. Для приведенных граничных условий разработана процедура расчета на основе МКЭ с кусочно-полиномиальными аппроксимациями по пространственной переменной для неизвестных полей поперечных смещений, линейной плотности импульса и изгибающего момента в сечении. Оптимизация движений звена производится с учетом изменяющихся линейной плотности и изгибной жесткости несущего стержня. Закон управления, понижающий нежелательные тепловые потери в обмотке электродвигателя, строится на фиксированном интервале времени путем совместной минимизации (с определенными весовыми коэффициентами) как терминальной энергии, так и ошибки дискретизации. Применимость численного алгоритма продемонстрирована на примере стержня с круглым поперечным сечением, радиус которого линейно меняется по длине.
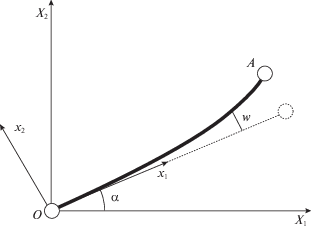
1. Постановка задачи управления. Рассмотрим движение электромеханической системы, схематически изображенной на рис. 1. Ее связующей частью является прямолинейный упругий стержень, поворачивающийся в плоскости $O{{X}_{1}}{{X}_{2}}$. Один конец стержня шарнирно закреплен в исходной точке O инерциальной декартовой системы отсчета $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$, к другому концу прикреплено твердое тело A. Длина стержня $\ell $ много больше его толщины и размеров прикрепленного тела. От электродвигателя постоянного тока с независимым возбуждением через абсолютно жесткий редуктор к стержню передается момент сил, приложенный в точке O и ортогональный плоскости $O{{X}_{1}}{{X}_{2}}$.
Для более удобного описания движения вводится система координат $O{{x}_{1}}{{x}_{2}}{{X}_{3}}$, разворачивающаяся вместе со стержнем. Предполагается, что плоскости $O{{X}_{1}}{{X}_{2}}$ и $O{{x}_{1}}{{x}_{2}}$ совпадают, а ось Ox1 всегда направленна по касательной к центральной линии стержня в точке O. В дальнейшем считается, что упругие деформации звена описываются в рамках линейной теории Эйлера–Бернулли об изгибе тонких прямолинейных упругих стержней [23]. Это означает, что упругие смещения $w = w(t,x)$ точек центральной линии стержня малы и перпендикулярны оси Ox1, а поперечные сечения остаются плоскими и ортогональными к этой линии. Угловая скорость вращения звена как целого мала по сравнению с собственной частотой низшей моды упругих колебаний жестко закрепленного стержня с той же нагрузкой. Уравнения динамики электромеханической системы при упомянутых предположениях выведены, например, в [24].
Плоские вращения стержня с точечной массой на конце описываются с помощью УЧП:
где $(t,x) \in \Omega = (0,T) \times (0,\ell )$ – область определения функции w. Заданы краевые условия:(1.2)
$\begin{array}{*{20}{c}} {w(t,0) = {{w}_{x}}(t,0) = {{w}_{{xx}}}(t,\ell ) = 0,} \\ {{{{(\kappa (x){{w}_{{xx}}}(t,\ell ))}}_{x}} = m({{w}_{{tt}}}(t,\ell ) + \ell \ddot {\alpha }(t)).} \end{array}$Здесь $\alpha $ – угол между осями $O{{x}_{1}}$ и $O{{X}_{1}}$, m – масса тела на конце стержня. Линейная плотность стержня $\rho $ и его изгибная жесткость $\kappa $ – функции координаты x вдоль оси стержня. Нижние индексы t и x обозначают соответственно частные производные по временной и пространственной координате. Даны также начальные условия в виде
где ${{w}_{0}}(x)$, ${{v}_{0}}(x)$ – достаточно гладкие функции, совместимые с ограничениями (1.2).Изменение углового момента системы вокруг оси OX3 описывается интегродифференциальным уравнением c начальными условиями
(1.4)
$\int\limits_0^\ell \rho {\text{*}}(x\ddot {\alpha }(t) + {{w}_{{tt}}}(0,x))xdx = \eta (t),\quad \alpha (0) = {{\alpha }_{0}},\quad \dot {\alpha }(0) = {{\omega }_{0}}.$Здесь $\eta $ – момент вокруг оси OX3, отрабатываемый электроприводом. Точечная масса A на конце стержня учтена с помощью дельта-функции интенсивности m, которая добавляется к линейной плотности $\rho (x)$, т.е.
Система уравнений, определяющих ток в обмотке электродвигателя, согласно [25], имеет вид
иЗдесь j – сила электрического тока в обмотке, $u(t)$ – подаваемое напряжение, $L$ – индуктивность, R – омическое сопротивление в цепи двигателя, $\Phi $ – эффективный магнитный поток, J – момент инерции ротора, $\nu $ – передаточное число редуктора. Система (1.6) определяет изменение тока в обмотке, а (1.7) описывает изменение скорости вращения ротора, повернутого на угол $\nu \alpha (t)$.
Исключая с помощью (1.1), (1.4)–(1.7) из рассмотрения переменные $\eta (t)$ и $j(t)$, можно получить интегродифференциальное уравнение баланса в электрической цепи:
(1.8)
$\begin{array}{*{20}{c}} {\int\limits_0^\ell \,[L(x\dddot \alpha (t) + {{w}_{{ttt}}}(t,x)) + R(x\ddot {\alpha }(t) + {{w}_{{tt}}}(t,x))]\rho {\text{*}}(x)xdx + } \\ {\, + LJ{{\nu }^{2}}\dddot \alpha (t) + RJ{{\nu }^{2}}\ddot {\alpha }(t) + {{\Phi }^{2}}{{\nu }^{2}}\dot {\alpha }(t) = \Phi \nu u(t).} \end{array}$В соответствии с (1.1) заменим в (1.8) выражения в круглых скобках под знаком интеграла. С учетом краевых условий (1.2) проведем ряд преобразований:
В результате вместо (1.8) приходим к дифференциальному уравнению
(1.9)
$\begin{array}{*{20}{c}} {A\dddot \alpha (t) + B\ddot {\alpha }(t) + C\dot {\alpha }(t) - D{{w}_{{txx}}}(t,0) - E{{w}_{{xx}}}(t,0) = \Phi \nu u(t),} \\ {A = LJ{{\nu }^{2}},\quad B = RJ{{\nu }^{2}},\quad C = {{\Phi }^{2}}{{\nu }^{2}},\quad D = L\kappa (0),\quad E = R\kappa (0).} \end{array}$С учетом (1.1), (1.4)–(1.7), начальное значение $\ddot {\alpha }$ выражается как
(1.10)
$\ddot {\alpha }(0) = {{\varepsilon }_{0}},\quad J{{\nu }^{2}}{{\varepsilon }_{0}} = \kappa (0)w_{0}^{{''}}(0) + \Phi \nu {{j}_{0}}.$В дальнейшем рассматривается система уравнений (1.1), (1.9) с начальными и краевыми условиями (1.2)–(1.4), (1.10). Для определенности решение строится при нулевых начальных условиях, соответствующих состоянию покоя двигателя и стержня. Задача оптимального управления ставится следующим образом. Найти закон изменения подаваемого напряжения u(t), который приводит к повороту звена на заданный угол из начального состояния покоя в покой за фиксированное время t = T. При этом управление доставляет минимум некоторому функционалу W[u] на допустимом классе функций $u \in \mathcal{U}$ при выполнении начальных и терминальных условий по времени:
(1.11)
$\begin{array}{*{20}{c}} {\alpha (T) = {{\alpha }_{T}},\quad \alpha (0) = \dot {\alpha }(0) = \ddot {\alpha }(0) = \dot {\alpha }(T) = \ddot {\alpha }(T) = 0,} \\ {w(0,x) = {{w}_{t}}(0,x) = w(T,x) = {{w}_{t}}(T,x) = 0,} \end{array}$2. Метод разделения переменных. В этом разделе решение для УЧП (1.1), (1.9) с краевыми и начальными условиями (1.2), (1.3) строится с помощью метода разделения переменных для случая однородного стержня ($\rho = {\text{const}}$ и $\kappa = {\text{const}}$). Для начала введем безразмерные переменные
В (1.1)–(1.3), (1.9) выразим старые переменные через новые. В дальнейшем для упрощения записи символ звездочки опускаем. В результате еще одной замены (переменной w на ${v}$, см. ниже) выписывается система
(2.1)
$\begin{gathered} {{{v}}_{{tt}}}(t,x) + {{{v}}_{{xxxx}}}(t,x) = 0,\quad {v}(t,x) = w(t,x) + x\alpha (t), \\ a\dddot \alpha (t) + \ddot {\alpha }(t) + b\dot {\alpha }(t) - c\left( {a{{{v}}_{{txx}}}(t,0) + {{{v}}_{{xx}}}(t,0)} \right) = {{u}_{*}}(t), \\ {v}(t,0) = {{{v}}_{{xx}}}(t,1) = 0,\quad {{v}_{{xxx}}}(t,1) = m{{v}_{{tt}}}(t,1),\quad \alpha (t) = {{{v}}_{x}}(t,0), \\ \end{gathered} $Системе (2.1) можно поставить в соответствие задачу на собственные значения:
(2.2)
$\begin{gathered} v_{k}^{{(4)}}(x) + \mu _{k}^{2}{{v}_{k}}(x) = 0, \\ (a\mu _{k}^{3} + \mu _{k}^{2} + b{{\mu }_{k}})v_{k}^{'}(0) = c(a{{\mu }_{k}} + 1)v_{k}^{{''}}(0), \\ {{v}_{k}}(0) = v_{k}^{{''}}(1) = 0,\quad v_{k}^{{(3)}}(1) = m\mu _{k}^{2}{{v}_{k}}(1),\quad {{\alpha }_{k}} = v_{k}^{'}(0), \\ \end{gathered} $Из структуры системы (2.2) сразу следует нулевое собственное число μ1 = 0 и полиномиальное решение ${{v}_{1}}(x) = {{\alpha }_{1}}x$, где ${{\alpha }_{1}} \in \mathbb{C}$ – произвольная константа. Если коэффициенты a и b одновременно не равны нулю, то задача не является самосопряженной и в числах μk при k > 1 всегда присутствует отрицательная вещественная часть, т.е. решение соответствует затухающим колебаниям точек стержня и тока в обмотке электропривода. Собственные функции можно искать в виде
(2.3)
$\begin{gathered} {{v}_{k}}(x) = \sum\limits_{n = 1}^4 \,{{c}_{{k,n}}}exp({{\lambda }_{{k,n}}}x), \\ {{\lambda }_{{k,n}}} = \sqrt {{\text{|}}{{\mu }_{k}}{\text{|}}} exp\left( {\frac{i}{4}arg( - \mu _{k}^{2}) + \frac{i}{2}(n - 1)\pi } \right). \\ \end{gathered} $С точностью до нормирующего множителя четыре коэффициента ${{c}_{{k,n}}}$, введенные в (2.3), и число μk определяются из краевых условий в (2.2).
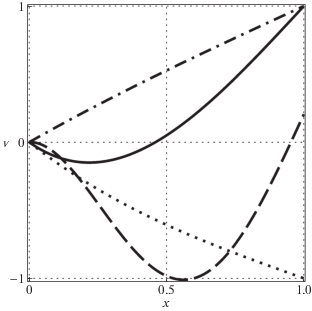
В качестве иллюстрирующего примера выберем следующие коэффициенты системы: a = 0.5, b = 0.9, c = 1. В табл. 1 для выбранных параметров приведены семь низших собственных чисел с учетом комплексной сопряженности четырех последних. Действительные части собственных функций ${{v}_{k}}$ для $k = 2,3,4,6$ изображены на рис. 2, а именно ${{v}_{2}}(x)$ (пунктирная линия), ${{v}_{3}}(x)$ (штрихпунктирная), ${{v}_{4}}(x)$ (сплошная), ${{v}_{6}}(x)$ (штриховая). Для наглядности функции сведены к одному масштабу с разными знаками множителя масштабирования.
Таблица 1.
Собственные числа для звена с однородным стержнем
| k | 1 | 2 | 3 | 4, 5 | 6, 7 |
|---|---|---|---|---|---|
| $\Re ({{\mu }_{k}})$ | 0 | –1.17 | –0.59 | –0.12 | –9.97 × 10–5 |
| $\Im ({{\mu }_{k}})$ | – | 0 | 0 | ±2.50 | ±16.37 |
| $\left| {\frac{{\Delta {{\mu }_{k}}}}{{{{\mu }_{k}}}}} \right|$, % | 0 | 2 × 10–8 | 2 × 10–9 | 2 × 10–6 | 4 × 10–6 |
В случае a = b = 0 задача становится самосопряженной и функции из (2.3) составляют ортогональный базис в гильбертовом пространстве $H_{0}^{2}((0,1);\mathbb{C})$ со скалярным произведением:
3. Проекционный подход. Применение метода разделения переменных, рассмотренного в предыдущем параграфе, затруднено из-за несамосопряженности дифференциального оператора в задаче о повороте звена с электроприводом. Требует особого внимания вопрос существования базиса в пространстве, которому принадлежит решение. Поиск существенно комплексных собственных чисел приводит к необходимости нахождения корней характеристического многочлена на комплексной плоскости.
Построение форм колебаний еще более проблематично для неоднородного стержня. В этом случае, за исключением особых видов распределения параметров, будут доступны лишь приближенные значения собственных функций. Проведенный спектральный анализ однородной системы используется исключительно для проверки численного алгоритма оптимизации, описанного ниже.
Для решения задачи оптимального управления (1.11) применим численный подход, основанный на МИДС [22]. Согласно этому подходу, для описания состояния стержня вводятся динамические переменные линейной плотности импульса $p(t,x)$ (в дальнейшем для краткости – просто импульса) и изгибающего момента в сечении $s(t,x)$ (кратко – момента). В соответствии с локальной формулировкой закона состояния функции
(3.1)
$f \triangleq s - \kappa {{w}_{{xx}}},\quad g \triangleq p - \rho ({{w}_{t}} + x\dot {\alpha }),$Используя с учетом (3.2) динамические переменные $p$ и $s$ вместо кинематической переменной w, уравнение движения (1.1) преобразуется в соотношение
которое определяет скорость изменение импульса, согласно второму закону Ньютона. В свою очередь ОДУ (1.9) переписывается в виде(3.4)
$A\dddot \alpha (t) + B\ddot {\alpha }(t) + C\dot {\alpha }(t) - D{{s}_{t}}(t,0) - Es(t,0) = \Phi \nu u(t).$Если определить две новые неизвестные функции, кинематическую q(t, x) и динамическую r(t, x) так, чтобы были справедливы равенства
(3.5)
$\begin{array}{*{20}{c}} {w(t,x) = q(t,x) + {{w}_{0}}(x),\quad p(t,x) = {{r}_{{xx}}}(t,x) + \rho (x){{v}_{0}}(x),} \\ {s(t,x) = - {{r}_{t}}(t,x) + m{{\rho }^{{ - 1}}}(x)(x - \ell ){{p}_{t}}(t,\ell ),} \end{array}$В согласии с (3.5) граничные условия (1.2) выражаются через новые переменные q и r однородно в виде
а начальные условия (1.3) даны какОриентацию осей инерциальной системы координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ можно всегда выбрать так, чтобы в момент t = 0 угол поворота звена равнялся нулю (см. рис. 1). Тогда произвольные начальные условия, определенные в (1.4) и (1.10), можно переписать в форме
(3.8)
$\alpha (0) = 0,\quad \dot {\alpha }(0) = {{\omega }^{0}},\quad \ddot {\alpha }(0) = {{\varepsilon }^{0}}.$Численное решение задачи (3.1)–(3.8) находится с применением МКЭ, см. [22]. Чтобы составить совместную конечномерную систему ОДУ, приближенную к исходной модели, приравниваются нулю проекции функций состояния f и g на линейную оболочку конечного набора тестовых функций:
(3.9)
$\int\limits_0^\ell \,f(t,x)h(x)dx = 0,\quad \int\limits_0^\ell \,g(t,x)h(x)\rho {\text{*}}(x)dx = 0,\quad \forall h \in {{\mathcal{S}}_{h}}.$Для учета массы, закрепленной на конце стержня, интегральная проекция функции g берется с добавочным весовым множителем ρ*, определенным в (1.5).
Приближенные гладкие функции $q \in {{\mathcal{S}}_{q}} \cap {{C}_{1}}$, $r \in {{\mathcal{S}}_{r}} \cap {{C}_{1}}$ и весовые функции $h \in {{\mathcal{S}}_{h}}$ – это кусочно-полиномиальные сплайны по $x$, такие, что
(3.10)
$\begin{gathered} {{\mathcal{S}}_{q}} = \left\{ {q:q(t,x) = \sum\limits_{n = 1}^{N + 2} \,{{w}_{{k,n}}}(t){{b}_{{N + 2 - n,n - 1}}}({{z}_{k}}(x)),\;x \in {{I}_{k}}} \right\}, \\ {{\mathcal{S}}_{r}} = \left\{ {r:r(t,x) = \sum\limits_{n = 1}^{N + 2} \,{{r}_{{k,n}}}(t){{b}_{{n - 1,N + 2 - n}}}({{z}_{k}}(x)),\;x \in {{I}_{k}}} \right\}, \\ {{\mathcal{S}}_{h}} = \left\{ {h:h(x) = \sum\limits_{n = 1}^N \,{{h}_{{k,n}}}{{b}_{{n - 1,N - n}}}({{z}_{k}}(x)),\;x \in {{I}_{k}}} \right\}, \\ \end{gathered} $Базисные функции на каждом элементе определяются с помощью полиномов Бернштейна
выраженных через масштабированную координату zk. При использовании этих полиномов только коэффициенты ${{w}_{{k,n}}}(t)$ и ${{r}_{{k,n}}}(t)$ с индексами $k = 1, \ldots M$ и $n = 0,1,N,N + 1$ влияют на значения функций q, r в граничных и узловых точках x = 0 и $x = {{x}_{k}}$. Добиться гладкости этих функций и выполнения граничных условий можно, как это делается далее, используя лишь коэффициенты ${{w}_{{k,n}}}(t)$ и ${{r}_{{k,n}}}(t)$ с индексами $n = N,N + 1$.Управление $u(t)$, т.е. функция напряжения в правой части (3.4), выбирается из класса многочленов заданной степени:
(3.11)
$u = {{u}_{0}} + \sum\limits_{k = 1}^K \,{{u}_{k}}{{t}^{k}} \in {{\mathcal{P}}_{K}},\quad {\mathbf{u}} = ({{u}_{1}}, \ldots ,{{u}_{K}}).$Здесь же введен вектор свободных параметров управления ${\mathbf{u}} \in {{\mathbb{R}}^{K}}$, а коэффициент u0 резервируется для выполнения первого терминального условия в (1.11) (см. далее).
Нахождение свободных параметров движения ${{w}_{{k,n}}}(t)$ и ${{r}_{{k,n}}}(t)$ для $k = 1, \ldots M$ и $n = 1, \ldots ,N$ сводится в случае выбранного типа управления к решению линейной системы ОДУ (3.9) с постоянными коэффициентами и полиномиальными правыми частями, зависящими от u. Теоретически это означает, что решения могут быть получены в явной форме. Дифференциальный порядок ${{N}_{d}}$ системы равен совместной размерности пространств ${{\mathcal{S}}_{q}}$ и ${{\mathcal{S}}_{r}}$ c учетом всех межэлементных и краевых ограничений плюс три, т.е. ${{N}_{d}} = 2MN + 3$. Это увеличение размерности на три происходит за счет добавления в систему дифференциального уравнения третьего порядка (3.4), необходимого для определения угла поворота $\alpha (t)$, угловой скорости $\dot {\alpha }(t)$ и ускорения $\ddot {\alpha }(t)$ (или силы тока j(t)).
Напомним, что управление $u(t)$ должно перевести электромеханическое звено из начального состояния покоя в конечное за фиксированное время T, при этом, в частности, $\alpha (T) = {{\alpha }_{T}}$. Поставим целью минимизацию следующего функционала:
(3.12)
$\begin{array}{*{20}{c}} {W[u] \to \mathop {min}\limits_{u \in {{\mathcal{P}}_{K}}} ,\quad W = {{W}_{0}} = \int\limits_0^T \,R{{j}^{2}}(t)dt,} \end{array}$При выборе определенного в (3.11) управления $u \in {{\mathcal{P}}_{K}}$ с низкой степенью многочлена $K < {{N}_{d}}$ не удастся в общем случае привести приближенную систему в состояние покоя. Однако даже если $K \geqslant {{N}_{d}}$ и построено управление приближенной системой, которое в конечный момент времени t = T обнуляет все неизвестные переменные (кроме α), исходная система, в которой реализовано то же самое управление, не перейдет гарантированно в состояние покоя из-за ошибок дискретизации. В терминах энергии остаточные затухающие колебания ограничены сверху по норме функционалом
(3.13)
$\begin{gathered} {{W}_{1}} = E(T),\quad E(t) = \int\limits_0^\ell \,\psi (t,x)dx + {{E}_{0}}(t), \\ {{E}_{0}}(t) = \frac{{m{{{({{w}_{t}}(t,\ell ) + \ell \dot {\alpha }(t))}}^{2}}}}{2} + \frac{{J{{\nu }^{2}}{{{\dot {\alpha }}}^{2}}(t)}}{2} + \frac{{L{{j}^{2}}(t)}}{2}, \\ 4\psi = {{\rho }^{{ - 1}}}(x){{p}^{2}}(t,x) + \rho (x){{({{w}_{t}}(t,x) + x\dot {\alpha }(t))}^{2}} + {{\kappa }^{{ - 1}}}(x){{s}^{2}}(t,x) + \kappa (x)w_{{xx}}^{2}(t,x). \\ \end{gathered} $Здесь функция времени E определяет электромеханическую энергию, запасенную манипуляционным звеном с учетом сосредоточенных элементов (E0), а подынтегральная функция $\psi $, согласно (3.1), (3.2), (3.5), задает через дуальные переменные $q$ и $r$ распределение в пространстве и времени линейной плотности механической энергии упругого стержня.
В МИДС ошибки в определении полей перемещений $w$, импульса $p$ и момента $s$ напрямую связаны с невязкой уравнений состояния (3.2) и могут быть оценены в энергетических единицах с помощью квадратичного функционала:
(3.14)
${{W}_{2}} = \frac{1}{T}\int\limits_0^T \,\int\limits_0^\ell \,\varphi (t,x)dxdt \geqslant 0,\quad \varphi = \frac{{{{f}^{2}}(t,x)}}{{2\kappa (x)}} + \frac{{{{g}^{2}}(t,x)}}{{2\rho (x)}},$Чтобы ограничить диапазон ошибок и таким образом повысить надежность моделирования, значение функционала состояния W2 может быть зафиксировано изопериметрическим условием ${{W}_{2}} = {{\varepsilon }_{2}} > 0$. Говоря о достоверности численного решения, необходимо назначить величину ${{\varepsilon }_{2}}$ много меньше значения средней энергии системы:
Если невозможно привести приближенную систему в терминальное состояние с нулевой энергией, разумно наложить еще одно изопериметрическое условие, в этот раз на конечную энергию ${{W}_{1}} = {{\varepsilon }_{1}} > 0$. При этом ради достоверности определения терминального состояния можно допустить, что ${{\varepsilon }_{2}} \ll {{\varepsilon }_{1}}$. С другой стороны, качество управления определяется степенью гашения колебаний, возникающих при повороте звена. Для количественной оценки успокоения звена можно использовать отношение величин терминальной и средней энергии и выбрать ${{\varepsilon }_{1}} \ll \overline E $.
В соответствии с теоремой Лагранжа [26] изопериметрические условия приводят к следующей оптимизационной задаче. Требуется найти закон управления $u{\text{*}}(t)$, который минимизирует модифицированную функцию цены:
(3.16)
$W[u] \to \mathop {min}\limits_{u \in {{\mathcal{P}}_{K}}} ,\quad W = {{W}_{0}} + {{\gamma }_{1}}{{W}_{1}} + {{\gamma }_{2}}{{W}_{2}}.$Здесь ${{\gamma }_{1}} \geqslant 0$ – весовой коэффициент, влияющий на энергию остаточных колебаний, а величина ${{\gamma }_{2}} \geqslant 0$ регулирует в допустимых пределах вычислительную ошибку. В предложенной постановке взвешенно минимизируется потеря энергии в системе с учетом ошибок управления и дискретизации.
После интегрирования системы ОДУ относительно времени для произвольного вектора управления u процедура минимизации заключается в определении наилучших параметров u* через решение линейной системы алгебраических уравнений, вытекающих из необходимых условий стационарности квадратичного функционала W, определенного в (3.16). Затем находятся функция управления $u{\text{*}}(t) = u(t,{\mathbf{u}}{\text{*}})$ и восстанавливаются функции поперечных смещений w*(t, x) = = $w(t,x,{\mathbf{u}}{\text{*}})$, импульса $p{\text{*}}(t,x) = p(t,x,{\mathbf{u}}{\text{*}})$, момента $s{\text{*}}(t,x) = s(t,x,{\mathbf{u}}{\text{*}})$ и угла поворота $\alpha {\text{*}}(t) = \alpha (t,{\mathbf{u}}{\text{*}})$. Зная значение функционала невязки W2 и средней энергии $\overline E $, можно вычислить величину Δ2 = = ${{W}_{2}}{\text{/}}\overline E $, которая будет служит мерой качества полученного решения.
4. Численные результаты. Чтобы показать эффективность предложенной в предыдущем разделе численной процедуры, выберем безразмерные параметры системы:
Выражения для $\kappa $ и $\rho $ соответствуют изменению изгибной жесткости и линейной плотности для стержня, выполненного из однородного материала с круглым сечением, радиус которого меняется линейно с ростом координаты x. Случай с σ > 0 означает, что неоднородный стержень сужается к нагруженному концу. Средняя изгибная жесткость и средняя плотность равны единице для любого σ. Из-за того что функции $\kappa $ и $\rho $ могут принимать только положительные значения, на величину σ накладываются естественные геометрические ограничения: $\sigma < 1{\text{/}}\ell $.
Зафиксируем параметры аппроксимации $M = N = 4$ и управления T = 10, K = 8, ${{\alpha }_{T}} = 1$, т.е. за время управления стержень поворачивается на один радиан. Дифференциальный порядок приближенной системы
равен ${{N}_{d}} = 35$. Здесь ${\mathbf{x}}(t) \in {{\mathbb{R}}^{{{{N}_{d}}}}}$ – вектор состояния, ${\mathbf{A}} \in {{\mathbb{R}}^{{{{N}_{d}} \times {{N}_{d}}}}}$ – постоянная матрица, ${\mathbf{b}} \in {{\mathbb{R}}^{{{{N}_{d}}}}}$ – вектор управляющих входов.Вначале рассмотрим спектральные характеристики управляемой системы (4.1), приближенно описывающей динамику звена с однородным стержнем (σ = 0). Для выбранных параметров конечно-элементной сетки низшие по абсолютной величине собственные числа матрицы A близки к соответствующим числам исходной бесконечномерной модели. В последней строке табл. 1 приведены в процентах относительные ошибки в определении значений первых семи собственных чисел, действительные и мнимые части которых даны в первых двух строках. Как видно, отклонения от точных значений незначительны, хотя и увеличиваются с номером k. Следует отметить, что старшие собственные числа матрицы A будут существенно расходиться с соответствующими величинами для распределенной системы.
Для модели с однородным стержнем и приведенными выше параметрами был выполнен ряд расчетов оптимизации управления при выборе различных весовых коэффициентов в функционале W, определенном в (3.16). В табл. 2 в зависимости от выбранных весовых коэффициентов ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ помещены значения тепловых потерь в обмотке двигателя W0, а также значения остаточной энергии в системе W1 и интегральной невязки уравнений состояния W2, выраженной в энергетических единицах. Когда функция цены не включает ни энергетическую норму остаточных колебаний, ни невязку уравнений состояния стержня (${{\gamma }_{1}} = {{\gamma }_{2}} = 0$), тепловые потери W0 оказываются малы по сравнению с терминальной энергией, запасаемой в звене. При этом ошибка дискретизации W2 слишком высока, чтобы говорить о достоверной оценке остальных величин.
Таблица 2.
Значение функционалов W0, W1 и W2 в зависимости от коэффициентов ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$
| γ1 | γ2 | W0 | W1 | W2 |
|---|---|---|---|---|
| 0 | 0 | 4.8 × 10–3 | 2.7 × 10–2 | 1.1 × 10–4 |
| 1 | 0 | 1.1 × 10–2 | 3.6 × 10–3 | 7.7 × 10–4 |
| 10 | 0 | 1.9 × 10–2 | 2.2 × 10–4 | 5.8 × 10–4 |
| 100 | 0 | 2.3 × 10–2 | 6.6 × 10–6 | 5.6 × 10–5 |
| 100 | 10 | 2.4 × 10–2 | 3.8 × 10–6 | 1.2 × 10–5 |
| 100 | 102 | 2.4 × 10–2 | 2.4 × 10–6 | 6.3 × 10–7 |
| 100 | 103 | 2.4 × 10–2 | 2.4 × 10–6 | 8.3 × 10–8 |
| 100 | 104 | 2.4 × 10–2 | 2.6 × 10–6 | 7.1 × 10–8 |
| 0 | +∞ | 1.2 × 10–2 | 7.4 × 10–2 | <10–14 |
| +∞ | 0 | 5.6 × 10–2 | 9.0 × 10–12 | 2.3 × 10–10 |
Вычислительная ошибка возрастает с введением в целевой функционал терминальной энергии W1 с некоторым весом (${{\gamma }_{1}} > 0$, ${{\gamma }_{2}} = 0$). С увеличением ${{\gamma }_{1}} > 0$ быстро падает значение W1, но при этом возрастают расходы энергии. Хотя точность приближенной модели увеличивается на порядок при ${{\gamma }_{1}} = 100$, ее не хватает для достоверной оценки терминального состояния системы (${{W}_{2}} \gg {{W}_{1}}$).
Когда при фиксированном коэффициенте ${{\gamma }_{1}} = 100$ начинает увеличиваться ${{\gamma }_{2}}$, ошибка W2 быстро уменьшается, достигая при ${{\gamma }_{2}} > {{10}^{3}}$ некоторого насыщения. При этом точность приведения системы в окрестность состояния с нулевой энергией несколько понижается, а суммарные тепловые потери за время поворота практически не изменяются.
Если не учитывать при оптимизации ни потери в электродвигателе, ни величину остаточных колебаний, можно построить особое управляемое движение, заданное с очень высокой степенью точности, о чем говорит предпоследняя строка табл. 2. В этой строке знак бесконечности для ${{\gamma }_{2}}$ означает, что в задаче оптимального управления выбран функционал W = W2.
Если же положить $W = {{W}_{1}}$, т.е. привести приближенную модель с помощью полиномиального управления как можно ближе к желаемому состоянию, ошибка дискретизации оказывается много больше остаточной энергии при t = T (${{W}_{2}} \gg {{W}_{1}}$), что обесценивает высокую точность приведения. К тому же возрастают и потери в двигателе.
Рассмотрим поворот звена со стержнем, сужающимся к нагруженному концу при $\sigma = 0.125$. Спектральные свойства системы представлены в табл. 3 при выбранных выше параметрах конечно-элементной сетки. Во второй строке приведены действительные части первых семи собственных чисел матрицы A, а в третьей – их мнимые части. В последней строке в процентном соотношении помещены сдвиги чисел в сравнении со звеном с однородным стержнем. Как видно (ср. с табл. 1), немного изменились собственные числа ${{\mu }_{4}}$ и ${{\mu }_{5}}$ (первая колебательная мода). Неоднородность стержня меньше влияет на действительные числа ${{\mu }_{2}}$ и ${{\mu }_{3}}$, соответствующие переходным процессам в электроприводе. Ещe слабее меняются старшие числа, отражающие почти не затухающие высокочастотные колебания звена. Это обусловлено тем, что усредненные по длине стержня изгибная жесткость и линейная плотность не изменяются.
Таблица 3.
Cобственные числа для звена с неоднородным стержнем
| k | 1 | 2 | 3 | 4, 5 | 6, 7 |
|---|---|---|---|---|---|
| $\Re ({{\mu }_{k}})$ | 0 | –1.20 | –0.59 | –0.11 | –1.13 × 10–4 |
| $\Im ({{\mu }_{k}})$ | – | 0 | 0 | ±2.64 | ±16.69 |
| $\left| {\frac{{\Delta {{\mu }_{k}}}}{{{{\mu }_{k}}}}} \right|$, % | 0 | 1.94 | 0.47 | 6.0 | 2.0 |
Зафиксируем значения ${{\gamma }_{1}} = 100$ и ${{\gamma }_{2}} = {{10}^{4}}$ в модифицированной задаче оптимального управления (3.16). Используя полиномиальные законы подачи напряжения (3.11), удается достичь достаточно малых значений терминальной энергии ${{W}_{1}} = 3.2 \times {{10}^{{ - 6}}}$ по сравнению со средней энергией, накапливаемой в системе: $\overline E = 0.052$. Тепловые потери за все время поворота равны ${{W}_{0}}$ = = 0.025. Относительная ошибка, получаемая при использовании найденного управления звеном с неоднородным стержнем, составляет $\Delta \approx 0.06\% $, при этом ${{W}_{2}} < 2 \times {{10}^{{ - 8}}} \ll {{W}_{1}}$.
Исходя из этих соотношений, можно полагать, что выбранные параметры аппроксимации достаточны для достоверного описания движения звена при предложенной стратегии оптимизации поворота. Для проверки качества полученного решения были проведены расчеты на той же сетке ($M = N = 4$), но для более высокой степени многочлена управления (N = 10). Для этого приближения при прочих равных условиях существенно понижается уровень ошибки W2 = = $8.2 \times {{10}^{{ - 9}}}$, несколько улучшается качество приведения системы в окрестность заданного состояния ${{W}_{1}} = 1.9 \times {{10}^{{ - 6}}}$ и практически не варьируется уровень энергетических потерь ${{W}_{0}} = 0.025$. Характер управления и траектории движения мало меняются. Разумеется, сходимость решения по параметрам конечно-элементной сетки M, N и управления K требует дальнейшего анализа.
Для наглядного представления оптимизированных процессов в электродвигателе на рис. 3 изображен закон изменения во времени напряжения $u{\text{*}}(t)$, подаваемого на обмотку двигателя (сплошная кривая), а также некоторые переменные состояния, выраженные в единицах напряжения согласно (1.6) и (1.7). Так, штрихпунктирная линия обозначает противо-ЭДС (электродвижущую силу) в обмотке, пропорциональную угловой скорости ротора $\nu \dot {\alpha }(t)$ при постоянном магнитном потоке Φ, характерном для двигателя с независимым возбуждением. Отметим, что за первую половину движения ротор монотонно увеличивает обороты, а потом постепенно замедляет вращения, останавливаясь в конце процесса управления.
Рис. 3.
Управление u(t) (сплошная) и масштабированные угловая скорость $\Phi \nu \dot {\alpha }(t)$ (штрихпунктирная), сила тока $Rj(t)$ (штриховая), момент сил $R\eta (t){\text{/}}\Phi {\text{/}}\nu $ (пунктирная)
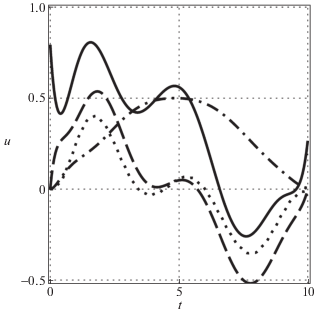
Падение напряжения $Rj(t)$ из-за активного сопротивления цепи показано на рис. 3 штриховой линией. Эта величина сравнима с изображенным пунктиром эффективным напряжением $R\eta (t){\text{/}}\Phi {\text{/}}\nu $, которое обусловлено полезной нагрузкой, передаваемой с коэффициентом ν–1 к мотору через редуктор. Управление u, как и сила тока j, за время поворота 2 раза меняет знак. Функции тока $j(t)$ и момента сил $\eta (t)$ достигают экстремальных значений в первой и третьей четверти временного интервала и стремятся к нулю в конце процесса. Как видно из графика, на коротком временном интервале вначале и конце движения осуществляется быстрое изменение напряжения, которое необходимо для компенсации переходных электромагнитных процессов в приводе с характерными временами $\mu _{2}^{{ - 1}}$ и $\mu _{3}^{{ - 1}}$ (порядка ~1 и ~2 соответственно, см. табл. 3).
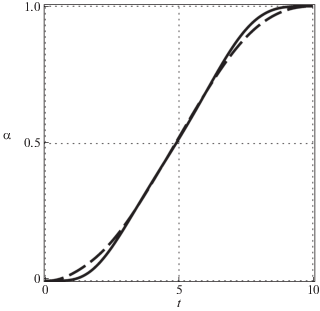
Угол поворота α как функция времени показан на рис. 4 штриховой линией. Для сравнения сплошной линией с точностью до квадратичных членов изображен поворот прикрепленной к звену массы A, равный $\alpha (t) + w(t,\ell ){\text{/}}\ell $. В момент окончания процесса управления угол поворота точно равен терминальному значению ${{\alpha }_{T}}$, а угловая скорость практически нулевая. Можно отметить, что упругие отклонения полезной нагрузки, показанные на графике, носят в основном квазистатический характер.
Рис. 4.
Углы поворота точечной массы $\alpha (t) + w(t,\ell ){\text{/}}\ell $ (сплошная) и касательной к стержню α(t) (штриховая)
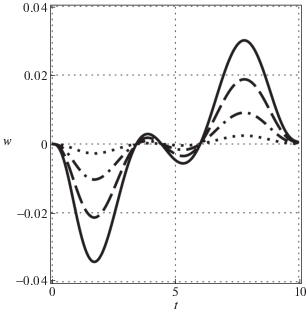
Это же подтверждает и распределение упругих смещений стержня $w(t,x)$ во времени, которые показаны на рис. 5 для четырех точек стержня при $x = \ell $ (сплошная кривая), $x = 3\ell {\text{/}}4$ (штриховая), $x = \ell {\text{/}}2$ (штрихпунктирная), $x = \ell {\text{/}}4$ (пунктирная). Амплитуда колебаний тем больше, чем дальше точка удалена от шарнирного закрепления. Можно заметить, что возникающие амплитуды отклонения от центральной линии, полученные для оптимального вектора управления, достаточно велики в первой и последней трети движения. Упругие смещения сравнительно малы в середине процесса и сходят на нет при t = T, что соответствует малым значениям терминальной энергии W1, величина которой приводилась выше.
Заключение. В представленной работе предложен алгоритм численного моделирования и оптимизации движений динамических систем, содержащих как распределенные, так и сосредоточенные параметры. Подход основан на использовании МИДС, в котором локальные законы состояния системы заменяются их интегральным представлением. В численной реализации применяется модификация метода Петрова–Галеркина, когда уравнения состояния проецируются на конечномерное пространство тестовых функций. Рассмотрен пример электромеханической системы, которая содержит упругий элемент, моделируемый в рамках теории Бернулли–Эйлера для поперечного изгиба балки. Неизвестными распределенными параметрами системы являются относительные перемещения точек прямолинейного тонкого стержня, изгибающий момент в его сечении, линейная плотность импульса, а также сосредоточенные параметры. В рассмотренном примере – это поворот ротора электродвигателя, его угловая скорость и сила тока в обмотке.
Развиваемый подход позволяет в явном виде дать энергетическую оценку качества решения. Численные расчеты показывают, что процесс оптимизации управления при некоторых условиях приводит к серьезному ухудшению точности аппроксимации. Даже для приближений достаточно высокой размерности не для всех законов управления удается обеспечить необходимое качество представленных решений. Для регуляризации численной процедуры решения задачи оптимального управления предлагается добавлять в функцию цены с некоторым весом квадратичный интеграл невязки уравнений состояния. Проведенные расчеты показывают эффективность выбранного подхода и позволяют предложить режимы движения, достоверность которых гарантирована высоким качеством приближенных решений.
Список литературы
Lions J.L. Optimal Control of Systems Governed by Partial Differential Equations. N.Y.: Springer-Verlag, 1971.
Ahmed N.U., Teo K.L. Optimal Control of Distributed Parameter Systems. N.Y.: North Holland, 1981.
Butkovsky A.G. Distributed Control Systems. N.Y.: Elsevier, 1969.
Krabs W. Optimal Control of Undamped Linear Vibrations. Lemgo: Heldermann, 1995.
Gugat M. Optimal Control of Networked Hyperbolic Systems: Evaluation of Derivatives // Advanced Modelling and Optimization. 2005. V. 7. P. 9–37.
Lagnese J.E., Leugering G., Schmidt E.J.P.G. Modeling, Analysis and Control of Dynamic Elastic Multi-Link Structures. Boston: Birkhäuser, 1984.
Leugering G. A Domain Decomposition of Optimal Control Problems for Dynamic Networks of Elastic Strings // Computational Optimization and Applications. 2000. V. 16. P. 5–29.
Banks S.P. State-Space and Frequency-Domain Methods in the Control of Distributed Parameter Systems. London: Peregrinus, 1983.
Curtain R.F., Zwart H.J. An Introduction to Infinite-Dimensional Linear Systems Theory. N.Y.: Springer-Verlag, 1995.
Chernousko F.L. Control of Elastic Systems by Bounded Distributed Forces // Applied Mathematics and Computation. 1996. V. 78. P. 103–110.
Gerdts M., Greif G., Pesch H.J. Numerical Optimal Control of the Wave Equation: Optimal Boundary Control of a String to Rest Infinite Time // Mathematics and Computers in Simulation. 2008. V. 79. № 4. P. 1020–1032.
Овсеевич А.И., Федоров А.К. Асимптотически оптимальное управление простейшей распределенной системой // ДАН. 2017. Т. 473. № 5. С. 525–528.
Романов И.В., Шамаев А.С. О задаче точного управления системой, описываемой уравнением струны с запаздыванием // АиТ. 2013. Вып. 11. С. 38–50.
Романов И.В., Шамаев А.С. О задаче граничного управления для системы, описываемой двумерным волновым уравнением // Изв. РАН. ТиСУ. 2019. № 1. С. 109–116.
Lewis R.W., Nithiarasu P., Seetharamu K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow. Chichester: Wiley, 2004.
Balas M.J. Finite-Dimensional Control of Distributed Parameter Systems by Galerkin Approximation of Infinite Dimensional Controllers // J. Mathematical Analysis and Applications. 1986. V. 114. P. 17–36.
Christofides P.D. Nonlinear and Robust Control of PDE Systems: Methods and Applications to Transport-Reaction Processes. Boston: Birkhäuser, 2001.
Belytschko T., Lu Y.Y., Gu L. Element-Free Galerkin Method // Intern. J. for Numerical Methods in Engineering. 1994. V. 37. P. 229–256.
Atluri S.N., Zhu T. A New Meshless Local Petrov-Galerkin (MLPG) Approach in Computational Mechanics // Computational Mechanics. 1998. V. 22. P. 117–127.
Bochev P.B., Gunzburger M.D. Least-Squares Finite Element Methods. N.Y.: Springer, 2009.
Kostin G.V., Saurin V.V. Dynamics of Solid Structures. Methods Using Integrodifferential Relations. Berlin: De Gruyter, 2018.
Kostin G.V. Modelling and Optimization of Controlled Longitudinal Motions for an Elastic Rod Based on the Ritz Method // 2018 14th Intern. Conf. “Stability and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference) (STAB). Moscow: IEEE, 2018. P. 1–4. https://doi.org/10.1109/STAB.2018.8408369
Доннелл Л.Г. Балки, пластины и оболочки. М.: Наука, 1982.
Костин Г.В. Динамика управляемых вращений нагруженного упругого звена в манипуляционной системе с электромеханическим приводом // Изв. АН СССР. Техн. кибернетика. 1990. № 3. P. 146–153.
Чиликин М.Г., Ключев В.И., Сандлер А.С. Теория автоматизированного электропривода. М.: Энергия, 1979.
Giaquinta M., Hildebrandt S. Calculus of Variations. I. Berlin: Springer-Verlag, 2004.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления