Известия РАН. Теория и системы управления, 2020, № 6, стр. 15-31
УСТОЙЧИВОСТЬ ИНТЕРВАЛЬНОГО СЕМЕЙСТВА ДИФФЕРЕНЦИАЛЬНО-АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
А. Д. Кононов a, А. А. Щеглова a, *
a Институт динамики систем и теории управления им. В.М. Матросова СО РАН
Иркутск, Россия
* E-mail: shchegl@icc.ru
Поступила в редакцию 18.10.2018
После доработки 14.02.2020
Принята к публикации 30.03.2020
Аннотация
Рассматривается линейная стационарная система дифференциально-алгебраических уравнений произвольно высокого индекса неразрешенности с интервальными коэффициентами. Для того чтобы возмущения не меняли вид и свойства общего решения, получены достаточные условия, при которых возмущенная система имеет такую же структуру общего решения, что и номинальная система. Эти условия представляют собой конечные соотношения, которым должны удовлетворять интервальные коэффициенты. В предположениях, обеспечивающих сохранение структуры, получены конструктивные оценки величины, определяющей размах неопределенностей, при выполнении которых рассматриваемое интервальное семейство робастно устойчиво. В частности, условия робастной устойчивости получены в предположении сверхустойчивости номинальной системы.
0. Введение. Рассматривается система обыкновенных дифференциальных уравнений
где A0 и B0 – заданные вещественные $(n \times n)$-матрицы, x(t) – искомая n-мерная функция. Предполагается, что ${\text{det}}{{A}_{0}} = 0$. Cистемы такого рода называются дифференциально-алгебраическими уравнениями (ДАУ). Важнейшей характеристикой ДАУ является индекс неразрешенности, отражающий сложность внутренней структуры системы.ДАУ вида (0.1) возникают при моделировании процессов во многих прикладных областях, в частности, в теории автоматического регулирования [1, c. 19], в теплотехнике [2], при проектировании электронных схем и электрических цепей [3, с. 259], в результате применения метода сферических гармоник к решению задачи переноса нейтронов [1, с. 21], при приближенном решении задачи фильтрации двухфазной несжимаемой жидкости методом ортогональных разложений [4, с. 86].
В работе изучается вопрос об асимптотической устойчивости семейства ДАУ с интервальными коэффициентами. Прежде чем привести постановку задачи, необходимо охарактеризовать специфику исследования робастных свойств таких систем. Основная трудность, возникающая в такого рода исследованиях, связана с тем, что даже в простейших случаях при сколь угодно малом возмущении коэффициентов может измениться внутренняя структура системы и, следовательно, вид общего решения, в результате чего структура и свойства невозмущенной системы (0.1) могут потерять для анализа всякое значение. В качестве иллюстрации рассмотрим пример индекса неразрешенности единица.
Пример 1. Система ДАУ
Возмущенная система
Уже из этого примера видно, что для обеспечения робастной устойчивости возмущения (даже достаточно малые) не могут быть произвольного вида. В данной работе для того, чтобы не возникала ситуация, представленная в примере 1, требуется, чтобы интервальные возмущения подчинялись некоторым конечным соотношениям, гарантирующим совпадение размерности пространства решений и структуры общего решения интервальных ДАУ и невозмущенной системы (0.1). Такие возмущения авторы назвали “сохраняющими внутреннюю структуру”.
Таким образом, в статье исследуется асимптотическая устойчивость интервального семейства
(0.2)
$({{A}_{0}} + \gamma {{\Delta }_{A}})x{\kern 1pt} '(t) + ({{B}_{0}} + \gamma {{\Delta }_{B}})x(t) = 0,\quad t \in T,$(0.3)
${\text{|}}{{\alpha }_{{i,j}}}{\text{|}} \leqslant {{g}_{{i,j}}},\quad {\text{|}}{{\beta }_{{i,j}}}{\text{|}} \leqslant {{h}_{{i,j}}},\quad i,j = \overline {1,n} ,$В литературе имеются результаты по робастной устойчивости и оценке радиуса устойчивости стационарных ДАУ [5–7], полученные посредством преобразования системы к канонической форме Кронекера–Вейерштрасса. В статье [8] обоснованы достаточные условия робастной устойчивости ДАУ произвольно высокого индекса неразрешенности в условиях, когда матрицы неопределенностей удовлетворяют некоторым условиям малости матричных норм. В [9–11] изучалась проблема робастной устойчивости ДАУ в случае, когда возмущение присутствует только в матрице B0.
Что касается нестационарных ДАУ, то известны результаты для систем индекса 1 с периодическими коэффициентами, использующие tractability index подход, базирующийся на построении проекторов на ядро [12, 13]. В [14] представлены необходимые и достаточные условия робастной устойчивости нестационарных ДАУ с интервальными коэффициентами для частного случая индекса один (так называемые impuls-free или удовлетворяющие критерию “ранг-степень”).
Для получения условий робастной устойчивости интервального семейства (0.2) в данной работе используется следующий подход. Сначала находятся достаточные условия того, что интервальные матрицы ΔA и ΔB не нарушают внутреннюю структуру ДАУ (0.1). Для этой цели привлекается структурная форма, которая эквивалентна исходной системе в смысле решений. Построение данной структурной формы, в отличие от канонической формы Кронекера–Вейерштрасса, носит конструктивный характер. Затем с применением известных результатов по робастной устойчивости систем обыкновенных дифференциальных уравнений, разрешенных относительно производной, получаются условия робастной устойчивости для преобразованной системы. Наконец, обосновывается эквивалентность в смысле решений преобразованного и исходного интервальных семейств. Таким образом, в предположениях, обеспечивающих сохранение структуры, найдены оценки для величины γ, определяющей размах неопределенностей, при выполнении которых система (0.2) робастной устойчива. В частности, условия робастной устойчивости получены в предположениии сверхустойчивости номинальной системы. Допускается произвольно высокий индекс неразрешенности.
1. Cтруктурная форма для системы ДАУ. Для ДАУ (0.1) определим $(n(r + 1) \times n)$-матрицы
(1.1)
${{\mathcal{B}}_{r}} = {\text{colon}}\left( {{{B}_{0}},O, \ldots ,O} \right),\quad {{\mathcal{A}}_{r}} = {\text{colon}}\left( {{{A}_{0}},{{B}_{0}},O, \ldots ,O} \right),$(1.2)
${{\Lambda }_{r}} = \left( {\begin{array}{*{20}{c}} O&O& \ldots &O&O \\ {{{A}_{0}}}&O& \ldots &O&O \\ {{{B}_{0}}}&{{{A}_{0}}}& \ldots &O&O \\ \vdots & \vdots & \ldots & \vdots & \vdots \\ O&O& \ldots &{{{A}_{0}}}&O \\ O&O& \ldots &{{{B}_{0}}}&{{{A}_{0}}} \end{array}} \right)$Предположим, что для некоторого $r(0 \leqslant r \leqslant n)$ в матрице ${{\mathcal{D}}_{r}}$ найдется неособенный минор $n(r + 1)$-го порядка, включающий в себя $\lambda = {\text{rank}}{{\Lambda }_{r}}$ столбцов матрицы ${{\Lambda }_{r}}$ и все столбцы матрицы ${{\mathcal{A}}_{r}}$. Такой минор будем называть разрешающим минором.
Введем обозначение
где Q – матрица перестановок столбцов11, такая, что все столбцы матрицы входят в разрешающий минор матрицы ${{\mathcal{D}}_{r}}$, а столбцы матрицы ${\text{colon}}\left( {{{B}_{1}},O, \ldots ,O} \right)$ не входят в этот минор. Блоки ${{B}_{2}}$ и ${{A}_{2}}$ имеют размеры $n \times d,$ $d = nr - \lambda $. О построении матрицы Q см. в [8].Обозначим
(1.5)
${{\Gamma }_{r}} = {{\mathcal{D}}_{r}}{\text{diag}}\left\{ {Q\left( {\begin{array}{*{20}{c}} O \\ {{{E}_{d}}} \end{array}} \right),Q, \ldots ,Q} \right\} = \left( {\left. {\begin{array}{*{20}{c}} {{{B}_{2}}} \\ O \\ O \\ \vdots \\ O \end{array}} \right|\left. {\begin{array}{*{20}{c}} {{{A}_{1}}}&{{{A}_{2}}} \\ {{{B}_{1}}}&{{{B}_{2}}} \\ O&O \\ \vdots & \vdots \\ O&O \end{array}} \right\|\begin{array}{*{20}{c}} O&O& \ldots &O&O \\ {{{A}_{1}}}&{{{A}_{2}}}& \ldots &O&O \\ {{{B}_{1}}}&{{{B}_{2}}}& \ldots &O&O \\ \vdots & \vdots & \ldots & \vdots & \vdots \\ O&O& \ldots &{{{A}_{1}}}&{{{A}_{2}}} \end{array}} \right),$Определение 1. Наименьшее значение r, при котором в матрице ${{\mathcal{D}}_{r}}$ найдется разрешающий минор, называется индексом неразрешенности ДАУ (0.1).
Замечание 1. В работе [8] показано, что в случае регулярного матричного пучка $c{{A}_{0}} + {{B}_{0}}$ в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор и выполняется условие
При этом индекс неразрешенности совпадает с индексом пучка.Лемма 1 [16]. Наличия разрешающего минора в матрице ${{\mathcal{D}}_{r}}$ необходимо и достаточно для существования оператора
(1.7)
$\mathcal{R} = {{R}_{0}} + {{R}_{1}}\frac{d}{{dt}} + \ldots + {{R}_{r}}\mathop {\left( {\frac{d}{{dt}}} \right)}\nolimits^r $(1.8)
$\tilde {A}\left( {\begin{array}{*{20}{c}} {x_{1}^{'}(t)} \\ {x_{2}^{'}(t)} \end{array}} \right) + \tilde {B}\left( {\begin{array}{*{20}{c}} {{{x}_{1}}(t)} \\ {{{x}_{2}}(t)} \end{array}} \right) = 0,$(1.9)
$\tilde {A} = \left( {\begin{array}{*{20}{c}} O&O \\ {{{E}_{{n - d}}}}&O \end{array}} \right) = \left( {{{R}_{0}}{{A}_{0}} + {{R}_{1}}{{B}_{0}}} \right)Q,\quad {{\tilde {B}}_{0}} = \left( {\begin{array}{*{20}{c}} {{{J}_{1}}}&{{{E}_{d}}} \\ {{{J}_{2}}}&O \end{array}} \right) = {{R}_{0}}{{B}_{0}}Q,$Прямым следствием леммы 1 является следующий результат.
Утверждение 1. Оператор вида (1.7), преобразующий ДАУ (0.1) к виду (1.8), (1.9), существует тогда и только тогда, когда относительно ${{R}_{0}},{{R}_{1}}, \ldots ,{{R}_{r}}$ разрешима алгебраическая система
(1.10)
$({{R}_{0}}\,\,{{R}_{1}}\,\, \ldots \,\,{{R}_{r}}){{\Gamma }_{r}} = \left( {{{E}_{n}}\,\,O\,\, \ldots \,\,O} \right),$Предположим, что в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор. Обозначим через Mr матрицу, определителем которой является этот минор. Покажем, что коэффициенты оператора (1.7) могут быть найдены по формуле
(1.11)
$({{R}_{0}}\,\,{{R}_{1}}\,\, \ldots \,\,{{R}_{r}}) = \left( {{{E}_{n}}\,\,O\,\, \ldots \,\,O} \right)M_{r}^{{ - 1}}.$Пусть ${{Q}_{\Lambda }}$ – матрица перестановок столбцов, такая, что
(1.12)
${{\Lambda }_{r}}{{\tilde {Q}}_{r}}{{Q}_{\Lambda }} = (\Lambda _{r}^{{[1]}}\,\,\Lambda _{r}^{{[2]}}).$Здесь и далее ${{\tilde {Q}}_{r}} = {\text{diag}}\{ Q, \ldots ,Q\} $ имеет на главной диагонали r блоков равных Q; $\Lambda _{r}^{{[1]}}$ – матрица размера $n(r + 1) \times \lambda $, состоящая из столбцов матрицы ${{\Lambda }_{r}}$, которые входят в разрешающий минор; $\Lambda _{r}^{{[2]}}$ – матрица размера $n(r + 1) \times (nr - \lambda )$, состоящая из столбцов, которые не входят в упомянутый минор.
Тогда
(1.13)
$M_{r}^{{ - 1}}{{\mathcal{D}}_{r}}{{\tilde {Q}}_{{r + 2}}}{\text{diag}}\{ {{E}_{{2n}}},{{Q}_{\Lambda }}\} = \left( {\left. {\begin{array}{*{20}{c}} {{{J}_{1}}}\vline & {{{E}_{d}}}OO \\ {{{J}_{2}}}\vline & O{{{E}_{{n - d}}}}O \\ \hline O\vline & OO{{{E}_{d}}} \\ O\vline & OOO \end{array} } \right\|\begin{array}{*{20}{c}} O{{{\Psi }_{1}}} \\ O{{{\Psi }_{2}}} \\ \hline O{{{\Psi }_{3}}} \\ {{{E}_{\lambda }}}{{{\Psi }_{4}}} \end{array} } \right),$Поскольку ${\text{rank}}{{\Lambda }_{r}} = \lambda $, то и ${\text{rank}}M_{r}^{{ - 1}}{{\Lambda }_{r}}\mathop {\tilde {Q}}\nolimits_r {{Q}_{\Lambda }} = \lambda $. На этом основании можно заключить, что ${{\Psi }_{1}} = O,$ ${{\Psi }_{2}} = O,$ ${{\Psi }_{3}} = O.$ Таким образом, коэффициенты оператора $\mathcal{R}$, вычисленные по формуле (1.11), будут решением системы (1.10).
Лемма 2 [8]. Пусть в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор и справедливо равенство (1.6). Тогда оператор $\mathcal{R}$ обладает левым обратным оператором $\mathcal{L} = {{L}_{0}} + {{L}_{1}}\tfrac{d}{{dt}}.$
Утверждение 2. Пусть в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор. Для того чтобы в матрице ${{\mathcal{D}}_{{r + 1}}}$ нашлась обратимая подматрица ${{M}_{{r + 1}}}$ порядка $n(r + 2)$, включающая в себя n + λ столбцов матрицы ${{\Lambda }_{{r + 1}}}$ и все столбцы матрицы $({{\mathcal{B}}_{{2,r + 1}}}\;{{\mathcal{A}}_{{r + 1}}})$ (см. (1.1), (1.3), (1.4)), необходимо и достаточно выполнения условия (1.6).
Доказательство вынесено в Приложение.
2. Возмущения, сохраняющие внутреннюю структуру системы. Пусть ДАУ (0.1) таковы, что в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор. Тогда, согласно леммам 1 и 2, существует оператор $\mathcal{R}$, который преобразует систему (0.1) к структурной форме (1.8), (1.9). Этот оператор имеет левый обратный оператор $\mathcal{L}$. Непосредственно из существования операторов $\mathcal{R}$ и $\mathcal{L}$ вытекает эквивалентность в смысле решений систем (0.1) и (1.8), (1.9).
Для того чтобы иметь возможность проводить анализ устойчивости ДАУ (0.2) c использованием информации о структуре и свойствах системы (1.8), (1.9), введем следующее определение.
Определение 2. Будем говорить, что возмущения $\gamma {{\Delta }_{A}}$ и $\gamma {{\Delta }_{B}}$, подчиняющиеся ограничениям (0.3), сохраняют внутреннюю структуру ДАУ (0.1), если при каждом фиксированном выборе матриц ${{\Delta }_{A}}$ и ${{\Delta }_{B}}$ существует оператор
(2.1)
$\tilde {\mathcal{R}} = \sum\limits_{j = 0}^r {{\tilde {R}}_{j}}\mathop {\left( {\frac{d}{{dt}}} \right)}\nolimits^j ,$(2.2)
$\left( {\begin{array}{*{20}{c}} O&O \\ {{{E}_{{n - d}}}}&O \end{array}} \right){{Q}^{{ - 1}}}x{\kern 1pt} '(t) + \left( {\begin{array}{*{20}{c}} {{{U}_{1}}}&{{{E}_{d}}} \\ {{{U}_{2}}}&O \end{array}} \right){{Q}^{{ - 1}}}x(t) = 0,$Найдем условия, при которых для системы (0.2) при каждом выборе возмущений ${{\Delta }_{A}}$ и ${{\Delta }_{B}}$ определен оператор $\tilde {\mathcal{R}}$.
Введем следующие обозначения:
(2.3)
$\left( {{{\Delta }_{{{{A}_{1}}}}}{{\Delta }_{{{{A}_{2}}}}}} \right) = {{\Delta }_{A}}Q,\quad \left( {{{\Delta }_{{{{B}_{1}}}}}{{\Delta }_{{{{B}_{2}}}}}} \right) = {{\Delta }_{B}}Q,$(2.4)
${{\Delta }_{{{{\Lambda }_{r}}}}} = \gamma \left( {\begin{array}{*{20}{c}} O&O& \ldots &O&{} \\ {{{\Delta }_{A}}}&O& \ldots &O&O \\ {{{\Delta }_{B}}}&{{{\Delta }_{A}}}& \ldots &O&O \\ \vdots & \vdots & \ldots & \vdots & \vdots \\ O&O& \ldots &{{{\Delta }_{B}}}&{{{\Delta }_{A}}} \end{array}} \right),$Разобьем ${{\Delta }_{{{{\Lambda }_{r}}}}}$ на блоки, аналогично тому, как это было сделано с матрицей Λr (см. (1.12)):
(2.5)
${{\Delta }_{{{{\Lambda }_{r}}}}}\mathop {\tilde {Q}}\nolimits_r {{Q}_{\Lambda }} = (\Delta _{\Lambda }^{{[1]}},\Delta _{\Lambda }^{{[2]}}).$Определим квадратную матрицу порядка $n(r + 1):$
(2.6)
${{\Delta }_{{{{M}_{r}}}}} = \left( {\left. {\begin{array}{*{20}{c}} {\gamma {{\Delta }_{{{{B}_{2}}}}}}&\vline & {\gamma {{\Delta }_{{{{A}_{1}}}}}}&{\gamma {{\Delta }_{{{{A}_{2}}}}}} \\ O&\vline & {\gamma {{\Delta }_{{{{B}_{1}}}}}}&{\gamma {{\Delta }_{{{{B}_{2}}}}}} \\ O&\vline & O&O \\ \vdots &\vline & \vdots & \vdots \\ O&\vline & O&O \end{array}} \right\|\Delta _{\Lambda }^{{[1]}}} \right),$Обозначим
где элементы матриц G и H задают масштабы изменения элементов матриц A0 и B0 (см. (0.3)).Утверждение 3. Пусть имеет место неравенство
(2.8)
$\gamma {\text{||}}F{\text{|}}{{{\text{|}}}_{1}} < \mathop {\frac{1}{{{\text{||}}M_{r}^{{ - 1}}{\text{||}}}}}\nolimits_1 ,$Тогда матрица ${{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}}$ обратима при любых матрицах неопределенностей ${{\Delta }_{A}} = \mathop {({{\alpha }_{{i,j}}})}\nolimits_{i,j = \overline {1,n} } $ и ${{\Delta }_{B}} = \mathop {({{\beta }_{{i,j}}})}\nolimits_{i,j = \overline {1,n} } ,$ элементы которых удовлетворяют неравенствам (0.3).
В самом деле [17, с. 142], матрица ${{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}}$ будет обратима, если имеет место оценка
(2.9)
${\text{||}}{{\Delta }_{{{{M}_{r}}}}}{\text{|}}{{{\text{|}}}_{1}} < \frac{1}{{{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}}}.$Легко видеть, что
(2.10)
${\text{||}}{{\Delta }_{{{{M}_{r}}}}}{\text{|}}{{{\text{|}}}_{1}} \leqslant \gamma {\text{||}}F{\text{|}}{{{\text{|}}}_{1}}.$Поэтому условие (2.8) гарантирует выполнение неравенства (2.9).
Теорема 1. Пусть в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор и выполняется условие (2.8). Для того чтобы при каждом фиксированном выборе возмущений ${{\Delta }_{A}}$ и ${{\Delta }_{B}}$, удовлетворяющих условиям (0.3), существовал оператор (2.1), преобразующий ДАУ (0.2) к виду (2.2), необходимо и достаточно выполнения равенства
(2.11)
$\left( {{{E}_{n}}\;O} \right)\mathop {({{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}})}\nolimits^{ - 1} \Delta _{\Lambda }^{{[2]}} = O,$(2.12)
$({{\tilde {R}}_{0}}\;{{\tilde {R}}_{1}}\;...\;{{\tilde {R}}_{r}}) = \left( {{{E}_{n}}\;O} \right)\mathop {\left( {{{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}}} \right)}\nolimits^{ - 1} .$Доказательство теоремы приведено в Приложении.
Поскольку в общем случае проверить равенство (2.11) не представляется возможным, найдем достаточные условия существования оператора $\tilde {\mathcal{R}}$.
Лемма 3. Пусть в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор и выполняется условие (2.8). И кроме того, при каждом выборе матриц ΔA и ΔB, подчиняющихся ограничениям (0.3),
(2.13)
$\left( {{{E}_{{n + d}}}\;{{O}_{\lambda }}} \right)M_{r}^{{ - 1}}\Delta _{\Lambda }^{{[2]}} = O$(2.14)
$M_{r}^{{ - 1}}{{\Delta }_{{{{M}_{r}}}}} = \left( {\begin{array}{*{20}{c}} * &O \\ * & * \end{array}} \right),$(2.15)
$\left( {{{E}_{{n + d}}}\;O} \right)\mathop {({{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}})}\nolimits^{ - 1} \Delta _{\Lambda }^{{[2]}} = O.$Доказательство леммы вынесено в Приложение.
Замечание 2. Очевидно, что предположения леммы 3 обеспечивают выполнение условия (2.11) и, следовательно, гарантируют существование оператора $\tilde {\mathcal{R}}$, преобразующего ДАУ (0.2) к виду (2.2). С другой стороны, условие (2.15) выглядит избыточным. Тем не менее, именно ограничение вида (2.15) потребуется в дальнейшем для того, чтобы обосновать левую обратимость оператора (2.1) и, в конечном итоге, доказать эквивалентность в смысле решений систем (0.2) и (2.2).
Теорема 2. Пусть:
1) в матрице ${{\mathcal{D}}_{r}}$ имеется разрешающий минор;
2) справедливо равенство (1.6);
3) для всех матриц ${{\Delta }_{A}}$ и ${{\Delta }_{B}}$, элементы которых подчиняются условиям (0.3), выполняются условия (2.13) и (2.14).
Если, кроме того,
(2.16)
$\gamma {\text{||}}F{\text{|}}{{{\text{|}}}_{1}} < \mathop {\frac{1}{{{\text{||}}M_{{r + 1}}^{{ - 1}}{\text{||}}}}}\nolimits_1 ,$Доказательство теоремы приведено в Приложении.
3. Достаточные условия робастной устойчивости ДАУ. В этом разделе в предположениях, обеспечивающих сохранение структуры, получены достаточные условия робастной устойчивости ДАУ.
Опираясь на результаты теоремы 1 и леммы 3, можно дать корректное определение рассматриваемого интервального семейства. В системе (0.2) матрицы возмущений должны подчиняться оценкам (0.3) и удовлетворять равенству (2.11), другими словами, обеспечивать существование оператора (2.1), преобразующего ДАУ (0.2) к виду (2.2). В частности, условие (2.11) выполнено, если имеют место алгебраические связи (2.13) и (2.14). Поскольку основные результаты работы получены в рамках предположений (2.13), (2.14), то можно сформулировать следующее определение.
Определение 3. В предположениях теоремы 1 под интервальным семейством ДАУ будем понимать систему (0.2), в которой матрицы возмущений ΔA и ΔB подчиняются оценкам (0.3) и удовлетворяют алгебраическим соотношениям (2.13) и (2.14).
Определение 4. Решением ДАУ (0.1) будем называть n-мерную вектор-функцию ${{x}_{*}}(t) \in {{{\mathbf{C}}}^{1}}(T)$, обращающую систему (0.1) в тождество при подстановке.
При каждом выборе возмущений ΔA и ΔB из рассматриваемого интервального семейства решение системы (0.2) будем понимать в смысле определения 4.
Замечание 3. В предположениях леммы 2 системы (0.1) и (1.8), (1.9) имеют одно и то же множество решений и, следовательно, обладают одними и теми же свойствами устойчивости. Пусть дифференциальная подсистема ДАУ (1.8), (1.9)
асимптотически устойчива, т.е. любое решение ${{x}_{1}}(t)$ этой системы обладает свойством ${\text{||}}{{x}_{1}}(t){\text{||}} \to 0,$ $t \to + \infty $. В свою очередь любое решение алгебраической подсистемы ДАУ (1.8) находится по формуле ${{x}_{2}}(t) = - {{J}_{1}}{{x}_{1}}(t)$ и, следовательно, ${\text{||}}{{x}_{2}}(t){\text{||}} \to 0$ при $t \to + \infty $. Поэтому будем называть систему (1.8), (1.9) и ДАУ (0.1) асимптотически устойчивыми, если этим свойством обладает система (3.1).Замечание 4. В предположениях теоремы 2 можно провести аналогичные рассуждения в отношении систем (0.2) и (2.2) при каждом выборе возмущений ΔA и ΔB из рассматриваемого интервального семейства. Так что будем называть интервальные семейства (0.2) и (2.2) асимптотически устойчивыми, если этим же свойством обладает каждая система из интервального семейства
В условиях теоремы 2 при каждом выборе матриц ΔA и ΔB для ДАУ (0.2) определен оператор $\tilde {R}$ (2.1), который преобразует (0.2) к виду (2.2). Коэффициенты этого оператора вычисляются по формуле (2.12). По построению в (2.2)
С учетом (2.12) можно получить представление
где(3.4)
$\begin{gathered} {{\Delta }_{{{{U}_{2}}}}} = ({{O}_{d}}{{E}_{{n - d}}}{{O}_{{nr}}})(\mathop {({{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}})}\nolimits^{ - 1} - M_{r}^{{ - 1}})\left( {\begin{array}{*{20}{c}} {{{B}_{1}}} \\ O \end{array}} \right) + \gamma ({{O}_{d}}{{E}_{{n - d}}}{{O}_{{nr}}})\mathop {({{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}})}\nolimits^{ - 1} \left( {\begin{array}{*{20}{c}} {{{\Delta }_{{{{B}_{1}}}}}} \\ O \end{array}} \right), \\ {{J}_{2}} = ({{O}_{d}}\;{{E}_{{n - d}}}){{R}_{0}}{{B}_{1}} \\ \end{gathered} $Определение 5. В условиях теоремы 2 будем говорить, что интервальное семейство (0.2) робастно устойчиво, если каждая система из интервального семейства (3.2)–(3.4) асимптотически устойчива.
Определим величины
где $j = \sqrt { - 1} $ – мнимая единица, $\omega $ – вещественный параметр, ${{\xi }_{1}}$ – наименьшее сингулярное число матрицы $j\omega {{E}_{{n - d}}} + {{J}_{2}}$, иПредположим, что все собственные числа матрицы J2 имеют положительные вещественные части, т.е.
(3.5)
$\mathop {min}\limits_{1 \leqslant i \leqslant n - d} {\text{Re}}{{\eta }_{i}}({{J}_{2}}) > 0.$Известно [18, с. 201–203], что в этом случае семейство ДАУ (3.2), (3.3) будет асимптотически устойчиво, если
илиЗаметим, что несмотря на то, что $\mu ({{J}_{2}}) \geqslant \nu ({{J}_{2}})$, условие (3.6) значительно проще для проверки, чем условие (3.7). Здесь и далее ||S||2 – спектральная норма матрицы:
Матрицу H, определяющую масштаб изменения элементов матрицы B0 (см. (0.3)), разобьем на блоки аналогично тому, как это было сделано в отношении матрицы $B$ (см. (1.3)):
где блок H1 имеет размер $n \times (n - d)$.Определим величину
(3.9)
$\theta = {\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}{\text{||}}F{\text{|}}{{{\text{|}}}_{1}}{\text{||}}{{B}_{1}}{\text{|}}{{{\text{|}}}_{1}}\; + \;{\text{||}}{{H}_{1}}{\text{|}}{{{\text{|}}}_{1}},$В соответствии с замечанием 4 интервальное семейство (2.2) будет асимптотически устойчиво тогда и только тогда, когда этим же свойством обладает семейство (3.2).
Перейдем к получению условий робастной устойчивости.
При доказательстве теоремы 2 показано, что предположение (2.16) влечет за собой оценку (2.9). В этом случае [17, с. 142]
(3.10)
${\text{||}}\mathop {\left( {{{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}}} \right)}\nolimits^{ - 1} - M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}} \leqslant \frac{{{\text{||}}M_{r}^{{ - 1}}{\text{||}}_{1}^{2}{\text{||}}{{\Delta }_{{{{M}_{r}}}}}{\text{|}}{{{\text{|}}}_{1}}}}{{1\; - \;{\text{||}}{{\Delta }_{{{{M}_{r}}}}}{\text{|}}{{{\text{|}}}_{1}}{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}}},$(3.11)
${\text{||}}\mathop {\left( {{{M}_{r}} + {{\Delta }_{{{{M}_{r}}}}}} \right)}\nolimits^{ - 1} {\text{|}}{{{\text{|}}}_{1}} \leqslant \frac{{{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}}}{{1\; - \;{\text{||}}{{\Delta }_{{{{M}_{r}}}}}{\text{|}}{{{\text{|}}}_{1}}{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}}}.$Из представления (3.4) и оценок (3.10) и (3.11) получим
Это неравенство можно усилить, воспользовавшись тем, что ${\text{||}}{{\Delta }_{{{{B}_{1}}}}}{\text{|}}{{{\text{|}}}_{1}} \leqslant \gamma {\text{||}}{{H}_{1}}{\text{|}}{{{\text{|}}}_{1}}$, условием (2.10) и обозначением (3.9):
(3.12)
${\text{||}}{{\Delta }_{{{{U}_{2}}}}}{\text{|}}{{{\text{|}}}_{1}} \leqslant \frac{{\gamma {\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}\theta }}{{1 - \gamma {\text{||}}F{\text{|}}{{{\text{|}}}_{1}}{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}}}.$Заметим, что в силу (2.8)
(3.13)
$1 - \gamma {\text{||}}F{\text{|}}{{{\text{|}}}_{1}}{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}} > 0.$С учетом известного соотношения между нормами ${\text{||}}{{\Delta }_{{{{U}_{2}}}}}{\text{|}}{{{\text{|}}}_{2}} \leqslant \sqrt {n - d} {\text{||}}{{\Delta }_{{{{U}_{2}}}}}{\text{|}}{{{\text{|}}}_{1}}$ условие (3.6) будет выполнено, если
Из последнего неравенства получаем оценку
(3.14)
$\gamma \leqslant \frac{{\nu ({{J}_{2}})}}{{{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}(\sqrt {n - d} \theta \; + \;{\text{||}}F{\text{|}}{{{\text{|}}}_{1}}\nu ({{J}_{2}}))}}.$Таким образом, имеет место следующий результат.
Теорема 3. Пусть выполнены все предположения теоремы 2, а также условия (3.5) и (3.14). Тогда система ДАУ (0.2) будет робастно устойчива.
Замечание 5. В условии (3.14) величину $\nu ({{J}_{2}})$ можно заменить на $\mu ({{J}_{2}})$. Возрастет или уменьшится выражение, стоящее в правой части неравенства (3.14), в общем случае установить невозможно.
4. Робастная устойчивость с использованием свойства сверхустойчивости номинальных ДАУ. В данном разделе с использованием свойства сверхустойчивости системы (0.1) получены достаточные условия робастной устойчивости интервальных ДАУ (0.2).
В работах [19, 20] обоснованы оценки радиуса сверхустойчивости для систем с интервальными коэффициентами, разрешенных относительно производной. К сожалению, получить такой же изящный результат для интервальных ДАУ невозможно, поскольку построение для системы (0.2) структурной формы (2.2), эквивалентной ей в смысле решений, связано с обращением интервальной матрицы.
Для матрицы ${{J}_{2}} = \mathop {({{\zeta }_{{i,j}}})}\nolimits_{i,j = \overline {1,n - d} } $ из (3.1) определим величину
Система (3.1) называется cверхустойчивой [18, с. 199], если
Если система сверхустойчива, то она будет асимптотически устойчива.
Нетрудно показать, что в предположениях леммы 2 система (0.1) будет асимптотически устойчива, если сверхустойчива система (3.1), т.е. если имеет место неравенство (4.1).
Как отмечалось выше, в условиях теоремы 2 интервальные семейства (0.2) и (2.2) обладают одними и теми же свойствами устойчивости. Легко видеть, что ДАУ (0.2) будут асимптотически устойчивы, если сверхустойчива интервальная система (3.2). Последнее имеет место в случае, когда для всех матриц из анализируемого интервального семейства справедливо неравенство
Найдем достаточные условия выполнения оценки (4.2). Для этого воспользуемся представлением (3.3), где ${{\Delta }_{{{{U}_{2}}}}} = \mathop {({{\delta }_{{i,j}}})}\nolimits_{i,j = \overline {1,n - d} } $ – интервальная матрица. Тогда
Рассмотрим сумму
По построению нулевая матрица принадлежит интервальному семейству ${{\Delta }_{{{{U}_{2}}}}}$, поэтому минимальное значение ${{\delta }_{{i,i}}}\; + \;{\text{|}}{{\delta }_{{i,i}}}{\text{|}}$ по всем $i = \overline {1,n - d} $ и по всем матрицам из представленного интервального семейства равно нулю. Используя этот факт и неравенство (3.12), получим
Очевидно, что интервальное семейство ДАУ (3.2) будет сверхустойчиво, если
(4.3)
$\gamma < \frac{{\sigma ({{J}_{2}})}}{{{\text{||}}M_{r}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}}\left( {\theta \; + \;{\text{||}}F{\text{|}}{{{\text{|}}}_{1}}\sigma ({{J}_{2}})} \right)}}.$Из приведенных выше рассуждений вытекает справедливость следующей теоремы.
Теорема 4. Пусть выполнены все предположения теоремы 2 и условие (4.1). Интервальное семейство ДАУ (0.2) будет робастно устойчиво, если выполняется неравенство (4.3).
5. Иллюстрирующий пример. Для простоты рассмотрим систему индекса 1:
(5.1)
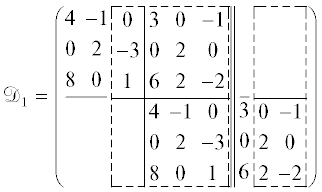
$\left( {\begin{array}{*{20}{c}} 3&0&{ - 1} \\ 0&2&0 \\ 6&2&{ - 2} \end{array}} \right)x{\kern 1pt} '(t) + \left( {\begin{array}{*{20}{c}} 4&{ - 1}&0 \\ 0&2&{ - 3} \\ 8&0&1 \end{array}} \right)x(t) = 0.$Начнем с предположений теоремы 2. В матрице
пунктирной линией выделены столбцы матрицы M1, определителем которой является разрешающий минор. При этом r = 1, d = 1, $Q = {{E}_{3}}$, ${\text{rank}}{{\Lambda }_{1}} = \lambda = 2.$ Используя явный вид матрицы Λ2, нетрудно вычислить ${\text{rank}}{{\Lambda }_{2}}$ = 5. Следовательно, условие (1.6) выполнено.Оператор
Поскольку
(5.2)
${{\alpha }_{{3,1}}} = 2{{\alpha }_{{1,1}}} + {{\alpha }_{{2,1}}}\quad \forall {{\alpha }_{{1,1}}},{{\alpha }_{{2,1}}}{\kern 1pt} :\;{\text{|}}{{\alpha }_{{1,1}}}{\text{|}} \leqslant {{g}_{{1,1}}},\quad {\text{|}}{{\alpha }_{{2,1}}}{\text{|}} \leqslant {{g}_{{2,1}}}$В свою очередь (2.14) означает, что
(5.4)
${{\alpha }_{{3,k}}} = 2{{\alpha }_{{1,k}}} + {{\alpha }_{{2,k}}}\quad \forall {{\alpha }_{{1,k}}},{{\alpha }_{{2,k}}}{\kern 1pt} :\;{\text{|}}{{\alpha }_{{1,k}}}{\text{|}} \leqslant {{g}_{{1,k}}},\quad {\text{|}}{{\alpha }_{{2,k}}}{\text{|}} \leqslant {{g}_{{2,k}}}$Условия (5.2) и (5.4) задают структуру матрицы ΔA:
(5.6)
${{\Delta }_{A}} = \left( {\begin{array}{*{20}{c}} {{{\alpha }_{{1,1}}}}&{{{\alpha }_{{1,2}}}}&{{{\alpha }_{{1,3}}}} \\ {{{\alpha }_{{2,1}}}}&{{{\alpha }_{{2,2}}}}&{{{\alpha }_{{2,3}}}} \\ {2{{\alpha }_{{1,1}}} + {{\alpha }_{{2,1}}}}&{2{{\alpha }_{{1,2}}} + {{\alpha }_{{2,2}}}}&{2{{\alpha }_{{1,3}}} + {{\alpha }_{{2,3}}}} \end{array}} \right),$(5.7)
$G = \left( {\begin{array}{*{20}{c}} {{{g}_{{1,1}}}}&{{{g}_{{1,2}}}}&{{{g}_{{1,3}}}} \\ {{{g}_{{2,1}}}}&{{{g}_{{2,2}}}}&{{{g}_{{2,3}}}} \\ {2{{g}_{{1,1}}} + {{g}_{{2,1}}}}&{2{{g}_{{1,2}}} + {{g}_{{2,2}}}}&{2{{g}_{{1,3}}} + {{g}_{{2,3}}}} \end{array}} \right).$Пусть для простоты элементы матриц G и H, определяющих масштабы изменения элементов матриц A0 и B0, ${{g}_{{i,j}}} = g = {\text{const}}$ ($i = \{ 1,2\} ,j = \{ 1,2,3\} $) ${{h}_{{i,j}}} = h = {\text{const}}$ ($i,j = \{ 1,2,3\} $). Тогда (см. (2.7) и (3.8)) ${\text{||}}F{\text{|}}{{{\text{|}}}_{1}} = 9g + 3h,$ ${\text{||}}{{H}_{1}}{\text{|}}{{{\text{|}}}_{1}} = 2h.$
Матрицу $M_{2}^{{ - 1}}$ по причине громоздкости выписывать не будем, но найдем
и оценка (2.16) принимает видВ частности, $\gamma < 0.059$ при $g = h = 0.5.$
Таким образом, для того чтобы возмущения системы (0.2) сохраняли структуру ДАУ (0.1) (другими словами, чтобы существовал оператор (2.1), преобразующий (0.2) в семейство (2.2), имеющее то же множество решений, что и система (0.2)), требуется, чтобы матрицы ΔA и G имели вид (5.6), (5.7), а размах неопределенностей удовлетворял неравенству (5.8).
Обратимся к условиям робастной устойчивости.
Легко видеть, что предположение (3.5) теоремы 3 имеет место. С учетом того, что ${\text{||}}{{B}_{1}}{\text{|}}{{{\text{|}}}_{1}} = 8$, ${\text{||}}M_{1}^{{ - 1}}{\text{|}}{{{\text{|}}}_{1}} = \frac{{59}}{{12}}$, в сделанных допущениях в соответствии с (3.9)
Несложно вычислить $\nu ({{J}_{2}}) = \frac{{2\sqrt 2 }}{3},$ поэтому условие (3.14) можно записать как
Итак, в условиях сохранения структуры по теореме 3 каждая система из семейства (0.2) будет асимптотически устойчива, если размах неопределенностей удовлетворяет условию (5.9). В частности, $\gamma \leqslant 0.00056$ при $g = h = 0.5.$ Если же возмущения матрицы A0 отсутствуют (g = 0), то $\gamma \leqslant 0.002.$
Рассмотрим предположения (4.1) и (4.3) теоремы 4. Очевидно, что $\sigma ({{J}_{2}}) = 1 > 0$, т.е. (4.1) имеет место. Оценка (4.3) в данном случае приобретает форму
В соответствии с утверждением теоремы 4 в том случае, если возмущения не нарушают структуру рассматриваемой системы, для асимптотической устойчивости семейства ДАУ (0.2) необходимо выполнение условия (5.10). В частности, $\gamma < 0.0008$ при $g = h = 0.5.$ В случае, когда g = 0, $\gamma \leqslant 0.003.$
Заключение. В работе получены достаточные условия, при которых интервальное семейство ДАУ имеет ту же структуру общего решения, что и номинальная система. Для интервальных ДАУ построена структурная форма, имеющая то же множество решений, что и исходное семейство. В предположениях, обеспечивающих сохранение структуры, найдены условия робастной устойчивости для ДАУ произвольно высокого индекса неразрешенности, у которых неопределенность присутствует не только в матрице при $x(t)$, но и в матрице при производной.
Список литературы
Бояринцев Ю.Е. Регулярные и сингулярные системы линейных обыкновенных дифференциальных уравнений. Новосибирск: Наука, 1980.
Серов Е.П., Корольков Б.П. Динамика парогенератора. М.: Энергоиздат, 1981.
Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем. М.: Радио и связь, 1988.
Коновалов А.Н. Задачи фильтрации многофазной несжимаемой жидкости. Новосибирск: Наука, 1988.
Byers R., Nichols N.K. On the Stability Radius of a Generalized State-space System // Linear Algebra Appl. 1993. № 188–189. P. 113–134.
Du N.H. Stability Radii of Differential-algebraic Equations with Structured Perturbations // Syst. Control Lett. 2008. № 57. P. 546–553.
Du N.H., Thuan D.D., Liem N.C. Stability Radius of Implicit Dynamic Equations with Constant Coefficients on Time Scales // Syst. Control Lett. 2011. № 60. P. 596–603.
Щеглова А.А., Кононов А.Д. Робастная устойчивость дифференциально-алгебраических уравнений произвольного индекса // АиТ. 2017. № 5. С. 36–55.
Fang C.-H., Chang F.-R. Analysis of Stability Robustness for Generalized State-space Systems with Structured Perturbations // Systems Control Lett. 1993. № 21. P. 109–114.
Lee L., Fang C.-H., Hsieh J.-G. Exact Uninderectional Perturbation Bounds for Robustness of Uncertain Generalized State-space Systems: Continuous-time Cases // Automatica. 1997. № 33. P. 1923–1927.
Qiu L., Davisov E.J. The Stability Robustness of Generalized Eigenvalues // IEEE Trans. Automat. Control. 1992. № 37. P. 886–891.
Du N.H., Linh V.H. Stability Radii for Linear Time-varying Differential-algebraic Equations with Respect to Dynamics Perturbations // J. Differ. Equat. 2006. № 230. P. 579–599.
Chyan C.J., Du N.H., Linh V.H. On Data-dependence of Exponential Stability and the Stability Radii for Linear Time-varying Differential-algebraic Systems // J. Differ. Equat. 2008. № 245. P. 2078–2102.
Lin Ch., Lam J., Wang J., Yang G.-H. Analysis on Robust Stability for Interval Descriptor Systems // System & Control Letters. 2001. № 42. P. 267–278.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1988.
Щеглова А.А. Преобразование линейной алгебро-дифференциальной системы к эквивалентной форме // Тр. IX Междунар. Четаевской конф. “Аналитическая механика, устойчивость и управление движением”. Иркутск, 2007. Т. 5. С. 298–307.
Треногин В.А. Функциональный анализ. М.: Наука, 1980.
Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука, 2002.
Поляк Б.Т., Щербаков П.С. Сверхустойчивые линейные системы управления I // АиТ. 2002. № 8. С. 37–53.
Поляк Б.Т., Щербаков П.С. Сверхустойчивые линейные системы управления II // АиТ. 2002. № 11. С. 56–75.
Ланкастер П. Теория матриц. М.: Наука, 1978.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления