Известия РАН. Теория и системы управления, 2021, № 1, стр. 24-29

0. Введение. Усложнение законов взаимного пространственного перемещения летательных аппаратов (ЛА) в процессе их противоборства, обусловленное в том числе и применением сверхманевренных (СМЛА) и гиперзвуковых (ГЗЛА) летательных аппаратов, приводит к необходимости ужесточения требований к устойчивости и точности их автоматического сопровождения.

Следящие измерители, обеспечивающие автоматическое сопровождение воздушных объектов по дальности, угловым координатам и их производным [1], являются основой информационного обеспечения существующих систем наведения [2]. Следует подчеркнуть, что от точности и устойчивости функционирования систем автоматического сопровождения во многом зависит результативность наведения. В связи с этим задача улучшения точности и устойчивости систем автоматического сопровождения, расширения поля условий их функционирования является весьма востребованной.

Анализ следящих измерителей позволяет выделить три особенности их функционирования, определяющие решение этой задачи.

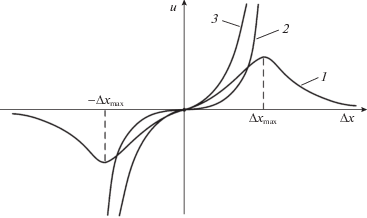
Первая связана с тем, что следящие измерители имеют ограниченную рабочую область, определяемую почти линейным участком дискриминационных характеристик [1]. Типовой вид такой характеристики для ошибки сопровождения Δx обобщенной координаты $x$ отображается на рис. 1 кривой 1, где $u$ – сигнал управления, $\left[ { - \Delta {{x}_{{{\text{max}}}}},\;\Delta {{x}_{{{\text{max}}}}}} \right]$ – рабочая зона.

Вторая особенность состоит в том, что ошибки сопровождения определяются соответствием (несоответствием) номера производной отслеживаемой координаты $x$ порядку астатизма следящей системы [3]. Если в законе изменения $x$ содержатся производные, номер которых превышает порядок астатизма следящей системы, то это приводит к нарастанию текущей ошибки Δx, выходу ее за пределы рабочего участка $ \pm \Delta {{x}_{{{\text{max}}}}}$, замене отрицательной обратной связи на положительную и срыву сопровождения.

В свою очередь в законах изменения пространственного положения СМЛА и ГЗЛА могут содержаться производные высоких порядков, особенно при движении по квазисинусоидальным траекториям.

Решить проблему сопровождения таких целей на базе классической теории оптимального управления удается с помощью линейных законов управления, содержащих старшие производные ошибки [4, 5]:

Однако присутствие в реальных задачах случайных погрешностей измерений требует в этом случае формирования оптимальных оценок этих старших производных (особенно по угловым координатам), что является отнюдь нетривиальной задачей и приводит к увеличению инерционности измерителей [5].

Решить задачу повышения устойчивости процедуры сопровождения можно, если применить кубическую зависимость управления от ошибок слежения:

показанную на рис. 1 кривой 2. Вместе с тем использование закона (0.2), предотвращая выход ошибок сопровождения за пределы рабочего участка $ \pm \Delta {{x}_{{{\text{max}}}}}$, приводит к снижению чувствительности управляющего напряжения $u$ к малым ошибкам Δx и соответственно к ухудшению точности сопровождения в установившемся режиме.

В связи с этим более рациональным является применение линейно-кубической зависимости

показанной на рис. 1 кривой 3. Однако для того, чтобы получить такую зависимость, необходимо в качестве минимизируемых использовать квадратично-биквадратные функционалы качества [4].

Третья особенность связана с тем, что время окончания сопровождения заранее не известно. При этом к следящему измерителю не предъявляется особых требований к точности сопровождения на различных временных участках работы. В рабочем диапазоне изменения дальности, угловых координат и их производных он должен обеспечивать примерно одинаковую точность в течение всего времени сопровождения. Эта особенность предопределяет целесообразность использования для синтеза процедур локальной оптимизации [6], обеспечивающей минимум выбранных функционалов качества в каждый текущий момент времени.

Цель статьи – на примере следящего угломера продемонстрировать эффективность реализуемого на практике многомерного варианта подобного (0.3) закона оптимального управления. В отличие от подобного примера из [6] здесь не ставится задача учета несоответствия динамических свойств цели и угломера, что приводит к более простому функционалу качества управления.

В первой части статьи кратко излагаются теоретические основы используемого метода [6] и демонстрируется процесс получения оптимального закона управления следящим угломером, тогда как во второй части будут приведены подробные результаты имитационного моделирования созданной системы.

При этом задача синтеза решается в детерминированной постановке. Влияние же небольших случайных воздействий на объект и измеритель его состояния компенсируется заменой в полученном законе управления значений переменных состояния на их калмановские оценки. И хотя из-за нелинейности закона управления (0.3) получаемый таким образом стохастический регулятор является лишь субоптимальным, он оказывается вполне работоспособным.

1. Постановка задачи. Пусть управляемый линейный объект, n-мерный вектор состояния ${{{\mathbf{x}}}_{{\text{у}}}}$ которого определяется уравнением

должен отслеживать требуемую траекторию ${{{\mathbf{x}}}_{{\text{т}}}}(t)$, заданную уравнением

Здесь $t$ – текущее время; ${{{\mathbf{F}}}_{{\text{у}}}}$ и ${{{\mathbf{F}}}_{{\text{т}}}}$ – матрицы внутренних связей процессов (1.1) и (1.2); ${{{\mathbf{B}}}_{{\text{у}}}}$ – матрица усиления r-мерного ($r \leqslant n$) сигнала управления ${\mathbf{u}}$; ${{{\mathbf{B}}}_{{\text{т}}}}$ и ${\mathbf{v}}$ – коэффициент передачи и управляющее воздействие системы (1.2), а подстрочные индексы “y” и “т” соответствуют управляемым и требуемым траекториям.

Цель управления состоит в обеспечении малости ошибки слежения

поэтому вектор ${\mathbf{u}}$ сигналов управления будем искать из условия локальной оптимизации изменяющегося во времени квадратично-биквадратного функционала качества, штрафующего большие значения элементов векторов $\Delta {\mathbf{x}}$ и управления ${\mathbf{u}}$: в котором ${\mathbf{K}} = {{{\mathbf{K}}}^{{\text{т}}}} > 0$ – положительно-определенная матрица штрафов за величину сигнала управления, ${\mathbf{Q}} = {{{\mathbf{Q}}}^{{\text{т}}}} \geqslant 0$ и ${\mathbf{P}} = {{{\mathbf{P}}}^{{\text{т}}}} \geqslant 0$ – неотрицательно-определенные матрицы квадратичных и биквадратных штрафов за величину ошибки слежения Δx соответственно.

2. Решение задачи. Получение локально-оптимального закона управления сводится [6] к минимизации по переменной u производной по времени функционала (1.4). Используя правила нахождения полной производной сложной функции и определенного интеграла от нее по его переменному верхнему пределу

а также формулы дифференцирования квадратичной и биквадратной форм в которых ∇_x – оператор градиента, приходим к соотношению где в соответствии с (1.1) и (1.2)

Здесь и далее для простоты опущена зависимость векторов и матриц от времени.

Учитывая в (2.3) формулу (2.4) для производной $\Delta {\mathbf{\dot {x}}}$, получаем минимизируемую по u квадратичную функцию

где C – не зависящая от u группа слагаемых:

Управление, минимизирующее выпуклую функцию (2.5), найдем, приравняв нулю ее градиент по u:

Решая данное линейное матричное уравнение, получаем искомый локально-оптимальный закон позиционного управления

Из выражения (2.6) следует, что сигнал управления содержит два слагаемых разных степеней относительно ошибки $\Delta {\mathbf{x}}$. Первое слагаемое ${{{\mathbf{K}}}^{{ - 1}}}{\mathbf{B}}_{{\text{у}}}^{{\text{т}}}{\mathbf{Q}}\Delta {\mathbf{x}}$ задает его линейную составляющую, а второе $2{{{\mathbf{K}}}^{{ - 1}}}{\mathbf{B}}_{{\text{у}}}^{{\text{т}}}(\Delta {{{\mathbf{x}}}^{{\text{т}}}}{\mathbf{P}}\Delta {\mathbf{x}}){\mathbf{P}}\Delta {\mathbf{x}}$ – кубическую составляющую. Также видно, что сигнал управления явно зависит от матрицы его усиления ${{{\mathbf{B}}}_{{\text{у}}}}$ системой управления (1.1) и матрицы K штрафов на величину сигналов управления, а весовые соотношения между линейной и кубической составляющими определяются элементами матриц Q и P штрафов квадратичного по Δx и биквадратного слагаемых целевого функционала (1.4).

Очевидно, что при малых ошибках Δx кубическая составляющая практически не влияет на величину сигнала управления (2.7), обеспечивая высокую линейную чувствительность к ним системы управления (рис. 1, кривая 3). Однако при больших ошибках Δx превалирующей становится кубическая составляющая, которая обеспечивает их энергичную отработку.

3. Пример. Исследование работоспособности предложенного алгоритма проведем на примере синтеза следящего радиолокационного угломера [1]. Пусть он имеет типовой привод антенны:

который предназначен для отработки пространственных перемещений цели в горизонтальной плоскости, определяемых кинематическим звеном:

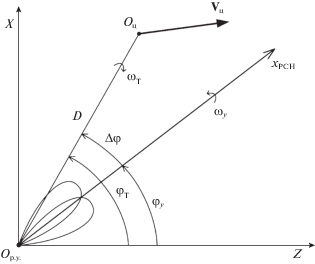
Здесь ${{\varphi }_{{\text{т}}}}$, ${{\varphi }_{{\text{у}}}}$ – бортовой пеленг сопровождаемого объекта и угол поворота антенны; ${{\omega }_{{\text{т}}}}$, ${{\omega }_{{\text{у}}}}$ – угловые скорости линии визирования и поворота антенны; T, $b$ – постоянная времени и коэффициент передачи угломера; ${{j}_{{\text{т}}}}$ – поперечное ускорение сопровождаемого объекта; D, $\dot {D}$ – дальность до цели и скорость ее изменения. Отметим, что, манипулируя в (3.2) законом изменения ускорения объекта ${{j}_{{\text{т}}}}$, можно реализовать изменение пространственного положения цели практически любой сложности.

Геометрические соотношения между координатами состояния показаны на рис. 2, где ${{O}_{{{\text{р}}{\text{.у}}{\text{.}}}}}$ и ${{O}_{{\text{ц}}}}$ – точки расположения радиолокационного угломера и цели, ${{{\mathbf{V}}}_{{\text{ц}}}}$ – вектор скорости цели, ${{x}_{{{\text{РСН}}}}}$ – положение равносигнального направления (РСН) в горизонтальной плоскости, определяющее величину ${{\varphi }_{{\text{у}}}}$.

Задача синтеза сигнала управления угломером (3.1) формулируется следующим образом. Необходимо сформировать сигнал управления ${{u}_{{\text{у}}}}$, оптимальный в смысле минимума квадратично-биквадратного функционала:

где $\Delta \varphi $, $\Delta \omega $ – ошибки слежения за углом и угловой скоростью:

Для решения этой задачи используем теоретические результаты, приведенные в разд. 1 и 2. Поставив соотношения (3.1), (3.2) в соответствие с (1.1), (1.2), а (3.3) – с (1.4), получаем, что в данном примере

Тогда на основе (2.6) находим матричную форму записи искомого скалярного закона управления:

В результате преобразований получаем

откуда имеем

Приводя здесь подобные члены, окончательно находим линейно-кубический закон управления

с коэффициентами

Заключение. Анализ соотношений (3.4), (3.5) позволяет сделать следующие выводы. Следящий угломер представляет многоконтурную систему с обратными связями по углу и угловой скорости. Сигнал управления зависит не только от значений ошибок $\Delta \varphi $ и $\Delta \omega $, но и от их кубов $\Delta {{\varphi }^{3}}$ и $\Delta {{\omega }^{3}}$, а также от смешанных произведений $\Delta {{\varphi }^{2}}\Delta \omega $ и $\Delta \varphi \Delta {{\omega }^{2}}$. Для получения сигнала управления не требуется знания старших производных угловых скоростей, а достаточно иметь бортовой пеленг, угловую скорость линии визирования, угол поворота антенны и скорость его изменения, что не накладывает ограничений на возможность формирования управления.

Полагая в (1.4) и (3.3) матрицу P диагональной, можно найти более простой вариант формирования сигнала управления. В свою очередь, манипулируя в функционале качества видом всего биквадратного члена, можно получить большое число различных видов управлений с другой степенью зависимости и связи линейных и нелинейных составляющих сигналов управления.

Более полные выводы о возможностях закона управления (3.4), (3.5) будут сделаны по результатам приведенного в ч. II данной статьи имитационного моделирования синтезированной здесь системы.