Известия РАН. Теория и системы управления, 2021, № 2, стр. 126-137

Введение. Одним из эффективных способов построения программных движений динамических систем с управлением является метод обратных задач динамики [1, 2], основная идея которого заключается в следующем. Сначала с учетом имеющихся требований и ограничений формируются желаемые значения переменных состояния системы, например как функции независимой переменной. Далее построенные функции подставляются вместо переменных состояния в уравнения динамической системы и полученная в результате этой подстановки система алгебраических уравнений относительно управляющих переменных решается аналитически или численно. Результатом решения является программное управление.

При синтезе программных движений на основе концепции обратных задач динамики часто используется подход, основанный на применении полиномов от независимой переменной [3, 4]. Решение различных терминальных задач управления с помощью многочленов рассматривалось, например, в [5–17]. Однако следует отметить, что указанный подход, как он используется в большинстве работ, не позволяет явным образом учитывать ограничения, наложенные на переменные состояния и управления. Численные процедуры синтеза программных движений механических систем с учетом ограничений, основанные на применении полиномов от независимой переменной, рассматривались, например, в [11, 12]. Некоторые идеи аналитического построения программных траекторий механических систем с учетом ограничений можно найти в книге [8] и, например, в работах [14, 18]. В [16, 19–21] для представленных классов дифференциально плоских динамических систем предложено аналитическое решение терминальных задач управления, удовлетворяющее ограничениям на переменные состояния. Тем не менее, задача синтеза программных движений с учетом ограничений, в том числе при помощи многочленов от независимой переменной, остается актуальной и до конца нерешенной.

В настоящей работе исследуется аналитическое построение программных движений механических систем на основе использования полиномов от времени. Программная траектория выбирается в классе монотонных на заданном временном отрезке многочленов третьего порядка исходя из начального и конечного состояний системы. За счет выбора времени движения решается задача учета ограничений на переменные состояния и управления.

1. Постановка задачи. Рассматривается задача синтеза программных движений для динамических систем, имеющих структуру уравнений Эйлера–Лагранжа и записанных в виде

где $q = {{\left( {{{q}_{1}}, \ldots ,{{q}_{m}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{m}}$ – вектор обощенных координат; $u = {{\left( {{{u}_{1}}, \ldots ,{{u}_{m}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{m}}$ – вектор управляющих сил и моментов; M(q) – матрица кинетической энергии, $M\left( q \right) = {{M}^{{\text{T}}}}\left( q \right) > 0$ при всех $q \in {{\mathbb{R}}^{m}}$; $C(q,\dot {q})\dot {q}$ – центробежные и кориолисовы силы; $D\dot {q}$ – демпфирование; $G(q) = {{[\partial P(q){\text{/}}\partial q]}^{{\text{T}}}}$, где P(q) – потенциальная энергия системы.

Программное движение системы (1.1) представляет собой пару функций $q = {{q}_{r}}\left( t \right)$, $u = {{u}_{r}}\left( t \right)$, такую, что уравнения системы (1.1) превращаются в тождества на заданном отрезке изменения независимой переменной $t \in \left[ {0,T} \right]$. В статье решается задача аналитического построения программных движений, удовлетворяющих фиксированным начальным и конечным условиям на переменные состояния q, $\dot {q}$ системы (1.1), а также ограничениям

где B_i, N_i и Q_i – некоторые заданные положительные числа, $i = \overline {1,m} $. Предполагается, что при синтезе программных движений для системы (1.1) есть свобода выбора времени движения T  и/или при всех $i = \overline {1,m} $ каких-либо величин среди начальных q_i(0), ${{\dot {q}}_{i}}\left( 0 \right)$ и конечных q_i(T), ${{\dot {q}}_{i}}\left( T \right)$ значений соответственно обобщенных координат и скоростей.

Заметим, что в случае локальной липшицевости функций переменных состояния q, $\dot {q}$, стоящих в левой части системы (1.1), для любой дважды кусочно непрерывно дифференцируемой программной траектории $q = {{q}_{r}}\left( t \right)$ кусочно непрерывное программное управление системой (1.1), найденное при помощи метода обратных задач динамики, запишется как

Следовательно, если для программной траектории $q = {{q}_{r}}\left( t \right)$ выполнены условия (1.2), то для программного управления (1.3) справедлива оценка ${\text{||}}{{u}_{r}}\left( t \right){\text{||}} \leqslant L$ при всех $t \in \left[ {0,T} \right]$, где постоянная L > 0 зависит от свойств матриц в (1.3) (например, их спектральных норм) и значений B_i, N_i и Q_i, $i = \overline {1,m} $. Здесь ||⋅|| – евклидова норма в ${{\mathbb{R}}^{m}}$.

2. Синтез программных движений для одной степени свободы. Рассмотрим сначала уравнения изменения состояния для одной из степеней свободы механической системы (1.1), записанные в виде динамической системы:

где ${{x}_{i}} = \left( {{{x}_{{1i}}},{{x}_{{2i}}}} \right) = \left( {{{q}_{i}},{{{\dot {q}}}_{i}}} \right) \in {{\mathbb{R}}^{2}}$, значение i, $1 \leqslant i \leqslant m$, фиксировано, q_i – обобщенная координата, ${{u}_{i}} \in \mathbb{R}$ – компонента вектора управляющих воздействий u, функции ${{f}_{i}}\left( {t,{{x}_{i}}} \right)$ и ${{g}_{i}}\left( {t,{{x}_{{1i}}}} \right)$ кусочно непрерывны по t и локально липшицевы по x_i и x_1i соответственно, причем ${{g}_{i}}\left( {t,{{x}_{{1i}}}} \right) \ne 0$ при всех ${{x}_{{1i}}} \in \mathbb{R}$ и $t \geqslant 0$. Здесь зависимость функций ${{f}_{i}}\left( {t,{{x}_{i}}} \right)$ и ${{g}_{i}}\left( {t,{{x}_{{1i}}}} \right)$ от t неявная и связана с возможной зависимостью этих функций от других, отличных от q_i и ${{\dot {q}}_{i}}$ обобщенных координат и скоростей.

Фиксируем произвольные начальные и желаемые конечные значения положения и скорости:

удовлетворяющие условиям

Будем полагать, что состояние $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$ системы (2.1) достижимо [4] из состояния $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$. Здесь T – время движения из точки $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$ в точку $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$ на фазовой плоскости $\left( {{{x}_{{1i}}},{{x}_{{2i}}}} \right)$. Далее без ограничения общности будем считать, что начальные и конечные значения переменных x_1i, x_2i для искомой программной траектории удовлетворяют неравенствам

Отметим, что, если условия (2.3) не выполнены, то при построении программной траектории на фазовой плоскости из начальной точки $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$ в конечную $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$ всегда можно использовать дополнительные промежуточные точки. Тогда за счет выбора их координат добьемся для каждой из промежуточных программных траекторий, образующих искомую траекторию как составную, выполнения соответствующих неравенств, аналогичных (2.3). Например, если имеет место равенство $\dot {x}_{{0i}}^{2} + \dot {x}_{{*i}}^{2} = 0$, то можно рассмотреть, как минимум, одну промежуточную точку с координатами $\left( {{{x}_{{li}}},{{{\dot {x}}}_{{li}}}} \right)$ на фазовой плоскости и построить сначала программную траекторию из начальной точки $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$ в промежуточную $\left( {{{x}_{{li}}},{{{\dot {x}}}_{{li}}}} \right)$, а затем из промежуточной точки в конечную $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$. При этом годятся любые значения x_li и ${{\dot {x}}_{{li}}}$, удовлетворяющие условиям

Далее, в качестве t – параметризованной кривой на фазовой плоскости $\left( {{{x}_{{1i}}},{{x}_{{2i}}}} \right)$, соединяющей точки $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$ и $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$, используем фазовый график [4] ${{\bar {p}}_{i}}(t) = ({{p}_{i}}(t),{{\dot {p}}_{i}}(t))$, $t \in [0,T]$, многочлена

где коэффициенты c_1i, c_2i находятся из условий ${{p}_{i}}(T) = {{x}_{{*i}}}$, ${{\dot {p}}_{i}}\left( T \right) = {{\dot {x}}_{{*i}}}$ и имеют вид

В силу ограничений (1.2) для многочлена (2.4) и его производных по времени первого и второго порядков при всех $t \in [0,T]$ необходимо выполнить условия $\left| {{{p}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}}$, $\left| {{{{\dot {p}}}_{i}}\left( t \right)} \right| \leqslant {{N}_{i}}$ и $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$ соответственно. Заметим, что в случае справедливости неравенств (2.2) и (2.3) для выполнения при всех $t \in [0,T]$ ограничений $\left| {{{p}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}}$ и $\left| {{{{\dot {p}}}_{i}}\left( t \right)} \right| \leqslant {{N}_{i}}$ достаточно обеспечить монотонность функций p_i(t) и ${{\dot {p}}_{i}}\left( t \right)$ на отрезке $t \in [0,T]$. При этом, если выполнены условия (2.2), (2.3), для строгой монотонности многочлена (2.4) и монотонности его производной по времени на отрезке $t \in [0,T]$ необходимо и достаточно, чтобы вторая производная многочлена, имеющая вид

была знакопостоянной на интервале $t \in \left( {0,T} \right)$. Отметим, что функция (2.6) линейная и в случае ${{c}_{{2i}}} \ne 0$ обращается в ноль при $t = - {{c}_{{1i}}}{\text{/}}(3{{c}_{{2i}}})$. Тогда для знакопостоянства второй производной по времени многочлена (2.4) на интервале $t \in \left( {0,T} \right)$ необходимо и достаточно, чтобы выполнялись условия c_2i = 0 или или

Наконец, в силу линейности по переменной t функция (2.6) при любых значениях ${{x}_{{0i}}}$, ${{\dot {x}}_{{0i}}}$, ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$ и T > 0 является монотонной на отрезке $t \in \left[ {0,T} \right]$. Следовательно, для выполнения ограничения $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$ при всех $t \in \left[ {0,T} \right]$ необходимо и достаточно, чтобы было справедливо неравенство

Отметим, что соответствующая компонента u_i программного управления (1.3), реализующая программную траекторию ${{x}_{{1i}}} = {{p}_{i}}\left( t \right)$, ${{x}_{{2i}}} = {{\dot {p}}_{i}}\left( t \right)$, $t \in \left[ {0,T} \right]$, системы (2.1), согласно [3, 4], имеет вид

Тогда в силу непрерывности функций ${{f}_{i}}\left( {t,{{x}_{i}}} \right)$ и ${{g}_{i}}\left( {t,{{x}_{{1i}}}} \right)$ в правой части системы (2.1) для любой положительной константы L_i > 0 можно подобрать такие значения постоянных B_i, N_i и Q_i, что при всех $t \in [0,T]$ имеет место неравенство $\left| {{{u}_{{ir}}}\left( t \right)} \right| \leqslant {{L}_{i}}$.

2.1. Учет ограничений за счет выбора времени движения. Воспользуемся свободой выбора времени T движения на фазовой плоскости из рассматриваемой начальной точки $\left( {{{x}_{{0i}}},{{{\dot {x}}}_{{0i}}}} \right)$ в конечную $({{x}_{{*i}}},{{\dot {x}}_{{*i}}})$. Используем далее обозначения

и

Справедлива следующая теорема.

Теорема 1. Пусть значения x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{i*}}}$, такие, что выполнены условия (2.3). Многочлен (2.4) с коэффициентами (2.5) и его производная по времени обладают соответственно свойством строгой монотонности и монотонности по переменной t на отрезке $t \in \left[ {0,T} \right]$ тогда и только тогда, когда $T \in {{I}_{{Ti}}}$. При этом ${{I}_{{Ti}}} = \left[ {{{T}_{{2i}}},{{T}_{{3i}}}} \right]$, если ${{T}_{{2i}}} \leqslant {{T}_{{1i}}}$, и ${{I}_{{Ti}}} = \left[ {{{T}_{{3i}}},{{T}_{{2i}}}} \right]$ в случае ${{T}_{{1i}}} \leqslant {{T}_{{2i}}}$.

Доказательство. Согласно условиям теоремы в силу справедливости неравенств (2.3) значения T_1i, T_2i и T_3i конечны и положительны.

Рассмотрим сначала неравенства (2.7), которые эквивалентны выполнению условий ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$ или ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$. Неравенства ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$ в силу соотношений (2.5) можно представить в виде $T \geqslant {{T}_{{2i}}}$, $T < {{T}_{{1i}}}$ при ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$ и $T \leqslant {{T}_{{2i}}}$, $T > {{T}_{{1i}}}$ в случае ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$. Аналогично неравенства ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$ эквивалентны выполнению условий $T \leqslant {{T}_{{2i}}}$, $T > {{T}_{{1i}}}$, если ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$, и $T \geqslant {{T}_{{2i}}}$, $T < {{T}_{{1i}}}$ при ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$.

Далее заметим, что для выполнения условий (2.8) необходимо, чтобы были справедливы неравенства ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$ или ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$. Условия ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$, $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$ с учетом соотношений (2.5) эквивалентны неравенствам $T > \max {\text{\;}}\{ {{T}_{{1i}}},{{T}_{{2i}}}\} $, $T \leqslant {{T}_{{3i}}}$ при ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$ и T < ${\text{min\;}}\{ {{T}_{{1i}}}$, T_2i}, $T \geqslant {{T}_{{3i}}}$ в случае ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$. Неравенства ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$, $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$ примут вид T < < ${\text{min\;}}\{ {{T}_{{1i}}},{{T}_{{2i}}}\} $, $T \geqslant {{T}_{{3i}}}$, если ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$, и $T > \max {\text{\;}}\{ {{T}_{{1i}}},{{T}_{{2i}}}\} $, $T \leqslant {{T}_{{3i}}}$ в случае ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$.

Следовательно, в случае ${{T}_{{2i}}} \leqslant T < {{T}_{{1i}}}$ выполнено ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$, если ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$, и ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$ при ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$. Далее легко показать, что при $0 < {{T}_{{2i}}} < {{T}_{{1i}}}$ справедливo неравенство ${{T}_{{3i}}} > {{T}_{{1i}}}$. Тогда в случае ${{T}_{{2i}}} < {{T}_{{1i}}} < T \leqslant {{T}_{{3i}}}$ получим, что ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$, $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$ при ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$ и ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$, $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$, если ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$. Таким образом, если выполнены условия ${{T}_{{2i}}} < {{T}_{{1i}}}$, ${{T}_{{2i}}} \leqslant T \leqslant {{T}_{{3i}}}$, $T \ne {{T}_{{1i}}}$, то функция (2.6) является знакопостоянной на интервале $t \in \left( {0,T} \right)$.

Аналогичным образом при ${{T}_{{1i}}} < {{T}_{{2i}}}$ доказывается знакопостоянство функции (2.6) на интервале $t \in \left( {0,T} \right)$, где ${{T}_{{1i}}} < T \leqslant {{T}_{{2i}}}$ или ${{T}_{{3i}}} \leqslant T < {{T}_{{1i}}}$. Наконец, при $T = {{T}_{{1i}}}$ имеет место равенство c_2i = 0, функция (2.6) является постоянной величиной и, следовательно, знакопостоянна. Достаточность доказана.

Для доказательства необходимости условий теоремы заметим, что в случае ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$ функция (2.6) отрицательна при всех $t \in \left( {0,T} \right]$ и, следовательно, ${{\dot {x}}_{{*i}}} < {{\dot {x}}_{{0i}}}$. Если ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$, то вторая производная по времени многочлена (2.4) положительна при всех $t \in \left( {0,T} \right]$ и ${{\dot {x}}_{{*i}}} > {{\dot {x}}_{{0i}}}$. Далее при ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$ если функция (2.6) сохраняет знак на интервале $t \in \left( {0,T} \right)$, то она отрицательна при всех $t \in \left[ {0,T} \right)$ и имеет место неравенство ${{\dot {x}}_{{*i}}} < {{\dot {x}}_{{0i}}}$. Аналогично в случае ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$ для знакопостоянства на интервале $t \in \left( {0,T} \right)$ функции (2.6) необходимым условием является ее положительность при всех $t \in \left[ {0,T} \right)$ и, следовательно, справедливость неравенства ${{\dot {x}}_{{*i}}} > {{\dot {x}}_{{0i}}}$.

Отметим, что при ${{\dot {x}}_{{0i}}}{{\dot {x}}_{{*i}}} \geqslant 0$, ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} \ne 0$ двойное неравенство $0 < {{T}_{{2i}}} \leqslant {{T}_{{1i}}}$ имеет место тогда и только тогда, когда справедливы неравенства ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$, ${{x}_{{*i}}} > {{x}_{{0i}}}$, ${{\dot {x}}_{{*i}}} \leqslant {{\dot {x}}_{{0i}}}$ или ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$, ${{x}_{{*i}}} < {{x}_{{0i}}}$, ${{\dot {x}}_{{*i}}} \geqslant {{\dot {x}}_{{0i}}}$.

Следовательно, если имеют место неравенства ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$ или ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$, то при 0 < < ${{T}_{{2i}}} \leqslant {{T}_{{1i}}}$ выполнены условия ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$ или ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$ соответственно и справедливо неравенство ${{T}_{{2i}}} \leqslant T < {{T}_{{1i}}}$. Далее при ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$ и ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$ получим, что в случае $0 < {{T}_{{2i}}} \leqslant {{T}_{{1i}}}$ имеют место соответственно неравенства ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} > 0$ и ${{\dot {x}}_{{0i}}} + {{\dot {x}}_{{*i}}} < 0$ и при $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$ выполняется условие ${{T}_{{1i}}} < T \leqslant {{T}_{{3i}}}$.

В случае ${{T}_{{1i}}} \leqslant {{T}_{{2i}}}$ аналогичным образом можно показать, что из неравенств ${{c}_{{1i}}} \geqslant 0$, ${{c}_{{2i}}} > 0$ или ${{c}_{{1i}}} \leqslant 0$, ${{c}_{{2i}}} < 0$ следует двойное неравенство ${{T}_{{1i}}} < T \leqslant {{T}_{{2i}}}$, а для выполнения условий ${{c}_{{1i}}} < 0$, ${{c}_{{2i}}} > 0$ или ${{c}_{{1i}}} > 0$, ${{c}_{{2i}}} < 0$ при $ - {{c}_{{1i}}}{\text{/}}\left( {3{{c}_{{2i}}}} \right) \geqslant T$ необходимым является условие ${{T}_{{3i}}} \leqslant T < {{T}_{{1i}}}$.

Наконец, равенство ${{c}_{{2i}}} = 0$ эквивалентно условию T = T_1i. Необходимость доказана.

В частности, заметим, что в случае ${{\dot {x}}_{{0i}}} = {{\dot {x}}_{{*i}}} \ne 0$ имеют место равенства ${{T}_{{1i}}} = {{T}_{{2i}}} = {{T}_{{3i}}}$ и ${{c}_{{1i}}} = {{c}_{{2i}}}$ = 0.

Следствием теоремы 1 является следующий результат.

Следствие 1. Пусть значения x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$ такие, что справедливы неравенства (2.2) и (2.3). Тогда для любого $T \in {{I}_{{Ti}}}$ многочлен (2.4) с коэффициентами (2.5) и его производная по времени при всех $t \in \left[ {0,T} \right]$ удовлетворяют ограничениям $\left| {{{p}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}}$ и $\left| {{{{\dot {p}}}_{i}}\left( t \right)} \right| \leqslant {{N}_{i}}$.

Далее исследуем соответствующее условие $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$, $t \in \left[ {0,T} \right]$, на вторую производную по времени многочлена (2.4) с коэффициентами (2.5). Рассмотрим выражения ${{\ddot {p}}_{i}}(0) = 2{{c}_{{1i}}}$ и ${{\ddot {p}}_{i}}(T) = 2{{c}_{{1i}}}$ + 6c_2iT в неравенстве (2.9) как функции переменной $T \in {{I}_{{Ti}}}$. Заметим, что первая и вторая производные по переменной T выражения для ${{\ddot {p}}_{i}}\left( 0 \right)$ обращаются в ноль при $T = 2{{T}_{{2i}}}$ и $T = 3{{T}_{{2i}}}$ соответственно. Аналогично первая и вторая производные по переменной T выражения для ${{\ddot {p}}_{i}}(T)$ равны нулю соответственно, если $T = 2{{T}_{{3i}}}$ и $T = 3{{T}_{{3i}}}$. Можно показать, что в случае выполнения условий теоремы 1 справедливы неравенства $2{{T}_{{2i}}} > {{T}_{{3i}}}$ и $2{{T}_{{3i}}} > {{T}_{{2i}}}$. Следовательно, для поиска максимальных по модулю значений ${{\ddot {p}}_{i}}(0)$ и ${{\ddot {p}}_{i}}(T)$ как функций переменной $T \in {{I}_{{Ti}}}$ достаточно проверить значения этих функций при $T = {{T}_{{2i}}}$ и $T = {{T}_{{3i}}}$.

При $T = {{T}_{{2i}}}$ имеют место равенства ${{c}_{{1i}}} = 0$, ${{c}_{{2i}}} = ({{\dot {x}}_{{*i}}} - {{\dot {x}}_{{0i}}}){\text{/}}(3T_{{2i}}^{2})$ и ${{\ddot {p}}_{i}}(0) = 0$. Таким образом, максимальное по модулю значение второй производной по времени многочлена (2.4) на отрезке $t \in \left[ {0,{{T}_{{2i}}}} \right]$ достигается при $t = {{T}_{{2i}}}$ и равно

В случае $T = {{T}_{{3i}}}$ справедливы равенства ${{c}_{{1i}}} + 3{{c}_{{2i}}}{{T}_{{3i}}} = 0$, ${{c}_{{1i}}} = ({{\dot {x}}_{{*i}}} - {{\dot {x}}_{{0i}}}){\text{/}}{{T}_{{3i}}}$ и ${{\ddot {p}}_{i}}\left( {{{T}_{{3i}}}} \right) = 0$. Следовательно, максимальное по модулю значение второй производной многочлена (2.4) на отрезке $t \in \left[ {0,{{T}_{{3i}}}} \right]$ достигается при t = 0 и равно

В частности, при $T = {{T}_{{1i}}}$ имеют место равенства ${{c}_{{2i}}} = 0$, ${{c}_{{1i}}} = ({{\dot {x}}_{{*i}}} - {{\dot {x}}_{{0i}}}){\text{/}}\left( {2{{T}_{{1i}}}} \right)$ и вторая производная по времени многочлена (2.4) при всех $t \in \left[ {0,{{T}_{{1i}}}} \right]$ является постоянной величиной:

Таким образом, имеет место следующая теорема.

Теорема 2. Пусть значения x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$, такие, что справедливы неравенства (2.3) и

Тогда для любого $T \in {{I}_{{Ti}}}$ вторая производная по времени многочлена (2.4) с коэффициентами (2.5) при всех $t \in \left[ {0,T} \right]$ удовлетворяет ограничению $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$.

На основе следствия 1 и теоремы 2 сформулируем следующий результат.

Теорема 3. Пусть значения x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$, такие, что справедливы неравенства (2.2), (2.3) и (2.14). Тогда для любого $T \in {{I}_{{Ti}}}$ многочлен (2.4) с коэффициентами (2.5) и его первая и вторая производные по времени при всех $t \in \left[ {0,T} \right]$ удовлетворяют ограничениям $\left| {{{p}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}}$, $\left| {{{{\dot {p}}}_{i}}\left( t \right)} \right| \leqslant {{N}_{i}}$ и $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$ соответственно.

Заметим, что, если требуемое значение времени движения T задано в постановке задачи, то выполнение условия $T \in {{I}_{{Ti}}}$ в теоремах 1–3 и следствии 1 обеспечим за счет выбора тех значений из x_0i, ${{\dot {x}}_{{0i}}}$, ${{x}_{{*i}}}$ и ${{\dot {x}}_{{*i}}}$, которые не фиксированы в условиях задачи. В этом случае соотношения в (2.11) для подходящих величин T_2i и T_3i рассмотрим как систему линейных алгебраических уравнений относительно соответствующих начальных и/или конечных значений положения и скорости. При этом необходимо, чтобы время движения T было таким, что полученные значения удовлетворяют условиям (2.2) и (2.3). Выполнение ограничения (2.14) требует дополнительной проверки.

3. Синтез программных движений для многих степеней свободы. Далее будем полагать, что для каждой из m степеней свободы механической системы (1.1) уравнения системы, соответствующие рассматриваемой степени свободы, могут быть представлены в виде (2.1), где ${{g}_{i}}\left( {t,{{x}_{{1i}}}} \right) \ne 0$ при всех ${{x}_{{1i}}} \in \mathbb{R}$ и $t \geqslant 0$, $i \in \overline {1,m} $.

Фиксируем произвольные начальные ${{x}_{{1i}}}\left( 0 \right) = {{x}_{{0i}}}$, ${{x}_{{2i}}}\left( 0 \right) = {{\dot {x}}_{{0i}}}$, $i = \overline {1,m} $, и желаемые конечные ${{x}_{{1i}}}\left( T \right) = {{x}_{{*i}}}$, ${{x}_{{2i}}}\left( T \right) = {{\dot {x}}_{{*i}}}$, $i = \overline {1,m} $, значения переменных q_i и ${{\dot {q}}_{i}}$, $i \in \overline {1,m} $. Здесь T – время движения в фазовом пространстве $\left( {{{q}_{1}},{{{\dot {q}}}_{1}}, \ldots ,{{q}_{m}},{{{\dot {q}}}_{m}}} \right)$ системы (1.1) из начальной точки c координатами $\left( {{{x}_{{01}}},{{{\dot {x}}}_{{01}}}, \ldots ,{{x}_{{0m}}},{{{\dot {x}}}_{{0m}}}} \right)$ в конечную точку c координатами $({{x}_{{*1}}},{{\dot {x}}_{{*1}}}, \ldots ,{{x}_{{*m}}},{{\dot {x}}_{{*m}}})$. Справедлива теорема, являющаяся следствием теоремы 3.

Следствие 2. Пусть значения x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$, $i \in \overline {1,m} $, такие, что справедливы соответствующие неравенства (2.2), (2.3), (2.14) и множество ${{I}_{T}} = {{I}_{{T1}}} \cap \ldots \cap {{I}_{{Tm}}}$ непустое. Тогда для любого $T \in {{I}_{T}}$ при всех $i \in \overline {1,m} $ многочлены (2.4) с коэффициентами (2.5) и их первые и вторые производные по времени удовлетворяют на отрезке $t \in \left[ {0,T} \right]$ ограничениям $\left| {{{p}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}}$, $\left| {{{{\dot {p}}}_{i}}\left( t \right)} \right| \leqslant {{N}_{i}}$ и $\left| {{{{\ddot {p}}}_{i}}\left( t \right)} \right| \leqslant {{Q}_{i}}$, $i \in \overline {1,m} $.

Отметим, что, если множество I_T пустое при заданных значениях x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$, $i \in \overline {1,m} $, то необходимо добиться непустоты I_T за счет выбора с учетом условий (2.2), (2.3) и (2.14) тех значений из x_0i, ${{\dot {x}}_{{0i}}}$ и ${{x}_{{*i}}}$, ${{\dot {x}}_{{*i}}}$, $i \in \overline {1,m} $, которые не фиксированы в постановке задачи.

Наконец, каждая из компонент u_i, $i = \overline {1,m} $, программного управления (1.3) имеет вид (2.10).

3.1. Движение с нулевыми начальными и конечными значениями обобщенных скоростей. В частности, рассмотрим задачу построения программных движений при условии, что ${{\dot {x}}_{{0i}}} = {{\dot {x}}_{{*i}}} = 0$, $i = \overline {1,m} $. Отметим, что для выполнения условий теорем 1–3 и следствий 1, 2 необходимо, чтобы хотя бы одно из соответствующих значений ${{\dot {x}}_{{0i}}}$ и ${{\dot {x}}_{{*i}}}$ было отлично от нуля, что в данном случае не выполняется при всех $i = \overline {1,m} $. Дополнительно к ограничениям (1.2) потребуем, чтобы искомая программная траектория удовлетворяла условиям ${{\ddot {q}}_{i}}(0) = {{\ddot {q}}_{i}}(T)$ = 0, $i = \overline {1,m} $.

Для синтеза программной траектории из начальной точки $\left( {{{x}_{{01}}},0, \ldots ,{{x}_{{0m}}},0} \right)$ в конечную точку $({{x}_{{*1}}},0, \ldots ,{{x}_{{*m}}},0)$ в пространстве состояний $\left( {{{q}_{1}},{{{\dot {q}}}_{1}}, \ldots ,{{q}_{m}},{{{\dot {q}}}_{m}}} \right)$ системы (1.1) используем дополнительные промежуточные точки с координатами $\left( {{{x}_{{j1}}},{{{\dot {x}}}_{{j1}}}, \ldots ,{{x}_{{jm}}},{{{\dot {x}}}_{{jm}}}} \right)$, $j = \overline {1,4} $, где значения x_ji, ${{\dot {x}}_{{ji}}}$, $j = \overline {1,4} $, $i = \overline {1,m} $, удовлетворяют условиям

Параметризованные временем кривые

в фазовом пространстве системы (1.1), соединяющие соответственно точки с координатами $\left( {{{x}_{{j - 1,1}}},{{{\dot {x}}}_{{j - 1,1}}}, \ldots ,{{x}_{{j - 1,m}}},{{{\dot {x}}}_{{j - 1,m}}}} \right)$ и $\left( {{{x}_{{j1}}},{{{\dot {x}}}_{{j1}}}, \ldots ,{{x}_{{jm}}},{{{\dot {x}}}_{{jm}}}} \right)$, $j = \overline {1,5} $, где T₀ = 0, ${{T}_{1}} + \ldots + {{T}_{5}} = T$, ${{x}_{{5i}}} = {{x}_{{*i}}}$, ${{\dot {x}}_{{5i}}} = {{\dot {x}}_{{*i}}} = 0$, $i = \overline {1,m} $, зададим при помощи многочленов

Здесь коэффициенты ${{c}_{{1{{i}_{j}}}}}$, ${{c}_{{2{{i}_{j}}}}}$, $j = \overline {1,5} $, $i = \overline {1,m} $, следующие:

Согласно следствию 2, рассмотренному для каждой из пяти промежуточных траекторий, образующих составную программную траекторию (3.3) из начальной точки с координатами $\left( {{{x}_{{01}}},0, \ldots ,{{x}_{{0m}}},0} \right)$ в конечную точку $({{x}_{{*1}}},0, \ldots ,{{x}_{{*m}}},0)$, значения T_j, $j = \overline {1,5} $, и x_ji, ${{\dot {x}}_{{ji}}}$, $j = \overline {1,4} $, $i = \overline {1,m} $, выбираются таким образом, что имеют место соотношения

Далее, условия ${{\ddot {q}}_{i}}\left( 0 \right) = {{\ddot {p}}_{{1i}}}\left( 0 \right) = 0$ и ${{\ddot {q}}_{i}}\left( T \right) = {{\ddot {p}}_{{5i}}}\left( T \right) = 0$, $i = \overline {1,m} $, обеспечим, выбрав соответственно значения T₁, ${{x}_{{1i}}}$, ${{\dot {x}}_{{1i}}}$ и T₅, ${{x}_{{4i}}}$, ${{\dot {x}}_{{4i}}}$, $i = \overline {1,m} $, такие, что

Заметим, что для непрерывности вторых производных по времени составных функций ${{x}_{{1i}}} = {{x}_{{1i}}}\left( t \right)$, $t \in \left[ {0,T} \right]$, $i = \overline {1,m} $, в (3.3) при $t = {{T}_{1}} + {{T}_{2}}$ и $t = {{T}_{1}} + {{T}_{2}} + {{T}_{3}}$ необходимо и достаточно, чтобы имели место равенства ${{\ddot {p}}_{{2i}}}\left( {{{T}_{1}} + {{T}_{2}}} \right) = 0$ и ${{\ddot {p}}_{{4i}}}\left( {{{T}_{1}} + {{T}_{2}} + {{T}_{3}}} \right) = 0$, $i = \overline {1,m} $. Указанные условия на значения вторых производных соответствующих многочленов выполним за счет выбора значений T₂, ${{x}_{{2i}}}$, ${{\dot {x}}_{{2i}}}$ и T₄, ${{x}_{{3i}}}$, $i = \overline {1,m} $, удовлетворяющих соотношениям

Наконец, производные второго порядка ${{\ddot {x}}_{{1i}}}\left( t \right)$, $t \in \left[ {0,T} \right]$, $i = \overline {1,m} $, для составной программной траектории (3.3) непрерывны при t = T₁ и $t = {{T}_{1}} + {{T}_{2}} + {{T}_{3}} + {{T}_{4}}$ тогда и только тогда, когда имеют место равенства

Условия (3.9) выполним, выбрав

где ε₁ > 1 – произвольный параметр. Аналогично добьемся справедливости равенств (3.10) за счет выбора

Отметим, что при любых значениях параметров ε₁ > 1, ε₂ > 1 и переменных x_2i, ${{\dot {x}}_{{2i}}}$, x_3i, $i = \overline {1,m} $, удовлетворяющих условиям (3.1) и (3.2), для значений x_1i, ${{\dot {x}}_{{1i}}}$, $i = \overline {1,m} $, (3.11) и x_4i, ${{\dot {x}}_{{4i}}}$, $i = \overline {1,m} $, (3.12) выполнены соотношения в (3.1) и (3.2).

В случае справедливости равенств (3.11), (3.12) имеют место соотношения ${{T}_{2}} = ({{\varepsilon }_{1}} - 1){{T}_{1}}$, ${{T}_{4}} = ({{\varepsilon }_{2}} - 1){{T}_{5}}$ и условия (2.14) для составной программной траектории (3.3) примут вид

Далее если требуемое значение времени движения T задано в постановке задачи, возьмем произвольные положительные значения T₁, T₃, T₅ и ε₁ > 1, ε₂ > 1 таким образом, чтобы было выполнено условие ${{\varepsilon }_{1}}{{T}_{1}} + {{T}_{3}} + {{\varepsilon }_{2}}{{T}_{5}} = T$. Тогда, рассмотрев соотношения (3.6) и (3.7) как систему линейных алгебраических уравнений относительно переменных x_2i, ${{\dot {x}}_{{2i}}}$ и x_3i, $i = \overline {1,m} $, при условии, что имеют место равенства (3.11), (3.12), получим

Отметим, что для любых значений ${{x}_{{0i}}} \ne {{x}_{{*i}}}$, $i = \overline {1,m} $, и положительных T₁, T₃, T₅, ε₁ > 1, ε₂ > 1 значения переменных x_2i, $i = \overline {1,m} $, (3.14) и x_3i, $i = \overline {1,m} $, (3.15) удовлетворяют соответствующим условиям в (3.1). При этом для выполнения ограничений $\left| {{{{\dot {x}}}_{{2i}}}} \right| \leqslant {{N}_{i}}$, $i = \overline {1,m} $, на переменные ${{\dot {x}}_{{2i}}}$, $i = \overline {1,m} $, записанные в виде (3.16), необходимо и достаточно, чтобы значения x_0i, ${{x}_{{*i}}}$, $i = \overline {1,m} $, и T₁, T₃, T₅, ε₁ > 1, ε₂ > 1 удовлетворяли неравенствам

В этом случае для значений (3.16) выполнены соответствующие условия в (3.2).

Наконец, неравенства (3.13) для x_2i, ${{\dot {x}}_{{2i}}}$ и x_2i, $i = \overline {1,m} $, имеющих вид (3.14)–(3.16), запишутся следующим образом:

4. Построение программных движений для параллельного дельта-робота. Рассмотрим динамику параллельного дельта-робота, записанную в виде [22]

где $\theta = {{\left( {{{\theta }_{1}},{{\theta }_{2}},{{\theta }_{3}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{3}}$ – углы между неподвижным основанием и рычагами; $\tau \in {{\mathbb{R}}^{3}}$ – моменты, создаваемые силовыми приводами и действующие на рычаги; $M\left( \theta \right) = {{M}^{{\text{T}}}}\left( \theta \right) > 0$ – матрица моментов инерции; $C(\theta ,\dot {\theta })$ – слагаемые, связанные с центробежными и кориолисовыми силами; G(θ) – слагаемые, связанные с действием силы тяжести. Положение подвижной конечной платформы робота в пространстве описывается при помощи вектора $X = {{\left( {x,y,z} \right)}^{{\text{T}}}}$ в прямоугольной декартовой системе координат.

Отметим, что одна из типовых задач управления движением дельта-робота состоит в подхвате и переносе различных объектов из одного положения в пространстве в другое при помощи инструмента, установленного на подвижной платформе. При этом подвижная платформа совершает перемещение в пространстве из некоторого начального положения ${{X}_{0}} = {{\left( {{{x}_{0}},{{y}_{0}},{{z}_{0}}} \right)}^{{\text{T}}}}$ в соответствующее конечное положение ${{X}_{*}} = {{({{x}_{*}},{{y}_{*}},{{z}_{*}})}^{{\text{T}}}}$. С использованием обратной кинематики робота [22] начальное X = X₀ и конечное $X = {{X}_{*}}$ положения подвижной платформы можно записать в переменных θ как $\theta = {{\theta }_{0}} = {{\left( {{{\theta }_{{01}}},{{\theta }_{{02}}},{{\theta }_{{03}}}} \right)}^{{\text{T}}}}$ и $\theta = {{\theta }_{*}} = {{({{\theta }_{{*1}}},{{\theta }_{{*2}}},{{\theta }_{{*3}}})}^{{\text{T}}}}$.

Решим задачу синтеза программного движения $\theta = {{\theta }_{r}}\left( t \right)$, $\tau = {{\tau }_{r}}\left( t \right)$, переводящего систему (4.1) из начального состояния $\theta \left( 0 \right) = {{\theta }_{0}}$, $\dot {\theta }\left( 0 \right) = 0$ при $\ddot {\theta }\left( 0 \right) = 0$ в конечное состояние $\theta \left( T \right) = {{\theta }_{*}}$, $\dot {\theta }(T) = 0$ таким образом, что $\ddot {\theta }\left( T \right) = 0$. При этом необходимо, чтобы искомая программная траектория $\theta = {{\theta }_{r}}\left( t \right)$ удовлетворяла при всех $t \in \left[ {0,T} \right]$ геометрическим ограничениям $\left| {{{\theta }_{{ir}}}\left( t \right)} \right| \leqslant \pi {\text{/}}2$, ограничениям на значения угловых скоростей $\left| {{{{\dot {\theta }}}_{{ir}}}\left( t \right)} \right| \leqslant {{N}_{i}}$ и ограничениям на значения угловых ускорений $\left| {{{{\ddot {\theta }}}_{{ir}}}\left( t \right)} \right| \leqslant {{Q}_{i}}$, $i = \overline {1,3} $. Здесь N_i, Q_i, $i = \overline {1,3} $, – заданные положительные значения. Будем также полагать, что время движения T не задано в постановке задачи.

Фиксируем произвольные положительные значения T₁, T₃, T₅ и ε₁ > 1, ε₂ > 1. Для синтеза программной траектории из начальной точки с координатами $\left( {{{\theta }_{{01}}},0,{{\theta }_{{02}}},0,{{\theta }_{{03}}},0} \right)$ в конечную точку $({{\theta }_{{*1}}},0,{{\theta }_{{*2}}},0,{{\theta }_{{*3}}},0)$ в фазовом пространстве системы (4.1) используем дополнительные промежуточные точки с координатами $\left( {{{\theta }_{{j1}}},{{{\dot {\theta }}}_{{j1}}},{{\theta }_{{j2}}},{{{\dot {\theta }}}_{{j2}}},{{\theta }_{{j3}}},{{{\dot {\theta }}}_{{j3}}}} \right)$, $j = \overline {1,4} $. Здесь значения θ_ji, ${{\dot {\theta }}_{{ji}}}$, $j = \overline {1,4} $, $i = \overline {1,3} $, удовлетворяют условиям ${{\dot {\theta }}_{{2i}}} = {{\dot {\theta }}_{{3i}}}$, $i = \overline {1,3} $, и соответствующим соотношениям (3.11), (3.12), (3.14)–(3.16), записанным в обозначениях θ.

Программная траектория $\theta = {{\theta }_{r}}\left( t \right)$, $t \in \left[ {0,T} \right]$, запишется покомпонентно следующим образом:

где $T = {{\varepsilon }_{1}}{{T}_{1}} + {{T}_{3}} + {{\varepsilon }_{2}}{{T}_{5}}$, ${{T}_{2}} = \left( {{{\varepsilon }_{1}} - 1} \right){{T}_{1}}$, ${{T}_{4}} = \left( {{{\varepsilon }_{2}} - 1} \right){{T}_{5}}$, многочлены p_ji(t), $j = \overline {1,5} $, $i = \overline {1,3} $, имеют соответствующий вид (3.4), записанный в обозначениях θ.

Заметим, что для выполнения заданных ограничений на значения функций (4.2) и их первых и вторых производных по времени необходимо и достаточно, чтобы выбранные значения T₁, T₃, T₅ и ${{\varepsilon }_{1}} > 1$, ${{\varepsilon }_{2}} > 1$ удовлетворяли соответствующим неравенствам (3.17), (3.18) и (3.19), записанным в обозначениях θ.

Искомое программное управление, являющееся решением рассматриваемой терминальной задачи для системы (4.1), имеет вид

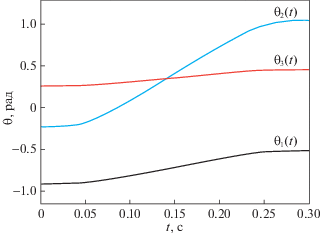
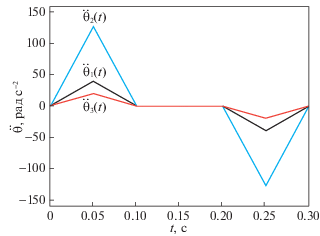
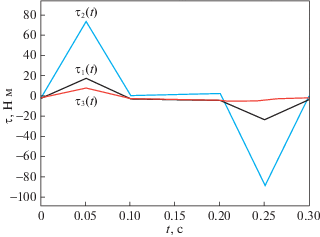
Результаты численного моделирования системы (4.1) с управлением (4.3) для значений физических и геометрических параметров модели, взятых из работы [22], представлены на рис. 1–4. В качестве начальных и конечных значений угловых координат рассматривались соответственно ${{\theta }_{0}} = {{( - 0.9106, - 0.2294,0.2568)}^{{\text{T}}}}$ и ${{\theta }_{*}} = {{\left( { - 0.516,1.04,0.4541} \right)}^{{\text{T}}}}$. При этом начальное и конечное положения подвижной конечной платформы робота в декартовой системе координат следующие: ${{X}_{0}} = {{\left( {0.2,0.1, - 0.5} \right)}^{{\text{T}}}}$ и ${{X}_{1}} = {{\left( {0.4, - 0.2, - 0.6} \right)}^{{\text{T}}}}$. Допустимые максимальные по модулю значения угловых скоростей и ускорений взяты соответственно N_i = 7 рад ⋅ c^–1 и ${{Q}_{i}} = 150$ рад ⋅ c^–2, $i = \overline {1,3} $. При планировании программной траектории были выбраны значения $T = 0.3$ с, ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 2$; T₁ = $T{\text{/}}(3{{\varepsilon }_{1}})$, ${{T}_{5}} = T{\text{/}}(3{{\varepsilon }_{2}})$.

Заключение. Для задачи планирования программных движений механических систем на основе использования полиномов третьего порядка от времени предложено аналитическое решение, учитывающее наличие ограничений на переменные состояния и управления. Программная траектория строится с учетом допустимых максимальных по модулю значений обобщенных координат, скоростей и ускорений. Выполнение заданных ограничений достигается за счет выбора времени движения. В частности, предложено решение задачи построения программной траектории с нулевыми начальными и конечными значениями обобщенных скоростей и ускорений, удовлетворяющее требуемым ограничениям на значения обобщенных координат, скоростей и ускорений. В качестве примера рассмотрено решение задачи управления движением параллельного дельта-робота. Для дальнейших исследований представляет интерес получение аналогичных результатов для программных движений, основанных на использовании полиномов более высоких, чем третий, порядков.