Известия РАН. Теория и системы управления, 2021, № 2, стр. 138-155

Введение. В настоящее время можно выделить два основных направления методов лабораторного тестирования систем управления движением космических аппаратов с точки зрения динамики – использование аэродинамических подвесов и применение аэродинамических столов, а также их комбинации. С помощью стенда с аэродинамическим столом благодаря воздушной подушке между поверхностью стола и опорой макета системы управления спутника обеспечивается свободное плоское поступательное движение и одноосное вращение аппарата. Такие стенды могут использоваться как для тестирования алгоритмов управления одиночным аппаратом, так и для отработки управления движением группы спутников [1–3].

Сферический аэродинамический подвес – наиболее распространенный способ лабораторной имитации углового движения спутника. Подвес представляет собой две полусферы, вложенные друг в друга. Внешняя полусфера имеет некоторое, обычно небольшое, число отверстий для выхода воздуха. За счет этого между внешней и внутренней сферами создается воздушная прослойка, практически исключающая трение. Подвес имеет три степени свободы, хотя обычно может неограниченно вращаться только относительно вертикали, так как на внутреннюю сферу устанавливается платформа, имитирующая спутник или его систему ориентации [4, 5].

Один из первых стендов был создан в Агентстве баллистических ракет США в 1959 г. [6]. Сложная конструкция пьедестала и платформы, на которой устанавливались элементы систем спутника, позволили добиться поворота до 120° по углу крена. Первый вопрос, для решения которого применялись аэродинамические подвесы, – влияние диссипации энергии (топливо в баках, нутационные демпферы, маховики) на движение спутника. В настоящее время крупные космические компании и агентства имеют в своем распоряжении стенды, предназначенные для моделирования движения макета спутника, включающего бóльшую часть его систем [7, 8].

Первый небольшой (грузоподъемностью до 100 кг) стенд со сферическим подвесом был создан в Стэнфорде в 1975 г. [9]. Сейчас небольшие стенды широко распространены в европейских и американских университетах. Так, платформа на аэродинамическом подвесе, имеющаяся в Мексиканском институте географии, имеет массу всего 35 кг. На платформе установлены акселерометры, гироскопы, магнитометр, солнечный датчик, магнитные катушки, маховики и система балансировки [10]. Угол крена ограничен 50°.

Одно из преимуществ небольшого макета на подвесе – возможность установить его внутри колец Гельмгольца. Кольца предназначены для имитации геомагнитного поля и его изменения в соответствие с движением спутника на орбите. Эта особенность хорошо согласуется с размерами и возможностями малых спутников: они зачастую имеют магнитные катушки в качестве основных управляющих элементов. Поэтому проведение экспериментов в имитационном магнитном поле становится одновременно важным и возможным, так как область однородности колец Гельмгольца невелика. Такой стенд имеется, например, в университетах Стретчклайда в Глазго [11], Фридриха II в Неаполе [12], в Массачусетском технологическом институте [13], Университете Бразилии [14]. Такие стенды позволяют установить на подвесе только специальный макет системы ориентации, а не всего спутника.

Одно из преимуществ использования сферического аэродинамического подвеса – простота интерпретации результатов, полученных в эксперименте, в терминах полета спутника в космическом пространстве. Движение обоих тел – спутника и макета в подвесе – описывается одними и теми же уравнениями, различаются лишь внешние возмущения и неполная свобода поворота макета по одному или двум углам. Основным источником возмущений, действующих на макет, является гравитационный момент, возникающий из-за смещения центра масс относительно центра вращения. При этом, несмотря на то, что момент является доминирующим, его можно уменьшить с помощью системы балансировки, состоящей из подвижных грузов на макете системы управления. Для корректной работы системы балансировки необходимо оценить положение центра масс макета. Если центр масс находится ниже центра вращения, макет движется подобно математическому маятнику. Макеты, у которых центр давления находится выше центра масс, предпочтительны – такой макет не заваливается набок, а совершает колебания небольшой амплитуды. Процедура балансировки может быть осуществлена с помощью ручного перемещения подвижных грузов путем оценки периода колебаний макета [15]. Однако такой подход основан на методе проб и ошибок и требует достаточно много времени для установки центра масс на приемлемом расстоянии от центра давления. Поэтому автоматическая система балансировки, когда массы на макете перемещаются с помощью линейных электромеханических приводов, значительно сокращает время для балансировки и увеличивает точность. Однако для автоматической балансировки требуется оценка положения центра масс. Такая оценка может быть получена как с помощью бортовых алгоритмов обработки измерений датчиков, так и с помощью внешней системы определения углового движения макета [16–18].

Для корректной настройки алгоритмов управления угловым движением макета на аэродинамическом подвесе необходимо не только уменьшить величину гравитационного момента с помощью балансировки, но и иметь оценку тензора инерции макета. Как правило, тензор инерции рассчитывается с помощью специальных программных пакетов, в которых задается положение и масса всех компонент макета. Однако распределение масс внутри каждого блока макета известно приблизительно, поэтому тензор инерции известен с довольно большой погрешностью. Оценить тензор инерции возможно с помощью измерений углового движения макета при управляемом движении на аэродинамическом подвесе, как это сделано в [19–21]. Однако в этих работах предполагается, что величина управляющего воздействия на макет известна, благодаря чему с помощью алгоритмов на основе метода наименьших квадратов или динамической фильтрации определяются как тензор инерции, так и положение центра масс макета. К сожалению, в распоряжении разработчиков системы управления не всегда имеется откалиброванный актюатор, такой, как маховики или магнитные катушки. Поэтому в отличие от предыдущих публикаций в настоящей работе для оценки тензора инерции и положения центра масс макета используется только информация о смещении груза системы балансировки. Рассматриваются два этапа балансировки макета. На первом этапе по измерениям системы определения углового положения макета и с помощью заданного смещения груза оценивается тензор инерции макета в связанной системе координат с центром в точке подвеса и положение центра масс относительно точки подвеса. На втором этапе в предположении известного тензора инерции проводится оценка положения центра масс в режиме реального времени и реализуется итерационная процедура помещения центра масс в требуемое положение с помощью системы подвижных грузов.

1. Стенд для имитации углового движения микроспутников. В настоящей работе рассматривается стенд для испытаний алгоритмов управления угловым движением макетов микроспутников, созданный компанией “Спутникс” [22]. В состав стенда входят имитатор магнитного поля, имитатор Солнца, макет системы ориентации микроспутника и аэродинамический подвес. Фото макета представлено на рис. 1. Этот макет благодаря воздушной подушке способен совершать трехосное угловое движение относительно точки подвеса.

Вследствие неидеальности балансировки положение точки подвеса не совпадает с центром масс макета, возникает гравитационный момент, который влияет на движение макета. Чтобы уменьшить влияние гравитационного момента, на макете установлена двухуровневая система балансировки: грубая ручная установка положения центра масс относительно центра подвеса с помощью грузов, перемещаемых вдоль осей системы координат, связанной с макетом, и программно-управляемая система балансировки. Эта система состоит из шести линейных приводов, по два привода вдоль каждой связанной с макетом оси системы координат (рис. 2). Линейный привод способен перемещать грузик в диапазоне [–5; 5] см с точностью 1 мм. Масса груза вместе с перемещаемой частью линейного привода составляет 15.6 г.

Для определения углового движения макета применяется система оптических измерений. Она основана на обработке изображений, получаемых с камеры, неподвижно установленной на имитаторе геомагнитного поля. На изображении распознаются специальные метки, установленные на макете (рис. 3), и определяется угловое положение макета относительно неподвижной лабораторной системы координат. Центр лабораторной системы координат находится в центре подвеса макета, ось $z$ направлена в зенит, оси $x$ и $y$ перпендикулярны друг другу и находятся в плоскости местного горизонта. Точность определения углового положения макета с помощью системы оптических измерений составляет σ_изм = 0.2°, частота поступающих измерений – около 5 Гц.

Цель статьи заключается в том, чтобы с помощью обработки данных системы независимых измерений в режиме пассивного движения макета на аэродинамическом подвесе оценить тензор инерции макета в системе координат, связанной с макетом и началом в центре масс, а также вектор положения центра масс макета относительно точки подвеса. Задача решается посредством перемещения грузов с помощью линейных приводов во время пассивного движения. Измерения углового положения макета во время экспериментов используются для постэкспериментальной обработки. С помощью метода наименьших квадратов определяются тензор инерции и положение центра масс, доставляющие минимальное значение квадрату разности прогноза измерений и полученных в эксперименте измерений углового положения.

Приведем основные приблизительные динамические характеристики макета системы ориентации. С помощью программы SolidWorks были рассчитаны предварительные компоненты тензора инерции без учета кабельной сети на макете. Эти компоненты тензора инерции в системе координат с началом в центре масс имеют следующие значения:

Масса всего макета составляет $m = 14.24$ кг.

2. Уравнения движения макета на аэродинамическом подвесе. Движение макета описывается с помощью динамических уравнений Эйлера. Используемые переменные можно разделить на две группы. Первую группу составляют компоненты ${{\omega }_{1}},\,\,{{\omega }_{2}},\,\,{{\omega }_{3}}$ абсолютной угловой скорости спутника ${\mathbf{\omega }}$, записанные в осях связанной с телом системы координат. Для описания ориентации используется кватернион $\left( {{\mathbf{q}},\,\,{{q}_{0}}} \right)$, где ${\mathbf{q}}$ – векторная, ${{q}_{0}}$ – скалярная часть кватерниона [23]. Динамические уравнения Эйлера движения твердого тела относительно неподвижной точки имеют вид

где механический момент ${\mathbf{M}}$ содержит как управление ${{{\mathbf{M}}}_{{{\text{упр}}}}}$, так и возмущающие моменты, т.е. ${\mathbf{M}} = {{{\mathbf{M}}}_{{{\text{упр}}}}} + {{{\mathbf{M}}}_{{{\text{возм}}}}}$. Для спутника ${\mathbf{J}}$ – это тензор инерции, вычисленный для связанной с телом системы координат, находящейся в центре масс. При этом оси обычно направлены по главным осям спутника. В случае макета возможны два варианта. Можно поместить связанную с макетом систему координат в его центр масс. В этом случае уравнения получаются те же, ${\mathbf{J}}$ – тензор инерции в главных центральных осях. Однако такой подход заставляет учитывать дополнительные возмущения и движение центра масс относительно центра вращения. Поэтому обычно применяется более естественный подход – описание движения макета относительно центра вращения. Это усложняет вид тензора ${\mathbf{J}}$, но упрощает запись действующих на спутник возмущений. Тензор инерции ${\mathbf{J}}$ можно представить как где ${{I}_{{ij}}}$ – компоненты тензора инерции ${\mathbf{I}}$ для центра масс макета, ${\mathbf{r}}$ – вектор, соединяющий центр вращения и центр масс. Будем считать, что ${\mathbf{I}}$ – тензор инерции всего макета, в том числе перемещаемых грузов, которые находятся изначально в несмещенном положении. Связь тензоров инерции с грузами и без них задается формулой где ${\mathbf{\hat {I}}}$ – исходный тензор инерции макета без балансировочных грузов, ${{{\mathbf{r}}}_{i}}$ – положение i-го груза в связанной системе координат, ${{m}_{i}}$ – его масса, $N$ – число грузов. В случае смещения грузов на вектор $d{{{\mathbf{r}}}_{i}}$ новый тензор инерции ${\mathbf{\tilde {I}}}$ будет иметь вид

Тогда изменение тензора инерции в случае смещения грузиков рассчитывается по следующей формуле:

Динамические уравнения (2.1) дополняются кинематическими уравнениями, которые при использовании кватерниона $\left( {{\mathbf{q}},\,\,{{q}_{0}}} \right)$ для описания углового положения имеют следующий вид:

Рассмотрим в качестве возмущающего момента гравитационный момент, который записывается в связанной с макетом системе координат в точке подвеса следующим образом:

где ${\mathbf{A}}$ – матрица направляющих косинусов, задающая переход от лабораторной системы координат в связанную с макетом систему координат, $m$ – масса всего макета, $g$ – ускорение свободного падения.

Приведем, как изменяется радиус-вектор положения центра масс ${\mathbf{r}}$, заданный в системе координат с центром в точке подвеса при смещении грузов на векторы $d{{{\mathbf{r}}}_{i}}$. До смещения грузов вектор вычисляется следующим образом:

где ${\mathbf{\hat {r}}}$ – радиус-вектор до центра масс макета без грузов, $\hat {m}$ – масса макета без грузов. После смещения грузов на $d{{{\mathbf{r}}}_{i}}$ положение центра масс ${\mathbf{\tilde {r}}}$  определяется из следующего выражения:

Тогда смещение центра масс находится из выражения

3. Методика оценки центра масс и тензора инерции макета на аэродинамическом подвесе с помощью системы балансировки. Для проведения лабораторных исследований алгоритмов определения углового движения и управления ориентацией необходимо, чтобы движение макета на аэродинамическом подвесе было максимально приближено к орбитальному движению. Однако этому препятствует смещение центра масс макета от точки подвеса, в результате чего возникает гравитационный момент. Для уменьшения его влияния на движение макета с помощью балансировочных грузов положение центра масс требуется установить близко в окрестности точки подвеса с максимально-возможной точностью. Чтобы корректно рассчитать смещение грузов необходимо иметь оценку как положения центра масс, полученную по измерениям системы определения движения макета. Кроме того, так как тензор инерции также непосредственно влияет на движение системы, а он известен только приблизительно по предварительным расчетам, то требуется разработать методику по его оценке совместно с оценкой положения центра масс.

Рассмотрим свободное движение макета на аэродинамическом подвесе, т.е. на макет не воздействует управляющий момент со стороны маховиков или магнитных катушек. Движение полностью определяется гравитационным моментом (2.5). Пусть в начальный момент грузы системы балансировки находятся в нулевом положении. Движение макета определяется уравнениями (2.1) и (2.4). Во время этого свободного движения накапливаются измерения системы определения углового положения макета, т.е. компоненты кватерниона, поступающие с некоторой частотой. Далее, в известный момент времени грузы смещаются на известную величину $d{{{\mathbf{r}}}_{i}}$, тем самым изменяя положение центра масс относительно точки подвеса по формуле (2.6) и тензор инерции по формуле (2.3). После смещения положения грузиков макет продолжает свободное движение, накапливаются измерения об угловом положении.

Таким образом, движение макета определяется следующими неизвестными параметрами: положением центра масс до смещения грузов ${\mathbf{r}}$, тензором инерции в связанной с центром масс системе координат до смещения грузиков ${\mathbf{I}}$, а также вектором начальной угловой скорости макета в связанной системе координат ${{{\mathbf{\omega }}}_{0}}$. Кватернион в начальный момент времени ${{\Lambda }_{0}}$ принимаем за первое измерение системы определения углового положения макета. Введем вектор оцениваемых параметров ${\mathbf{\xi }}$:

Вектор $\xi $ полностью задает свободное угловое движение макета на аэродинамическом подвесе. С помощью интегрирования уравнений движения можно получить прогноз углового положения макета ${{\hat {\Lambda }}_{k}}$ в каждый момент времени ${{t}_{k}}$. Построим функцию следующего вида:

где ${{\Lambda }_{k}}$ – кватернион углового положения, полученный с помощью системы независимых измерений.

Задача оценки тензора инерции и положения центра масс сводится к задаче минимизации функции (3.1), которая производится численно.

Следует заметить, что положение центра масс вследствие температурных деформаций макета может изменяться во времени. Поэтому разумно оценивать положение центра масс макета и балансировать его в режиме реального времени непосредственно при тестировании алгоритмов управления угловым движением.

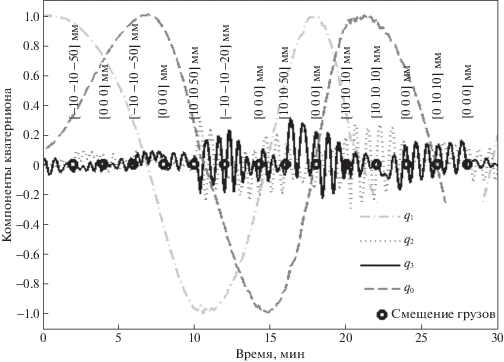
4. Оценка тензора инерции и положения центра масс на аэродинамическом подвесе. Был проведен ряд экспериментов по методике, описанной выше. Раз в 2 мин грузы перемещались на известную величину. На рис. 4 представлены компоненты кватерниона, полученные с помощью системы определения углового положения, точками обозначены моменты смещения грузиков, а в квадратных скобках дан вектор смещения грузов $d{\mathbf{r}}$.

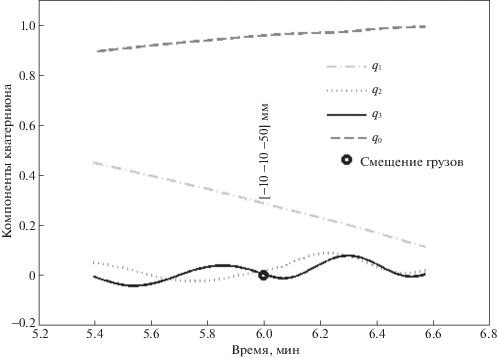
Рассмотрим в качестве примера отрезок измерений в окрестности третьего смещения грузов (рис. 5).

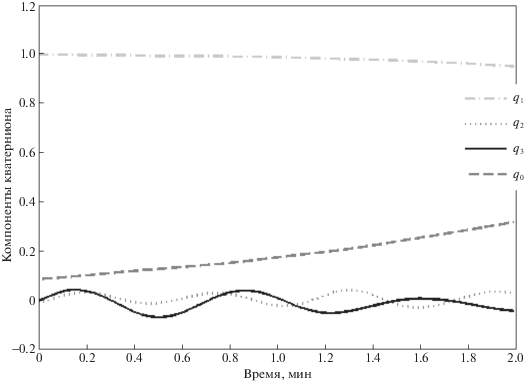
Зададим начальное значение для вектора определяемых параметров: положение центра масс макета ${{{\mathbf{r}}}_{0}} = {{[0\,\,0\,\, - {\kern 1pt} {{10}^{{ - 4}}}{\text{]}}}^{{\text{T}}}}$ м; момент инерции зададим согласно расчетам из программы SolidWorks ${{{\mathbf{I}}}_{0}} = {\mathbf{\hat {I}}}$; вектор угловой скорости ${{{\mathbf{\omega }}}_{0}}$ оценим с помощью дифференцирования матрицы направляющих косинусов по первым двум измерениям углового положения. На рис. 6, а представлено сравнение компонент кватерниона, полученных с помощью системы определения углового положения и с помощью интегрирования уравнений движения, из которого видно, что оценки компонент кватерниона сильно отклоняются от измеренных значений, что можно объяснить неточным значением начального приближения вектора оцениваемых параметров ${{\xi }_{0}} = {{[{{{\mathbf{r}}}_{0}};{{{\text{I}}}_{0}};{{\omega }_{0}}{\text{]}}}^{{\text{T}}}}$.

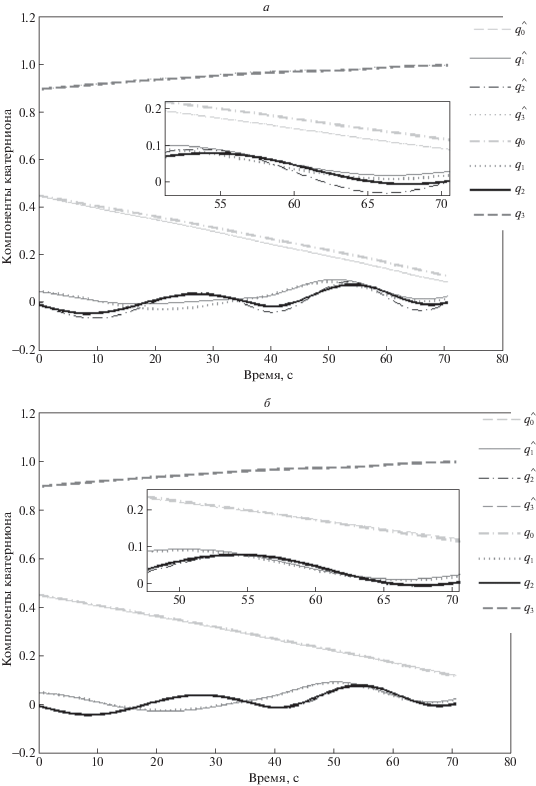
Запустим итерационную процедуру, которая найдет такой вектор $\xi $, который доставит минимум функционалу (3.1). Для минимизации функции используется алгоритм Левенберга–Марквардта. В результате минимизации получены следующие искомые параметры:

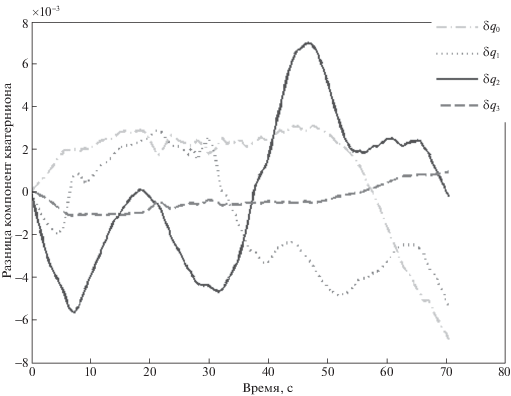
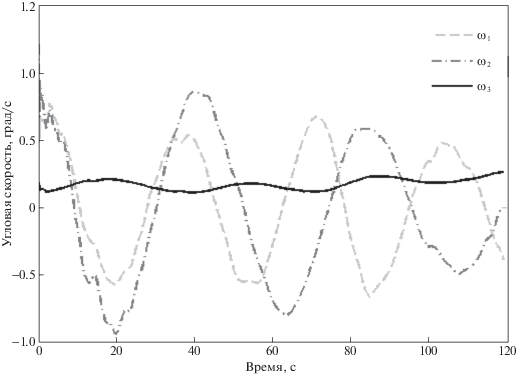
Тензор инерции несколько отличается от рассчитанного с помощью программы SolidWorks, но близок к нему. На рис. 6, б представлено сравнение измеренного и полученного с помощью интегрирования по оцененным параметрам кватерниона ориентации. Визуально эти графики совпадают, но на рис. 7 можно увидеть покомпонентную разность, которая не превышает значения $7 \times {{10}^{{ - 3}}}$, что соответствует ошибке 0.8° по угловому положению. На рис. 8 можно увидеть компоненты вектора угловой скорости. Излом кривых в точке около 37 с вызван смещением грузов.

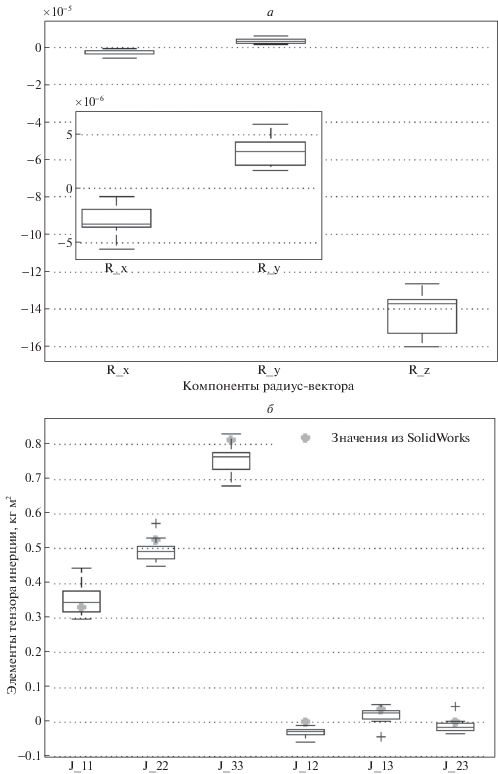
На рис. 9, а представлена диаграмма размаха оценок положения центра масс для 20 экспериментов, из которой можно заключить, что разброс значений для вертикальной компоненты составляет около 10^–5 м, а для горизонтальных компонент – около $5 \times {{10}^{{ - 6}}}$ м. На рис. 9, б приведена диаграмма размаха оценки компонент тензора инерции макета, из которой можно заключить, что разброс по определению диагональных элементов тензора инерции составляет около 0.1 кг ⋅ м². Для оценки значений недиагональных элементов разброс составляет около 0.05 кг ⋅ м². На рис. 9,б также представлены значения элементов тензора инерции, рассчитанные с помощью программы SolidWorks. Расчетные значения осевых моментов инерции по третьей и второй оси заметно отличаются от среднего значения по результатам экспериментов, что может свидетельствовать об ошибках в расчетах распределения масс в компонентах макета.

5. Автоматическая балансировка в режиме реального времени. Для оценки положения центра масс в режиме реального времени по поступающим измерениям углового положения используется алгоритм на основе расширенного фильтра Калмана [24, 25]. На этом этапе будем считать, что оценка тензора инерции известна в результате применения алгоритма на основе метода наименьших квадратов, рассмотренного в разд. 3 статьи. Кроме того, тензор инерции практически не изменяется, тогда как положение центра масс может значительно измениться вследствие термических деформаций платформы макета во время экспериментов под действием нагрева со стороны имитатора Солнца. Это может привести к значительным возмущениям со стороны гравитационного момента.

Для случая определения положения центра масс макета в режиме реального времени используется вектор состояния макета, содержащий векторную часть кватерниона ориентации, вектор угловой скорости и положение центра масс относительно точки подвеса:

Дискретная модель изменения вектора состояния записывается следующим образом:

где ${\mathbf{x}}_{k}^{{}} = {\mathbf{x}}\left( {{{t}_{k}}} \right)$, ${{t}_{k}}$ – тактовый момент времени, $\Delta t = {{t}_{{k + 1}}} - {{t}_{k}}$, $k$ – номер такта алгоритма определения движения, ${{0}_{{3 \times 3}}}$ – нулевая матрица размерности $3 \times 3$, ${{{\mathbf{E}}}_{{n \times n}}}$ – единичная матрица размерности $n \times n$, ${{{\mathbf{w}}}_{k}}$ – дискретная белая нормально распределенная ошибка модели движения с ${\text{M}}({{{\mathbf{w}}}_{k}}) = 0$ и ${\text{M}}({{{\mathbf{w}}}_{k}}{\mathbf{w}}_{i}^{{\text{T}}}) = Q{{\delta }_{{ki}}}$, ${{\delta }_{{ki}}}$ – символ Кронекера, ${{{\mathbf{F}}}_{k}}$ – матрица динамики, полученная в результате линеаризации уравнений движения (2.1), (2.4), ${{{\mathbf{W}}}_{{\mathbf{y}}}}$ – кососимметрическая матрица с элементами, определенными вектором y, ${\mathbf{F}}_{{{\text{гир}}}}^{k} = 2\left( {{{{\mathbf{W}}}_{{{\mathbf{J}}{{\omega }_{k}}}}}{{{\mathbf{W}}}_{{{{\omega }_{k}}}}} - {{{\mathbf{W}}}_{{{{\omega }_{k}}}}}{\mathbf{J}}{{{\mathbf{W}}}_{{{{\omega }_{k}}}}}} \right)$ – матрица гироскопического момента.

В (5.1) принята следующая дискретная модель изменения радиус-вектора центра масс в жестко связанной с макетом системе координат с центром в точке подвеса:

где ${{{\mathbf{r}}}_{k}} = {\mathbf{r}}\left( {{{t}_{k}}} \right)$, ${{{\mathbf{w}}}_{{\mathbf{r}}}}$ – дискретная белая нормально распределенная случайная величина с ${\text{M}}({\mathbf{w}}_{k}^{{\text{T}}}) = 0$ и ${\text{M}}({\mathbf{w}}_{k}^{r}{\mathbf{w}}{{_{i}^{r}}^{{\text{T}}}}) = {{{\mathbf{Q}}}^{r}}{{\delta }_{{ki}}}$. Случайная природа изменения положения центра масс может быть обусловлена влиянием неучтенного в модели термического изменения объема материалов, из которых состоит макет.

В качестве вектора измерений рассматривается векторная часть кватерниона ${\mathbf{z}} = {\mathbf{q}}$. Тогда дискретная модель измерений имеет вид

где ${\mathbf{H}} = \left[ {{{{\mathbf{E}}}_{{3 \times 3}}}\,\,\,{{0}_{{3 \times 3}}}\,\,{{0}_{{3 \times 3}}}} \right]$, ${{\psi }_{k}}$ – белая нормально распределенная, не зависящая от w_k ошибка измерений с нулевым математически ожиданием ${\text{M}}({{\psi }_{k}}) = 0$ и ковариационной матрицей ${\text{M}}({{\psi }_{k}}\psi _{i}^{{\text{T}}})$ = = Rδ_ki.

Работа расширенного фильтра Калмана состоит из двух этапов – прогноза вектора состояния на момент получения измерения и его коррекции при обработке результатов измерения. На этапе прогноза априорная оценка вектора состояния ${\mathbf{\hat {x}}}_{{k + 1}}^{ - }$ вычисляется с использованием непрерывных уравнений движения с начальными условиями, которые задаются апостериорной оценкой вектора состояния на предыдущем шаге ${\mathbf{\hat {x}}}_{k}^{ + }$:

где ${\mathbf{f}}({\mathbf{x}},t)$ – функция правых частей, которая может быть получена из уравнений (2.1) и (2.4). Также на этапе прогноза необходимо найти ковариационную матрицу ошибок вектора состояния ${{{\mathbf{P}}}_{k}} = {\text{M}}(\Delta {{{\mathbf{x}}}_{k}}\Delta {\mathbf{x}}_{k}^{{\text{T}}})$, где $\Delta {{{\mathbf{x}}}_{k}} = {{{\mathbf{\hat {x}}}}_{k}} - {{{\mathbf{x}}}_{k}}$ – ошибка оценки фильтра Калмана. Априорная матрица ${\mathbf{P}}_{{k + 1}}^{ - }$ вычисляется с помощью дискретного уравнения следующим образом:

На этапе коррекции апостериорная оценка вектора состояния ${\mathbf{\hat {x}}}_{{k + 1}}^{ + }$ и апостериорная ковариационная матрица ${\mathbf{P}}_{{k + 1}}^{ + }$ вычисляются по формулам

где

Для работы дискретного фильтра Калмана в начальный момент времени требуется задать вектор состояния x₀, ковариационные матрицы ошибок модели движения Q, ошибок измерений ${\mathbf{R}}$ и ошибок знания начального вектора состояния ${{{\mathbf{P}}}_{0}}$. Величину матрицы Q можно оценить экспериментально, исходя из величины неучтенных в модели движения возмущений. Ковариационная матрица R, как правило, задается диагональной, где по диагонали расположены дисперсии ошибок измерений, которые определяются экспериментально, т.е. ${\mathbf{R}} = {\text{diag}}(\sigma _{{{\text{изм}}}}^{2},\sigma _{{{\text{изм}}}}^{2},\sigma _{{{\text{изм}}}}^{2})$. Матрица P₀ задается исходя из начального незнания вектора состояния x₀.

Рассмотрим участок измерений без перемещения грузов, который представлен на рис. 10. Будем подавать на вход измерения и на каждом шаге получать оценку положения центра масс макета. На рис. 11 приведена оценка угловой скорости макета, а на рис. 12 – оценка вектора положения центра масс макета. В результате после сходимости оценка положения центра масс составила, м:

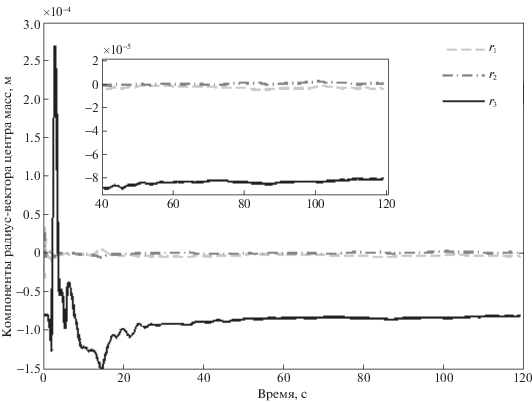
Ошибка относительно положения центра масс, оцененного с помощью метода наименьших квадратов, составила $2 \times {{10}^{{ - 6}}}$ м.

Рассмотрим теперь, что произойдет с оценками положения центра масс при смещении грузов. Пусть грузы смещаются на вектор $[ - 10; - 10; - 50]$ мм, это соответствует смещению центра масс, согласно приведенным выше параметрам, на величину $[ - 1; - 1; - 5] \times {{10}^{{ - 5}}}$ м. На рис. 13, а представлен пример, когда в уравнения движения в фильтре Калмана не подается информация о смещении грузов. Видно, что с момента, равного приблизительно 120 с, оценка положения центра масс начала отслеживать текущее значение положения центра масс, причем изменение вектора положения центра масс близко к расчетному $[ - 1; - 1; - 5] \times {{10}^{{ - 5}}}$ м. На рис. 13, б приведен пример, когда в уравнения движения в фильтре Калмана подается информация о смещении грузов на заданное значение. В момент 120 с оценки положения центра масс резко смещаются на величину $[ - 1; - 1; - 5] \times {{10}^{{ - 5}}}$ м, но по третьей компоненте это значение постепенно сходится к значению $1.1 \times {{10}^{{ - 5}}}$ м вместо расчетного $1.4 \times {{10}^{{ - 5}}}$ м. Это может быть обусловлено тем, что расчетное значение смещения положения центра масс несколько ошибочно из-за неточности линейных приводов, ошибки исполнения или в результате смещения положения центра масс за счет термического расширения.

Теперь продемонстрируем совместную работу алгоритма определения центра масс макета и автоматических балансиров. Пусть требуемое положение центра масс задается вектором [0; 0; $ - 10] \times {{10}^{{ - 5}}}$ м. В этом случае можно уменьшить влияние гравитационного момента на движение аэродинамического подвеса. По оценке положения центра масс, полученной с помощью фильтра Калмана, раз в 25 с будем сдвигать грузики на такую величину, чтобы положение центра масс было равно желаемому значению. Однако вследствие ошибок оценки положения центра масс и плавного смещения центра масс вследствие термических эффектов требуется постепенное уточнение положения центра масс. Таким образом, из-за последовательных периодических смещений  грузиков  центр масс системы устанавливается в некоторой окрестности требуемого значения. На рис. 14 представлены оценки положения центра масс, полученные фильтром Калмана, а на рис. 15 – значения перемещения грузов для балансировки, рассчитанные по текущим значениям положения центра масс раз в 25 с. В результате после четырех итераций с точностью около $1 \times {{10}^{{ - 5}}}$ м установилось требуемое положение центра масс.

Таким образом, продемонстрирована работа системы определения положения центра масс относительно точки подвеса и системы перемещения грузов для уменьшения влияния гравитационного момента на движение макета на аэродинамическом подвесе за счет смещения центра масс макета ближе к центру подвеса.

Заключение. При тестировании алгоритмов управления угловым движением спутников на наземных стендах с аэродинамическим подвесом необходимо уменьшить влияние возмущающего гравитационного момента на движение макета системы ориентации. В работе предложена связка алгоритмов для двухэтапной балансировки макета микроспутника. На первом этапе оцениваются положение центра масс макета относительно центра вращения подвеса и компоненты тензора инерции макета с помощью известного перемещения грузов системы балансировки во время свободного неуправляемого движения. Эта методика была протестирована на стенде компании “Спутникс”, точность оценки положения центра масс составила около 10 мкм, а точность оценки диагональных элементов тензора инерции – около 0.1 кг ⋅ м². Оценка тензора инерции и первое приближение положения центра масс используется на втором этапе автоматической балансировки. За счет термических деформаций положение центра масс смещается при длительных экспериментах, поэтому оно оценивается с помощью алгоритма на основе фильтра Калмана в режиме реального времени, и на основе этой информации грузы смещаются для помещения центра масс макета в требуемое положение. В результате экспериментального исследования разработанной методики на стенде удалось обеспечить требуемое положение центра масс относительно центра подвеса с точностью около 10 мкм, что является приемлемым значением для тестирования бортовых алгоритмов управления ориентацией.